1. Introduction
The concept of entropy as a measure of information was introduced by Shannon [
1] and has since been discussed in many books (e.g., see [
2], [
3]). Entropy has played a central role in the field of communications, providing limits on both data compression and channel capacity [
2]. Entropy-based signal processing techniques and analysis have also enjoyed a great deal of success in a diverse set of applications ranging from ecological system monitoring [
4] to crystallography [
5]. Successful application of entropy-based approaches is often predicated on having analytical expressions for the entropy of a given signal model, particularly in the communications field (e.g., see [
6]. For some probability distributions expressions for differential entropy are well known (e.g., see Table 17.1 in reference [
2]) while for others such expressions have not yet been derived.
This work derives the differential entropy for harmonic signals with non-uniform (Beta) distributed phase. In a number of applications the signal under study is harmonic and the primary uncertainty mechanism giving rise to the probability distribution is the phase noise which can be distributed non-uniformly. Optical communications strategies, for example, often involve the phase modulation of a carrier signal and subsequent demodulation at the receiver. The measured photocurrent at the receiver takes the general form [
7]
where
is a scalar amplitude,
contains the desired information, and
represents the noise. In differential phase shift keying, the probability distribution function associated with
has been modeled both as a Gaussian and as a uni-modal (but not Gaussian) distribution [
7], [
8]. Specifically, Ho [
9] found the distribution to be a convolution of a Gaussian and a non-central chi-squared distribution with two degrees-of-freedom.
An additional situation in which the signal model (
1) appears is in interferometric measurement or detection systems [
10]. In these applications the goal is still the same as in communications: to recover the parameter
given phase noise
. The work of Arie
et al. considered a Gaussian phase model [
10] while Freitas [
11] considered a non-Gaussian phase-noise model. Calculation of the differential entropy for the case of a sinusoid with non-uniform phase distributions does not appear in the literature however.
This paper will therefore derive the differential entropy for the sine wave for the case when the phase angle is Beta-distributed. The Beta distribution is an extremely flexible distribution possessing finite support and can be made, via appropriate choice of parameters, to approximate a number of other well-known distributions. The uniform distribution, for example, is a special case of the Beta distribution. It will be shown, in fact, that for appropriate choice of parameters the differential entropy for the Beta-distributed phase case reduces to that of the well-known expression for differential entropy associated with a uniform distributed phase.
2. Mathematical Development and Results
The following notation will be utilized. The differential entropy for a continuous random variable,
X, with probability density function
is given by
where
is the support set of
X. Here log usually means
. If the log is taken to the base
e, the notation
is used. Consider the sinusoidal signal written as:
where
θ is uniformly distributed on
(A similar discussion applies if
or
, where
ω and
ϕ are constants). It is well known that this signal has a probability density function given by
and possesses zero mean and variance
[
12]. For this distribution the associated differential entropy can be computed by introducing the transformation
which yields the probability density function
where
is the Gamma function. Equation (
4) defines the Beta distribution, with differential entropy given by
where
is the Beta function and
is the Digamma function (see Cover & Thomas [
2] p. 486) so
Consequently
Note that
can be positive or negative, depending on the value of
A. This is a well known result, e.g., see [
6]. Indeed the entropy of arbitrary Beta distributions is known [
13]. Next it will be shown that the result given by Equation (
7) is a special case of the differential entropy of a sine-wave with a Beta-distributed phase angle.
The probability density function for a Beta-distributed random variable on [0,1] is expressed as:
where
,
.
The transformation
provides
as the Beta distribution on the interval
. Consequently, the sine wave
, where
θ is Beta-distributed on
has probability density function:
The differential entropy for
Z in nats, is calculated as follows:
Letting
, so
and
, gives:
so
where we have made the substitution for the Beta function
.
Setting
in the first integral of Equation (
13) leads to:
which is equal to
from formula 4.253(1) of Gradshteyn and Ryzhik [
14]. Similarly, setting
in the second integral gives:
Finally, setting
in the third integral and noting that
, we obtain
Collecting terms gives
The last term is the average of the function
over the Beta distribution. Unfortunately, there does not appear to be an analytic solution for this integral.
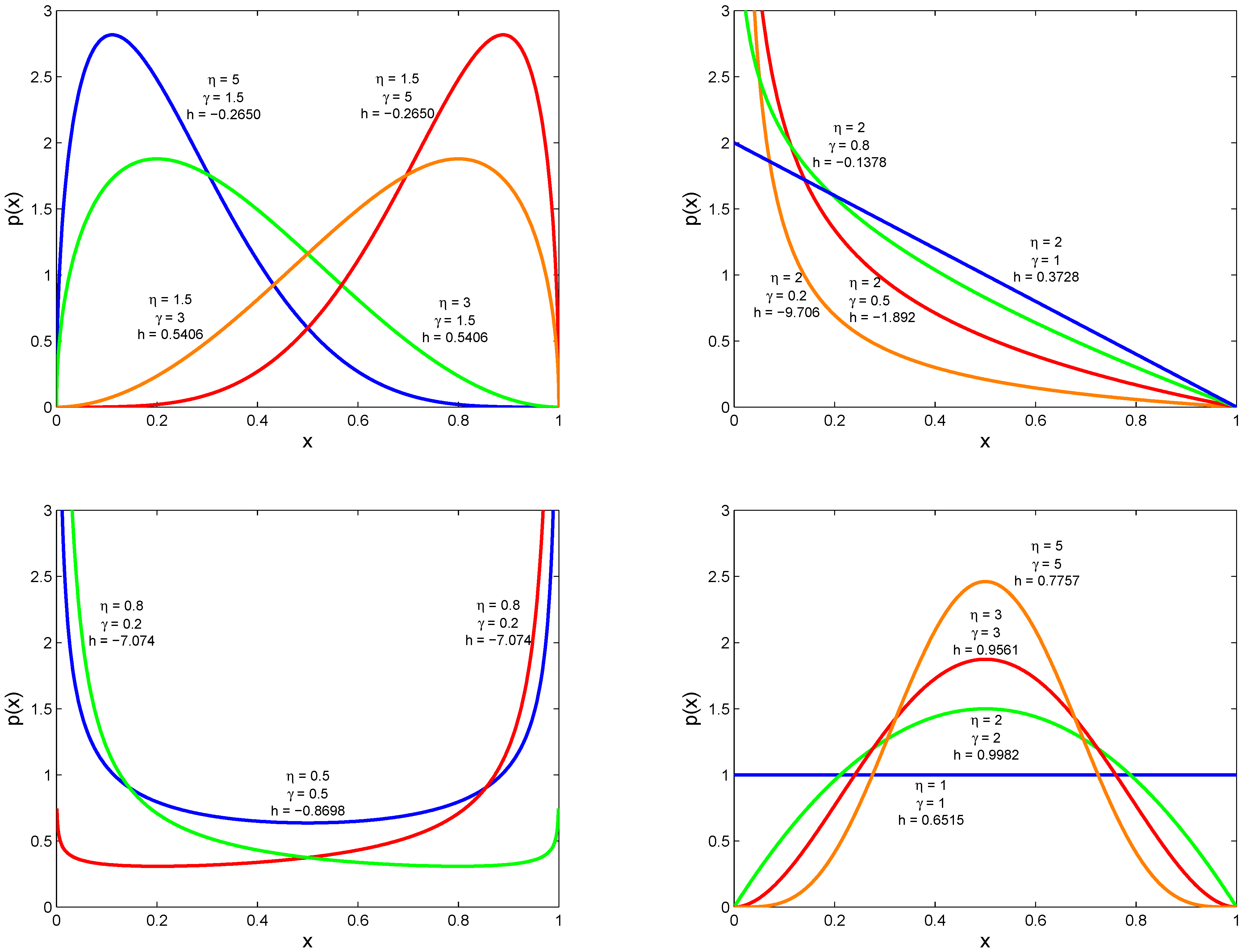
A variety of Beta distributions (taken from Hahn and Shapiro, [
15]) are shown in
Figure 1, along with the corresponding differential entropy,
h, for a sine wave of amplitude
. These entropies are expressed in bits, so the values of
obtained from Equation (
17) are divided by
. The last term in (
17) is calculated by standard numerical integration techniques.
Figure 1.
Beta distributions with different parameter values and the associated entropy values, h, (in bits).
Figure 1.
Beta distributions with different parameter values and the associated entropy values, h, (in bits).
We now derive an analytic approximation for the integral term in Equation (
17) which is valid when
and
. This technique is based on the following integral found in Gradshteyn and Ryzhik ([
14], formula 3.768(11)):
and its companion (formula 3.768(12)):
both expressed in terms of generalized hypergeometric series. In fact,
is defined by:
where
denotes the product
for
and
.
is similarly defined. Note that Mathematica also gives expressions for the integrals in (
18) and (
19); these formulas are in terms of the
generalized hypergeometric series and, with a bit of manipulation, can be shown to be equivalent to the expressions above.
We make use of the power series expansion:
which converges for
, and apply it to
since
for
. This gives
We wish to choose
N such that the first
N terms of this series converge closely enough to
for purposes of calculating the integral in Equation (
17). We have found that this approximation will be valid when
and
. If either
η or
γ is less than unity, then the contribution to the integral near the endpoints at
and
will exceed the precision of the power series convergence near those points.
Accordingly,
Collecting the coefficients of like powers of
, we can write
as
where
and
This is an unusual approximation since it is clear that the coefficients diverge as
. However, the coefficients have alternating signs and our calculations show that the approximation is increasingly good for small values of
N up to about
, at which point we begin losing precision. For example consider the approximation obtained with
terms. In this case the coefficients are given by the values shown in
Table 1.
Table 1.
Coefficients for the approximation of using terms.
Table 1.
Coefficients for the approximation of using terms.
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3.776 | -24 | 138 | -674.67 | 2656.5 | -8500.8 | 22433 | -49443 | 91934 | -145278 | 196126 | -226922 | 225346 |
| j | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| 192011 | 140090 | -87167 | 45967 | -20359 | 7477.6 | -2237.1 | 531.30 | -96.38 | 12.55 | -1.043 | 0.0417 | |
We further expand Equation (
21) by expressing powers of
as linear combinations of sines and cosines of multiples of
x (see Gradshteyn and Ryzhik, [
4] pp. 25-26). In general, for any positive integer n,
and
Combining (
21), (
22), and (
23) leads to the conclusion that
is (approximately) expressible as a linear combination of terms of the form
,
, and constant terms. Consequently, the integral in Equation (
17):
can be written as a linear combination of integrals of the form:
which are given analytically by Equations (
18) and (
19).
Results for this analytic approximation are shown in
Table 2 for two values of
N. The last term of Equation (
17) is shown, as well as the resulting value of differential entropy
in nats. Again, the amplitude of the sine wave is taken to be
. Clearly the approximation is a good one, particularly for
. We find that for a wide variety of Beta parameters the error in the approximation is
. For larger values of
N, we find that the quality of the results degrade. Specifically, we find that the values in the range
give the best results.
Table 2.
Accuracy of the Analytical Approximations of the Entropy for Various Values of and .
Table 2.
Accuracy of the Analytical Approximations of the Entropy for Various Values of and .
| | | Entropy (in nats) |
|---|
| | | Analytical Approximation | | Analytical Approximation |
|---|
| η | γ | Numerical Integration | | | Numerical Integration | | |
|---|
| 1 | 1 | -0.6931 | -0.6677 | -0.6793 | 0.4516 | 0.4771 | 0.4654 |
| 2 | 2 | -0.3278 | -0.3268 | -0.3274 | 0.6919 | 0.6928 | 0.6922 |
| 3 | 3 | -0.2141 | -0.2140 | -0.2141 | 0.6627 | 0.6628 | 0.6628 |
| 5 | 5 | -0.1264 | -0.1264 | -0.1264 | 0.5377 | 0.5377 | 0.5377 |
| 2 | 1 | -0.6931 | -0.6677 | -0.6793 | 0.2584 | 0.2839 | 0.2723 |
| 1.5 | 3 | -0.4970 | -0.4916 | -0.4948 | 0.3747 | 0.3801 | 0.3769 |
| 1.5 | 5 | -0.7485 | -0.7377 | -0.7443 | -0.1837 | -0.1729 | -0.1794 |
| 3 | 1.5 | -0.4970 | -0.4916 | -0.4948 | 0.3747 | 0.3801 | 0.3769 |
| 5 | 1.5 | -0.7485 | -0.7377 | -0.7443 | -0.1837 | -0.1729 | -0.1794 |