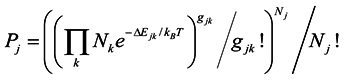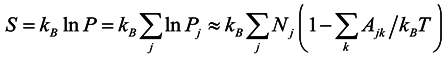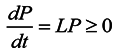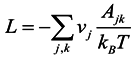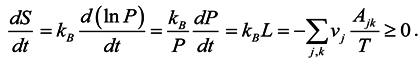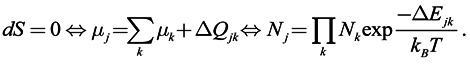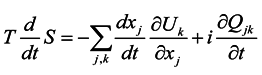1. Introduction
Parallels between economic and biological systems have not gone unnoticed. Common roots stem from the formulation of evolutionary theory based on natural selection [
1]. Darwin was inspired by the idea that favorable variation is preserved under a struggle for existence when reading Malthus [
2]. The tenet of self-directed and self-regulatory processes was first posited by classical liberalism as being manipulated by an ‘invisible hand’ [
3], and was later reworded as laissez-faire policy [
4] and is today given, albeit in more refined terms, as free-market principles [
5].
It is time to re-inspect the fundamental resemblance between economic and biological systems using the 2
nd law of thermodynamics, which was recently formulated as an equation of motion for natural processes [
6,
7,
8]. In this form, evolution by natural selection can be recognized as being guided by the 2
nd law. This relationship is in agreement with earlier reasoning about the governing role of the 2
nd law, known also as the principle of increasing entropy, in directing numerous natural processes, animate as well as inanimate [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18].
Certainly in the past too, the principle of increasing entropy has invigorated cross-disciplinary thinking [
19,
20] and given rise to evolutionary economics, thermoeconomics and econophysics [
21,
22,
23,
24,
25,
26,
27,
28]. However, the inspiration has not been exhausted, because
the entropy law, in the words of Georgescu-Roegen
is still surrounded by many conceptual difficulties and equally numerous controversies [
19].
Common considerations about entropy contrast with the principal findings of this study. It is reasoned here that economic activities are not confined by the 2nd law but are actually manifestations of it. The entropy of an entire economic system does not decrease due to its diverse activities at the expense of entropy increase in its surroundings. Rather, it follows from the conservation of energy that both the economy and its surroundings are increasing in entropy (decreasing in available energy) when mutual differences in energy densities are leveling off as a result of economic activity. The key here is that according to the statistical physics of open systems increasing entropy means dispersal of energy, rather than as increasing disorder. Finally, we understand the ultimate motivation of economic activities, not as the maximizing of profit or productivity, but rather to disperse energy.
These conclusions stem from the same statistical theory [
6,
7,
8] that has been recently applied to understand diverse evolutionary processes [
29,
30,
31,
32,
33,
34,
35,
36,
37] The 2
nd law is found to yield functional structures, hierarchical organizations, skewed distributions and sigmoid cumulative curves that also characterize economies. Here, we use the thermodynamic formalism to address some fundamental questions of economics. What drives economic growth and diversification? Where do the law of diminishing returns, the Pareto principle, the balance of supply and demand, and the principle of comparative advantage come from? Why is it so difficult to predict economic growth and decline?
These questions are approached here from a strictly material and operational standpoint. It is understood that this standpoint of thermodynamics which relates everything directly or indirectly in terms of energy may immediately strike some as deficient. For example, is not information, as an essential guide of economic activities, immaterial? However, it has been argued that no information can be stored or processed without being represented in a physical form that, in turn, is subject to the laws of thermodynamics [
38,
39,
40]. Moreover we fully acknowledge that physics in its traditional deterministic and reductionist form applicable for closed systems is rightfully rejected in attempting to account for behavior of open systems,
e.g., for human endeavors. However the 2
nd law, when formulated properly using the statistical physics of open systems, reveals that nature is an intrinsically interdependent system and its evolution is inherently a non-deterministic process. Thus, our holistic account aims to remove doubts and concerns commonly leveled against physicalism. Yet, our objective is not to turn economics into physics, but to clarify economic activity in the context of the 2
nd law, which accounts for all irreversible motions in nature.
We will proceed to describe an economy as an energy transduction system, first in qualitative and then in mathematical terms. Thereafter the intractable nature of economic progression and regression is clarified, and, as well, accompanied structural, functional and organizational changes are exemplified. Some familiar economic relationships and regularities are derived from the ubiquitous natural law. Finally, the subjective nature of decision making is discussed.
2. Economy as an Energy Transduction System
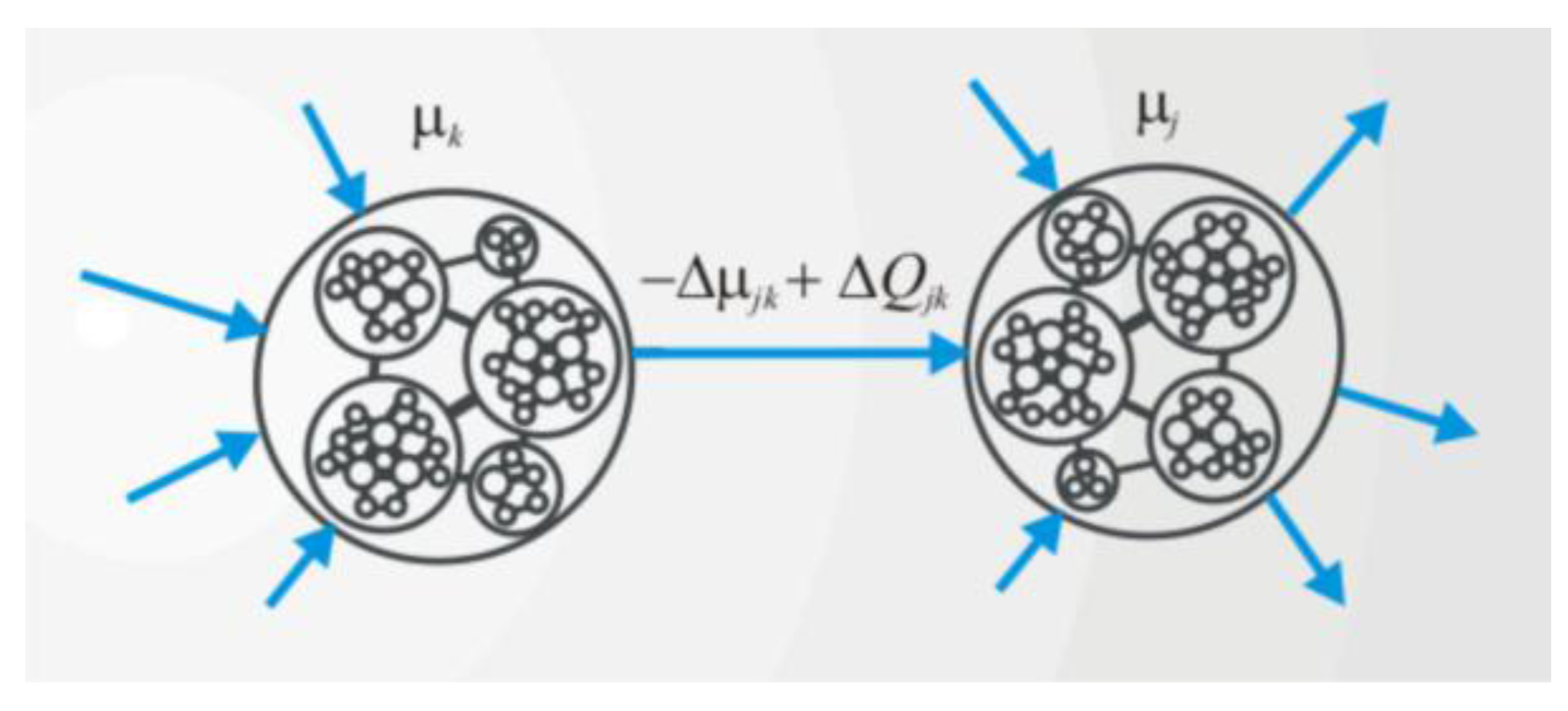
According to our naturalistic approach, an economy is an energy transduction system. To describe its characteristics and evolution in a self-similar manner using the statistical physics of open systems, all entities of the system are regarded as systems themselves (
Figure 1). Each entity is associated with an energy density that results from its physical production processes. When all entities are valued by their energy density, it is possible to deduce from the corresponding density differences where an economic system is on its way. Its motion, as flows of energy, will direct, along available channels wherever constraints allow, from high densities to low densities. Entropy, the additive logarithmic probability measure, quantifies the system’s evolutionary course toward increasingly more probable states.
We begin by defining elementary concepts so as to leave less room for misunderstandings. Products in numbers
Nj that result from production activities are indexed by
j. They are made from various raw materials or semi-finished products available in numbers
Nk. Agricultural, industrial, logistical, informational,
etc., processes that transform
Nk to
Nj also couple quanta of energy, Δ
Qjk per each unit product. The energy supply may be in various forms including labor which, in terms of physics, is work. Each material entity
j, is associated with an energy content denoted by
Gj relative to the average energy
kBT of the system per entity. For historical reasons the everyday meaning of ambient temperature
T relates via
kB to the average energy density of the geophysical system as sensed by thermometers In the same way body temperature is measure for the average energy density of the biological system. In the same sense the common
kBT is a meaningful concept for a sufficiently statistical economic system where entities interact with each other frequently [
41]. In previous studies economic systems have been compared on the basis of the average energy density [
42]. A pool of indistinguishable (identical) entities
Nj, that are the result of natural processes such as chemical reactions, is a repository of energy denoted by the density
ϕj =
Njexp(
Gj/
kBT) [
43].
Figure 1.
Self-similar description of an economy as an energy transduction system. Each entity is regarded as a system (circle) of its own in interactions (lines and arrows) with its surrounding systems (larger circles). The energy difference Δμjk between the j and k system and the external energy flux ΔQjk (grey background) that couples to the transformations are the driving forces of economic activities. The energy differences are the forces that generate flows of energy (blue arrows) and propel the economic system toward a thermodynamic stationary state where energy density differences within the system and in respect to its surroundings have leveled, hence there is neither growth or decline. The steady state is maintained by the incessant to-and-fro flows of energy between the system and its surroundings.
Figure 1.
Self-similar description of an economy as an energy transduction system. Each entity is regarded as a system (circle) of its own in interactions (lines and arrows) with its surrounding systems (larger circles). The energy difference Δμjk between the j and k system and the external energy flux ΔQjk (grey background) that couples to the transformations are the driving forces of economic activities. The energy differences are the forces that generate flows of energy (blue arrows) and propel the economic system toward a thermodynamic stationary state where energy density differences within the system and in respect to its surroundings have leveled, hence there is neither growth or decline. The steady state is maintained by the incessant to-and-fro flows of energy between the system and its surroundings.
It is worth emphasizing that we discern a distinct entity as different from another entity in energetic terms, not by its configurations (
e.g., having isergonic topological or geometric properties). In other words, the mutual order of energetically identical entities in the system is immaterial. In terms of economic energetics, any of these identical commodities is of equal value. This way Gibbs’ formalism [
43,
44,
45] allows us to relate any entity
k to any other
j in an economy by comparing the corresponding potentials
μk =
kBTln
ϕk and
μj =
kBTln
ϕj. When
μk + Δ
Qjk >
μj, more products
Nj can be made from the available raw-materials
Nk and any input energy Δ
Qjk. On the other hand when
μk + Δ
Qjk <
μj, there is a surplus of products that the economic system would then be searching for ways to reduce. Thus, the free energy, known also as the affinity
Ajk =
μk + Δ
Qjk –
μj, is the driving force of economic activities that generate diverse flows of energy in both material forms and radiation, which are in terms of physics scalar and vector potentials.
We emphasize that each entity, including information via its physical representation, is assigned an energy density resulting from its production process. For example, a speech does not exist without being physically produced and represented as transient fluctuations about the ambient average air pressure. Admittedly the associated energy content in this example is minuscule but not negligible. The speech must exist to be heard. Subsequently it may be interpreted (processed) to unleash flows from gigantic reservoirs of energy. Thus, according to the natural tenet, even the most “immaterial” goods and services do not exist without physical forms. The energetic “costs” of representations can be very small but essential to understanding the thermodynamic imperatives, most notably conservation of energy in the flows of energy that all economic activities are also subject to.
The view of economic activities as energy flows that direct down along energy gradients, is plain. Yet it may appear unfamiliar because production processes are not usually perceived as spontaneous but actively driven as if the motion was “uphill”. We emphasize that the driving force is precisely the free energy (known also as exergy), including any external influx ΔQjk, e.g., work. The total force, when positive (Ajk > 0), makes the production of Nj a probable process (dNj/dt > 0), i.e., the energy flow is statistically speaking always “downhill”. According to our natural approach, all processes, regardless of being either conscious or unconscious, must follow the law of energy dispersal.
An economy, just as an ecosystem, is powered by an energy influx from its high-energy surroundings, e.g. by consuming fossil fuels and capturing solar radiation. Conversely, all products that have emerged from endergonic production processes are subsequently subject to exergonic degradation when exposed to low-energy surroundings and cut off from the sources that powered their production or carried out repairs and restorations. Thus, goods are limited by life spans just as are living entities. Therefore economic, like chemical potentials μj, are constantly regenerated using surrounding supplies. This leads to incessant circulation of matter in both economic systems and ecosystems. Under these conditions random variation in syntheses or deliberate design of production may yield more effective mechanisms of energy transduction which will be naturally selected by the flows themselves to level the density differences even more effectively.
3. Economic Evolution as an Energy Dispersal Process
The physical portrayal of an economy as an energy transduction system associates all interacting entities with energy densities. The density differences within the system and in respect to its surroundings are the forces that direct flows of energy to diminish the differences. This notion is a generalization of Carnot’s observation that
wherever there exists a difference of temperature, motive force can be produced [
46].
The concept of probability,
P, is a concise measure to capture the energetic state of the entire economic system in its myriad of motions due to numerous flows being directed by diverse forces. According to the self-similar formalism
P = Π
Pj, is a product of probabilities so that each
Pj is associated with a subsystem composed of entities
j in numbers
Nj (for the derivation see references [
6,
8]):
The scale-independent notation shows, in a recursive manner, that
Nj are themselves also made of various entities
k each distinct ingredient available in numbers
Nk (
Figure 1). The form Π
Nk in the numerator ensures that if any of the
k-ingredients is missing, no
j-product can be made (
Pj = 0). The degeneracy
gjk denotes the number of
k-components that remain indistinguishable (symmetric) even after being assembled in the
j-product. The energy difference Δ
Ejk = Δ
Gjk – Δ
Qjk in the production process is bridged by the intrinsic difference Δ
Gjk =
Gj –
Gk between the raw materials and products and by the external influx Δ
Qjk. The division by the factorial
Nj! means that the combinatorial configurations of identical
Nj in the system are indistinguishable. The nominator is raised to the power of
Nj because the production process may combine the raw materials into any of the indistinguishable products.
The total logarithmic, hence additive, probability measure of the economic state is entropy
S =
kBln
P. It takes into account all densities of energy and paths of transformations:
where the energy difference,
i.e., free energy
Ajk = Δ
μjk – Δ
Qjk is the motive force that directs the transformations from
Nk to
Nj. The potential difference Δ
μjk =
μj – Σ
μk contains co-products and by-products of
Nj in Σ
k with the opposite sign. The Stirling’s approximation implies that the system is well-defined by being sufficiently statistical,
i.e.,
Ajk/
kBT << 1 to absorb or emit quanta without a marked change in its average energy density
kBT. Otherwise, if
S is not a sufficient statistic for
kBT [
41], the embedded entities,
e.g. semi-finished products
Nk themselves would be transforming rapidly. Obviously then the assembly of
Nj would be jeopardized. For example, it would be difficult to build a house from bricks that themselves were still soft and deforming. In such a case, the production process must be analyzed at a lower level of hierarchy [
47,
48] where the submerged evolutionary processes involving the
k-entities,
e.g., the fabrication of bricks, would be described using the same self-similar formalism.
The economy evolves from one state to another by diminishing free energy. The equation of probable motion resulting from the dispersal of energy down along the diverse gradients by various activities is obtained from Equations 3.1 and 3.2 by differentiating and using the chain rule (
dPj/
dNj)(
dNj/
dt):
where the process generator:
drives a series of state changes by way of numerous flows
vj =
dNj/
dt that consume the motive forces
Ajk. The population change
dNj and the time step
dt have been denoted as continuous only for convenience whereas actual processes advance in quantized steps Δ
Nj during Δ
t.
The 2
nd law of thermodynamics in the form of an equation of motion for the overall probability (Equation 3.3) is a powerful description of an evolving economy. Yet, it is not
P itself but numerous activities and material flows that are amenable for monitoring the economic state. In a sufficiently statistical system each flow:
is proportional to the corresponding motive force by a conductance (production capacity)
σjk > 0 to satisfy the continuity
vj = –Σ
vk between the density
ϕj and diverse densities
ϕk [
6,
49].
The linear relationship in Equation 3.5 is familiar from Onsager’s reciprocal relations which are considered to be valid close to the stationary state [
50,
51]. Here the condition
Ajk/
kBT << 1 of being a sufficiently statistical system is assumed but it is not unusual that the assumption does not hold. This critical phenomenon is also familiar from fluid mechanics when a flow changes from laminar to turbulent. When the transformation mechanism
σjk itself is evolving or when the free energy
Ajk is comparable to the average energy density
kBT, the linear relationship between the flow and force (Equation 3.5) fails, but this is no obstacle for the self-similar description. When the condition of being sufficiently statistical is not satisfied at a particular level of hierarchy, the process would need to be described in a finer detail at a level further down in the hierarchy. For example, a series of improvements on a production line will increase the throughput by increasing
σjk. The time-dependence of the evolving conduction system is fully contained in the recursive, scale-independent system description according to Equations 3.1–3.5.
The statistically sufficient assumption Ajk/kBT << 1 will fail also when energy is not distributed effectively enough within the system to maintain its integrity, i.e. to maintain common kBT. The economy is subject to disintegration when an economic sector is receiving high influx (or another is draining high efflux). The rapidly growing subsystem acquires greater independence when it is not connected effectively enough to distribute acquired assets to others. Eventually when the high influx ceases, redistribution processes catch up and the excursion for independence ends. The disintegration and reintegration processes are fully contained in the self-similar formalism.
We emphasized that the energy density differences
Ajk (Equation 3.5) drive the flows, not the differences in number densities
Nj, which are commonly used in economic [
52] as well as in ecological models,
e.g., written as sets of coupled differential equations [
53]. These models based on the law of mass action [
54] erroneously picture that transformation rates would be changing during kinetic courses even when the system is sufficiently statistical. Consequently it may appear as if kinetics was inconsistent with thermodynamics.
The equation of motion for an evolving economy (Equation 3.3) can be rewritten using the definition of entropy
S =
kBln
P as the law of increasing entropy [
6,
8]:
The equation of motion says that entropy
S is increasing when energy density differences, contained in
Ajk, are decreasing by way of various flows
vj. The non-negativity of
dS/
dt is apparent from the quadratic form obtained by inserting Eqaution 3.5 in 3.6. The formula obtained from statistical physics of open systems is consistent with the basic maxim of chemical thermodynamics [
45],
i.e., the entropy maximum corresponds to the free energy minimum as well as with the classical form of
dS given by Carnot [
46], the Gouy-Stodola theorem [
55,
56] and the mathematical foundations of thermodynamics [
50,
57,
58].
The form of Equation 3.6 makes it explicit that it is the energy density difference between the system and its surroundings that drives the probable motions. The economy will prosper when the difference from its surroundings is positive and conversely the economy will decline when the difference is negative. The significance of surroundings is apparent, for example, when an economy is curtailed by an embargo. It is emphasized that both during economic progression and regression, the entropy of the economy, just as the entropy of its surroundings, are increasing. There is no room for a provisional proposition that the entropy of a system could possibly decrease at the expense of entropy increase at its exterior (or
vice versa). Such generosity would violate the conservation of energy because the system and its surroundings share the same flows at their mutual interfaces [
8].
Eventually, when no further and faster means to consume free energy and no additional sources are found, the economy reaches a steady-state, just as an ecosystem attains a climax, the mature state with maximal gross transduction [
59,
60]. The maximum entropy state is characterized by a distribution of entities without mutual density differences [
6]
The steady-state populations
Nj and
Nk of energy transduction mechanisms are governed by the mutual energy differences Δ
Ejk = Δ
Gjk – Δ
Qjk relative to the average energy
kBT per entity in the particular system. The everyday notion of temperature
T, when given in units of Kelvin and multiplied with
kB, refers to the average energy of ambient atmospheric gas per molecules that the thermometer is sensitive to. In the same physical sense the average energy density of an economy can be quantified. However, it would extremely tedious to tabulate changes in energy in every transaction. Instead, various economic barometers are used to sense the status of the economic system. The maximum entropy state
Smax =
kBΣ
Njss, where all energy density differences have vanished, is a dynamic stationary state so that variations Δ
Nj about the steady-state populations
Njss are rapidly averaged out by economic activities that correspond to conserved flows (ΣΔ
NjΔ
μjk = 0). In modern times, apart from some transient periods, economies have not been in stationary states. Instead the average energy influx from the surroundings has been and is still growing due to more and more effective agricultural, industrial, logistical and informational processes [
61].
4. Origin of Non-Deterministic Economic Evolution
The 2nd law in the form of an equation of motion clarifies the fundamentals that underlie difficulties in providing accurate economic forecasts. The equation of evolution (Equation 3.3), despite being simple, cannot be solved analytically, e.g., integrated in a closed form, because when there are multiple degrees of freedom the variables L and P cannot be separated from each other as they both depend on Nj and Aj. The non-integrable characteristics of the evolving system mean that economic trajectories are non-deterministic. The uncertainty stems from the following factors.
First, an economy, just as in any other thermodynamic system, is composed of interacting entities. In other words, a potential
μk is in a functional relation to other potentials
μj via available transformation mechanisms (
Figure 1). In a market
μk can be transformed to
μj by various transactions, here expressed using numerous flow equations (Equation 3.5), so that the products and other economic entities, just as any other forms of energy, are interdependent. Owing to the continuity
vj = –Σ
vk in the transformations it is impossible to change one entity without affecting others. The energy flows
vj and driving forces
Ajk are inseparable in
L from each other when there are three or more degrees of freedom (agents). Flows affect driving forces that, in turn, affect the flows. A decision taken by a player will change sets of states accessible by other players that, in turn, by their own decisions, affect the sets of accessible states of others. When the currents are not conserved, the
ceteris paribus assumption does not hold and the equation of motion cannot be solved by a transformation to yield an analytical formula to determine the system’s time course. Hence evolutionary courses, including economic growth and decline, are non-integrable,
i.e. trajectories of an evolving economy cannot be predicted in detail. The problem is exactly the same as was encountered first in the context of the three body problem [
62] and later recognized to seed also chaotic behavior [
63,
64]. The non-deterministic course toward a defined solution–here, the free energy minimum–identifies the problem of predicting economic growth among many other natural processes in computational terms, as non-polynomial time complete [
34,
65].
Second, to understand the origins of intractability of evolving economies, it is crucial to recognize that changes of state are dissipative. It is impossible to transform an entity into another distinct one without acquiring at least a quantum of energy from the surroundings or expelling a quantum to the surroundings [
6,
7,
8]. When assembling from semi-finished products, it is easy to see that some of the external energy becomes incorporated in the product. It is the essential ingredient that distinguishes the product from raw-materials. Owing to the energy influx (or efflux) an open, evolving system is capable of transformations that cause net changes in identities, whereas a closed and stationary system is limited to isergonic exchange of identities. The equation of motion (Equation 3.3) and the flow equation (Equation 3.5) differ from the conventional physical formalism that has been devised for closed, conserved systems which display only isergonic and deterministic dynamics. Such an invariant description by normalized probabilities is not sufficient to account for an open, non-conserved economy. The open system will grow or shrink in its energy content due to energy influx or efflux until it has arrived at a stationary state,
i.e. attained an energy balance in its surroundings. As long as the system’s energy content is changing, there is no norm, which would be necessary to find a unitary transformation to solve the characteristic equation. Thus, economic growth, just as ecological succession [
35], is a process without invariants of motion. Since, the Noether’s theorem [
66] does not hold and Liouville’s theorem is not satisfied for this non-Hamiltonian system, much of the powerful machinery of physics devised for closed, deterministic systems is disabled when analyzing economic systems. This means that it is impossible to predict (determine) future states because these do not pre-exist, instead a particular state at each moment results from the irreversible evolutionary processes.
It is concluded that the difficulties in forecasting economic growth or decline are not exclusively due to incomplete knowledge of the system’s properties but rather follow from the inherent characteristics of natural processes. Of course it has been recognized already for a long time that the conventional closed system formalism does not describe open systems appropriately. However, the evolutionary equations are not usually derived directly from the fundamental principle using statistical physics. Instead, stochastic processes such as Markovian chains or deterministic analytical formulae are used [
67] to model inherently non-deterministic evolutionary courses. Certainly these are practical approximations but are not explicit in communicating why it is difficult to forecast economic growth and decline.
The flow Equation 3.5 can be used to build an economic model and the state Equation 3.6 to monitor the economic status. The model system will respond to influxes and effluxes by non-deterministic evolution. The obtained scenarios are representative to the degree that the input is realistic and that the model accommodates relevant interaction mechanisms within the system and with its surroundings. The scale-independent formalism allows one to model both micro- and macroeconomics. Also, when using a self-similar model, computational capacity can be dynamically allocated to refine the description into significant details, or instead, coarse-graining it from insignificant factors. In any case, to gain certainty and scope in prognoses by deterministic finite automaton is a tedious process because an evolving state space is huge and searches through it are intractable [
68].
The intrinsically non-integrable behavior of an evolving economy does not, of course, mean that information of its diverse potentials μk, flows vj and available jk-transformation paths would not help to estimate the current state and to project toward future states. But the prognoses, even when based on the same premises, will diverge when extended over longer and longer periods of time. Furthermore, it is emphasized that mere information gathering and its exposition are thermodynamic processes themselves that will inevitably affect the course of economy. This has, of course, been understood in practice and regulated by legislation, but has here been associated with the fundamental properties of non-conserved systems with degrees of freedom where forces and flows are inseparable from each other. For example, the use of insider information is prohibited because it would endanger the overall progression by limiting conceivable actions.
5. Natural Selection Criterion
The principle of increasing entropy is not only about increasing but increasing as fast as possible. This has been recognized in the form of the maximum entropy production principle [
17]. This principle has in it that a system that is capable of assuming many conformations will tend to assume one, or frequently return to one, that maximizes the rate of dissipation of the powering energy gradients. This dissipation promotes entropy production even when some of the energy is captured as exergy because of the statutorially poor energy efficiency of any work. The natural law manifests itself here in iterative improvement of the energy transduction machinery. An economy develops to hold increasingly more effective mechanisms just an ecosystem evolves to house increasingly more effective species. Natural selection for the most effective mechanisms of energy dispersal is often pictured to be driven only by mutual competition, sometimes referred to as an arms race, whereas less attention has been given to the gains that are obtained by evolution to hierarchical organizations, sometimes viewed as co-evolution, co-operation or even altruism.
The energy gradients are the motive forces of physical process just as they are of economic activities but we note that these forces are not sensed by the system when there is no mechanism to funnel the flows of energy. For example, a voltage difference has no effect without a conducting path just as supplies of raw materials and customers’ purchasing power constitute an energy density difference but which has no effect on the economic state as long as there is no flow to equalize the gradient. This stationary state will change first when a production line, as a mechanism of energy transduction, begins to pump out a particular flow of products according to Equation 3.5. A prototype mechanism is superior to nothing, and serves only to trigger the development of more refined machinery.
The key to understanding natural selection as a bias for more and more effective machinery is to recognize that entities are limited by life spans and hence must be regenerated. Consequently, the competition for common resources is incessant. This competition tends to increase work rates, which in turn increases the rate of entropy production. When several mechanisms of transduction, characterized by the transduction coefficients σjk > 0, consume a common pool of free energy, the magnitudes of flows from the same source via distinct mechanisms distribute according to σjk. When a particular mechanism is unable to acquire enough flow from the common resources even for its own regeneration, it will, in biological terms, face extinction as a result of competition. Technological developments alter energy flows and redirect economic growth just as advantageous genetic mutations change the food chain and affect biological evolution. Eventually the most effective paths of economic productivity funnel all flows and leave nothing for the least effective means of energy dispersal, that then ‘run out of business’. This thermodynamic principle for maximal entropy production, equivalent to the maximal energy dispersal, is universal.
When a comparative advantage appears among mechanisms, the energy flows will redirect accordingly. A rerouting may happen rapidly, especially when the consumed free energy can be used to boost the particular superior mechanistic capacity. In economic terms, profit is invested in increasing the production capacity. In biological terms, food is invested in raising the population. In terms of our statistical physics formulation of evolutionary theory those mechanisms that channel most of the energy are naturally selected through the flows [
1,
6,
7,
69]. According to the self-similar hierarchical theory, natural selection is systemic notion since a mechanism, just as an individual or a group, is a system. Given sufficient undiminishing energy sources, evolution is not merely manifesting itself in ‘selfish’ rivalries but also in integration by specialization, co-operation and even ‘altruistic’ conduct that aim at increasing the total rate of energy dispersal to arrive at win-win circumstances.
We note that the natural bias for the maximal energy dispersal down along the steepest gradients was anticipated in the economical context as being directed by ‘an invisible hand’. However, we emphasize that, according to the 2
nd law, the primary motive of economic activities is the most effective dispersal of energy, whereas it is of secondary importance whether the processes are defined as conscious or unconscious. Therefore, legislation and its enforcement that also consume free energy in redirecting flows and in altering mechanisms, are regarded as natural forces. Also in biological systems natural selection is at work both when particular traits are intentionally sought by breeding and when they appear in response to unintentional forces [
1]. The selection between mechanisms by the rate of entropy increase is a particularly stringent criterion when free energy is becoming depleted. This condition is usually referred to as ‘operating on a small margin’. As well, unit costs are reduced by way of voluminous transformations (‘economies of scale’).
Since the kinetic mechanisms (
e.g. production lines) themselves are assembled by synthesizing flows, mere random variations may, once in a while, give rise to an improved mechanism, although we usually think of rationalized production as a result of engineering design and coordinated actions. It is important that regardless of an action being accidental or intentional, a revised mechanism, when it increases the consumption of free energy, will tend to be adopted. Economic growth via technological improvements, just as biological evolution via genetic mutations, is mostly ‘tinkering’ [
70].
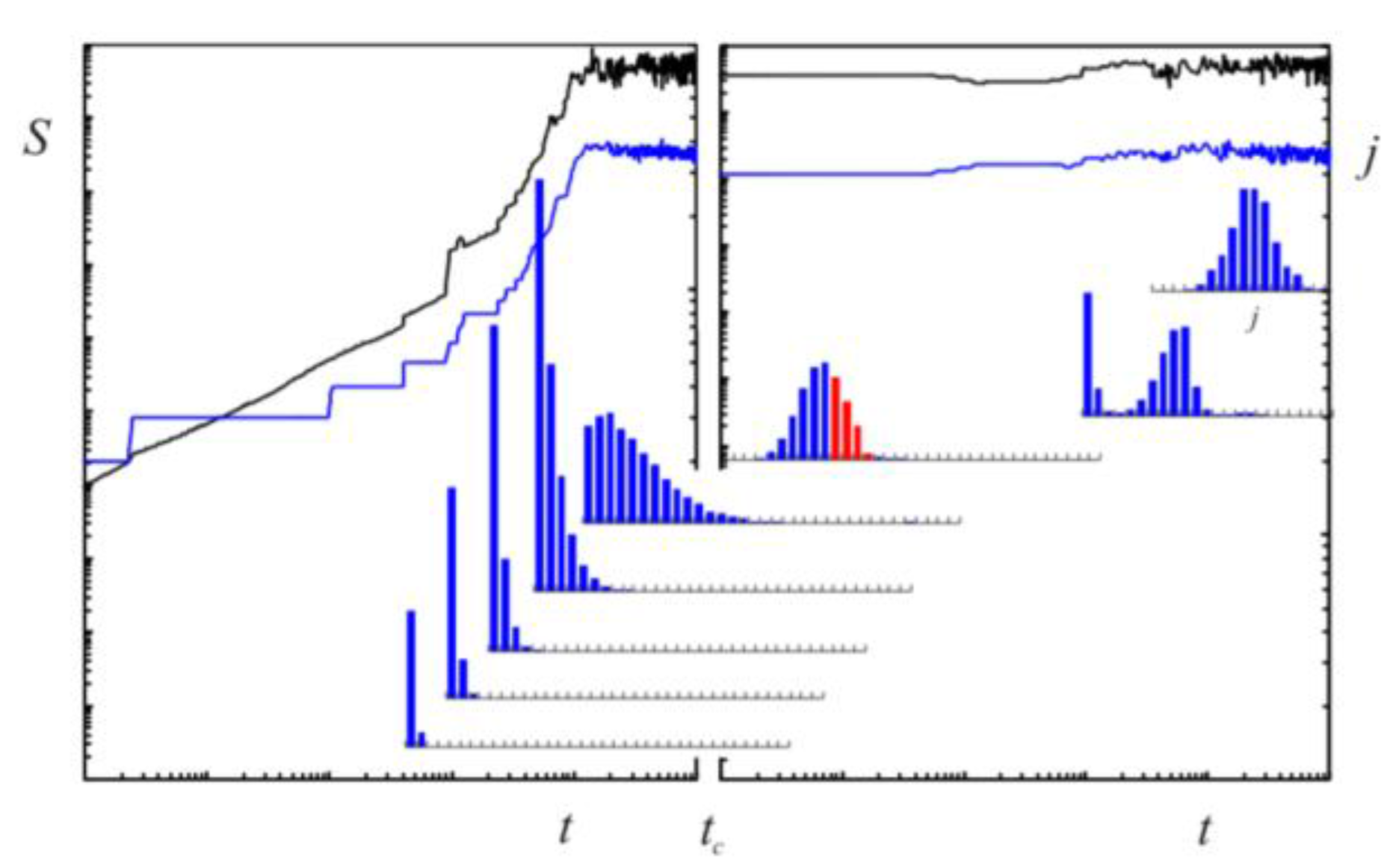
The interplay between the energy gradients, flows and mechanisms is particularly intriguing every time a new, highly effective mechanism appears in the system (
Figure 2). Then a stationary state would be punctuated by a rapid evolution when the highly effective mechanism is consuming the free energy accessible to it and cumulating new densities that may quickly become out of balance with other densities. Soon the system will redirect its course to correct for the overshoot. Owing to its autocatalytic nature,
i.e. positive feedback mechanisms, the trajectory toward a steady state may proceed in an oscillatory manner. Even large modern economies may first experience periods of fast growth that later terminate to severe declines when highly effective mechanisms emerged and succeeded in drawing large assets but remained poorly integrated in the system,
e.g. due to lack of effective control and redistribution mechanisms. Eventually evolution settles to a stasis when excess resources have been consumed. The intermittent course of punctuations and stases [
71], also referred to as self-organized criticality [
72,
73], is inherent in evolution. This is in conflict with the desire for a steady economic growth where the system would retain its integrity by evolving so that
dS/
dt > 0 while all
Ajk/
kBT << 1.
Figure 2.
Simulated evolution of an economy based on the 2nd law of thermodynamics. Flows, including sporadic variation (up to 10% in the flows), direct down along the steepest gradients of free energy according to Equation 3.5. Entropy (S black line) is increasing as long as the system emerges with novel, increasingly more effective mechanisms of various kinds (j blue line) that are able to acquire more and more energy from the surroundings. When a new mechanism appears, the growth rate increases whereas the stationary state is approached with diminishing returns. During the evolutionary course the distribution that was sampled at various times t (blue bar charts), shifts from simple mechanisms at low-j fractions to sophisticated machinery at high-j fractions. Each fraction is proportional to a population’s effectiveness in energy transduction relative to the others. A catastrophe is introduced at tc. It demolishes a fraction of the stationary state production capacity (red bars). Consequently, entropy will momentarily plummet as it takes time for the system to recover by restoring the skewed distribution. Scales of axes are in arbitrary units because the simulation is based on scale-independent formalism. See appendix for technical details.
Figure 2.
Simulated evolution of an economy based on the 2nd law of thermodynamics. Flows, including sporadic variation (up to 10% in the flows), direct down along the steepest gradients of free energy according to Equation 3.5. Entropy (S black line) is increasing as long as the system emerges with novel, increasingly more effective mechanisms of various kinds (j blue line) that are able to acquire more and more energy from the surroundings. When a new mechanism appears, the growth rate increases whereas the stationary state is approached with diminishing returns. During the evolutionary course the distribution that was sampled at various times t (blue bar charts), shifts from simple mechanisms at low-j fractions to sophisticated machinery at high-j fractions. Each fraction is proportional to a population’s effectiveness in energy transduction relative to the others. A catastrophe is introduced at tc. It demolishes a fraction of the stationary state production capacity (red bars). Consequently, entropy will momentarily plummet as it takes time for the system to recover by restoring the skewed distribution. Scales of axes are in arbitrary units because the simulation is based on scale-independent formalism. See appendix for technical details.
![Entropy 11 00606 g002]()
6. Evolving Energy Landscape
The thermodynamic description of an economy via Equations 3.1–3.7, despite their concise notation, is very precise. Numerous terms denote all potentials
μj, their mutual differences, all transforming flows
vj and all
jk-transforming mechanisms. However, to model an economy to the precision of an atom and a quantum is neither practical nor instructive, but coarse-grained simulations of natural processes are easy to set up and execute according to Equation 3.5 [
29,
30,
31,
32,
33,
34,
35,
36,
37].
Simulations serve to exemplify the principal characteristics and non-deterministic features of evolution but much can be understood directly from the equation of motion (Equation 3.6) when it is pictured as an energy landscape in evolution [
7]. To that end the rate of entropy change
dS/
dt is rewritten as an energy balance for the flows
by multiplying
dln
P with the average energy
kBT. Time-dependent tangential vectors as directional derivates
Dj = (
dxj/
dt)(∂/∂
xj) span an energy landscape, properly referred to as an affine manifold, in the continuum limit [
7,
8,
49,
74] (
Figure 3). Heights of the manifold are high potentials
μk/
kBT = ln[
Nkexp(
Gk/
kBT)] at the site
xk and valleys are low potentials
μj/
kBT = ln[
Njexp(
Gj/
kBT)] at
xj. Their difference in the continuum limit is denoted by the gradient –∂
Uk/∂
xj and the external energy by the field ∂
Qjk/
c∂
t in the orthogonal direction denoted (redundantly) by
i. The various economic activities generate continuous flows
vj =
dxj/
dt from the heights to the valleys. During evolution the landscape is leveling due to numerous flows.
The energy landscape given by Equation 6.1 is curved,
i.e. non-Euclidean [
75]. This means that a distance between two points is directional and the sum of triangle’s angles between three points is not equal to 180°. These are not exotic properties of a curved space-time, but well-established,
e.g. in information theory [
41]. These characteristics are also familiar from economic systems. The directionality means that putting together a product from raw-materials by coupling the influx of energy to the assembly is not the same as breaking apart the product into raw-materials where the efflux of energy is released. The two opposite processes differ by the net direction of energy flux. The assembly is typically endergonic whereas the disassembly is an exergonic process. The triangle inequality means that the overall cost of a product depends on the particular semi-finished products that are used in its assembly. The less energy is required in the assembly, the more Euclidean (even) the landscape is. Production processes are optimized to transform along the paths of least action (the variational principle),
i.e. along the least curved paths. That would be the most economical trajectory. This motion along the optimal paths corresponds to minimal squandering. Another way to state the same principle is described in “constructal theory” [
76].
Figure 3.
Economy is pictured in a self-similar manner as systems within systems (encircled cyclic paths) that are embedded in the surrounding energy landscape. The diverse high-energy densities in the hierarchical organization are associated with transduction mechanisms that direct flows of energy (blue arrows) among themselves and from the surroundings down to the economy. Eventually the landscape may develop to open up for new flows (dashed arrow to right), so that a previously confined steady-state systems will face evolution, e.g., perceived as economic restructuring due to integration.
Figure 3.
Economy is pictured in a self-similar manner as systems within systems (encircled cyclic paths) that are embedded in the surrounding energy landscape. The diverse high-energy densities in the hierarchical organization are associated with transduction mechanisms that direct flows of energy (blue arrows) among themselves and from the surroundings down to the economy. Eventually the landscape may develop to open up for new flows (dashed arrow to right), so that a previously confined steady-state systems will face evolution, e.g., perceived as economic restructuring due to integration.
The non-stationary energy landscape composed of finite material densities is curved by the amount of net dissipation ∂
Qjk/∂
t in the
jk-transformations. The external energy (
i.e. work) drives the production process in addition to the potential difference between the raw-materials and products. However at a local region, as Gauss noted, the curved landscape can be viewed as nearly Euclidean [
8,
77]. In other words, to a good approximation the high-density source
μk does not deplete during the outflow, and the low-density sink
μj does not fill during the inflow. In economic terms, the Euclidean approximation means that prices of raw-materials and products do not alter during an on-going transaction. In practice, it is of course noticed that, in particular, huge bargains do change the prices of subsequent deals. Contracts aim at predictability but only time-limited offers are given, ultimately because nature is, when depicted as an energy density landscape, inherently non-Euclidean.
To picture an economy as a landscape that evolves by flows of energy is admittedly abstract but allows one to use notions that have been established in other contexts. Mathematically speaking the evolving landscape is an affine manifold undergoing a geometric flow [
75]. In terms of physics, the evolving landscape is a thermalizing system of interacting densities. In biological terms, the evolving landscape is a maturing food-web of interacting species. In economic terms, the evolving landscape is a growing market economy of players.
7. Motives of Integration and Disintegration
Economies, just as ecosystems do, organize themselves in nested hierarchical systems to improve on energy dispersal. At each level of hierarchy a larger system provides the surroundings for its integral subsystems. Throughout the hierarchy the incentive of activities is nevertheless the same, the dispersal of energy. The holistic description of an economy as a nested hierarchy of energy transduction systems is self-similar with regard to energy transductions so that the landscape contains basins within basins (Equations 3.3. and 6.1). In other words, the global economy is comprised of national economies, each housing economic zones that in turn accommodate districts, firms, households and so on.
Likewise, the biosphere is comprised of ecosystems, each housing populations of individuals that in turn encompass organs, cells, organelles and so on [
78]. Biological systems were integrated already eons ago into the biosphere, which also houses systems within systems. For example, a eukaryotic cell houses cellular organelles, chloroplasts and mitochondria that are thought to have once been independent organisms [
79]. Also at higher levels of hierarchical organization various forms of symbiosis and co-operation are found.
Restructuring of activities will contribute to economic growth. Two similar units,
e.g. firms that generate similar potentials (
e.g. products) by drawing from the same resources
μk will be in competition with each other [
12]. Such a system is not stable according to the Lyapunov criterion [
44,
64]. This situation, referred to in the biological context as competitive exclusion, may resolve if the units differentiate in respect to each other [
80] or one of them disappears, or becomes assimilated to the other in a merger.
On-going economic integration emerges with numerous technological standards to ensure and boost the consumption of free energy. The value of standardization increases with an increasingly larger system. Likewise, biological standards such as universal metabolites, amino acid chirality consensus and common genetic code have allowed intimate integration of the biosphere by differentiation based on the same base constituents [
29].
Product differentiation or specialization in integrated activities leads to an increase in entropy production, denoted by an increasing number of terms in the sums of Equation 3.4. New mechanisms access new potentials or more effectively utilize those that were not fully exploited. It is well observed that economic growth generates further economic growth, just as biological diversity builds on diversity. As well, many policies promote economic diversification. Despite efforts to diversify activities some particular potentials may remain limiting or specific mechanisms may appear as bottlenecks of economic growth. Likewise, shortage of water curtails growth and diversification of terrestrial ecosystems. Ultimately the Second Law itself imposes, by depleting the surrounding energy density, a limit of growth for all systems [
61].
In a highly integrated and versatile economy numerous flows rapidly redirect along alternative paths in response to changing potentials and mechanistic innovations or failures. An economy with effective infrastructure will quickly redirect its flows along newly emergent gradients and adapt to forces imposed by its surroundings. Furthermore, a wealthy society has a large capacity, i.e. a high-energy content to influence its surroundings and to resist changes. In contrast, a disjointed and one-sided economy is slow in adjusting its course in response to altered surroundings. Furthermore, a poor community has hardly any influence on its surroundings and its feeble potentials are soon exhausted in attempts to oppose changes.
Integration, however, is not an end in itself. When the integrated machinery is not superior in its energy transduction to its internalized subsystems working as independent systems, we suggest that the organization is bound to disassemble. The integration at each level of hierarchy is supported or opposed by a subsystem depending on its local subjective view of its surroundings. According to the 2
nd law (Equation 3.6) subjectivity will be shaped only by perceived proximate gradients. A subsystem supports integration when it gains in
dS/
dt. Conversely, we propose that a subsystem will tend to break loose when the integration seems to afford a smaller rate of
dS/
dt than the system could produce independently. How this driving force for integration (or disintegration) actually transpires as flows in any particular system will depend upon available mechanisms. Consistently, it has been proposed that new levels may appear in a dynamical hierarchy only if that results in a more rapid overall energy gradient depletion [
81].
To attribute economic integration to the universal law of energy dispersal may at first appear counterintuitive since the dispersal means spreading while economic activities are accumulating aggregates [
82]. However, an aggregate, such as an intense technological infrastructure, is a mechanism that allows the economy to extract resources from its surroundings. For example, crude oil sources are the high-energy surroundings that are intensively drawn from by the global economic system. Conversely, when an economy disintegrates, energy flows out of the system as the interactions break apart. Then, aggregate units, such as railway, power and telephone networks, have become higher in energy density than the relatively impoverished surroundings, and these high-energy infrastructures will be subject to plunder. Likewise, in biological terms, a big carcass is a generous supply for other organisms. At each level of hierarchy the surroundings, must be higher in the total energy content for the system to profit from them. In the converse case, the surroundings will profit from the system. The law is the same, only the viewpoint is different.
Today we witness economic globalization that is motivated by attempts to access and consume increasingly larger surrounding pools of free energy so as to keep the economy growing. The integration aims at boosting energy transduction by enhancing interactions and adjusting subsystemic mechanisms to funnel flows ever more rapidly. This manifests,
e.g., as division of labor and specialization, and yields comparative advantages and disadvantages. These internal changes, referred to as restructuring, are basic to economic integration where interactions assemble subsystems to systems. Trust between partners is a sign of mutual understanding of interdependence and adherence to the common system. The co-operative functions of an integrated system are enforced,
e.g., by practices, rules, tabus, legislation and traditions. In accord with earlier ideas [
83] cultures have emerged and devised hierarchical organizations to facilitate effective dispersal of energy.
8. Roots of Economic Relations and Regularities
The natural process of energy dispersal, despite being non-deterministic, imposes certain relations and regularities on economic systems by requiring that, while energy is conserved globally, flows of energy direct down along the steepest gradients.
A typical economic growth curve is an overall sigmoid on linear scales and dominated by a power-law region on a log-log plot [
84,
85]. Initially the free energy is high and growth is soon nearly exponential. As a result of the transforming activities, free energy diminishes. The diminishing difference Σ
μk(
t) + Δ
Qjk –
μj(
t) ≥ 0 per unit time represents profit from the viewpoint of a producer of
μj. The producer may invest acquired free energy in increasing its production capacity, as well as in obtaining more raw materials and energy, in hopes of maintaining rapid growth to improve its entropy production status. However, eventually, when no new innovations and no supplies are found, the free energy declines. This particular business branch is maturing and its growth is slowing down. Finally, when the free energy vanishes altogether, no more profit can be made, but to make a living is still possible when the market is saturated with products, just as animate populations tend to be in balance in a mature ecosystem.
It follows from the diminishing difference Σ
μk(
t) + Δ
Qjk –
μj(
t) ≥ 0 that an additional input Δ
Nk will give an additional output Δ
Nj with diminishing marginal returns. Often this classical law by Ricardo is supplemented with a caveat that only “after a certain point”, the diminishing returns would first set in. This empirical observation of initially increasing marginal products results from the aforementioned initial growth that may be prolonged by restructuring of activities, increasing capacity, efficacy and specializing. As a result of autocatalysis, the initial growth curve is concave and only later becomes convex yielding an overall sigmoid, nearly logistic form [
86].
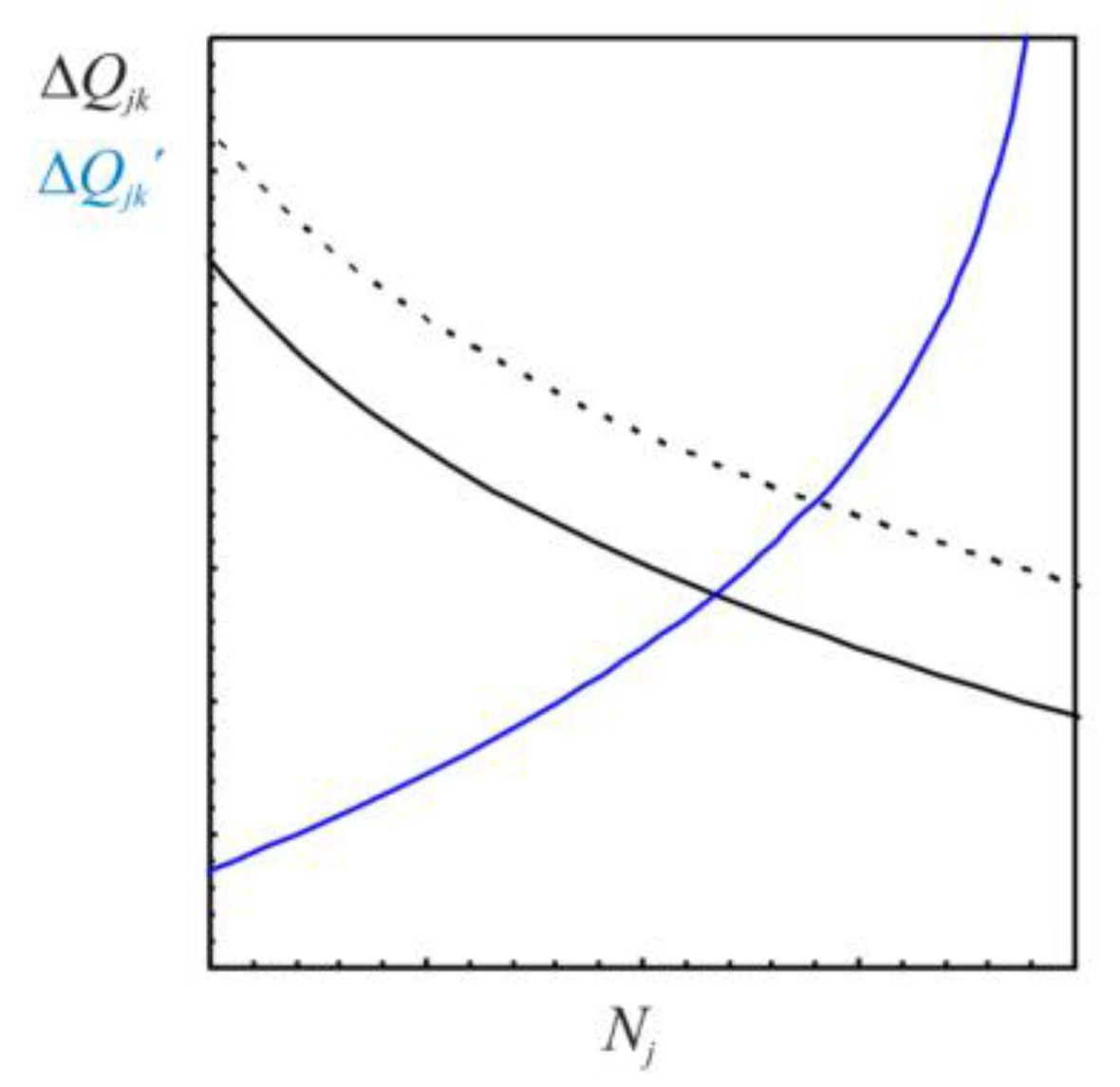
At the market equilibrium, Σ
μk + Δ
Qjk =
μj, the demand and supply are equal,
i.e., in balance. For a given supply the increase in consumer demand, denoted by an increase in Δ
Qjk, gives rise to a difference, Σ
μk + Δ
Qjk >
μj + Δ
Qjk´ that is balanced by raising the price denoted by Δ
Qjk´. For a given demand the increase in producer’s supply gives rise to a difference that is balanced by lowering the price, assuming as usual that no other alternatives would open up (
Figure 4). The money associated with potential contributes to the transaction motive, just as does the external energy Δ
Qjk. Also a value-added tax, customs,
etc., are associated with potentials that influence rates of transformations (Equation 3.5) and affect the market equilibrium (Equation 3.7), and also indirectly when the collected assets are returned to the system. In general a change in a particular commodity price will also affect the demand and supply of other products, and then elasticity behaves non-deterministically. These intractable responses can be simulated using the flow equations Equation 3.5.
Figure 4.
Demand (black) and supply (blue curve) relate by purchasing power ΔQjk and pricing ΔQjk´ to the quest for the balance (Equation 3.7) between energy densities ϕj and ϕk associated with the products (Nj) and raw-materials (Nk).
Figure 4.
Demand (black) and supply (blue curve) relate by purchasing power ΔQjk and pricing ΔQjk´ to the quest for the balance (Equation 3.7) between energy densities ϕj and ϕk associated with the products (Nj) and raw-materials (Nk).
From the physical perspective the free market economy, by its statistically independent actions of trade and transactions, is free to seek the steepest gradient and thus is likely to move, according to Equations 3.6 and 6.1, by most voluminous flows along steepest gradients toward a local balance. Considering that natural processes are non-deterministic it would be difficult to command an economy along the steepest gradients. This idea of freedom was once voiced as laissez-faire. However, it should be noted that although integration in hierarchical organizations structures energy dispersal processes, it also fosters statistical independence in transformations, e.g., by legislation that prohibits monopolies, cartels and use of insider information.
Our examination of economic relationships from this physical principle is not intended to be exhaustive but exemplary. There are also relationships whose validity is questioned [
87],
e.g. the Phillips curve [
88] that seems to fail in relating inflation and unemployment rates under stagflation. Although the physical counterpart of money is energy in its nearly immaterial form,
fiat currency is an agreement. Since deterministic agreements hold strictly only under steady-state conditions, the trust in money is not fully firm during non-Euclidean growth and decline conditions. The mistrust in money is particularly apparent in a time of war when in disrupted regions the economy disintegrates. When taking these aspects of trust into account, the dependence given by the Phillips curve can be understood so that the size of a quantum,
i.e. the unit of money as the transaction motive, is decreasing
relative to the average energy density (
kBT) of an economy that is growing. Obviously, unemployment is reduced during the growth period as the growth is consuming the labor force, literally
Ajk. Conversely, a reducing economy faces deflation risk and increasing unemployment.
9. Economic Stability, Fluctuations and Oscillations
Economic systems are rarely subject to steady surroundings or free from internal perturbations but the stationary-state properties are worth a study to understand the nature of stability and the causes of disturbances.
The natural distributions are nearly log-normal and their cumulative curves are sigmoid [
31,
89]. The size of a particular population
Nj in Equation 3.7 depends on its ability to acquire energy from its surroundings relative to all other mechanisms in the same system. For example in a developed economy, characterized by high
kBT, the most abundant fractions associate with median-income households. These dominant fractions of the distribution on a log-log plot follow the power-law, which in the context of incomes, is referred to as the Pareto principle. The low-income fractions associated with the poorest are smaller, as are the high-income fractions of the long tail [
90] associated with the richest [
91]. The corresponding distribution of a developing economy, characterized by low
kBT, peaks at the lower fractions [
92,
93]. Usually the income distributions are taken as inequality indicators [
94] whereas here insight to the evolving distribution of wealth is drawn from the law of energy dispersal. Earlier these skewed distributions and their cumulative curves viewed as power-laws have been obtained using statistical physics concepts [
95], in particular self-similarity in scaling [
28], or using Tsallis’ entropy [
96], but not explicitly from the 2
nd law, although maximum principles have been understood as being in control [
87].
When an economy is growing, the distribution shifts higher in energy because during development new more productive mechanisms are adopted and infrastructure is built, while less productive processes and outdated traditions are abandoned (
Figure 2). The rate of production and fast circulation of matter using external energy is of the prime importance to reach increasingly higher total economic status as represented by
S. For example, automation will free up resources for other purposes and so speed up the regeneration of potentials that in turn serve as raw materials for other product potentials. These fervent actions follow directly from the fact that economic potentials are metastable,
i.e. they are subject to degradation. Increasingly higher turnover requires more energy or more effective use of energy. Therefore economic growth is inevitably coupled with increasing consumption of energy.
The same scaling laws and relationships between overall energy intake and diversity in economic systems hold also for biological systems, where distributions of individuals within a species are skewed, nearly log-normal distributions that peak at the fractions that contribute most to the energy transduction [
31,
59]. The energy influx and the size of an ecosystem, usually given per area, scale the average energy dispersion and the most abundant fraction of the distribution [
32].
The stationary state economy is a conserved system maintained by a steady through-flux without net flows of energy (
dQjk/
dt = 0). Its isergonic motions,
i.e., dynamics on the Euclidean energy landscape, are along statistically predictable trajectories determined solely by the potential and kinetic energy equilibrium condition 2
K +
U = 0 as the net flux 〈
Q〉 = 0. The steady-state kinetic energy to-and-fro flows correspond to commodity exchange without net profit or loss. The stationary state structure-functional diversity,
i.e., the maximum entropy partition of energy transduction mechanisms, can be referred to as the Pareto-efficient economy in the context of game theory or as the Nash equilibrium that is maintained by mixed strategy [
97]. However, the stationary state is often only evanescent since the surroundings seldom stay invariant for long, and a system will subsequently tend to senesce and become recycled [
12].
The steady-state economy is stable against fluctuations in
Nj according to the Lyapunov criterion
δS < 0 and
dδS/
dt > 0 [
44,
64]. Any excess or shortage ±
δNj will be soon be abolished by an opposing gradient that drives the reverse flow
dNj/
dt and returns the system back to a maximum entropy partition. The same phenomenon is familiar from population fluctuations in ecosystems that are maintained by a steady influx of energy accompanied by a steady thermal outflow. We emphasize that any particular steady state of a dissipative system is stable only against variations in the existing densities and mechanisms, but must adapt to changes in surroundings as well as those imposed by new mechanisms. Variations in production may yield new superior mechanisms to provide access to new resources. Then the system is once again on an evolutionary track. Thus, for any economy, just as for an ecosystem, there is no absolute guaranty of stability. Furthermore, owing to the limited life span of any dissipative system, there are always systems within systems at various developmental phases on their way toward maturity.
When the surrounding energy density varies periodically, such as by an annual rhythm, it imposes a corresponding variation on ecosystems and also on economic systems. Sporadic changes in surroundings are perceived as fluctuations and perturbations. For example, gross national product declines temporarily when a natural disaster demolishes some energy transduction machinery. Likewise, in biological systems photosynthesis plunges when fire burns a forest. Also, in chemical systems concentrations fluctuate, and temperature varies in physical systems. Since evolution aims at the
Smax state, stability is naturally sought by all mechanisms. Accordingly, contemporary human endeavors at the global scale aspire after a greater control of increasingly larger surroundings,
e.g. by meteorite surveillance and accompanied precautionary measures. These conscious actions aim at contributing to the global homeostasis that has been maintained approximately for eons by biotic means. This proposition was articulated by the Gaia theory [
98] and recently shown to follow from the 2
nd Law [
33].
Endogenous fluctuations, oscillations and economic trends are of particular interest in hopes of understanding how they originate and propagate, as well as how to interfere with them and to lessen their adverse consequences. These autocatalytic and progressive phenomena are not exclusive to economic systems but manifest alike as ecosystems’ correlated population fluctuations and chemical systems’ oscillations, as well as induced emission in physical systems. In all cases, when a powerful transduction mechanism appears for the first time in the system, voluminous flows will be generated and they will be, in turn, invested in increasing the transduction capacity. There are many ecological examples where introduction of exogenous species has caused major changes in endogenous populations.
When a new mechanism emerges, novel potentials build up fast, but one-sidedly, to result in an unbalanced ecological or economic structure. In particular, an autocatalytic process will readily drive a system into imbalance, i.e., away from the distribution given by Equation 3.7. When inserting an autocatalytic dependence, dNj/dt ∝ Nj, into Equation 3.6 we realize that then δS < 0 and also dδS/dt < 0, which means that the Lyapunov stability criterion is violated. Therefore the autocatalytic processes will easily disrupt the balance. When a powerful mechanism appears in an economy, densities associated with raw-materials, semi-finished products, savings etc., will easily become over-depleted by the over-populating products or assets. These self-reinforcing kinetic mechanisms are reasons for intrinsic economic perturbations. For example, energy densities associated with fuels, food supplies, stocks, etc., but represented in modern electronic forms, can be transformed swiftly from one form to another. A rapid accumulation of huge deposits and large deficits signals an imbalance and entails an inevitable restructuring to regain the steady-state partition.
When the flows redirect to restore the balance, their consequences, despite the natural objective of attaining a steady state, may themselves be devastating. Since economic systems, just as with ecosystems, depend on energy influx, the restructuring processes will affect a system’s mechanistic abilities to draw from its surroundings. When the corrective actions undershoot the balance, it takes time to restore the vital mechanisms to regain the high-entropy status that preceded the crisis (
Figure 2). Indeed government interference is often directed to slow down activities to prevent overheating or a ‘bubble’ and conversely to speed up and maintain activities to prevent recession. However it is not easy to predict consequences of these decisions because the ensuing motion is by its nature non-deterministic. For example, legislative measures targeted on specific potentials and mechanisms will often give rise to unexpected side-effects. On the other hand, general measures tend to be slow. For example, raising the interest rate and reducing the amount of money affect the whole economy. An interest rate, like a tax, will, as an additional transaction cost, shift the balance given by Equation 3.7 and slow down the rates given by Equation 3.5. The reduction in the amount of money will cut the overall liquid potential for transactions. Similarly, shortage of sunlight or of a vital ingredient such as water will curtail the growth of an ecosystem. Despite progress in economic monitoring and ecosystem surveillance, it is difficult to keep track of all potentials and flows, and to recognize various autocatalytic mechanisms in order to respond appropriately and in a timely fashion. Thus, our herein presented statistical formalism for open systems does not provide simple solutions about how to act in a particular case but gives understanding of the inherent difficulties in predicting and directing non-deterministic processes.
10. On Decision Making
The principle of increasing entropy is simple, yet it is not always obvious how to decide among alternative actions and to choose the one that generates flows along the steepest gradients. However, when goods j and ĵ are perfect substitutes there is no difficulty to choose the one with the lowest unit price. According to an entropy related utility function, the consumer favors the product j over ĵ when (dS/dNj)(dNj/dt) > (dS/dNĵ)(dNĵ/dt). The consumer, as a thermodynamic system, makes decisions among alternatives on a subjective basis about the factors affecting its capability to further entropy production. Also the producer makes decisions based on a subjective view of energy gradients. Each player in the market will prefer a particular series of transformations, usually referred to as a strategy, to move from one state to another higher in entropy production. For this natural reason the views of consumer and producer are not identical but they do not have to be opposite either, rather, more like parallel in a highly integrated economy.
Since the players are interdependent via direct or indirect flows of energy, every action is accompanied by reactions, usually referred to as its complement [
99]. Consequently, flows keep redirecting as the entire economic system evolves to level the energy density differences among players and in respect to the surroundings. The entropy of the entire economic system is an additive measure for the overall global process that sums up from the numerous local processes all directing down along the gradients. Thus, there is no need for each and every player to be aware of the global course which results from their numerous individual actions and mutual interactions. Synergistic actions, collaborations or even altruistic behavior indicate that free energy is drawn by mutual interactions whereas individual efforts, competitions or even selfish deeds imply activities at a lower level in the hierarchical organization.
We emphasize that the decision making is subjective without a universal standard of ‘rational choice’ because the gradients are subjectively experienced. To optimize the non-deterministic dispersal process, each player aims at taking into account in its decision making the effects caused by decisions made by others. It is natural that the decision making seems at times inconsistent. A choice that appears most prosperous and consistent with previous decisions is not necessarily chosen when it is coupled with a significant risk of ending up with lowered dS/dt. Consequently, behavior is varied, i.e. mixed strategies are used to ensure that on the average dS/dt will remain high. Put otherwise–to ensure maximal energy flows through the system. It is also conceivable that players shun strictly consistent conducts because, in general, deterministic demeanor is not the optimal response to non-deterministic natural courses.
A large economy provides for its subsystems (players) numerous opportunities, i.e. various energy gradients. A decision to exploit a particular one may, despite careful considerations, after all reduce the rate dS/dt. The risk has been realized because a particular subsystem may not have been informed of other crucial currents so as to anticipate its future status more realistically. The evolving economic landscape may also change rapidly so that once prosperous conditions have turned into poor circumstances. Due to its inherently non-deterministic and chaotic characteristics, economic development (growth or decline) may direct itself along unexpected trajectories. The integrated dissipation sums up the loss in terms of lost energy and matter from the economy. All in all, the physical portrayal of decision making does not expose its intricacies, but provides fundamental insights into the non-deterministic process.
11. Discussion
In this study the cross-disciplinary examination of economics is not an end in itself but a consequence of applying the universal natural law of energy dispersal. Economic systems are not described as mimicking biological systems but both are seen to be manifestations of the ubiquitous natural law that is equally valid also for chemical and physical systems. Admittedly, the principle of increasing entropy seems technically trivial in its mathematical form but its conceptual consistency draws from the principles of hierarchy theory. Self-similarity in energy transduction and dissipative transformations are the key elements that overshadow disciplinary divisions of historical origin.
Traditionally, economic activities are viewed as being motivated because they provide means for human welfare, or simply because they make profit possible. Our definition of economic activity as a means to increase entropy production sums up numerous terms just as does the gross national product (GNP), the familiar measure for all produced goods and services. However, we emphasize that not all and every productivity counts for the economic growth measured by entropy production that turns negative,
e.g. due to temporary over production. In a command economy or in a poorly operating market it may take a while before the adverse behaviors are noticed and corrective actions are taken. Indeed, recent studies have revealed that the stability of an economy against incessant endogenous perturbations is compromised when most of its agents are sparsely linked and only a few central hubs have a large number of connections [
100,
101]. Economic evolution directs naturally toward highly integrated hierarchical systems where statistically independent actions secure maximal flows of energy that rapidly level all accessible gradients of energy. Ensembles of arbitrary actions will be statistically random.
Information deserves no special status in the thermodynamic description of economic activities. Information in its physical representations is a commodity like any other, although its value, measured by entropy increase resulting from instructed actions is often high [
40]. Information asymmetry [
102] means that informed agents are simply more appropriately equipped with mechanisms than their uninformed counterparts. Adverse selection,
e.g., encountered in the principal-agent problem, follows from the subjective nature of decision making that is an inherent characteristic of changing open systems. It is in the interest of the economic system to use various mechanisms, including those that are referred to as rules, traditions and legislation, to promote growth, on the one hand by protecting owner’s rights in accumulating aggregates that are needed to assemble powerful mechanisms, and on the other hand by ensuring that its agents are informed and equipped with adequate mechanisms,
e.g. acquired during education.
Utility, that essential but elusive concept, is herein identified with the rate of entropy production; the ultimate but invisible incentive is to disperse energy. Economies evolve by diminishing free energy, equivalent ultimately to increasing entropy, toward more probable distributions of matter under an influx of energy. This reasoning, based on statistical physics, does not undervalue decision making in directing economic activities but allows us to rationalize or framework human behavior.
It is not surprising that a statistical description yields statistical laws and regularities that are characteristic of diverse economic systems, but it is intriguing that the same theory also provides insight into the decision making by individual agents. The self-similar hierarchical formalism considers an individual as a system of its own whose decision making results from a natural process eventually driven by many, and even conflicting, forces. This naturalized view of economic activity, however, does not deny the concept of free will but realizes that it is constrained by bearing free energy configurations.