Chaotic and Hyperchaotic Self-Oscillations of Lambda Diode Composed by Generalized Bipolar Transistors
Abstract
Featured Application
Abstract
1. Introduction
2. Mathematical Description of Third Order and Fourth Order Model
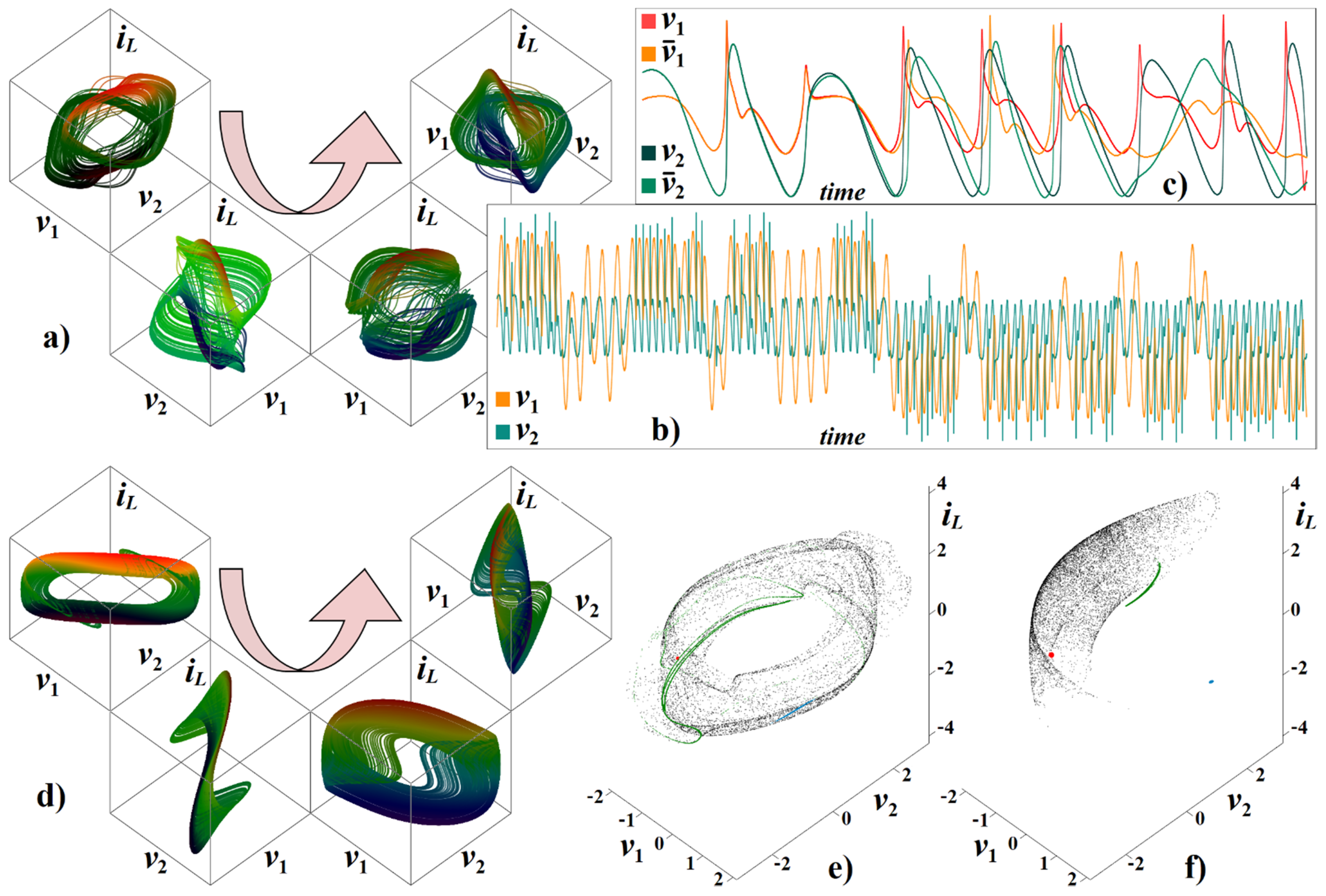
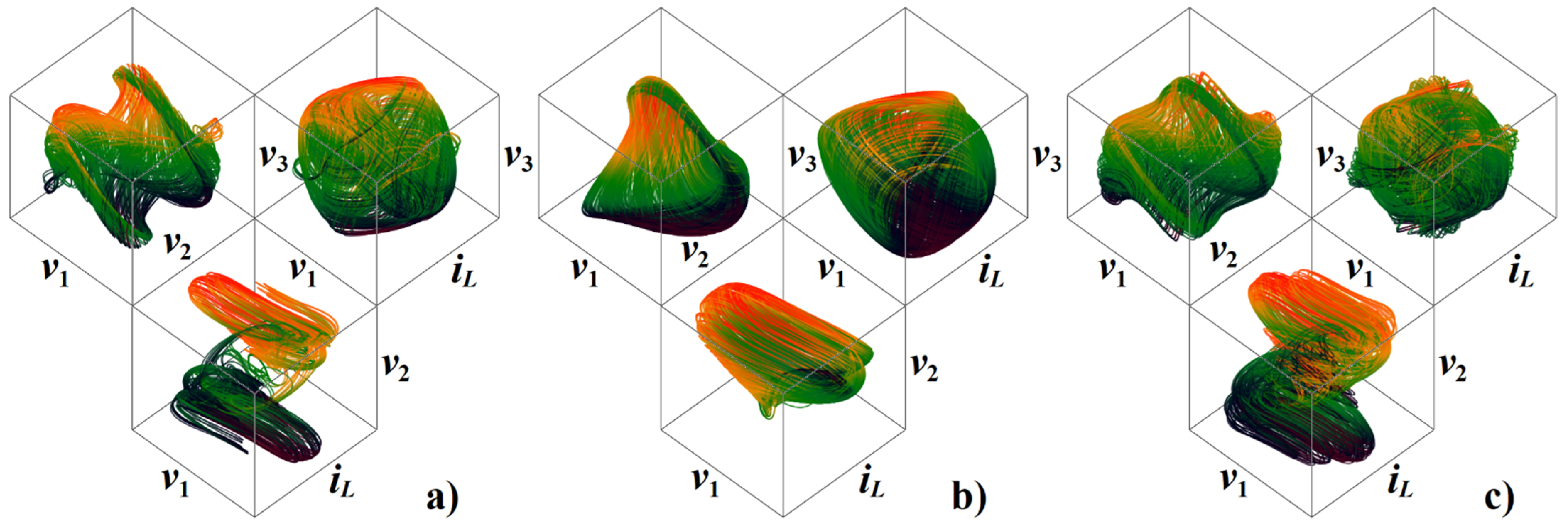
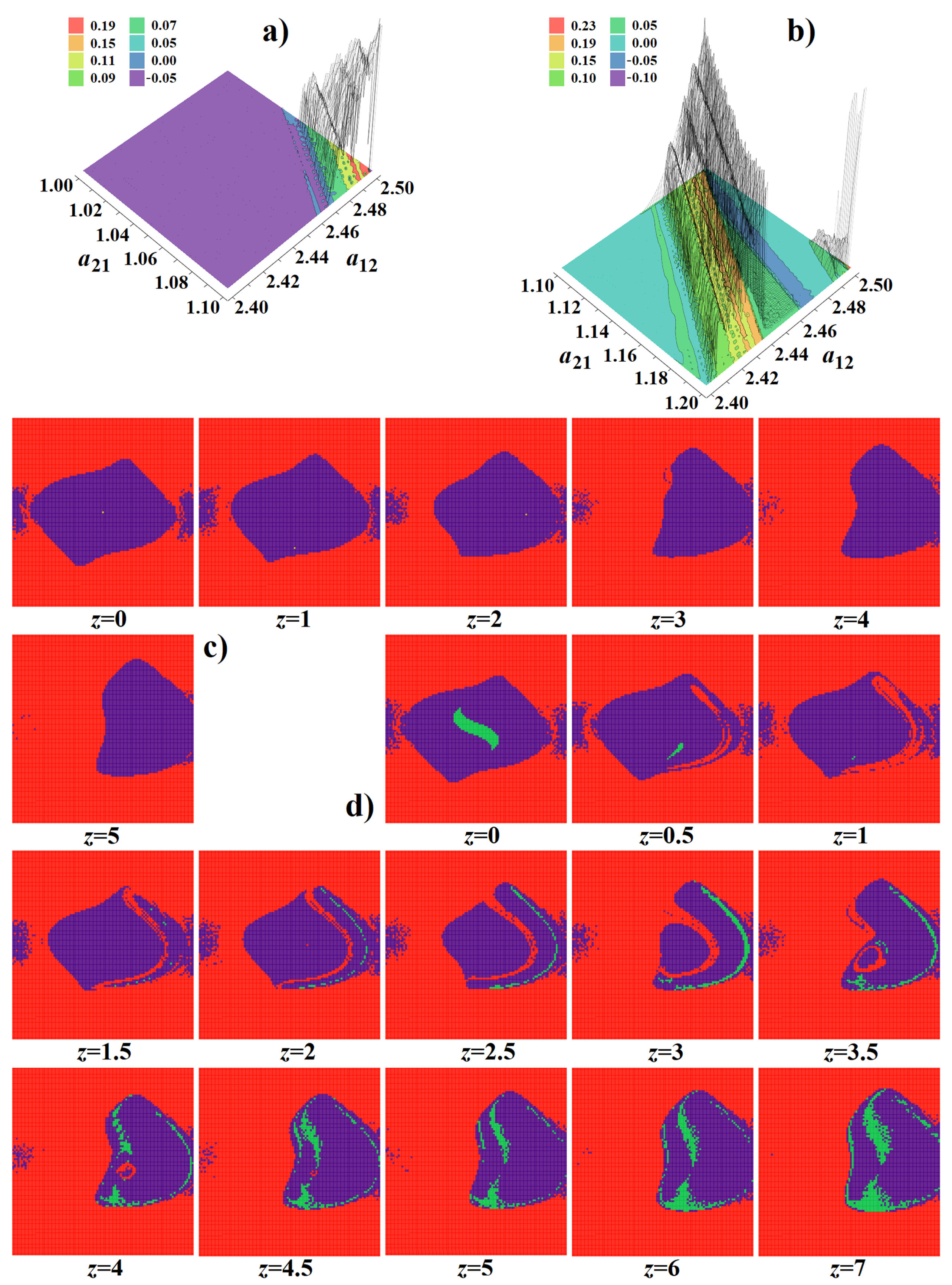
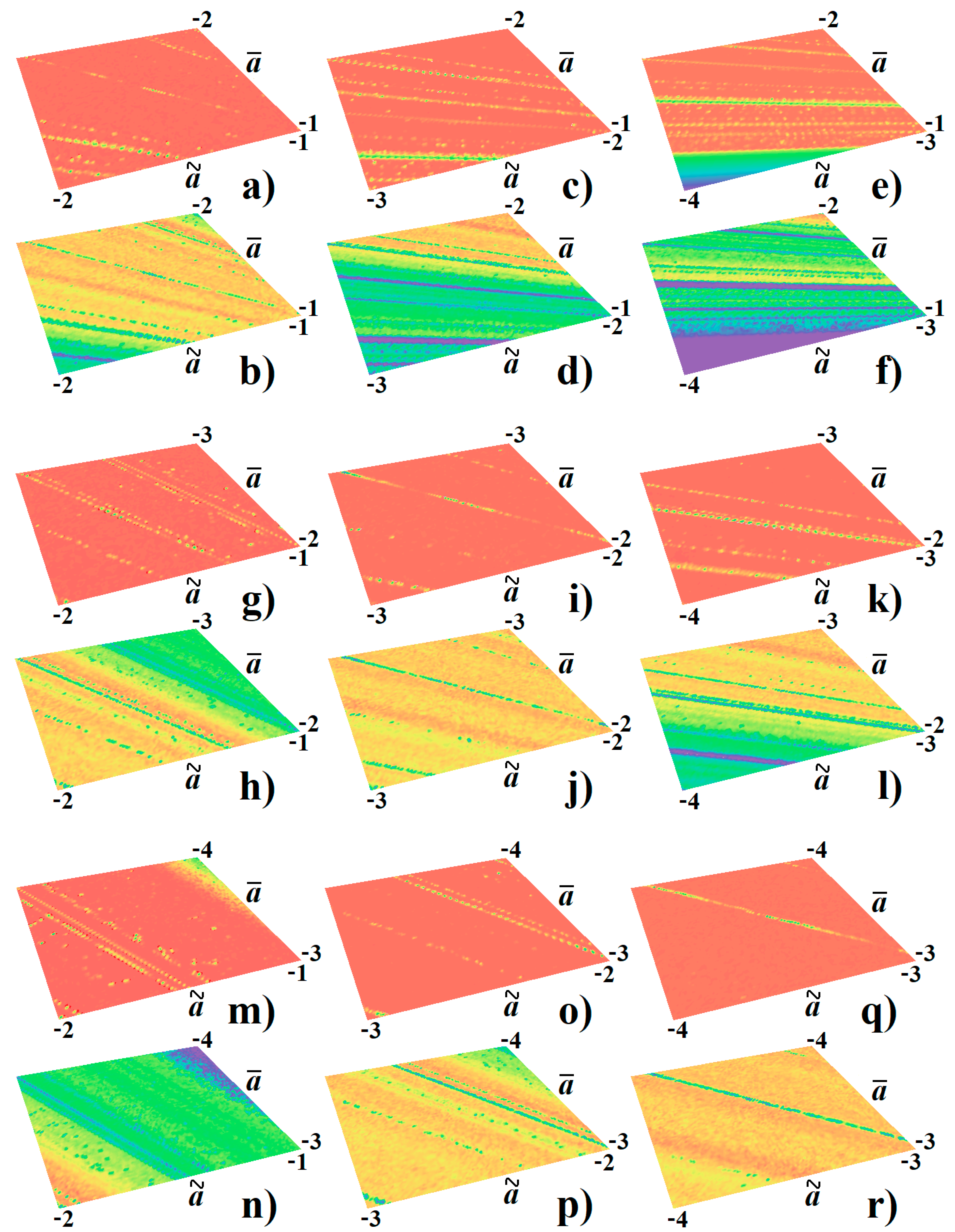
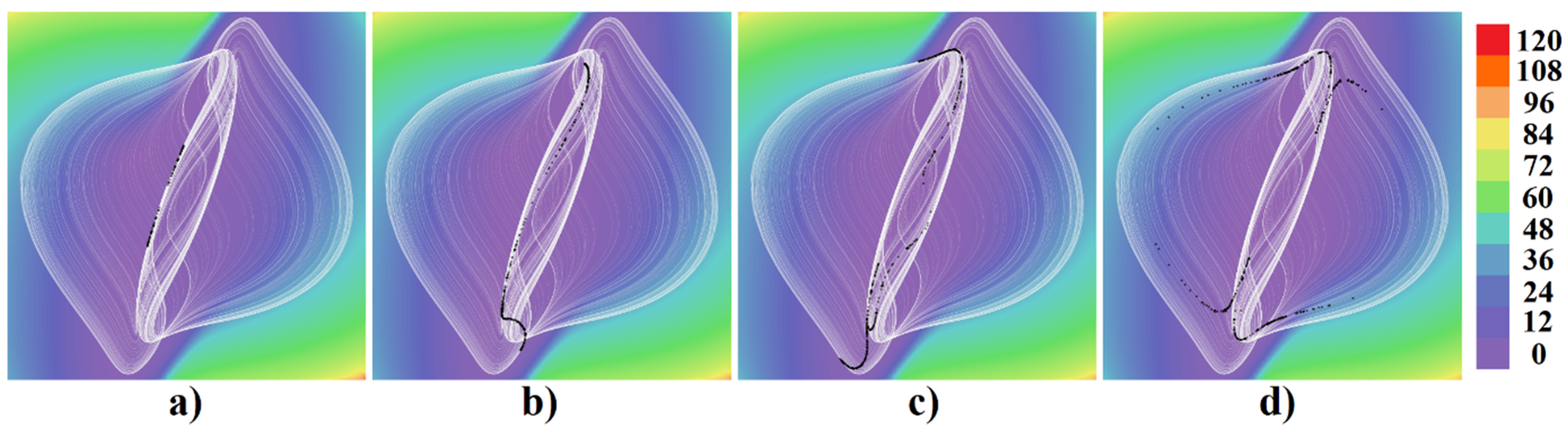
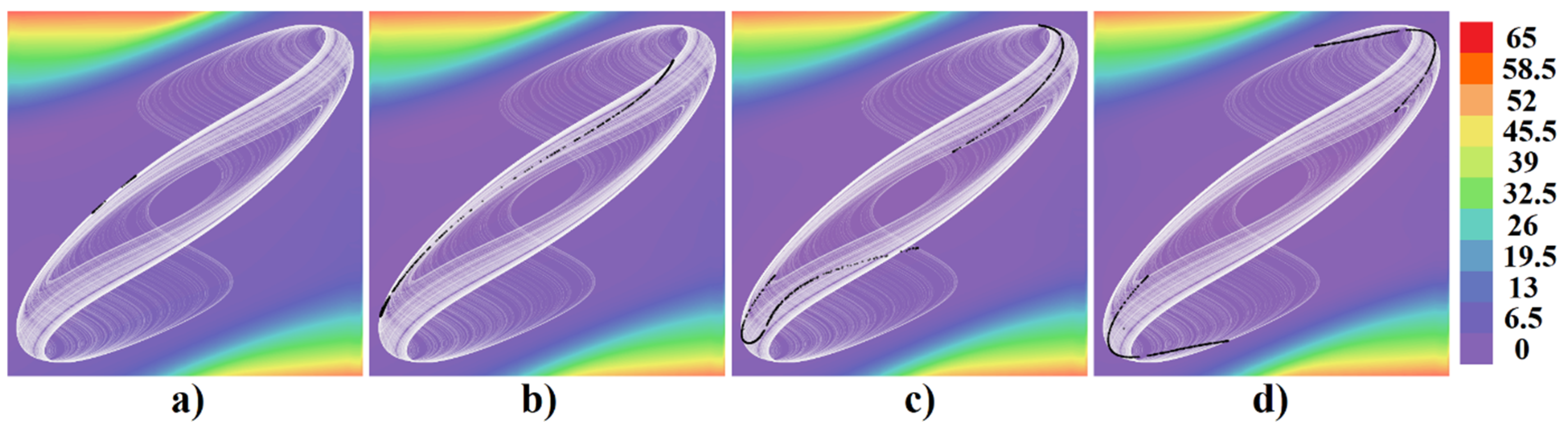
3. Numerical Analysis and Localization of Chaotic Behavior
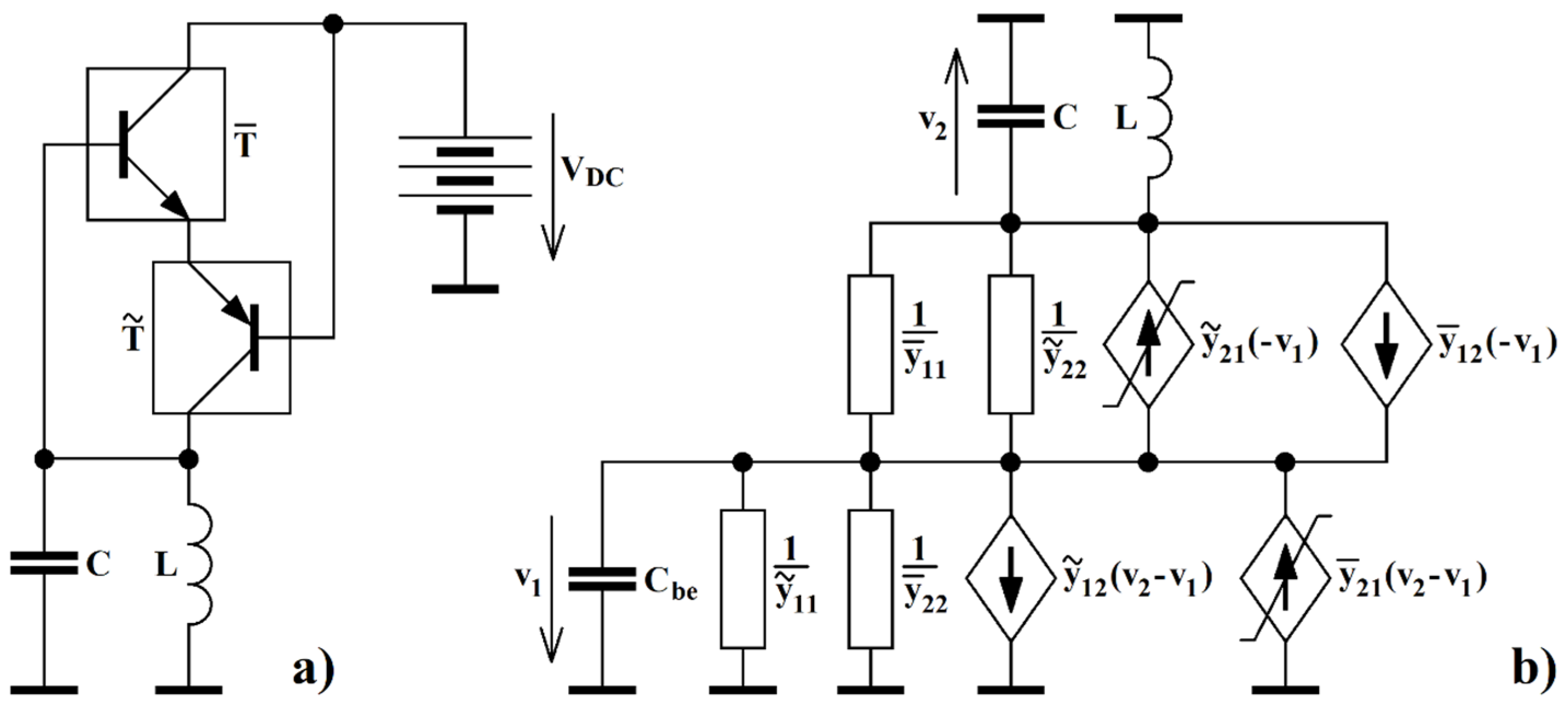
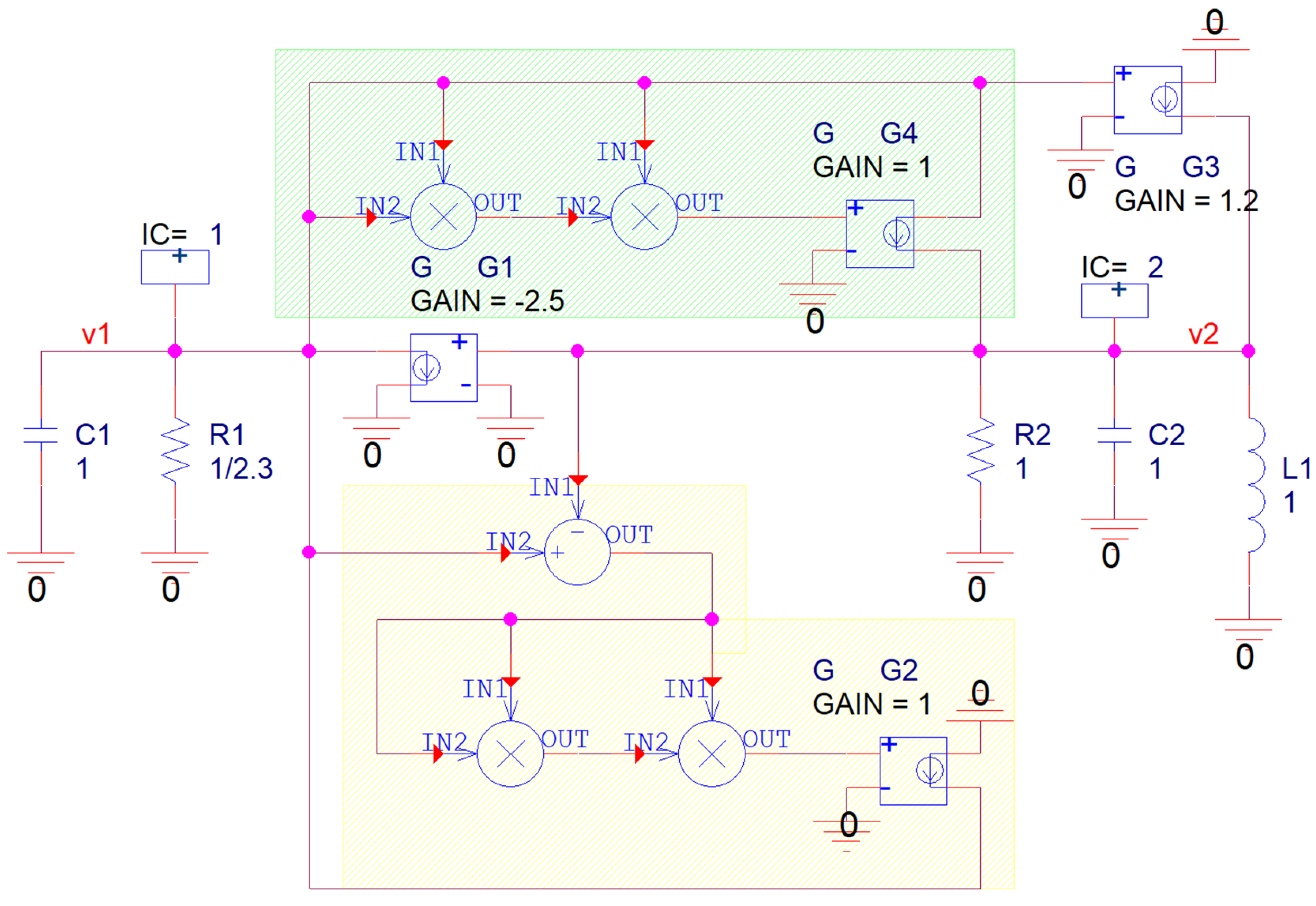
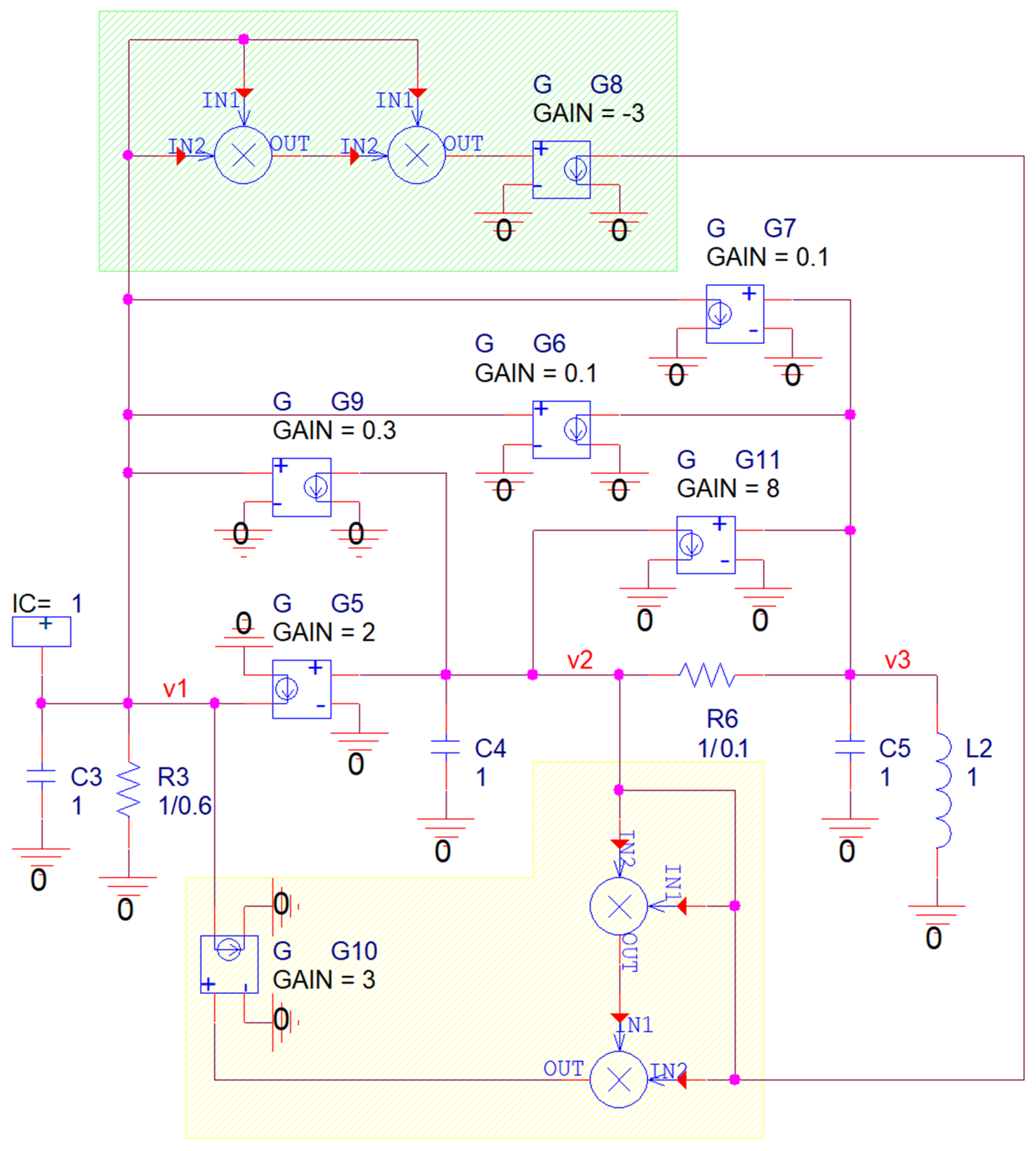
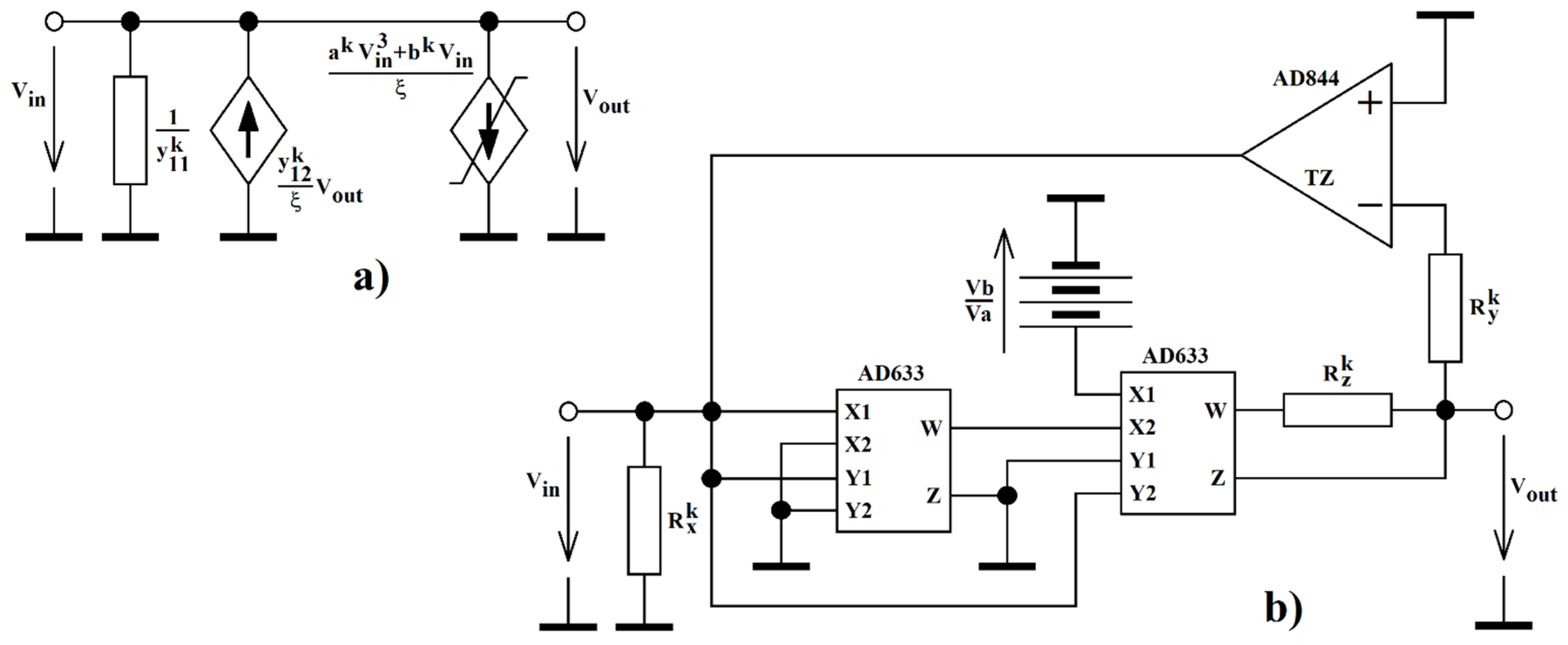
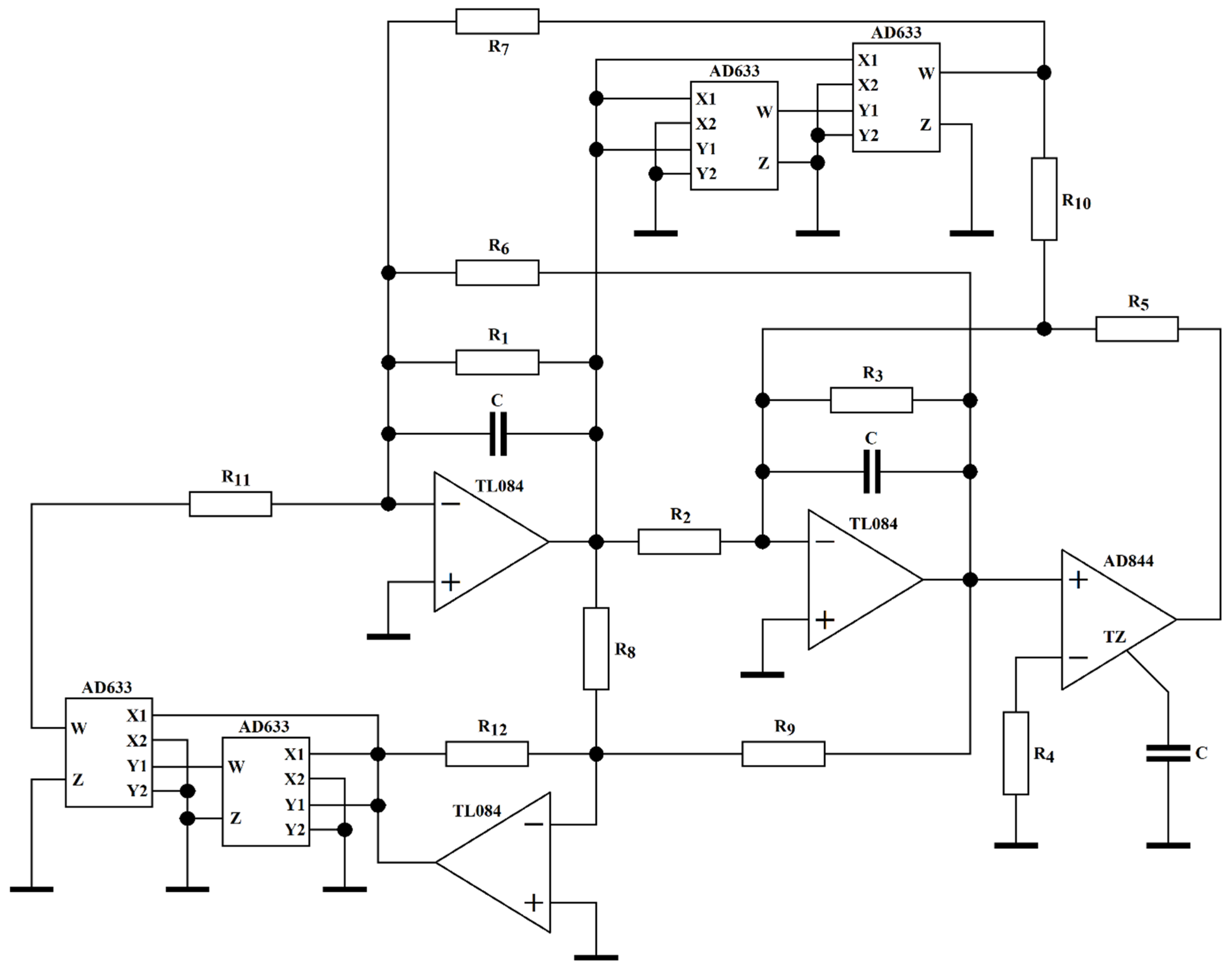
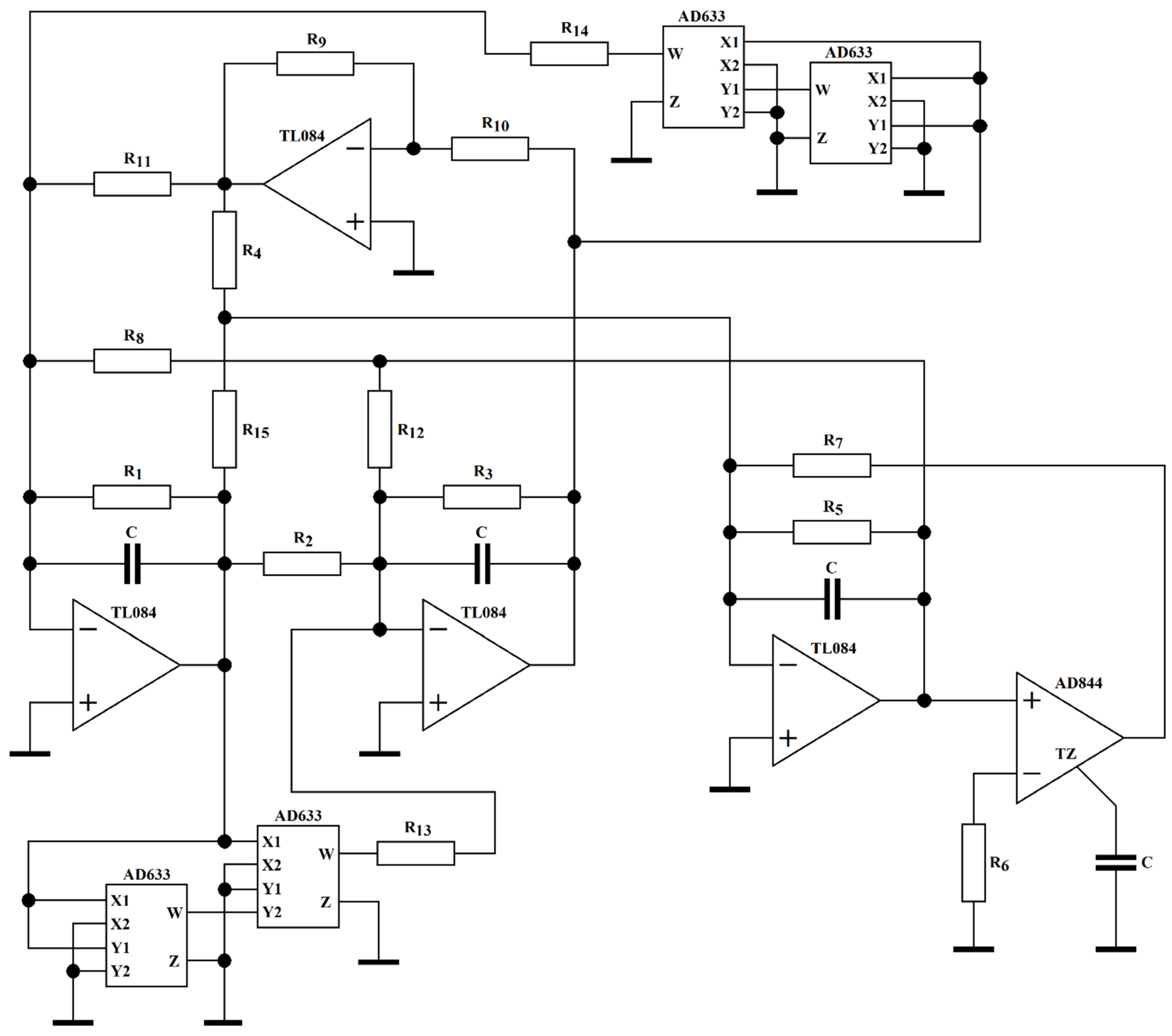
4. Design of Flow-Equivalent Lumped Circuit
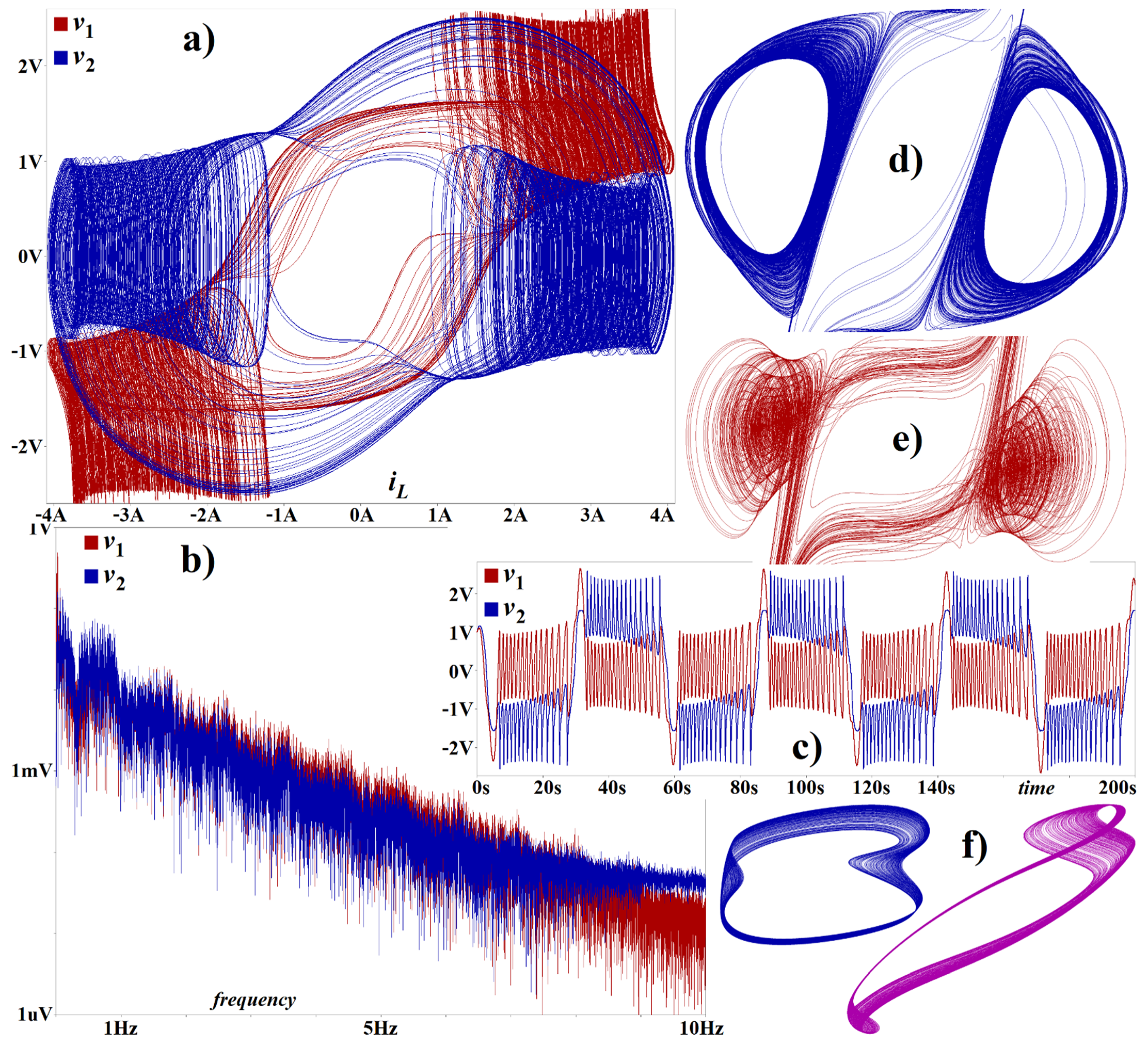
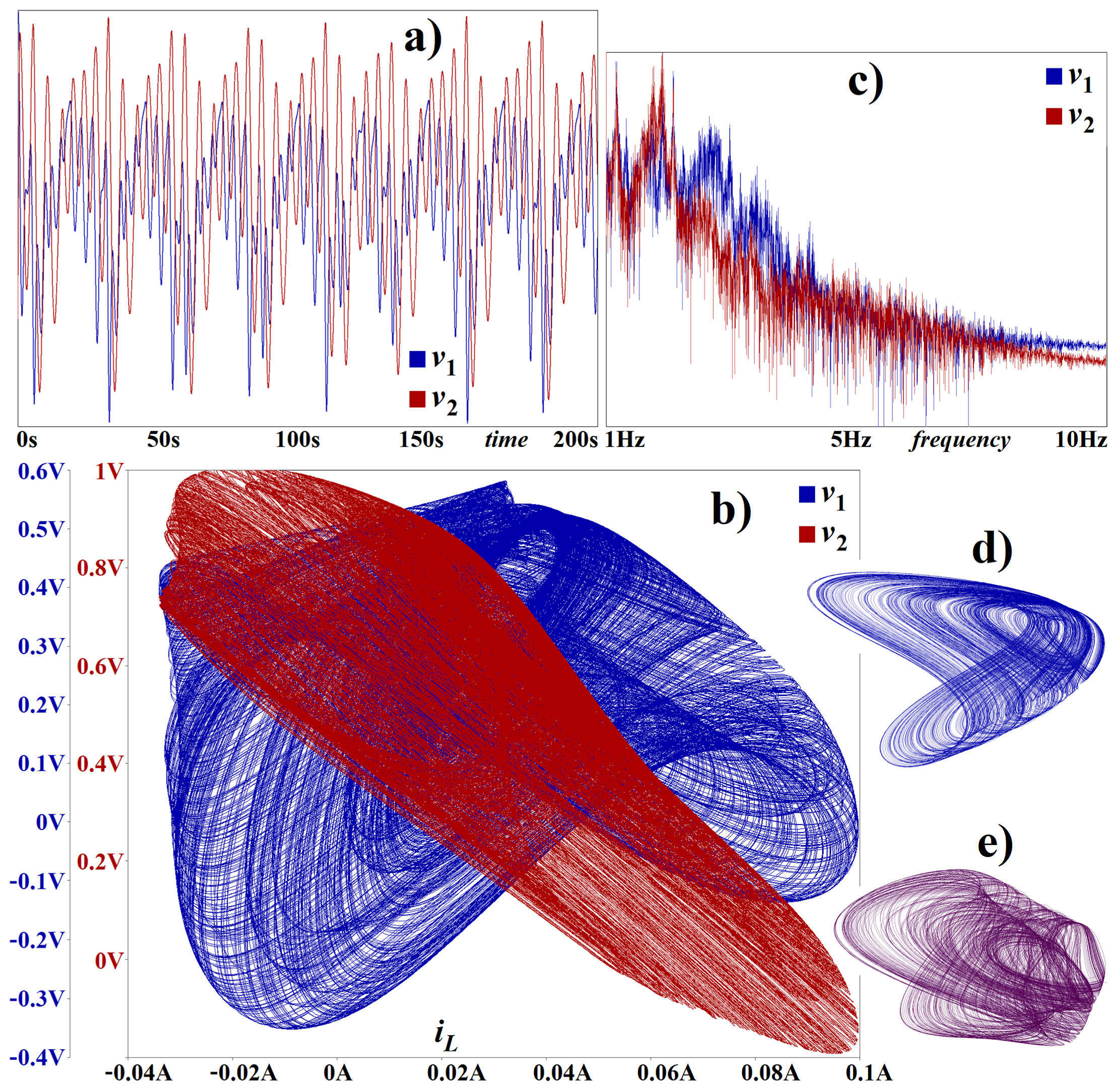
5. Experimental Measurement
6. Discussion
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Matsumoto, T. A chaotic attractor from Chua’s circuit. IEEE Trans. Circuits Syst. 1984, 31, 1055–1058. [Google Scholar] [CrossRef]
- Guzan, M. Variations of boundary surface in Chua’s circuit. Radioengineering 2015, 24, 814–823. [Google Scholar] [CrossRef]
- Chua, L.O.; Lin, G.-N. Canonical realization of Chua´s circuit family. IEEE Trans. Circuits Syst. 1990, 37, 885–902. [Google Scholar] [CrossRef]
- Kilic, R. Experimental study of CFOA-based inductorless Chua´s circuit. Int. J. Bifurc. Chaos 2004, 14, 1369–1374. [Google Scholar] [CrossRef]
- Itoh, M. Spread spectrum communication via chaos. Int. J. Bifurc. Chaos 1999, 9, 155–213. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Pham, V.-T.; Golpayegani, S.M.R.Z.; Jafari, A.M. A new cost function for parameter estimation of chaotic systems using return maps as fingerprints. Int. J. Bifurc. Chaos 2014, 24, 1450134. [Google Scholar] [CrossRef]
- Petrzela, J. Optimal piecewise-linear approximation of the quadratic chaotic dynamics. Radioengineering 2012, 21, 20–28. [Google Scholar]
- Ogorzalek, M.J. Order and chaos in a third-order RC ladder network with nonlinear feedback. IEEE Trans. Circuits Syst. 1989, 36, 1221–1232. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Kennedy, M.P. Construction of classes of circuit-independent chaotic oscillators using passive-only nonlinear devices. IEEE Trans. Circuits Syst.-I Fundam. Theory Appl. 2001, 48, 289–307. [Google Scholar] [CrossRef]
- Petrzela, J.; Polak, L. Minimal realizations of autonomous chaotic oscillators based on trans-immittance filters. IEEE Access 2019, 7, 17561–17577. [Google Scholar] [CrossRef]
- Kilic, R.; Yildrim, F. A survey of Wien bridge-based chaotic oscillators: Design and experimental issues. Chaos Solitons Fractals 2008, 38, 1394–1410. [Google Scholar] [CrossRef]
- Rajagopal, K.; Li, C.; Nazarimehr, F.; Karthikeyan, A.; Duraisamy, P.; Jafari, S. Chaotic dynamics of modified Wien bridge oscillator with fractional order memristor. Radioengineering 2019, 28, 165–174. [Google Scholar] [CrossRef]
- Kennedy, M.P. Chaos in the Colpitts oscillator. IEEE Trans. Circuits Syst. 1994, 41, 771–774. [Google Scholar] [CrossRef]
- Kvarda, P. Chaos in Hartley´s oscillator. Int. J. Bifurc. Chaos 2011, 12, 2229–2232. [Google Scholar]
- Yener, S.C.; Kuntman, H.H. Fully CMOS memristor based chaotic circuit. Radioengineering 2014, 23, 1140–1149. [Google Scholar]
- Itoh, M. Synthesis of electronic circuits for simulating nonlinear dynamics. Int. J. Bifurc. Chaos 2001, 11, 605–653. [Google Scholar] [CrossRef]
- Petrzela, J.; Gotthans, T.; Guzan, M. Current-mode network structures dedicated for simulation of dynamical systems with plane continuum of equilibrium. J. Circuits Syst. Comput. 2018, 27, 1830004. [Google Scholar] [CrossRef]
- Pham, V.-T.; Ali, D.S.; Al-Saidi, N.M.G.; Rajagopal, K.; Alsaadi, F.E.; Jafari, S. A novel mega-stable chaotic circuit. Radioengineering 2020, 29, 140–146. [Google Scholar] [CrossRef]
- Karimov, T.; Nepomuceno, E.G.; Druzhina, O.; Karimov, A.; Butusov, D. Chaotic oscillators as inductive sensors: Theory and practice. Sensors 2019, 19, 4314. [Google Scholar] [CrossRef]
- Petrzela, J. On the existence of chaos in the electronically adjustable structures of the state variable filters. Int. J. Circuit Theory Appl. 2016, 44, 1779–1797. [Google Scholar] [CrossRef]
- Endo, T.; Chua, L.O. Chaos from phase-locked loops. IEEE Trans. Circuits Syst. 1988, 35, 987–1003. [Google Scholar] [CrossRef]
- Hamill, D.C.; Jeffries, D.J. Subharmonics and chaos in a controlled switched-mode power converter. IEEE Trans. Circuits Syst. 1988, 35, 1059–1061. [Google Scholar] [CrossRef]
- Zhou, X.; Li, J.; Youjie, M. Chaos phenomena in dc-dc converter and chaos control. Procedia Eng. 2012, 29, 470–473. [Google Scholar] [CrossRef]
- Niu, Q. Study on bifurcation and chaos in boost converter based on energy balance model. Energy Power Eng. 2009, 1, 38–43. [Google Scholar] [CrossRef]
- Fossas, E.; Olivar, G. Study of chaos in the buck converter. IEEE Trans. Circuits Syst. I Fund. Theory Appl. 1996, 43, 13–25. [Google Scholar] [CrossRef]
- Petrzela, J. Strange attractors generated by multiple-valued static memory cell with polynomial approximation of resonant tunneling diodes. Entropy 2018, 20, 697. [Google Scholar] [CrossRef] [PubMed]
- Petrzela, J. New chaotic oscillator derived from class C single transistor-based amplifier. Math. Probl. Eng. 2020, 2640629. [Google Scholar] [CrossRef]
- Minati, L.; Frasca, M.; Oswiecimka, P.; Faes, L.; Drozd, S. Atypical transistor-based chaotic oscillators: Design, realization, and diversity. Chaos 2017, 27, 073113. [Google Scholar] [CrossRef] [PubMed]
- Kiers, K.; Klein, T.; Kolb, J.; Price, S.; Sprott, J.C. Chaos in a nonlinear analog computer. Int. J. Bifurc. Chaos 2004, 14, 2867–2873. [Google Scholar] [CrossRef]
- Gotthans, T.; Petrzela, J. Experimental study of the sampled labyrinth chaos. Radioengineering 2011, 20, 873–879. [Google Scholar]
- Cooper, M.; Heidlauf, P.; Sands, T. Controlling chaos—forced van der Pol equation. Mathematics 2017, 5, 70. [Google Scholar] [CrossRef]
- Pham, V.-T.; Kingni, S.T.; Volos, C.H.; Jafari, S.; Kapitaniak, T. A simple three-dimensional fractional-order chaotic system without equilibrium: Dynamics, circuitry implementation, chaos control and synchronization. AEU-Int. J. Electron. Commun. 2017, 78, 220–227. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; Zambrano-Serrano, E.; Volos, C.H.; Jafari, S.; Kengne, J.; Rajagopal, K. A new fractional-order chaotic system with different families of hidden and self-excited attractors. Entropy 2018, 20, 564. [Google Scholar] [CrossRef] [PubMed]
- Petrzela, J. Fractional-order chaotic memory with wideband constant phase elements. Entropy 2020, 22, 422. [Google Scholar] [CrossRef]
- Pinchus, S. Approximate entropy (ApEn) as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrzela, J. Chaotic and Hyperchaotic Self-Oscillations of Lambda Diode Composed by Generalized Bipolar Transistors. Appl. Sci. 2021, 11, 3326. https://doi.org/10.3390/app11083326
Petrzela J. Chaotic and Hyperchaotic Self-Oscillations of Lambda Diode Composed by Generalized Bipolar Transistors. Applied Sciences. 2021; 11(8):3326. https://doi.org/10.3390/app11083326
Chicago/Turabian StylePetrzela, Jiri. 2021. "Chaotic and Hyperchaotic Self-Oscillations of Lambda Diode Composed by Generalized Bipolar Transistors" Applied Sciences 11, no. 8: 3326. https://doi.org/10.3390/app11083326
APA StylePetrzela, J. (2021). Chaotic and Hyperchaotic Self-Oscillations of Lambda Diode Composed by Generalized Bipolar Transistors. Applied Sciences, 11(8), 3326. https://doi.org/10.3390/app11083326





