To NFT or Not: A Strategic Analysis for Fashion Brands Developing Digital Products in the Metaverse

Abstract

This paper examines the strategic decisions of fashion brands to develop and sell non-fungible tokens (NFTs) within the metaverse. We construct two operational models based on whether NFTs are adopted: the traditional fashion model without NFT (Scenario T) and the digital fashion model with NFT (Scenario D). By comparing the equilibrium outcomes of fashion brands in Scenarios T and D, we derive valuable insights into the implementation of digital strategies in the fashion industry. Our analysis reveals three key findings. First and foremost, the proportion of fashion customers to conventional customers, as well as the digital value and cost of NFTs, are direct factors influencing the adoption of digital strategies by fashion brands. Secondly, opportunistic pricing by manufacturers is an indirect factor influencing fashion brands’ strategic choices, and a fixed production price contract can effectively avoid this case. Finally, we find that personalized pricing and a free NFT strategy are effective tools to boost fashion brands’ digital revenues.

1. Introduction

As a cornerstone of the global economy, the fashion industry generated USD 1.74 trillion in revenue in 2023 [1], with projections to reach USD 2 trillion by 2028 [2]. Driven by gaming, NFTs, virtual reality (VR), and augmented reality (AR), the metaverse has significantly increased consumer demand for virtual interactions, particularly in digital fashion. A cross-generational survey of US consumers (Gen Z, Millennials, Gen X) shows that 49% of respondents are interested in purchasing NFTs from luxury brands [3], signaling NFTs as a new growth driver for the industry [4].

However, digital transformation in the industry remains uneven: while leading brands like Gucci, Nike, and Louis Vuitton have actively developed and marketed NFT products [5], most brands—especially small and medium-sized enterprises (SMEs)—adopt a wait-and-see approach. This strategic divergence stems from two key challenges: (1) Limited NFT market scale and heterogeneous preferences: Statista forecasts a global NFT user base of only 11.67 million by 2026, indicating a market scale below the threshold for mass commercial investment [6]. Empirical data from the US [7], China [8], and Indonesia [9] show that 50–60% of respondents have sustained interest in fashion NFTs, creating a dual market of “fashion customers” (valuing digital assets) and “conventional customers” (preferring physical products). The former sees NFTs as scarce social status symbols, while the latter questions the practical value of virtual goods. The market share distribution is a pivotal variable in brands’ NFT investment decisions. (2) Technological gaps: Developing “physical + digital” hybrid products requires integrating blockchain authentication, smart contract development, and 3D modeling, demanding significant R&D investments and design reengineering. These barriers disproportionately affect resource-constrained SMEs [10,11].

Against this backdrop, this study addresses three critical questions:

• For fashion brands: What are the core motivations driving brands to adopt digital strategies? Under what conditions are fashion brands willing to develop and sell digital products?
• For manufacturers: How do manufacturers perceive brands’ digital strategies? Are manufacturers willing to support digital fashion initiatives?
• For consumers: How do consumers evaluate brands’ digital strategies? Do fashion customers and conventional customers hold conflicting perceptions? Is there a balanced strategy to satisfy both customer segments?

To address these questions, we develop a classical supply chain model involving a fashion brand and a manufacturer. In the model, the brand designs products and issues production orders to the manufacturer, who produces and supplies goods to the brand’s retail channel for sale to consumers. The brand decides whether to adopt a digital strategy (e.g., developing NFTs). We examine two scenarios: (1) a traditional fashion model without NFT (Scenario T); and (2) a digital fashion model with NFT (Scenario D). Our main findings are as follows:

Firstly, the decision to adopt a digital strategy hinges on three core factors: the number of fashion customers, the digital value of NFTs, and the digital cost of NFTs. From a profit perspective, the number of fashion customers and the digital value of NFTs are positive variables, while the digital cost of NFTs is a negative variable. Fashion brands will adopt digital strategies only if the benefits derived from the positive variables outweigh the impact of the negative variables.

Secondly, manufacturers exhibit interesting behavioral dynamics: if a brand profits from digital strategies, manufacturers may seek to increase production price (even without participating in NFTs development); if the brand incurs losses, manufacturers may voluntarily reduce production price to support the brand. To avoid manufacturers’ “opportunistic” behavior, brands can sign a fixed production contract. Extended analysis shows this strategy is feasible, with manufacturers generally accepting such contracts.

Finally, pricing strategies and marketing approaches are equally critical for the successful implementation of digital strategies by fashion brands. Different pricing or marketing strategies can significantly impact the profitability of fashion brands. This paper conducts a comparative analysis of common pricing, personalized pricing, and free NFT strategies, providing valuable insights to further optimize the digital transformation of fashion brands.

The theoretical contributions of this paper are as follows: (1) The existing literature on digital products primarily focuses on digital content (e.g., Netflix, Spotify) [12], where consumers only obtain usage rights [13]. Digital assets like NFTs discussed herein differ fundamentally: their ownership allows secondary transactions (e.g., resale on Opensea), giving consumers collectible value and value-added utility. Their pricing strategies also diverge from digital content uses subscription-tiered models (e.g., membership levels, subscription durations) [14], while NFTs are priced via ownership transactions. (2) In consumer segmentation, this paper uses “willingness to purchase NFTs” as a criterion based on empirical research, defining “fashion customers” (willing to pay for NFTs) and “conventional customers” (only accepting physical products). This is the first model to incorporate the concept of “digital asset identification”. (3) Compared to traditional supply chain research, this paper introduces an operational strategy for fashion supply chains involving NFT development, establishing two retail product modes: “physical + digital” and “physical only.” This complements the existing supply chain literature. Additionally, it expands on pricing and marketing strategies for NFT sales (e.g., personalized pricing, gifting tactics).

The rest of this paper is organized as follows. We review the relevant literature in Section 2. In Section 3, we describe the problem, the model, and obtain equilibrium results. We analyze the comparison between fashion brand, manufacturer, and consumer for different scenarios in Section 4. Section 5 provides some discussion on pricing strategy. Conclusions and future research directions can be found in Section 6. All proofs are in the Appendix A and Appendix B.

2. Literature Review

The theoretical framework of this work primarily engages with four streams of literature: digital transformation, metaverse business strategy, digital products, and consumer behavior.

2.1. Digital Transformation

Digital transformation serves as a key pathway for enterprises to enhance competitiveness and achieve sustainable development [15], bringing process optimization, efficiency improvements, and innovation opportunities [16]. With the rapid advancement of digital technologies like the Internet of Things (IoT), cloud computing, blockchain, and artificial intelligence (AI), the term “digital transformation” now describes the disruptive impact of these technologies on businesses [17]. Verhoef et al. argue that business model innovation is the outcome of digital transformation, with digital technologies serving as the tools to enable it [18]. Ancillai et al. further reveal the relationship between digital technology and business model innovation [19], while Klos et al. propose a framework for digital business model transformation that effectively supports this theory [20]. Thus, examining the role of digital technology in enterprise digital transformation and operations management forms a critical theoretical foundation for this study.

In terms of digital technology applications, extensive practice has been conducted in both industry and academia. For example, blockchain, as a distributed ledger technology, is characterized by decentralization, transparency, and immutability [21]. Shen et al. explore how original brands use blockchain to disclose product origins and combat market encroachment by counterfeiters [22]. Niu et al. apply blockchain in cross-border e-commerce to address product quality ambiguity [23]. Artificial intelligence (AI), adept at simulating human cognition and behavior, serves as a powerful tool for automating business processes and enhancing predictive accuracy [21]. Yang et al. introduce a cloud-based AI system that profoundly impacts dynamic pricing and information disclosure for fresh produce [24]. Cui et al. discuss how AI bot applications influence suppliers’ quoting strategies, revealing AI’s unique value in procurement processes [25]. Additional research on digital technology applications in digital transformation and operations management can be found in the literature [26].

This paper is closely tied to blockchain technology applications in the digital transformation of fashion enterprises. Specifically, the NFTs discussed herein are blockchain-based products. Current fashion industry applications of blockchain primarily focus on product traceability [27], supply chain transparency [28], authenticity verification [29], and sustainability [30]. Few studies have explored strategies for fashion brands to develop NFTs using blockchain. For instance, Wang et al. quantitatively analyze the market prospects of fashion NFTs, finding that consumers are interested in and willing to purchase them [8]. Liu et al. demonstrate that blockchain-based NFT digital assets can create win-win outcomes for enterprises in terms of profits and environmental benefits [31]. Additionally, Sung et al. show that NFT marketing helps luxury brands increase profitability [32]. As such, this research is theoretically grounded in fashion brand digital transformation and supported by real-world cases of luxury brands like Gucci and LV selling NFTs [33].

2.2. Metaverse Business Strategy

With the rapid advancement of digital technologies, the concept of the metaverse is increasingly mentioned in discussions of digital transformation [34]. Defined as a virtual space that mirrors the real world, the economic activities within this space form the core of metaverse business strategies [35]. In recent years, tech giants like Facebook (now Meta), Microsoft, and Google have invested heavily in the metaverse, continuously shifting economic growth toward metaverse-centric strategies [36]. Driven by these leaders, research on metaverse applications has emerged across industries such as gaming [37], fashion [38], agro-food [39], transportation [40], and healthcare [41]. This section thus focuses on metaverse-centered business models, systematically mapping their development directions to provide a panoramic view of metaverse-driven business model innovation.

The value creation mechanisms of metaverse business strategies can be categorized into five dimensions. First, value appreciation is achieved through virtual products or digital assets, primarily via the tokenization of physical products (e.g., NFT sneakers). This process creates scarcity barriers and activates collectible value systems by fostering functional complementarity between virtual assets and physical goods [42]. Second, the integration of traditional physical retail channels with metaverse spaces reconfigures the channel ecosystem. No-table applications include the creation of metaverse virtual retail stores and the embedding of virtual showrooms within physical outlets, enabling synergistic optimization of online-offline channel dynamics [35]. Third, bidirectional interaction between products and channels in hybrid reality environments generates novel consumption chains. For instance, consumers can purchase NFT credentials in physical stores to unlock metaverse immersive experiences, or complete transactions in the metaverse for physical logistics fulfillment, forming closed-loop consumption ecosystems [43]. Fourth, the exploitation of user virtual identities emerges as a growth driver. By designing personalized assets such as avatar skins and equipment, businesses can precisely activate demand for virtual products and establish emotional engagement [44]. Fifth, the construction of metaverse user co-creation communities reshapes brand–user relationship paradigms. Through open content production and real-time interaction mechanisms, these communities significantly enhance user participation and strengthen brand community identification [45].

This paper focuses on fashion enterprises’ metaverse strategies, particularly the value creation mechanisms of NFT products. The core hypothesis—that NFT buyers gain additional digital value—is theoretically supported by Joy et al. and Alexander, who show that NFTs attract consumers through uniqueness, scarcity, and collectability. Post-purchase, these attributes enable personalized metaverse display, wearability, and interaction, enhancing psychological utility [46,47]. Economically, Sung et al. highlight NFTs’ tradability, which allows resale-driven returns and strengthens purchase intent [32]. Thus, this inquiry into fashion brands’ NFT investment strategies serves as a critical validation of metaverse business models in a vertical industry context.

2.3. Digital Products

Digital products are electronic content goods delivered and consumed online, such as software, digital art, streaming media, and video games [48]. As Watkins et al. note, digital content goods differ fundamentally from traditional goods: their transactions involve granting usage rights rather than transferring ownership [13]. Due to their easy replicability and low transmission costs, digital goods face higher piracy risks, making digital rights management (DRM) and anti-piracy measures critical to marketing [49]. Avinadav et al. examine DRM investment and pricing strategies for digital products to maximize profits for manufacturers and retailers [12]. Kim et al., meanwhile, explore a “pay-what-you-want” pricing model to combat piracy, finding it both feasible and an effective complement to technical measures like DRM [50].

Subscription-based pricing represents another key area for digital content [14]. Li et al. discuss pricing models for digital music, highlighting the distinction between ownership and physical music, and compare ownership-based, subscription-based, and hybrid pricing [51]. Yu et al. analyze bundling strategies for digital content and devices, such as Microsoft’s Office Suite bundles for laptops [52]. Alaei et al. further investigates optimal subscription plans for digital goods [53].

Unlike digital content, NFTs are blockchain-based digital assets characterized by ownership transactions, shifting this study beyond subscription pricing frameworks. Inspired by Li et al.’s analysis of digital music pricing (subscription, ownership, hybrid models) [51], we optimize pricing models and marketing strategies for this new asset class.

2.4. Consumer Behavior

The study of consumer behavior theory has long been a focal point in marketing management and behavioral science [54], with scholars extensively exploring psychological tendencies [55], behavioral mechanisms [56], and loyalty [57]. In operations management, pricing research incorporating consumer behavior has grown significantly through the lens of consumer segmentation and heterogeneity [58].

Regarding retail channel preference heterogeneity, Yu et al. analyze consumer preferences for direct, resale, and agency channels, providing insights to guide retailers’ channel decisions [59]. For environmental attribute preferences, Li and Wang develop a subsidy pricing model for electric vehicles, distinguishing between green and non-green consumers [60]. Strategic consumers represent a critical focus in purchasing behavior research. Unlike myopic consumers who only decide “whether to buy”, Pun and DeYong define strategic consumers as those who decide “whether, when, and what to buy”, exploring their role in manufacturer-counterfeiter competition [61]. Additional segmentation research covers risk-neutral vs. risk-averse consumers [62], novice vs. expert consumers (product authenticity recognition) [22], and conspicuous vs. follower consumers [63].

A review of this literature shows that operations management studies on consumer behavior predominantly focus on group segmentation, including preference heterogeneity (channel, attribute) and typological differences (strategic/myopic, conspicuous/follower). This paper focuses on NFTs—emerging fashion commodities—where Statista reports 49% of respondents are willing to buy fashion NFTs, versus 51% uninterested or unaware [3]. Following Li and Wang’s green/non-green consumer framework [60], we define “fashion customers” (NFT-interested) and “conventional customers” (NFT-uninterested). This constitutes an innovative addition to consumer behavior research in operations management.

3. Model

We consider a typical fashion supply chain composed of a manufacturer and a fashion brand. The fashion brand has a design department (designer) and a retail department (retailer). The fashion brand procures products from the manufacturer. The supply process is as follows: the designer provides design files, the manufacturer produces fashion products, and the retailer sells them to the market. With the maturity of blockchain technology, developing digital versions of fashion products has become a prevalent trend in the fashion industry. Some renowned luxury brands like Givenchy, Gucci, and Louis Vuitton have already started selling NFT products and reaped significant profits [33]. However, not all fashion brands have entered the NFT market. In particular, small or lesser-known brands have yet to take action. To disclose the conditions under which fashion brands implement digital strategies, this paper adopts a game-theoretic approach to discuss two strategies: (1) The fashion brand sells only physical fashion products, which is referred to as “traditional fashion” (Scenario T). (2) The fashion brand sells both physical and digital fashion products, which are referred to as “digital fashion” (Scenario D). Figure 1 illustrates the structures of the traditional and digital fashion strategies.

Data from the industry and some existing surveys helped us to determine the settings for some of the parameters. According to a report on NFTs published by BoF Insights, about 50% of respondents from the US have the intention to buy NFTs, and they consider their digital image important [7]. This result is also corroborated by data from the Chinese and Indonesian markets. Wang et al. showed that among 33 random Chinese respondents aged 16–30, about 57.6% were interested in NFTs, believing that they have a unique appeal and provide an additional psychological utility similar to a limited edition physical luxury product [8]. Syailendra et al. conducted a questionnaire survey with 250 Indonesian consumers, which showed that more than 80% of the respondents were interested in digital-physical NFT products, and 58% of the respondents indicated that the scarcity of NFTs could generate additional collector value [9]. Accordingly, we refer to existing industry reports to segment NFT’s customers into those who are willing to purchase NFT, and who generate additional digital value $v_d$ as fashion customers (market share $\alpha$), while those who are not willing to purchase NFT are called conventional customers (market share $1-\alpha$).

The development of NFT is not free, and some of the product managers explained to us about the cost of minting NFTs. Mateusz, a product manager from ULAM LABS, said, “At its core, NFT minting is about converting a digital asset (whether it’s an artwork, a music or a utility token) into a part of the blockchain, making it secure, verifiable and tradable. However, this process incurs a range of transaction fees, platform fees and other upfront costs that can vary significantly depending on the blockchain network chosen”. According to our validation, the unit cost of minting NFTs in Solana and Ether platforms is around USD 0.015–USD 150 [64]. Another product manager from RetroStyle Games, Dmytro, gives more detailed data on NFT costs, which can be accessed if interested: https://retrostylegames.com/blog/how-much-does-it-cost-to-create-an-nft-collection/ (accessed on 19 June 2025). For this reason, in this paper, we set the production cost of the NFT to be $c_d$.

In addition, we also set the settings for some other common parameters. The designer’s design cost is set to $C$, which is a fixed cost. The unit production price charged by the manufacturer is $w$, which represents the cost of materials and production, and the retailer’s unit product price is $p$.

3.1. Traditional Fashion Model Without NFT

In the traditional fashion industry, it is well known that the fashion value of products declines over time. This means that fashion items are likely to become obsolete and less fashionable, leading to a decrease in their prices. Strategic customers are aware of this and often prefer to purchase products during discount periods to maximize their psychological utility. With real-world references in mind, we set up a fashion brand to sell its products to customers over two periods, $t\in \left\{1,2\right\}$. All customers are present at the beginning of the first period and exit the market after purchasing the product.

Through branding and advertising, customers can evaluate the fashion value of new products. The fashion value, $v$, is uniformly distributed between zero and one, with the market size normalized to one. A customer who purchases a product at time $t$ derives consumption utility ${\theta }^{ t-1}\left(v-p_t\right)$, where $\theta \in \left(0,1\right)$ is the decline factor for the fashion item. A smaller $\theta$ implies a lower evaluation of the fashion product’s value over time, leading to lower consumption utility if it is purchased in the second period. Referring to [61], the total utility for a customer purchasing the product at time $t$ with price $p_t$ is

$$\begin{array}{cc}u\left(p_t\right)={\theta }^{ t-1}\left(v-p_t\right)& t\in \left\{1,2\right\}.\end{array}$$

The game sequence of the traditional fashion model is shown in Figure 2.

Initially, the fashion brand designer sends the design file to the manufacturer and specifies the order quantity, $q$. Next, the manufacturer sets the unit production price, $w$. Then, the retailer determines the retail prices, $p_1$ and $p_2$. Finally, customers decide whether to purchase the product and the timing of their purchase. We derive the customer’s utility to make the optimal choice in the two periods: (1) If $u_1>0$ and $u_1>u_2$, the customer purchases in the first period. (2) If $u_2>0$ and $u_2>u_1$, the customer purchases in the second period.

Furthermore, we obtain the quantity purchased by the customer in the two periods, i.e., the demand function is as follows:

$$q_t^T=\left\{\begin{array}{cc}{\displaystyle {\int }_{\frac{p_1-\theta p_2}{1-\theta }}^{1}dv}& t=1\\ {\displaystyle {\int }_{p_2}^{\frac{p_1-\theta p_2}{1-\theta }}dv}& t=2\end{array}\right..$$

The total profit of the manufacturer and the fashion brand are characterized by

$$\begin{gathered} \begin{array}{ll}{\pi }_M^T=w^T\left(q_1^T+q_2^T\right)& \mathrm{and} \\ \\ {\pi }_{FB}^T=\left(p_1^T-w^T\right)q_1^T& +\left(p_2^T-w^T\right)q_2^T-C.\end{array} \end{gathered}$$

It is worth noting that the profit of the fashion brand encompasses both the designer and the retailer, with shared information and no internal competition. In this paper, we consider the fashion brand as a unified decision-making entity. We assume that all products offered by the fashion brand are accepted by the market, resulting in no leftover inventory.

3.2. Digital Fashion Model with NFT

With the growing development of blockchain technology, the emergence of NFTs has further enriched the business model of digital fashion. These NFTs based on blockchain technology can be shared and displayed on social media platforms such as the metaverse, thus giving customers a unique and trendy fashion experience [32]. It is a very different model from traditional methods.

As shown in Figure 3, in the digital fashion model, the designer develops an NFT version of the fashion product with blockchain, which incurs a digital cost per unit of NFTs, $c_d$. It is important to clarify that in the digital fashion model, the retailer sells a composite fashion product that includes both the physical and digital products. In other words, when the customer purchases the physical product, an NFT version of that product can be accessed by scanning the label and can be used on platforms such as the metaverse.

However, not all customers are interested in digital fashion. Some customers enjoy and are willing to pay for NFTs, which we define as fashion customers (denoted by F), while others are not in NFTs and are defined as conventional customers (denoted by C). We denote $v_d$ as the digital value of NFTs, with $v_d>0$.

We consider that when a fashion product is sold with NFTs, the utility of the fashion customer is $u_F={\theta }^{ t-1}\left(v-p_t+v_d\right)$ and the utility of the conventional customer is $u_C={\theta }^{ t-1}\left(v-p_t\right)$. It is important to note that the market proportion of the fashion customer is $\alpha$ and the proportion of the conventional customer is $1-\alpha$, with $\alpha \in \left(0,1\right)$. Furthermore, we discuss the timing and quantity of purchases for fashion and conventional customers as follows:

$$\begin{gathered} \begin{array}{ll}{q}_{F\_t}^D=\left\{\begin{array}{cc}\alpha {\displaystyle {\int }_{\frac{p_1-\theta p_2-\left(1-\theta \right)v_d}{1-\theta }}^{1}dv}& t=1\\ \alpha {\displaystyle {\int }_{p_2-v_d}^{\frac{p_1-\theta p_2-\left(1-\theta \right)v_d}{1-\theta }}dv}& t=2\end{array}\right. & \mathrm{and} \\ \\ q_{C\_t}^D=\left\{\begin{array}{cc}\left(1-\alpha \right){\displaystyle {\int }_{\frac{p_1-\theta p_2}{1-\theta }}^{1}dv}& t=1\\ \left(1-\alpha \right){\displaystyle {\int }_{p_2}^{\frac{p_1-\theta p_2}{1-\theta }}dv}& t=2\end{array}\right..& \end{array} \end{gathered}$$

In the digital fashion model, the total profits of the manufacturer and the fashion brand are, respectively:

$$\begin{array}{cc}{\pi }_M^D=w^D\left(q_{F\_t}^D+q_{C\_t}^D\right)\hspace{1em}\hspace{1em}\mathrm{and}\hspace{1em}\hspace{1em}\hspace{1em}& \\ {\pi }_{FB}^D=\left[p_1^D\left(q_{F\_1}^D+q_{C\_1}^D\right)+p_2^D\left(q_{F\_2}^D+q_{C\_2}^D\right)\right]-w^D\left(q_{F\_t}^D+q_{C\_t}^D\right)-c_d\left(q_{F\_t}^D+q_{C\_t}^D\right)-C.\end{array}$$

The fashion brand’s profits from the designer and the retailer include the sales profit $p_1^D\left(q_{F\_1}^D+q_{C\_1}^D\right)+p_2^D\left(q_{F\_2}^D+q_{C\_2}^D\right)$, the production cost $w^D\left(q_{F\_t}^D+q_{C\_t}^D\right)$, the design cost $C$, and the digital cost of NFTs $c_d\left(q_{F\_t}^D+q_{C\_t}^D\right)$. The equilibrium outcomes in Scenarios T and D are summarized in

Table 1. The equilibrium outcomes of Scenarios T and D.

	Scenario T	Scenario D
$w^{*}$	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{1}{2}}\left(1+\alpha v_d-c_d\right)$
$p_1^{*}$	${\displaystyle \frac{1}{2\left(\theta +3\right)}}\left(\theta +5\right)$	${\displaystyle \frac{1}{2\left(\theta +3\right)}}\left[\alpha v_d\left(\theta +5\right)+\left(1+\theta \right)c_d+\theta +5\right]$
$p_2^{*}$	${\displaystyle \frac{1}{\theta +3}}\left(\theta +3\right)$	${\displaystyle \frac{1}{\theta +3}}\left(\alpha v_d\left(\theta +2\right)+c_d+\theta +2\right)$
$q_1^{*}$	${\displaystyle \frac{1}{2\left(\theta +3\right)}}$	$q_{F\_1}={\displaystyle \frac{\alpha }{2\left(\theta +3\right)}}\left[\left(2\theta +6-\left(2\theta +5\right)\alpha \right)v_d-c_d+1\right]$
		$q_{C\_1}={\displaystyle \frac{\left(1-\alpha \right)}{2\left(\theta +3\right)}}\left[-\left(2\theta +5\right)v_d\alpha -c_d+1\right]$
$q_2^{*}$	${\displaystyle \frac{1}{2\left(\theta +3\right)}}$	$q_{F\_2}={\displaystyle \frac{\alpha }{2\left(\theta +3\right)}}\left(\alpha v_d-c_d+1\right)$
		$q_{C\_2}={\displaystyle \frac{\left(1-\alpha \right)}{2\left(\theta +3\right)}}\left(\alpha v_d-c_d+1\right)$
${\pi }_M^{*}$	${\displaystyle \frac{1}{2\left(\theta +3\right)}}$	${\displaystyle \frac{1}{2\left(\theta +3\right)}}{\left(\alpha v_d-c_d+1\right)}^2$
${\pi }_{FB}^{*}$	${\displaystyle \frac{1}{4\left(\theta +3\right)}}-C$	${\displaystyle \frac{1}{4\left(\theta +3\right)}}{\left(\alpha v_d-c_d+1\right)}^2-C$

(the proof is in Appendix B: A1).

4. Results

4.1. Optimal Pricing Comparison

Lemma 1. 

The development of NFTs by fashion brands will result in higher retail prices for their products, i.e., $p_t^D>p_t^T.$

Compared to traditional fashion models, the implementation of digital strategies by fashion brands has resulted in an increase in the selling price of their products. In Scenario D, the fashion brand sells a combination of “physical + digital” products to consumers instead of only physical products. The development of NFTs by fashion brands incurs a digital cost $c_d$, which is ultimately borne by consumers, resulting in higher prices.

Lemma 2. 

The development of NFTs by fashion brands will result in smaller discount levels on products, i.e., ${\displaystyle \frac{p_2^T}{p_1^T}}<{\displaystyle \frac{p_2^D}{p_1^D}}.$

Lemma 2 indicates that fashion brands offer higher levels of discounts in Scenario T. The appeal of “discounts” to customers cannot be ignored. Discounts capture the attention of consumers, who always prefer higher levels of discounts. During events such as “Black Friday”, many fashion companies offer significant discounts, such as 50% off. Therefore, it is not the price that catches the consumer’s eye, but the discount level. For example, a survey revealed that consumers were more likely to enter a store when they saw a “discount” [36]. Based on this finding, we suggest that fashion brands should promote the “discount” strategy at the right time in Scenario T.

Lemma 3. 

The development of NFTs by fashion brands has the potential to result in higher price reductions for products, i.e., only when $c_d<\alpha v_d$; then, we have $\left(p_1^D-p_2^D\right)>\left(p_1^T-p_2^T\right).$

Lemma 3, together with Lemma 2, suggests that a higher discount does not necessarily mean more savings in terms of actual payments. In Scenario D, if the digital cost of NFTs is lower $\left(c_d<\alpha v_d\right)$, the level of price reduction for its product will be greater, and consumers will receive greater utility for purchasing in the second period. Conversely, if the digital cost is higher $\left(c_d>\alpha v_d\right)$, the level of price reduction for the product in Scenario T will be greater. Therefore, we suggest that if $c_d<\alpha v_d$ holds, the fashion brand in Scenario D should sell its product by presenting its price reduction level to consumers as much as possible, as in “Save $20”, rather than in the form of discounts such as “80% of the original price.”

4.2. Profit Analysis of Fashion Brands

Proposition 1. 

Only when $c_d<1-\left(2\theta +5\right)\alpha v_d$, there exists a market demand for fashion brands to develop NFTs, i.e., $\left\{q_{F\_1}^D,q_{C\_1}^D,q_{F\_2}^D,q_{C\_2}^D\right\}>0.$

Regardless of whether fashion brands develop NFTs, the market demand for their products serves as the fundamental basis for their market behavior. According to Lemma 1, the retail price of products increases after the introduction of NFTs by fashion brands. This indicates that consumer utility will consequently change, and since consumer utility is a critical determinant of product demand, it plays a pivotal role in shaping market outcomes. Therefore, we find the limitation of $q^D>0$ in Scenario D, i.e., $c_d<1-\left(2\theta +5\right)\alpha v_d$.

Proposition 2. 

Only when $c_d<\alpha v_d+1$, a price reduction strategy can be implemented by the fashion brands to develop NFTs, i.e., $p_1^D>p_2^D.$

Price reduction strategies are commonly used by fashion brands to promote sales, and they are equally applicable to NFTs. From real-world observations, it can be noted that fashion products often follow a specific cycle known as the “discount period”. This refers to occasions when fashion brands lower prices to promote their products, such as during “Black Friday” in the United States and “Double Eleven” in China. Accordingly, we derive the constraint condition, denoted as $c_d<\alpha v_d+1$, for implementing price reduction strategies to promote NFTs after their development by fashion brands.

Proposition 3. 

Only when ${\Phi }_D^{*}=\left\{c_d<\alpha v_d\right\}$, the development of NFTs by fashion brands will increase profits, i.e., ${\pi }_{FB}^D>{\pi }_{FB}^T.$

As rational decision-makers, profitability is the key factor for fashion brands when determining whether to implement a digital strategy. In the traditional fashion scenario, fashion brands have already established a mature business model. If the development of NFTs can lead to further profit growth, fashion brands will have a stronger incentive to pursue digital transformation. Accordingly, we derive the critical condition for fashion brands to implement a digital strategy, denoted as ${\Phi }_D^{*}=\left\{c_d<\alpha v_d\right\}$.

Proposition 4. 

In Scenario D, we have the following:

• The higher the digital value of NFTs, the higher the profit of the fashion brand, i.e., ${\displaystyle \frac{\mathsf{\partial }{\pi }_{FB}^D}{\mathsf{\partial }{v}_d}}>0$;
• The greater number of fashion customers, the higher the profit of the fashion brand, i.e., ${\displaystyle \frac{\mathsf{\partial }{\pi }_{FB}^D}{\mathsf{\partial }\alpha }}>0.$

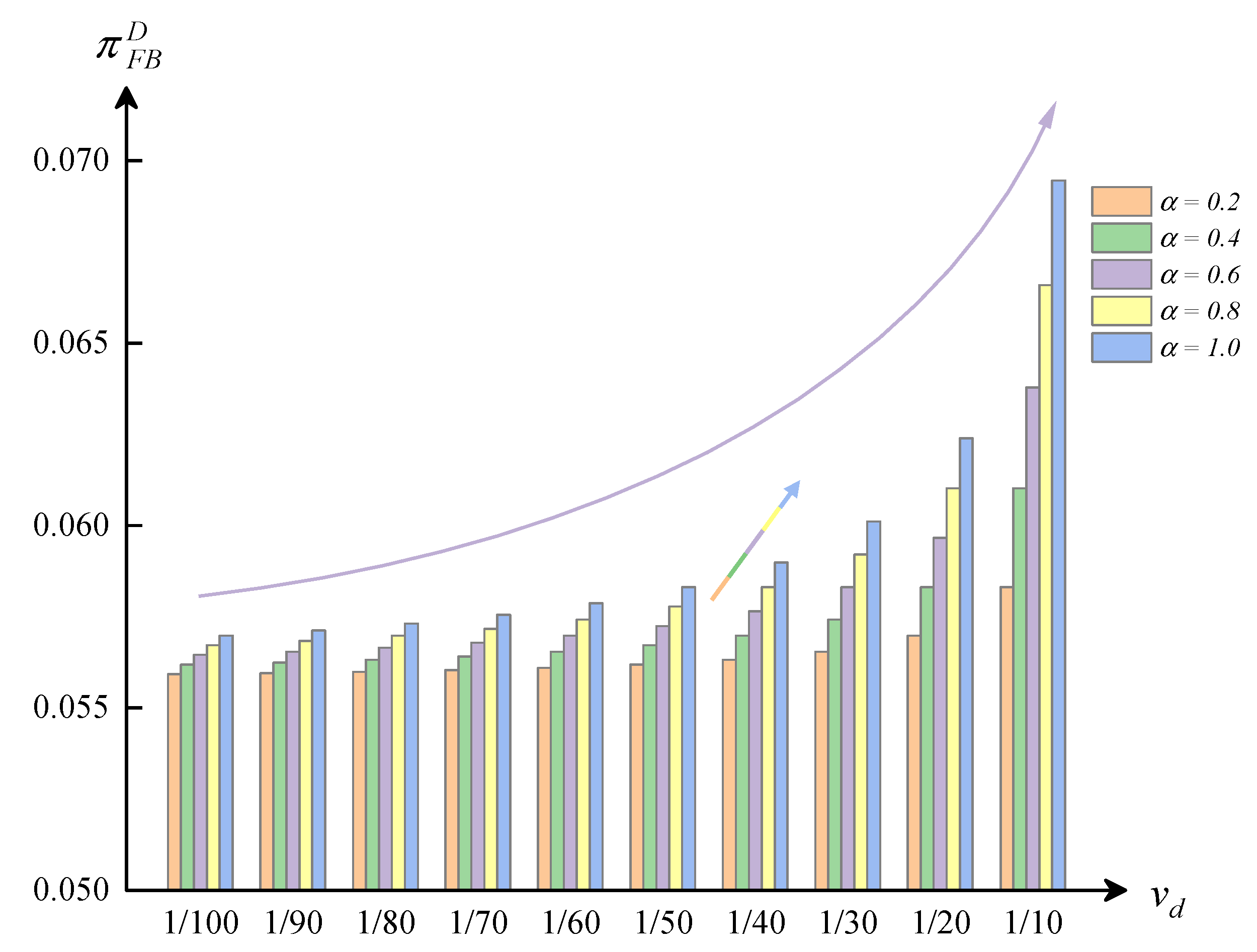
The digital value of NFTs and the proportion of fashion customers positively impact NFT development for fashion brands, especially profit, as shown in Figure 4. On the one hand, a higher digital value increases product retail prices, i.e., ${\displaystyle \frac{\mathsf{\partial }{p}^D}{\mathsf{\partial }{v}_d}}>0$. On the other hand, digital value directly boosts fashion customers’ psychological utility, raising demand for products, i.e., ${\displaystyle \frac{\mathsf{\partial }{q}^D}{\mathsf{\partial }{v}_d}}>0$. Similarly, a greater number of fashion customers means greater profit for fashion brands.

Proposition 5. 

In Scenario D, we have the following:

• The smaller the fashion decline factor, the higher the profitability of the fashion brand, i.e., ${\displaystyle \frac{\mathsf{\partial }{\pi }_{FB}^D}{\mathsf{\partial }\theta }}<0$;
• The lower the NFT’s cost, the greater the fashion brand’s profitability, i.e., ${\displaystyle \frac{\mathsf{\partial }{\pi }_{FB}^D}{\mathsf{\partial }{c}_d}}<0.$

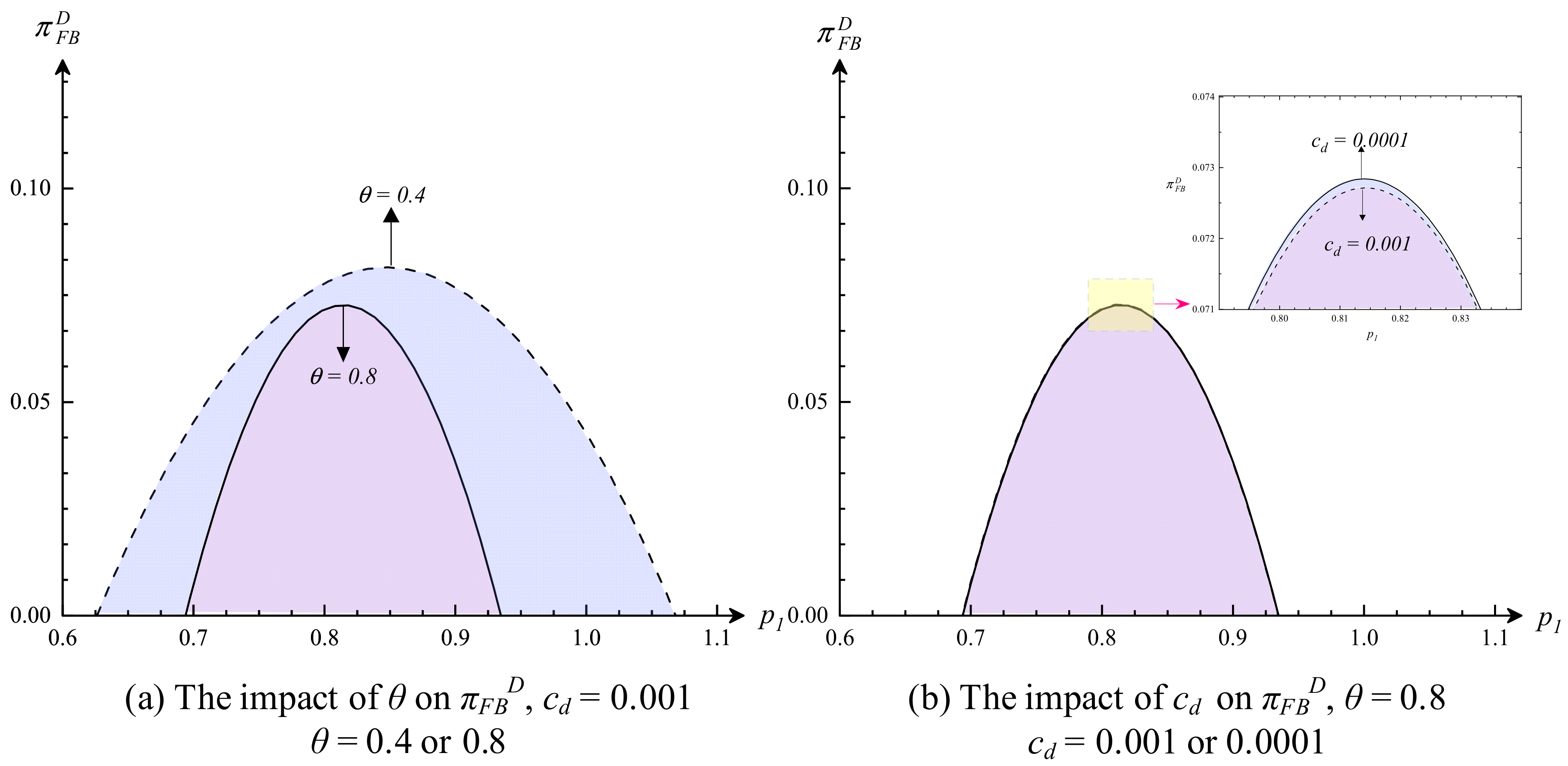
Proposition 5 focuses on the impact of the fashion decline factor and digital cost on the profitability of a fashion brand that develops NFTs, as shown in Figure 5. First, a higher fashion decline factor means the product becomes obsolete faster, and more consumers will be willing to buy fashionable products in period 2. Due to the two-stage pricing strategy of fashion brands, in period 2, the product price will drop significantly because of the decline in fashion value, which in turn reduces the profit of the fashion brand. Second, the higher the digital cost is, the lower the fashion brand’s profit. This conclusion is easy to obtain because the cost–price relationship leads to higher product prices and lower consumer demand, which in turn reduces the fashion brand’s profitability.

4.3. Behavioral Analysis of Manufacturers

Proposition 6. 

Only when $c_d<\alpha v_d$, the manufacturer will obtain a rise in profit due to the fashion brands to develop NFTs, i.e., ${\pi }_M^D>{\pi }_M^T.$

The production price and order quantity are direct factors influencing the profitability of manufacturers. By comparing the profits of manufacturers under Scenarios T and D, we find that: (1) If condition $c_d<\alpha v_d$ is satisfied, both the production price and order quantity increase ($w^D>w^T$ and $q^D>q^T$), leading to higher profits for manufacturers in Scenario D (${\pi }_M^D>{\pi }_M^T$). (2) Conversely, if condition $c_d>\alpha v_d$ is met, both the production price and order quantity decrease ($w^D<w^T$ and $q^D<q^T$), resulting in a loss for manufacturers in Scenario D (${\pi }_M^D<{\pi }_M^T$). Therefore, manufacturers can achieve profit growth from the development of NFTs by fashion brands only when condition $c_d<\alpha v_d$ is satisfied.

Proposition 7. 

In a scenario where fashion brands develop NFTs to generate higher profits, the manufacturer raises the production price, i.e., when ${\pi }_{FB}^D>{\pi }_{FB}^T$, then $w^D>w^T.$

When fashion brands profit from developing NFTs, manufacturers exhibit opportunistic behavior by raising the production price of products. The key reason behind this phenomenon is the decentralized decision-making between manufacturers and fashion brands, where each party aims to maximize its own profit. The development of NFTs by fashion brands triggers changes in market demand, prompting manufacturers to act opportunistically.

4.4. Demand Analysis of Customers

In this subsection, we show consumers’ attitudes towards the development of NFTs by fashion brands through a comparison of the quantity of products sold in scenarios T and D.

Proposition 8. 

Only when $c_d<\alpha v_d$, the fashion brands develop NFTs with more sales, i.e., $q^D>q^T.$

The quantity of product sales is an important indicator in the fashion industry. Based on the traditional fashion model, we observe three changes if fashion brands develop NFTs. First, fashion brands incur an additional digital cost for NFTs ($c_d$). Second, market consumers become segmented into two groups: fashion customers, who account for a proportion $\alpha$, and conventional customers, who account for a proportion $1-\alpha$. Finally, fashion customers perceive NFTs as having digital value ($v_d$), whereas conventional customers have no interest in NFTs. Consequently, we find that the sales quantity in Scenario D will exceed that in Scenario T only if the digital cost of NFTs satisfies condition $c_d<\alpha v_d.$

Proposition 9. 

The price reduction strategy is favored by consumers, i.e., $q_1^T=q_2^T$ and $q_1^D=q_2^D.$

Proposition 9 shows that the two-stage pricing strategy is effective in curbing the decline in sales due to product obsolescence. In the second period, consumers’ evaluation of fashion products generates a decline, a characteristic represented by the fashion decline factor, $\theta$. Naturally, consumers will reduce their purchases due to the decrease in the fashion value of the product. The results showed that with the price reduction strategy, the fashion brand did not experience a decrease in the quantity of sales in the second period. In other words, the price reduction strategy is effective.

Proposition 10. 

The role of the fashion customer in digital fashion.

The fashion customer is more attractive to the fashion brand. By comparing the quantity sold by the fashion brand, we find that if the market ratio of fashion customers and conventional customers is the same, then the fashion brand sells more products to fashion customers. As illustrated in Figure 6, when $\alpha ={\displaystyle \frac{1}{2}}$, we can easily obtain that $q_F^D>q_C^D$. This means that, with the same proportion, the fashion customer has a higher purchasing demand than the conventional customer.

Proposition 11. 

The quantity of products purchased by fashion customers vs. conventional customers in Scenario D is as follows:

• When ${\alpha }_1<\alpha \le 1$, we have $q_F^D>q_C^D$; otherwise $q_F^D<q_C^D.$
• When ${\alpha }_2<\alpha \le 1$, we have $q_{F\_1}^D>q_{C\_1}^D$; otherwise $q_{F\_1}^D<q_{C\_1}^D.$
• When ${\alpha }_3<\alpha \le 1$, we have $q_{F\_2}^D>q_{C\_2}^D$; otherwise $q_{F\_2}^D<q_{C\_2}^D.$
• Only when $\max \left\{{\alpha }_1,{\alpha }_2,{\alpha }_3\right\}<\alpha \le 1$, can we have $q_F^D>q_C^D$, $q_{F\_1}^D>q_{C\_1}^D$, and $q_{F\_2}^D>q_{C\_2}^D.$

Proposition 11 provides a detailed analysis of the comparison between fashion customers and conventional customers in terms of product purchase quantities. This serves as a further discussion of Proposition 10. The variables ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ represent the equilibrium purchase quantities of fashion and conventional customers during the entire sales period, the first-stage sales period, and the second-stage sales period, respectively, as shown in Figure 6. If the market share of fashion customers satisfies condition $\max \left\{{\alpha }_1,{\alpha }_2,{\alpha }_3\right\}<\alpha \le 1$, implementing a digital strategy in such a market offers significant advantages. In the real world, fashion brands often collaborate with celebrities to promote their products with the goal of expanding the proportion of target customers. Proposition 11, therefore, provides a visualized benchmark for the consumer share that fashion brands should aim for when developing NFTs.

4.5. Generalizability Analysis on the Results

In this section, we consider that the main conclusions of this paper are still in the exploratory stage of mathematical and theoretical modeling and have not yet been able to be supported by the validation of industry data. Therefore, we specially add a note about the generalizability of the results, in order to improve the academic rigor of this paper.

First, the digital fashion strategy drives up the prices of fashion products. This result applies to scenarios of new technology introduction or new product development, not limited to the specific case of fashion brands developing NFTs. For enterprises, developing new products or introducing new technologies is essentially an investment in additional production costs. In the “cost-price” transmission, rising costs will push up prices. Choi’s research [65] on the diamond industry also supports this conclusion and statement.

Second, profit comparison is a key criterion for fashion brands to decide whether to implement the digital fashion strategy. Facing the emergence of new products and technologies, decision—makers tend to cautiously weigh the positive (potential benefits) and negative (additional costs) factors brought by them, seeking a balance between the two (i.e., the key conditions influencing decisions) to determine whether to take action. This result is supported by Niu et al.’s research [66], whose topic covers the implementation conditions of AI live streaming for global brands.

Finally, consumer segmentation and their market proportion are key factors influencing fashion brands’ implementation of the digital fashion strategy. Referring to industry reports on consumers’ NFT purchase willingness differences, this paper segments two groups: fashion customers and conventional customers. This is common in consumer segmentation literature (e.g., literature [60] distinguishes green and non-green customers). Moreover, our research shows that the more fashion customers there are, the stronger the fashion brands’ willingness to adopt digital fashion. Shen et al.’s research [63] on identifying “novice customers” and “expert customers” of product origin also supports this finding.

In summary, the findings of this paper can be supported by conclusions from the existing literature in other research directions and have certain generalizability.

5. Discussion

In the previous section, we have compared the equilibrium outcomes of fashion brands in traditional and digital fashion models and obtained the motivational conditions under which fashion brands are willing to develop NFTs. However, we believe that there are still parts of the setup that can be further updated by combining real-world scenarios with the relevant literature. For this reason, we expand three new scenarios about fashion brands developing NFTs for diffuse communication and discussion among readers.

5.1. Scenario $\tilde{\mathrm{D}}$: The Fixed Production Contract

In the discussion in Section 4.3, we found that the manufacturer is likely to be snobbish, and he is likely to increase the production price when the fashion brand implements the digital fashion model, as described in Proposition 7. To avoid the manufacturer’s snobbish behavior, we refer to the research of Ku et al. [67] and Wang et al. [68]. Their settings provide us with new ideas. In their research, the production price is set as a fixed price contract, and this setting is feasible in reality. For this reason, we provide the fixed production contract scenario, i.e., $w^{\tilde{D}}=w^T={\displaystyle \frac{1}{2}}$.

We denote this case as Scenario $\tilde{\mathrm{D}}$, where the profit functions of the manufacturer and the fashion brand are as follows:

$$\begin{gathered} {\pi }_M^{\tilde{D}}=w^{\tilde{D}}{q}_{F\_t}^{\tilde{D}}+w^{\tilde{D}}{q}_{C\_t}^{\tilde{D}} \mathrm{and} \\ {\pi }_{FB}^{\tilde{D}}=\left[p_1^{\tilde{D}}\left(q_{F\_1}^{\tilde{D}}+q_{C\_1}^{\tilde{D}}\right)+p_2^{\tilde{D}}\left(q_{F\_2}^{\tilde{D}}+q_{C\_2}^{\tilde{D}}\right)\right]-\left[\left(w^{\tilde{D}}+c_d\right)\left(q_{F\_t}^{\tilde{D}}+q_{C\_t}^{\tilde{D}}\right)\right]-C. \end{gathered}$$

We obtain the equilibrium outcomes in Scenario $\tilde{\mathrm{D}}$ by backward induction, as shown in

Table 2. The equilibrium outcomes of Scenario $\tilde{\mathrm{D}}$.

Scenario $\tilde{\mathrm{D}}$
$w^{\tilde{D}}$	${\displaystyle \frac{1}{2}}$
$p_1^{\tilde{D}}$	${\displaystyle \frac{\left(2c_d+1\right)\theta +4\alpha v_d+2c_d+5}{2\left(\theta +3\right)}}$	$p_2^{\tilde{D}}$	${\displaystyle \frac{\left(1+\theta \right)\alpha v_d+2c_d+\theta +2}{\theta +3}}$
$q_1^{\tilde{D}}$	${\displaystyle \frac{2\left(\alpha v_d-c_d\right)+1}{2\left(\theta +3\right)}}$	$q_2^{\tilde{D}}$	${\displaystyle \frac{2\left(\alpha v_d-c_d\right)+1}{2\left(\theta +3\right)}}$
${\pi }_M^{\tilde{D}}$	${\displaystyle \frac{2\left(\alpha v_d-c_d\right)+1}{2\left(\theta +3\right)}}$	${\pi }_{FB}^{\tilde{D}}$	${\displaystyle \frac{{\left(2\alpha v_d-2c_d+1\right)}^2}{4\left(\theta +3\right)}}-C$

.

Lemma 4. 

The equilibrium outcome results in Scenario $\tilde{\mathrm{D}}$ vs. Scenario D are shown below:

• $q^{\tilde{D}}-q^D={\displaystyle \frac{\left(\alpha v_d-c_d\right)}{\theta +3}}>0.$
• ${\pi }_M^{\tilde{D}}-{\pi }_M^D=-{\displaystyle \frac{{\left(\alpha v_d-c_d\right)}^2}{2\left(\theta +3\right)}}<0$
• ${\pi }_{FB}^{\tilde{D}}-{\pi }_{FB}^D={\displaystyle \frac{3{\left(\alpha v_d-c_d\right)}^2-2\left(\alpha v_d-c_d\right)}{4\left(\theta +3\right)}}>0.$

The fixed production price contract enables fashion brands to develop NFTs at higher profits. First of all, with the fixed production price implemented by the manufacturer, the retail price of the fashion brand’s products is lower. The fixed production price avoids possible opportunistic behavior by the manufacturer, and the fashion brand is able to make retail price decisions at a fixed transaction price, which in a certain sense reduces the pricing costs of the fashion brand. Secondly, the sales quantity of fashion brand increases. As a result of lower retail prices, consumer utility increases, which in turn boosts market demand, and the fashion brand obtains higher profits as a result. However, it should be clear that the manufacturer’s profit still shows an increase compared to the traditional fashion model, i.e., ${\pi }_M^{\tilde{D}}>{\pi }_M^T$. Therefore, there is a motivation for manufacturer to implement the fixed production price model.

Proposition 12. 

The conditions for the fashion brand to implement the digital strategy in Scenario $\tilde{\mathrm{D}}$ are the same as those in Scenario D, but he prefers fixed production price contracts.

The fashion brand in Scenario $\tilde{\mathrm{D}}$ is more motivated to implement the digital strategy. First, from Proposition 3, we know that in the digital strategy, the fashion brand’s profit in Scenario $\tilde{\mathrm{D}}$ is greater than that in Scenario D, i.e., ${\pi }_{FB}^{\tilde{D}}>{\pi }_{FB}^D$. Second, comparing the fashion brand’s profit in Scenario $\tilde{\mathrm{D}}$ and Scenario T, we find that the motivation for the fashion brand to implement the digital strategy is ${\Phi }_{\tilde{D}}^{*}=\left\{\alpha v_d>c_d\right\}$, and ${\Phi }_{\tilde{D}}^{*}={\Phi }_D^{*}$. In other words, the condition for the fashion brand to implement the digital strategy in Scenario $\tilde{\mathrm{D}}$ is the same as that in Scenario D. Finally, we find that the fixed production price model is more favorable for the fashion brand to shift from traditional fashion to digital fashion.

5.2. Scenario P: The Personalized Retail Price

In this section, we discuss the feasibility of personalized pricing for fashion brands. In Scenario D, we set up the fashion brand to sell “physical + digital” fashion products at a common price to both fashion and conventional customers. We consider this bundling setup to be a scheme of price discrimination because conventional customers do not want the NFT but pay for it. In Richards et al.’s research, we found that customers who face price discrimination have the psychological utility of being “unfair”, which leads to the risk of reduced willingness to buy [69]. For a comprehensive understanding of the mediating mechanisms between price discrimination, psychological utility, and consumer willingness to buy, refer to the theoretical elaboration in the literature [70]. To avoid losing conventional customers, we refer to some of the literature on personalized pricing, such as Chen et al. [71] and Xu et al. [72], and update the pricing model of the fashion brand, i.e., Scenario P. This means that the fashion brand sells “physical + digital” fashion products to the fashion customer at price $p_{F\_t}^P$, and sells only “physical” fashion products to the conventional customer at price $p_{C\_t}^P$, and obviously, $p_{F\_t}^P>p_{C\_t}^P$. The profit function of the fashion brand in Scenario P is:

$${\pi }_{FB}^P=\left(p_{F\_1}^P{q}_{F\_1}^P+p_{C\_1}^P{q}_{C\_1}^P+p_{F\_2}^P{q}_{F\_2}^P+p_{C\_2}^P{q}_{C\_2}^P\right)-w^P\left(q_{F\_t}^P+q_{C\_t}^P\right)-c_d\left(q_{F\_1}^P+q_{F\_2}^P\right)-C$$

Similarly, we obtain the equilibrium outcomes in Scenario P via backward induction, as shown in

Table 3. The equilibrium outcomes of Scenario P.

Scenario P
$w^P$	${\displaystyle \frac{\alpha \left(v_d-c_d\right)+1}{2}}$
$p_{F\_1}^P$	${\displaystyle \frac{\left(\alpha \left(v_d-c_d\right)+2c_d+1\right)\left(1+\theta \right)+4v_d+4}{2\left(\theta +3\right)}}$	$p_{F\_2}^P$	${\displaystyle \frac{\alpha \left(v_d-c_d\right)+\left(1+\theta \right)v_d+2c_d+\theta +2}{\theta +3}}$
$p_{C\_1}^P$	${\displaystyle \frac{\alpha \left(1+\theta \right)\left(v_d-c_d\right)+\theta +5}{2\left(\theta +3\right)}}$	$p_{C\_2}^P$	${\displaystyle \frac{\alpha \left(v_d-c_d\right)+\theta +2}{\theta +3}}$
$q_1^P$	${\displaystyle \frac{\alpha \left(v_d-c_d\right)+1}{2\left(\theta +3\right)}}$	$q_2^P$	${\displaystyle \frac{\alpha \left(v_d-c_d\right)+1}{2\left(\theta +3\right)}}$
${\pi }_M^P$	${\displaystyle \frac{{\left(\alpha \left(v_d-c_d\right)+1\right)}^2}{2\left(\theta +3\right)}}$	${\pi }_{FB}^P$	${\displaystyle \frac{4\alpha \left(1-\alpha \right){\left(v_d-c_d\right)}^2+{\left(\alpha \left(v_d-c_d\right)+1\right)}^2}{4\left(\theta +3\right)}}-C$

.

Lemma 5. 

The equilibrium outcome results in Scenario F vs. Scenario D are shown below:

• $q^P-q^D={\displaystyle \frac{\left(1-\alpha \right)c_d}{\theta +3}}>0.$
• ${\pi }_M^P-{\pi }_M^D={\displaystyle \frac{c_d\left((2v_d-c_d)\alpha +2-c_d\right)(1-\alpha )}{2\left(\theta +3\right)}}>0.$
• ${\pi }_{FB}^P-{\pi }_{FB}^D={\displaystyle \frac{\left(1-\alpha \right)\left(3\alpha c_d^2-6\alpha c_d{v}_d+4\alpha v_d^2-c_d^2+2c_d\right)}{4\left(\theta +3\right)}}>0.$

The personalized pricing model leads to increased benefits for both the manufacturer and the fashion brand. First, the personalized pricing strategy increases consumer utility for conventional customers, which in turn leads to an increase in the quantity of “physical” products sold by the fashion brand, and therefore more orders for the manufacturer. In addition, the manufacturer increases her production fees, which in turn increases her profit. For a fashion brand, the personalized pricing strategy not only increases the quantity of products sold but also reduces the digital cost of NFTs. The fashion brand only needs to develop digital products for fashion customers instead of all customers, which further increases the profit of the fashion brand. Therefore, the personalized pricing strategy is a better option for fashion brands as well as manufacturers.

Proposition 13. 

The fashion brand is more likely to implement the digital strategy in Scenario P than in Scenario D, i.e., ${\Phi }_P^{*}>{\Phi }_D^{*}.$

Personalized pricing allows fashion brands to implement digital strategies under loose conditions. By comparing the profits of fashion brands in Scenario P and Scenario T, we find that the fashion brand will implement a digital strategy when ${\Phi }_P^{*}=\left\{v_d>c_d\right\}$ is satisfied. Furthermore, ${\Phi }_P^{*}=\left\{v_d>c_d\right\}>{\Phi }_D^{*}=\left\{\alpha v_d>c_d\right\}$ indicates that the personalized pricing model is more effective than the Scenario D model in achieving the goal of a digital strategy.

5.3. Scenario F: The Free NFT

In this section, we consider a new model in which NFTs are given to customers as gifts, defined as Scenario F. In the real world, the freebie strategy is a very well-established marketing scheme, i.e., free characters in video games, etc. Numerous studies have demonstrated the positive effects of this strategy. For example, studies by Lee et al. and B jointly discussed the effect of gift promotions on consumers’ willingness to return products, and their results both indicated that consumers were less willing to return products when merchants offered gifts [73]. In contrast, Roll et al. surveyed a sample of 150 respondents and showed that consumers preferred free gifts to price discounts [74]. Further, Liu et al. reveals that the essential reason for this phenomenon is that consumers feel a sense of luck when they are offered a free gift, which in turn increases their willingness to purchase the target product [75].

Therefore, we have updated the settings regarding the free NFT. In Scenario F, the fashion brand develops the digital product at a fixed cost and gives it to the consumer as a gift. The profit function of the fashion brand in Scenario F is updated to

$${\pi }_{FB}^F=\left(p_1^F{q}_1^F+p_2^F{q}_2^F\right)-w^F\left(q_1^F+q_2^F\right)-F_d-C,$$

where $F_d$ is the fixed cost paid by the fashion brand for the development of the digital product.

Table 4. The equilibrium outcomes of Scenario F.

Scenario F
$w^F$	${\displaystyle \frac{\alpha v_d+1}{2}}$
$p_1^F$	${\displaystyle \frac{\left(\alpha v_d+1\right)\left(\theta +5\right)}{2\left(\theta +3\right)}}$	$p_2^F$	${\displaystyle \frac{\left(\alpha v_d+1\right)\left(\theta +2\right)}{\theta +3}}$
$q_1^F$	${\displaystyle \frac{\alpha v_d+1}{2\left(\theta +3\right)}}$	$q_2^F$	${\displaystyle \frac{\alpha v_d+1}{2\left(\theta +3\right)}}$
${\pi }_M^F$	${\displaystyle \frac{{\left(\alpha v_d+1\right)}^2}{2\left(\theta +3\right)}}$	${\pi }_{FB}^F$	${\displaystyle \frac{{\left(\alpha v_d+1\right)}^2}{4\left(\theta +3\right)}}-F_d-C$

shows the equilibrium outcomes in Scenario F.

Lemma 6. 

The equilibrium outcome results in Scenario F vs. Scenario D are shown below:

• $q^F-q^D={\displaystyle \frac{c_d}{\theta +3}}>0.$
• ${\pi }_M^F-{\pi }_M^D={\displaystyle \frac{c_d\left(2\alpha v_d-c_d+2\right)}{2\left(\theta +3\right)}}>0.$
• Only if $F_d<{\displaystyle \frac{c_d\left(2\alpha v_d-c_d+2\right)}{4\left(\theta +3\right)}},$${\pi }_{FB}^F-{\pi }_{FB}^D>0$; otherwise, ${\pi }_{FB}^F-{\pi }_{FB}^D<0.$

The free digital product model is favored by consumers and manufacturers with the cost being borne by fashion brand alone. First of all, consumers preferred Scenario F to basic Scenario D. Hence, this conclusion is obtained from $q^F>q^D$. The free digital product makes the product less expensive for consumers to buy, and both fashion and conventional customers are happy about this. Second, the manufacturer can obtain more revenues in Scenario F. The manufacturer obtains a double increase in the production price and the quantity of orders, and gains more profits than in Scenario D. Finally, the fixed digital cost significantly affects the fashion brand’s profit. Only at $F_d<{\displaystyle \frac{c_d\left(2\alpha v_d-c_d+2\right)}{4\left(\theta +3\right)}}$, the fashion brand will choose strategy F. Otherwise, the fashion brand chooses Scenario D in order to obtain more profits.

Proposition 14. 

The conditions for fashion brands to implement a digital strategy in Scenario F are easier than those in Scenario D, i.e., ${\Phi }_F^{*}<{\Phi }_D^{*}$.

The fashion brand is more inclined to implement a digital strategy in Scenario F than in Scenario D. To compare the access conditions of scenarios F and D, we transformed them into the same dimension, i.e., the total digital cost of NFTs that the fashion brand has to pay. In Scenario F, the highest total digital cost that a fashion brand has to pay to ensure higher profits than the traditional fashion model is ${\widehat{C}}_d^F={\Phi }_F^{*}=F_d<{\displaystyle \frac{\alpha v_d\left(\alpha v_d+2\right)}{4\left(\theta +3\right)}}$. However, in Scenario D, the highest total cost that a fashion brand has to pay is ${\widehat{C}}_d^D={\Phi }_D^{*}{q}^D=c_d{q}^D<{\displaystyle \frac{\alpha v_d\left(\alpha v_d-c_d+1\right)}{\theta +3}}$. We find that ${\widehat{C}}_d^D-{\widehat{C}}_d^F={\displaystyle \frac{\alpha v_d\left(3\alpha v_d-4c_d+2\right)}{4\left(\theta +3\right)}}>0$, and therefore, the fashion brand is more inclined to use a free giveaway strategy for the sale of the digital product.

5.4. Discussion of the Models and Results

In this section, we comprehensively compare and discuss the differences in the results and model settings of the five models. In addition, in order to present the relevant conclusions with a more intuitive presentation for the reader’s understanding,

Table 5. The differences in model settings in scenarios T, D, $\tilde{\mathrm{D}}$, P, and F.

	Without NFT	With NFT
Scenarios	Scenario T	Scenario D	Scenario $\tilde{\mathbf{D}}$	Scenario P	Scenario F
Definition of models	The traditional fashion model	The digital fashion with NFT, a common pricing model	The digital fash-ion with NFT, a fixed production contract model	The digital fashion with NFT, a personalized pricing model	The digital fashion with NFT, a free NFT model
To NFT or not	×	√	√	√	√
Types of products	physical	Physical + digital	Physical + digital	Physical + digital	Physical + digital
Segmentation of consumer groups	Conventional	Conventional and fashion	Conventional and fashion	Conventional and fashion	Conventional and fashion
The digital cost of NFT	×	$c_d$, unit cost of production, affects product pricing	$c_d$, unit cost of production, affects product pricing	$c_d$, unit cost of production, affects product pricing	$F_d$, fixed production costs, small lot production, no impact on product pricing
The variables affecting the sales NFT of fashion brands	×	$c_d$, $\alpha$, and $v_d$	$c_d$, $\alpha$, and $v_d$	$c_d$, $\alpha$, and $v_d$	$F_d$, $\alpha$, and $v_d$
Manufacturer’s production price	$w^T$	$w^D$	Fixed production price: $w^{\tilde{D}}=w^T$	$w^P$	$w^F$
Fashion brands’ retail price	$p_t^T$	$p_t^D$	$p_t^{\tilde{D}}$	Personalized price: $p_{C\_t}^P$ and $p_{F\_t}^P$	$p_t^F=p$
Quantity of products sold	$q^T$	Only if ${\Phi }_D^{*}=\left\{c_d<\alpha v_d\right\}$, then $q^D>q^T$.	$q^{\tilde{D}}>q^D$	$q^P>q^D$	$q^F>q^D$
Profits of the manufacturer	${\pi }_M^T$	Only if ${\Phi }_D^{*}=\left\{c_d<\alpha v_d\right\}$, then ${\pi }_M^D>{\pi }_M^T$.	${\pi }_M^{\tilde{D}}<{\pi }_M^D$	${\pi }_M^P>{\pi }_M^D$	${\pi }_M^F>{\pi }_M^D$
Profits of the fashion brand	${\pi }_{FB}^T$	Only if ${\Phi }_D^{*}=\left\{c_d<\alpha v_d\right\}$, then ${\pi }_{FB}^D>{\pi }_{FB}^T$.	${\pi }_{FB}^{\tilde{D}}>{\pi }_{FB}^D$	${\pi }_{FB}^P>{\pi }_{FB}^D$	Only if $F_d<{\displaystyle \frac{c_d\left(2\alpha v_d-c_d+2\right)}{4\left(\theta +3\right)}}$, then ${\pi }_{FB}^F>{\pi }_{FB}^D$.

lists these differences.

Our work focuses on the strategic choices of NFTs, with the fashion supply chain consisting of manufacturers and fashion brands as the object of the study. The main conclusions of this paper, obtained by comparing the equilibrium outcomes of supply chain members under different scenarios, are as follows.

First, we constructed the traditional fashion model without NFT (Scenario T) and the digital fashion model with NFT (Scenario D). And by referring to the research of Li et al., Syailendra et al., and Mateusz [7,9,64], we identified the key parameters such as conventional customers, fashion customers, digital value of NFT, and the digital cost of NFT, which ensured the basic theoretical support for the model setting.

Further, by comparing the equilibrium outcomes in Scenario T and Scenario D, we obtain the key conditions for fashion brands to implement digital fashion strategies. That result is different from the conclusion of Alaei et al.’s study on pricing of digital content products [53], mainly because there is a difference between pricing of NFT products and pricing of digital content product subscriptions, where NFT is a sale of ownership, while digital content products are rented with the right to use them. In direct correlation with our results are the studies by Shen et al. [22] and Niu et al. [23] on the application of blockchain technology, and our results are supported by the results of their studies.

Finally, we discuss and update some of the settings in Scenario D to expand the application case for fashion brands to implement digital strategies. For example, we find that the manufacturer is snobbish, and she will overcharge the fashion brand for producing the physical product, while a fixed price contract can avoid this situation, i.e., Scenario $\tilde{\mathrm{D}}$. This extension is supported by Ku et al., where a fixed price contract is effective in their study [67], which is a further optimization of the model (Scenario D) that is the basis of this paper in terms of supply chain cooperation. In Scenario P, we further optimize the pricing strategy of fashion brands selling NFTs. We update the common pricing to personalized pricing in order to reduce the “unfair” effect of price discrimination on consumers, as mentioned in Richards et al.’s study [69]. This allows us to further rationalize the pricing strategy of NFTs. In Scenario F, we modified the NFT cost by updating the unit marginal cost to fixed cost. Meanwhile, in terms of marketing strategy inspired by the research of Liu et al. [75], we set up a free NFT strategy. This setting makes the findings of this paper more rigorous and enriches the discussion related to NFT marketing strategy.

6. Conclusions

6.1. Major Findings

As blockchain and digital twin technologies mature, the metaverse is emerging as an innovative frontier in the fashion industry. The development of NFTs and the implementation of digital strategies are becoming essential for fashion brands aiming to capture consumer attention. Notably, fashion giants and luxury brands are leading the charge in adopting these strategies, while many other fashion companies remain cautious observers. It is from this real-world contrast that we hope to further discuss the motivations of fashion companies to develop NFTs and provide useful insights into the evolution of the fashion industry.

Our findings highlight the critical relationship between the proportion of fashion customers, the digital value of NFTs, and the digital costs in influencing the adoption of digital fashion strategies. The motivation for fashion brands to develop NFTs arises only when the positive gains from the digital fashion model exceed the negative impacts. In such cases, creating digital versions of products not only mitigates the negative utility from declining fashion value but also presents a profitable opportunity. It is essential to consider the behavior of both manufacturers and consumers. Manufacturers may capitalize on the implementation of digital strategies by increasing production costs. On the other hand, consumers exhibit heterogeneity; fashion customers are willing to pay for digital products, whereas conventional customers may resist price increases. Consequently, appropriate contract or pricing strategies hold significant theoretical importance in the digital fashion model. Specifically, our fixed price contract, developed from a long-term partnership perspective, effectively mitigates manufacturers’ opportunistic behaviors. We also discussed personalized pricing and free giveaways. Practically, these strategies enhance the motivation for fashion brands to adopt digital strategies and result in more favorable evaluations from both consumers and manufacturers.

6.2. Managerial Insights

Our findings offer valuable managerial insights for companies observing digital fashion trends, particularly niche fashion brands interested in the metaverse. The key recommendations include:

We suggest that fashion brands should conduct detailed market research, first and foremost with consumers, which will enable them to more accurately predict consumer market share and consumer acceptance of digital products. Second, for metaverse platform companies, the display platform of digital products will directly affect consumers’ intuitive feelings toward digital products, and consumers will choose to cooperate with a good platform; this will be twice the result with half the effort.

We suggest that fashion brands should employ professional designers to improve the quality of their digital products as much as expected revenue allows. Of course, we also recommend fashion brands to increase the advertising of their products to lead fashion concepts and further increase the proportion of fashion customers.

Our research further suggests that the contract and pricing strategies in the digital fashion model are very important and that fashion brands need to develop appropriate sales strategies for digital fashion.

6.3. Limitations and Future Research Directions

It is important to note that although our work has led to some interesting conclusions, enriching the research on the implementation of NFT strategies in the fashion industry, there are still some limitations in the related modeling setup. First, this paper assumes that the designer’s cost expenditure is a fixed cost. This setting ignores the fact that, in reality, there are differences in the competence levels of designers. The variable design cost deserves further discussion in future research. Second, we assume that all players in the fashion supply chain are rational individuals who make decisions based on profit optimization. However, successful decision-makers are often irrational when facing new technologies or new product development, such as being overconfident. The role of factors like overconfidence in the implementation of digital strategies by fashion brands can be further explored in the future. Third, although we referred to some scholars’ studies and classified fashion customers and conventional customers based on consumers’ willingness to purchase NFTs, in light of recent studies, we can further discuss the impact of NFT scarcity and collectability value on conspicuous consumers to complement this paper. Finally, the difference between NFT products and traditional digital content products mainly lies in the distinction between ownership and usage rights. Future research could explore the price transmission mechanism of NFT secondary sales.