Abstract
The emergence of the new retail model of community group buying (CGB) has brought a significant impact on the traditional retail of community nanostores while community nanostores, as the leaders of the community, have the natural advantage of becoming the pick-up points of the CGB platform. Therefore, as the two core formats in the new community retail ecosystem, the CGB platform and community nanostore exhibit both competitive and complementary characteristics. Aiming at the community retail market composed of the CGB platform and the community nanostore, this study constructed a Hotelling game model to portray the competition and cooperation between these two channels and explored the impacts of different operational strategies on the equilibrium decisions and optimal profits of community retail market participants through comparative analysis. The research revealed that when retailers adopt the non-cooperation strategy, the community nanostore will occupy a larger market share, and the spillover effect between channels brought by the cooperation strategy is the main factor influencing retailers’ operation strategy. In addition, the type of pick-up point operated by the community nanostore will also affect the cooperation willingness of the CGB platform.
1. Introduction
Community new retail is a new retail model derived from the community environment that takes the community as the center and community residents as the service objects, and with the help of advanced technologies such as the internet, big data, and artificial intelligence, it realizes the deep integration of online and offline retail to meet the convenient, efficient, and diversified shopping needs of community residents. As one of the typical representatives of new retail in the community, community group buying (CGB) has been sought after by major capitals in recent years [1,2]. Different from the traditional retail’s immediate transaction model, CGB adopts a “pre-sale + pick-up” mechanism [3], that is, the CGB carries out pre-sale through the platform or the community leader’s release of product links and integrates the needs of the community for centralized procurement, and goods are subsequently delivered to designated pick-up points for user retrieval the following day [1]. By leveraging its unique operational framework and price competitiveness derived from economies of scale, CGB has gained rapid consumer adoption among community residents, thereby injecting new vitality into retail industry development and stimulating innovation in market penetration strategy [4]. According to data from the E-Commerce Research Center, China’s CGB market achieved a transaction volume of CNY 322.8 billion in 2023, representing a 53.71% year-on-year growth, with user penetration reaching 678 million individuals and an 8.3% annualized increase [5]. By 2025, the transaction value of China’s CGB market will reach CNY 1.2 trillion, and the user scale is expected to exceed 900 million [6]. With the intensifying competition in China’s domestic CGB market, international expansion has become a critical strategy for some CGB platforms. Consequently, CGB has achieved varying degrees of development globally. For example, Uruguay’s CGB market reached USD 30 million in 2022 and is projected to double to USD 60 million by 2025 [7]. Additionally, Verified Market Reports (VMR) indicates that the global CGB market was valued at USD 10.5 billion in 2022 and is expected to grow to USD 25.8 billion by 2030 [8]. These metrics underscore the sector’s substantial growth potential. However, intensified market competition, user acquisition slowdown, and tightening regulatory oversight have rendered purely price-centric competition unsustainable in achieving long-term viability. CGB platforms need to adjust their operational strategies in a timely manner to achieve new growth and profitability [2,9]. In this context, community nanostores, as natural pick-up points in communities, play a crucial role in CGB [9]. Generally speaking, community nanostores are defined as hyper-localized retail micro-enterprises embedded within residential ecosystems, predominantly operated by individuals, couples, or families [10]. Compared with chain convenience stores [11,12], community nanostores exhibit the following characteristics: (i) they are located within 5–10 min walking distance from residents, which is closer to them; (ii) the variety of products is relatively streamlined, focusing on the high-frequency daily needs of community residents, with lower investment risks; and (iii) the services provided are more personalized and diversified, and it is easier to establish a relationship of familiarity and trust with community residents.
Based on the above attributes, we can observe that CGB platforms and community nanostores, as two core formats of community new retail, exhibit both competitive and complementary characteristics. On the one hand, CGB platforms and community nanostores compete with each other in the community retail terminal market, and the invasion of the CGB has exerted certain competitive pressure on community nanostores. Specifically, CGB platforms reduce supply chain costs and product prices through centralized procurement, placing traditional nanostores at a price disadvantage. In addition, the innovative model of “pre-sale + self-pick-up” and the rich variety of goods in CGB platforms further improve the shopping experience of community residents, leading to some customers of community nanostores turning to CGB platforms. On the other hand, traditional nanostores still attract considerable patronage due to their superior geographical proximity and instant service capabilities. However, in the face of the diversified transformation of community residents’ consumption demands and the market impact brought by the community new retail industry, community nanostores urgently need to transform and upgrade their traditional models to cope with the increasingly fierce competitive pressure. Crucially, the inherent complementarity between CGB platforms and nanostores—manifested in operational models, product categories, and service methods—enables them to collectively fulfill residents’ diverse needs, creating strong incentives for collaboration. Through cooperation, CGB platforms can bring traffic resources to nanostores as self-pick-up points and increase the turnover of offline nanostores. At the same time, CGB platforms can also use the community network resources of nanostores to further reduce their last-mile delivery costs and enhance their stickiness with self-pick-up residents relying on offline scenarios. This dynamic interplay of competition and cooperation between CGB platforms and community nanostores not only affects the operation strategies of community retail market participants but also changes the competitive landscape of the community retail market. Because of these situations, this paper intends to explore the interactions between online and offline channels in the community retail market and investigates the following critical questions:
- What operation strategy can the CGB platform choose to maximize its profit? And what are the factors that influence its decision?
- What prerequisites must be met for the community nanostore to formulate a cooperative alliance with the CGB platform?
- How do strategic interactions between the CGB platform and the community nanostore influence the equilibrium decision and optimal profit for community retail market stakeholders?
To address the aforementioned questions, this paper considers a duopoly community retail market composed of a CGB platform and a community nanostore, and we develop game theoretic models for both non-cooperation and cooperation strategy scenarios between the platform and the nanostore. For the cooperation strategy, we further analyze how heterogeneous types of pick-up points operated by the community nanostore influence the platform’s operational decisions. By comparing equilibrium outcomes across scenarios, we identify the optimal operational strategy and its specific conditions for the CGB market.
The primary contributions of this paper are as follows. (i) Existing research on CGB has mainly focused on delivery route optimization [13,14], the analysis of CGB participation intention [12,15,16], and CGB operational strategies [2,9,17], and the literature highly relevant to this paper’s focus on operational strategies emphasizes the impact of CGB platforms on other members [2,18] and the preferred operational strategy of the nanostore [9,17]. In contrast, this paper fills a gap in existing research by examining channel interactions between retailers and optimal strategy selection for platforms from the perspective of the CGB platform. (ii) As a critical entry point for channel interactions, spillover effects [19,20,21] are a central consideration in this paper. However, prior studies have predominantly explored unidirectional spillover effects [19,22] between channels or analyzed the impact of introduced factors on unilateral [23,24] or bilateral [20,25] spillover effects. The novel inclusion of bidirectional spillover effects not only represents a key innovation of this study but also extends the theoretical boundaries of spillover effect research. (iii) Within the community retail context, we pioneer the incorporation of pick-up point heterogeneity into the analysis of CGB platforms’ partnership strategies, which represents a crucial yet underexplored dimension in CGB channel interaction research. (iv) Although the existing literature on channel interaction issues is relatively mature [26,27,28,29], this paper’s focus on strategic interactions among retailers in CGB enriches the research context of online–offline channel competition and cooperation.
The remaining parts of this paper are organized as follows: Section 2 reviews and summarizes the relevant literature; Section 3 elaborates on the research problem investigated in this study and proposes certain hypotheses; Section 4 focuses on model construction, solution, and comparative analysis; Section 5 validates the conclusions through numerical analysis; Section 6 provides corresponding management insights based on the research findings.
2. Literature Review
In this section, we will review the relevant literature. The literature related to this paper primarily involves two streams: community group buying (CGB) and competition and cooperation between online and offline channels.
2.1. Community Group Buying (CGB)
Currently, research on CGB has primarily focused on logistics route optimization [13,14,30,31], surveys on willingness to participate in CGB [12,15,16,32], and operational strategies for CGB [1,2,9,17,18]. Given the focus of this study, we focus on the review of literature related to CGB operational strategies.
The existing literature has examined the operational decisions of CGB participants from various perspectives. Sun et al. [9] constructed game models for the nanostore and the community e-tailer under competitive, cooperative, and coopetitive strategy within the context of CGB. By comparing the nanostore profits across these three operational strategies, they determined the preferred strategy for the nanostore. Their findings reveal that the nanostore generally preferred competitive and coopetitive strategies in most scenarios. Lan et al. [1] used the group leaders as the coordination tool, introduced the promotion effort and service level into the decision-making system, and designed the revenue sharing–commission coordination contract to realize the coordination of the CGB supply chain. Wang et al. [2] observed that the emergence of CGB raised fairness concerns among other participating merchants. They constructed and compared game scenarios under baseline conditions, fairness neutrality, and fairness-aware frameworks. The results indicated that after online retailers entered the market, profits from suppliers and wholesalers increased significantly while offline retailers’ profits exhibited multiple prospects. Shu et al. [17] examined whether nanostores should position themselves as leaders and their decision-making in competitive environments through an analysis of three scenarios. The study found that nanostores’ preferred strategies depend on their own and competitors’ investment cost parameters and that nanostores without cost advantages may benefit from acting as the first leaders. Zhang et al. [18] developed three distinct models of the “store strategy” to investigate its impact on the CGB platform and community leader. Comparative analysis revealed that after adopting the store strategy, the platform maintained unchanged online product pricing regardless of whether the strategy was implemented.
The above literature primarily focused on the impact of CGB platforms on other supply chain members [1,2,18] and the preferred operational strategies of nanostores in the context of CGB [9,17]. In contrast, we emphasize the dynamic strategic choices between the CGB platform and the nanostore under competitive community retail market conditions. Furthermore, we incorporate the influence of nanostore pick-up point types on platform operational strategy, which is a factor critical to understanding CGB dynamics but has not yet received sufficient attention or systematic investigation.
2.2. Competition and Cooperation Between Online and Offline Channels
In essence, the strategic interactions between the CGB platform and the community nanostore explored in this study can be categorized as competition and cooperation between online and offline channels [20,26,28,33,34]—a topic that has been extensively researched in the field of operations and management.
The development and widespread adoption of e-commerce have intensified competition between online and offline channels [19,25]. Many researchers have employed modeling approaches to characterize the competitive dynamics and conflicts between online channels and traditional channels, thereby exploring supply chain members’ channel strategy preferences and conditions [21,22,28,35,36]. With the further intensification of competition in the retail market, many manufacturers or suppliers choose to open new sales channels based on the original sales channels to realize profit growth, which has led to increasingly prevalent dual-channel competition issues [20,33,37,38,39]. In this case, many scholars have designed scientific and reasonable coordination [33,38,39] or cooperation [25,26,27,40] mechanisms to mitigate channel conflicts without harming the interests of supply chain members. Furthermore, the application of advanced technologies such as big data and artificial intelligence [29], as well as the diversification and upgrading of consumer demands [17], has drawn academic attention to emerging retail models such as omni-channel business models [29,41,42], CGB [2,9,18] and livestream e-commerce [20,43,44,45].
As evidenced by the existing literature, channel competition is prevalent in retail markets while the decision of supply chain members to collaborate [25,26,40] has emerged as a focal point of scholarly inquiry. The above literature provides a theoretical foundation and references for our research, whereas this paper, which is based on the strategic interactions within the community retail market, will further enrich the study of online–offline channel competition and cooperation across diverse industries and contexts.
Additionally, the existing literature indicates that with the change in the market competition environment and the deepening interdependencies among stakeholders, the spillover effect [19,20,21,22,25] has become an important entry point for many scholars to study the interaction of channels. Some scholars analyze the impact of the spillover effect generated by diverse factors (e.g., information technology spillover [23], innovation spillover [46], consumer awareness spillover [47], brand spillover [24,48]) on competitive markets and industry participants within supply chain systems of varying contexts. However, existing studies have predominantly focused on unidirectional spillover effects between channels [19,21,22] or examined the impact of an introduced factor on unilateral [23,24,47] or bilateral [20,24,25,46] spillover effects while rarely considering bidirectional spillover effects between channels. Specifically, the interactive relationship between online and offline channels may result in mutually influential spillover effects.
In the community retail market, the CGB platform and the community nanostore both compete and complement each other. By simultaneously considering the impact of their interaction on the operational decisions of both sides, this paper not only provides a more realistic depiction of the community retail market but also more comprehensively captures the dynamic linkages between retailers of different channels. Therefore, the novel incorporation of bidirectional spillover effects between channels in this research framework yields substantive contributions to both strategic management theory and practical retail operations optimization. Table 1 systematically summarizes the similarities and differences between this paper and relevant research studies.

Table 1.
Distinctions between this study and related literature.
3. Problem Description and Basic Assumptions
Within the context of CGB, we examine a community retail market comprising a CGB platform (denoted by ) and a community nanostore (denoted by ). Empirical observations reveal a significant product category overlap between CGB platforms and nanostores (e.g., standardized goods with high demand frequency such as daily necessities, snacks, and beverages) [12]. Accordingly, it is assumed that the products provided by the CGB platform and the community nanostore to community residents are homogeneous [42], that is, the basic utility of residents purchasing a unit of goods through the two channels is the same , and the value of is sufficiently large to ensure full market coverage [49]. However, residents are heterogeneous with respect to their preferences for two channels. In this case, the CGB platform and the community nanostore compete in the community retail market. In addition, due to divergent procurement channels, the CGB platform and the community nanostore source goods from their respective suppliers at distinct wholesale prices and . Without loss of generality, we normalize the suppliers’ marginal production cost for a unit product to 0 [50,51].
To further analyze their strategic interactions, we develop a duopoly competition model based on a stylized Hotelling framework, which can capture the spatial differentiation inherent in the community retail market [50]. Assuming that the CGB platform and the community nanostore are located at the two ends of the Hotelling line segment with a length of 1 (the CGB platform is located at 0 and the community nanostore is located at 1), the community residents are uniformly distributed along this line, and the position of the residents represents their ideal channel preference [52]. Therefore, the market shares of the CGB platform and the community nanostore are and , respectively. In addition to residents completely located at both ends, other consumers will incur certain unit transportation costs, [38,52].
Considering the differences in the operation models between the CGB platform and the community nanostore, our assumptions about their cost structures exhibit inherent asymmetry. Specifically, the community nanostore will generate fixed operating costs and variable costs , whose cost function is [51,53], to enhance the service level (e.g., employee training, adding convenience services, and meeting diverse customer needs) in the course of their actual operation. The fixed costs of the nanostore include expenses such as store rent, basic equipment, and staff salaries [9], which remain relatively constant regardless of the nanostore’s business performance. For the service variable costs, we assume that the community nanostore exhibits no economies of scale in variable service costs [34,54]; this means that the additional service costs (e.g., service time, consumables, or energy costs) required per unit increase in transactions grow strictly proportionally without reductions in per-unit service costs due to scale expansion. In contrast, the primary cost for the CGB platform lies in the variable expenses of last-mile delivery orders. By cooperating with pick-up points, the CGB platform can shift its last-mile delivery costs to partners, thereby reducing direct logistical burdens [3]. Therefore, we exclude the logistics and delivery costs of community group buying (CGB) platforms from our model.
As mentioned, to reduce delivery costs, the CGB platform typically chooses to partner with in-community pick-up points to fulfill last-mile order delivery while the community nanostore, as the community leader, often become the preferred choice for partnership by the CGB platform [9]. Consequently, the CGB platform and the community nanostore face two strategic choices: non-cooperation or cooperation. For convenience, we refer to the non-cooperation strategy as “N” and the cooperation strategy as “C”. As shown in Figure 1, the channel structure of community retail markets varies under different operational strategies. When the non-cooperation strategy is adopted, the CGB platform completes product delivery by assigning orders to other self-pick-up points. In this scenario, the online and offline channels of the community retail market operate independently and compete with each other, and the CGB platform and the community nanostore are only responsible for the residents of their respective channels. When the cooperation strategy is adopted, the CGB platform will hand over the ordered goods to the community nanostore, and the nanostore, as a pick-up point, needs to assist the CGB platform in completing the order of the last kilometer delivery. At this time, the community nanostore needs to be responsible for both online platform users and offline residents in the community.
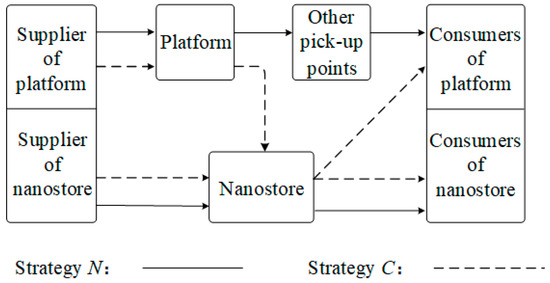
Figure 1.
Channel structure of community retail market under different strategies.
From this, it can be seen that the selection of the CGB operation strategy not only influences the competitive landscape between online and offline channels in the community retail market but also affects the scope of interaction between community nanostore and residents, and the resulting spillover effect between the channels is the main factor affecting the decision-making behavior of all stakeholders. Based on the above background, we construct the Hotelling model to characterize the competition and cooperation among different channels in the community retail market and explore the optimal strategy selection and conditions of the CGB platform and the community nanostore driven by the profit-maximizing objective. Additionally, we examine the impacts of different operation strategies on the equilibrium decisions and optimal profits of community retail market participants through comparative analysis.
Assuming that community residents and consumers only engage in one transaction of unit goods [55], the game sequence among community retail market participants is structured as follows. (1) The CGB platform and the community nanostore decide whether to cooperate. (2) Suppliers determine their respective wholesale prices based on the operational strategy selected by retailers. (3) The community nanostore determines its offline service level. (4) The CGB platform and the community nanostore set the commodity prices. (5) Community residents make the final channel purchase choice.
For the convenience of subsequent analysis and explanation, the relevant symbols and meanings used in the model in this article are summarized in Table 2.

Table 2.
Model notations.
4. Models and Analysis
In this section, we construct the game models of the non-cooperation strategy and the cooperation strategy involving the CGB platform and the community nanostore and further consider the impact of the type of community nanostore pick-up point on the willingness of both parties to cooperate for the cooperation scenario.
4.1. Model N
As shown in Figure 1, when a non-cooperation strategy is adopted, the CGB platform and the community nanostore compete with each other in the community retail terminal market, and there is no cross-interaction between online and offline channels. At this time, the pick-up points of the CGB platform are mostly located in scattered locations such as community owners’ homes (e.g., the homes of baby moms, retired seniors, etc.), community management offices with public attributes (e.g., security kiosks, property offices, community service centers, etc.), and stores with services (e.g., courier stations, restaurants, barbershops, etc.). In this scenario, the utility functions of community residents from purchasing commodities through the CGB platform and the community nanostore are, respectively, as follows:
Among them, represents the basic utility obtained by community residents from purchasing commodities; denotes the utility loss caused by residents’ payment of commodity prices; and represent the utility losses caused by the inconvenience costs incurred by residents in purchasing goods through online and offline channels, respectively; represents the increased utility of offline channel residents brought about by the improvement of service level of the community nanostore. From the rationale of the Hotelling model, let (1) = (2); we can get the location of the community residents’ indifferent point . Therefore, community residents will choose to purchase goods from the CGB platform when their location is within , and they will obtain higher utility by purchasing goods from the community nanostore when they are located in . At this point, the profit functions of the CGB platform, the community nanostore, and their respective suppliers are as follows:
According to the game sequence in H4, we can derive the equilibrium in Lemma 1 through backward induction, and the superscript “∗” denotes the equilibrium result throughout this paper.
Lemma 1.
In the non-cooperation strategy scenario, the indifference point of community residents is: . The equilibrium decisions and optimal profits of each member in the community retail market are as follows:
Proof of Lemma 1.
The proof process is shown in Appendix A. □
Proposition 1.

The equilibrium results under the non-cooperation strategy reveal the following:
(i) , , and ;
(ii) The impact of unit transportation cost on the equilibrium results are shown in Table 3, where .

Table 3.
The influences of under the strategy N.
Proof of Proposition 1.
The proof process is shown in Appendix A. □
Proposition 1 shows the following. (i) When the CGB platform and the community nanostore adopt the non-cooperation strategy, the community nanostore occupies a larger market share in the community retail market and is in a dominant position, and the supplier of the nanostore that observes this market pattern can take advantage of the opportunity to obtain greater benefits by setting higher wholesale prices. At this point, the community nanostore must set a higher pricing level than the CGB platform to ensure a certain profit margin due to its higher comprehensive costs (including purchasing costs, fixed operating costs of stores, and variable costs generated by providing services). In this case, the CGB platform, which is in a weaker position in the community retail market, can only attract community residents by lowering its product price. (ii) In the case of non-cooperation, the unit transportation cost of residents’ purchase of goods is the only factor affecting the equilibrium result. Higher unit transportation costs indicate stronger purchase intentions among residents, creating a seller-favorable market. Consequently, the CGB platform, the community nanostore, and their respective suppliers will increase their respective prices as the unit transportation cost rises to capture greater profits. In this scenario, the community nanostore can reduce the service level without significantly affecting residents’ purchase intentions. The reduction in service level makes residents inclined to online channels, so the market share of the CGB platform expands. However, the increase in purchase cost caused by the increase in unit transportation cost and the reduction in service level also lead to a decrease in the utility obtained by residents when purchasing goods.
4.2. Model C
In community retail practice, CGB platforms often face diverse types of pick-up point choices when allocating orders. To better visualize the attribute differences between community nanostores and other types of pick-up points within the community, as detailed in Table 4, we systematically compare several representative pick-up point types including nanostores through an analysis of their operational models. This comparison explicitly reveals the strategic motivations for collaboration between the CGB platform and the nanostore.

Table 4.
Comparison of different types of pick-up points.
When the cooperation strategy is adopted, the community nanostore will serve as a pick-up point, assisting the CGB platform in completing the delivery of online orders while maintaining its offline retail operations. From the perspective of the reality of the community retail market, there are two motivations for the cooperation between the CGB platform and the community nanostore: on the one hand, compared with the pick-up point locations mentioned in the non-cooperation strategy in Section 4.1, the community nanostore has incomparable superiority in terms of geographic location, infrastructure, operational efficiency, staff expertise, and community embeddedness, which significantly enhance service convenience for online platform users, thereby amplifying residents’ purchasing willingness on the group buying platform. On the other hand, the cooperation will drive the online traffic from the CGB platform to the offline community nanostore, and the interaction between the community nanostore and the pick-up consumers may stimulate the potential demand of the pick-up consumers, which will bring additional sales revenues to the nanostore. In summary, the cooperation strategy can bring a cross-channel spillover effect to the CGB platform and the community nanostore. However, while the cooperation strategy brings convenience and benefits to community retailers, it concurrently exposes the community nanostore to the risk of market share encroachment by the CGB platform, thereby indirectly undermining the offline channel profitability of the nanostore. Consequently, the CGB platform and the community nanostore need to comprehensively evaluate the impact of the spillover effect in their operational decision-making processes, which constitutes the primary analytical focus of this paper.
It should be noted that under the cooperation strategy, the nanostore becomes the pick-up point of the CGB platform, which will incur additional operating costs (such as storage and labor costs) while earning commission income from the platform. Considering that the commission set by the CGB platform is generally low at present [56], and the nanostore’s resources can provide the storage space and docking personnel required by the pick-up point, the commission revenue obtained by the community nanostore as a pick-up point can partially offset the additional operational costs. Consequently, this arrangement has a relatively minor impact on the overall profitability of the community nanostore. To further focus on analyzing the spillover effect on supply chain members in the community retail market, this section excludes discussions regarding the commission income and associated operational costs arising from the nanostore’s participation as a pick-up point under the cooperation strategy.
For the convenience of subsequent modeling, we refer to the practice in the relevant literature [34,57] and assume denotes the convenience utility derived by the CGB platform users under the cooperation strategy, where a higher denotes the greater convenience brought by cooperation. Since cooperation will bring a cross-selling effect [58,59] to the community nanostore, we assume that [60] denotes the spillover consumption generated for the community nanostore through cooperation, with a larger reflecting increased additional consumption generated by residents of the CGB platform when picking up goods at the community nanostore. Furthermore, considering the differences in the type of the community nanostore pick-up point in the real situation, this section establishes game models between the CGB platform and the basic community nanostore pick-up point or the service-oriented community nanostore pick-up point, aiming to investigate how the type of nanostore pick-up point influences the platform operational strategy selection and equilibrium decision-making among community retail market participants.
4.2.1. Model CA
When the CGB platform chooses to cooperate with the basic nanostore pick-up point, the community nanostore only serves as a place of commodity transit responsible for receiving CGB goods without engaging in value-added services such as product promotion, processing, or after-sales. For instance, convenience stores in first- and second-tier cities like Hangzhou (Zhejiang Province) and Chengdu (Sichuan Province), along with some local-brand community chain convenience stores (e.g., Jinhu Convenience Store in Taiyuan, Shanxi Province), choose to cooperate with CGB platforms when expanding their business and do not provide additional services for CGB consumers in addition to basic commodity receipt, storage, and notification pick-up business. It can be seen that the basic pick-up point mainly utilizes the physical attributes of the community nanostore, and achieves the purpose of attracting traffic to the convenience store by becoming a CGB pick-up point, increasing the arrival rate and frequency of community residents and thus stimulating the potential demand of online consumers for the offline nanostore. Therefore, when the CGB platform chooses to cooperate with the community nanostore and the nanostore is the based pick-up point (this case is denoted by the superscript “CA”), the utility obtained by the community residents through the CGB platform and the community nanostore are respectively expressed as follows:
Similarly, let (10) = (11), we can get the location of the community residents’ indifferent point . Thus, the profit functions of the CGB platform, the community nanostore, and their respective suppliers are as follows:
Here, indicates the utility change caused by the convenience brought by cooperation to platform residents; denotes the consumption spillover generated by the platform residents at the nanostore under the cooperation strategy. Consistent with Section 4.1, the application of backward induction yields the equilibrium outcomes presented in Lemma 2.
Lemma 2.
When the CGB platform chooses to cooperate with the basic community nanostore, the equilibrium results are as follows:
Proof of Lemma 2.
The proof process is shown in Appendix A. □
Proposition 2.

Under the strategy CA, the influences of and on members of the community retail market are shown in Table 5.

Table 5.
The influences of and under the strategy CA.
Proof of Proposition 2.
The proof process is shown in Appendix A. □
Proposition 2 reveals the following insights. (i) Under the CA strategy, the wholesale price of suppliers in the community retail market and the profit level of supplier of the CGB platform increase with an increase in the unit transportation cost of residents. This result is consistent with that in the case of the N strategy, which proves the robustness of the previous conclusion. However, when retailers switch from non-cooperation to cooperation, the improvement in convenience utility and consumption spillover brought about by cooperation have important impacts on residents’ channel preferences and the service level of the nanostore, thereby indirectly affecting the equilibrium decisions and profit levels of members in the community retail market. Therefore, in the case of cooperation, the unit transportation level has a non-monotonic impact on the service level of the nanostore, market share allocation, retailers’ pricing and profits, the profit of the nanostore supplier, and residents’ utility. It is necessary to comprehensively measure the effects of convenience utility and consumption spillover. (ii) The convenience provided by the cooperation strategy reduces the hassle costs for community residents when purchasing goods through the platform. Higher convenience strengthens residents’ willingness to buy via the CGB platform, prompting a shift of some consumers from offline to online channels. This intensifies competition in the community retail market, leading suppliers to lower wholesale prices to incentivize retailers to increase order quantities. Consequently, the demand redistribution in the community retail market diminishes profits for both the community nanostore and its supplier. (iii) The convenience derived from cooperation exerts a non-monotonic impact on the service level of the nanostore, the platform’s market share, and the profits of the platform and its supplier, which will be affected by the comprehensive effect of consumption spillover. When the consumption spillover brought by the cooperation for the community nanostore is small, the cooperation cannot bring more revenue to the nanostore, and at this time, with the increase in convenience, the nanostore can only choose to reduce the service level to ensure the profit margins to reduce the expenditure of operating costs, and the reduction in the service level makes the market demand further tilted to the platform. When the consumption spillover is large, the additional income of the nanostore increases. In this case, rising convenience drives the nanostore to enhance service levels to retain consumers and mitigate excessive market share erosion by the CGB platform.
Proposition 3.

Under the strategy CA, the influences of on members of the community retail market are shown in Table 6.

Table 6.
The influences of under the strategy CA.
Proof of Proposition 3.
The proof process is shown in Appendix A. □
Proposition 3 indicates the following. (i) The greater the consumption spillover brought by cooperation to the community nanostore is, the more additional consumption is generated by platform users during pick-up in the nanostore, and the profit of the nanostore increases. With the increase in consumption spillover, the nanostore is willing to reduce the service level to encourage more community residents to purchase goods on the platform so that the nanostore can obtain more consumption spillover benefits while reducing operating costs. However, the decrease in service level has led to a reduction in the market share of the community nanostore, and its supplier has to lower wholesale price to stimulate the nanostore to increase order quantity, resulting in a decrease in the overall profit level of the supplier. (ii) A decline in the offline market share corresponds to an expansion in the platform’s online market share. The surge in platform demand, coupled with reduced nanostore service level, incentivizes the platform to raise product prices to gain greater profitability and the platform supplier who observes this market change also increases its wholesale price to capture more revenue. (iii) The impact of consumption spillover on the community nanostore pricing is non-monotonic and contingent on the unit hassle cost of community residents. When the unit hassle cost of purchasing goods by community residents is high, it indicates a stronger willingness to purchase the goods. At this time, increasing pricing with the increase in consumption spillover will not significantly reduce the purchasing desire of community residents. When the unit hassle cost is low, consumers’ desire to purchase decreases. With the increase in consumption spillover, the nanostore needs to lower prices to retain consumers and maintain a certain market share.
Proposition 4.
Comparison of the equilibrium solutions between strategy CA and strategy N.
(i) , ;
(ii) and when ; when . Here, , , and .
Proof of Proposition 4.
The proof process is shown in Appendix A. □
Proposition 4 states the following. (i) For the community nanostore supplier, the wholesale price and profit level under the cooperation strategy are always lower than those under the non-cooperation strategy. This is because the cooperation between the CGB platform and the community nanostore breaks the community retail market pattern under non-cooperation, and intensifies market competition, and some offline residents shift to online channels, forcing the nanostore supplier to lower wholesale prices to stimulate order quantity, resulting in a decrease in its profit level. (ii) For the community nanostore, when the consumption spillover is higher than threshold , the platform users can bring a large consumption spillover income, and the nanostore will reduce the service level to increase the market demand of the platform. When the consumption spillover further increases to the threshold , the market share of the CGB platform reaches a certain level, at which time the platform supplier can increase the wholesale price to obtain more profits.
Proposition 5.
The conditions for cooperation between the CGB platform and the basic community nanostore are thus:
(1) For the CGB platform, when , there is ; then, the optimal strategy of the platform is non-cooperation (N); when , there is ; then, the optimal strategy of the platform is cooperation (CA).
(2) For the community nanostore, when , there is , then, the optimal strategy of the nanostore is non-cooperation (N); when , there is ; then, the optimal strategy of the nanostore is cooperation (CA).
(3) In summary, only when the consumption spillover meets can the CGB platform reach cooperation with the basic community nanostore.
Among them, , , and .
Proof of Proposition 5.
The proof process is shown in Appendix A. □
Proposition 5 reveals the following strategic interplay between the CGB platform and the basic community nanostore pick-up point under varying consumption spillover levels: (i) when , there is and , and the platform and the nanostore choose not to cooperate; (ii) when , there is but , and the platform still chooses not to cooperate while the nanostore wants to reach cooperation to obtain more revenue; (iii) when , there is and , and the cooperation strategy becomes the optimal choice for both parties. From this, it can be seen that when the community nanostore only provides basic services as a pick-up point, it has greater profit margins and a stronger willingness to cooperate than the CGB platform. Only when the consumption spillover generated by platform users in the nanostore is large enough can the CGB platform benefit from cooperation with the community nanostore.
4.2.2. Model CB
When the CGB platform collaborates with the service-oriented community nanostore pick-up point (denoted by the superscript “CB”), the nanostore not only serves offline residents but also provides identical services to platform pick-up users. For instance, many family-operated nanostores in third- and fourth-tier cities and nanostores with high viscosity in terms of community residents will give full play to their social attributes in the community and strengthen the interaction with online-platform pick-up consumers while serving offline residents. In addition to basic pick-up services, online residents will also be provided with additional services such as the temporary storage of items, free shopping bags, and after-sales of goods. In this scenario, the service level of the community nanostore not only directly affects the shopping experience of offline residents but also indirectly affects the platform users who carry out pick-up in the nanostore.
Based on the actual situation, the impact of the community nanostore’s services on platform users is mainly reflected in two aspects. (i) The nanostore improves the perceived utility and purchase willingness of the platform users by providing high-quality pick-up services (i.e., service spillover). Assuming that the degree of service spillover of the community nanostore services to the platform users is [61,62], a larger value indicates that the utility gained by pick-up users due to the nanostore services is greater. (ii) The positive interaction between the nanostore and pick-up users improves the favorable impression of the platform users on the nanostore and further promotes the pick-up users to generate more additional consumption in the nanostore (i.e., consumption spillover) [16]. Assuming that the influence factor of consumption spillover of the community nanostore services to platform pick-up users is , indicates the total consumption spillover generated by the unit pick-up user in the nanostore, and a larger value indicates that the total consumption spillover generated by the community nanostore services from the platform users in the nanostore is greater.
Under this framework, the utilities of community residents purchasing through the CGB platform and the community nanostore are respectively defined as follows:
And the profit functions of participants in the community retail market are as follows:
Among them, denotes the utility increase brought to platform residents by the nanostore pick-up point with service spillover under the cooperation strategy; represents the total consumption generated by platform residents in the nanostore under the presence of service spillover.
Lemma 3.
When the CGB platform chooses to cooperate with the service-oriented community nanostore, the equilibrium results are as follows:
Proof of Lemma 3.
The proof process is shown in Appendix A. □
Proposition 6.

Under the strategy CB, the influences of parameters and on the equilibrium results are shown in Table 7:

Table 7.
The influences of and under the strategy CB.
Proof of Proposition 6.
The proof process is shown in Appendix A. □
Proposition 6 shows the following. (i) Similar to strategy N and strategy CA, under the CB strategy, suppliers’ wholesale prices and the profit levels of the CGB platform supplier continue to increase with rising unit transportation costs, which further ensures the robustness of the prior research results on transportation costs. (ii) Furthermore, the trend of the impact of changes in consumption spillover on the relevant equilibrium results under the CB strategy is completely consistent with that under the CA strategy. This indicates that regardless of whether the community nanostore chooses to be a basic or service-oriented pick-up point, when the CGB platform and the community nanostore reach a cooperation intention, the consumption spillover brought by the cooperation has the same monotonicity in its impact on the equilibrium decisions and optimal profits of the supply chain members in the community retail market. The difference is that when the CGB platform cooperates with the service-oriented nanostore, the emergence of service spillover will affect the equilibrium decisions of the supply chain members, thereby indirectly changing the efficiency of the impact of consumption spillover on the relevant results. Collectively, Proposition 6 provides necessary evidence for the robustness of the equilibrium results under different strategies.
Proposition 7.

Under the strategy CB, the impacts of service spillover intensity () and total consumption spillover () on community retail market are shown in Table 8, where , , , and .

Table 8.
The influences of and under the strategy CB.
Proof of Proposition 7.
The proof process is shown in Appendix A. □
Proposition 7 suggests the following. (i) The existence of service spillover improves the overall service level of the community retail market, and the purchasing willingness of the community residents is also enhanced. Observing this market shift, suppliers raise wholesale prices to capture a share of the incremental revenue generated by retailers. Especially for the CGB platform, service spillover exerts a more pronounced utility enhancement on the platform users. Consequently, the platform’s supplier experiences profit growth proportional to the intensity of service spillover. (ii) The impact of service spillover on the service level of the nanostore, platform market share, and profitability and the profitability of the nanostore and its suppliers is moderated by the total consumption spillover generated through cooperation. When total consumption spillover exceeds the threshold , both the community nanostore and its supplier achieve profit growth as service spillover intensifies. When total consumption spillover further increases to the threshold , the market share and profitability of the CGB platform rise with stronger service spillover. When total consumption spillover surpasses the threshold , the nanostore will increase its service level with the enhancement of service spillover to prevent the offline market share from being overly eroded by the platform.
Proposition 8.
Comparison of strategy CB with strategy N and strategy CA.
(i) Strategy CB vs. strategy N: when , ; when , .
(ii) Strategy CB vs. strategy CA: ; when , .
Proof of Proposition 8.
The proof process is shown in Appendix A. □
Proposition 9.
The conditions for cooperation between the CGB platform and the service-oriented community nanostore.
(1) For the CGB platform, when , there is ; then, the optimal strategy of the platform is non-cooperation (N); when , there is ; then, the optimal strategy of the platform is cooperation (CB).
(2) For the community nanostore, when , there is ; then, the optimal strategy of the nanostore is non-cooperation (N); when , there is ; then, the optimal strategy of the nanostore is cooperation (CB).
(3) In summary, only when the consumption spillover satisfies can the CGB platform reach cooperation with the basic community nanostore.
Here, and
Proof of Proposition 9.
The proof process is shown in Appendix A. □
Proposition 9 reveals that when the CGB platform chooses to cooperate with the community nanostore, and the community nanostore is a service-oriented pick-up point, the platform and nanostore need to consider more parameter changes when making decisions, with consumption spillover magnitude remaining a pivotal determinant. As consumption spillover changes, the platform and the nanostore face the following strategic alternatives. (i) When , and , the optimal choice between the platform and the nanostore is non-cooperation. (ii) When , , and , the cooperation strategy can realize the win–win outcome of the platform and the nanostore. (iii) Except in the above two scenarios, the CGB platform and the community nanostore cannot reach a unified consensus.
5. Numerical Analysis
Building upon the preceding model analysis that has systematically examined the impact of spillover effects on community group purchasing operational strategies, we conduct numerical simulations using Mathematica 14.2 software to further investigate the influence of spillover-related parameters on equilibrium outcomes under different strategic scenarios. Through this numerical analysis, we gain intuitive insights into the extent and directional trends of how spillover effects shape equilibrium decisions among community retail market participants, redistribute market structures, and influence retailers’ collaborative incentives. These simulations not only validate the stability of the model results but also enhance the explanatory power of the findings for real-world community retail market dynamics. In this case, we assign , , and under fundamental constraints. Concurrently, we set the service spillover intensity to and to observe how variations in consumption spillover under distinct service spillover levels influence the trend of key equilibrium outcomes.
5.1. Comparison of Wholesale Prices for Suppliers in the Community Retail Market
Figure 2 and Figure 3 illustrate the trends in wholesale prices for suppliers in the community retail market. As can be seen from the figures, regardless of the level of service spillover, the wholesale price of the CGB platform supplier always increases with an increase in consumption spillover while the wholesale price of the community nanostore supplier always decreases with an increase in consumption spillover. Moreover, the wholesale prices of the platform supplier with service spillover are always higher than those without service spillover, which also supports the conclusions about supplier wholesale prices in Propositions 3 and 8. In addition, observing Figure 2, it is found that when the level of service spillover is high (), the wholesale price of the platform supplier in the case of cooperation with a service-oriented nanostore is always higher than that in the case of non-cooperation, while Figure 3 shows that when service spillover is at a low level (), the wholesale price of the service-oriented nanostore supplier is always lower than that of the non-cooperation nanostore supplier, which further verifies the conclusion of Proposition 8.
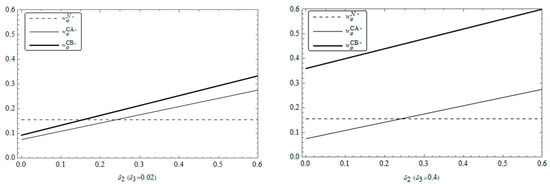
Figure 2.
Changes in the wholesale price of the CGB platform supplier with and .
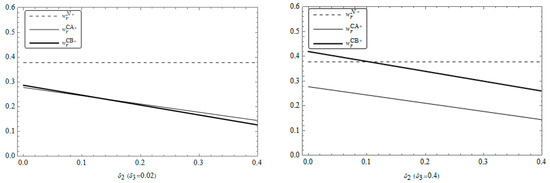
Figure 3.
Changes in the wholesale price of the community nanostore supplier with and .
5.2. Comparison of Service Level and Market Share of the Community Nanostore
Figure 4 and Figure 5 depict the influence of consumption spillover and service spillover on the service level and market share of the community nanostore. Key observations include the following. Regardless of the service spillover level, the service level of the nanostore consistently exhibits a negative correlation with consumption spillover while the online channel market share shows a positive correlation with consumption spillover. When the service spillover is at a low level (), the service level of the nanostore and the platform’s market share under different strategies vary dynamically with consumption spillover; when the service spillover is at a high level (), the service level of the service-oriented nanostore remains lower than that under the non-cooperation scenario. This demonstrates that the service level of the nanostore significantly influences community residents’ channel selection, thereby shaping the segmentation of the community retail market.
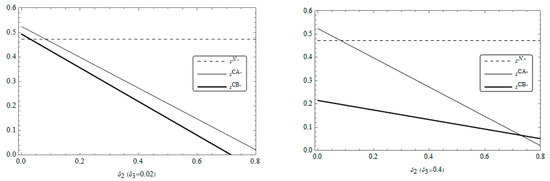
Figure 4.
Changes in service level of the community nanocore supplier with and .
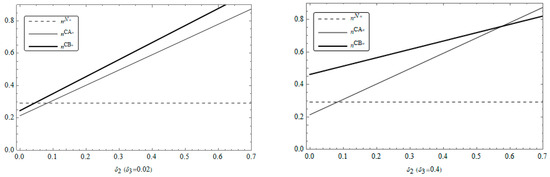
Figure 5.
Changes in market share of the online channel with and .
5.3. Comparison of Cooperation Range Between the CGB Platform and the Community Nanostore
Figure 6 shows that when the community nanostore is a service-oriented pick-up point, the cooperation range between the CGB platform and the community nanostore changes with the spillover of consumption and service. By comparison, it is found that service spillover has a more significant impact on the CGB platform. When the service spillover is at a low level (), the result is similar to that of the nanostore as a basic pick-up point, where the platform’s willingness to cooperate is lower than that of the nanostore, and the cooperation range between the platform and the nanostore is narrower (). When the service spillover is at a high level (), the cooperation range of the platform expands (), and the cooperation willingness is obviously increased. This indicates that the platform demonstrates a stronger preference for collaboration with the service-oriented nanostore pick-up point.
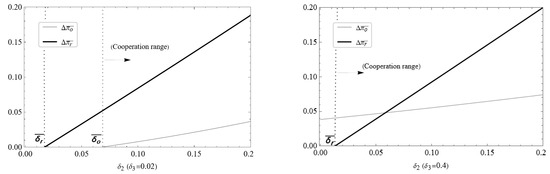
Figure 6.
Changes in cooperation range with and .
6. Conclusions
6.1. Main Conclusions
In this paper, we have considered a community retail market composed of a CGB platform and a community nanostore. We have constructed game-theoretic models for both non-cooperation and cooperation strategies and further analyzed the impacts of different types of nanostore pick-up points on the operational decisions of the CGB platform under the cooperation scenario. Through comparative analysis, the main conclusions are as follows:
(i) When they adopt the non-cooperation strategy, the community nanostore dominates a larger market share in the community retail market, and the commodity pricing of the nanostore and the wholesale price of its supplier are always higher than the commodity pricing of the platform and the wholesale price of its supplier.
(ii) The convenience provided by the cooperation strategy reduces the hassle costs for community residents purchasing through the platform, intensifying competition between online and offline channels in the retail market, and the profitability of the nanostore and its upstream supplier diminishes as convenience increases.
(iii) Under cooperation, the change in consumption spillover brought by the CGB platform pick-up users for the community nanostore has a moderating effect on the service level of the nanostore, and the change in the service level not only directly affects the channel preference of the community residents but also indirectly affects both the willingness of the platform to cooperate with the nanostore as well as the profit levels of the various members of the community retail market.
(iv) When the community nanostore is a basic pick-up point, the nanostore has a larger profit margin and a stronger willingness to cooperate than the platform, and the CGB platform can benefit from cooperation with the community nanostore only when the consumption spillover is large enough.
(v) When the CGB platform considers cooperating with the service-oriented community nanostore pick-up point, service spillover positively enhances both the profitability of the platform and its supplier as well as the consumption spillover from platform pick-up users. The higher the degree of service spillover is, the stronger the cooperation willingness of the CGB platform will be.
6.2. Theoretical Contributions
This paper has considered a duopoly community retail market composed of a CGB platform and a community nanostore. We have developed non-cooperation and cooperation strategy game models involving the platform and the nanostore with a focus on examining how spillover effects influence retailers’ operational decisions. For cooperation strategy, we have further analyzed how the pick-up point heterogeneity of the community nanostore impacts the platform’s operational decisions. Compared to the existing research, the theoretical contributions of this paper lie in the following aspects:
(i) The literature highly relevant to our research focus on operational strategies emphasizes the impact of CGB platforms on other members [2] and the preferred operational strategy of the nanostore [9]. In contrast, this paper has filled a gap in the existing research by examining channel interactions between retailers and optimal strategy selection for platforms from the perspective of the CGB platform.
(ii) Prior studies about spillover effects have predominantly explored unidirectional spillover effects [22] between channels or analyzed the impacts of introduced factors on unilateral [24] or bilateral [20] spillover effects, and the introduction of the bidirectional spillover effect is an important innovation of this paper.
(iii) We have pioneered the incorporation of pick-up point heterogeneity into the analysis of CGB platforms’ partnership strategies, which is a crucial yet underexplored dimension in CGB channel interaction research.
(iv) Our study focused on strategic interactions among retailers in CGB can enrich the research context of online–offline channel competition and cooperation.
6.3. Management Implications
Based on the above findings, we obtain the following managerial implications:
(i) Considering bidirectional spillover effects, community retailers should avoid unilateral focus on others’ impacts while strategically considering how their operational decisions reciprocally influence competitors or partners, which can trigger a chain reaction in the community retail market. Therefore, when faced with the choice between cooperation or non-cooperation strategy, the CGB platform should prioritize cooperation facilitation and service spillover parameters—these indicators reflect the extent to which the cooperation strategy influences community residents’ channel preferences, thereby affecting the platform’s market share and profits in the community retail market. For the community nanostore, it should focus on monitoring consumption spillover indicators, which directly relate to their spillover revenue and profit. Meanwhile, the nanostore should not overlook the impact of their service levels on community residents to prevent their market share from being excessively eroded by online channels.
(ii) When adopting a non-cooperation strategy, community nanostores can maintain market share through dense store networks and brand advantages by continuously optimizing supply chains, enhancing service levels, and rationally increasing product pricing to increase operating revenue. For instance, the local brand Red Flag Chain Nanostore in Chengdu, Sichuan Province closely relies on its community-centric convenience services and high-density offline stores to provide diverse products and services, effectively shielding its offline traffic from disruptions by CGB and e-commerce platforms.
(iii) The cooperation strategy brings convenience to platform pick-up residents while affecting the market share and profit space of the community nanostore, so the platform and nanostore can flexibly adjust the cooperation mode according to the changes in consumption spillover and find a balance between competition and cooperation. For example, platforms may negotiate with nanostores to designate high-frequency, low-margin goods (e.g., fresh produce, daily necessities) as pick-up categories, avoiding direct competition with nanostores’ core profit drivers (e.g., tobacco, alcohol, prepared foods). And nanostores can differentiate product assortments to convert platform traffic into in-store purchases, thereby amplifying spillover revenue.
(iv) CGB platforms can combine community environments to provide differentiated cooperation mechanisms for different nanostore pick-up point types. When CGB platforms choose to cooperate with basic nanostore pick-up points, platforms can leverage their traffic dominance to negotiate terms, potentially reducing commissions or even charging nanostores for access to platform users. When partnering with service-oriented pick-up-points, platforms can incentivize nanostores to offer premium services, strengthening service spillover and consumption spillover while enhancing resident loyalty to both parties.
6.4. Research Limitations
This paper has primarily provided insights into the dynamic competition and cooperation between CGB platforms and community nanostores with a focus on channel-level interactions (e.g., pricing, service differentiation, and operational strategy selection). However, it has not fully considered other factors that may influence the ecosystem of the community new retail market. Notably, two key limitations are as follows:
(i) Consumer behavior: The model assumes that residents’ channel choices are determined by their physical proximity within the community retail market. In reality, consumer preferences for channels can change significantly, driven by shifts in socioeconomic trends (e.g., post-pandemic demand for contactless services) or consumer preferences (e.g., some consumer groups prioritizing instant gratification or relying on social media for commercial interactions). These changes can reshape the community retail market landscape and influence operational strategies of supply chain members.
(ii) Technological innovation: While the model focuses on operational costs in assessing the profit structure of community nanostores, over the long term, technological advancements and applications (e.g., AI-powered unmanned stores, automated management systems, and smart inventory and data analytics systems) could substantially reduce operational costs for nanostores. This reduction may diminish their reliance on partnerships with CGB platforms, ultimately affecting their overall profitability and strategic choices.
Considering the impact of the above limitations on model construction and research results, we will discuss more realistic and complex community retail scenarios in future research to comprehensively analyze how different factors affect the operation of the community retail market.
Author Contributions
Conceptualization, J.Z. and Y.W. (Yong Wang); methodology, J.Z.; software, J.Z. and Y.C.; validation, J.Z., Y.W. (Yong Wang), Y.C., and Y.W.; formal analysis, J.Z.; investigation, Y.W. (Yue Wen); resources, Y.W. (Yong Wang); writing—original draft preparation, J.Z.; writing—review and editing, J.Z.; visualization, J.Z.; supervision, Y.C.; project administration, Y.W. (Yue Wen); funding acquisition, Y.W. (Yue Wen) and Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 71672015, and the Scientific and Technological Research Program of Chongqing Municipal Edu-cation Commission, grant number KJQN202400847.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors thank the editors and reviewers for their hard work.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Proof of Lemma 1.
Firstly, let (1) = (2); we can get the indifferent point of community residents . Substituting into (3) and (4), we have the profits of two retailers in the price competition stage as follows:
To verify the existence of the optimal solutions and , we take the second-order conditions (SOCs) that because . Then, let the first-order conditions (FOCs) ; we can derive the retailers’ optimal prices: and .
Then, substituting and into (8) yields the following:
To ensure the concavity, we need to satisfy the SOC that , that is, . Under this precondition, we can obtain the function of service level by the FOC in the service decision stage, that is, . By simplifying (5) and (6), we have and .
Similarly, the SOCs are given by . Thus, we can derive the optimal wholesale prices of suppliers by the FOCs , that is, , . To guarantee that the wholesale prices are positive, and should be satisfied, that is, and . In summary, we need . Bringing and backward, we obtain the results in Lemma 1. □
Proof of Proposition 1.
According to Lemma 1, it can be shown that , , and hold.
In addition,, , , , , , , , , and under the condition . Therefore, Proposition 1 is proven. □
Proof of Lemma 2.
The solution steps here are consistent with Lemma 1. Firstly, let (10) = (11); we can get the indifferent point of community residents under the CA strategy: . Substituting into (12) and (13), we have the following:
Since the SOCs hold because of and , let the FOCs ; we can derive the optimal solutions:
and .
Furthermore, by substituting and into (17), we can get the SOC . To ensure the existence of equilibrium solutions, the SOC should satisfy that , that is . Under this precondition, we can obtain that according to the FOC. By simplifying (14) and (15), we have the following functions for suppliers.
,
Their SOCs can be given as: . Thus, we derive the equilibrium wholesale prices of suppliers by letting as follows: and .
Similarly, we need and to ensure that the solution is positive. To sum up, the following technical conditions are required to ensure the existence of equilibrium solutions: , , and . Based on the above conditions, bringing and backward, we obtain the equilibrium results in Lemma 2. □
Proof of Proposition 2.
According to Lemma 2, the proof can be derived as follows:
and because of the conditions mentioned in the proof of Lemma 2. In addition, and when , that is, , , and . Proposition 2 is proven. □
Proof of Proposition 3.
Similarly, according to Lemma 2, we can have the following:
and hold because of the condition ;
, , and are valid according to the condition ; when .
And if , that is, . Proposition 3 is proven. □
Proof of Proposition 4.
Comparing the equilibrium results of Lemma 1 and Lemma 2, it can be derived that , and ;
when , that is, . And when . Since holds because of , thus, . Proposition 4 can be proven. □
Proof of Proposition 5.
Let , and from the previous equilibrium results, we can obtain that . Since , is an increasing function with respect to ; then, yields . According to the monotonicity of and the zero point theorem, when , there is , that is, .
Similarly, if , . Since , is also an increasing function with respect to . Let ; we can derive that . Therefore, when , , that is, . In addition, since , i.e., , only when the consumption spillover can both and be satisfied. Proposition 5 is proven. □
Proof of Lemma 3.
The solution steps here are consistent with Lemma 1. Firstly, let (18) = (A1); we can obtain the indifferent point . Substituting into (A2) and (A3), we have the following:
Since , let ; we can derive the following:
Furthermore, substituting and into (A7), we can get the SOC . In this case, we need , that is, , to ensure the existence of equilibrium solutions. Based on this precondition, we can obtain that by the FOC . By simplifying (A4) and (A5), functions for suppliers are as follows:
Their SOCs can be given as . Thus, we derive the equilibrium wholesale prices of suppliers as follows:
Similarly, and should be satisfied simultaneously to guarantee positive solutions. In summary, the following conditions are required to ensure the existence of equilibrium solutions: , , and . Finally, bringing and backward, we obtain the equilibrium results in Lemma 3. □
Proof of Proposition 6.
According to Lemma 3, we can have the following:
(i) , and
(ii), , , , , , , , and when . Proposition 6 is proven. □
Proof of Proposition 7.
According to Lemma 3, the proof can be derived as follows:
(i) , and .
Since , holds because of the conditions mentioned in the proof of Lemma 3.
(ii) , , and
Based on the constraints in the proof of Lemma 3 and simplifying the above results, we can derive that if ; and if ; and and if . Since , that is, , , that is, ; thus, . Proposition 7 is proven. □
Proof of Proposition 8.
By comparing the equilibrium solutions in Lemma 1, Lemma 2, and Lemma 3, we can obtain the following: if ; if ; and if . Proposition 8 is proven. □
Proof of Proposition 9.
The proof process is similar to that of Proposition 5. Let ; we can have that from the equilibrium results of Lemma 1 and Lemma 3.
Since , is an increasing function with respect to ; then, let ; we can derive that . Due to the monotonicity of and the zero point theorem, when , there is , that is, . Similarly, let ; it can be obtained that . Since , is also an increasing function with respect to . Let ; we can derive that
Therefore, when , there is , that is, .
In summary, only when the consumption spillover can both and be satisfied. Proposition 9 is proven. □
References
- Lan, C.; Yu, X. Revenue Sharing-Commission Coordination Contract for Community Group Buying Supply Chain Considering Promotion Effort. Alex. Eng. J. 2022, 61, 2739–2748. [Google Scholar] [CrossRef]
- Wang, Y.; Song, H. A Game Theoretic Strategic Model for Understanding the Online-Offline Competition and Fairness Concern Under Community Group Buying. J. Ind. Manag. Optim. 2023, 19, 1670–1696. [Google Scholar] [CrossRef]
- Li, C.; Shi, X. Optimisation of Multi-Level Logistics Network for Agricultural Products under Community Group Buying Model. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2276414. [Google Scholar] [CrossRef]
- Lu, S.; Ahn, J. The Impacts of Relational Benefits on the Behavior of Customers in Online Community-Based Group Buying. Total Qual. Manag. Bus. Excell. 2025, 36, 553–571. [Google Scholar] [CrossRef]
- China Fresh E-commerce & Community Group Purchase Market Data Report of 2023. Available online: https://www.100ec.cn/zt/2023sxsqscbg/ (accessed on 5 February 2025).
- 2025 Community Chain Industry Market Research and Analysis: Comprehensive Insights into Community Chain Development Trends. Available online: https://www.chinairn.com/news/20250328/142620881.shtml (accessed on 23 May 2025).
- The Development Trend, Growth, Scale and Share of the Group-Buying Market in Uruguay. Available online: https://www.zcqtz.com/news/2935294.html (accessed on 3 May 2025).
- Community Group Buying Market Size, Growth, Market Overview and Forecasts. Available online: https://www.verifiedmarketreports.com/zh/product/community-group-buying-market/ (accessed on 3 May 2025).
- Sun, S.; Zhang, B. Operation Strategies for Nanostore in Community Group Buying. Omega 2022, 110, 102636. [Google Scholar] [CrossRef]
- Ge, J.; Honhon, D.; Fransoo, J.C.; Zhao, L. Manufacturer Competition in the Nanostore Retail Channel. Eur. J. Oper. Res. 2020, 286, 360–374. [Google Scholar] [CrossRef]
- Liu, L.; Yan, Y.; Tian, X.; Jiang, Z. Impact of Text and Image Information on Community Group Buying Performance: Empirical Evidence from Convenience Chain Stores. Sustainability 2024, 16, 4344. [Google Scholar] [CrossRef]
- Tian, X.; Jiang, H.; Zhao, X. Product Assortment and Online Sales in Community Group-Buying Channel: Evidence from a Convenience Store Chain. J. Retail. Consum. Serv. 2024, 79, 103838. [Google Scholar] [CrossRef]
- Yu, B.; Shan, W.; Sheu, J.-B.; Diabat, A. Branch-and-Price for a Combined Order Selection and Distribution Problem in Online Community Group-Buying of Perishable Products. Transp. Res. B Methodol. 2022, 158, 341–373. [Google Scholar] [CrossRef]
- Liu, Z.; Niu, Y.; Guo, C.; Jia, S. A Vehicle Routing Optimization Model for Community Group Buying Considering Carbon Emissions and Total Distribution Costs. Energies 2023, 16, 931. [Google Scholar] [CrossRef]
- Hongsuchon, T.; Li, J. Accessing the Influence of Consumer Participation on Purchase Intention Toward Community Group Buying Platform. Front. Psychol. 2022, 13, 887959. [Google Scholar] [CrossRef] [PubMed]
- Guan, Z.; Shi, X.; Ying, H.; Xue, R.; Qiao, X. An Empirical Study on Traditional Offline Retailer’s Switching Intention towards Community-Based Group Buying Program: A Push-Pull-Mooring Model. Electron. Mark. 2024, 34, 18. [Google Scholar] [CrossRef]
- Shu, L.; Li, X.; Liang, X. Optimal Strategies for Nanostores under Competition in Community Group Buying. Kybernetes 2023, 53, 2723–2748. [Google Scholar] [CrossRef]
- Zhang, N.; Yu, L.; Liu, K.; Ye, Z.; Jia, M. “Store Strategy”: A New Omni-Channel Strategy in Community Group Buying. Manag. Decis. Econ. 2024, 46, 1358–1372. [Google Scholar] [CrossRef]
- Dong, S.; Qin, Z.; Yan, Y. Effects of Online-to-Offline Spillovers on Pricing and Quality Strategies of Competing Firms. Int. J. Prod. Econ. 2022, 244, 108376. [Google Scholar] [CrossRef]
- Yang, W.; Govindan, K.; Zhang, J. Spillover Effects of Live Streaming Selling in a Dual-Channel Supply Chain. Transp. Res. E Logist. Transp. Rev. 2023, 180, 103298. [Google Scholar] [CrossRef]
- Wang, K.; Lin, J.; Liu, G.; Liu, Q. Strategic Introduction of Logistics Retail and Finance under Competition and Channel Spillover. Transp. Res. E Logist. Transp. Rev. 2022, 165, 102863. [Google Scholar] [CrossRef]
- Zhen, X.; Xu, S.; Li, Y.; Shi, D. When and How Should a Retailer Use Third-Party Platform Channels? The Impact of Spillover Effects. Eur. J. Oper. Res. 2022, 301, 624–637. [Google Scholar] [CrossRef]
- Han, K.; Chang, Y.B.; Hahn, J. Information Technology Spillover and Productivity: The Role of Information Technology Intensity and Competition. J. Manag. Inf. Syst. 2011, 28, 115–146. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, F.; Zhou, Y. Brand Spillover as a Marketing Strategy. Manag. Sci. 2022, 68, 5348–5363. [Google Scholar] [CrossRef]
- Yan, R.; Pei, Z. The Strategic Value of Cooperative Advertising in the Dual-Channel Competition. Int. J. Electron. Commer. 2015, 19, 118–143. [Google Scholar] [CrossRef]
- Liu, W.; Liang, Y.; Tang, O.; Ma, X. Channel Competition and Collaboration in the Presence of Hybrid. Transp. Res. E Logist. Transp. Rev. 2022, 160, 102658. [Google Scholar] [CrossRef]
- Song, H.; Wang, R.; Tang, Y. Competition or Cooperation: Strategy Analysis for a Social Commerce Platform. Eur. J. Oper. Res. 2024, 318, 560–574. [Google Scholar] [CrossRef]
- Wang, R.; Nan, G.; Kou, G.; Li, M. Separation or Integration: The Game between Retailers with Online and Offline Channels. Eur. J. Oper. Res. 2023, 307, 1348–1359. [Google Scholar] [CrossRef]
- Yu, J.; Ren, Y.; Zhou, C. Strategic Interactions in Omnichannel Retailing: Analyzing Brand Competition and Optimal Strategy Selection. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 2557–2581. [Google Scholar] [CrossRef]
- Song, W.; Yuan, S.; Yang, Y.; He, C. A Study of Community Group Purchasing Vehicle Routing Problems Considering Service Time Windows. Sustainability 2022, 14, 6968. [Google Scholar] [CrossRef]
- Xu, S.; Ou, X.; Govindan, K.; Chen, M.; Yang, W. An Adaptive Genetic Hyper-Heuristic Algorithm for a Two-Echelon Vehicle Routing Problem with Dual-Customer Satisfaction in Community Group-Buying. Transp. Res. E Logist. Transp. Rev. 2025, 194, 103874. [Google Scholar] [CrossRef]
- Xu, X.; Hu, Z. Effect of Introducing Virtual Community and Community Group Buying on Customer’s Perceived Value and Loyalty Behavior: A Convenience Store-Based Perspective. Front. Psychol. 2022, 13, 989463. [Google Scholar] [CrossRef]
- David, A.; Adida, E. Competition and Coordination in a Two-Channel Supply Chain. Prod. Oper. Manag. 2015, 24, 1358–1370. [Google Scholar] [CrossRef]
- Lei, B.; Li, G.; Cheng, T.C.E. Friend or Foe? Examining Local Service Sharing between Offline Stores and e-Tailers. Omega 2024, 123, 102988. [Google Scholar] [CrossRef]
- Li, J.; Konus, U.; Langerak, F.; Weggeman, M.C.D.P. Customer Channel Migration and Firm Choice: The Effects of Cross-Channel Competition. Int. J. Electron. Commer. 2017, 21, 8–42. [Google Scholar] [CrossRef][Green Version]
- Tang, Y.; Sethi, S.P.; Wang, Y. Games of Supplier Encroachment Channel Selection and E-tailer’s Information Sharing. Prod. Oper. Manag. 2023, 32, 3650–3664. [Google Scholar] [CrossRef]
- Zhang, Y.; Hezarkhani, B. Competition in Dual-Channel Supply Chains: The Manufacturers’ Channel Selection. Eur. J. Oper. Res. 2021, 291, 244–262. [Google Scholar] [CrossRef]
- Sun, S.; Liu, T. Pricing and Sales-Effort Coordination Facing Free Riding Behaviors between a Brick-and-Mortar Retailer and a Platform Store Owned by the Manufacturer. Transp. Res. E Logist. Transp. Rev. 2023, 179, 103285. [Google Scholar] [CrossRef]
- Liu, C.; Dan, B.; Zhang, X.; Zhang, H. Composite Contracts for Dual-Channel Supply Chain Coordination with the Existence of Service Free Riding. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 789–808. [Google Scholar] [CrossRef]
- Li, Y.; Chu, M.; Bai, X. To Fight or Not? Product Introduction and Channel Selection in the Presence of a Platform’s Private Label. Transp. Res. E Logist. Transp. Rev. 2024, 181, 103373. [Google Scholar] [CrossRef]
- Kim, J.-C.; Chun, S.-H. Cannibalization and Competition Effects on a Manufacturer’s Retail Channel Strategies: Implications on an Omni-Channel Business Model. Decis. Support Syst. 2018, 109, 5–14. [Google Scholar] [CrossRef]
- Tang, P.; Chen, J.; Raghunathan, S. Physical Stores as Warehouses for Online Channels: Implications for Channel Choices Under Competition. Inf. Syst. Res. 2023, 34, 1554–1581. [Google Scholar] [CrossRef]
- Fan, T.; Wang, L.; Song, Y. Impact of Live Commerce Spillover Effect on Supply Chain Decisions. Ind. Manag. Data Syst. 2022, 122, 1109–1127. [Google Scholar] [CrossRef]
- Niu, B.; Yu, X.; Li, Q.; Wang, Y. Gains and Losses of Key Opinion Leaders’ Product Promotion in Livestream E-Commerce. Omega 2023, 117, 102846. [Google Scholar] [CrossRef]
- Liu, J. Quality-Differentiated Distribution Strategies between Live Streaming and Online Channels. J. Retail. Consum. Serv. 2025, 82, 104056. [Google Scholar] [CrossRef]
- Hu, B.; Mai, Y.; Pekeč, S. Managing Innovation Spillover in Outsourcing. Prod. Oper. Manag. 2020, 29, 2252–2267. [Google Scholar] [CrossRef]
- Song, W.; Chen, J.; Li, W. Spillover Effect of Consumer Awareness on Third Parties’ Selling Strategies and Retailers’ Platform Openness. Inf. Syst. Res. 2021, 32, 172–193. [Google Scholar] [CrossRef]
- Wu, H.; Li, G.; Zheng, H.; Zhang, X. Contingent Channel Strategies for Combating Brand Spillover in a Co-Opetitive Supply Chain. Transp. Res. E Logist. Transp. Rev. 2022, 164, 102830. [Google Scholar] [CrossRef]
- Chen, L. Analysis of Online Platforms’ Free Trial Strategies for Digital Content Subscription. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 2107–2124. [Google Scholar] [CrossRef]
- Huang, L. Channel Strategies for Competing Retailers: Whether and When to Introduce Live Stream? Eur. J. Oper. Res. 2024, 312, 413–426. [Google Scholar] [CrossRef]
- Wang, X.; Han, X.; Chen, Y. Optimal Manufacturer Strategy for Live-Stream Selling and Product Quality. Electron. Commer. Res. Appl. 2024, 64, 101372. [Google Scholar] [CrossRef]
- Xie, J.; Zhu, W.; Wei, L.; Liang, L. Platform Competition with Partial Multi-Homing: When Both Same-Side and Cross-Side Network Effects Exist. Int. J. Prod. Econ. 2021, 233, 108016. [Google Scholar] [CrossRef]
- Li, G.; Li, L.; Sun, J. Pricing and Service Effort Strategy in a Dual-Channel Supply Chain with Showrooming Effect. Transp. Res. E Logist. Transp. Rev. 2019, 126, 32–48. [Google Scholar] [CrossRef]
- Qin, X.; Liu, Z.; Tian, L. The Strategic Analysis of Logistics Service Sharing in an E-Commerce Platform. Omega 2020, 92, 102153. [Google Scholar] [CrossRef]
- Zhang, T.; Choi, T.-M.; Cheng, T.-C. Competitive Pricing and Product Strategies in the Presence of Consumers’ Social Comparisons. Eur. J. Oper. Res. 2024, 312, 573–586. [Google Scholar] [CrossRef]
- The Decline of Group Leaders: Plummeting Commissions and the Phase-Out of Leaders in Community Group Buying. Available online: https://news.qq.com/rain/a/20221017A08FUH00 (accessed on 7 February 2025).
- Gao, F.; Agrawal, V.V.; Cui, S. The Effect of Multichannel and Omnichannel Retailing on Physical Stores. Manag. Sci. 2022, 68, 809–826. [Google Scholar] [CrossRef]
- Nageswaran, L.; Cho, S.-H.; Scheller-Wolf, A. Consumer Return Policies in Omnichannel Operations. Manag. Sci. 2020, 66, 5558–5575. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Xia, Y.; Aneja, Y.P. Returns Operations in Omnichannel Retailing with Buy-Online-and-Return-to-Store. Omega 2023, 119, 102874. [Google Scholar] [CrossRef]
- Yan, S.; Archibald, T.W.; Han, X.; Bian, Y. Whether to Adopt “Buy Online and Return to Store” Strategy in a Competitive Market? Eur. J. Oper. Res. 2022, 301, 974–986. [Google Scholar] [CrossRef]
- Xia, J.; Niu, W. Adding Clicks to Bricks: An Analysis of Supplier Encroachment under Service Spillovers. Electron. Commer. Res. Appl. 2019, 37, 100876. [Google Scholar] [CrossRef]
- Xue, M.; Zhang, J.; Zhu, G. Quantity Decision Timing with Spillover Effect and Asymmetric Demand Information. Transp. Res. E Logist. Transp. Rev. 2020, 142, 102048. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).