New Practice of E-Commerce Platform: Evidence from Two Trade-In Programs
Abstract
:1. Introduction
- We consider VPN programs and compare the implementation effects of VPN and ON programs. We also analyze the impacts of the two different trade-in programs on the pricing decisions of brand owners and e-commerce platforms for two successive-generation products and discuss their preferences for both trade-in programs, then advise brand owners and e-commerce platforms on their choices.
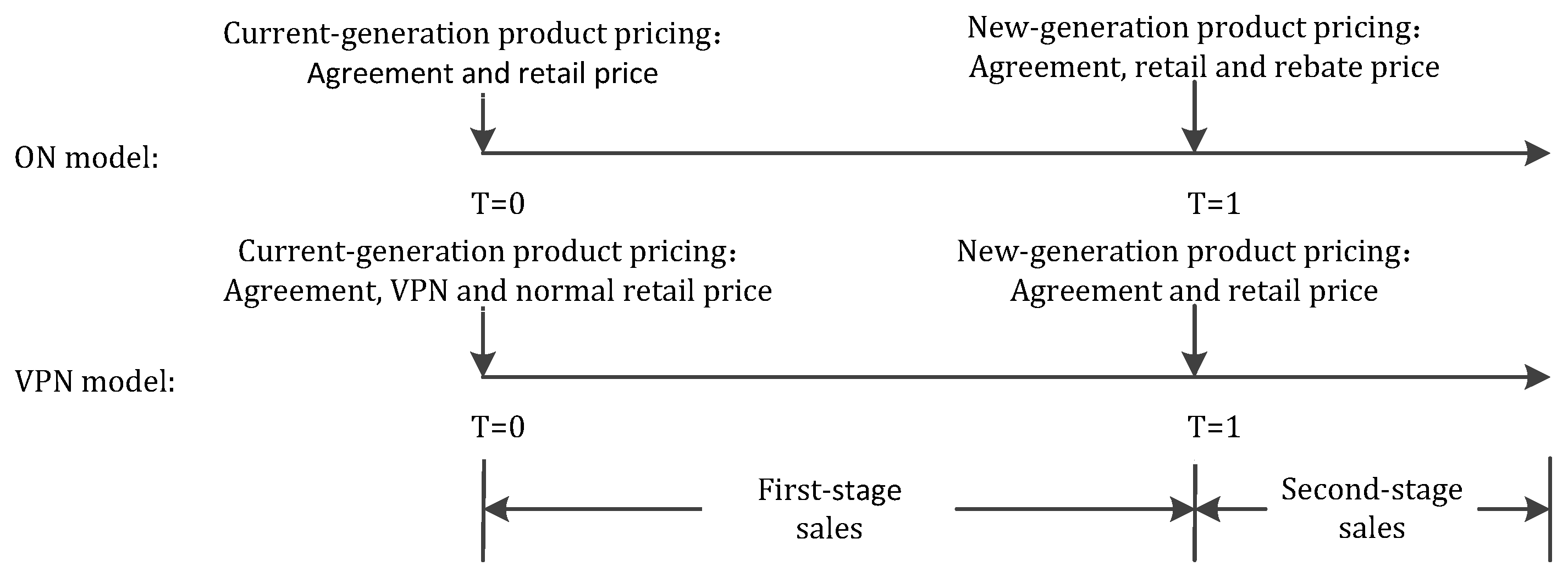
- Based on the two-stage sales of two successive-generation products, we develop Stackelberg game models between a brand owner and a B2C e-commerce platform with both trade-in programs and derive pricing strategies for two-generation products. Product rollover is often common in industry practice, and 3C products are more representative, namely, computer, communications, and consumer electronic products.
2. Literature Review
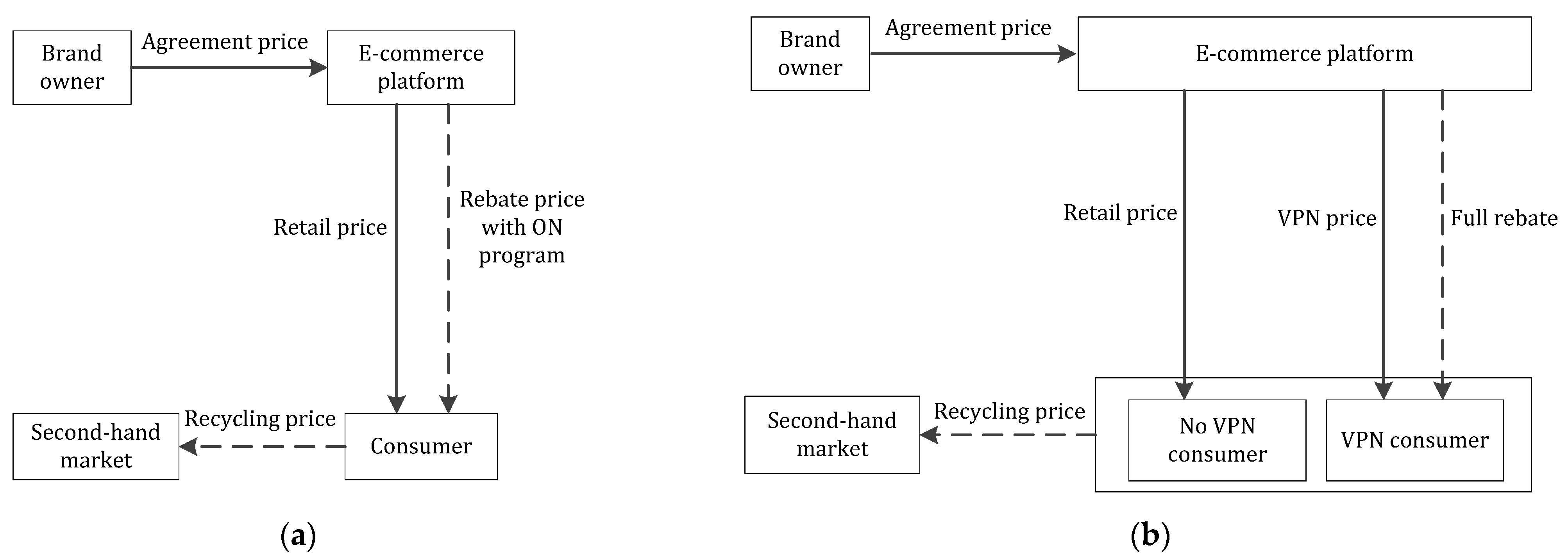
3. Problem Description
4. The Model
4.1. Product Demand
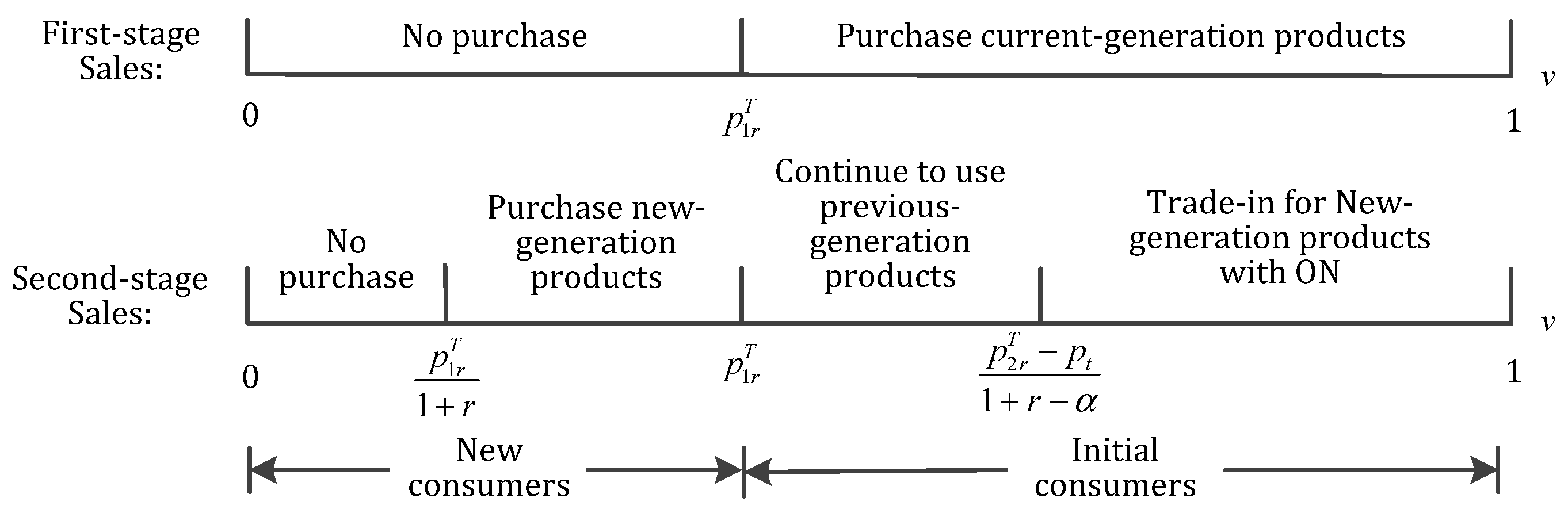
4.1.1. Demand with ON Program
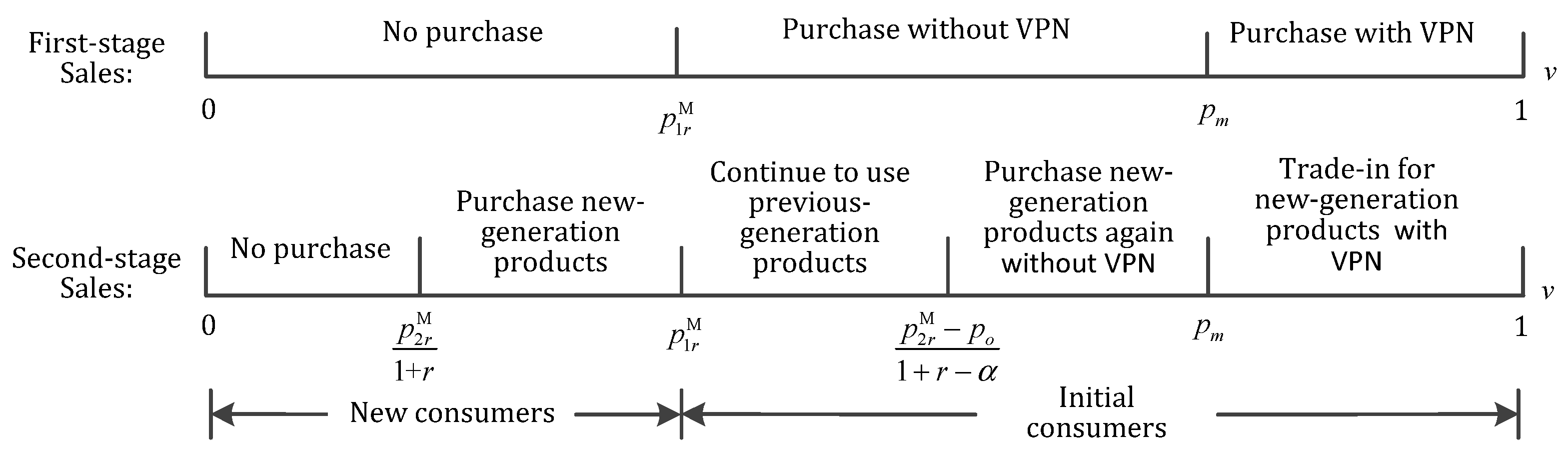
4.1.2. Demand with VPN Program
4.2. ON Model
4.3. VPN Model
5. Results and Analysis
5.1. Model Results
5.2. Analysis of Results
- (1)
- Both and are positively correlated with the net revenue brought by recycling of per unit of old products (s value).
- (2)
- Both and are negatively correlated with the remaining rate of customer perceived value of the previous-generation products at second-stage sales (α value).
- (3)
- If s > α, is positively correlated with discount factor (τ value) and improvement rate of consumer-perceived value of new-generation products (r value). If s < α, they are negatively correlated. If s = α, , which is only linearly correlated with the unit production cost of current-generation products ( value).
- (4)
- and τ are not correlated (this means that the discount factor will not affect the agreed price of new-generation products).
- (1)
- is positively correlated with the net revenue brought by recycling per unit of old products (s value), negatively correlated with discount factor (τ value), and does not correlate with α, β, or r values.
- (2)
- is negatively correlated with α value, positively correlated with β value, and has no correlation with s, τ values.
- (1)
- and are positively correlated with s value, while is not correlated with s value.
- (2)
- is negatively correlated with α value, is positively correlated with α value, while is not correlated with α value.
- (3)
- If , , , and are all positively correlated with τ value. If , , , and are all negatively correlated with τ value. If , , , and are all not correlated with τ value.
6. Numerical Simulation
6.1. Impacts of Main Parameters on {, , }
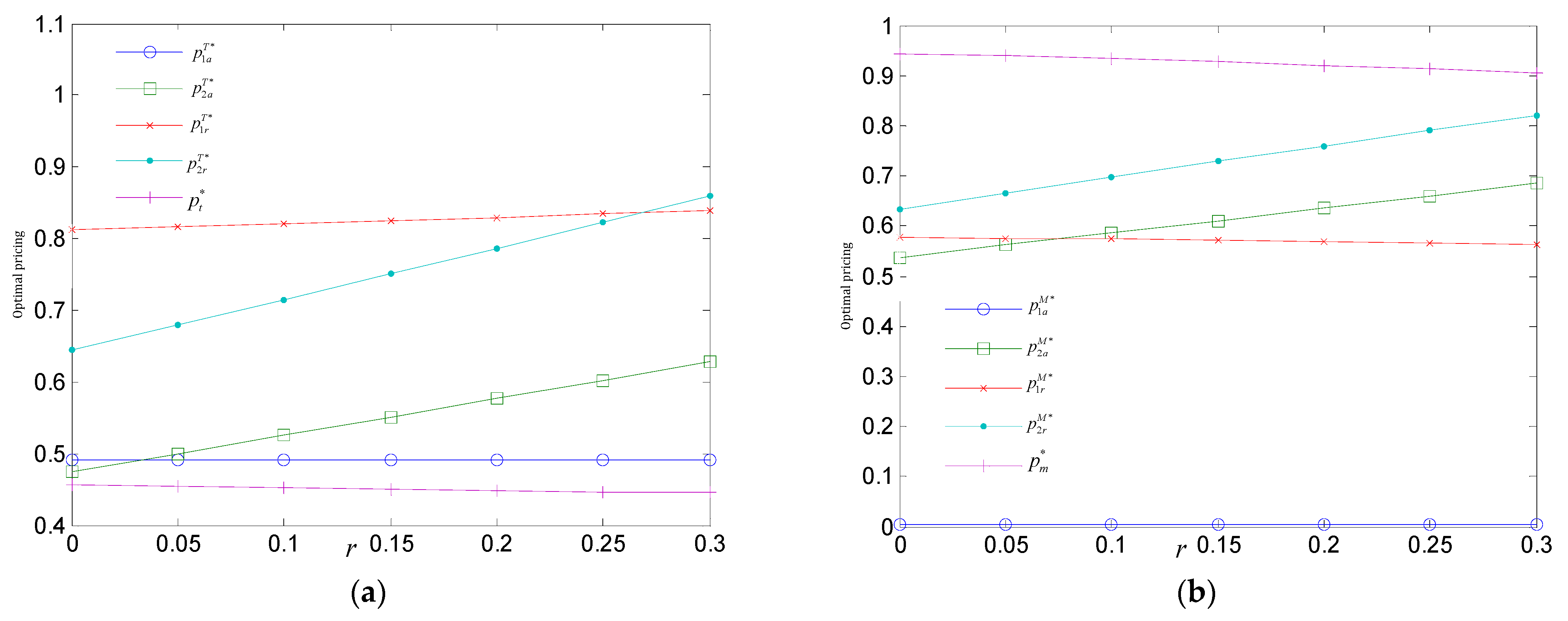
6.2. Impacts of Improvement Rate r on Pricing with Two Trade-In Programs
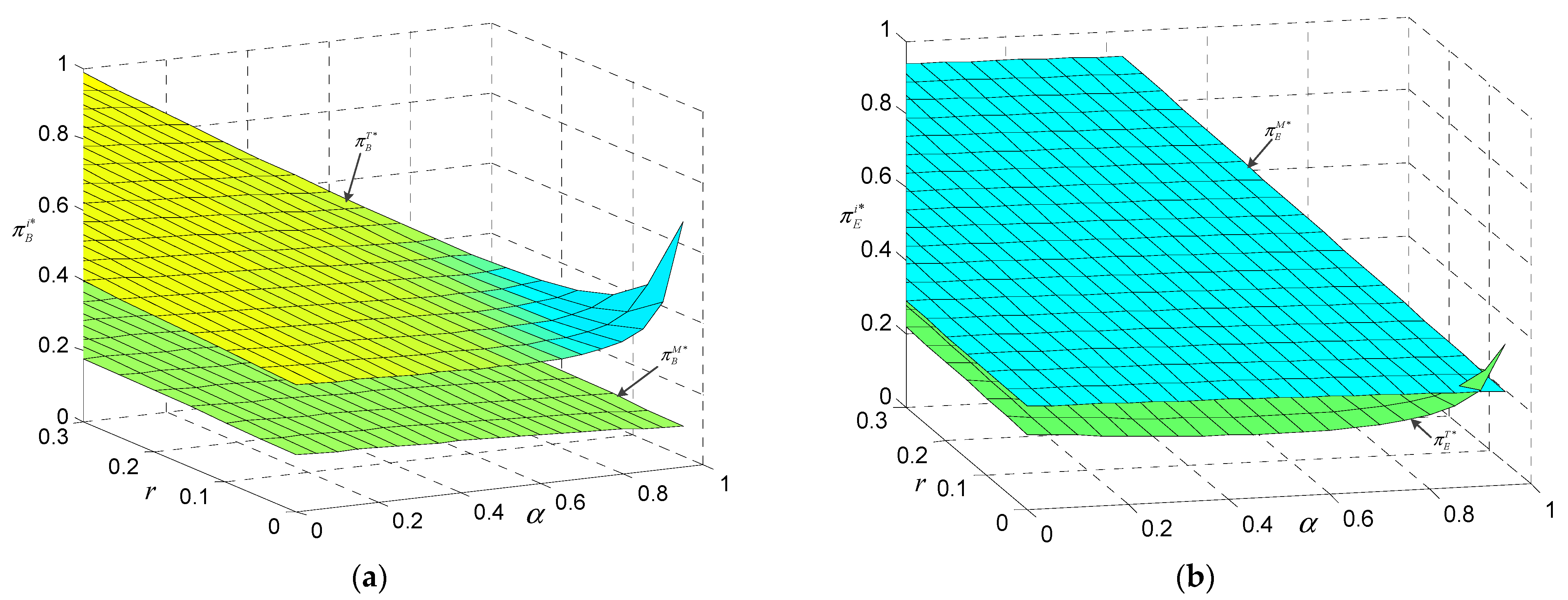
6.3. Preferences of Two Trade-In Programs
6.4. The Dominant Scenario of Two Trade-In Programs
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ON | Old-for-new |
| VPN | Value-preserved-for-new |
References
- Hahn, G.J. Industry 4.0: A supply chain innovation perspective. Int. J. Prod. Res. 2020, 58, 1425–1441. [Google Scholar] [CrossRef]
- Gayialis, S.P.; Kechagias, E.P.; Konstantakopoulos, G.D.; Papadopoulos, G.A.; Tatsiopoulos, I.P. An approach for creating a blockchain platform for labeling and tracing wines and spirits. In Proceedings of the IFIP International Conference on Advances in Production Management Systems, Nantes, France, 5–9 September 2021; pp. 81–89. [Google Scholar]
- Manavalan, E.; Jayakrishna, K. A review of Internet of Things (IoT) embedded sustainable supply chain for Industry 4.0 requirements. Comput. Ind. Eng. 2019, 127, 925–953. [Google Scholar] [CrossRef]
- Xiahou, X.; Harada, Y. B2C e-commerce customer churn prediction based on K-means and SVM. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 458–475. [Google Scholar] [CrossRef]
- Pournader, M.; Ghaderi, H.; Hassanzadegan, A.; Fahimnia, B. Artificial intelligence applications in supply chain management. Int. J. Prod. Econ. 2021, 241, 108250. [Google Scholar] [CrossRef]
- Chiang, W.Y.K.; Monahan, G.E. Managing inventories in a two-echelon dual-channel supply chain. Eur. J. Oper. Res. 2015, 162, 325–341. [Google Scholar] [CrossRef]
- Hu, H.; Wu, Q.; Han, S.; Zhang, Z. Coordination of dual-channel supply chain with perfect product considering sales effort. Adv. Prod. Eng. Manag. 2020, 15, 192–203. [Google Scholar] [CrossRef]
- Hu, Y.S.; Zeng, L.H.; Huang, Z.L.; Cheng, Q. Optimal channel decision of retailers in the dual-channel supply chain considering consumer preference for delivery lead time. Adv. Prod. Eng. Manag. 2020, 15, 453–466. [Google Scholar] [CrossRef]
- Gayialis, S.P.; Kechagias, E.P.; Konstantakopoulos, G.D. A city logistics system for freight transportation: Integrating information technology and operational research. Oper. Res. 2022. [Google Scholar] [CrossRef]
- Kechagias, E.P.; Miloulis, D.M.; Chatzistelios, G.; Gayialis, S.P.; Papadopoulos, G.A. Applying a system dynamics approach for the pharmaceutical industry: Simulation and optimization of the quality control process. WSEAS Trans. Environ. Dev. 2021, 17, 983–996. [Google Scholar] [CrossRef]
- Zimon, D.; Tyan, J.; Sroufe, R. Drivers of sustainable supply chain management: Practices to alignment with UN sustainable development goals. Int. J. Qual. Res. 2020, 14, 219–236. [Google Scholar] [CrossRef]
- Cao, K.Y.; Xu, X.Y.; Bian, Y.W.; Sun, Y.H. Optimal trade-in strategy of business-to-consumer platform with dual-format retailing model. Omega 2019, 82, 181–192. [Google Scholar] [CrossRef]
- Bai, J.; Hu, S.; Gui, L.; So, K.C.; Ma, Z.J. Optimal subsidy schemes and budget allocations for government-subsidized trade-in programs. Prod. Oper. Manag. 2021, 30, 2689–2706. [Google Scholar] [CrossRef]
- Zhao, S.; You, Z.; Zhu, Q. Quality choice for product recovery considering a trade-in program and third-party remanufacturing competition. Int. J. Prod. Econ. 2021, 240, 108239. [Google Scholar] [CrossRef]
- Glover, J.L.; Champion, D.; Daniels, K.J.; Dainty, A.J. An Institutional Theory perspective on sustainable practices across the dairy supply chain. Int. J. Prod. Econ. 2014, 152, 102–111. [Google Scholar] [CrossRef] [Green Version]
- Sawik, B. Selected multiple criteria supply chain optimization problems. Appl. Manag. Sci. 2020, 20, 31–58. [Google Scholar]
- Bernal, G.; Paola, J.; Mantilla, M.; Eduardo, C.; Castro, O.; Arturo, J. The sustainable supply chain: Concepts, optimization and simulation models, and trends. Ingeniería 2020, 25, 355–377. [Google Scholar] [CrossRef]
- Li, K.J.; Fong, D.K.H.; Xu, S.H. Managing trade-in programs based on product characteristics and customer heterogeneity in business-to-business markets. Manuf. Serv. Oper. Manag. 2011, 13, 108–123. [Google Scholar] [CrossRef]
- Zhang, F.Q.; Zhang, R.Y. Trade-in remanufacturing, customer purchasing behavior, and government policy. Manuf. Serv. Oper. Manag. 2018, 20, 601–616. [Google Scholar] [CrossRef]
- Xiao, Y.B.; Zhou, S.X. Trade-in for cash or for upgrade? Dynamic pricing with customer choice. Prod. Oper. Manag. 2020, 29, 856–881. [Google Scholar] [CrossRef]
- Li, Y.J.; Feng, L.P.; Govindan, K.; Xu, F.C. Effects of a secondary market on original equipment manufactures’ pricing, trade-in remanufacturing, and entry decisions. Eur. J. Oper. Res. 2019, 279, 751–766. [Google Scholar] [CrossRef]
- Zhu, X.X.; Wang, M.M.; Chen, G.F.; Chen, X.S. The effect of implementing trade-in strategy on duopoly competition. Eur. J. Oper. Res. 2016, 248, 856–868. [Google Scholar] [CrossRef]
- Liu, J.C.; Zhai, X.; Chen, L.H. Optimal pricing strategy under trade-in program in the presence of strategic consumers. Omega 2019, 84, 1–17. [Google Scholar] [CrossRef]
- Hu, S.; Ma, Z.J.; Sheu, J.B. Optimal prices and trade-in rebates for successive-generation products with strategic consumers and limited trade-in duration. Transp. Res. E Logist. Transp. Rev. 2019, 124, 92–107. [Google Scholar] [CrossRef]
- Lim, W.S.; Tang, C.S. Optimal product rollover strategies. Eur. J. Oper. Res. 2006, 174, 905–922. [Google Scholar] [CrossRef]
- Koca, E.; Souza, G.C.; Druehl, C.T. Managing product rollovers. Decis. Sci. 2010, 41, 403–423. [Google Scholar] [CrossRef]
- Liang, C.; Cakanyildirim, M.; Sethi, S.P. Can strategic customer behavior speed up product innovation? Prod. Oper. Manag. 2018, 27, 1516–1533. [Google Scholar] [CrossRef]
- Seref, M.M.H.; Carrillo, J.E.; Yenipazarli, A. Multi-generation pricing and timing decisions in new product development. Int. J. Prod. Res. 2016, 54, 1919–1937. [Google Scholar] [CrossRef]
- Liang, C.; Çakanyıldırım, M.; Sethi, S.P. Analysis of product rollover strategies in the presence of strategic customers. Manag. Sci. 2014, 60, 1033–1056. [Google Scholar] [CrossRef] [Green Version]
- Ye, T.F.; Wang, N.; Wang, N.X. Analysis on product rollover strategies: The innovation level perspective. Ind. Market. Manag. 2020, 88, 59–69. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Bhattacharya, S.; Krishnan, V.V. Pricing information goods: A strategic analysis of the selling and pay-per-use mechanisms. Market. Sci. 2015, 34, 218–234. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, S.M.; Randhawa, R.S.; Sun, H. Optimal per-use rentals and sales of durable products and their distinct roles in price discrimination. Prod. Oper. Manag. 2014, 23, 393–404. [Google Scholar] [CrossRef]
- Chiang, W.K.; Chhajed, D.; Hess, J.D. Direct marketing, indirect profits: A strategic analysis of dual-channel supply-chain design. Manag. Sci. 2003, 49, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Zhou, T.; Liu, B.H. The comparison between selling and leasing for new and remanufactured products with quality level in the electric vehicle industry. J. Ind. Manag. Optim. 2021, 17, 1505–1529. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.Y.; Zheng, H.Q.; Sun, X.Y.; Li, W. Customized investment decisions for new and remanufactured products supply chain based on 3D printing technology. Sustainability 2022, 14, 2502. [Google Scholar] [CrossRef]
- Wu, C.H. Product-design and pricing strategies with remanufacturing. Eur. J. Oper. Res. 2012, 222, 204–215. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, Z.; Wu, Q.; Han, S. Manufacturer’s customer satisfaction incentive plan for duopoly retailers with Cournot or collusion games. Adv. Prod. Eng. Manag. 2020, 15, 345–357. [Google Scholar] [CrossRef]
- Arifoğlu, K.; Tang, C.S. A two-sided incentive program for coordinating the influenza vaccine supply chain. Manuf. Serv. Oper. Manag. 2022, 24, 235–255. [Google Scholar] [CrossRef]
- Rajput, R.; Venkataraman, S.V. A violent market price contract for agribusiness supply chain. Ann. Oper. Res. 2021. [Google Scholar] [CrossRef]


| Notation | Description |
|---|---|
| The superscript | |
| , denotes the ON and VPN model, respectively. | |
| The brand owner’s decision variables | |
| The brand owner’s agreement price at first-stage sales (second-stage sales). | |
| The e-commerce platform’s decision variables | |
| The e-commerce platform’s retail price at first-stage sales (second-stage sales). | |
| The e-commerce platform’s VPN price at first-stage sales. | |
| The e-commerce platform’s rebate price at second-stage sales. | |
| Parameters | |
| The brand owner’s unit production cost of current-generation products (new-generation products). | |
| s | The e-commerce platform’s average net revenue per unit of old products recovered through ON and VPN programs. |
| v | . |
| r | . |
| value, the more durable the previous-generation products. | |
| Recycling the price of old products at the second-hand market during the second-stage sales. Note that, in the ON model, the rebate price set by the e-commerce platform is significantly higher than the recycling price, otherwise the conditions for implementing the ON program are not available. Let po be given exogenously. | |
| . | |
| . | |
| Functions | |
| The demand for current-generation products at first-stage sales. | |
| The demand of initial consumers to trade-in for new-generation products with an ON program at second-stage sales. | |
| The demand of new consumers to purchase new-generation products at second-stage sales. | |
| Demand for current-generation products with (without) a VPN program at first-stage sales. | |
| The demand of the initial consumers who had participated in a VPN program to trade-in for new-generation products at second-stage sales. | |
| The demand of the initial consumers who did not participate in a VPN program to purchasing new-generation products again at second-stage sales. | |
| The brand owner’s profit. | |
| The e-commerce platform’s profit. | |
| . |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Lou, T.; Li, J.; Zuo, W.; Chen, X.; Ma, L. New Practice of E-Commerce Platform: Evidence from Two Trade-In Programs. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 875-892. https://doi.org/10.3390/jtaer17030045
Hu Q, Lou T, Li J, Zuo W, Chen X, Ma L. New Practice of E-Commerce Platform: Evidence from Two Trade-In Programs. Journal of Theoretical and Applied Electronic Commerce Research. 2022; 17(3):875-892. https://doi.org/10.3390/jtaer17030045
Chicago/Turabian StyleHu, Qiang, Tingyuan Lou, Jicai Li, Wenjin Zuo, Xihui Chen, and Lindong Ma. 2022. "New Practice of E-Commerce Platform: Evidence from Two Trade-In Programs" Journal of Theoretical and Applied Electronic Commerce Research 17, no. 3: 875-892. https://doi.org/10.3390/jtaer17030045
APA StyleHu, Q., Lou, T., Li, J., Zuo, W., Chen, X., & Ma, L. (2022). New Practice of E-Commerce Platform: Evidence from Two Trade-In Programs. Journal of Theoretical and Applied Electronic Commerce Research, 17(3), 875-892. https://doi.org/10.3390/jtaer17030045







