Bundling Strategies for Ride-Hailing Platforms Based on Price and Service Level

Abstract

The increasing popularity of ride-hailing applications has given rise to a new channel in which ride-hailing platforms are bundled into aggregation platforms to earn additional orders by charging commissions and slotting fees. Such bundled channels, unlike traditional reseller electronic ones, may flutter prices, service levels, market demands, and then further affect their profits. These divergent attitudes raise an interesting and key question about whether and under what conditions bundled channels should be introduced to ride-hailing platforms. In this paper, we provide an analytical framework for ride-hailing and aggregation platforms in unbundled and bundled scenarios, respectively. We build a Stackelberg game model in which ride-hailing and aggregation platforms as leaders obtain prices by constructing Nash equilibria, while drivers as followers determine service levels given to two platforms. Drivers’ best responses in terms of service levels for two platforms, as well as platforms’ optimal pricing strategies and profits are achieved. To capture access conditions of the ride-hailing platform and the profit contention between two platforms, we further conduct sensitivity analysis on cost coefficients of service levels, price and cross-price substitutions, service level and cross-service level substitutions, revenue-sharing ratio, cost, as well as commission and slotting fee. Based on numerical examples and analysis of the results, some interesting managerial insights about bundling strategies are gained for ride-hailing platforms.

1. Introduction

Amid a steady rise of the bundling mode on the ride-hailing market recently, the shared mobility ecosphere is expected to be reinvented. Ride-hailing, including carpooling, slugging, the Dial-a-ride, and taxi-sharing, has become a rather popular transportation model over the last decade. It directly integrates advanced information technologies and mobility resources to meet regional traveling needs in a timely and distributed fashion. Ride-hailing platforms are moving on to actively seek cooperation with aggregation platforms for flows. Through aggregating the existing ride-hailing services, rather than operating new platforms, aggregation platforms avert the head-on competition with those ride-hailing platforms and also reduce costs significantly as it now does not need to invest everlasting capital to attract users. Using these bundled services in aggregation platforms, users no longer need to download, install or register multiple ride-hailing applications, instead of helping them call faster and shorten the waiting time. The aggregation platform provides riders with the possibility of shopping around for the best deal. Ride-hailing platforms bundling them on the aggregation platform are becoming a trend and deserve to be widely studied.

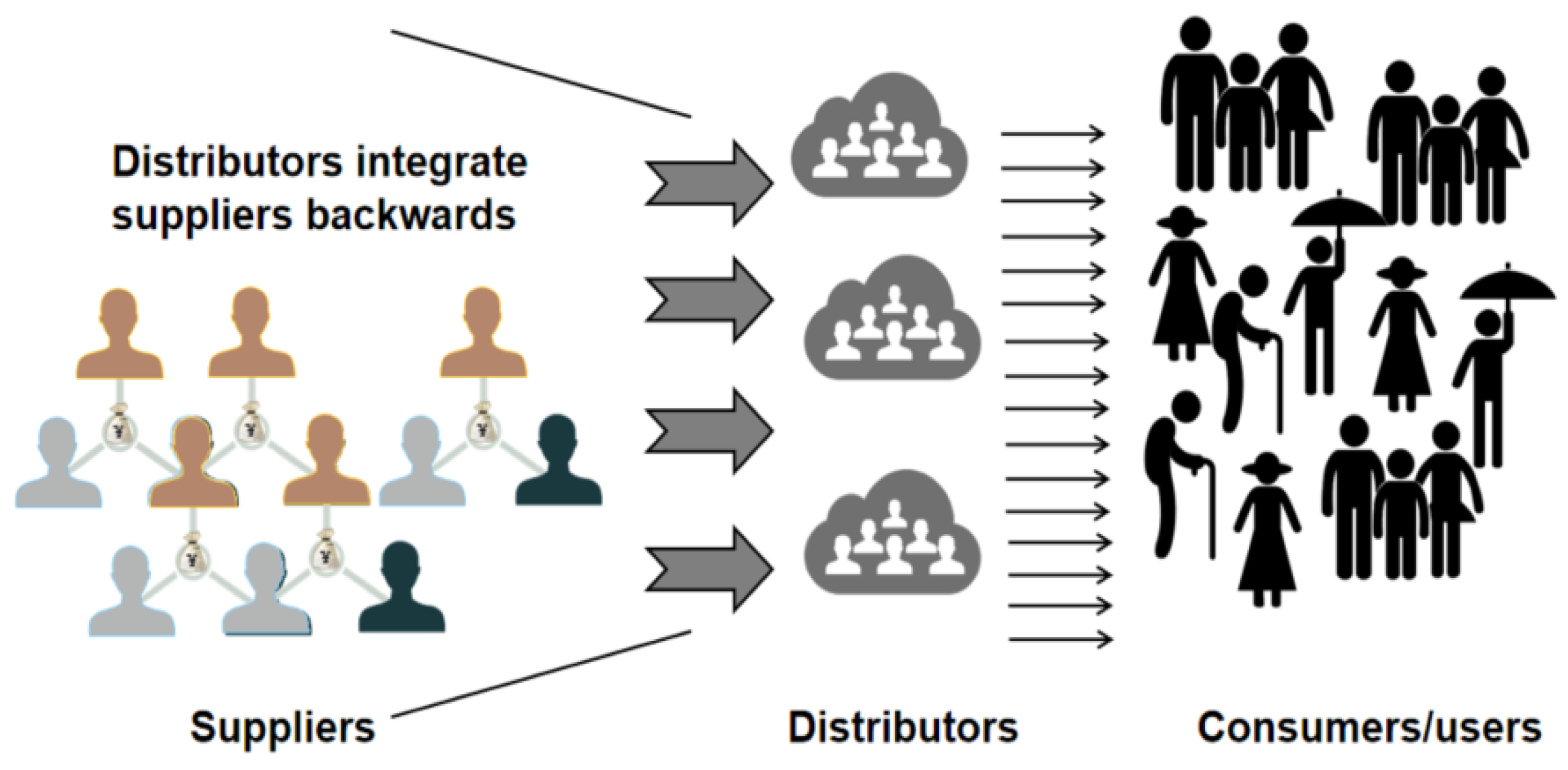
There are two ages before the emergence of aggregation platforms, i.e., pre-internet and internet ages. The aggregated case in [1], however, is what we understand as the internet platform. The value chain for any given consumer-facing market is divided into three parts: suppliers, distributors, and users. In the pre-internet age, this integration was often achieved by controlling and reverse integrating suppliers’ resources, such as newspapers, television stations, taxis, and hotel chains. 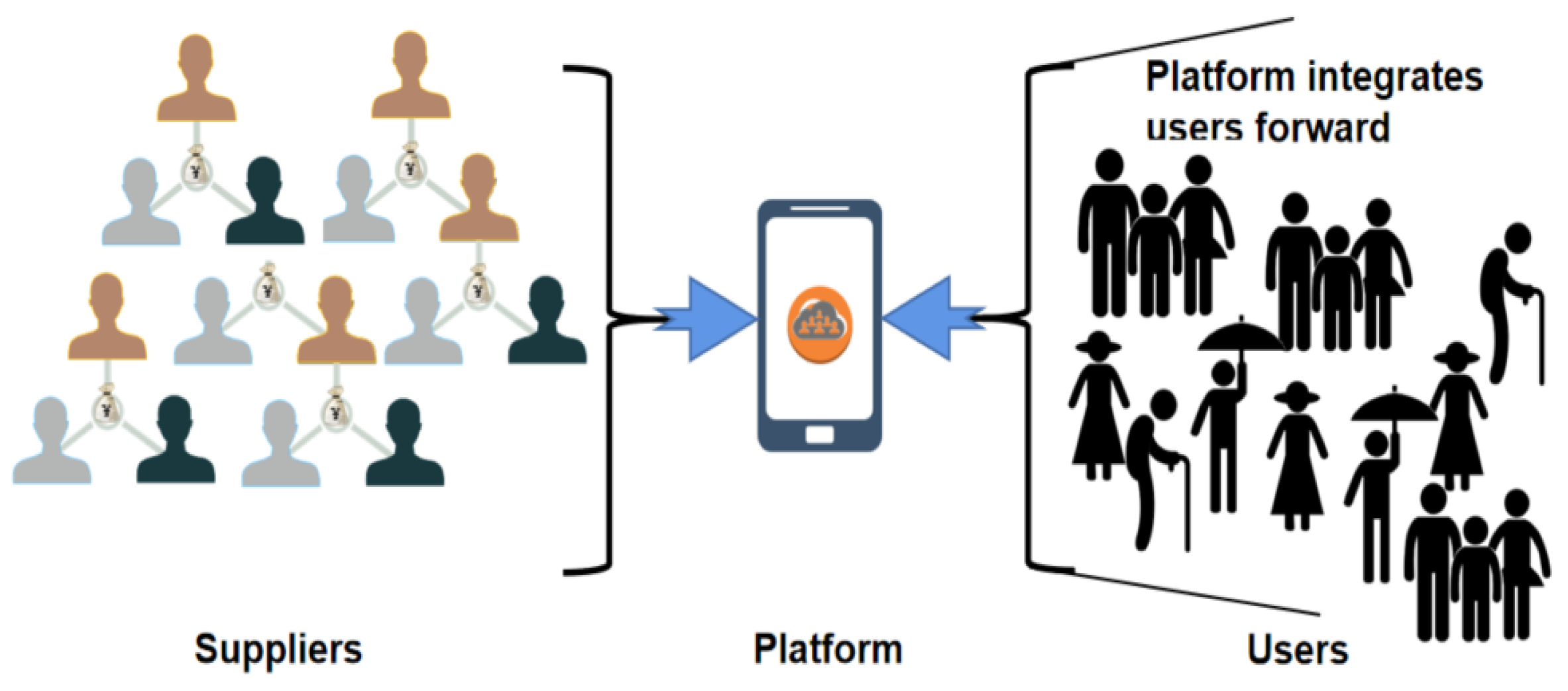Compared with a large number of consumers, it is easier and more valuable for distributors to connect with suppliers, as shown in Figure 1. After the advent of the Internet, the rules changed. The marginal cost of an Internet platform is infinitely close to zero so that the advantages of traditional distributors are offset, which also makes it possible for users to establish contact with the platform with almost zero cost. 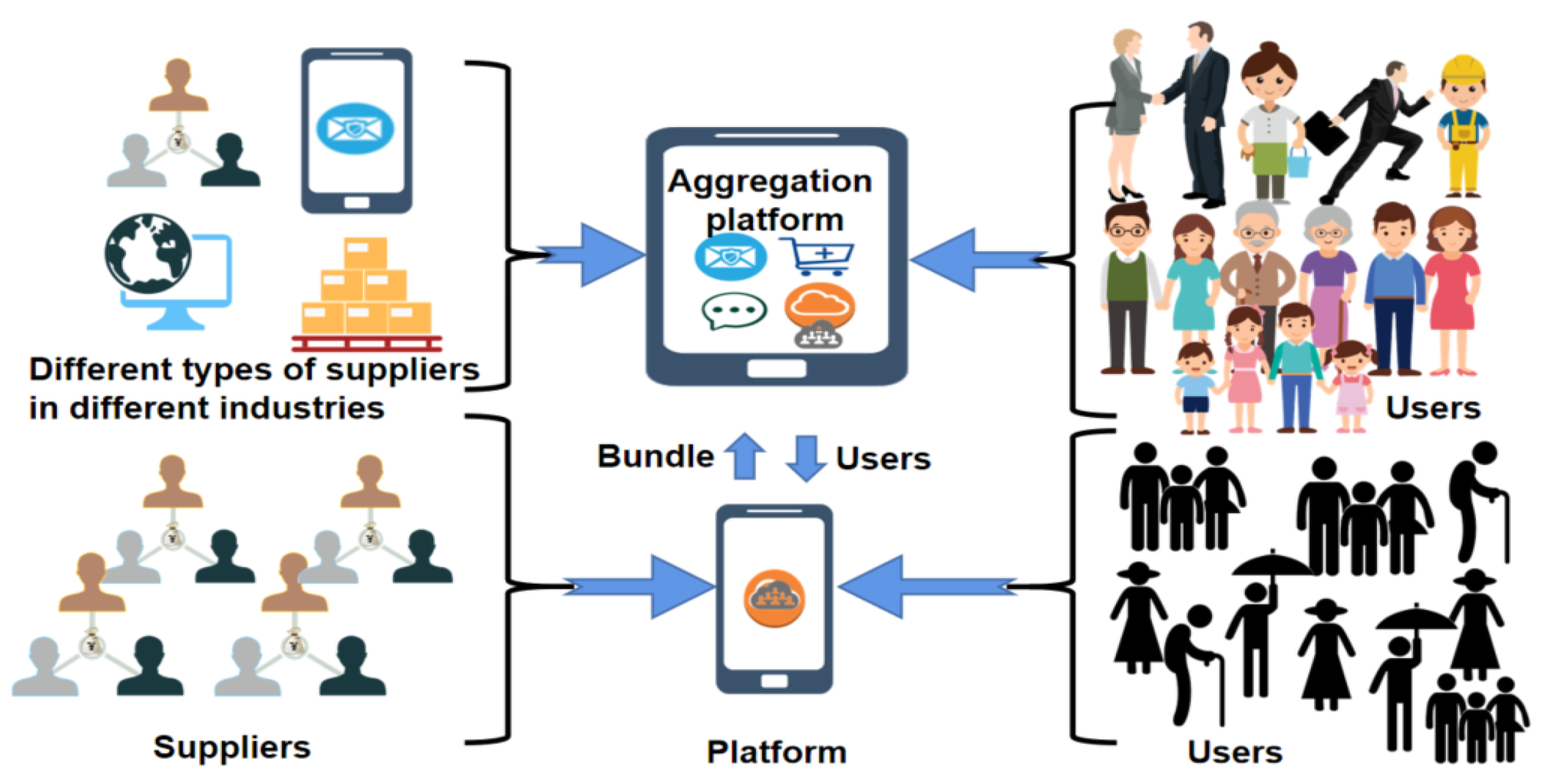The internet platform integrates users forward, evolving into WeChat public accounts, TikTok, Didi, Uber, and Airbnb, as seen in Figure 2. At present, when internet platforms are established, the aggregation and information sharing between different internet channels will stimulate greater vitality. The functional aggregation platform attracts more modular and commoditized small platforms to enter it by some rules. Thus, more platform suppliers attract more user demand to reduce the overall user acquisition cost, see Figure 3.

With certain theoretical rationality and innovation, the bundling strategy for ride-hailing platforms is feasible in practice and worthy of research and popularization. Amap (Alibaba-owned AutoNavi) as the first aggregation platform in the ride-hailing market in China, aggregates more than 40 providers such as Didi, Shenzhou, Shouqi, Caocao, and others, providing a variety of models and vehicle types across the country with over 100 million daily activity users. DiDi Chuxing as both a ride-hailing platform and an aggregation platform, accesses some services like Landao Chuxing, Liangzi Chuxing, and Henghao Yongche. With the help of Amap’s digital upgrade program, Hengdao Chuxing has been reduced several times of costs to acquire travel flow. Furthermore, Amap contributes to more than 90% of Hubei Yichang Transportation Group’s orders. The aggregation platform will also access more ride-hailing providers in the future. The full aggregation of the existing capacity in the ride-hailing market can effectively reduce the vehicle idle, bringing about 10% more improvement in urban travel. If the aggregation model is not well received, dozens of ride-hailing platforms develop their applications and subsidies fanatically, to throw the industry and society into chaos. Internet platforms with large flow, to a large extent, choose to be aggregation platforms to improve the viscosity of users, requiring very little costs, and achieve realizable cash value of the travel flow.

The bundling mode is a social focus; however, it still has a blank space in the licensing mechanism. There are so many significant problems that deserved to be explored. We pick some core issues as follows.

(i)

What are the motivations for ride-hailing platforms to adopt or not to adopt the bundling mode?

(ii)

How will ride-hailing and aggregation platforms respond to the introduction of bundling services?

(iii)

Is the equilibrium between the ride-hailing platform and the aggregation platform in line with the total profit maximization?

This paper aims to dig deeper into the above mentioned issues. We present an analytical framework on the Stackelberg game where the driver group serves to each platform on the service level and each platform as a leader dictates prices for the driver group. We set up a Nash equilibrium between the ride-hailing platform and the aggregation platform to obtain optimal prices. We present some sensitivity analysis to capture the bundling option of the ride-hailing platform in unbundled and bundled cases. There is little literature on the bundling modes of ride-hailing platforms and aggregation platforms. Drawing on channel selection in marketing, we liken the problem of bundling option to the channel selection problem. This paper aims to fill in the research gap in pricing and multi-channel layouts of ride-hailing platforms. We summarize the main contributions of this paper as follows:

(i)

We dictate bundling options on the multi-channel selection and pricing, that are fairly common in practice but have not yet received sufficient research attention. This paper highlights the pricing reactions caused by the introduction of bundling modes on ride-sharing and aggregation platforms.

(ii)

Observing that ride-hailing platforms are gaining more and more orders in bundled channels, we consider a framework in which the driver group services for ride-hailing and aggregation platforms. Each platform is in a position to decide price and influences the drivers’ service levels. We focus on bundling modes in the presence of interactions with traditional direct channels, as opposed to focusing on the effect of bundling modes introduced on direct sell. Further, the equilibrium between the ride-hailing platform and the aggregation platform is explored to maximize total profits.

(iii)

The motivation of the ride-hailing platform to adopt or not adopt bundling mode is the key to introduce the bundling service. One key distinction between unbundled and bundled formats is that there is an additional price, whereas in the bundling mode it is decided by the ride-hailing platform, but requires sharing-revenue with the aggregation platform and paying slotting fees. We test six groups of parameters to obtain the access conditions for the ride-hailing platform by introducing the bundling mode and the boundary line of profit competition between the two platforms, where four pairs (cost coefficients of service levels provided for the two platforms, service level and cross-service level substitutions, revenue-sharing ratios of the two platforms, cost prices of the two platforms) have regular boundaries, and two pairs (price and cross-price substitutions, commission and slotting fee charged by the aggregation platform) have irregular boundaries.

The remainder of the paper is organized as follows. Section 2 reviews the recent studies on the multi-channel structures, prices and service levels, slotting fees and revenue-sharing, and game models. Section 3 introduces the unbundled model (Model N for short) and bundled model (Model B for short), and some notations and assumptions as the basis of this paper. In Section 4, we describe the decision making processes of ride-hailing and aggregation platforms. We also construct Nash equilibria between the two platforms in Model N and Model B in this section, respectively. Section 5 gives some analysis and numerical examples. Section 6 discusses main results. Finally, conclusions and future work are drawn in Section 7.

2. Literature Review

Our research is closely related to four streams of literature, including business models of various ride-hailing platforms, multi-channel structures, price and service level modes, slotting fee and revenue-sharing, and game models. We now describe how our research relates to the literature in these areas.

2.1. Business Models

Nowadays, there are large ride-hailing platforms in various countries of the world, e.g., Uber, Didi, Lyft, Gett, Mytaxi (Hailo), Ola Cabs, BlaBla Car, Careem, and Kako Taxi. The increase of novel business models are introduced to different ride-hailing platforms year by year all over the world [2,3,4]. Feng et al. show that the on-demand hailing system is more efficient when the traffic intensity is low or high, while the street-hailing system could be more competent in regular traffic intensity or the low density of taxis distributed [5]. Turoń in reference [6] indicates several main business models concerning business-to-consumer (B2C) roundtrip, business-to-business (B2B) mode, one-way models, the non-profit business model, as well as a hybrid form in the form of B2B and B2C entities. A business model based on open innovations has five main characteristics: both uses its own and external solutions, cooperation with specialists, meet customer expectations to improve market advantage, use available ideas, and develop knowledge, skills, licenses, or technology [2,4]. Wan Mohamad et al. mention the new initiative Uber + Travel, whose partners are online travel agency, Chinese Airlines, and a few travel services providers to provide the tourists with the smooth traveling experience [7]. The purpose of the research is to identify factors that increase energy consumption to compare real consumption with data obtained from operators [8].

2.2. Multi-Channel Structures

Our work is related to the rich stream of literature on the determinants of multi-channel structures. Drawing on channel selection in marketing, we liken the bundled service problem to the channel selection problem for the ride-hailing platform. Multi-channel management has been extensively researched on the choice of multi-channel supply chain in e-commerce or direct sales [9,10]. Turning to related works lie on the issue of pricing conflict, reporting that prices, profits, demands, and consumer welfare are influenced by channel structures, cost of participants, and customer preferences of channels [11,12]. The equilibrium solutions in various channel structures indicate that e-channel does not always lead to lower prices, but can enhance total consumer welfare.

2.3. Price and Service Level Modes

This paper is also in the specific stream of pricing strategies. Interestingly, dynamic or surge pricing is controversial and has been questioned by riders, drivers, scholars, and policymakers. By contrast, the research in [13] studies the pricing problem as a queueing-theoretic economic model. They show that dynamic pricing does not provide more payoff than static pricing with a large market limit. Research on this problem proceeds from why the price differences between a conventional retailer channel and a direct online channel [14,15]. A key distinction between unbundled and bundled formats is that there is an additional price, whereas in the bundling option they are decided by the ride-hailing platform, but that price is available on the aggregation platform. On the other hand, there is little research on non-discriminating pricing policy by manufacturers [11]. Additionally, service level plays a strategic role in the dual-channel competitive market. Retail services have significant effects on customers’ channel choice, demand, and loyalty [16,17,18].

2.4. Slotting Fee and Revenue-Sharing

Slotting fee and revenue-sharing contract are the two pricing instruments by the aggregation platform in our problem. Generally speaking, a slotting fee is a one-time charge that manufacturers pay to place their products on retail shelves. In this paper, the platform usage fee’s analogy to slotting fee seems so very appropriate. Bloom et al. in reference [19] summarize two earlier viewpoints regarding the role of slotting fees: product quality [20] and empty shelves [21]. More recently, a new viewpoint argues that slotting fees arise from the operational costs or vertical margin differences. In China’s electronics retail market, slotting fees have long been criticized for creating unfair competition [22]. On the other hand, the fixed-ratio revenue-sharing contract is the most common scheme studied so far to solve the profit assignment problem [23,24].

2.5. Stackelberg Game and Nash Equilibrium

Several studies have indicated that the game schemes have a greater impact on competition outcomes and supply chain performance [25,26]. In this work, we consider two types of game schemes, namely, Stackelberg game and Nash game. In the Nash game, the ride-hailing platform and the aggregation platform determine the prices simultaneously and are equally powerful in the system. The Nash game allows us to deal with another supply-chain structure, in which the supplier and the retailer are equally powerful. Mixed equilibrium has been proposed as a consequence to study the equilibrating behavior of multiple players in the ridesharing system [27]. In the Stackelberg game, the platform is the leader, and the driver group is the follower. The Stackelberg game depicts a common supply-chain system in reality, in which the platform is more powerful than the driver group. Many studies on price strategies have bi-level programming to access the effects of transportation policies on traffic flows and system performance. Commonly, the decisions made by policy-makers or operators reside in the upper-level, and travelers respond through an equilibrate adjustment process in the lower-level [28]. Stackelberg game provides a good perspective to integrate the ride-hailing platform and users (both drivers and riders) in the transportation system. The diversity of objective functions varied in response to different decisions. The main reason for choosing to minimize the total generalized travel cost rather than maximizing the overall occupancy ratio or minimizing the total number of solo drivers is that the last two objectives as mentioned above too often might result in several optimal solutions, which does not help with decision-making [29,30].

3. Basic Setting

In this section, we will give a rough picture of unbundled and bundled models. Notations and some assumptions as the basis of this paper are also presented in this section.

3.1. Model Description

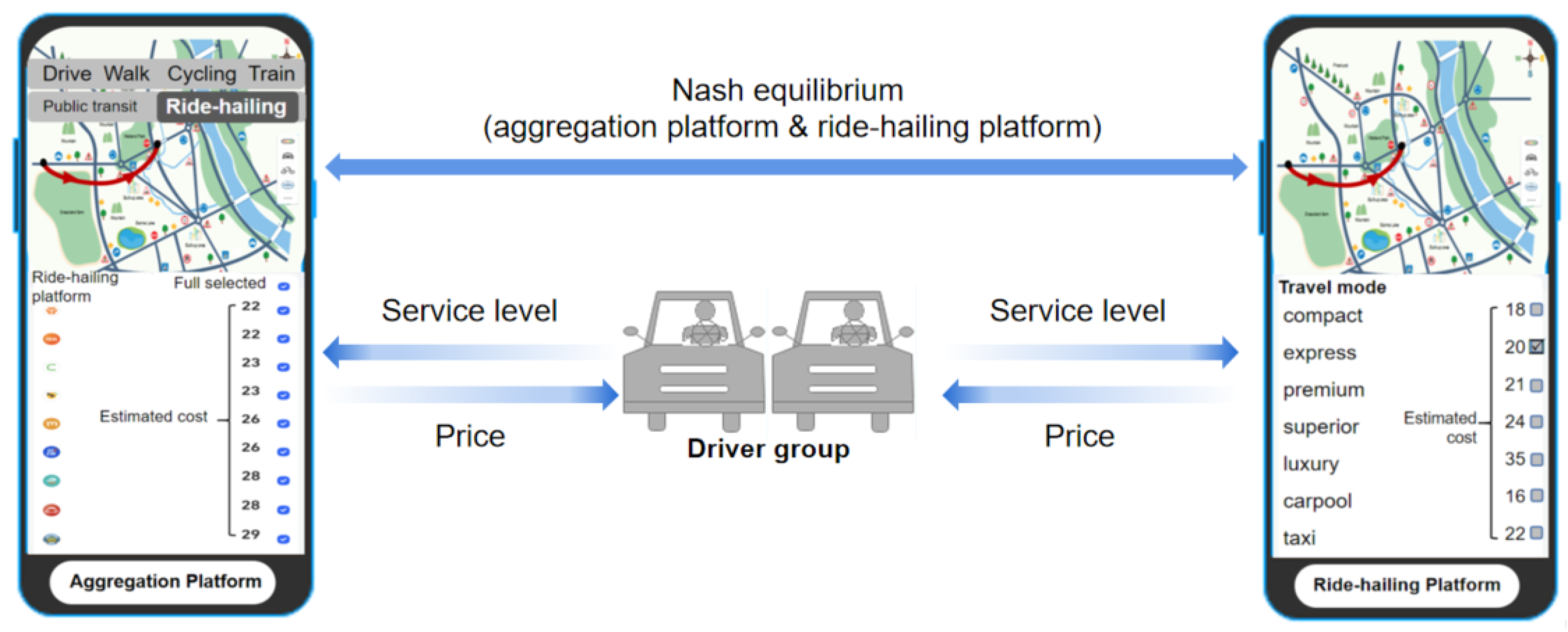
The order sales system consists of a ride-hailing platform, an aggregation platform, and a driver group. Price and service level are core factors interacting among those three stakeholders. This paper formulates the decision making process of the ride-hailing platform without and with the bundling mode. There are two Stackelberg games where the driver group serves each platform respectively on the service levels, and each platform as a leader dictates prices for the driver group. Then, we set up Nash equilibria between the ride-hailing platform and the aggregation platform to obtain optimal prices without and with the bundling modes, respectively. Therefore, we consider the following two scenarios: unbundled mode (Model N for short) and bundled mode (Model B for short), as illustrated in Figure 4 and Figure 5, respectively.

Model N: The ride-hailing platform is not bundled on the aggregation platform. The ride-hailing platform and the aggregation platform as leaders give prices respectively, followed by the driver group providing service levels for the two platforms. There are two Stackelberg games: between the ride-hailing platform and the driver group, between the aggregation platform and the driver group. The competition between the two platforms is formulated by a Nash equilibrium.

Model B: The ride-hailing platform bundles its partial business on the aggregation platform. On the basis that the ride-hailing platform and the aggregation platform both keep the direct channel, there is an additional sales channel established by the aggregation platform to provide orders for the ride-hailing platform. A Stackelberg game is built to obtain service levels of the driver group, followed by capturing prices of the bundled channel and the direct channel for the ride-hailing platform jointly in the upper-level. Another Stackelberg game between the aggregation platform (leader) and the driver group (follower), determines the price in the upper-level and service levels in the lower-level. Furthermore, the aggregation platform charges the ride-hailing platform commission and slotting fee. The competition between the two platforms is formulated by a Nash equilibrium.

3.2. Notation and Assumptions

The following notations will be used to develop the proposed model, see

Table 1. Notation and description.

Parameters	Description
$\theta$	Demand percentage that the aggregation platform provides to the ride-hailing platform
$\alpha ,\beta$	Price substitution and cross-price substitution
$\gamma ,\delta$	Service level substitution and cross-service level substitution
$\lambda ,\sigma$	Commission and slotting fee
$c_r,c_a$	Cost prices of the ride-hailing/aggregation platform, respectively
${\eta }_r,{\eta }_a$	Cost coefficients of service levels in the ride-hailing/aggregation platform, respectively
$w_r,w_a$	Revenue-sharing ratios of the ride-hailing/aggregation platform, respectively
$D_1,D_2$	Base demands of the ride-hailing/aggregation platform, respectively
Variables	Description
$p_{rn},p_{rb},p_{rt}$	Prices of the ride-hailing platform in Model N, Model B, bundle channel, respectively
$p_{an},p_{ab}$	Prices of the aggregation platform in Model N and Model B, respectively
$s_{rn},s_{rb}$	Service levels of the ride-hailing platform in Model N and Model B, respectively
$s_{an},s_{ab}$	Service levels of the aggregation platform in Model N and Model B, respectively

.

We make the following assumptions as the basis of this paper:

Assumption 1.

The marginal cost of the order is zero.

Assumption 2.

Orders from the ride-hailing platform are homogeneous.

Assumption 3.

Drivers service for both aggregation and ride-hailing platforms.

Assumption 1 describes a situation where an additional unit can be produced without any increase in the total cost of production. Offering another unit of an order can have zero marginal costs when that order is non-rivalrous, meaning that a rider can get an order without impairing the ability of others to simultaneously consume it as well. Assumption 2 indicates the ride-hailing platform offers the same orders to the aggregation platform and its own channel. Assumption 3 means that drivers are multi-homing for both aggregation and ride-hailing platforms.

4. The Model

In this section, we will give the standard form of demand function and its derivatives, the decision making processes of Model N and Model B.

4.1. Standard Form of Demand Function and Its Derivatives

Linear demand functions in price and service level have been adopted in [15,31,32,33,34,35,36] and many others. The order demand decreases with the rise of price and increases with the rise of service level on its own channel. Meanwhile, this demand grows with the rise of price and falls with the rise of service level on rival channels.

Let $D_r$ and $D_a$ be the demands of the one platform and the other platform, respectively, $D_1$ and $D_2$ represent the base demands of the one platform and the other platform, respectively. Denote $p_r$ and $p_a$ by the prices of the one platform and the other platform, respectively, $s_r$ and $s_a$ by the service levels, respectively. The parameter $\alpha$ measures the price substitution of its own channel. The parameter $\beta$ is the cross-price substitution of the rival channel. Besides, the parameter $\gamma$ is the demand sensitivity of its own service level. The parameter $\delta$ is the sensitivity of the service level of another platform. Parameters satisfy $0<\beta \le \alpha <1$ and $0<\delta \le \gamma <1$. $\alpha \ge \beta$ means that the ownership price effect is before the cross-price effect, while $\gamma \ge \delta$ means that the ownership service level effect is before the cross-service level effect. The standard demand functions of the one platform and the other platform are described, respectively, as follows:

$$\begin{array}{cc}& D_r=D_1-\alpha p_r+\beta p_a+\gamma s_r-\delta s_a,\hfill \\ & D_a=D_2-\alpha p_a+\beta p_r+\gamma s_a-\delta s_r.\hfill \end{array}$$

Some derivatives of the demand functions are given in

Table 2. Specific demand functions of two platforms.

Reference	Demand Function	Require
Dan et al. [31]	$D_r=D_1-\alpha p_r+\beta p_a+\gamma s_r$	$s_r=s_a$
	$D_a=D_2-\alpha p_a+\beta p_r-\delta s_a$
Lu and Liu [32]	$D_r=D_1-\alpha p_r+\beta p_a+\gamma s_r$	$D_1+D_2=\overline{D},s_r=s_a$
	$D_a=D_2-\alpha p_a+\beta p_r-\delta s_a$
Ding et al. [33]	$D_r=D_1-p_r+\beta p_a-s_r+\delta s_a$	$D_1=D_2$
	$D_a=D_2-p_a+\beta p_r-s_a+\delta s_r$
Wei et al. [34]	$D_r=D_1-p_r+\beta p_a$
	$D_a=D_2-p_a+\beta p_r$
Panda et al. [15]	$D_r=D_1-\alpha p_r+\beta p_a$	$D_1+D_2=\overline{D}$, $\overline{D}$ is the fixed demand of the market
	$D_a=D_2-\alpha p_a+\beta p_r$
Gurnani et al. [35]	$D_r=D_1-p_r+e_1+e_2+e_3$	$e_1$: selling effort, $e_2$: the other platform’s quality level, $e_3$: cross-price substitution
	$D_a=D_2-p_a+e_1+e_2+e_3$
Qin et al. [36]	$D_r=D_1-p_r+\beta p_a+\gamma s_r-\delta s_a$	$D_1=D_2$
	$D_a=D_2-p_a+\beta p_r+\gamma s_a-\delta s_r$

.

4.2. Model

In Model N, let $p_{rn}$ ($p_{rn}\ge c_r$) and $p_{an}$ ($p_{an}\ge c_a$) be prices of ride-hailing and aggregation platforms, respectively, while $c_r$ and $c_a$ are costs of each order in ride-hailing and aggregation platforms, respectively, including the fuel cost, toll and parking fees. Let $s_{rn}$ and $s_{an}$ be service levels of ride-hailing and aggregation platforms respectively where $s_{rn},s_{an}\in [s_l,s_h]$. Following the demand functions $D_r$ and $D_a$ in Section 4.1, we have demand functions of ride-hailing and aggregation platforms, i.e., $D_{rn}$ and $D_{an}$, respectively, as shown in

Table 3. Expressions of Model N and Model B.

	Model N	Model B
	Demand function
Platform R	$D_{rn}=D_1-\alpha p_{rn}+\beta p_{an}+\gamma s_{rn}-\delta s_{an}$	$D_{rb}=D_1-\alpha p_{rb}+\beta (p_{rt}+p_{ab})+\gamma s_{rb}-\delta s_{ab}$
Bundle channel		$D_{rt}=\theta D_2-\alpha p_{rt}+\beta (p_{rb}+p_{ab})+\gamma s_{rb}-\delta s_{ab}$
Platform A	$D_{an}=D_2-\alpha p_{an}+\beta p_{rn}+\gamma s_{an}-\delta s_{rn}$	$D_{ab}=(1-\theta )D_2-\alpha p_{ab}+\beta (p_{rb}+p_{rt})+\gamma s_{ab}-\delta s_{rb}$
	Utility of the driver group in the lower level
	${\pi }_{dn}=w_r(p_{rn}-c_r)D_{rn}+w_a(p_{an}-c_a)D_{an}$	${\pi }_{db}=w_r(p_{rb}-c_r)D_{rb}+w_r(p_{rt}-c_r)D_{rt}$
	$-{\displaystyle \frac{1}{2}}{\eta }_r{s}_{rn}^2-{\displaystyle \frac{1}{2}}{\eta }_r{s}_{an}^2$	$+w_a(p_{ab}-c_a)D_{ab}-{\displaystyle \frac{1}{2}}{\eta }_r{s}_{rb}^2-{\displaystyle \frac{1}{2}}{\eta }_a{s}_{ab}^2$
	Optimal service levels of the driver group in the lower level
Platform R	${\overline{s}}_{rn}={\displaystyle \frac{\gamma }{{\eta }_r}}{w}_r(p_{rn}-c_r)-{\displaystyle \frac{\delta }{{\eta }_r}}{w}_a(p_{an}-c_a)$	${\overline{s}}_{rb}={\displaystyle \frac{\gamma }{{\eta }_r}}{w}_r(p_{rt}+p_{rb}-2c_r)-{\displaystyle \frac{\delta }{{\eta }_r}}{w}_a(p_{ab}-c_a)$
Platform A	${\overline{s}}_{an}={\displaystyle \frac{\gamma }{{\eta }_a}}{w}_a(p_{an}-c_a)-{\displaystyle \frac{\delta }{{\eta }_a}}{w}_r(p_{rn}-c_r)$	${\overline{s}}_{ab}={\displaystyle \frac{\gamma }{{\eta }_a}}{w}_a(p_{ab}-c_a)-{\displaystyle \frac{\delta }{{\eta }_a}}{w}_r(p_{rt}+p_{rb}-2c_r)$
	Update demand functions
	${\overline{D}}_{rn}=D_1-\alpha p_{rn}+\beta p_{an}+\gamma {\overline{s}}_{rn}-\delta {\overline{s}}_{an}$	${\overline{D}}_{rb}=D_1-\alpha p_{rb}+\beta (p_{rt}+p_{ab})+\gamma {\overline{s}}_{rb}-\delta {\overline{s}}_{ab}$
	${\overline{D}}_{an}=D_2-\alpha p_{an}+\beta p_{rn}+\gamma {\overline{s}}_{an}-\delta {\overline{s}}_{rn}$	${\overline{D}}_{rt}=\theta D_2-\alpha p_{rt}+\beta (p_{rb}+p_{ab})+\gamma {\overline{s}}_{rb}-\delta {\overline{s}}_{ab}$
		${\overline{D}}_{ab}=(1-\theta )D_2-\alpha p_{ab}+\beta (p_{rb}+p_{rt})+\gamma {\overline{s}}_{ab}-\delta {\overline{s}}_{rb}$
	Utility of the platform in the upper level
Platform R	${\pi }_{rn}=(1-w_r)(p_{rn}-c_r){\overline{D}}_{rn}$	${\pi }_{rb}=(1-w_r)\left((p_{rt}-c_r){\overline{D}}_{rt}+(p_{rb}-c_r){\overline{D}}_{rb}\right)-\lambda p_{rt}{\overline{D}}_{rt}-\sigma$
Platform A	${\pi }_{an}=(1-w_a)(p_{an}-c_a){\overline{D}}_{an}$	${\pi }_{ab}=(1-w_a)(p_{ab}-c_a){\overline{D}}_{ab}+\lambda p_{rt}{\overline{D}}_{rt}+\sigma$

with other expressions of Model N and Model B. Platform R represents the ride-hailing platform, and Platform A represents the aggregation platform in Table 3. Let $w_r\in (0,1)$ and $w_a\in (0,1)$ be revenue-sharing ratios, which are used to be incentive percentage-based rewards for the driver group on ride-hailing and aggregation platforms, respectively. Let ${\eta }_r$ and ${\eta }_a$ be cost coefficients of the driver group for ride-hailing and aggregation platforms, respectively. According to Yan and Pei (2009), the costs of service levels in ride-hailing and aggregation platforms are ${\eta }_r{s}_{rn}^2/2$ and ${\eta }_r{s}_{an}^2/2$, respectively.

For any given prices $p_{rn}$ and $p_{an}$, the driver group obtains service levels by maximizing the utility ${\pi }_{dn}$. It is clearly that for any given $p_{rn}$ and $p_{an}$, ${\pi }_{dn}$ is jointly quadric concave in $s_{rn}$ and $s_{an}$. Through the first-order necessary condition, we have service levels ${\overline{s}}_{rn}$ and ${\overline{s}}_{an}$. Update demand functions $D_{rn}$ and $D_{an}$ to ${\overline{D}}_{rn}$ and ${\overline{D}}_{an}$, respectively. Then, the profit-maximization model of the ride-hailing platform in the upper-level is ${max}_{p_{rn}\ge c_r}{\pi }_{rn}$. The aggregation platform aims to maximize the profit as ${max}_{p_{an}\ge c_a}{\pi }_{an}$.

In the next, we give the decision making process of Model B. In Model B, the ride-hailing platform is bundled on the the aggregation platform, which means that the ride-hailing platform is going to seize the market share from the aggregation platform. Let $p_{rb}\ge c_r$, $p_{rt}\ge c_r$ and $p_{ab}\ge c_a$ be prices of three channels in this model, which are the direct channel of the ride-hailing platform, the bundled channel of the ride-hailing platform and the direct channel of the aggregation platform, respectively. Denote that the driver group offers service levels $s_{rb},s_{ab}\in [s_l,s_h]$ to the ride-hailing platform and the aggregation platform, respectively. The demand functions of the direct channel and the bundled channel of the ride-hailing platform are denoted by $D_{rb}$ and $D_{rt}$, respectively. Thus, the total demand of the ride-hailing platform is $D_{rb}+D_{rt}$. Let $\theta \in [0,1]$ be the potential proportion of orders that ride-hailing platform acquires from the aggregation platform. Then, the base demand of the direct channel and the bundled channel of the ride-hailing platform orders are $\theta D_2$ and $(1-\theta )D_2$, respectively. The demand function of the aggregation platform is down to $D_{ab}$. The driver group obtains profits from the three channels, while costs ${\eta }_r{s}_{rb}^2/2$ and ${\eta }_a{s}_{ab}^2/2$ to obtain orders from ride-hailing and aggregation platforms, respectively.

For any given $p_{rb}$, $p_{rt}$ and $p_{ab}$, the utility of the driver group ${\pi }_{db}$ is jointly quadric concave in $s_{rb},s_{ab}$. By the first-order necessary condition of ${\pi }_{db}$, we have service levels ${\overline{s}}_{rb},{\overline{s}}_{ab}$. Then, $D_{rb},D_{rt},D_{ab}$ are updated as ${\overline{D}}_{rb},{\overline{D}}_{rt},{\overline{D}}_{ab}$, respectively. The aggregation platform provides the bundled channel to increase order volume of the ride-hailing platform and increase its revenue by charging the commission and slotting fees. Letting $\lambda \in (0,1)$ be the commission ratio, the revenue-sharing of the aggregation platform is $\lambda p_{rt}{\overline{D}}_{rt}$. Let $\sigma \ge 0$ be the slotting fee including a fixed technical service fee and a fixed settle-in fee (deposit). The ride-hailing platform in Model B has the profit-maximization model: ${max}_{p_{rt}\ge c_r,p_{rb}\ge c_r}{\pi }_{rb}$. The aggregation platform aims to maximize the profit, which is expressed as ${max}_{p_{ab}\ge c_a}{\pi }_{ab}$.

4.3. Theoretical Analysis

In the competition between the ride-hailing platform and the aggregation platform, each platform selects its pricing policy in a noncooperative manner, seeking to maximize its interests at a maximal profit until an equilibrium is achieved. A choice of pricing policy $p_{rn}^{*},p_{an}^{*}$ constitutes a Nash equilibrium in Model N if, ${\pi }_{rn}\left(p_{rn}^{*},p_{an}^{*}\right)\ge {\pi }_{rn}\left(p_{rn},p_{an}^{*}\right),\forall p_{rn}\ge c_r$, and ${\pi }_{an}\left(p_{rn}^{*},p_{an}^{*}\right)\ge {\pi }_{an}\left(p_{rn}^{*},p_{an}\right),\forall p_{an}\ge c_a$.

We give the following Assumption 4 to derive that ${\pi }_{rn}$ and ${\pi }_{an}$ are strongly concave in $p_{rn}$ and $p_{an}$, respectively. By solving first-order conditions of ${\pi }_{rn}$ and ${\pi }_{an}$ simultaneously, we obtain the optimal prices and service levels in Proposition 1. To simplify writing, we denote $K_1={\gamma }^2/{\eta }_r+{\delta }^2/{\eta }_a,K_2=\gamma \delta /{\eta }_r+\gamma \delta /{\eta }_a,K_3={\gamma }^2/{\eta }_a+{\delta }^2/{\eta }_r$.

Assumption 4.

$\alpha >max\{K_1{w}_r,K_3{w}_a\}$.

Proposition 1.

In Model N, if Assumption 4 holds, the optimal prices of ride-hailing and aggregation platforms are, respectively, given by

$$\begin{array}{cc}{p}_{rn}^{*}=\hfill & [(K_2{w}_a-\beta )(D_2-2K_3{w}_a{c}_a+K_2{w}_r{c}_r+\alpha c_a)\hfill \\ \hfill & +2(K_3{w}_a-\alpha )(D_1-2K_1{w}_r{c}_r+K_2{w}_a{c}_a)]/\hfill \\ \hfill & \left[(K_2{w}_r-\beta )(K_2{w}_a-\beta )-4(K_3{w}_a-\alpha )(K_1{w}_r-\alpha )\right],\hfill \\ p_{an}^{*}=\hfill & [(K_2{w}_r-\beta )(D_1-2K_1{w}_r{c}_r+K_2{w}_a{c}_a)\hfill \\ \hfill & +2(K_1{w}_r-\alpha )(D_2-2K_3{w}_a{c}_a+K_2{w}_r{c}_r+\alpha c_a)]/\hfill \\ \hfill & \left[(K_2{w}_a-\beta )(K_2{w}_r-\beta )-4(K_1{w}_r-\alpha )(K_3{w}_a-\alpha )\right],\hfill \end{array}$$

(1)

with $p_{rn}^{*}\ge c_r$ and $p_{an}^{*}\ge c_a$. If the prices in (1) are lower than the costs, then the optimal prices are $p_{rn}^{*}=c_r$ and $p_{an}^{*}=c_a$.

The optimal service levels provided by the driver group to ride-hailing and aggregation platforms, respectively, are

$$\begin{array}{cc}& s_{rn}^{*}={\displaystyle \frac{\gamma }{{\eta }_r}}{w}_r(p_{rn}^{*}-c_r)-{\displaystyle \frac{\delta }{{\eta }_r}}{w}_a(p_{an}^{*}-c_a),\hfill \\ & s_{an}^{*}={\displaystyle \frac{\gamma }{{\eta }_a}}{w}_a(p_{an}^{*}-c_a)-{\displaystyle \frac{\delta }{{\eta }_a}}{w}_r(p_{rn}^{*}-c_r).\hfill \end{array}$$

Proof. 

The gradient of ${\pi }_{rn}$ with respect to the variable $p_{rn}$ is

$${\nabla }_{p_{rn}}{\pi }_{rn}=(1-w_r)\left(D_1-2\alpha p_{rn}+\alpha c_r+\beta p_{an}+2K_1{w}_r(p_{rn}-c_r)-K_2{w}_a(p_{an}-c_a)\right).$$

With Assumption 4, the second-order partial derivatives of ${\pi }_{rn}$ with respect to the variable $p_{rn}$ is

$${\partial }^2{\pi }_{rn}=2\left(w_r{K}_1-\alpha \right)(1-w_r)<0.$$

Thus, ${\pi }_{rn}$ is concave in $p_{rn}$. Similarly, ${\pi }_{an}$ is concave in $p_{an}$. This means that any stationary point of ${\pi }_{rn}$ or ${\pi }_{an}$ must be its globally optimal solution. By solving their stationarity conditions, we can obtain the conclusions immediately. □

A choice of pricing policy $(p_{rb}^{*},p_{rt}^{*},p_{ab}^{*})$ constitutes a Nash equilibrium in Model B if, ${\pi }_{rb}\left(p_{rb}^{*},p_{rt}^{*},p_{ab}^{*}\right)\ge {\pi }_{rb}\left(p_{rb},p_{rt},p_{ab}^{*}\right)$, $\forall p_{rb},p_{rt}\ge c_r$, and ${\pi }_{ab}\left(p_{rb}^{*},p_{rt}^{*},p_{ab}^{*}\right)\ge {\pi }_{ab}\left(p_{rb}^{*},p_{rt}^{*},p_{ab}\right)$, $\forall p_{ab}\ge c_a$. Through formulating a Nash equilibrium between the ride-hailing platform and the aggregation platform, we obtain the optimal prices and service levels. We give Assumption 5 for the convexity results of ${\pi }_{rb}$ and ${\pi }_{ab}$, i.e., ${\pi }_{rb}$ is jointly quadric concave in $p_{rb}$ and $p_{rt}$, and ${\pi }_{ab}$ is quadric concave in $p_{ab}$.

To simplify writing, we denote

$$\begin{array}{c}{L}_1={\displaystyle \frac{(1-w_r)(\alpha c_a-\beta c_r-2K_1{w}_r{c}_r)-(1-w_r-\lambda )(\theta D_2-2K_1{w}_r{c}_r+K_2{w}_a{c}_a)}{(1-w_r-\lambda )(K_2{w}_a-\beta )}},\hfill \\ L_2={\displaystyle \frac{(2-2w_r-\lambda )(\beta +K_1{w}_r)}{(1-w_r-\lambda )(K_2{w}_a-\beta )}},L_3={\displaystyle \frac{(1-w_a)\left(\beta -K_2{w}_r+2L_2(K_3{w}_a-\alpha )\right)}{(1-w_a)\left(K_2{w}_r-\beta +2L_4(\alpha -K_3{w}_a)\right)+\lambda (K_2{w}_a-\beta )}},\hfill \end{array}$$

$$L_4={\displaystyle \frac{2(K_1{w}_r-\alpha )}{K_2{w}_a-\beta }},L_5={\displaystyle \frac{(1-w_a)\left((1-\theta )D_2+\alpha (c_a-2L_1)+2K_2{w}_r{c}_r+2(L_1-c_a)K_3{w}_a\right)}{(1-w_a)\left(K_2{w}_r-\beta +2L_4(\alpha -K_3{w}_a)\right)+\lambda (K_2{w}_a-\beta )}}.$$

Assumption 5.

$\lambda <1-w_r,\alpha >max\left\{{\displaystyle \frac{2-2w_r-3\lambda /2}{4(1-w_r-\lambda )}}+K_1{w}_r,4{(\beta +K_1{w}_r)}^2+K_1{w}_r,K_3{w}_a\right\}$.

Proposition 2.

In Model B, if Assumption 5 holds, the optimal prices of the direct channel of ride-hailing platform, the bundled channel of the ride-hailing platform, and the direct channel of the aggregation platform are, respectively, given by

$$\begin{array}{cc}{p}_{rb}^{*}=\hfill & ((1-w_r)(D_1+\alpha c_r-\beta c_r-4K_1{w}_r{c}_r+K_2{w}_a{c}_a)+L_5(2-2w_r\hfill \\ \hfill & -\lambda )(\beta +K_1{w}_r)+(1-w_r)(\beta -K_2{w}_a)(L_1+L_2{L}_5+L_4{L}_5\hfill \\ \hfill & +L_3{L}_4{L}_5\left)\right)/(L_3(\beta +K_1{w}_r)(2w_r-\lambda -2)+2(1-w_r)(\alpha \hfill \\ \hfill & -K_1{w}_r)+L_3(1-w_r)(L_2+L_3{L}_4)(K_2{w}_a-\beta )),\hfill \\ p_{rt}^{*}=\hfill & L_5+L_3{p}_{rb}^{*},and{p}_{ab}^{*}=L_1+L_4{L}_5+(L_2+L_3{L}_4)p_{rb}^{*},\hfill \end{array}$$

(2)

with $p_{rb}^{*}\ge c_r$, $p_{rt}^{*}\ge c_r$ and $p_{ab}^{*}\ge c_a$. If the prices in (2) are lower than the costs, then the optimal prices are $p_{rb}^{*}=c_r$, $p_{rt}^{*}=c_r$ and $p_{an}^{*}=c_a$. The service levels provided by the driver group to the ride-hailing platform and the aggregation platform, respectively, are

$$\begin{array}{cc}{s}_{rb}^{*}=\hfill & {\displaystyle \frac{\gamma }{{\eta }_r}}{w}_r\left(L_5+(L_3+1)p_{rb}^{*}-2c_r\right)-{\displaystyle \frac{\delta }{{\eta }_r}}{w}_a(L_1+L_4{L}_5+(L_2+L_3{L}_4)p_{rb}^{*}-c_a),\hfill \\ s_{ab}^{*}=\hfill & {\displaystyle \frac{\gamma }{{\eta }_a}}{w}_a\left(L_1+L_4{L}_5+(L_2+L_3{L}_4)p_{rb}^{*}-c_a\right)-{\displaystyle \frac{\delta }{{\eta }_a}}{w}_r\left(L_5+(L_3+1)p_{rb}^{*}-2c_r\right).\hfill \end{array}$$

Proof. 

The Hessian matrix of ${\pi }_{rb}$ with respect to $p_{rt}$, $p_{rb}$ is

$${\partial }^2{\pi }_{rb}=\left[\begin{array}{cc}2(1-w_r)(K_1{w}_r-\alpha )& (2-2w_r-\lambda )(\beta +K_1{w}_r)\\ (2-2w_r-\lambda )(\beta +K_1{w}_r)& 2(1-w_r-\lambda )(K_1{w}_r-\alpha )\end{array}\right].$$

By Assumption 5, it is not difficult to see that the above matrix is negative definite and hence ${\pi }_{rb}$ is concave in $p_{rb},p_{rt}$. Similarly, we can show that ${\pi }_{ab}$ is also concave with respect to $p_{ab}$. By solving their stationarity conditions, we can obtain the conclusions immediately. □

Based on Proposition 2, we can give the optimal profits of the two platforms as follows. The optimal profits of the ride-hailing platform in Model N and Model B respectively are

$$\begin{array}{cc}\hfill {\pi }_{rn}^{*}=& (1-w_r)(E_1+E_2{p}_{an}^{*}-c_r)\left(D_1-\alpha (E_1+E_2{p}_{an}^{*})+\beta p_{an}^{*}+w_r{K}_1(E_1+E_2{p}_{an}^{*}-c_r)-w_a{K}_2(p_{an}^{*}-c_a)\right),\hfill \\ \hfill {\pi }_{rb}^{*}=& \left((1-w_r)(L_5+L_3{p}_{rb}^{*}-c_r)-\lambda \right)\left(\theta D_2-\alpha (L_5+L_3{p}_{rb}^{*})+\beta \left(L_1+L_4{L}_5+(L_2+L_3{L}_4+1)p_{rb}^{*}\right)\right)\hfill \\ & +(1-w_r)(p_{rb}^{*}-c_r)\left(D_1-\alpha p_{rb}^{*}+\beta \left(L_1+L_5+L_4{L}_5+(L_2+L_3+L_3{L}_4)p_{rb}^{*}\right)\right)+\left((1-w_r)\right(L_5+(L_3+1)p_{rb}^{*}\hfill \\ & -2c_r)-\lambda )\left(w_r{K}_1\left(L_5+(L_3+1)p_{rb}^{*}-2c_r\right)-w_a{K}_2\left(L_1+L_4{L}_5+(L_2+L_3{L}_4)p_{rb}^{*}-c_a\right)\right)-\sigma .\hfill \end{array}$$

The optimal profits of the aggregation platform in Model N and B, respectively, are

$$\begin{array}{cc}\hfill {\pi }_{an}^{*}=& (1-w_a)(p_{an}^{*}-c_a)\left(D_2-\alpha p_{an}^{*}+\beta (E_1+E_2{p}_{an}^{*})+w_a{K}_3(p_{an}^{*}-c_a)-w_r{K}_1(E_1+E_2{p}_{an}^{*}-c_r)\right),\hfill \\ \hfill {\pi }_{ab}^{*}=& (1-w_a)\left(L_1+L_4{L}_5+(L_2+L_3{L}_4)p_{rb}^{*}-c_a\right)((1-\theta )D_2-\alpha (L_1+L_4{L}_5)+\left(\beta (L_3+1)-\alpha (L_2+L_3{L}_4)\right)p_{rb}^{*}+\beta L_5\hfill \\ & +w_a{K}_3\left(L_1+L_4{L}_5+(L_2+L_3{L}_4)p_{rb}^{*}-c_a\right)-w_r{K}_2\left(L_5+(L_3+1)p_{rb}^{*}-2c_r\right))+\lambda (L_5+L_3{p}_{rb}^{*})(\theta D_2-\alpha (L_5+L_3{p}_{rb}^{*})\hfill \\ & +\beta \left(L_1+L_4{L}_5+(L_2+L_3{L}_4+1)p_{rb}^{*}\right)+w_r{K}_1\left(L_5+(L_3+1)p_{rb}^{*}-2c_r\right)-w_a{K}_2\left(L_1+L_4{L}_5+(L_2+L_3{L}_4)p_{rb}^{*}-c_a\right))+\sigma .\hfill \end{array}$$

In the next, we give the motivation for the ride-hailing platform to adopt or not adopt the bundling mode.

• If ${\pi }_{rb}^{*}>{\pi }_{rn}^{*}$, the ride-hailing platform will adopt the bundling mode.
• if ${\pi }_{rb}^{*}<{\pi }_{rn}^{*}$, the ride-hailing platform will not adopt the bundling mode.
• If ${\pi }_{rb}^{*}={\pi }_{rn}^{*}$, there will be no difference for the ride-hailing platform to adopt or not adopt the bundling mode.

We further obtain that for the aggregation platform, the bundling mode always cuts into the profit of the aggregation platform. Moreover, the ride-hailing platform is at a disadvantage with a lower profit all the time in market competition in Model N. In Model B, the competition between the two platforms is inconclusive. We summarize these observations as follows.

• The profit of the aggregation platform in Model N is less than that in Model B, that is ${\pi }_{ab}^{*}<{\pi }_{an}^{*}$.
• In Model N, the profit of the ride-hailing platform is less than that of the aggregation platform, that is ${\pi }_{rn}^{*}<{\pi }_{an}^{*}$.
• In Model B, if ${\pi }_{rb}^{*}>{\pi }_{ab}^{*}$, the ride-hailing platform is at a competitive advantage; if ${\pi }_{rb}^{*}<{\pi }_{ab}^{*}$, the aggregation platform is at a competitive advantage; if ${\pi }_{rb}^{*}={\pi }_{ab}^{*}$, the ride-hailing platform and the aggregation platform are on an equal footing.

5. Analytical and Numerical Comparison

In this part, we used MATLAB to verify the impacts of six pairs of parameters on the bundling strategy for the ride-hailing platform (${\pi }_{rn}$ and ${\pi }_{rb}$) and the profit in Model B (${\pi }_{ab}$ and ${\pi }_{rb}$), that is

(i)

${\eta }_r$ and ${\eta }_a$: cost coefficients of service levels provided for the two platforms;

(ii)

$\alpha$ and $\beta$: price substitution and cross-price substitution;

(iii)

$\gamma$ and $\delta$: service level substitution and cross-service level substitution;

(iv)

$w_r$ and $w_a$: revenue-sharing ratios of the two platforms;

(v)

$c_r$ and $c_a$: cost prices of the two platforms;

(vi)

$\lambda$ and $\sigma$: commission and slotting fee charged by the aggregation platform.

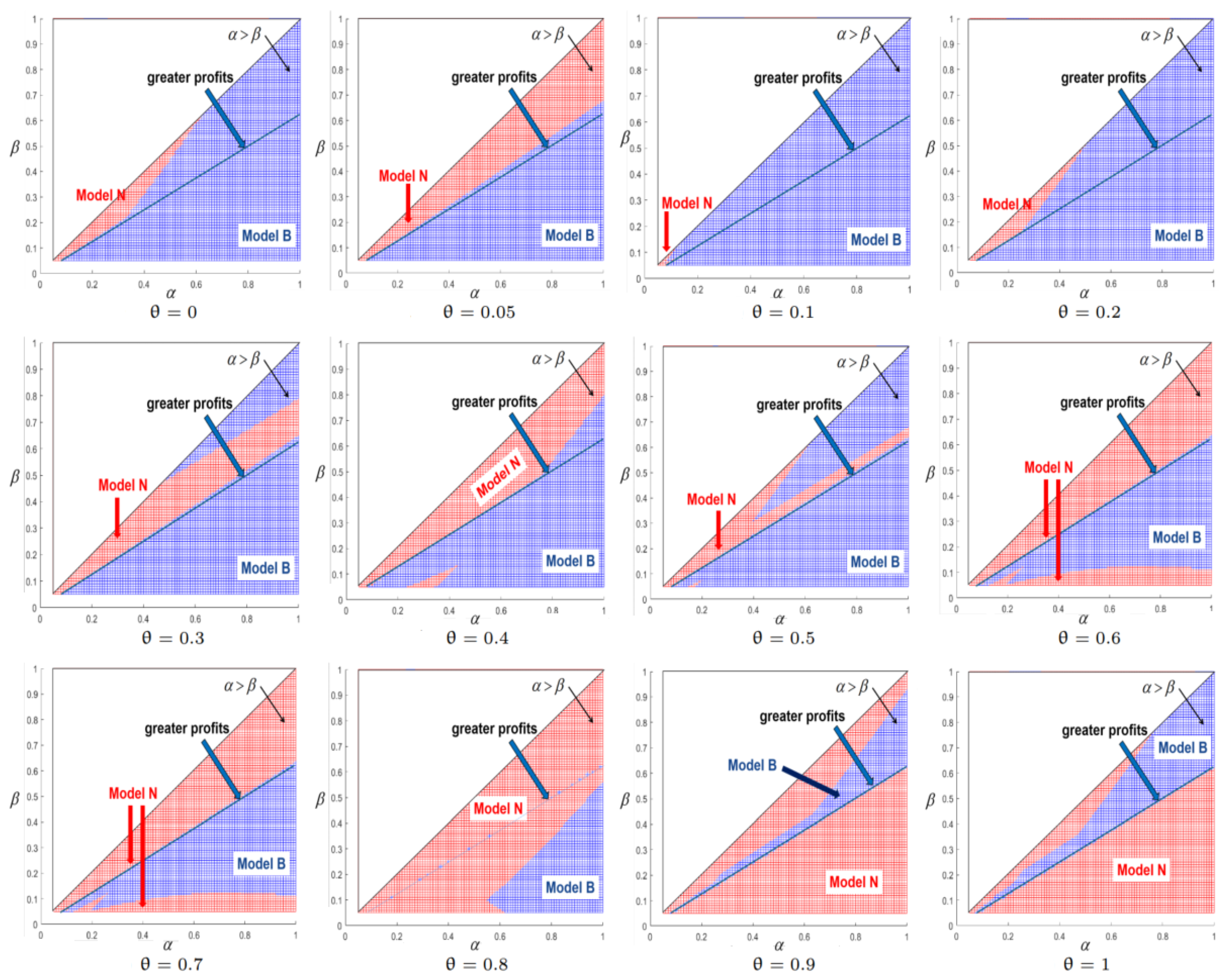
To make it clear, in this section, we use the red legend color to represent the ride-hailing platform in Model N, the blue legend color to represent the ride-hailing platform in Model B, the yellow legend color to represent the aggregation platform in Model N, and the green legend color presents the aggregation platform in Model B. In addition, we obtain some combinations of parameters of the ride-hailing platform with the change of the demand scale $\theta$. For figures with obvious rules, we summarize some results of critical points and boundaries under some specific parameters setting.

5.1. Cost Coefficients of Service Levels (${\eta }_r$ and ${\eta }_a$)

For ${\eta }_r$ and ${\eta }_a$, cost coefficients of service levels in the ride-hailing platform and the aggregation platform, respectively, the boundaries and critical points of the bundling option for the ride-hailing platform are shown in Figure 6 and Figure 7 and profits for two platforms are shown in Figure 8 and Figure 9. The values of the remaining parameters in Figure 6, Figure 7, Figure 8 and Figure 9 were set as $\alpha =0.8$, $\beta =0.2$, $\gamma =0.5$, $\delta =0.15$, $w_r=0.7$, $w_a=0.7$, $c_r=8$, $c_a=8$, $\lambda =0.1$, $\sigma =50$, $D_1=200$, and $D_2=300$.

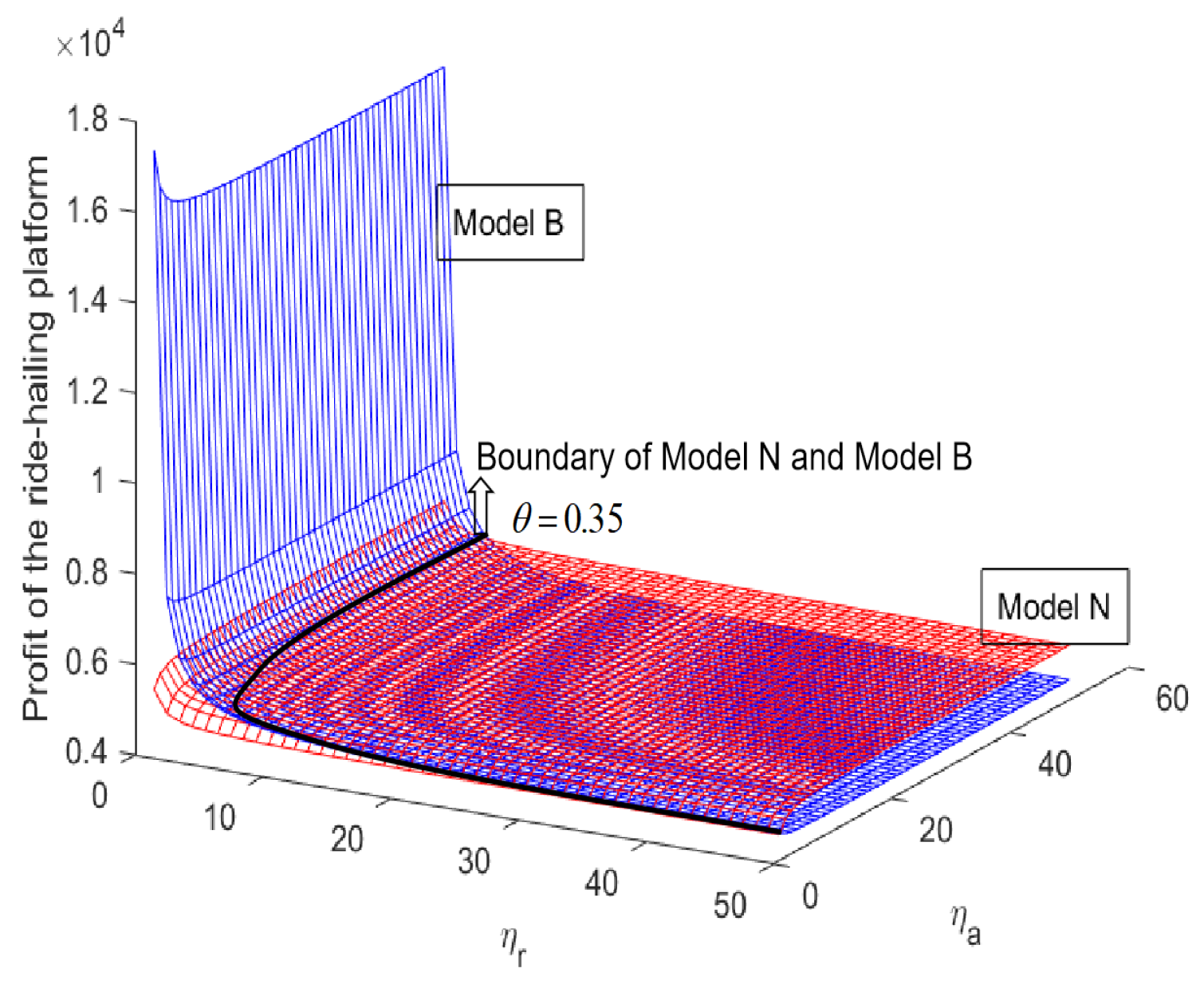
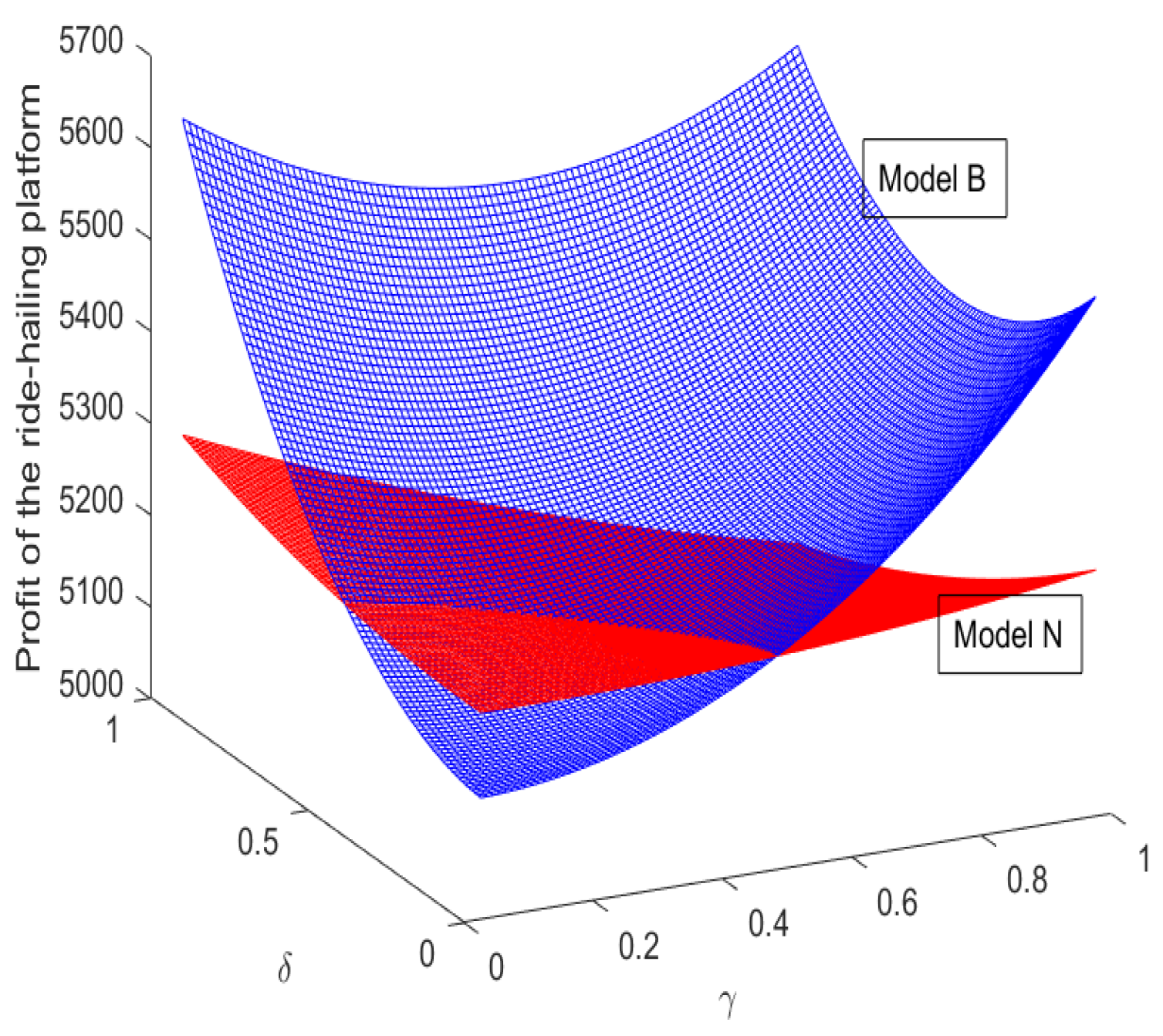
Figure 6 creates a three-dimensional surface plot as a sample for the case of $\theta =0.35$, where the red grid surface fills in Model N and the blue face grid surface fills in Model B. The function plotted the values in the ride-hailing platform’s profit (${\pi }_{rn}$ and ${\pi }_{rb}$) as heights above a grid in the ${\eta }_r-{\eta }_a$ plane where ${\eta }_r$ and ${\eta }_a$ are both on the ranges of [1, 50] with one unit step.

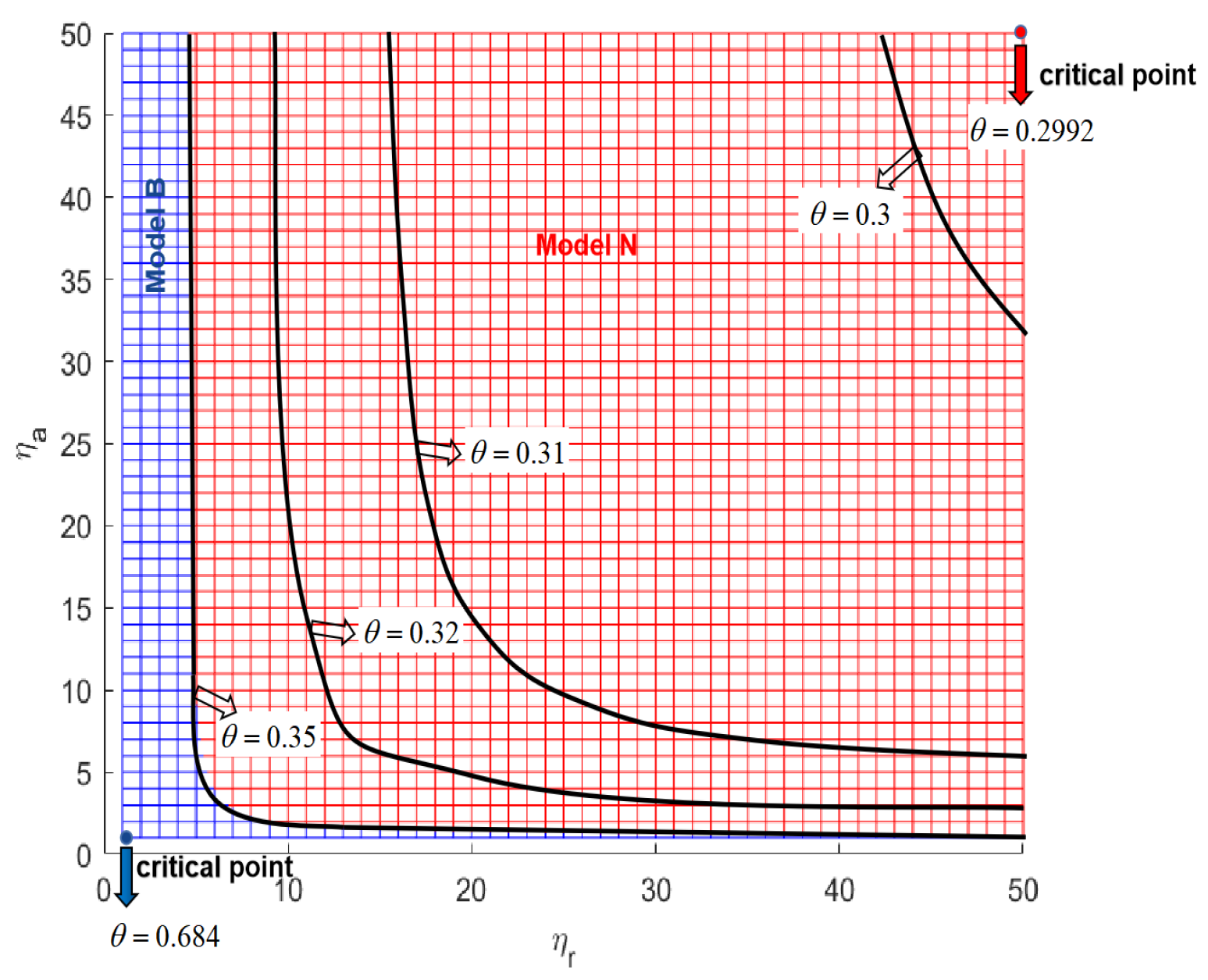
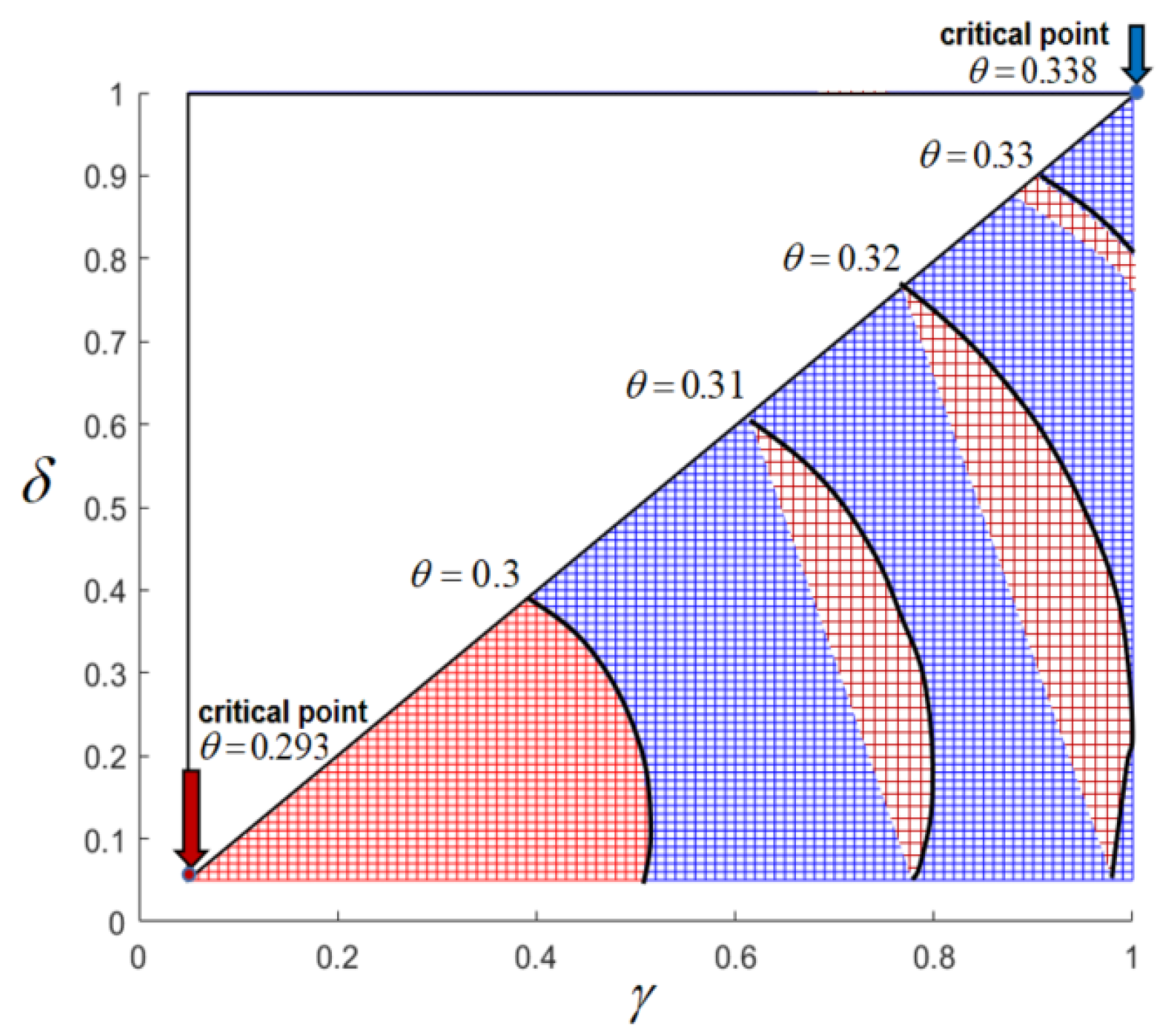
In Figure 7, projecting grid surfaces as like in Figure 6 onto ${\eta }_r-{\eta }_a$ plane, the color with the greater profit will cover the other color. Therefore, we give boundaries between the red and the blue with the growth of $\theta$ where the red line starts to appear on the ${\eta }_r-{\eta }_a$ plane (i.e., ${\eta }_r=50,{\eta }_a=50$), the critical point is $\theta =0.2992$. As the rise of $\theta$, the area of the red gradually expands until it is all covered with the red on the ${\eta }_r-{\eta }_a$ plane, at which the critical point is $\theta =0.684$. Some examples of boundary curves are also shown in this figure, in which $\theta$ are 0.3, 0.31, 0.32, and 0.35, respectively. From the critical point $\theta =0.2992$, the tinier change of the demand percentage $\theta$ brought the greater profit of the ride-hailing platform in Model N. It is observed that the more demand the ride-hailing platform obtained from the aggregation platform, the less profit it has when the ride-hailing platform is bundled on the aggregation platform in Model B. This can be explained by the revenue-sharing that causes the ride-hailing platform to pay more with the increasing demand.

There are some samples of boundaries in Figure 7. If $\theta$, the base demand percentage provided by the aggregation platform to the ride-hailing platform, is within [0, 0.2992], then the ride-hailing platform chooses Model N. If $\theta$ is within [0.2992, 0.684], then the ride-hailing platform chooses different models under some conditions. For example, when $\theta =0.3$, if ${\eta }_a<2.853\times {10}^{12}\times {\eta }_r^{-6.789}+23.62$ then it chooses Model B; if ${\eta }_a>2.853\times {10}^{12}\times {\eta }_r^{-6.789}+23.62$, then it chooses Model N; if ${\eta }_a=2.853\times {10}^{12}\times {\eta }_r^{-6.789}+23.62$, then there is no difference between Model N and Model B. When $\theta =0.31$, if ${\eta }_a<1.288\times {10}^{11}\times {\eta }_r^{-7.984}+7.213$ then it chooses Model B; if ${\eta }_a>1.288\times {10}^{11}\times {\eta }_r^{-7.984}+7.213$, then it chooses Model N; if ${\eta }_a=1.288\times {10}^{11}\times {\eta }_r^{-7.984}+7.213$,then there is no difference between Model N and Model B. When $\theta =0.33$, the boundary curve is ${\eta }_a=8.72\times {10}^{11}\times {\eta }_r^{-12.32}+3.377$. If $\theta$ is within (0.684, 1], then the ride-hailing platform chooses Model B.

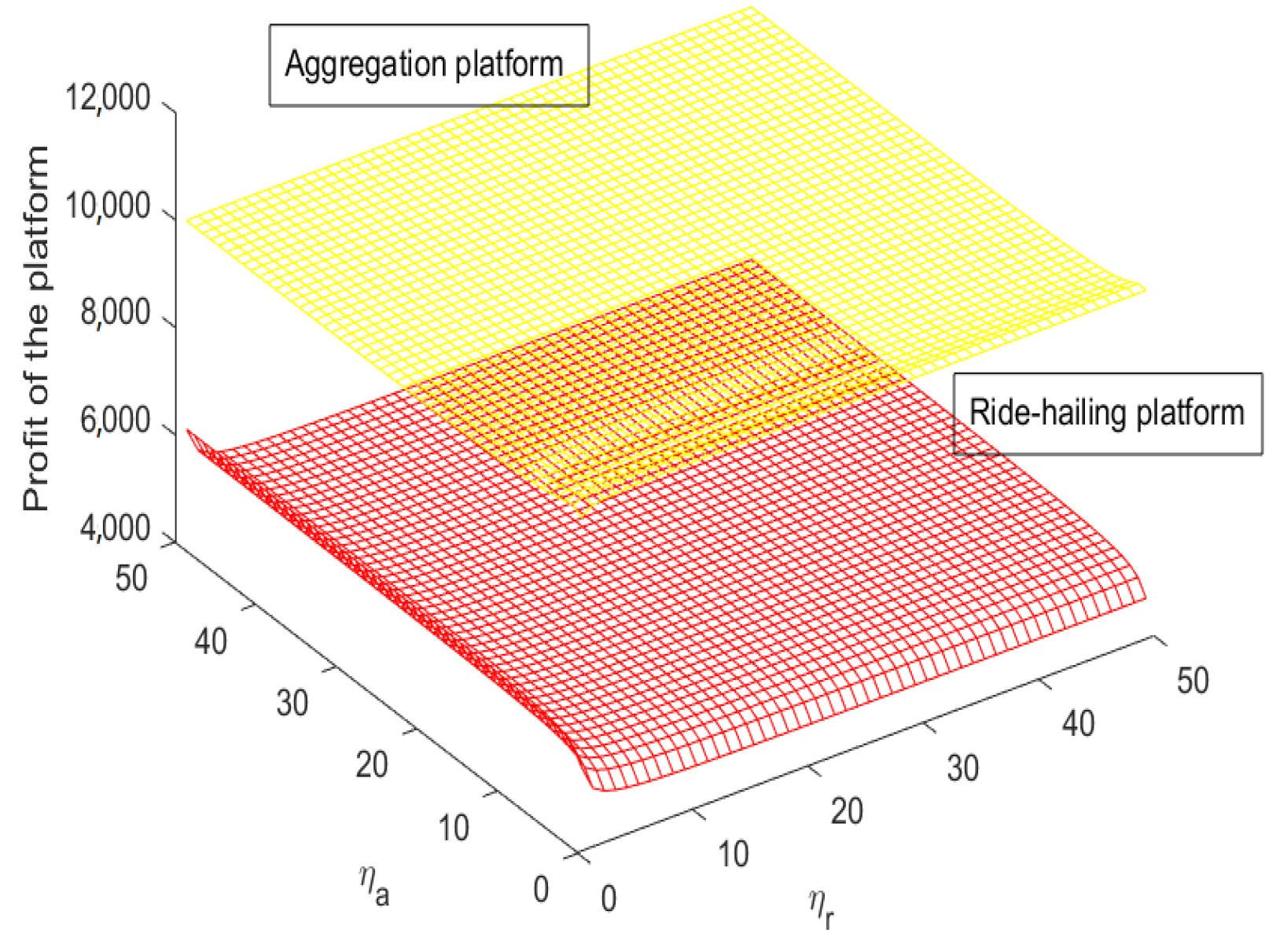
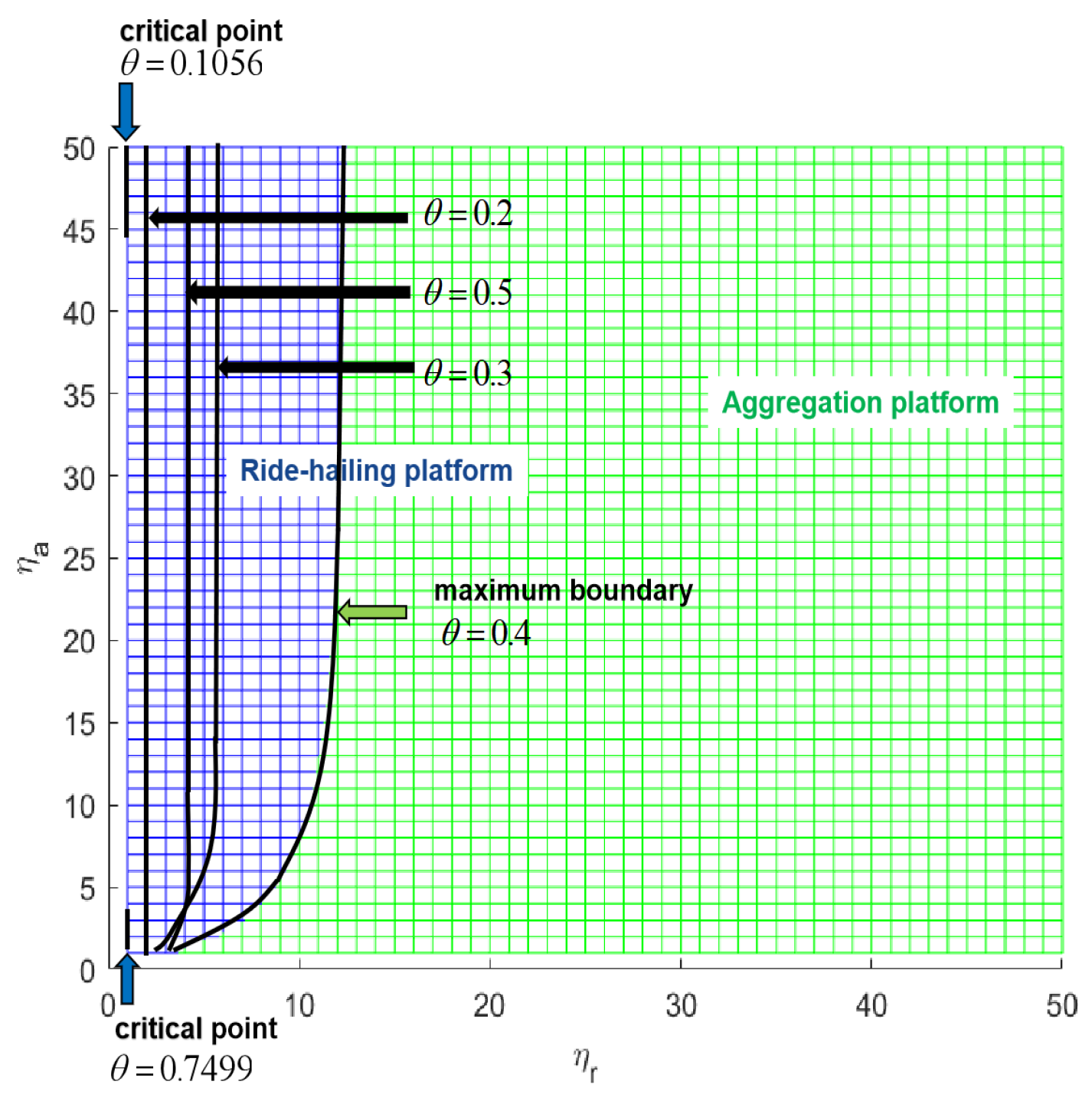
In Figure 8, the ride-hailing platform is at a disadvantage with the lower profit all the time in market competition in Model N. In Figure 9, the competition between the aggregation platform and the ride-hailing platform in Model B, projecting grid surfaces onto ${\eta }_r-{\eta }_a$ plane, the color with the greater profit will cover the other color. Therefore, we give boundaries between the green and the blue with the growth of $\theta$ where the blue line starts to appear on the ${\eta }_r-{\eta }_a$ plane (i.e., ${\eta }_r=1,{\eta }_a=50$), the critical point is $\theta =0.1056$. Then, with the rise of $\theta$, the area of the blue gradually expands at the maximum region with $\theta =0.4$, followed by the progressively smaller areas until the blue disappears at $\theta =0.7499$. Some examples of boundary curves are also shown in this figure, in which $\theta$ takes 0.2, 0.3, 0.4, and 0.5, respectively. From the critical point $\theta =0.1056$, the tinier change of the demand percentage $\theta$ brings the greater profit of the ride-hailing platform. It is observed that the more demand the ride-hailing platform obtained from the aggregation platform, the less profit it has when the ride-hailing platform is bundled on the aggregation platform in bundle mode.

5.2. Price Substitution and Cross-Price Substitution ($\alpha$ and $\beta$)

For $\alpha$ and $\beta$, the boundaries of the bundling option for the ride-hailing platform are shown in Figure 10 and the profit game between the two platforms in two models are shown in Figure 11. The values of the remaining parameters in Figure 10 and Figure 11 were set as $\gamma =0.5$, $\delta =0.15$, $w_r=0.7$, $w_a=0.7$, ${\eta }_r=48$, ${\eta }_a=40$, $c_r=8$, $c_a=8$, $\lambda =0.1$, $\sigma =50$, $D_1=200$, and $D_2=300$.

In Figure 10, based on three-dimensional surface plots where the ride-hailing platform’s profit value (${\pi }_{rn}$ and ${\pi }_{rb}$) as heights in the $\alpha -\beta$ plane, projecting grid surfaces onto $\alpha -\beta$ plane. With $\alpha >\beta$, only the lower triangle region was shown on the $\alpha -\beta$ plane. In Figure 10, the distinctions between red and blue areas were not clear with $\theta =0,0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1$, respectively. Unlike Figure 7, boundary curves were also irregular with the change of $\theta$. However, whatever the value of $\theta$, the alpha–beta combination on the blue line (i.e., $\beta =0.6484\alpha -0.0084$) rather than other blue regions for the ride-hailing platform always yielded a greater profit.

In Figure 11, projecting grid surfaces onto the $\alpha -\beta$ plane, the color with the greater profit covered the other color. Since the game between the two platforms in Model N is similar to Figure 8, we do not give the figure description that the aggregation platform always has a greater profit than the ride-hailing platform whatever the combination of $\alpha$ and $\beta$. It is necessary for the ride-hailing platform to choose Model B. In Figure 11, the competition between the aggregation platform and the ride-hailing platform in Model B, the distinctions between green and blue areas are not all clear with $\theta =0.31,0.4,0.5,0.6,0.7,0.8,0.9,1$. Unlike Figure 9, boundary curves are irregular with the change of $\theta$. Starting with $\theta =0.31$ until $\theta =1$, the ride-hailing platform has greater profits with some conditions.

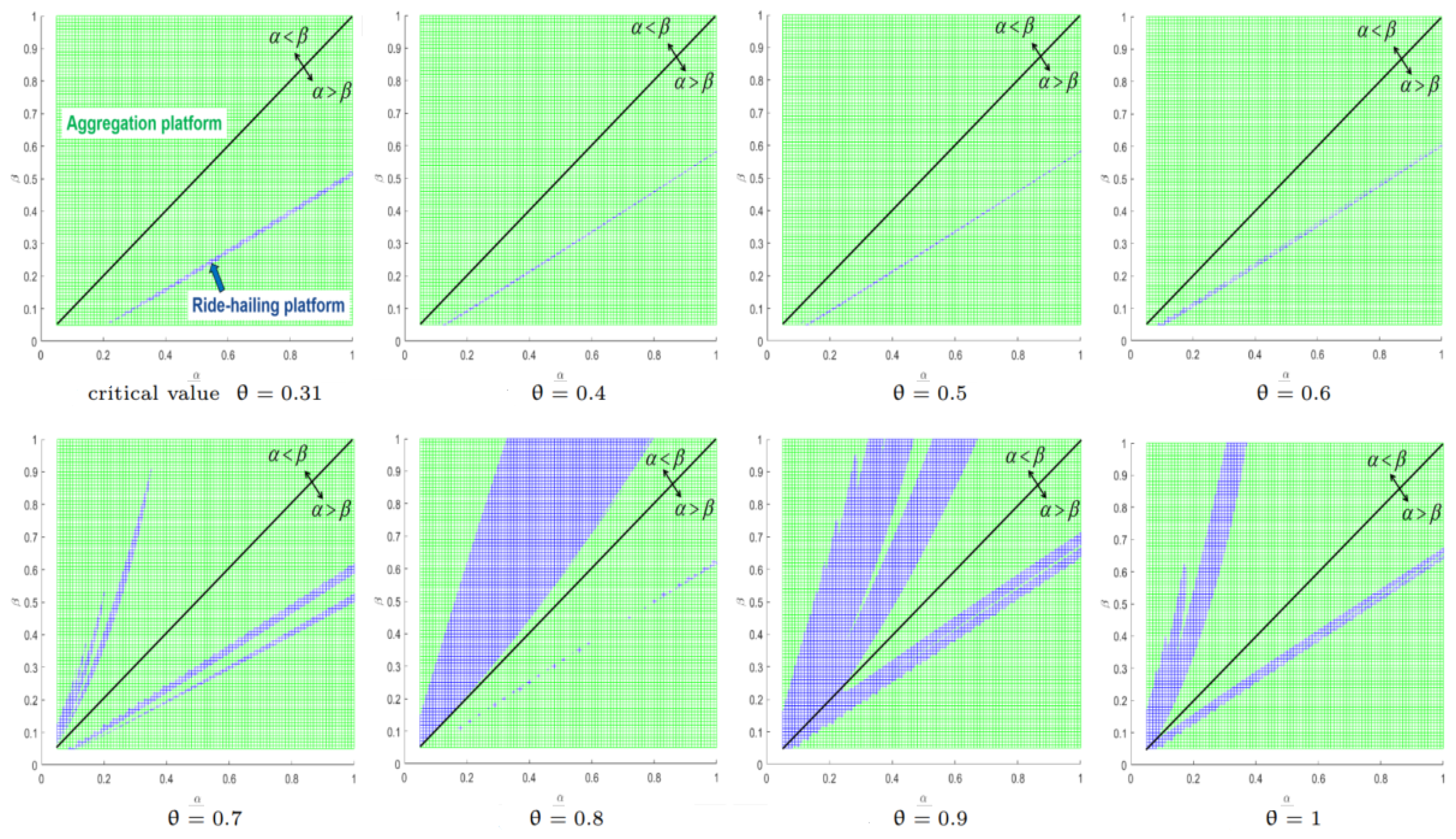
5.3. Service Level Substitution and Cross Service Level Substitution ($\gamma$ and $\delta$)

Through testing, the aggregation platform used to have a greater profit than the ride-hailing platform in both Model N and Model B whatever the combination of $\gamma$ and $\delta$. Thus, the service levels were at the disadvantage stage all the time in market competition. Regardless of the competition with the aggregation platform, however, there are differences for the ride-hailing platform to choose the bundling option. The boundaries of the bundling option for the ride-hailing platform are shown in Figure 12 and Figure 13. The values of the remaining parameters in Figure 12 and Figure 13 were set as $\alpha =0.8$, $\beta =0.2$, $w_r=0.7$, $w_a=0.7$, ${\eta }_r=48$, ${\eta }_a=40$, $c_r=8$, $c_a=8$, $\lambda =0.1$, $\sigma =50$, $D_1=200$, and $D_2=300$.

Figure 12 creates a three-dimensional surface plot as a sample of $\theta =0.3$. The function plotted the values in the ride-hailing platform’s profit (${\pi }_{rn}$ and ${\pi }_{rb}$) as heights above a grid in the $\gamma -\delta$ plane where $\gamma$ and $\delta$ are both on the ranges of [0.05, 1] with the step 0.01. In Figure 13, projecting grid surfaces onto $\gamma -\delta$ plane, the color with a greater profit will cover the other. Therefore, we give regular boundaries between the red and the blue with the growth of $\theta$ where the red line starts to appear on the $\gamma -\delta$ plane (i.e., $\gamma =0.05,\delta =0.05$), the critical point is $\theta =0.293$. Then, as a rise of $\theta$, the area of the red expanded until it is all covered with the red, at which the critical point is $\theta =0.338$. Some examples of boundary curves are also shown in this figure, in which $\theta$ was set as 0.3, 0.31, 0.32, and 0.33, respectively.

If $\theta$, the base demand percentage provided by the aggregation platform to the ride-hailing platform, is within [0, 0.293], then the ride-hailing platform chooses Model N. If $\theta$ is within [0.293, 0.338], then the ride-hailing platform chooses different models under some conditions. For example, when $\theta =0.3$, if $\gamma <-4.749{\delta }^{3.939}+0.5059$, then it chooses Model N; if $\gamma >-4.749{\delta }^{3.939}+0.5059$, then it chooses Model B; if $\gamma =-4.749{\delta }^{3.939}+0.5059$, then there is no difference between Model N and Model B. If $\theta$ is within [0.338, 1], then the ride-hailing platform chooses Model B.

5.4. Revenue Sharing Ratios of the Two Platforms ($w_r$ and $w_a$)

For ${\omega }_r$ and ${\omega }_a$, the bundling option for the ride-hailing platform is very single with the change of $\theta$. To be specific, the ride-hailing platform always chooses Model B except for the case of ${\omega }_r=1$ and ${\omega }_a=1$, and its profit always peaks at ${\omega }_r=0.9$ and ${\omega }_a=1$. In Model N, if ${\omega }_a<0.5111{\omega }_r+0.4889$, the aggregation platform has a greater profit than the ride-hailing platform, else if ${\omega }_a>0.5111{\omega }_r+0.4889$, the ride-hailing platform has a greater profit than the aggregation platform, then if ${\omega }_a=0.5111{\omega }_r+0.4889$, the ride-hailing platform and the aggregation platform have no difference in profits. In Model B, the aggregation platform has always more profits except for the case of ${\omega }_r=0.9$ and ${\omega }_a=1$. In other words, the ride-hailing platform’s profit can only choose and peak at ${\omega }_r=0.9$ and ${\omega }_a=1$. The values of the remaining parameters were set as $\alpha =0.8$, $\beta =0.2$, $\gamma =0.5$, $\delta =0.15$, ${\eta }_r=48$, ${\eta }_a=40$, $c_r=8$, $c_a=8$, $\lambda =0.1$, $\sigma =50$, $D_1=200$, and $D_2=300$.

5.5. Cost Prices of Two Platforms ($c_r$ and $c_a$)

For $c_r$ and $c_a$, the boundaries of the bundling option for the ride-hailing platform are shown in Figure 14 and Figure 15 and the differences of profits for two platforms are shown in Figure 16 and Figure 17. The values of the remaining parameters in Figure 14, Figure 15, Figure 16 and Figure 17 were set as $\alpha =0.8$, $\beta =0.2$, $\gamma =0.5$, $\delta =0.15$, $w_r=0.7$, $w_a=0.7$, ${\eta }_r=48$, ${\eta }_a=40$, $\lambda =0.1$, $\sigma =50$, $D_1=200$, and $D_2=300$.

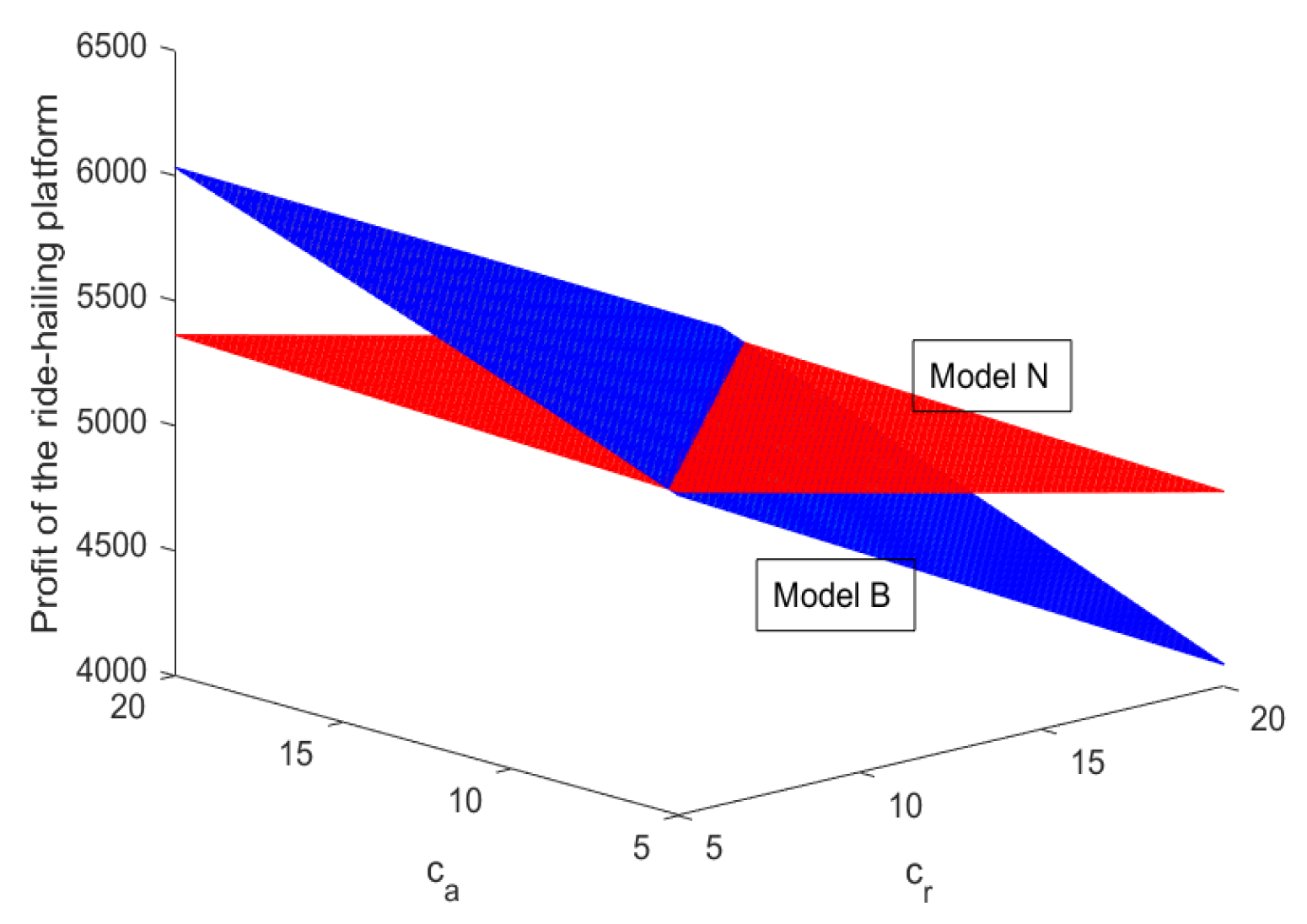
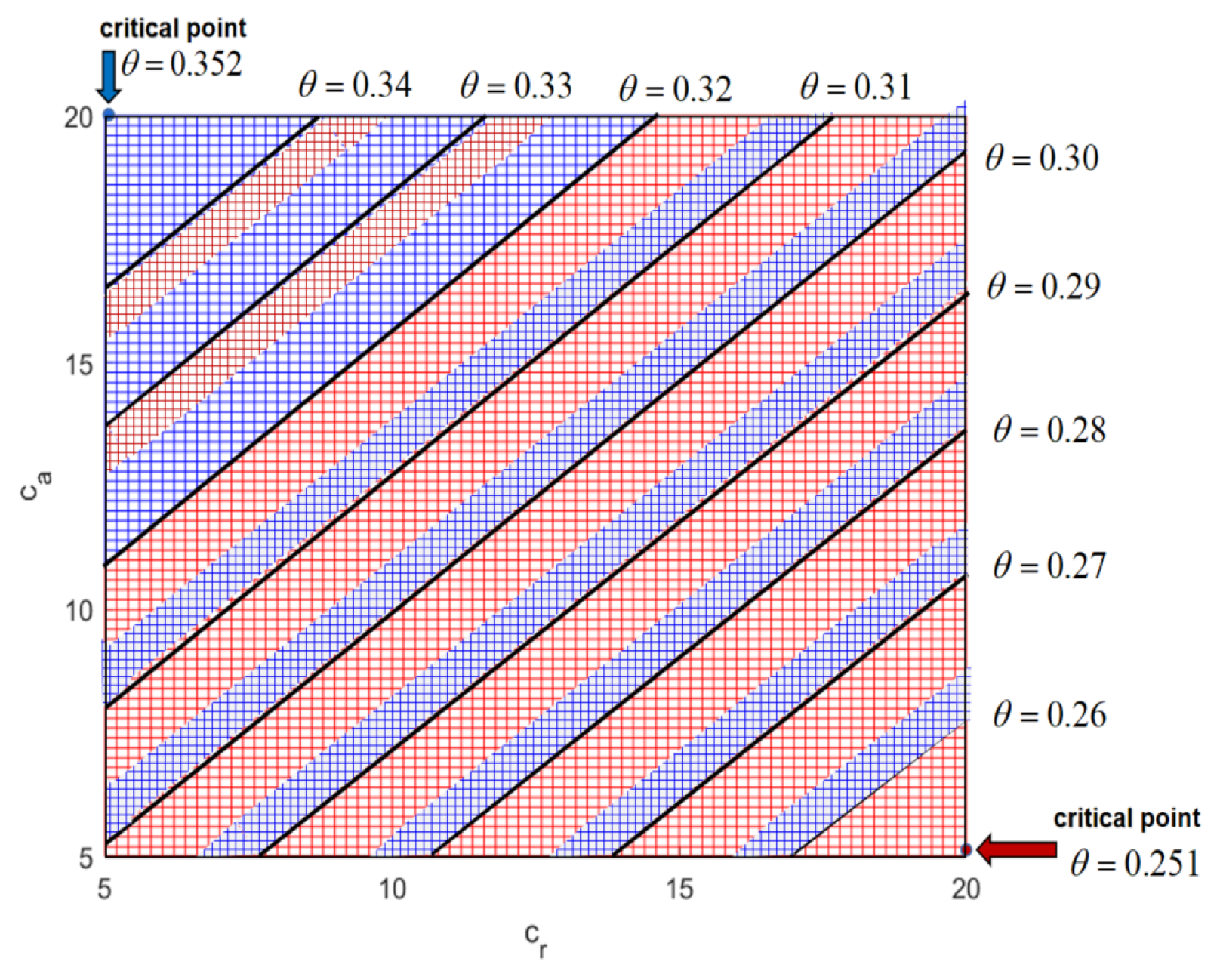
Figure 14 creates a three-dimensional surface plot as a sample for the case of $\theta =0.3$, where the red grid surface fills in Model N and the blue fills in Model B. The function plotted the values in the ride-hailing platform’s profit (${\pi }_{rn}$ and ${\pi }_{rb}$) as heights above a grid in the $c_r-c_a$ plane where $c_r$ and $c_a$ are both on the ranges of [5, 20] with the step 0.2. In Figure 15, we see grid surfaces projected onto the $c_r-c_a$ plane. Therefore, the regular linear boundaries are present between the red and the blue with the changes of $\theta$. Where the red started to appear on the $c_r-c_a$ plane (i.e., $c_r=20,c_a=5$), the critical point was $\theta =0.251$. Then, with the rise of $\theta$, the area of the red gradually expands until it is all covered with the red on the $c_r-c_a$ plane, at which the critical point is $\theta =0.352$. Some examples of boundary curves are shown in this figure, in which $\theta$ was set as 0.26, 0.27, 0.28, 0.29, 0.30, 0.31, 0.32, 0.33, and 0.34, respectively.

If $\theta$, the base demand percentage provided by the aggregation platform to the ride-hailing platform, is within [0, 0.251], then the ride-hailing platform chooses Model N. If $\theta$ is within [0.251, 0.352], then the ride-hailing platform chooses Model B under some conditions. If $c_a<0.9333c_r+272.3\theta -81.15$, then it chooses Model N; if $c_a<0.9333c_r+272.3\theta -81.15$, then it chooses Model B; if $c_a=0.9333c_r+272.3\theta -81.15$, then there is no difference between Model N and Model B. If $\theta$ is within [0.352, 1], then the ride-hailing platform chooses Model B.

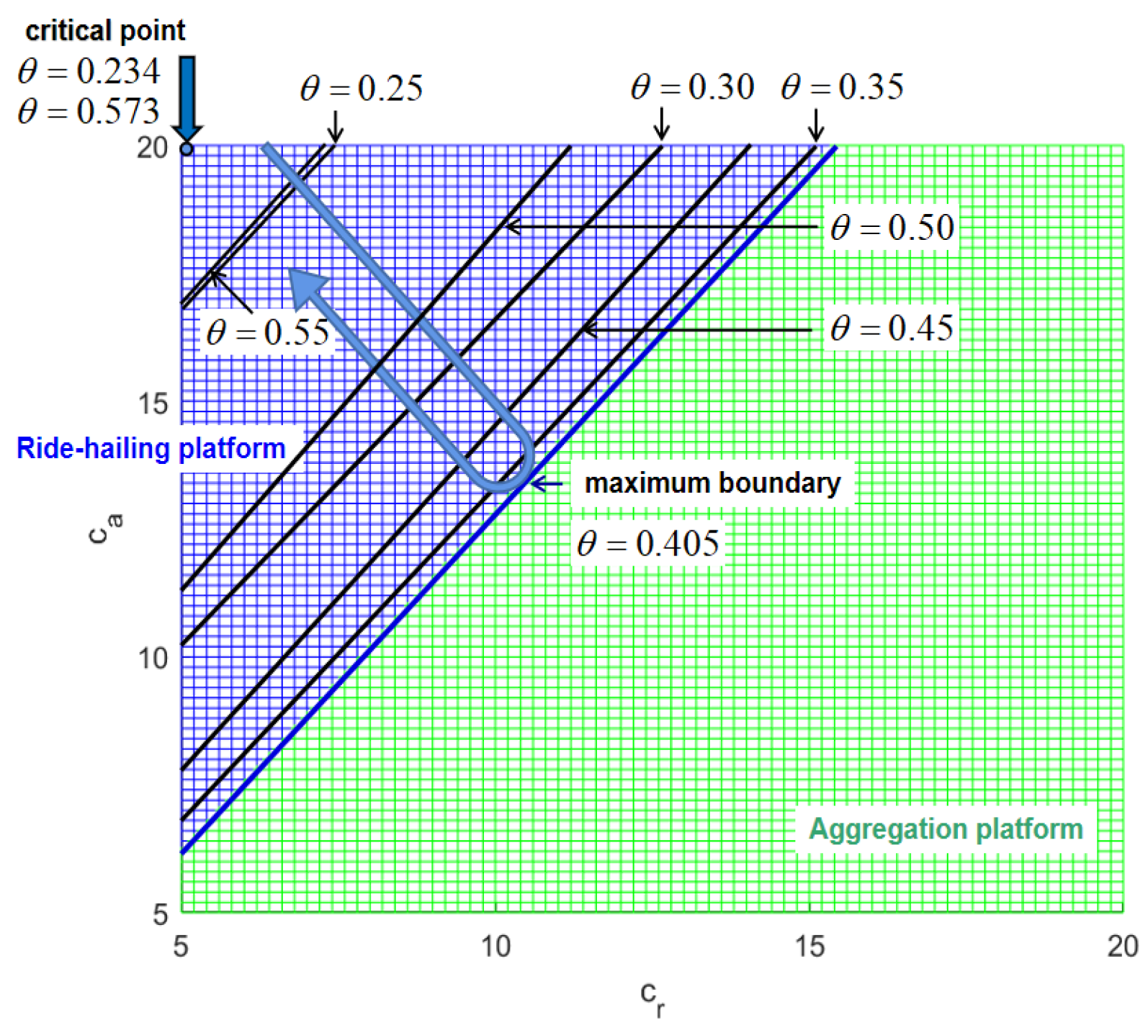
In Figure 16, the aggregation platform always has a greater profit than the ride-hailing platform whatever the combinations of $c_r$ and $c_a$. Thus, the ride-hailing platform is at a disadvantage all the time in market competition in Model N. In Figure 17, projecting grid surfaces onto $c_r-c_a$ plane, the color with the greater profit will cover the other color. Therefore, we give boundaries between the green and the blue with the changes of $\theta$ in Model B. The location where the blue starts and disappears on the $c_r-c_a$ plane is both on $c_r=5,c_a=20$, which corresponds to the critical point $\theta =0.234$ and $\theta =0.573$, respectively. To be specific, with the rise of $\theta$ beginning at 0.234, the area of the blue gradually expands at the maximum region with $\theta =0.405$, followed by the progressively smaller areas until the blue disappears at $\theta =0.573$. Some examples of boundary curves are also shown in this figure, in which $\theta$ was set as 0.25, 0.3, 0.35, 0.45, 0.50, and 0.55, respectively.

The change rate of $\theta$ is inconsistent with the change range of the intercept of the boundary on the $c_a$ axis. In Model B, the ride-hailing platform lowers costs compared the aggregation platform to gain more profits. If $\theta$ is within [0, 0.234] and [0.573, 1], the aggregation platform always has more profits than the ride-hailing platform. If $\theta$ is within [0.234, 0.573], the ride-hailing platform has more profits on the competition between the aggregation platform under some conditions. For example, with $\theta =0.405$, the ride-hailing platform chooses cost $c_r$ with the condition $c_r<0.7536c_a+0.3275$.

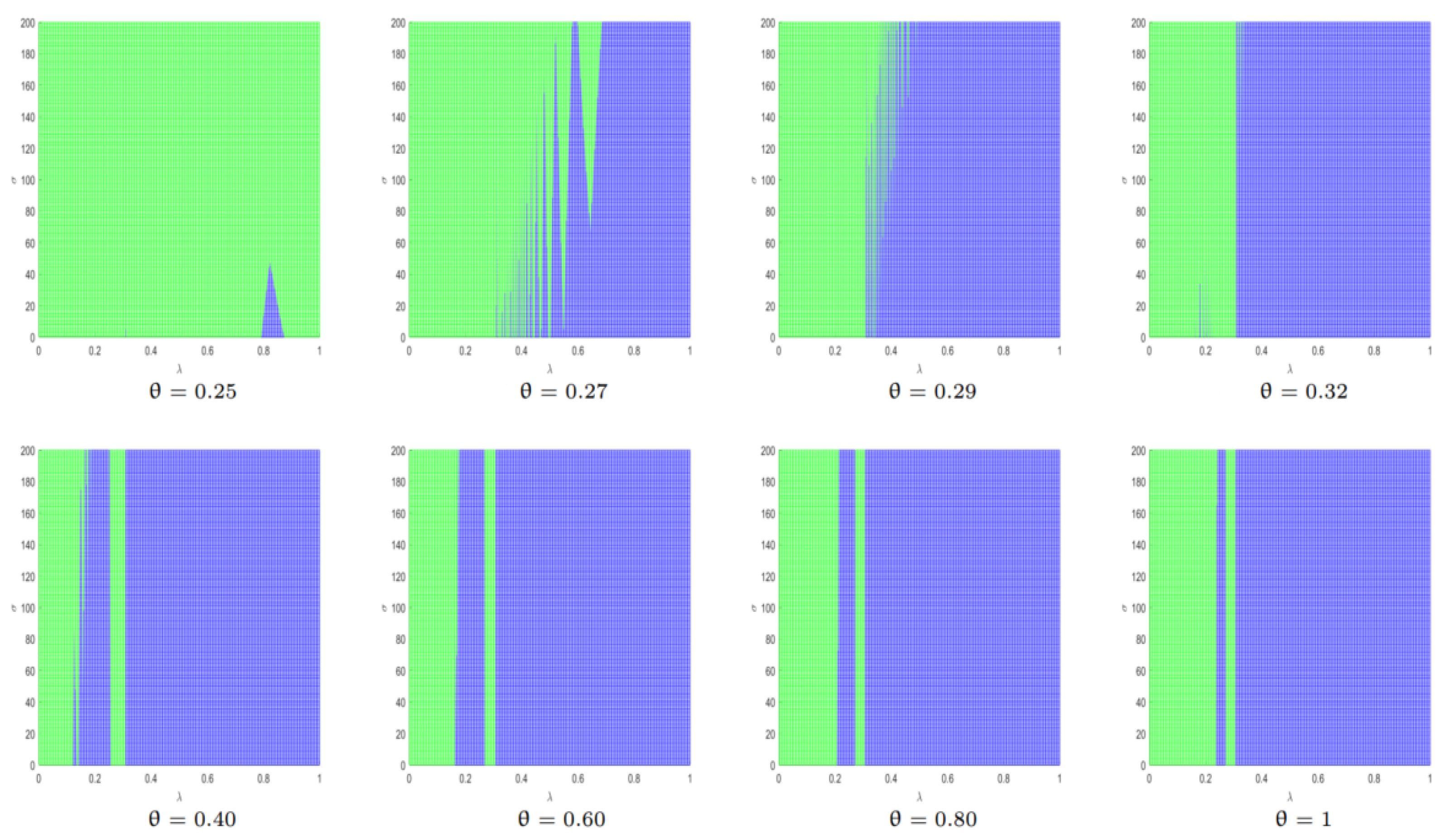
5.6. Commission and Slotting Fee ($\lambda$ and $\sigma$)

For $\lambda$ and $\sigma$, the boundaries of the bundling option for the ride-hailing platform are shown in Figure 18 and the differences of profits for two platforms are shown in Figure 19. The values of the remaining parameters in Figure 18 and Figure 19 were set as $\alpha =0.8$, $\beta =0.2$, $\gamma =0.5$, $\delta =0.15$, $w_r=0.7$, $w_a=0.7$, ${\eta }_r=48$, ${\eta }_a=40$, $c_r=8$, $c_a=8$, $D_1=200$, and $D_2=300$.

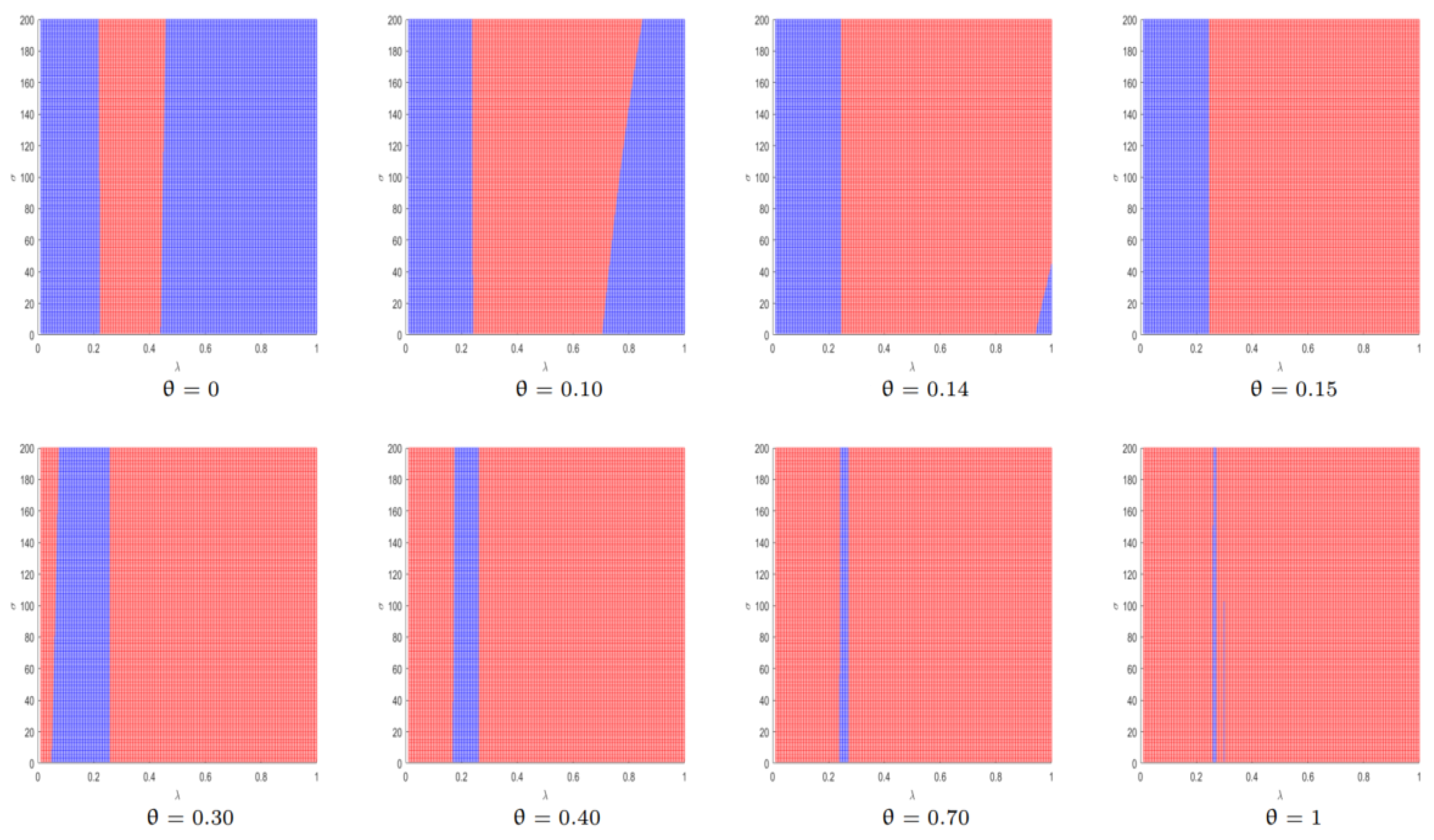
In Model N, the ride-hailing platform (${\pi }_{rn}$) has a fixed profit of 5203.9 with no regard as the changes of $\lambda$ and $\sigma$. In Figure 18, projecting grid surfaces with the heights (${\pi }_{rn},{\pi }_{rb}$) onto $\lambda -\sigma$ plane, the color with the greater profit will cover the other color, where $\lambda$ is on the range of [0, 1] with the step 0.01 and $\sigma$ is on the range of [0, 200] with one step. The boundaries change irregular, which present between the red and the blue with the changes of $\theta$ in Figure 18. When $\theta =0$, most of $\lambda -\sigma$ strategy combinations tend to Model B for the ride-hailing platform. With the rise of $\theta$, however, strategy combinations of Model N increase, which makes the values of $\lambda$ climb at first and then fall. The area of the red gradually expands until it almost covers the $\lambda -\sigma$ plane. When $\theta =1$, the majority of strategy combinations stand for Model N. Some examples of boundary curves are also shown in this figure, in which $\theta$ was set as 0, 0.10, 0.14, 0.15, 0.30, 0.40, 0.70, and 1, respectively.

Figure 19 describes the profits competition between the aggregation platform and the ride-hailing platform in Model B with the irregular strategy combinations of $\lambda$ and $\sigma$. Projecting profits ($p_{ab}$ and $p_{rb}$) grid surfaces onto $\lambda -\sigma$ plane, the color with a greater profit will cover the other color. Thus, we give advantaged areas of green and blue with the changes of $\theta$. Starting from $\theta =0.247$, the blue appeared on the $c_r-c_a$ plane on $\lambda =0.31$. With the rise of $\theta$ until $\theta =0.316$, the blue steadily filled up the area to the right of $\lambda =0.31$, i.e., $\lambda \in [0.31,1]$ and $\sigma \in [0,200]$. Followed by the blue appearing at $\lambda =0.26$, it then expanded toward $\lambda$ less than 0.26. At $\theta =0.569$, the blue accounted for the largest part on $\lambda -\sigma$ plane, followed by the decrease of the left area of $\lambda =0.26$. Some examples of boundary curves were also shown in this figure, which $\theta$ was 0.25, 0.27, 0.29, 0.32, 0.40, 0.60, 0.80, and 1, respectively. In Model B, the ride-hailing platform can gain more profit than the aggregation platform all the time by avoiding $\lambda \in [0,0.15)\bigcup (0.26,0.31)$.

6. Main Results and Discussion

We verified the impacts of six pairs of parameters for the ride-hailing platform on the bundle option and the competition in bundle mode, where four pairs (i, iii, iv, v) have regular boundaries, and two pairs (ii, vi) have irregular boundaries. On the one hand, the ride-hailing platform chooses to bundle in the aggregation platform under some conditions. The ride-hailing platform is at a disadvantage with the lower profit all the time in market competition in non-bundled mode. Thus, we study some conditions on the competition between the ride-hailing platform and the aggregation platform in the bundling mode. With the test in Section 5, we conclude some valuable issues of the results obtained.

(i) for ${\eta }_r$ and ${\eta }_a$: cost coefficients of service levels provided for the two platforms.

For the bundle option of the ride-hailing platform, the tinier change of the demand percentage $\theta$ brought the greater profit of the ride-hailing platform in non-bundle mode. It is observed that the more demand the ride-hailing platform obtained from the aggregation platform, the less profit it has when the ride-hailing platform is bundled on the aggregation platform in bundle mode. This can be explained by the revenue-sharing that causes the ride-hailing platform to pay more with the increasing demand. As the rise of the demand from the aggregation platform to the ride-hailing platform $\theta$, the base demand percentage provided by the aggregation platform to the ride-hailing platform, is within [0, 0.2992), then the ride-hailing platform intends to choose not bundling in the aggregation platform. If $\theta$ is within [0.2992, 0.684], then the ride-hailing platform chooses different models under some conditions. If $\theta$ is within [0.684, 1], then the ride-hailing platform always chooses to bundle in the aggregation platform.

Under the competition between the aggregation platform and the ride-hailing platform in bundle mode, with the rise of $\theta$, the ride-hailing platform has the greater profit than the aggregation platform within the range of $\theta \in [0.1056,0.7499]$. The ride-hailing platform has the maximum ratio profit with $\theta =0.4$. From the critical point $\theta =0.1056$, the tinier change of the demand percentage $\theta$ brings the greater profit of the ride-hailing platform. It is observed that the more demand the ride-hailing platform obtained from the aggregation platform, the less profit it has when the ride-hailing platform is bundled on the aggregation platform in bundle mode.

(ii) $\alpha$ and $\beta$: price substitution and cross-price substitution.

With the assumption of $\alpha >\beta$, only the lower triangle region was shown on $\alpha -\beta$ plane. Boundary curves were irregular with the change of $\theta$. However, whatever the value of $\theta$, the alpha–beta combination on the line of $\beta =0.6484\alpha -0.0084$ rather than other regions for the ride-hailing platform always yielded a greater profit. On the other hand, under the competition between the aggregation platform and the ride-hailing platform in bundle mode, the distinctions are not all clear and boundary curves are irregular with the change of the demand offered by the aggregation platform.

(iii) $\gamma$ and $\delta$: service level substitution and cross-service level substitution.

There are regular boundaries with the decrease of $\theta$ for the bundle mode. If $\theta$, the base demand percentage provided by the aggregation platform to the ride-hailing platform, is within [0, 0.293), then the ride-hailing platform chooses the non-bundle mode. If $\theta$ is within [0.293, 0.338], then the ride-hailing platform chooses different models under some conditions. Else if $\theta$ is within [0.338, 1], then the ride-hailing platform chooses the bundle mode.

(iv) $w_r$ and $w_a$: revenue-sharing ratios of the two platforms.

For ${\omega }_r$ and ${\omega }_a$, the bundling option for the ride-hailing platform is very single with the change of $\theta$. To be specific, the ride-hailing platform always chooses Model B except a couple of special cases. In Model N, if ${\omega }_a<0.5111{\omega }_r+0.4889$, the aggregation platform has a greater profit than the ride-hailing platform, else if ${\omega }_a>0.5111{\omega }_r+0.4889$, the ride-hailing platform has a greater profit than the aggregation platform, then if ${\omega }_a=0.5111{\omega }_r+0.4889$, the ride-hailing platform and the aggregation platform have no difference in profits. In Model B, the aggregation platform has always more profits except a certain cases.

(v) $c_r$ and $c_a$: cost prices of the two platforms.

Therefore, the regular linear boundaries are present for the bundle option of the ride-hailing platform with the changes of $\theta$. If $\theta$, the base demand percentage provided by the aggregation platform to the ride-hailing platform, is within [0, 0.251], then the ride-hailing platform chooses the non-bundle mode. If $\theta$ is within [0.251, 0.352], then the ride-hailing platform chooses the bundle mode under some conditions. If $\theta$ is within [0.352, 1], then the ride-hailing platform chooses the bundle mode. Under the competition between the aggregation platform and the ride-hailing platform in Model B, if $\theta$ is within [0, 0.234] and [0.573, 1], the aggregation platform always has more profits than the ride-hailing platform. Otherwise, if $\theta$ is within [0.234, 0.573], the ride-hailing platform has more profits on the competition between the aggregation platform under some conditions.

(vi) $\lambda$ and $\sigma$: commission and slotting fee charged by the aggregation platform.

For the bundle option of the ride-hailing platform, boundaries change irregularly. When $\theta =0$, the ride-hailing platform tends to bundle in the aggregation platform for most of $\lambda -\sigma$ strategy combinations. With the rise of $\theta$, however, strategy combinations of Model N become more, which makes the values of $\lambda$ climb at first and then fall. The area of the red gradually expands until it almost covers the $\lambda -\sigma$ plane. When $\theta =1$, the majority of strategy combinations stand for Model N. Under the competition between the aggregation platform and the ride-hailing platform in Model B with the irregular strategy combinations of $\lambda$ and $\sigma$. In Model B, the ride-hailing platform can gain more profit than the aggregation platform all the time by avoiding $\lambda \in [0,0.15)\bigcup (0.26,0.31)$.

7. Conclusions

This paper provided a new perspective for the channel selection problem on the ride-hailing platform by introducing bundled services. We presented an analytical framework for the ride-hailing platform in unbundled and bundled cases, providing two Stackelberg games in which the driver group serves to two asymmetric platforms at the service level and each platform as the leader decides the price for the driver group. Considering the ride-hailing and aggregation Stackelberg games simultaneously, we set up a Nash equilibrium between the two platforms to obtain prices. We dug deeply about the motivation for the ride-hailing platform to adopt the bundling option, and platform strategies for introducing bundled services. The equilibrium between the ride-hailing platform and the aggregation platform is in line with the total profit maximization with the decreased profit of the aggregation platform and the increased profit of the ride-hailing platform.

We verified the impacts of six pairs of parameters on the bundling option for the ride-hailing platform and the profit game in Model B (the bundled model), where four pairs (cost coefficients of service level provided for two platforms, service level substitution and cross-service level substitution, revenue-sharing ratios of two platforms, cost prices of two platforms) have regular boundaries, and two pairs (price substitution and cross-price substitution, commission and slotting fee charged by the aggregation platform) have irregular boundaries. We obtained the bundling option for the ride-hailing platform in regular four parameter pairs and some examples with irregular two parameter pairs. As the aspect of the bundling option for the ride-hailing platform, more strategies (cost coefficients of service level provided for two platforms, service level substitution, and cross-service level substitution) on Model B the ride-hailing platform can be chosen as the demand provided by the aggregation platform decreases. On the contrary, fewer strategies of cost prices the ride-hailing platform can be chosen with the falls of demand. Moreover, in the strategy set of revenue-sharing ratios, the ride-hailing platform is more advantageous to choose Model B besides two cases. We then gave the profit game between the aggregation platform and the ride-hailing platform in regular four parameter pairs and some examples with irregular two parameter pairs. In Model N (the unbundled model), the aggregation platform always has higher profits than the ride-hailing platform. As the demand rises and then declines, more strategies of costs and cost coefficients of service level on Model B the ride-hailing platform can be chosen. The aggregation platform has much more profits than the ride-hailing platform regardless of service level substitution and cross-service level substitution as well as revenue-sharing ratios.

In the future, we will study the ride-hailing platform by considering the elastic travel demand. In the early days of the emergence of aggregation platforms, accepting bundled services seems the right choice for ride-hailing platforms. However, if too many platforms enter, the demand allocated by aggregation platforms to ride-hailing platforms will decrease. This will inevitably lead to competition among ride-hailing platforms on the aggregation platforms. As aggregation platforms grow, it is worth considering the number of bundled ride-hailing platforms introduced to aggregation platforms.