T-Smart: Trust Model for Blockchain Based Smart Marketplace

Abstract

With the innovation of embedded devices, the concept of smart marketplace came into existence. A smart marketplace is a platform on which participants can trade multiple resources, such as water, energy, bandwidth. Trust is an important factor in the trading platform, as the participants would prefer to trade with those peers who have a high trust rating. Most of the existing trust management models for smart marketplace only provide a single aggregated trust score for a participant. However, they lack the mechanism to gauge the level of commitment shown by a participant while trading a particular resource. This work aims to provide a fine-grained trust score for a participant with respect to each resource that it trades. Several parameters, such as resource availability, success rate, and turnaround time are used to gauge the participant’s level of commitment, specific to the resource being traded. Moreover, the effectiveness of the proposed model is validated through security analysis against ballot-stuffing and bad-mouthing attacks, along with simulationbased analysis and a comparison in terms of accuracy, false positive, false negative, computational cost and latency. The results indicate that the proposed trust model has 7% better accuracy, 30.13% lower computational cost and 31.74% less latency compared to the existing benchmark model.

1. Introduction

The evolution of sensor-enabled smart gateways in smart homes has led to creative collaboration practices among participants of smart communities [1]. Such collaborations involve the exchange of resources (such as water, internet bandwidth, energy) in the form of trading, where a participant may request resources from other participants in exchange of a digital currency, such as ether [1,2]. This type of trading platform is also known as a smart marketplace (SMP) [1,3]. SMP, as a resource trading platform, faces a range of privacy- and security-related challenges, such as vulnerability and controller compromise, which are addressed through authentication- and cryptography-based solutions in the literature [4,5,6].

In SMP, a participant node can act dishonestly, either to promote itself or to malign the reputation of other nodes [7,8]. Through this, a dishonest participant can maneuver requester participants to trade resources with it instead of the honest participants and dominate the trade by carrying out attacks, such as bad-mouthing and ballot-stuffing. In a bad-mouthing attack, the malicious participant tries to lower the trust score of an honest participant by providing false reviews and, therefore, reducing their chance of being selected as a service provider. This attack can also be carried out by group of dishonest participants to defame an honest participant. In a ballot-stuffing attack, the malicious participant tries to boost the trustworthiness of other malicious participants by providing false favorable recommendations. This can increase their chance of being selected as a trustworthy participant. This attack can also be carried out by a group of dishonest participants to support each other. In order to handle these attacks and maintain the true reputation of the participating nodes, there is a need for a better trust management scheme.

A number of trust management schemes have been proposed for the smart marketplace (SMP), such as [9,10,11,12], where trust calculation is based on the direct observations of each participant with respect to others during peer-to-peer (P2P) interactions, such as trading activities, and the indirect feedback obtained from other participants. For example, to accurately measure the trust of a resource seller, a participant must share their trust score with multiple other SMP participants [13,14,15,16]. Similarly, other works such as [8,17,18,19] propose to strengthen the trust computing mechanism and refine the properties of participants using a number of other techniques, such as unified trust management. Ref. [20] utilized commitment as a measure to gauge resource provider’s honesty towards a resource.

Most of the existing trust management schemes for SMP are designed considering the fact that the participants can trade only one type of resource, such as energy or internet bandwidth. Hence, such schemes are not suitable for a participant who tends to trade multiple resources at a time [7]. Besides, these schemes suffer from issues of unfair trust calculation based on unreliable information shared by dishonest participants [20]. Additionally, trust information (direct observation and indirect feedback) is exchanged in a manner that decelerates the process of trust computing and produces inconsistent results [7,8,15,16]. Moreover, other trust models typically assume third party controllers to be a pre-trusted entity [21], which is often not feasible for most SMP implementations [7].

The goal of this research is to present a trust management model that can provide a detailed trust profile (separate trust score per individual resource) of a participant in the role of a seller or buyer of various resources. Moreover, the model is resilient to various types of bad-mouthing and ballot-stuffing attacks and provides a fair trust score of the participants.

Our Contribution: In this paper, we have presented a trust management model for detailed trust profiling of SMP participants as follows:

• The model computes separate trust score per resource for a participant to ensure fair and genuine trust management.
• Trust of a participant is calculated based on past experiences, feedback provided by other participants and the level of commitment a participant has shown to carrying out the transactions.
• Ethereum Blockchain is used to ensure the security, validation, and trust for all the participants within the smart marketplace.

The proposed work has been implemented using Solidity and Python. Simulations were performed with trustworthy and dishonest participants in a smart marketplace. Our results have shown that the proposed framework comprehensively captures the trust of the participants and helps to improve trading among honest participants, and also identify dishonest participants.

2. Related Work

Advancements in digital technology have substantially changed the pace of operations by enabling business to business (B2B) to efficiently handle huge amounts of data and manage transactions [22], especially in e-commerce smart marketplaces [23]. To enhance the profitability and efficiency of e-commerce firms, blockchain technology is incorporated in SMP. Blockchain technology has helped enhance the payment speed and data transmission dependability and transparency of data transmission [24,25]. Blockchain helps to ensure that the information involved is anonymized and immutable. The exchanging of data among different participants gives rise to security issues, especially when trading participants have interchangeable roles in SMP [26]. The major advantage of utilising blockchain is that it provides a secure decentralised database. Additionally, the importance of trust management in e-commerce businesses cannot be overstated, as each participant would always prefer to transact with a party with a good reputation to prevent being victimized by less reputable parties.

Trust and credibility mechanisms have been extensively researched to support the activities of participants in the SMP [17,20]. In a particular context, trust and credibility structures aim to estimate the trustworthiness of prospective participants, to minimize risk due to their likely unreliability. In fact, the importance of trust-based schemes is shown by their adoption in virtually every decision-making and trading interaction in SMP activities [19,20]. For instance [27,28,29] have classified trust management components into five main components, namely: trust composition, trust spread, trust aggregation, trust update, and trust creation. Similarly, Study [30,31] sets out the key characteristics of an efficient reputation scheme consisting of three main properties, including, first, the use of past experience of participants to detect potential future behavior of other participants in the system. Second, decisions on new experiences can be guided by previous experiences. Third, ratings on existing experiences need to be obtained, including planning rewards to persuade participants to release feedback that needs to be disseminated to the population. Other work, such as [32], have examined and addressed the importance of feedback in trustworthiness models to develop trust management framework.

To address issues related to trust management in an SMP environments, many works, such as [7,33,34], suggested a trust management mechanism based on a central controller that is responsible for distributing the trust obtained across the network. However, these trust models can have many limitations, such as latency issues, central point of failure, and other computational complexities [28,32,35]. Similarly, two trustworthiness computational models have been presented by [36]; they are used to distribute trust evaluations in a shared Hash table managed by a group of trusted participants. These models comprise, first, a subjective model consisting of local trust matrix (direct observation) and the indirect feedback received and, second, an objective model. However, options are also constrained and only applicable to social-based participants [7,35].

Additionally, models such as [37,38] use recommendations to compute trust based on information gathered from a neighbouring participant, where trust is computed by the pre-selected participant. Such approaches help with cost reduction by assuming a participant as an intermediary; however, such models lead to unreliable information due to their reliance on a single SMP data source for computing trust.

Other models, such as [36,39], have based their trust assessment on direct observations, and the history of interactions and recommendations from other system participants. In addition, the studies considered different classes of trust properties, such as commitment, honesty and co-operation, depending on the social relationship between the participants. However, the solutions are not feasible enough, since each participant must store all the trust pieces of information, including the history and recommendations of the other participants in the lookup table [7,28,35].

The concept of grouping was also used in many approaches, such as [8,13], to address trust management issues. These approaches combine individuals with a comparable trust score and allow trade amongst them, avoiding the selection of an untrustworthy trading partner. However, these solutions usually demand high computational resources and may lead to double spending issues [35]. When groups are formed based only on how similar the profiles of the potential group members are, then it is not guaranteed that groups will remain homogeneous over time [40]. This, and other similar group challenges, are usually referred as group recommendation (affiliation problems) [29].

To make trading decisions, the existing work uses an aggregated trust score for participants rather than a resource-specific (separate trust score for each unique resource) and role-specific (seller/buyer) trust score for each participant. Such techniques are incapable of determining a participant’s fair and genuine trust score. Additionally, current models are vulnerable to attacks such as bad-mouthing and ballot stuffing, since participants may behave dishonestly to advance their own careers or to smear the reputations of others. Moreover, the computation of the trust score in SMP may result in cost and latency problems.

3. System Model

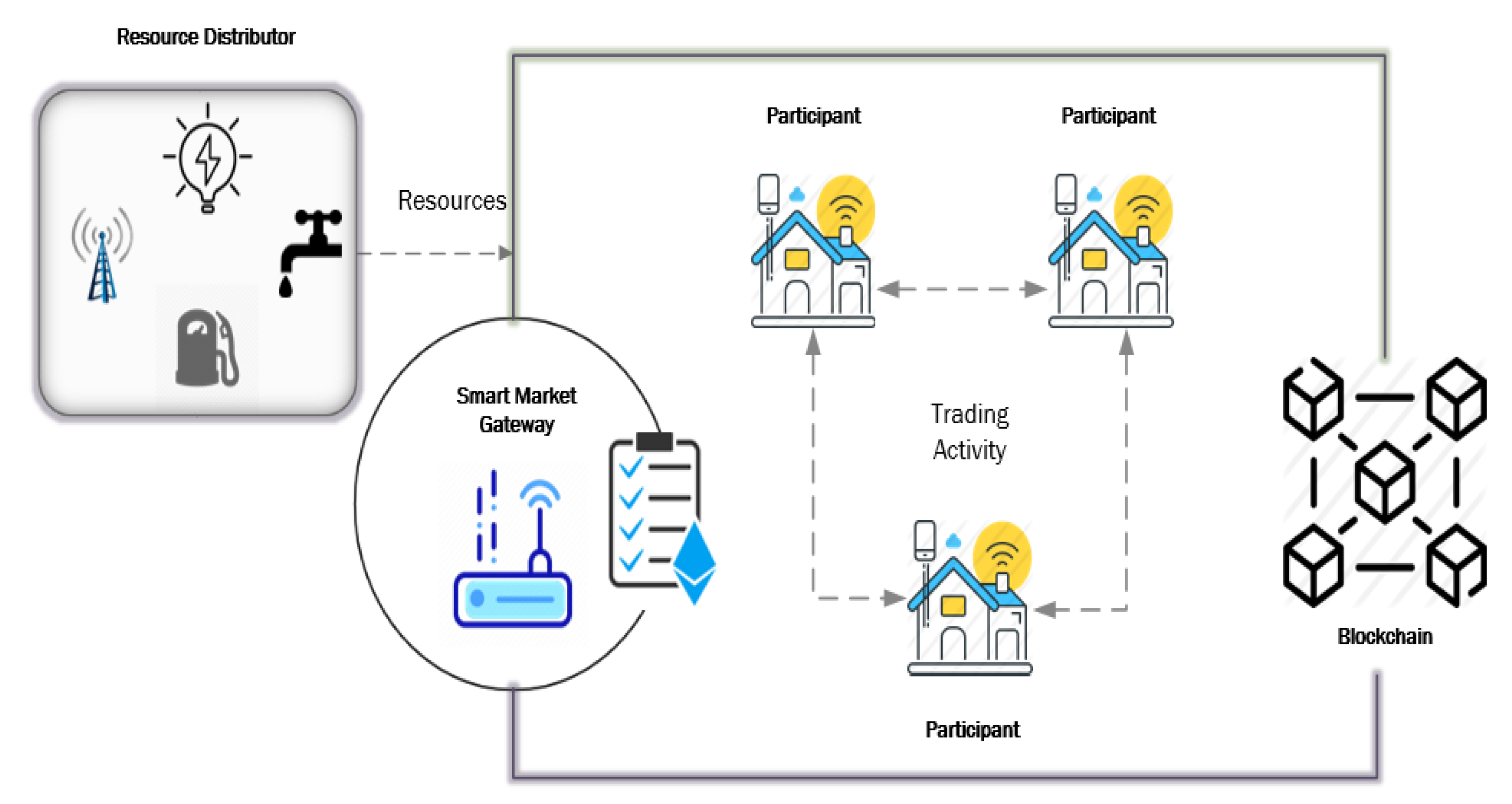
This section discusses our system model, including network model, trading model, and the threat model.

3.1. Network Model

Our network model for SMP is derived from [1], where the SMP consists of a tamper-proof smart gateway known as the Smart Market Gateway (SmGW). Each smart home has a sensor-enabled smart gateway that is used to connect with SmGW in SMP. A given set of smart home participants $P=\{p^1,p^2,p^3,\dots p^q\}$, A smart home in SMP can engage in a resource trade, either as a seller or a buyer, as shown in Figure 1. Resource Distributor (RD) represents the resource providing entities to smart homes, such as electricity and telecommunication companies. The SMP is built on z semi-centralized private Ethereum blockchain technology, as transactions performed on Ethereum blockhain are much faster than those performed on bitcoin. All participating smart homes are computationally capable and have full access to the shared ledger where all transactions are registered. Moreover, all SMP participants have a separate Ethereum Account (EA) and can directly access blockchain Smart Contracts across the network.

3.2. Trade Model

The stakeholders engaged in the execution of a transaction include: a set of smart home participants P (sellers and buyers) and the Smart Market Gateway (SmGW). A seller participant might become a buyer participant at a given time t, and vice versa. The seller sends the offer to the SmGW, to be placed on the auction board. The offer contains the price, quantity, type of resource being sold, and the resource ownership ID. SmGW verifies the resource by sending the $id$ of a seller along with the resource ownership ID to RD before placing the bid on the auction board. After a successful negotiation between the potential buyer and the seller, the buyer surrenders the payment and the seller surrenders the resource by executing their respective Smart Contracts, completing the trading activity. Moreover, SMP allows a participant to trade a variety of resources, such as energy, internet bandwidth, nd water. Additional information regarding the trading model can be found in [1].

3.3. Threat Model

In this work, the following features are considered for Adversary A:

• Adversary $\mathcal{A}$ can carry out a variety of attacks, such as ballot-stuffing and bad-mouthing attacks in the SMP.
• It is presumed that smart gateway is tamper-proof, and thus cannot be breached.
• It is presumed that the adversary does not compromise the blockchain.

4. The Trust Management Model

This section presents the proposed trust model that can be utilized to gauge the trust of participants in the SMP.

4.1. Trust Computation and Modeling

The proposed trust model is designed to record the trust of each participant separately as a seller and a buyer for each of the traded resource, such as water, energy, and bandwidth. Given a set of all type of resources $R^{*}$= { $r_1$, $r_2$, $r_3$, … , $r_n$} and $r_x$ is a given resource in $R^{*}$, then the trust can be computed based on participants’ previous trust, participants’ commitment ($C_p^{r_x}$) [20], and their feedback (${fb}_p^{r_x}\left(t\right)$). Hence, the trust score for a given participant is computed as,

$${TS}_p^{r_x}\left(t\right)=\alpha \left({TS}_p^{r_x}(t-1)\right)+\beta \left(C_p^{r_x}\right)+\phi ({fb}_p^{r_x}\left(t\right))$$

(1)

where $\alpha$,$\beta$,$\phi$ are weights with values ranging from 0 to 1. n is the number of resources (energy, water and bandwidth) and p is the participant for which trust is being computed. Once the trust score is computed, it is then stored in blockchain. The process of calculating trust score is illustrated in Algorithm 1.

Algorithm 1: Computing trust score for SMP participants.

4.1.1. Commitment ($C_p^{r_x}$)

Three distinct parameters were considered when computing the $C_p^{r_x}$ of a given participant. These include the resource integrity, success rate and turnaround time. The $C_p^{r_x}$ of a given participant is evaluated by the system when bids are received in the auction board, as described in lines 1–10 of Algorithm 1. This is performed based on the trading history of the concerned participant. The evaluation process is further explained in the following subsections.

Resource Availability: Resource Availability plays an important role in calculating trust for a participant. A resource must be available before it is broadcast onto the auction board. SmGW verifies the availability of a resource by taking into account the $id$ of a seller participant along with the resource ownership ID and confirming it with RD before allowing a participant to broadcast their bids on the auction board. In this model, a resource is unavailable even if a seller participant has broadcast their bids and yet not agreed to sell them. Let $N_{r_x}$ be the number of times a single resource was requested to be listed over a time and $A_{r_x}$ be the number of times the resource was available out of $N_{r_x}$. Hence, the availability of a resource is computed as given in Equation (2). Therefore, once a buyer participant requests a given resource, the system computes the provider’s resource availability (RA) according to line 5 of Algorithm 1.

$$R{A}_{r_x}=A_{r_x}/N_{r_x}$$

(2)

Success Rate: Success rate is the number of successful trades concluded for a resource $r_{x}s$. Let $S_{r_x}$ be the number of successful trades conducted out of $A_{r_x}$. The success rate can be calculated as given in Equation (3).

$$S{R}_{r_x}=S_{r_x}/A_{r_x}$$

(3)

Turn Around Time: Turnaround time is the delay in responding to a request either from a seller or buyer perspective. The turnaround time can be calculated depending on the state of the participant (seller or buyer). These processes are explained in the following subsections.

a. For participant as seller: In this regard, the turnaround time $\left(T{A}_{r_x}\right)$ for a given resource is the difference between the time of delivery $\left(t_{dev}\right)$ and time of request $\left(t_{req}\right)$ for a resource. It is defined as the time difference when a buyer participant has requested a particular resource from seller participant up to the time the resource is successfully delivered by the seller participant. Hence, turnaround time can be calculated as

$$T{A}_{r_x}=(t_{dev}-t_{req})/(t_{dev}+t_{req})$$

(4)

b. For participant as buyer: In this regard, the turnaround time $\left(T{A}_{r_x}\right)$ for a given resource is the time that the payment is given by the buyer $\left(t_{pay}\right)$ when the seller participant agrees to sell the resource, after receiving acknowledgement of buyer participant $\left(t_{ack}\right)$. It is defined as the time difference when a seller participant has acknowledged as selling the resource up to the time of release of payment by the buyer participant. Hence, the turnaround time for buyer participant can be calculated as

$$T{A}_{r_x}=(t_{pay}-t_{ack})/(t_{pay}+t_{ack})$$

(5)

Different weights w have been assigned depending upon the turnaround time for a participant.

$$w=\left\{\begin{array}{cc}0.4\hfill & T{A}_{r_x}<0.5sec\hfill \\ 0.3\hfill & T{A}_{r_x}>0.51and<1sec\hfill \\ 0.2\hfill & T{A}_{r_x}>1.01and<1.5sec\hfill \\ 0.1\hfill & T{A}_{r_x}>1.51sec\hfill \end{array}\right.$$

From the above Equations (2)–(5), the ($C_p^{r_x}$) for seller participant can be computed as:

$$C_p^{r_x}=\alpha \left(R{A}_{r_x}\right)+\tau \left(S{R}_{r_x}\right)+\epsilon \left(T{A}_{r_x}\right)$$

(6)

For the buyer participant, ($C_p^{r_x}$) can be computed as:

$$C_p^{r_x}=\delta \left(S{R}_{r_x}\right)+\mu \left(T{A}_{r_x}\right)$$

(7)

where $\tau$ and $\delta$∈$\beta$, $\epsilon$ and $\mu$∈$\gamma$. And $\alpha$, $\beta$, $\gamma$ represents the weights. The availability of a resource is given the highest priority, whereas turnaround time is given the lowest priority: $\alpha =0.5$, $\beta =0.2$, $\gamma =0.1$.

4.1.2. Feedback ${fb}_p^{r_x}\left(t\right)$

Participants’ feedback ${fb}_p^{r_x}\left(t\right)$ represents the feedback a participant (buyer or seller) provides regarding other participant after the completion of trade at time t. The system collects ${fb}_p^{r_x}$ of each participant based on their experience. Hence, the participant feedback determines the integrity of the resource delivered to a given participant. For given participants {$p^{*},p^{\prime }$}, $f{b}_{p^{*}\to p^{\prime }}^{r_x}$ represents the behavior of $p^{*}$ towards $p^{\prime }$ during trading activities, where $p^{*},p^{\prime }\in P$. Genuine feedback provided by a participant (seller or buyer) adds to the trust calculation of other participants. In the case of dispute or false feedback from a dishonest participant, the SmGW resolves the dispute and the dishonest participant’s trust score will be negatively impacted. For this, we assumed that both the buyer participant and seller participant can open a dispute to SmGW in case they behave honestly and still receive false feedback, to claim back their feedback trust.

Additionally, ${fb}_p^{r_x}\left(t\right)$ represents the aggregated feedback that the whole SMP community perceives for a single participant specific to a given resource. It is computed by taking the average of the individual feedback provided by various participants to a given participant with respect to a specific resource, based on their experience when traded in SMP.

Given the state of the participant (buyer, seller), the individual feedback of the participant, whether a buyer or seller, with respect to a given resource $r_x\in R^{*}$, at time t ranging from $[0,1]$, is given as $f{b}_{p^{*}\to p^{\prime }}^{r_x}$, where $p^{*},p^{\prime }$ and both can act as a seller and buyer or vice versa.

Participants’ feedback helps to evaluate other participant that behave dishonestly by providing a good or bad reputation each time, as described in line 15 of Algorithm 1. The feedback provided by individual participant is verified by the feedback score of other participants for the same resource, which helps to identity the activity of an honest and dishonest participant and prevent attacks. Thus participants’ feedback can be aggregated and computed as:

$${fb}_p^{r_x}\left(t\right)=\sum _{n=1}^{k}f{b}_{p^{*}\to p^{\prime }}^{r_x}/k$$

(8)

where k is the number of participants that provided feedback.

5. Security Analysis

This section provides the security analysis of the resilience of our proposed model to bad-mouthing and ballot-stuffing attacks. For this analysis, we provide the lower and upper bounds of trust values gained from our proposed model and prove that our proposed model is highly resistant against such types of attacks. A list of symbols used in security analysis are mentioned in

Table 1. Symbols with Description.

Symbol	Description
$\mathcal{N}$	Total number of participant in SMP
z	Member of $\mathbb{N}$
$\sigma$	Percentage of honest participants
$m_{TS}^p$	Minimum trust score given to participant p by another participant.
$T{S}_p^t$	Trust score given to p by another participant at time t
$H,D$	Subset of honest and dishonest participants.
$\mathcal{S}$	Set of honest participants
$\alpha$	Weight of previous trust score
$\beta$	Weight of individual feedback trust score
$\gamma$	Weight of aggregated feedback trust score
$\phi$	Weight of commitment-based trust
$\mathcal{P}$	Predication for a participant
$M_h\left(T{S}_{\sigma }\right)$	The mean trust value of an honest participant $\sigma$, measured by all participants
$M_d\left(T{S}_d\right)$	The mean trust value of a dishonest participant, measured by all participants

.

In our model, the trust score $T{S}_p^{r_x}$ is updated after each transaction has occurred. The interaction time is defined as $\{t_1,t_2\dots ..t_n\}$, when a buyer participant requests a seller participant.

Lemma 1.

Let an SMP contain several participants. For each honest participant$p^h$, where$\forall p^{*},p^{\prime },p^h\in 1,\cdots ,\mathcal{N}$, then

$$0.5\le m_{TS}^{p^h}\le f{b}_{p^{*}\to p^{\prime }}^{r_x}\left(t\right)\le 1$$

(9)

Proof. 

Given the individual feedback, $f{b}_{p^{*}\to p^{\prime }}^{r_x}\left(t\right)$, and $p^{*}$ and $p^{\prime }\in P$ are participants, the satisfaction value $S{V}_p\left(t\right)$ at a time t is in a range of 0.5 $\le m_{TS}^{p^h}\le 1$. Then, we can deduce that

$$m_{TS}^{p^h}\le f{b}_{p^{*}\to p^{\prime }}^{r_x}\left(t\right)\le 1.$$

(10)

□

Lemma 2.

Let an SMP with several participants, along with a certain number of honest participants, be σ, where $\sigma >0$.

For bad-mouthing attacks against honest participants σ, $\forall p,p^{\prime },p^h\in 1,\cdots ,\mathcal{N}$, such that

$${fb}_{p^h}^{r_x}\left(t\right)\ge {\sigma }_{m_{TS}^{p^h}}\times T_{z-1}^{min}$$

(11)

where

$$m_{TS}^{p^h}\ge 0.5$$

$$T_z^{min}=min[T_z^{r{p}^h}r,p^h\in \{1,\cdots ,\mathcal{N}\},p^h\in H,z\in \mathbb{N}]$$

 Case 1: An SMP with $\mathcal{N}$ number of participants, along with a certain number of honest participants $\sigma$, where $\sigma >0$. Under a bad-mouthing attack for each honest participant $p^h$ in $\sigma$, $\forall p^h\in 1,\cdots ,\mathcal{N}$, where 0$\le m_{TS}^{p^h}\le 1$, we derive:

$$T_H=\underset{z\to \infty }{lim}T{S}_{p^h}^z\ge (m_{TS}^{p^h}\times \beta \times \phi )/(1-\alpha -\gamma \times \phi )$$

(12)

Proof. 

From the above, we can deduce that

$$T{S}_{p^h}^z\ge T_z^{min}$$

(13)

From the results obtained from lemmas 1 and 2

$$T_z^{min}\ge (\alpha \times T_z^{min}+\beta \times m_{TS}^{p^h}+\gamma \times {\sigma }_{m_{TS}^{p^h}}\times \phi \times T_z^{min})*\phi$$

Thus,

$$\underset{z\to \infty }{lim}{T}_z^{min}\ge (\alpha +\gamma \times {\sigma }_{m_{TS}^{p^h}}\times \phi )\times \underset{z\to \infty }{lim}{T}_z^{min}+\beta \times m_{TS}^{p^h}\times \phi$$

Hence,

$$\underset{z\to \infty }{lim}{T}_z^{min}\ge (\beta \times m_{TS}^{p^h}\times \phi )/(1-\alpha -\gamma \times {\sigma }_{m_{TS}^{p^h}}\times \phi )$$

Given Equation (13), we have

$$T_H=\underset{z\to \infty }{lim}T{S}_{p^h}^z\ge (\beta \times m_{TS}^{p^h}\times \phi )/(1-\alpha -\gamma \times {\sigma }_{m_{TS}^{p^h}}\times \phi )$$

□

 Case 2: An SMP with $\mathcal{N}$ number of participants, along with a certain number of honest participants $\sigma$, where $\sigma >0$. Under a ballot-stuffing attack for each dishonest participant $p^d$, $\forall p^d\in \{1,\cdots ,\mathcal{N}\}$, we derive

$$T_D=\underset{z\to \infty }{lim}T{S}_{p^d}^z\le 1-(\beta \times m_{TS}^{p^d}\times \phi )/(1-\alpha -\gamma \times {\sigma }_{m_{TS}^{p^d}}\times \phi )$$

(14)

where 0$\le m_{TS}^{p^d}\le 1$ $z\in \mathbb{N}$

Proof is as in Case 1.

Theorem 3.

AN SMP with $\mathcal{N}$ number of participants containing a certain number of honest participants σ, where $\sigma >0$. Under a bad-mouthing attack the mean trust $M_h\left(T{S}_{\sigma }\right)$ for a honest participant is measured as:

$$\begin{array}{c}\hfill M_h\left(T{S}_{\sigma }\right)\ge \sigma \times T{S}_{p^h}\ge [(\sigma \times \beta \times m_{TS}^{p^h}\times \phi )/(1-\alpha -\gamma \times {\sigma }_{m_{TS}^{p^h}}\times \phi )]\end{array}$$

(15)

Proof. 

Let $\mathcal{S}$ be the set of honest participants; then,

$$\begin{array}{c}\hfill M_h\left(T{S}_{\sigma }\right)=\underset{z\to \infty }{lim}1/\mathcal{S}\sum _{i=1}^{\mathcal{S}}T{S}_{p^h}^z\\ \hfill =\underset{z\to \infty }{lim}1/\mathcal{S}\sum _{i=1}^{\mathcal{S}}\mathcal{P}\left(p^h\right)\times T{S}_{p^h}^z\\ \hfill +\mathcal{P}\left(p^d\right)\times T{S}_{p^d}^z\\ \hfill =\underset{z\to \infty }{lim}\sigma \times T{S}_{p^h}^z+(1-\sigma )\times ϵ\end{array}$$

□

$ϵ\ge 0$ is the worst value given by a bad-mouthing attack for $ϵ$ is as 0. Therefore, by using these values, we have

$$\begin{array}{c}\hfill M_h\left(T{S}_{\sigma }\right)\ge \underset{z\to \infty }{lim}\sigma \times T{S}_{p^h}^z+(1-\sigma )\times 0\ge \sigma \times T{S}_h\ge \\ \hfill (\sigma \times \beta \times m_{TS}^{p^h}\times \phi )/(1-\alpha -\gamma \times {\sigma }_{m_{TS}^{p^h}}\times \phi )\end{array}$$

Theorem 4.

An SMP with $\mathcal{N}$ number of participants containing a certain number of honest participants σ, where $\sigma >0$. Under a ballot-stuffing attack, the mean trust $M_d\left(T{S}_d\right)$ for a dishonest participant is measured as:

$$\begin{array}{c}\hfill M_d\left(T{S}_d\right)\le \sigma \times T{S}_{p^d}+1-\sigma \le \\ \hfill 2-\sigma -[(\sigma \times \beta \times m_{TS}^{p^h}\times \phi )/(1-\alpha -\gamma \times {\sigma }_{m_{TS}^{p^h}}\times \phi )]\end{array}$$

(16)

Proof. 

Let d be dishonest participants in SMP

$$\begin{array}{c}\hfill M_d\left(T{S}_d\right)=\underset{z\to \infty }{lim}1/\mathcal{N}\sum _{i=1}^{\mathcal{N}}T{S}_{p^d}^z\\ \hfill =\underset{z\to \infty }{lim}1/\mathcal{N}\sum _{i=1}^{\mathcal{N}}\mathcal{P}\left(p^h\right)\times T{S}_{p^h}^z\\ \hfill +\mathcal{P}\left(p^d\right)\times T{S}_{p^d}^z\\ \hfill =\underset{z\to \infty }{lim}\sigma \times T{S}_{p^d}^z+(1-\sigma )\times ϵ\end{array}$$

$ϵ\le 1$, so the best value given by ballot-stuffing attack for $ϵ$ is as 1. Therefore, using these values, we have

$$\begin{array}{c}\hfill M_d\left(T{S}_d\right)\le \underset{z\to \infty }{lim}\sigma \times T{S}_{p^d}^z+(1-\sigma )\times 1\le \\ \hfill \sigma \times T{S}_{p^d}+1-\sigma \le 2-\sigma \\ \hfill -(\sigma \times \beta \times m_{TS}^{p^h}\times \phi )/(1-\alpha -\gamma \times {\sigma }_{m_{TS}^{p^h}}\times \phi )\end{array}$$

□

6. Performance Analysis

This section presents the simulation setup adopted for the implementation of our proposed model (T-smart) as well as the performance parameters used.

6.1. Simulation Setup

T-smart is implemented using Solidity and Python. Metamask [41] was used as an Ethereum wallet. Simulations used a proof-of-authority (POA) consensus mechanism under Rinkeby testnet [42]. A PC with Intel(R) Core(TM) i5-3230M CPU @ 2.60 GHz was used for the experiments. Transaction details for our contract deployment are available on Etherscan: https://rinkeby.etherscan.io accessed on 28 April 2021. Models were implemented in the same setup scenario to avoid bias and to achieve the best observation and results. The same weights were applied for both models, as described in Section 4.1. In addition, the following parameter settings were adopted in the simulations:

• The SMP population was kept to 30 participants (both sellers and buyers).
• Each trading interaction involved two participants (buyer and seller) chosen in random way. Interactions were conducted in minutes and 60 interactions were carried out in 60 min so that each of the 30 participants acted as a seller or buyer in different cases.
• Percentage of dishonest participants is varied between $10\%,20\%,30\%,40\%,$ and $50\%$.
• Model is also assessed by varying the number of participants from 10, 20 and 30 participants with $30\%$ dishonest participants.

Furthermore, we programmed the dishonest participants in four different categories. Category A contains dishonest participants that lack certain resources and yet claim to have them. Category B contains dishonest participants that have all the resources they claim but a lower success rate in their tradings due to back-off and aborting trading interactions before completion. Category C contains dishonest participants that have both resource availability and a high success rate but have a high delay, leading to a high turnaround time during their trading. Category D contains dishonest participants that might have a high success rate, resource availability, low turnaround time during their trading activities but provide bad feedback to other participants that they trade with. In line with this, the dishonest participants can belong to one or more categories at a time. For example, a dishonest participant can belong to a single category, two categories, three categories or even all four categories.

6.2. Performance Parameters

To evaluate the performance of the T-smart, different parameters have been used, such as trust scores, detection accuracy, computational cost, transaction latency and satisfaction level. Detection accuracy is defined as the proportion of true positive and true negative participants detected and it is computed as:

$$DA=(TP+TN)/(TP+TN+FP+FN)$$

where TP = true positive, TN = true negative, FP = false positive and FN = false negative. Computational cost comprises the transaction cost and execution cost consumed by the smart contract during trading activities. Transaction cost is defined as the gas consumed during the deployment and implementation of smart contract into the blockchain. Execution cost is the gas consumed in the implementation of the smart contract. Satisfaction is defined as the perceived level of pleasure obtained with respect to cost.

Using the above parameters, the effectiveness of T-smart can be tested against the benchmark model. The results obtained for these performance parameters are shown in Section 7.

7. Results and Evaluation

Simulation-based experiments were carried out to determine the performance of T-smart and compare it with [8], in terms of commitment, trust score, detection accuracy, false positive, false negative, computational overhead, and transaction latency. Initially, 30 participants were studied, of which $30\%$ remained as dishonest and remaining as trustful (trust value ≥ 0.5).

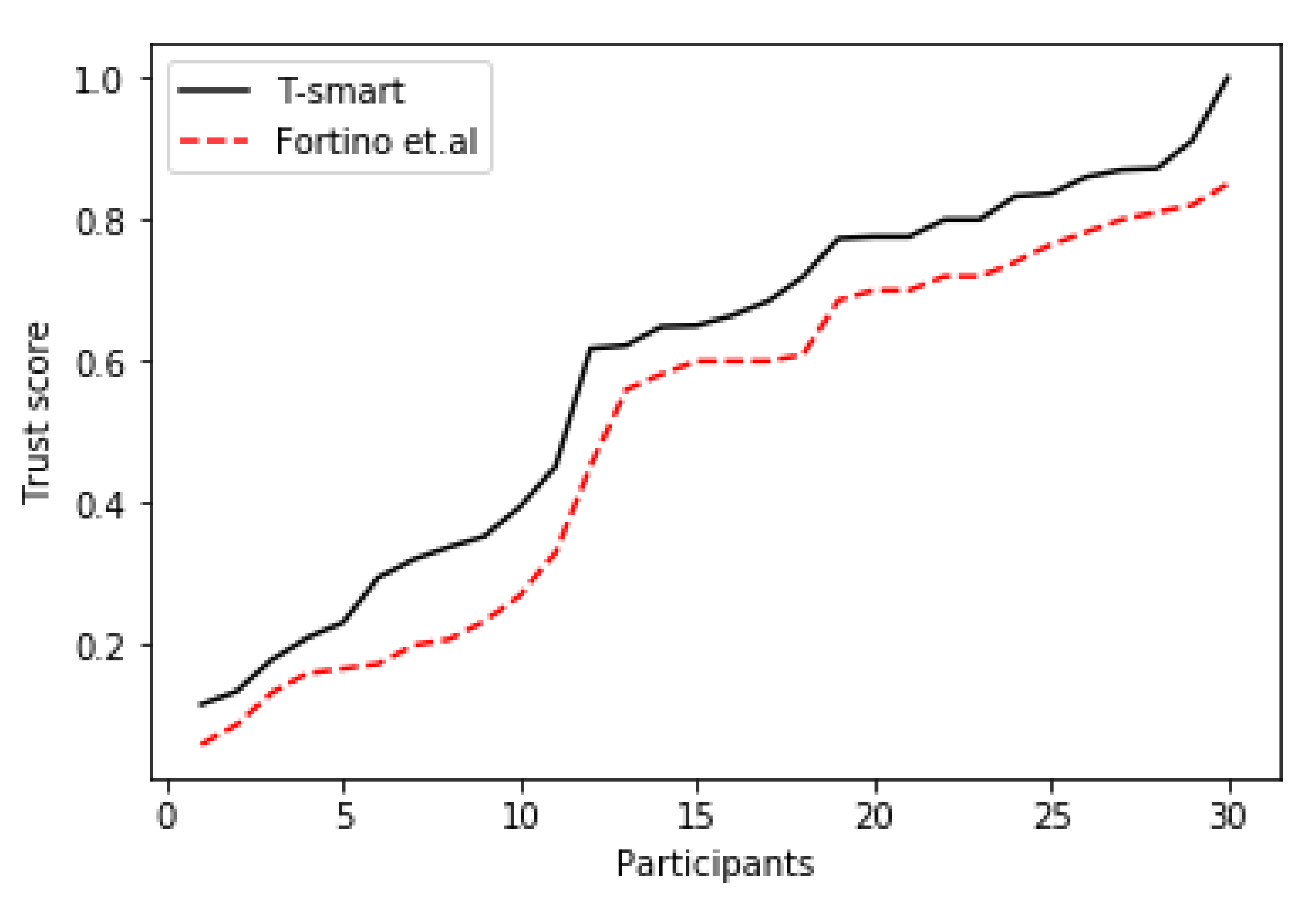
7.1. Trust Score Comparison

Figure 2 represents the results for both models in terms of trust score, which clearly indicates that the trust score of T-smart is much higher then the model presented in [8]. Simulation results shows that T-smart achieved more than $8.74\%$ trust score as compared to the benchmark model. A truthful participant is always seen to be more trustworthy. T-smart is able to compute a fair trust score in the presence of dishonest participants, utilizing factors listed in Section 4. However, the benchmark model is not able to compute fair trust scores for participants. This is due to the false recommendations received by dishonest participants, which the benchmark model failed to accurately detect. As a result, participants’ trust scores are miscalculated using the benchmark model, especially while calculating the trust score of dishonest nodes. T-smart is capable of calculating the trust of a participant, depending upon the previous trust score, feedback, and the performance in terms of commitment to fulfilling the requests made by various participants.

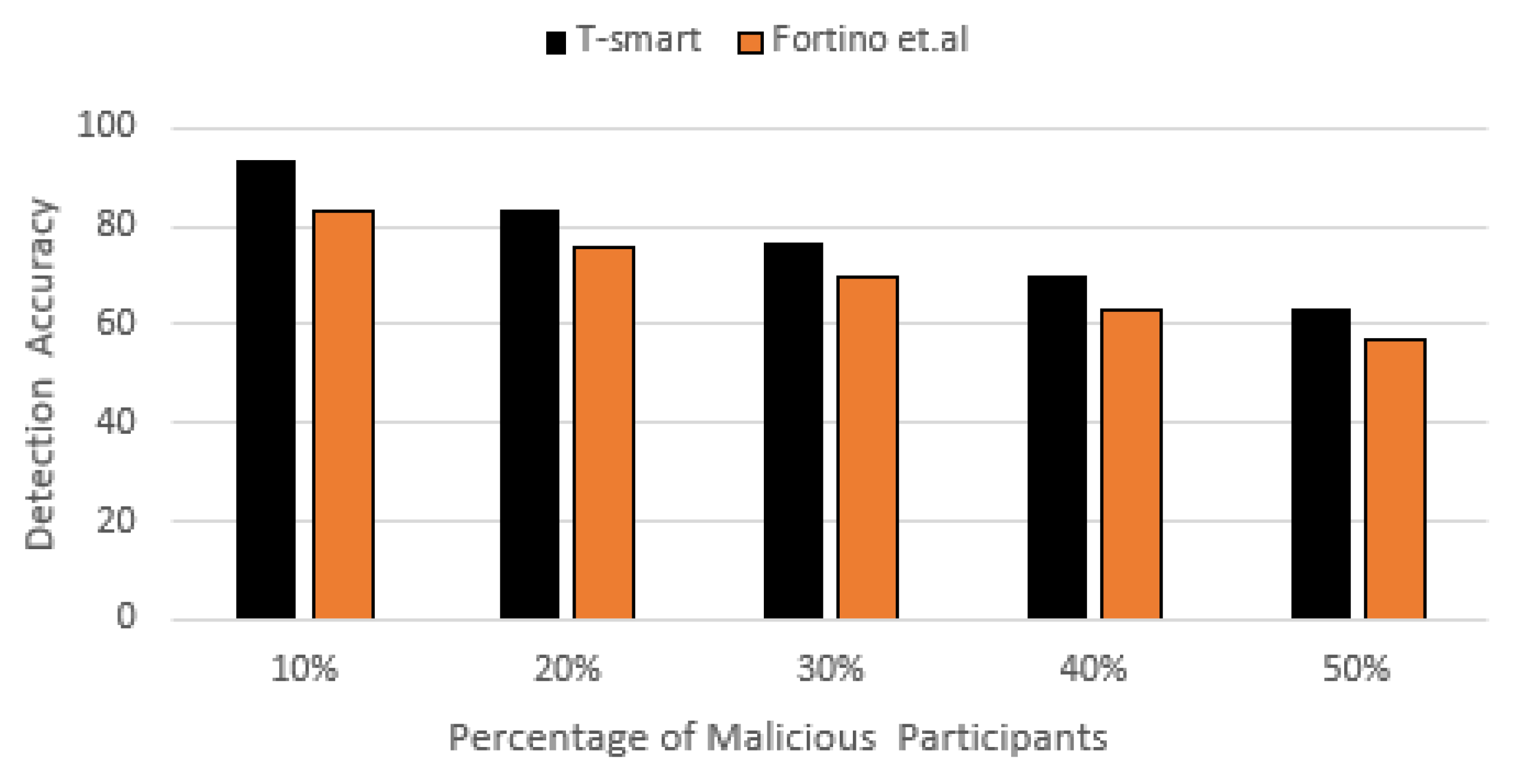
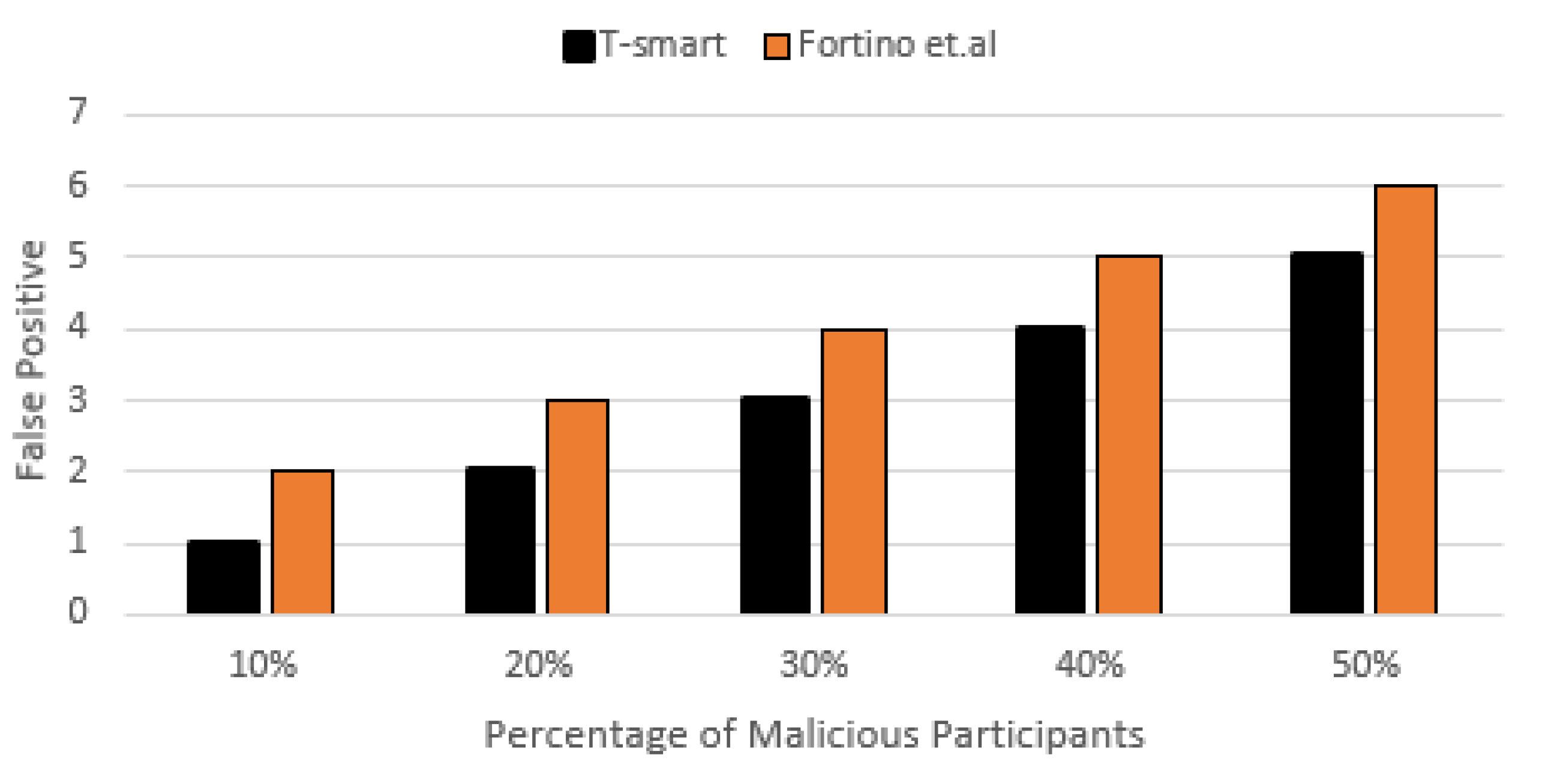
7.2. Increasing Number of Dishonest Participants 10–50%

The effectiveness of T-smart is evaluated under an increasing number of dishonest participants $10\%,20\%,30\%,40\%,$ and $50\%$, with respect to the total number of participants in the SMP, i.e., 30. The results obtained for accuracy, false positive, and false negative, for both T-smart and [8] are discussed in the following.

7.2.1. Detection Accuracy

Figure 3 illustrates the detection accuracy of dishonest nodes for the proposed trust model in comparison with [8]. Our results show that T-smart achieved more than $90\%$ accuracy under $10\%$ dishonest nodes, with an increase in the number of dishonest nodes that the detection accuracy degrades; however, even at $50\%$ dishonest nodes T-smart achieves $63.33\%$ detection accuracy. Moreover, T-smart managed to achieve $7\%$ better detection accuracy compared to [8] under varying dishonest nodes.

7.2.2. False Positive and False Negative

The results shown in Figure 4 and Figure 5 illustrate that the proposed trust model managed to achieve low false positives and false negatives at $10\%$ dishonest participants and, even with $50\%$ dishonest participants in SMP, the results are within the acceptable range. Moreover, irrespective of the percentage of dishonest nodes, T-smart performs better for both false positives and false negatives compared to [8]. This is due to the ability of T-smart to tackle false information provided by other participants based on the factors described in Section 4.

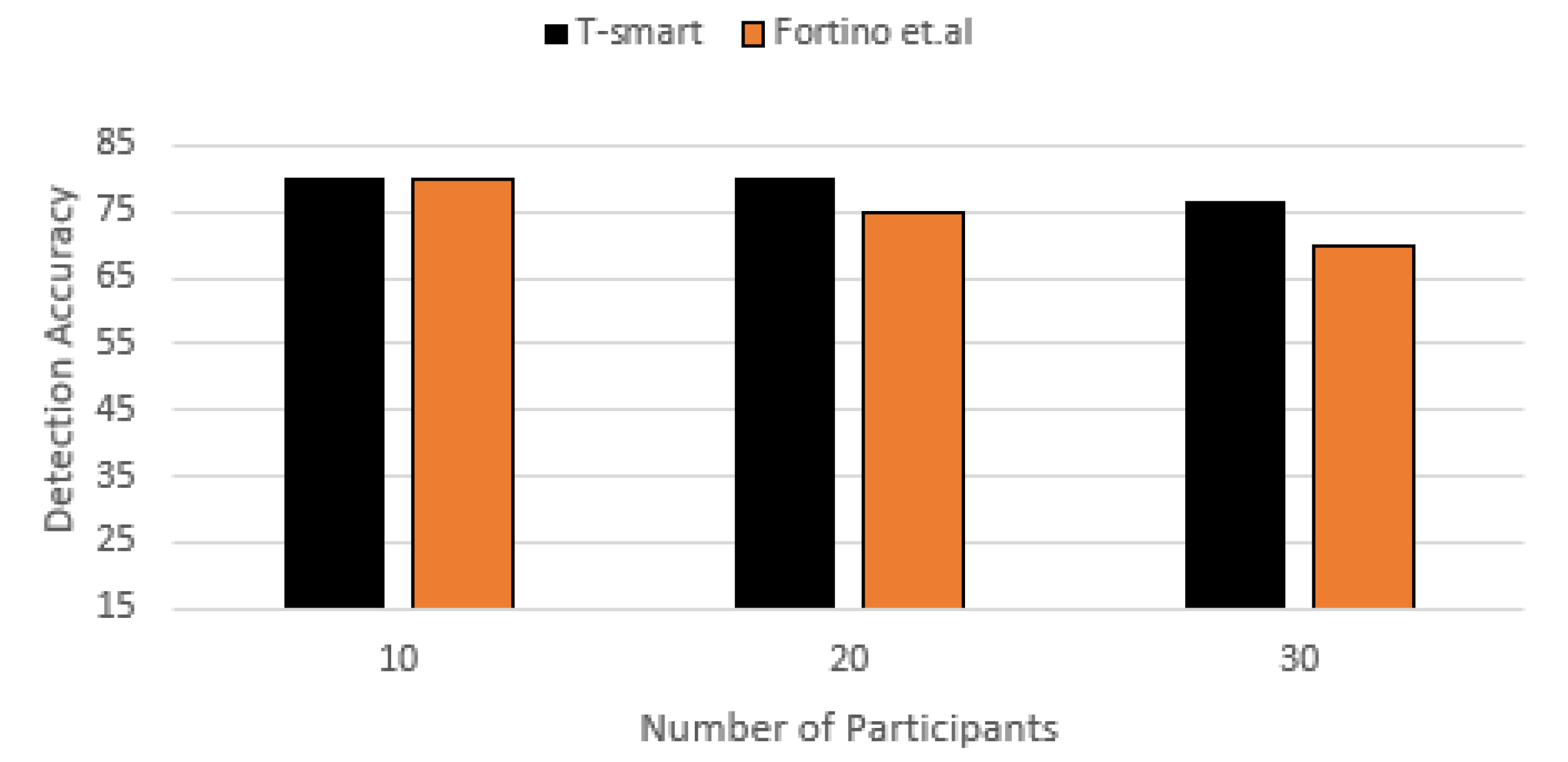
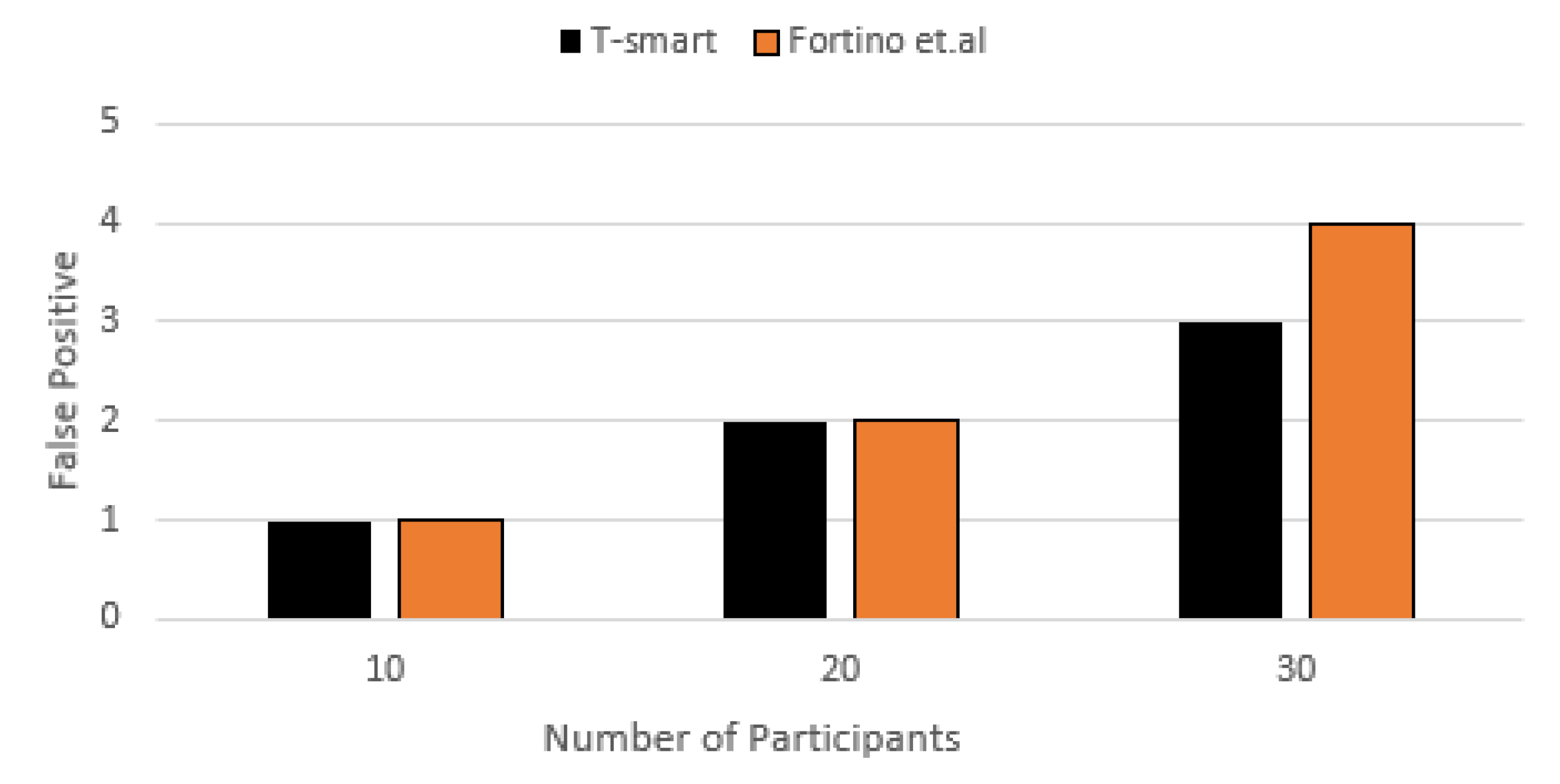
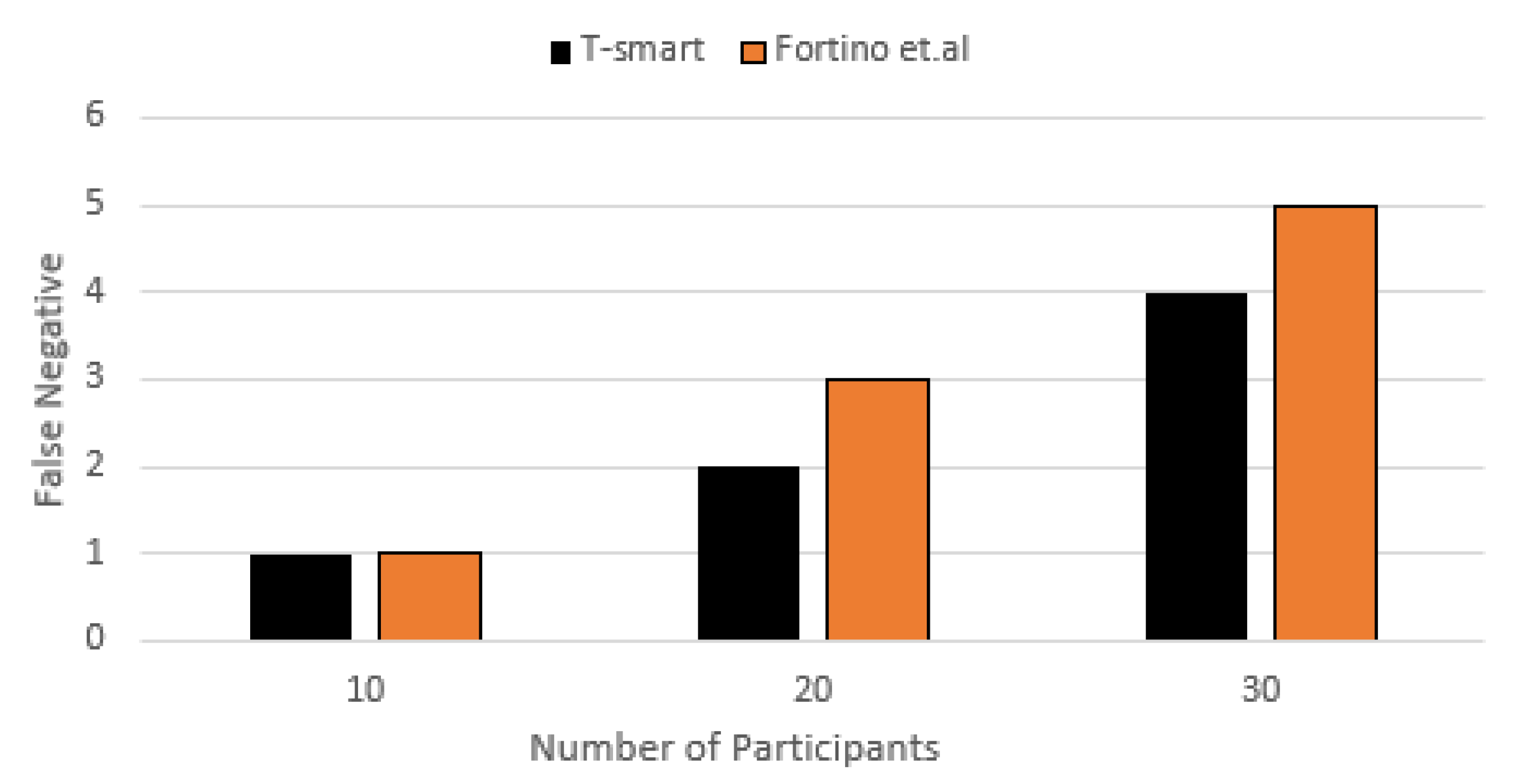
7.3. Increasing Number of Participants

The effectiveness of T-smart is evaluated under an increasing number of participants 10, 20 and 30, while keeping the percentage of dishonest nodes fixed at $30\%$. The results obtained for accuracy, false positive, and false negative for both T-smart and [8] are discussed in the following.

7.3.1. Detection Accuracy

Figure 6 illustrates the detection accuracy of dishonest nodes for the proposed trust model in comparison with [8]. The results show that T-smart achieved more than $80\%$ accuracy under 10 participants; with an increase in the number of participants, the detection accuracy degrades slightly. However, even at 30 participants, T-smart achieves $76.66\%$ detection accuracy. Moreover, on average, T-smart managed to achieve $3.9\%$ better detection accuracy compared to [8] under $30\%$ dishonest nodes.

7.3.2. False Positive and False Negative

The results shown in Figure 7 and Figure 8 illustrate that, for a small number of participants, i.e., 10, both the T-smart and [8] record only one false positive and false negative. However, with an increase in the number of participants, i.e., 20 and 30, the performance of [8] degrades at higher rate compared to the proposed model.

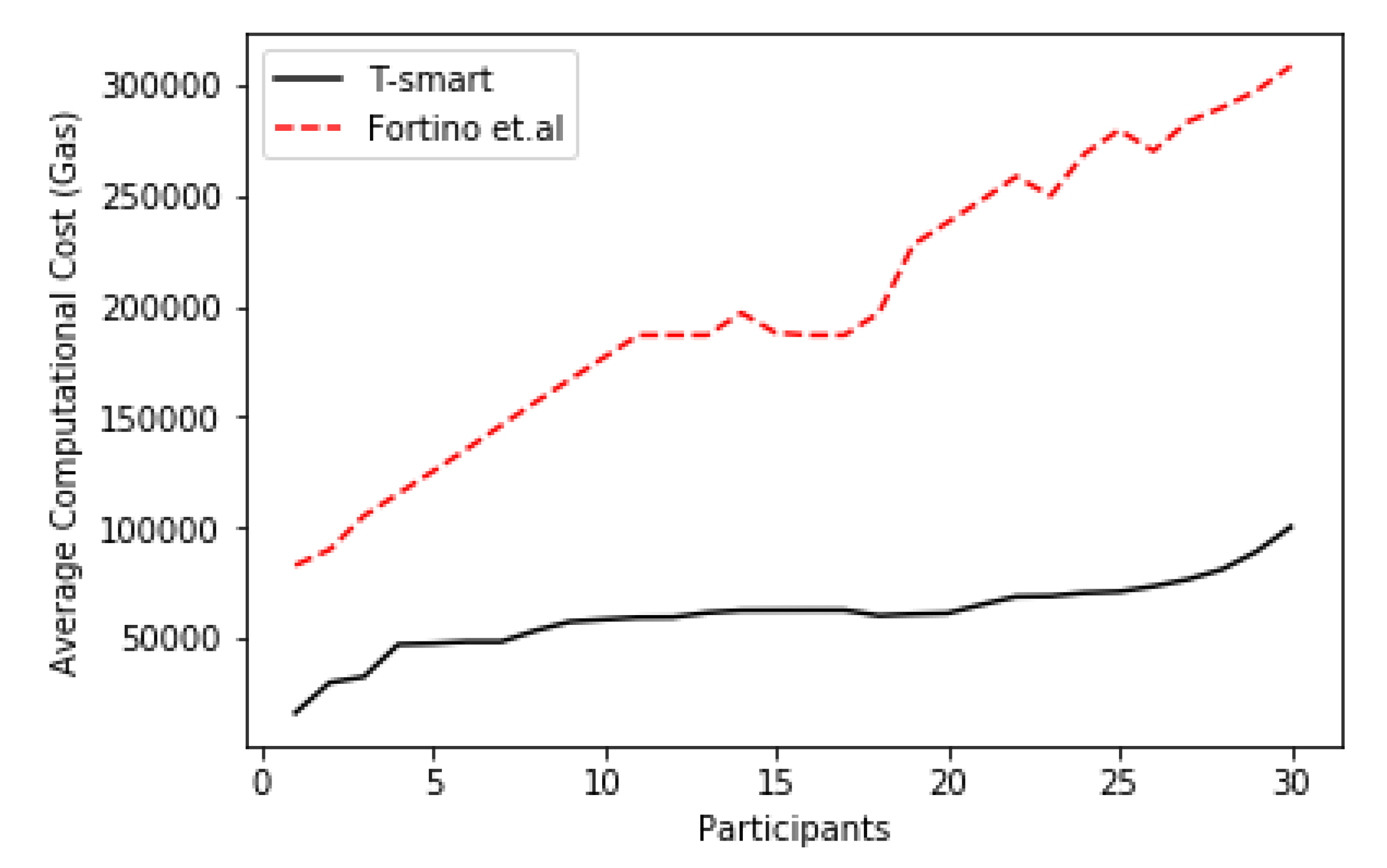
7.4. Average Computational Cost

The average computational cost for both models is presented in Figure 9. Both the execution and transaction costs are part of the computational cost. The results in Figure 9 show that the cost of T-smart is significantly lower than [8]. The average computational cost of 30 participants in our model is $30.13\%$ lower than the benchmark model. Generally, the increase in computational cost with an increase in the number of participants is least effected as compared to [8]. This iis due to the elimination of clustering algorithms, which consume more computations and thus increase the gas consumption in [8].

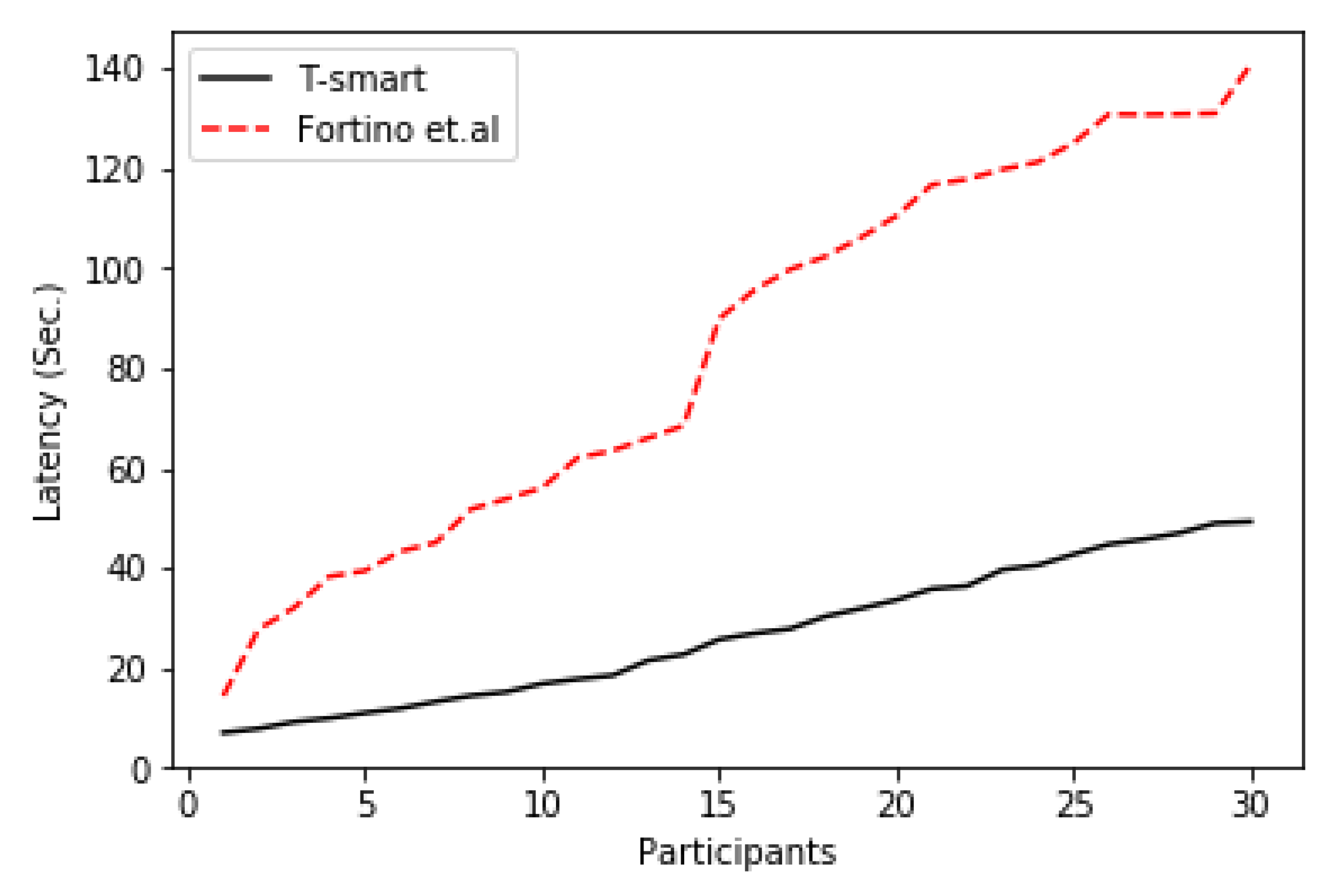
7.5. Average Transaction Latency

The average transaction latency for both models is presented in Figure 10. It can be observed that the T-smart has much lower latency as compared to the benchmark model. Besides this, latency in the T-smart was slightly changed with an increase in the number of participants, whereas that of benchmark model faced a dramatic change. The average latency of 30 participants in our model is $31.74\%$ lower than the benchmark model. This is because the PoA consensus mechanism is maintained by selected trusted entities, whereas the benchmark model uses proof-of-work (POW), where a miner needed to be selected to add transactions to the blockchain, slowing down the entire process and contributing to a higher latency.

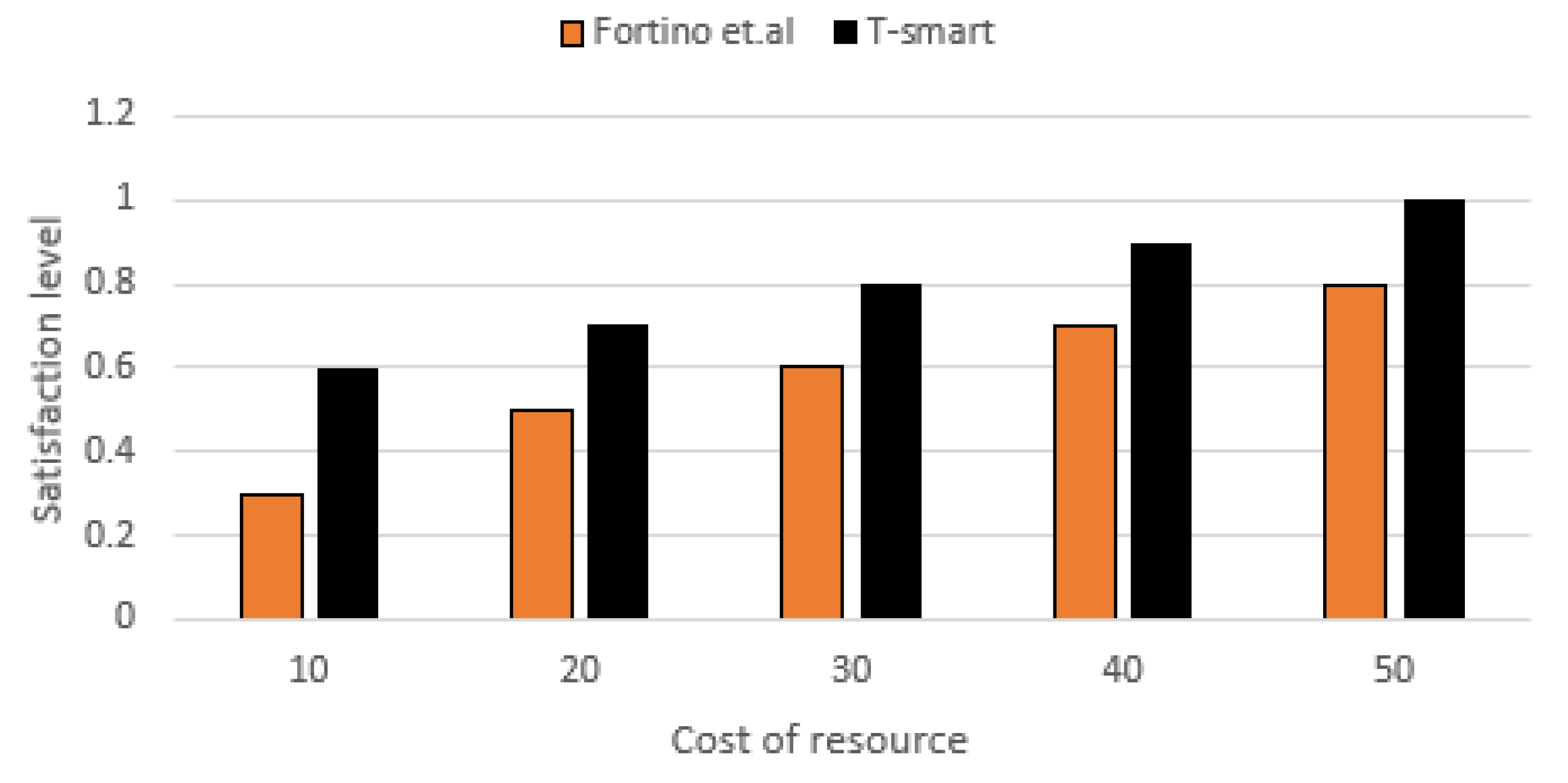
7.6. Satisfaction Level with Respect to Cost

Figure 11 shows the level of satisfaction of the participant (buyer) with respect to the cost (prize) of an individual resource. The simulation results show that, using the T-smart, the buyer participant achieves a higher level of satisfaction compared to the benchmark model. In addition, a seller with a higher trust score in a given resource type(s) (e.g., bandwidth and energy) might not have a good trust score in another resource type e.g., water. However, due to its good reputation in bandwidth and energy, the seller can achieve a high overall trust score and a higher profit. Figure 11 shows that the level of satisfaction increases with the increase in resource costs (prize). This is due to a higher tendency that a high-trust scored seller in a particular resource would tend to maximize its profit while maintaining a higher level of satisfaction. This is due to its high level of satisfaction, which has led to the attraction of a high number of buyers. While selling the same resources at cheaper rates may not provide better satisfaction.

8. Discussions

This section emphasizes our model’s contribution to theory and the business world. Additionally, it discusses how traders can utilize the study findings to enhance and protect their business. Furthermore, the section discusses how academics can incorporate a conceptual model into theory creation and how the findings contribute to theory development.

8.1. Business Environment

Proposed model is focused on aligning the decentralized business model and blockchain-related technologies with the requirements of various business problems in the domain of trust and security. It has been shown that the basic business processes underlying different smart markets and IoT-based smart environments can be readily implemented utilizing blockchain technology, which can then assist in managing trust while guaranteeing fairness and dependability. The work is relevant to the developing area of blockchain applications and may be of interest to academics and theorists interested in studying blockchain processes for value creation. Additionally, this will influence how traders interact during trading operations. Besides, this will have a long-term transformative effect on the market’s structure and trust management. While researching new rules that may alleviate the burden of utilizing and supporting two distinct trust management systems, traders and officials can leverage them to their advantage and work to increase the profits and capabilities during trading cycles.

8.2. Useability

SMPs should transition away from information sharing and data management throughout the trading cycle and toward commodity-based, resource-specific trust ratings and participant assistance during the trading cycle. Due to the difficulty of developing trust-based trading systems with complex algorithms, new SMPs based on trust management must prioritize providing participants with reliable trading opportunities or technological advancements in efficient trading processes. This work demonstrated how blockchain technology can be used to provide a realistic solution for trust-management-based trade cycles by using participants’ unique trust ratings for each resource. Additionally, the study demonstrates blockchain’s potential contribution to trust management and its associated benefits. As smart market participants are always on the lookout for more effective means of managing trust, this innovation transformation makes sense from an SMP perspective.

8.3. Limitations

This research has two fundamental scalability constraints. The first is that the suggested model was evaluated on a small sample size. The second relates to the architectural design of the blockchain. Additional constraints include the model’s limited consideration of dishonest attacks.

Malicious conduct in the context of resource trade is complicated and is influenced by a variety of variables. Thus, in the future, it will be subject to more thorough research on participant behavior linked to trust during the trading cycle in a blockchain network environment. Another area of future study that has been explored is determining the variables that affect user behavior on blockchain-based trading platforms. Besides, the proposed model’s effect on human behavior in a large trading environment can only be proven via the model’s fundamental functions and components being technically feasible.

Scalability is the primary constraint on blockchain technology. As general solutions for enhancing the scalability of blockchain technology are being developed, it is reasonable to anticipate that these solutions might be applicable to the trust management area as well. Thus, future research should prioritize addressing the problem of scalability.

9. Conclusions

This work proposes a blockchain-based, semi-distributed trust management mechanism for participants in a smart marketplace SMP. In the considered environment, participants can trade multiple resources with each other by considering their trust scores. T-smart helps to determine the trust score of participants based on several factors, such as previous trust score, feedback and commitment. In addition, the T-smart provides a resource-specific trust-score-computing mechanism that reveals the level of satisfaction each participant has recorded in a given resource type. In comparison, T-smart provides a scalable solution for SMP using blockchain technology with a PoA consensus mechanism that is effectively contrary to the benchmark model. Besides this, we have demonstrated the resilience and robustness of T-smart against bad-mouthing and ballot-stuffing attacks through security analysis. The results indicate that T-smart achieved 7% better accuracy, 30.13% lower computational cost and 31.74% less latency as compared to the benchmark model. The model is more effective than other models in establishing a participant’s trust during trading activities. Each participant is able to ascertain which party is more trustworthy before deciding on a transaction. Additionally, the model is resilient against bad-mouthing and ballot-stuffing attacks. In future we aim to extend the scalability of our model to a higher number of participants and develop a countermeasure strategy by designing more effective algorithms for other dishonest attacks using multiple machine-learning techniques.