Eye-Tracking Characteristics: Unveiling Trust Calibration States in Automated Supervisory Control Tasks
Abstract
:1. Introduction
2. Background
3. Materials and Methods
3.1. Participants
3.2. Experimental Materials
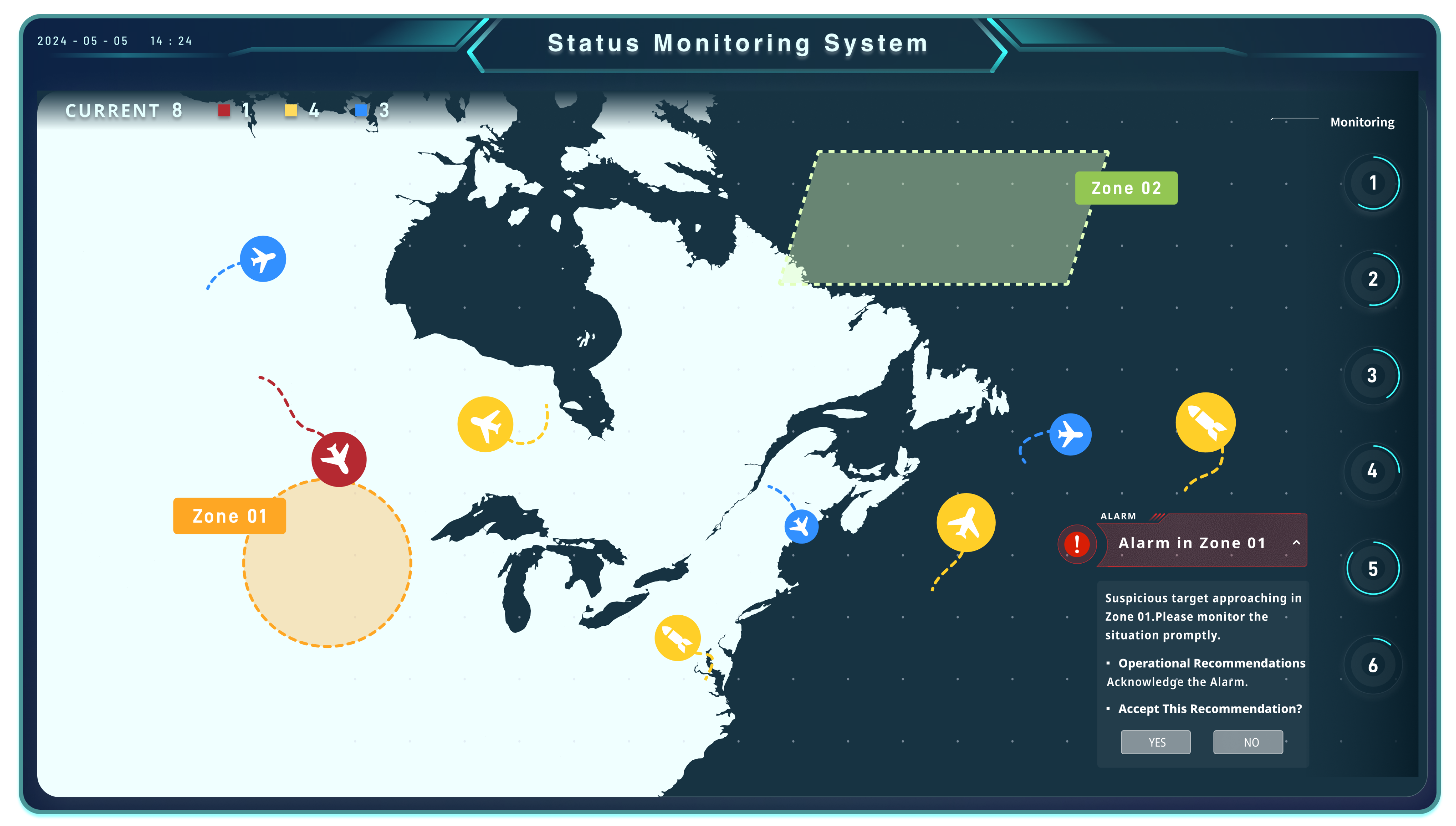
3.3. Experimental Tasks
- Selecting “yes” prompted the system to log the alert details in the backend.
- Selecting “no” caused no system response but still logged the decision in the backend.
3.4. Data Collection
- Real-time interaction data
- System log data
- Self-report scale data
- Eye-tracking data
- Raw eye-tracking data: This dataset included only raw fixation point coordinates represented as (x, y) pairs. Before inputting the data for analysis, preprocessing steps were applied, including handling missing data, down-sampling, and normalization. Missing data points were filled using the value from the preceding data point.
- Feature-extracted data: This dataset contained extracted features based on three primary eye-tracking metrics: pupil diameter, fixation, and saccade characteristics. These features were used to analyze participants’ attention and trust-related behaviors.
3.5. Trust State Classification and Regression Model Based on Two-Layer Random Forest
- (1)
- First Layer: Random Forest Classification Model
- (2)
- Second Layer: Random Forest Regression Model
3.6. Model Evaluation
3.6.1. Confusion Matrix
- True positive (TP): The model correctly predicts a positive instance.
- True negative (TN): The model correctly predicts a negative instance.
- False positive (FP): The model incorrectly predicts a negative instance as positive.
- False negative (FN): The model incorrectly predicts a positive instance as negative.
3.6.2. First-Layer Random Forest Classification Model Evaluation
- Accuracy: The proportion of correctly predicted instances out of the total instances. It evaluates the model’s overall classification performance.
- Precision: The proportion of true positive predictions among all positive predictions made by the model. A higher precision indicates stronger ability to distinguish negative samples.
- Recall: The proportion of actual positive samples that were correctly predicted by the model. A higher recall indicates stronger ability to detect positive samples.
3.6.3. Second-Layer Random Forest Regression Model Evaluation
- RSS, MSE, RMSE, and MAE provide measures of accuracy, indicating how closely the model’s predictions align with the actual data.
- RSS (residual sum of squares): Measures the total squared difference between predicted and actual values.where is the actual value, is the predicted value, and n is the number of observations.
- MSE (mean squared error): The average of the squared differences between predicted and actual values. It penalizes larger errors more heavily.
- RMSE (root mean squared error): The square root of MSE, providing an interpretable error measure in the same units as the target variable.
- MAE (mean absolute error): The average of the absolute differences between predicted and actual values. It gives equal weight to all errors.
- reflects the model’s ability to explain the variance in the data comprehensively. An value closer to 1 indicates better performance, signifying that the model captures more information from the actual labels.
- (coefficient of determination): Measures the proportion of the variance in the dependent variable that is predictable from the independent variables. It evaluates the model’s ability to capture the variability in the data,where TSS is the total sum of squares:
4. Data Computation and Analysis
4.1. Construction and Computation of the Dynamic Trust Mathematical Model
4.2. Trust State Annotation
4.3. Feature Engineering
- Most eye-tracking metrics can be used to evaluate human–machine trust states.
- Metrics such as fixation index, saccade duration, fixation–saccade time ratio, and pupil diameter change rate show a very strong correlation with human–agent trust states.
4.4. Hyperparameter Configuration for the Classifier
- (1)
- Hyperparameter Selection for the First-Layer Random Forest Classification Model
- (2)
- Hyperparameter Selection for the Second-Layer Random Forest Regression Model
5. Results
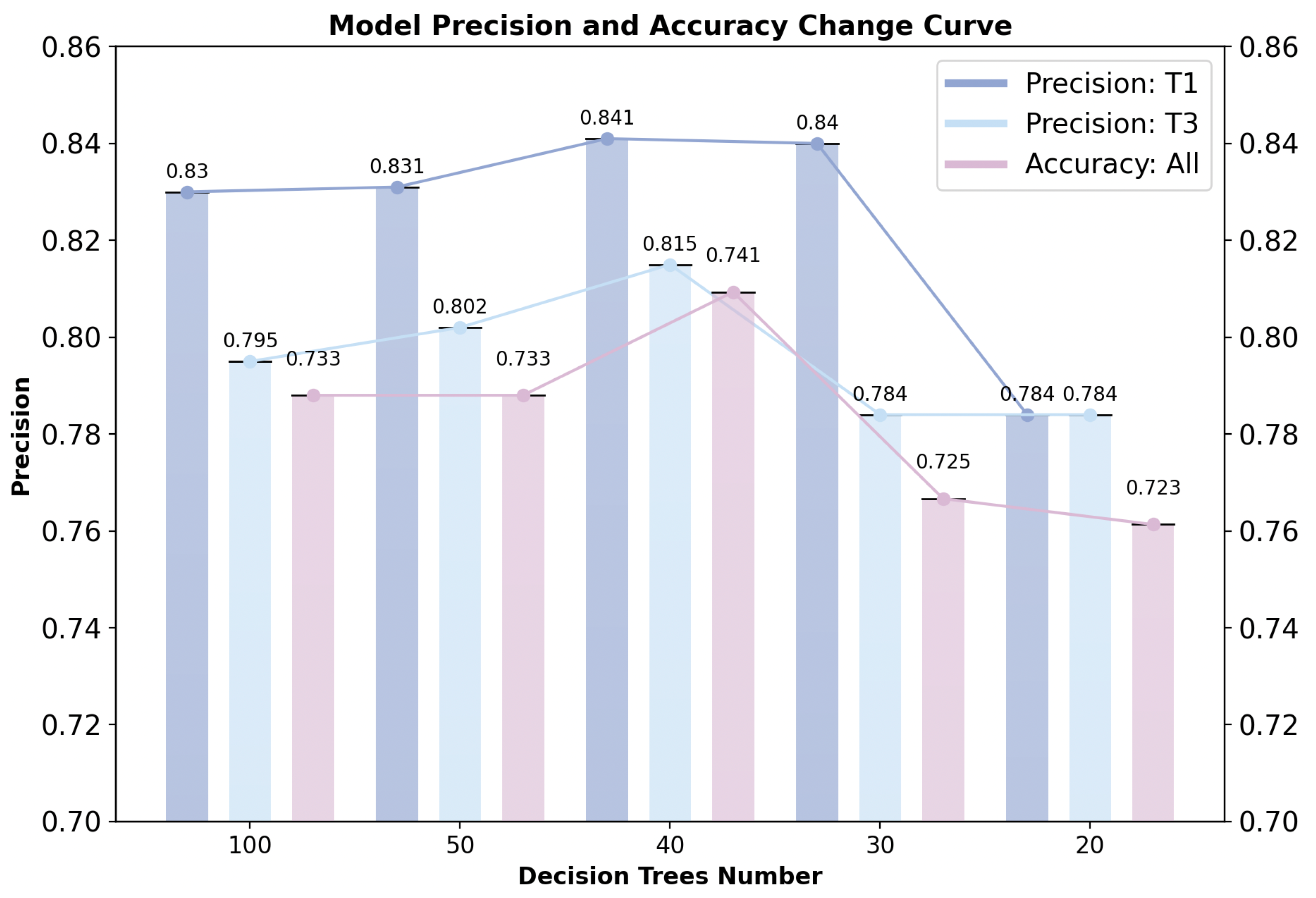
5.1. First-Layer Random Forest Classification Model
- (1)
- Classification Results
- (2)
- Importance of Eye-Tracking Metrics
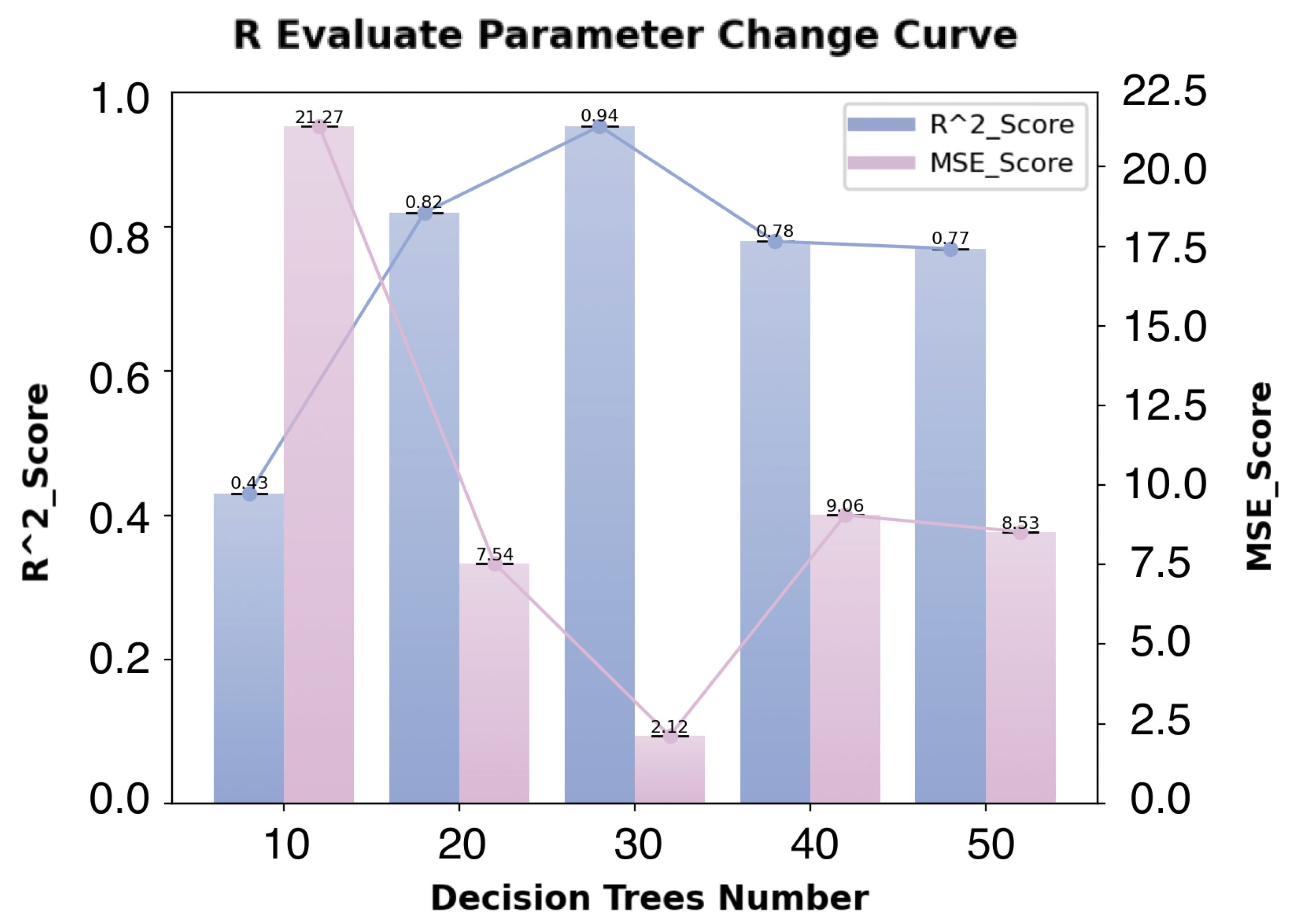
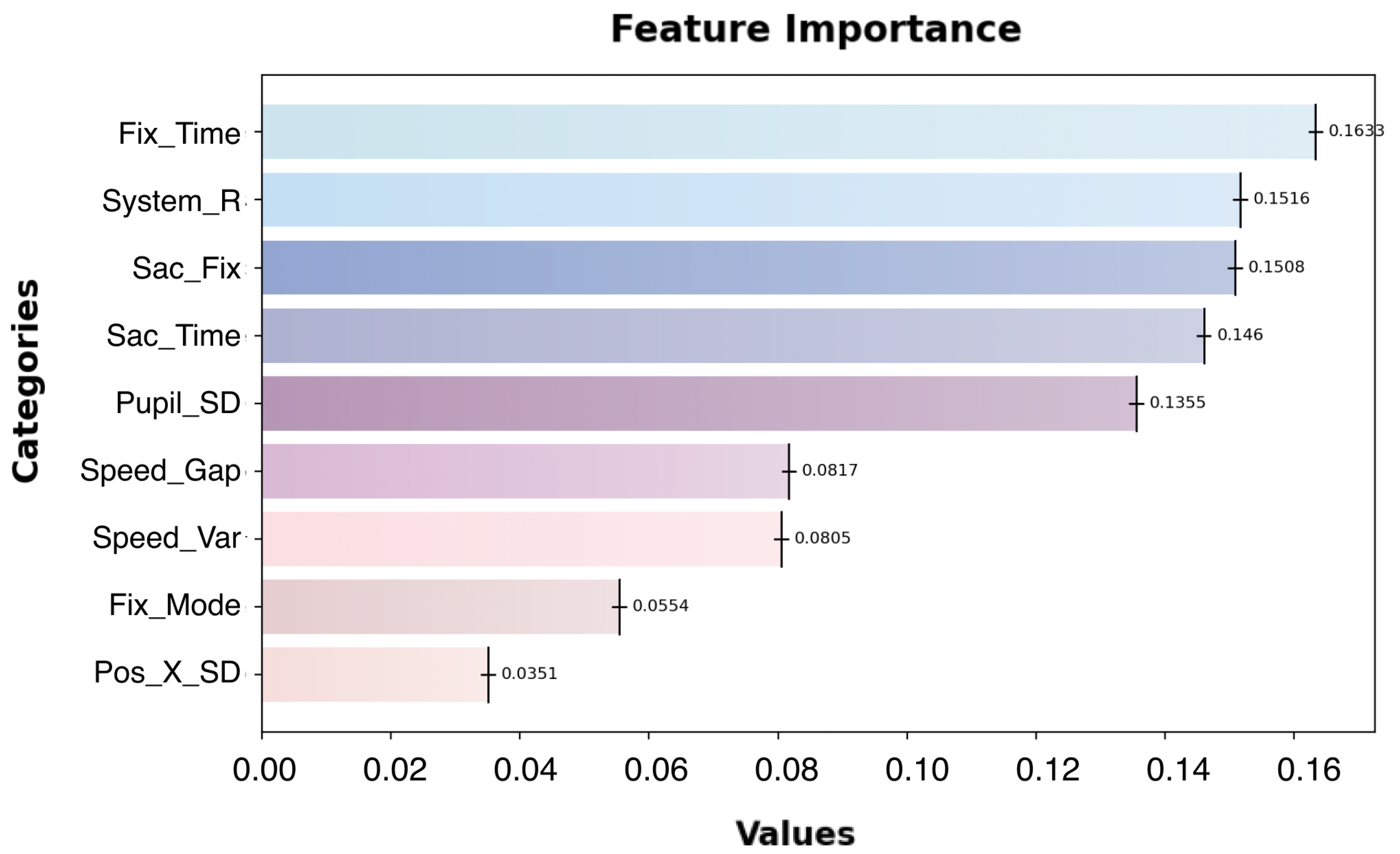
5.2. Second-Layer Random Forest Regression Model
- (1)
- Feature Importance
- (2)
- Model Fitting Results
6. Discussion
6.1. Trust Measurement and Trust Calibration
6.2. Contribution of Eye-Tracking Metrics to Trust Calibration in Human–Agent Interaction
6.3. Limitations and Future Directions
- (1)
- Theoretical Scope
- (2)
- Practical Complexity
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Final Scale
- (1)
- I believe there could be negative consequences when using the system.
- (2)
- I feel I must be cautious when using the system.
- (3)
- It is risky to interact with the system.
- (4)
- I believe the system will act in my best interest.
- (5)
- I trust the system will do its best to assist me when I need help.
- (6)
- I believe the system is genuinely interested in understanding my needs and preferences.
- (7)
- I think the system is competent and effective in its functions.
- (8)
- I believe the system performs its role very well.
- (9)
- I trust that the system has all the functionalities I would expect from it.
- (10)
- If I use the system, I feel I can depend on it completely.
- (11)
- I can always rely on the system for support.
- (12)
- I trust the information presented to me by the system.
References
- Inga, J.; Ruess, M.; Robens, J.H.; Nelius, T.; Rothfuß, S.; Kille, S.; Dahlinger, P.; Lindemann, A.; Thomaschke, R.; Neumann, G.; et al. Human-machine symbiosis: A multivariate perspective for physically coupled human-machine systems. Int. J. Hum.-Comput. Stud. 2023, 170, 102926. [Google Scholar] [CrossRef]
- Buçinca, Z.; Malaya, M.B.; Gajos, K.Z. To trust or to think: Cognitive forcing functions can reduce overreliance on AI in AI-assisted decision-making. Proc. ACM Hum.-Comput. Interact. 2021, 5, 1–21. [Google Scholar] [CrossRef]
- Chignell, M.; Wang, L.; Zare, A.; Li, J. The evolution of HCI and human factors: Integrating human and artificial intelligence. ACM Trans. Comput.-Hum. Interact. 2023, 30, 1–30. [Google Scholar] [CrossRef]
- Wischnewski, M.; Krämer, N.; Müller, E. Measuring and understanding trust calibrations for automated systems: A survey of the state-of-the-art and future directions. In Proceedings of the 2023 CHI Conference on Human Factors in Computing Systems, Hamburg, Germany, 23–28 April 2023; pp. 1–16. [Google Scholar]
- Mehrotra, S.; Degachi, C.; Vereschak, O.; Jonker, C.M.; Tielman, M.L. A systematic review on fostering appropriate trust in Human-AI interaction: Trends, opportunities and challenges. ACM J. Responsible Comput. 2024, 1, 1–45. [Google Scholar] [CrossRef]
- Lakkaraju, H.; Bastani, O. “How do I fool you?” manipulating user trust via misleading black box explanations. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, San Jose, CA, USA, 21–23 October 2020; pp. 79–85. [Google Scholar]
- Zhang, Z.T.; Hußmann, H. How to manage output uncertainty: Targeting the actual end user problem in interactions with AI. In Proceedings of the IUI Workshops, Virtual, 13–17 April 2021. [Google Scholar]
- Lee, J.D.; See, K.A. Trust in automation: Designing for appropriate reliance. Hum. Factors 2004, 46, 50–80. [Google Scholar] [CrossRef]
- Shin, D. The effects of explainability and causability on perception, trust, and acceptance: Implications for explainable AI. Int. J. Hum.-Comput. Stud. 2021, 146, 102551. [Google Scholar] [CrossRef]
- Bach, T.A.; Khan, A.; Hallock, H.; Beltrão, G.; Sousa, S. A systematic literature review of user trust in AI-enabled systems: An HCI perspective. Int. J. Hum.- Interact. 2024, 40, 1251–1266. [Google Scholar] [CrossRef]
- Razin, Y.S.; Feigh, K.M. Converging measures and an emergent model: A meta-analysis of human-automation trust questionnaires. ACM Trans. Hum.-Robot. Interact. 2024, 13, 1–14. [Google Scholar] [CrossRef]
- Gulati, S.; Sousa, S.; Lamas, D. Design, development and evaluation of a human-computer trust scale. Behav. Inf. Technol. 2019, 38, 1004–1015. [Google Scholar] [CrossRef]
- McGuirl, J.M.; Sarter, N.B. How are we doing? Presenting system confidence information to support trust calibration and adaptive function allocation. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting; SAGE Publications: Los Angeles, CA, USA, 2003; Volume 47, pp. 538–542. [Google Scholar]
- Zhang, Y.; Liao, Q.V.; Bellamy, R.K. Effect of confidence and explanation on accuracy and trust calibration in AI-assisted decision making. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 295–305. [Google Scholar]
- Chen, J.; Mishler, S.; Hu, B. Automation error type and methods of communicating automation reliability affect trust and performance: An empirical study in the cyber domain. IEEE Trans. Hum.-Mach. Syst. 2021, 51, 463–473. [Google Scholar] [CrossRef]
- Faas, S.M.; Kraus, J.; Schoenhals, A.; Baumann, M. Calibrating pedestrians’ trust in automated vehicles: Does an intent display in an external HMI support trust calibration and safe crossing behavior? In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems, Virtual, 8–13 May 2021; pp. 1–17. [Google Scholar]
- Albayram, Y.; Jensen, T.; Khan, M.M.H.; Fahim, M.A.A.; Buck, R.; Coman, E. Investigating the effects of (empty) promises on human-automation interaction and trust repair. In Proceedings of the 8th International Conference on Human-Agent Interaction, Virtual, 10–13 November 2020; pp. 6–14. [Google Scholar]
- Barda, A.J.; Horvat, C.M.; Hochheiser, H. A qualitative research framework for the design of user-centered displays of explanations for machine learning model predictions in healthcare. BMC Med Inform. Decis. Mak. 2020, 20, 257. [Google Scholar] [CrossRef] [PubMed]
- Gebru, B.; Zeleke, L.; Blankson, D.; Nabil, M.; Nateghi, S.; Homaifar, A.; Tunstel, E. A review on human–machine trust evaluation: Human-centric and machine-centric perspectives. IEEE Trans. Hum.-Mach. Syst. 2022, 52, 952–962. [Google Scholar] [CrossRef]
- Lu, Y.; Sarter, N. Eye tracking: A process-oriented method for inferring trust in automation as a function of priming and system reliability. IEEE Trans. Hum.-Mach. Syst. 2019, 49, 560–568. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, J.; Chen, M.; Li, Z.; Zang, J.; Qu, X. EEG-based assessment of driver trust in automated vehicles. Expert Syst. Appl. 2024, 246, 123196. [Google Scholar] [CrossRef]
- Deng, M.; Chen, J.; Wu, Y.; Ma, S.; Li, H.; Yang, Z.; Shen, Y. Using voice recognition to measure trust during interactions with automated vehicles. Appl. Ergon. 2024, 116, 104184. [Google Scholar] [CrossRef]
- Wickens, C. Attention: Theory, principles, models and applications. Int. J. Hum.-Interact. 2021, 37, 403–417. [Google Scholar] [CrossRef]
- Duan, W.; Zhou, S.; Scalia, M.J.; Yin, X.; Weng, N.; Zhang, R.; Freeman, G.; McNeese, N.; Gorman, J.; Tolston, M. Understanding the evolvement of trust over time within Human-AI teams. Proc. ACM Hum.-Comput. Interact. 2024, 8, 1–31. [Google Scholar] [CrossRef]
- McDermott, P.L.; Brink, R.N.T. Practical guidance for evaluating calibrated trust. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting; SAGE Publications: Los Angeles, CA, USA, 2019; Volume 63, pp. 362–366. [Google Scholar]
- Huang, S.H.; Bhatia, K.; Abbeel, P.; Dragan, A.D. Establishing appropriate trust via critical states. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3929–3936. [Google Scholar]
- Bansal, G.; Buçinca, Z.; Holstein, K.; Hullman, J.; Smith-Renner, A.M.; Stumpf, S.; Wu, S. Workshop on Trust and Reliance in AI-Human Teams (TRAIT). In Proceedings of the 2023 CHI Conference on Human Factors in Computing Systems, Hamburg, Germany, 23–28 April 2023; pp. 1–6. [Google Scholar]
- Alizadeh, F.; Vereschak, O.; Pins, D.; Stevens, G.; Bailly, G.; Caramiaux, B. Building appropriate trust in Human-AI interactions. In Proceedings of the 20th European Conference on Computer-Supported Cooperative Work (ECSCW 2022), Coimbra, Portugal, 27 June–1 July 2022; Volume 6. [Google Scholar]
- Yang, F.; Huang, Z.; Scholtz, J.; Arendt, D.L. How do visual explanations foster end users’ appropriate trust in machine learning? In Proceedings of the 25th International Conference on Intelligent User Interfaces, Cagliari, Italy, 17–20 March 2020; pp. 189–201. [Google Scholar]
- Xu, A.; Dudek, G. Optimo: Online probabilistic trust inference model for asymmetric human-robot collaborations. In Proceedings of the Tenth Annual ACM/IEEE International Conference on Human-robot Interaction, Portland, OR, USA, 2–5 March 2015; pp. 221–228. [Google Scholar]
- Guo, Y.; Yang, X.J. Modeling and predicting trust dynamics in human–robot teaming: A Bayesian inference approach. Int. J. Soc. Robot. 2021, 13, 1899–1909. [Google Scholar] [CrossRef]
- Lee, J.; Moray, N. Trust, control strategies and allocation of function in human-machine systems. Ergonomics 1992, 35, 1243–1270. [Google Scholar] [CrossRef]
- Manzey, D.; Reichenbach, J.; Onnasch, L. Human performance consequences of automated decision aids: The impact of degree of automation and system experience. J. Cogn. Eng. Decis. Mak. 2012, 6, 57–87. [Google Scholar] [CrossRef]
- Yang, X.J.; Wickens, C.D.; Hölttä-Otto, K. How users adjust trust in automation: Contrast effect and hindsight bias. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting; SAGE Publications: Los Angeles, CA, USA, 2016; Volume 60, pp. 196–200. [Google Scholar]
- Müller, R.; Reindel, D.F.; Stadtfeld, Y.D. The benefits and costs of explainable artificial intelligence in visual quality control: Evidence from fault detection performance and eye movements. Hum. Factors Ergon. Manuf. Serv. Ind. 2024, 34, 396–416. [Google Scholar] [CrossRef]
- Lu, Y.; Sarter, N. Modeling and inferring human trust in automation based on real-time eye tracking data. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting; SAGE Publications: Los Angeles, CA, USA, 2020; Volume 64, pp. 344–348. [Google Scholar]
- Hergeth, S.; Lorenz, L.; Vilimek, R.; Krems, J.F. Keep your scanners peeled: Gaze behavior as a measure of automation trust during highly automated driving. Hum. Factors 2016, 58, 509–519. [Google Scholar] [CrossRef] [PubMed]
- Gold, C.; Körber, M.; Hohenberger, C.; Lechner, D.; Bengler, K. Trust in automation–before and after the experience of take-over scenarios in a highly automated vehicle. Procedia Manuf. 2015, 3, 3025–3032. [Google Scholar] [CrossRef]
- Victor, T.W.; Tivesten, E.; Gustavsson, P.; Johansson, J.; Sangberg, F.; Ljung Aust, M. Automation expectation mismatch: Incorrect prediction despite eyes on threat and hands on wheel. Hum. Factors 2018, 60, 1095–1116. [Google Scholar] [CrossRef]
- Parasuraman, R.; Manzey, D.H. Complacency and bias in human use of automation: An attentional integration. Hum. Factors 2010, 52, 381–410. [Google Scholar] [CrossRef]
- Maman, Z.S.; Chen, Y.J.; Baghdadi, A.; Lombardo, S.; Cavuoto, L.A.; Megahed, F.M. A data analytic framework for physical fatigue management using wearable sensors. Expert Syst. Appl. 2020, 155, 113405. [Google Scholar] [CrossRef]
- Li, Q.; Song, Y.; Zhang, J.; Sheng, V.S. Multiclass imbalanced learning with one-versus-one decomposition and spectral clustering. Expert Syst. Appl. 2020, 147, 113152. [Google Scholar] [CrossRef]
- Tobii Technology. Tobii Pro Fusion User Manual; Technical Report; Tobii Technology: Danderyd Municipality, Sweden, 2023. [Google Scholar]
- Bandicam Company. Bandicam Screen Recorder. 2008. Available online: https://www.bandicam.com (accessed on 23 May 2024).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F. Scikit-learn: Machine learning in python Fabian. J. Mach. Learn. Res. 2011, 12, 2825. [Google Scholar]
- Deng, X.; Liu, Q.; Deng, Y.; Mahadevan, S. An improved method to construct basic probability assignment based on the confusion matrix for classification problem. Inf. Sci. 2016, 340, 250–261. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. Int. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- McDonald, J.B.; Xu, Y.J. A generalization of the beta distribution with applications. J. Econom. 1995, 66, 133–152. [Google Scholar] [CrossRef]
- De Winter, J.C.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273. [Google Scholar] [CrossRef] [PubMed]
- IBM Corporation. IBM SPSS Statistics 28.0 User’s Guide; Technical Report; IBM Corporation: Armonk, NY, USA, 2021; Available online: https://www.ibm.com/docs/en/SSLVMB_28.0.0/pdf/IBM_SPSS_Statistics_Core_System_User_Guide.pdf (accessed on 17 June 2024).
- Kraus, J.M.; Forster, Y.; Hergeth, S.; Baumann, M. Two routes to trust calibration: Effects of reliability and brand information on trust in automation. Int. J. Mob. Hum. Comput. Interact. (IJMHCI) 2019, 11, 1–17. [Google Scholar] [CrossRef]
- Ribeiro, D.D.S.; Barbosa, G.D.J.; Silva, M.D.C.; Lopes, H.; Barbosa, S.D.J. Exploring the impact of classification probabilities on users’ trust in ambiguous instances. In Proceedings of the 2021 IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC), St Louis, MO, USA, 10–13 October 2021; pp. 1–9. [Google Scholar]






| True/Predicted | Alarms | No Alarms |
|---|---|---|
| Danger Exists | Hits | Misses |
| No Danger Exists | False Alarms | Correct Rejections |
| No. | Interaction Data | System Data | Scale Data | Eye-Tracking Data |
|---|---|---|---|---|
| 1 | No | Hit | Complete the trust scale 1 time for each of the 6 subtasks on a scale of 1–100 | Eye-tracker real-time collection of eye-tracking data throughout |
| 2 | Yes | Not Hit | ||
| 3 | No | False Alarm | ||
| 4 | Yes | Hit | ||
| 5 | Yes | Correctly Reject | ||
| 6 | No | Hit |
| True/Predicted | T1 | T2 | T3 |
|---|---|---|---|
| T1 | T | F | F |
| T2 | F | T | F |
| T3 | F | F | T |
| Reliability Level | RMSE |
|---|---|
| 50% | 0.0367 |
| 70% | 0.0226 |
| 80% | 0.0678 |
| 90% | 0.0664 |
| Comprehensive | 0.0521 |
| No. | Eye-Tracking Metric | Spearman Coefficient | Correlation Result |
|---|---|---|---|
| 1 | Fixation Duration Mean/Fixation Duration Standard Deviation | 0.803 | Strong correlation |
| 2 | Fixation Index | 0.853 | Strong correlation |
| 3 | Horizontal Search Range | 0.663 | Moderate correlation |
| 4 | Vertical Search Range | 0.255 | Weak correlation |
| 5 | Fixation Transition Time | 0.859 | Strong correlation |
| 6 | Fixation–Saccade Time Ratio | 0.809 | Strong correlation |
| 7 | Saccade Velocity Range | 0.496 | Moderate correlation |
| 8 | Saccade Velocity Variance | 0.542 | Moderate correlation |
| 9 | Saccade Velocity Mean | 0.492 | Moderate correlation |
| 10 | Pupil Diameter Change Rate | 0.916 | Strong correlation |
| Evaluation Metric | Results |
|---|---|
| T1 Precision | 0.80 |
| T3 Precision | 0.84 |
| T1 Recall | 0.88 |
| T3 Recall | 0.51 |
| T1 as T3 Error Rate | 0.0000 |
| T3 as T1 Error Rate | 0.0006 |
| Eye-Tracking Metric | Description |
|---|---|
| Sac_Fix (saccade–fixation ratio) Sac_Time (saccade time) | Proportion of time spent on saccades relative to total time spent on saccades and fixations. Total time spent on saccadic eye movements. |
| Fix_Time (fixation time) | Time spent fixing on specific areas of interest (AOIs). |
| Pos_X_SD (horizontal gaze dispersion) | Standard deviation of gaze positions along the horizontal axis. |
| Speed_Var (saccade velocity variance) | Variability in the velocity of saccadic eye movements. |
| Fix_Mode (fixation mode) | Most frequent fixation duration observed during a task. |
| Pupil_SD (pupil diameter standard deviation) | Standard deviation of pupil size changes during the task. |
| Speed_Gap (saccade velocity range) | Range between the maximum and minimum velocities of saccadic movements. |
| Speed_Mean (saccade velocity mean) | Average velocity of saccadic movements. |
| Criteria | Result |
|---|---|
| MSE | 1.8439 |
| RMSE | 1.3579 |
| 0.8993 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Hou, W.; Ma, H.; Hong, L. Eye-Tracking Characteristics: Unveiling Trust Calibration States in Automated Supervisory Control Tasks. Sensors 2024, 24, 7946. https://doi.org/10.3390/s24247946
Wang K, Hou W, Ma H, Hong L. Eye-Tracking Characteristics: Unveiling Trust Calibration States in Automated Supervisory Control Tasks. Sensors. 2024; 24(24):7946. https://doi.org/10.3390/s24247946
Chicago/Turabian StyleWang, Keran, Wenjun Hou, Huiwen Ma, and Leyi Hong. 2024. "Eye-Tracking Characteristics: Unveiling Trust Calibration States in Automated Supervisory Control Tasks" Sensors 24, no. 24: 7946. https://doi.org/10.3390/s24247946
APA StyleWang, K., Hou, W., Ma, H., & Hong, L. (2024). Eye-Tracking Characteristics: Unveiling Trust Calibration States in Automated Supervisory Control Tasks. Sensors, 24(24), 7946. https://doi.org/10.3390/s24247946





