Characteristic Analysis and Error Compensation Method of Space Vector Pulse Width Modulation-Based Driver for Permanent Magnet Synchronous Motors
Abstract
1. Introduction
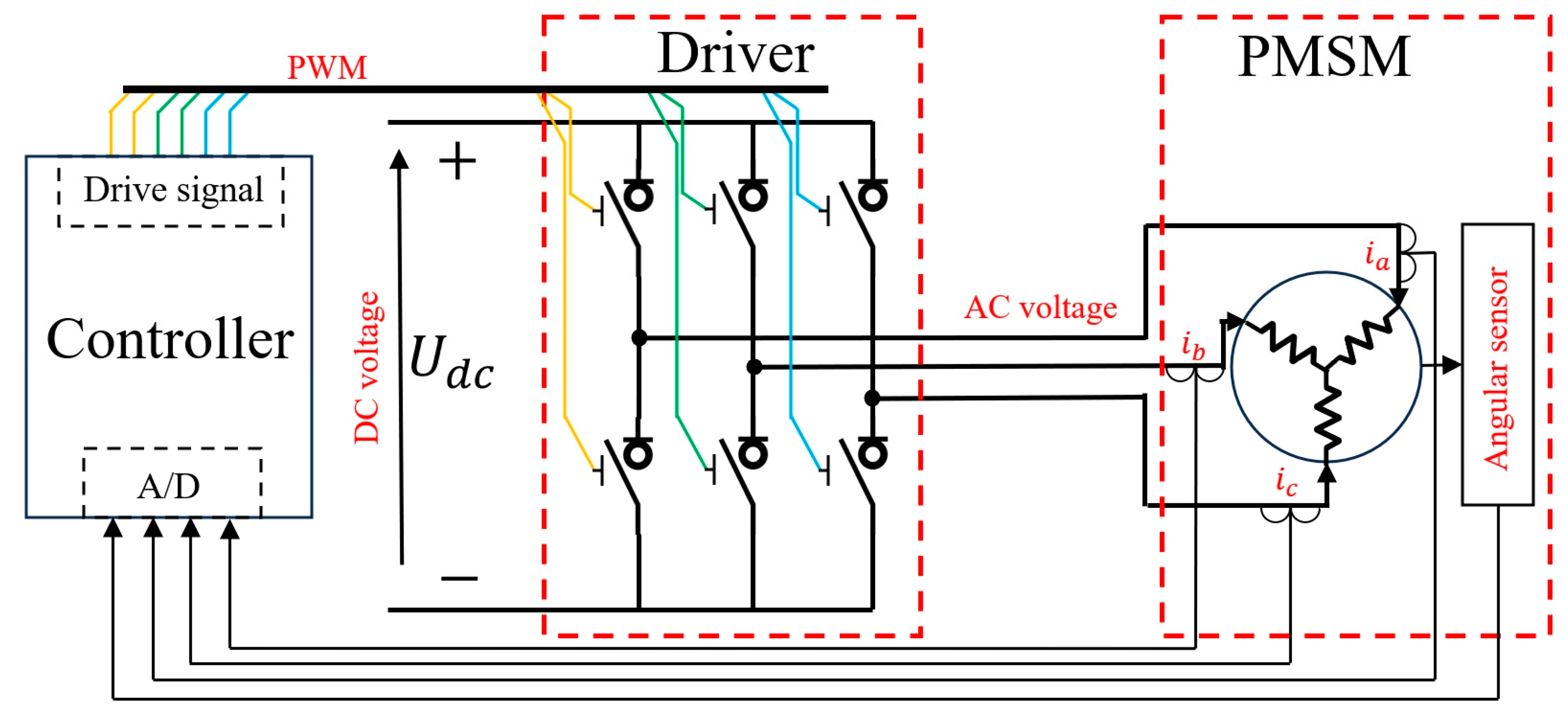
2. Characterization of Space Vector Pulse Width Modulated Drivers
2.1. Overview of SVPWM Techniques
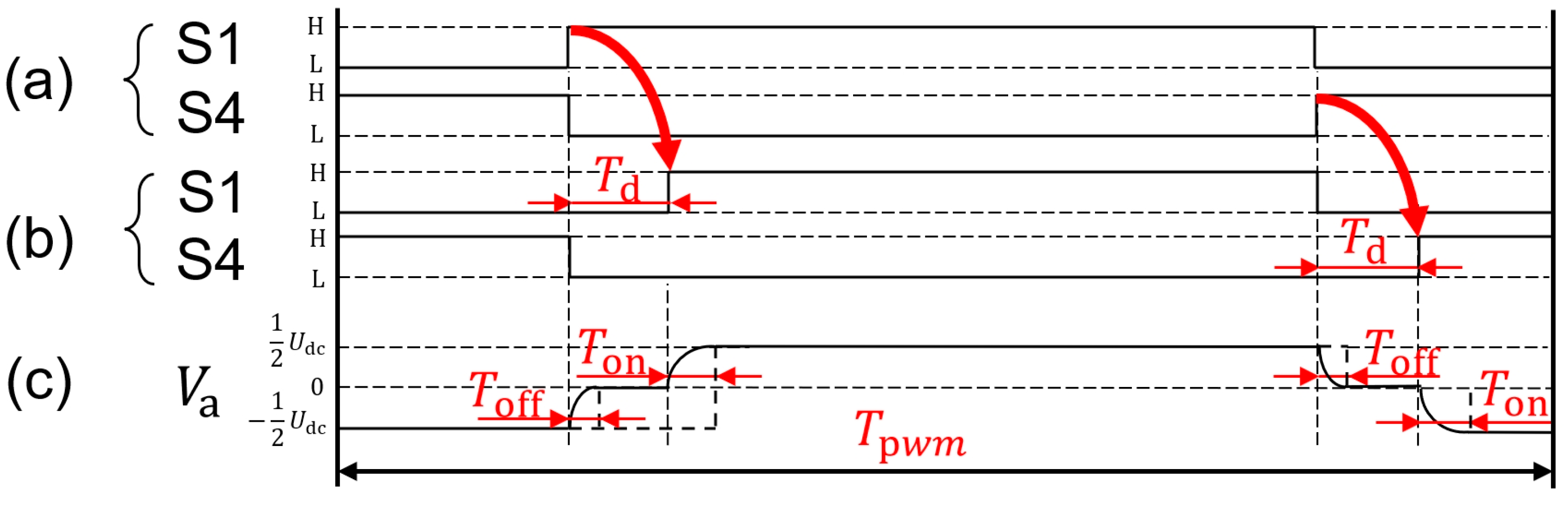
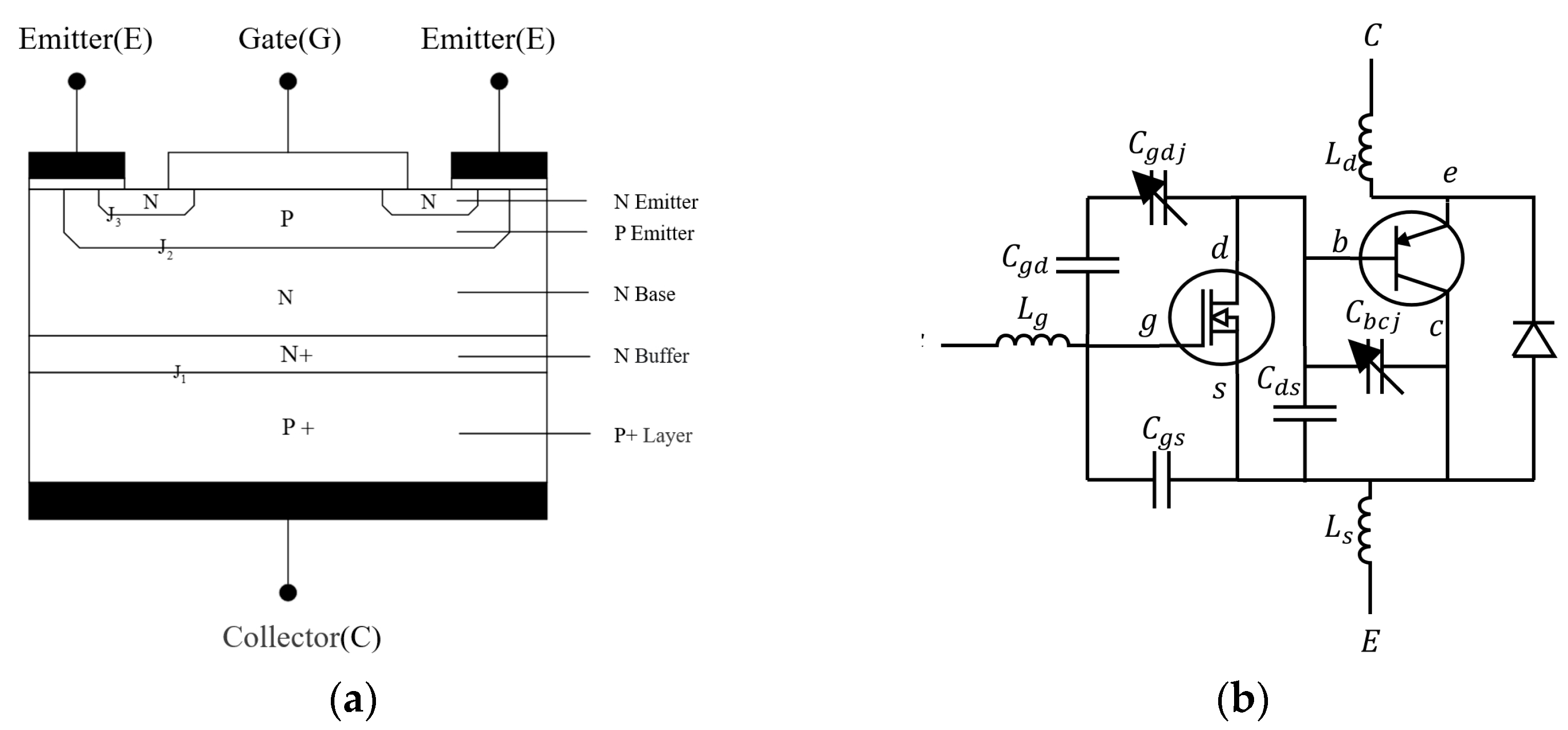
2.2. IGBT Internal Structure and On–Off Time Analysis
2.3. Effect of Voltage on IGBT Switching Time
2.4. Effect of Current on IGBT Switching Time
3. Drive Characterization Modeling
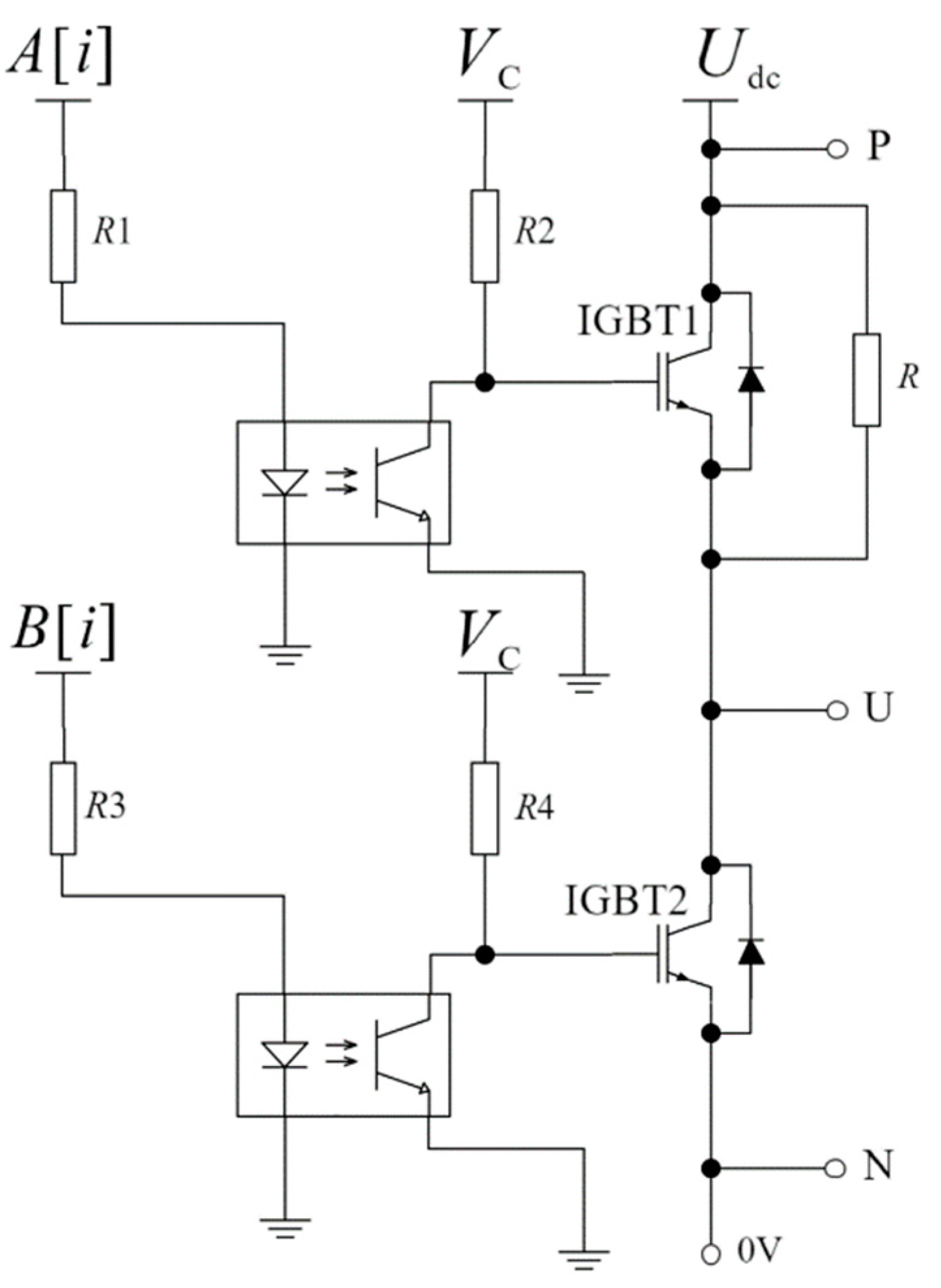
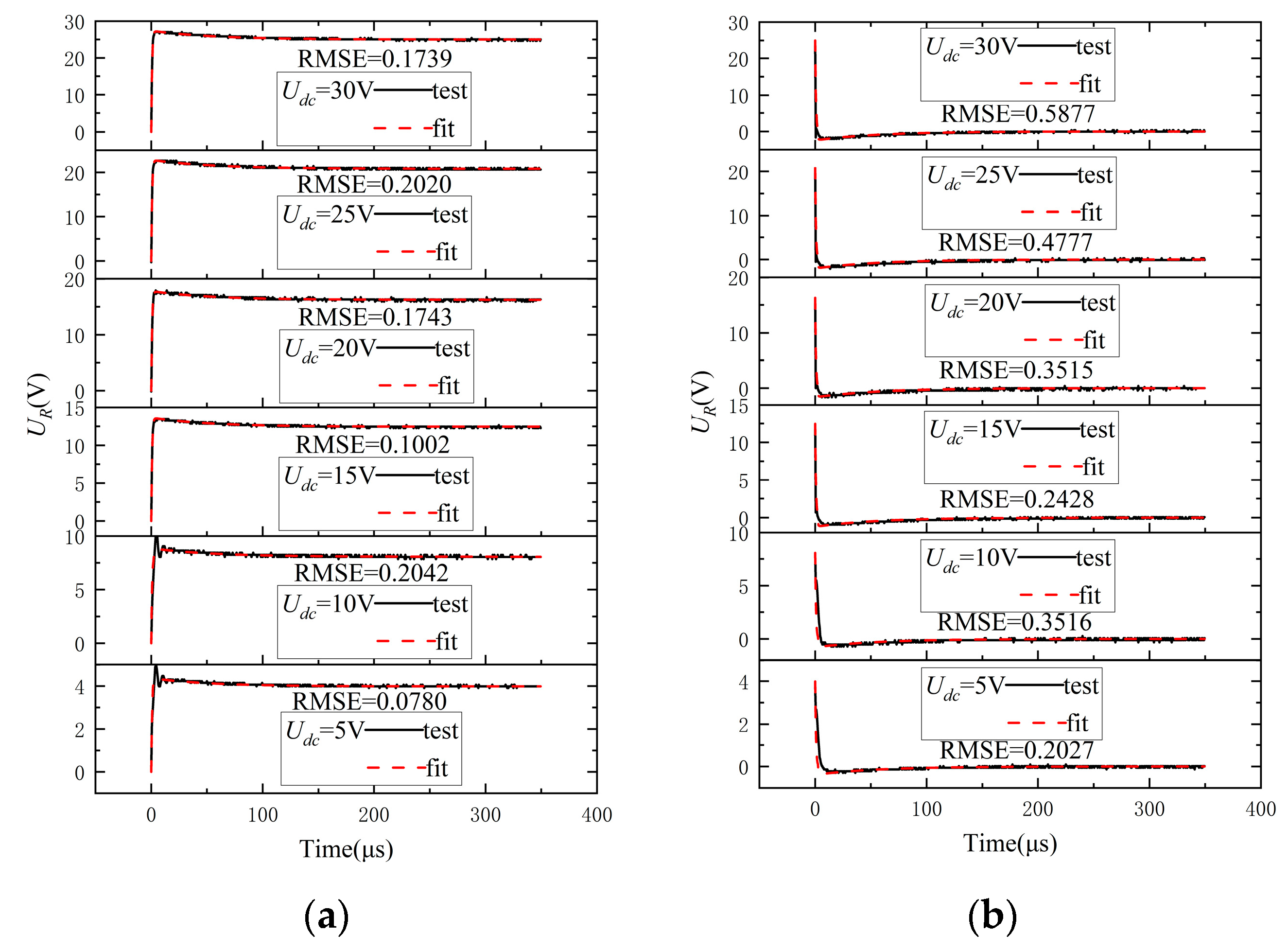
3.1. IGBT On–Off Test Method
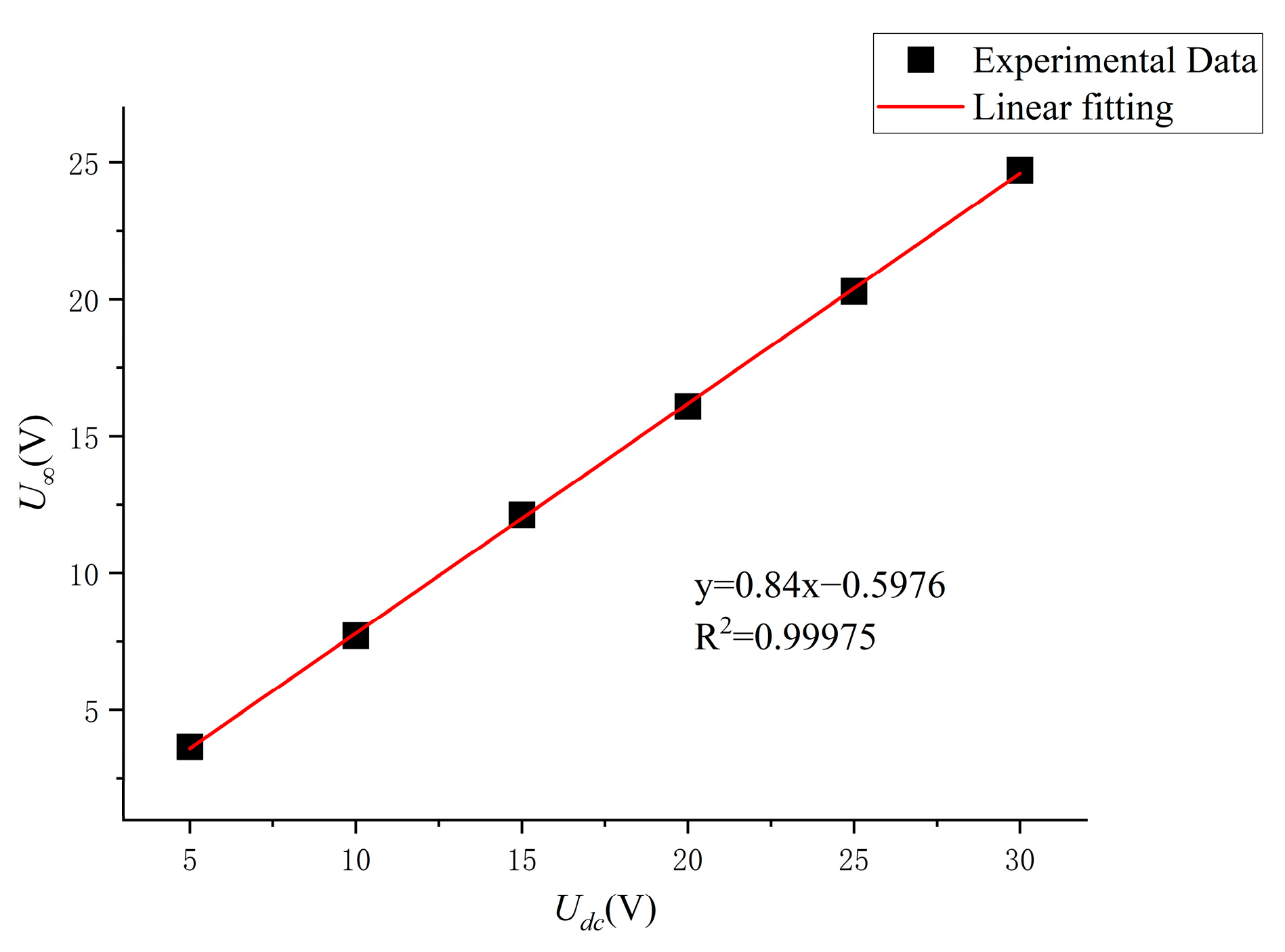
3.2. IGBT Conduction Test Analysis
3.3. Analysis of IGBT Turn-Off Testing
3.4. Driver On–Off Modeling
4. Driver Error Compensation Method Based on IGBT Switching Characteristics
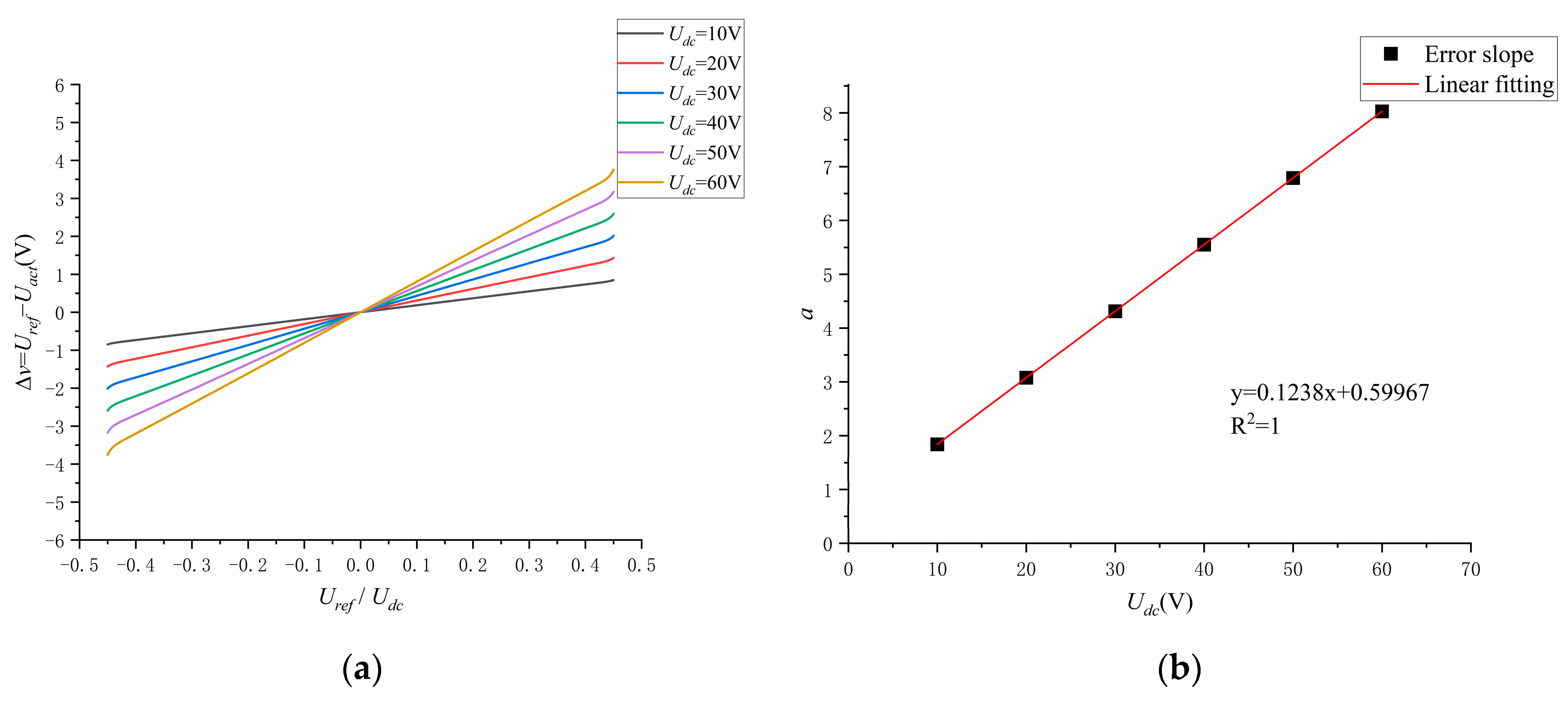
4.1. Driver Input–Output Error Model
4.2. Voltage Compensation Method
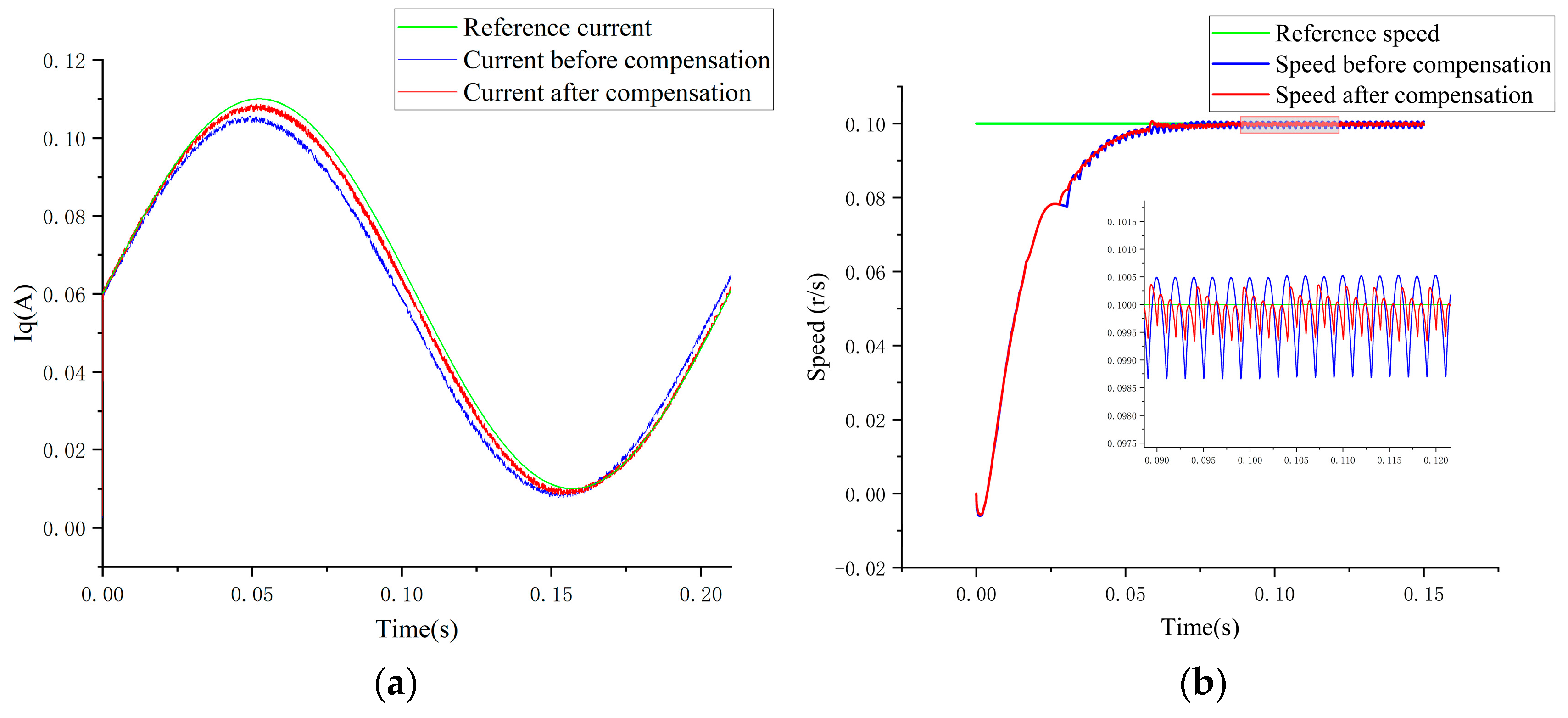
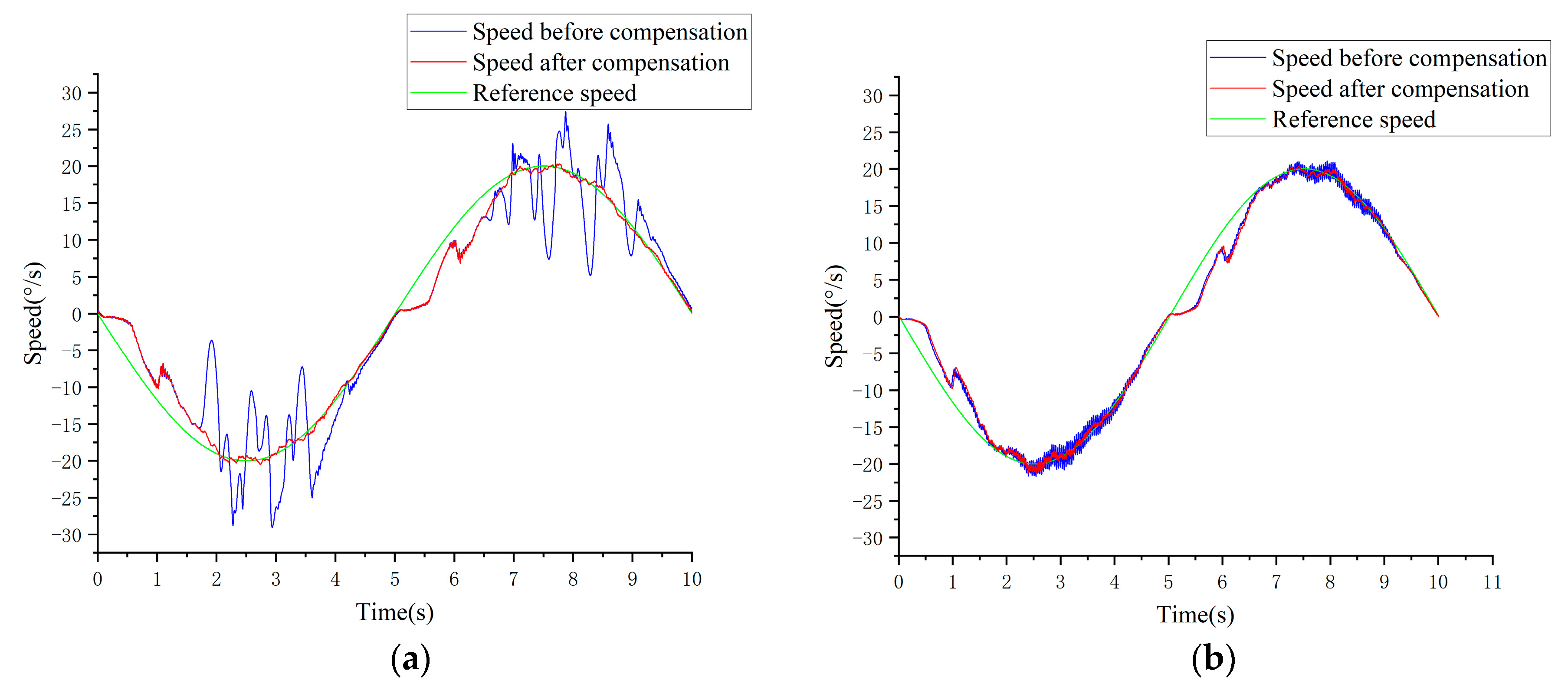
5. Simulation Results and Analysis
6. Experimentation Results and Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Zhou, K.; Wang, H.; Blaabjerg, F. Analysis and Mitigation of Dead-Time Harmonics in the Single-Phase Full-Bridge PWM Converter with Repetitive Controllers. IEEE Trans. Ind. Appl. 2018, 54, 5343–5354. [Google Scholar] [CrossRef]
- Wei, J.; Xue, J.; Zhou, B. Dead-time effect analysis and suppression for open-winding PMSM system with the four-leg converter. Trans. China Electrotech. 2018, 33, 4078–4090. [Google Scholar] [CrossRef]
- Han, K.; Sun, X. Dead-time On-line Compensation Scheme of SVPWM for Permanent Magnet Synchronous Motor Drive System with Vector Control. Proc. CSEE 2018, 38, 620–627. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Deng, Y. Torque Ripple Minimization of PMSM Based on Robust ILC Via Adaptive Sliding Mode Control. IEEE Trans. Power Electron. 2018, 33, 3655–3671. [Google Scholar] [CrossRef]
- Wang, W.; Wang, W. Compensation for Inverter Nonlinearity in Permanent Magnet Synchronous Motor Drive and Effect on Torsional Vibration of Electric Vehicle Driveline. Energies 2018, 11, 2542. [Google Scholar] [CrossRef]
- Mao, Y.; Zuo, S.; Wu, X.; Duan, X. High frequency vibration characteristics of electric wheel system under in-wheel motor torque ripple. J. Sound. Vib. 2017, 400, 442–456. [Google Scholar] [CrossRef]
- Liu, G.; Wang, D.; Jin, Y.; Wang, M.; Zhang, P. Current-Detection-Independent Dead-Time Compensation Method Based on Terminal Voltage A/D Conversion for PWM VSI. IEEE Trans. Ind. Electron. 2017, 64, 7689–7699. [Google Scholar] [CrossRef]
- Guha, A.; Narayanan, G. Small-Signal Stability Analysis of an Open-Loop Induction Motor Drive Including the Effect of Inverter Deadtime. IEEE Trans. Ind. Appl. 2016, 52, 242–253. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Q.; Cai, X. Mixed PWM for Dead-Time Elimination and Compensation in a Grid-Tied Inverter. IEEE Trans. Ind. Electron. 2011, 58, 4797–4803. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, P.; Xu, Y. Dead Zone Compensation Strategy for Inverter of PMSM Based on Direct Axis Voltage Analysis. J. Electr. Eng. 2021, 16, 51–58. [Google Scholar] [CrossRef]
- Li, Y.-S.; Wu, P.-Y.; Ho, M.-T. Dead-Time Compensation for Permanent Magnet Synchronous Motor Drives. In Proceedings of the 2020 International Automatic Control Conference (CACS), Hsinchu, Taiwan, 4–7 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, Z.; Pei, Y.; Wang, L.; Yang, Q.; Lu, X.; Yang, F. Research on Switching Characteristics of SiC MOSFET in Pulsed Power Supply with Analytical Model. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 325–330. [Google Scholar] [CrossRef]
- Da Costa Gonçalves, P.F.; Dhale, S.; Batkhishig, B.; Yang, J.; Nahid-Mobarakeh, B. Comparative Study Between Finite Control Set Model Predictive Control and Digital Sliding-Mode Control for the Reduction of Current Harmonics in Six-Phase PMSM Drives. In Proceedings of the 2023 IEEE International Electric Machines & Drives Conference (IEMDC), San Francisco, CA, USA, 15–18 May 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Zhang Q and Fan, Y. "The Online Parameter Identification Method of Permanent Magnet Synchronous Machine under Low-Speed Region Considering the Inverter Nonlinearity. Energies 2022, 15, 4314. [Google Scholar] [CrossRef]
- Geng, Y.; Han, P.; Chen, R.; Le, Z.; Lai, Z. On-line dead-time compensation method for dual three phase PMSM based on adaptive notch filter. IET Power Electron. 2021, 14, 2452–2465. [Google Scholar] [CrossRef]
- Lee, J.-H.; Sul, S.-K. Inverter Nonlinearity Compensation Through Deadtime Effect Estimation. IEEE Trans. Power Electron. 2021, 36, 10684–10694. [Google Scholar] [CrossRef]
- Luo, L.; Rao, Z.; Yan, Y.; Bai, Z. Analysis of an Improved Voltage-balancing Control Method of Modular Multilevel Converter Based on Amplitude-adjustable Carrier. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kota Kinabalu, Malaysia, 7–10 October 2018; pp. 335–340. [Google Scholar] [CrossRef]
- Iwamuro, N.; Laska, T. Correction to “IGBT History, State-of-the-Art, and Future Prospects” [Mar 17 741-752]. IEEE Trans. Electron Devices 2018, 65, 2675. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, B.; Wang, B. The influence of IGBT switching mechanism on the dead-time of inverters. Electr. Mach. Control. 2014, 18, 62–68+75. [Google Scholar] [CrossRef]
- Si, G.; Shen, Z.; Zhang, Z.; Kennel, R. Investigation of the limiting factors of the dead time minimization in a H-bridge IGBT inverter. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Sze, S.M.; Lee, M.-K. Physics of Semiconductor Devices; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]







| Parameters | Value |
|---|---|
| 10 | 1.83765 | 0.99998 |
| 20 | 3.07563 | 0.99997 |
| 30 | 4.31361 | 0.99996 |
| 40 | 5.55159 | 0.99996 |
| 50 | 6.78957 | 0.99996 |
| 60 | 8.02755 | 0.99996 |
| Name | Value |
|---|---|
| Stator Equivalent Resistance | 9.9 Ω |
| Stator Equivalent Inductance | 17.9 mH |
| Continuous Torque | 23.8 N·m |
| Torque Constant | 9.5 N·m/A |
| Moment of Inertia | 0.02 kg∙m2 |
| Number of Pole Pairs | 15 |
| Viscous Damping Coefficient | 0.001 |
| Module | Name | Value |
|---|---|---|
| LD-170095 | Stator Equivalent Resistance | 9.9 Ω |
| Stator Equivalent Inductance | 17.9 mH | |
| Continuous Torque | 23.8 N·m | |
| Continuous Current | 2.5 A | |
| Maximum Torque | 71 N·m | |
| Maximum Current | 7.5 A | |
| Torque Constant | 9.5 N·m/A | |
| Moment of Inertia | 0.02 kg∙m2 | |
| Number of Pole Pairs | 15 | |
| Maximum Rated Power Consumption | 30.1 W | |
| Maximum Rotational Speed | 190 rpm | |
| PM25RLA120 | Maximum Collector-Emitter Voltage | 1200 V |
| Collector Current | 15 A | |
| Collector Current (Peak) | 30 A | |
| Recommendation dead time | ||
| Recommendation PWM input frequency | ≤20 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Wu, W.; He, Q. Characteristic Analysis and Error Compensation Method of Space Vector Pulse Width Modulation-Based Driver for Permanent Magnet Synchronous Motors. Sensors 2024, 24, 7945. https://doi.org/10.3390/s24247945
Chen Q, Wu W, He Q. Characteristic Analysis and Error Compensation Method of Space Vector Pulse Width Modulation-Based Driver for Permanent Magnet Synchronous Motors. Sensors. 2024; 24(24):7945. https://doi.org/10.3390/s24247945
Chicago/Turabian StyleChen, Qihang, Wanzhen Wu, and Qianen He. 2024. "Characteristic Analysis and Error Compensation Method of Space Vector Pulse Width Modulation-Based Driver for Permanent Magnet Synchronous Motors" Sensors 24, no. 24: 7945. https://doi.org/10.3390/s24247945
APA StyleChen, Q., Wu, W., & He, Q. (2024). Characteristic Analysis and Error Compensation Method of Space Vector Pulse Width Modulation-Based Driver for Permanent Magnet Synchronous Motors. Sensors, 24(24), 7945. https://doi.org/10.3390/s24247945






