CA Modeling of Microsegregation and Growth of Equiaxed Dendrites in the Binary Al-Mg Alloy
Abstract
:1. Introduction
2. Description of the Model
2.1. Modelling of Component Diffusion and Solid Phase Growth
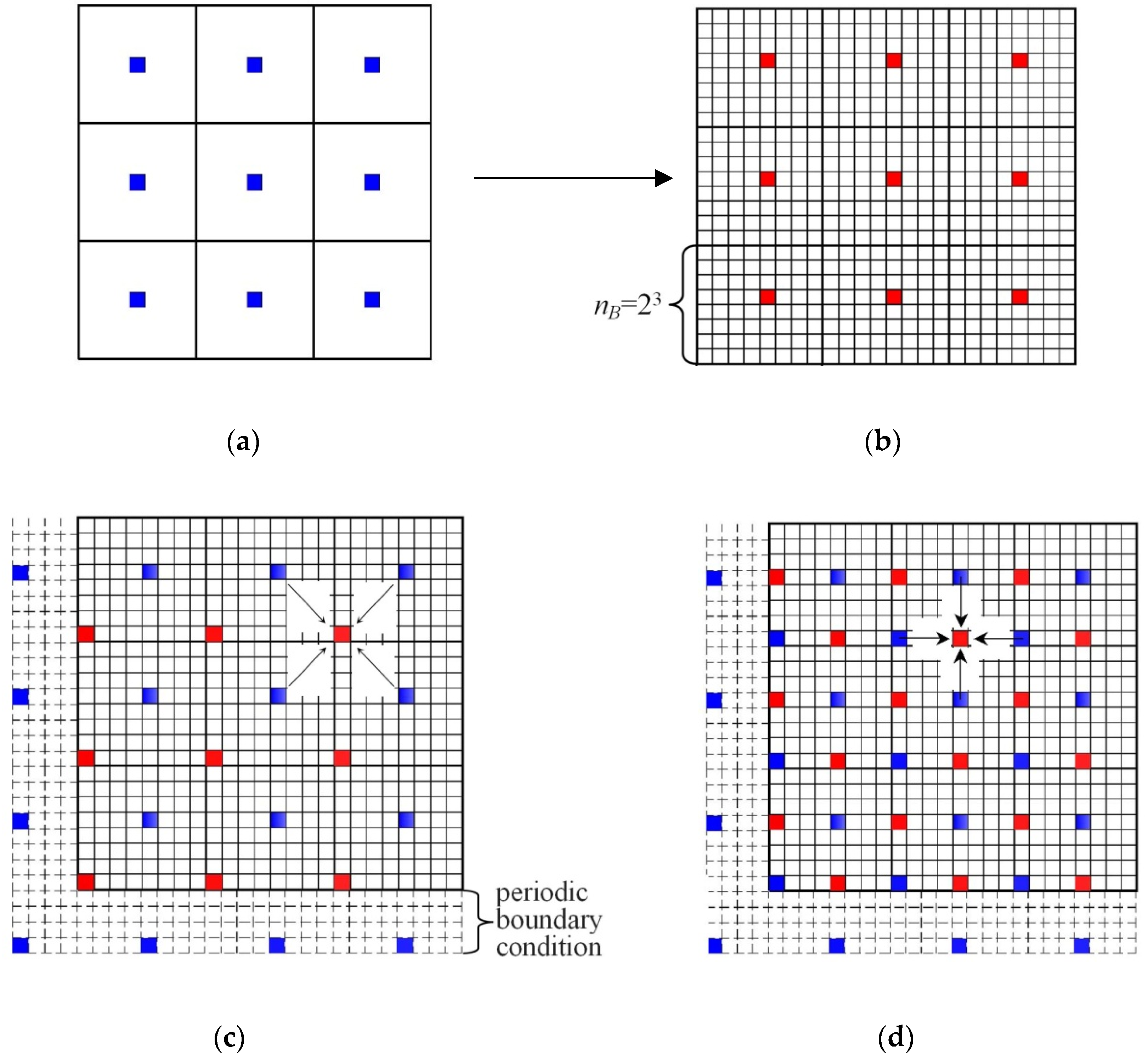
2.2. Temperature Field Approximation and Interpolation
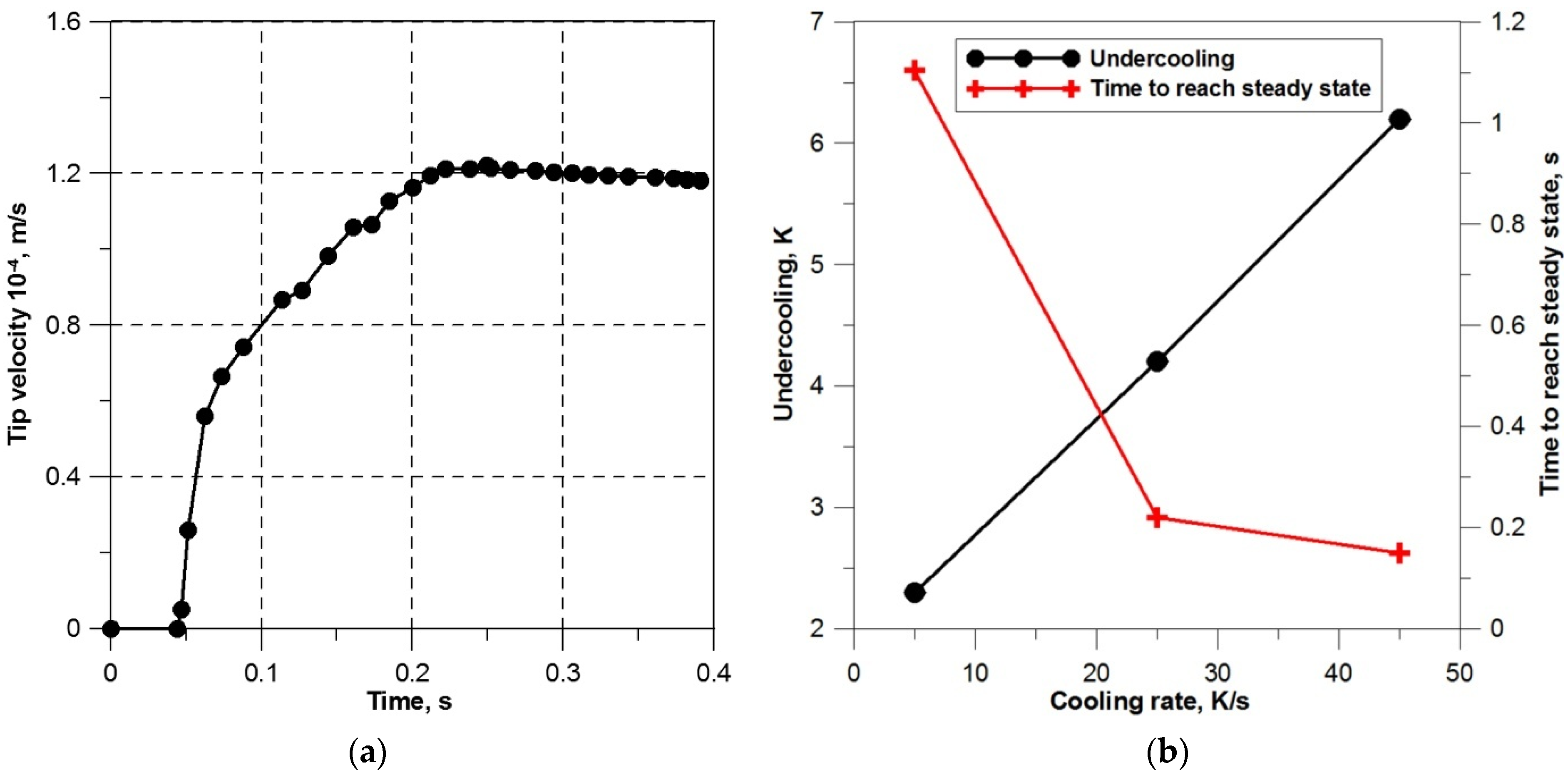
2.3. Nucleation and Initial Growth Period under Transient Diffusion Conditions
2.4. Optimisation of the Time Step for Model Equations
3. Numerical Simulations Results
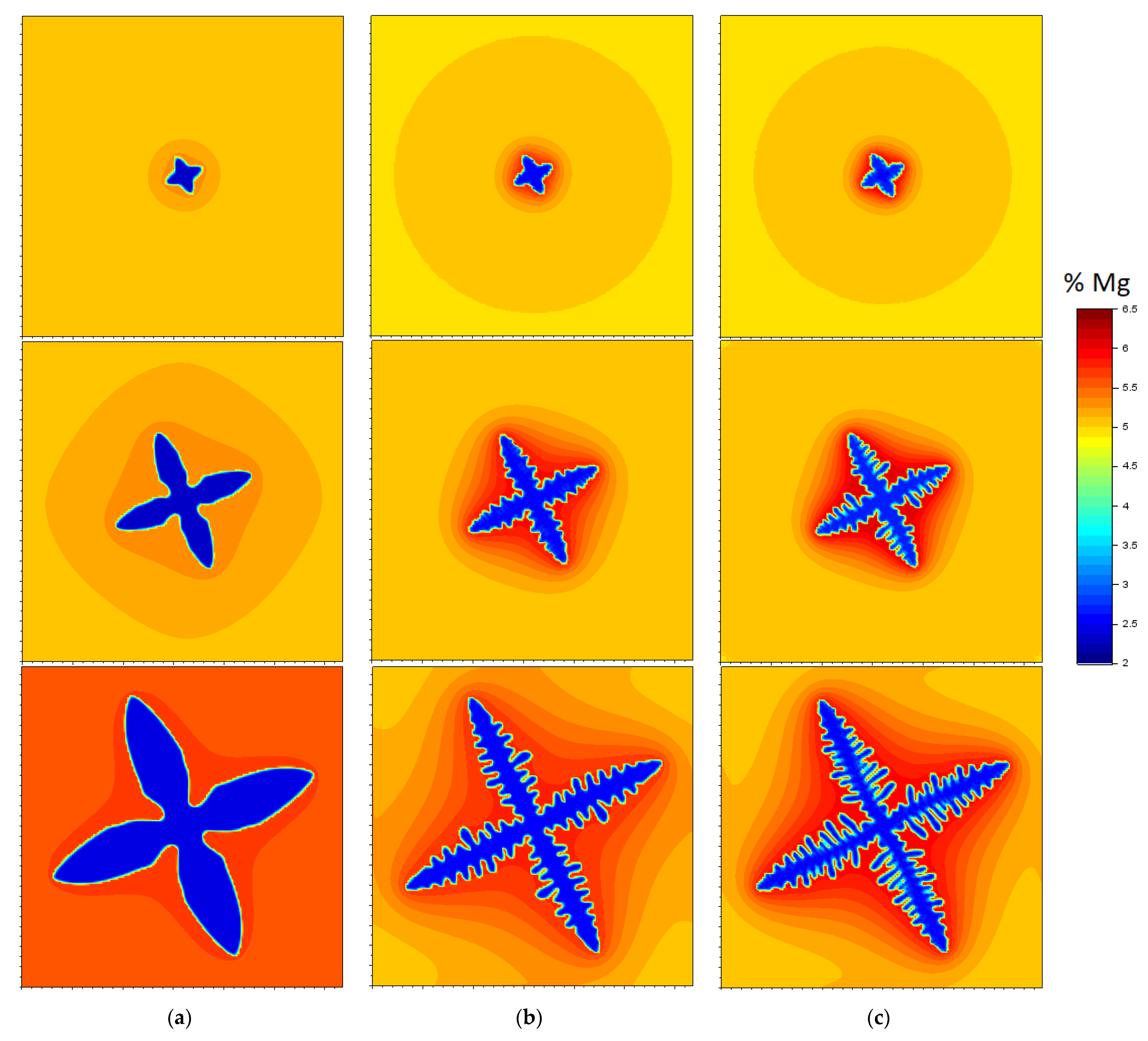
3.1. Free Growth of a Single Dendrite
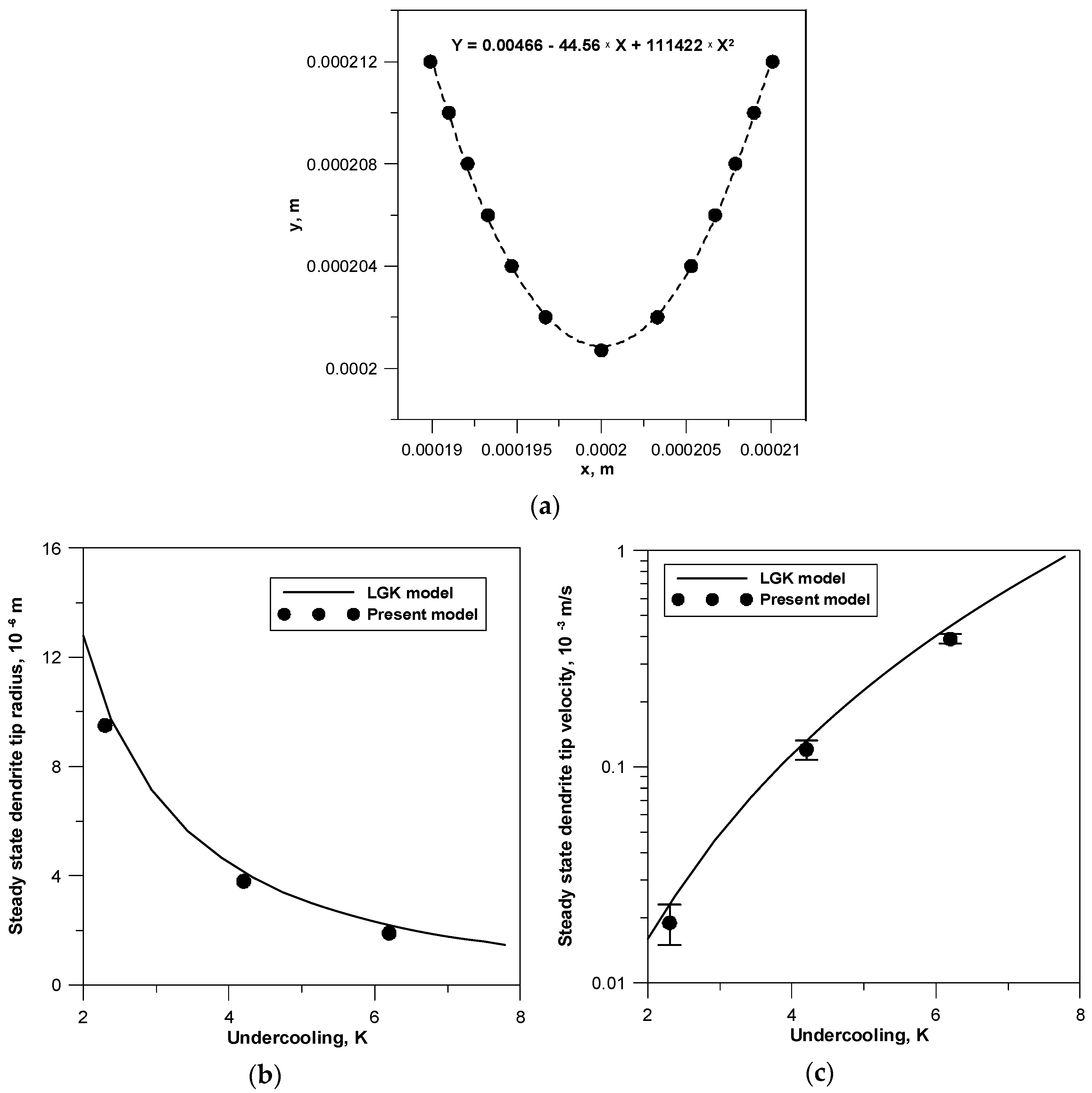
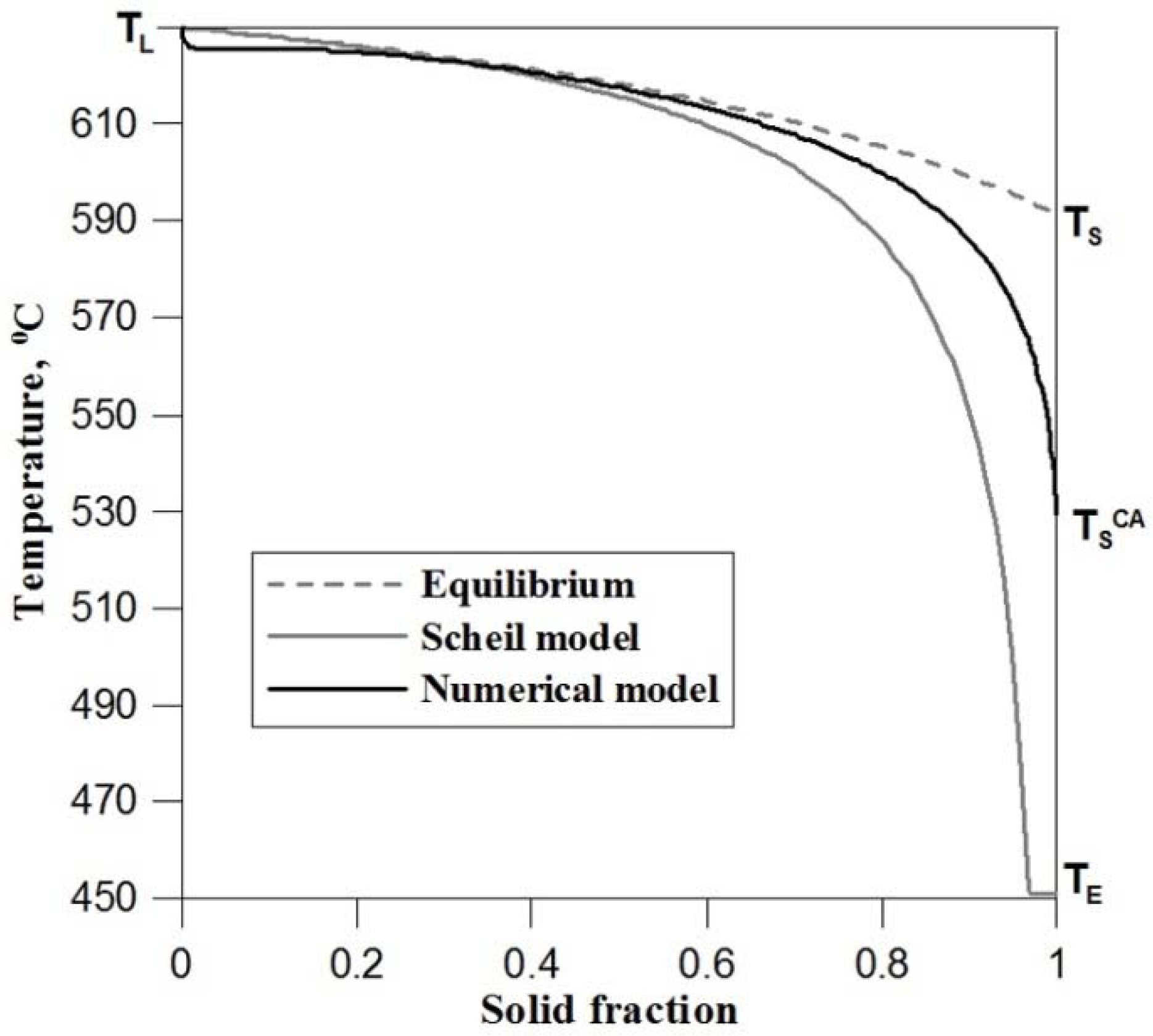
3.2. Validation of the Numerical Model
3.3. Multiple Dendrite Growth Simulation
4. Experimental Tests
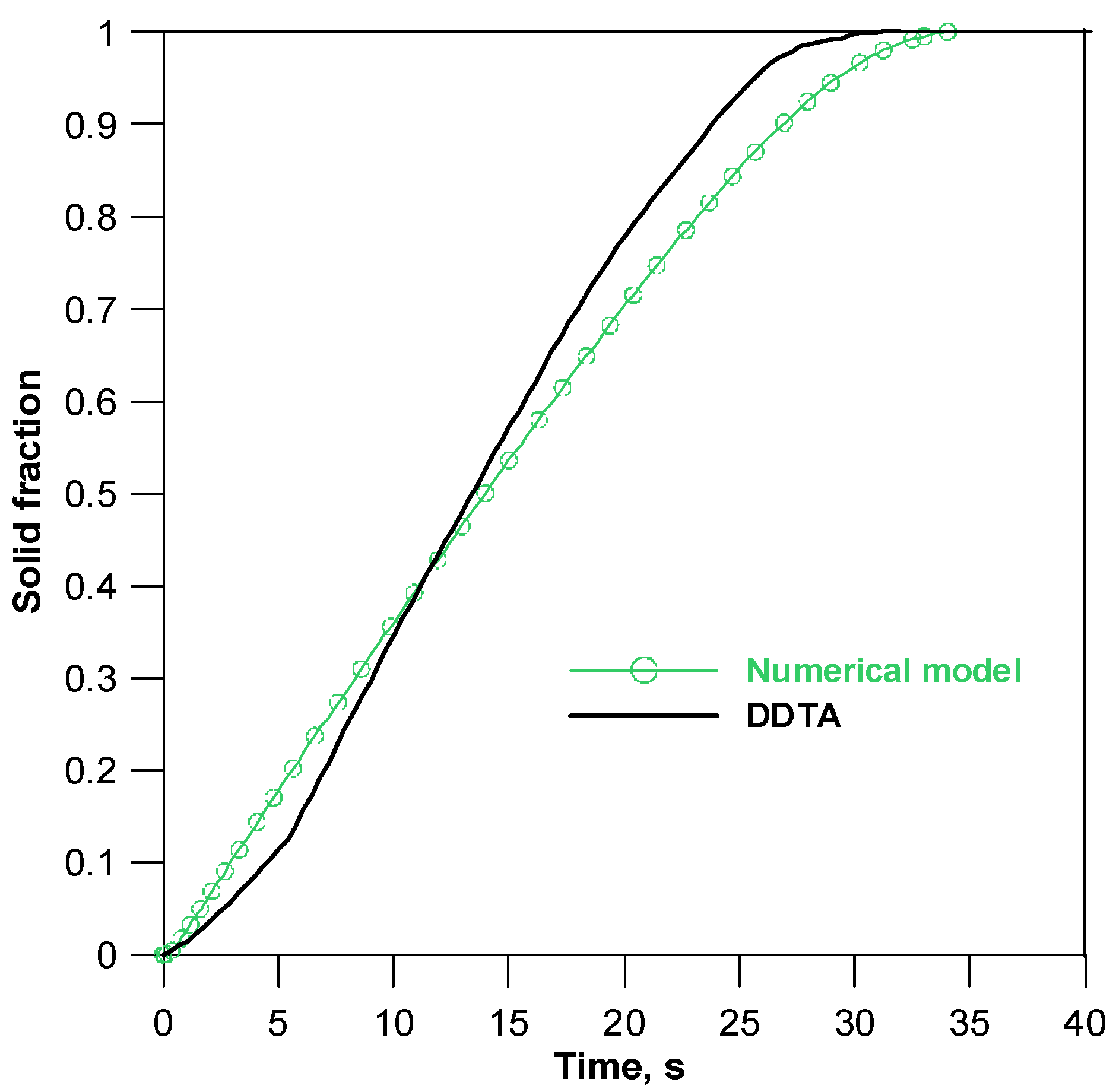
4.1. Tests of the Solidification Process Using the DDTA Method
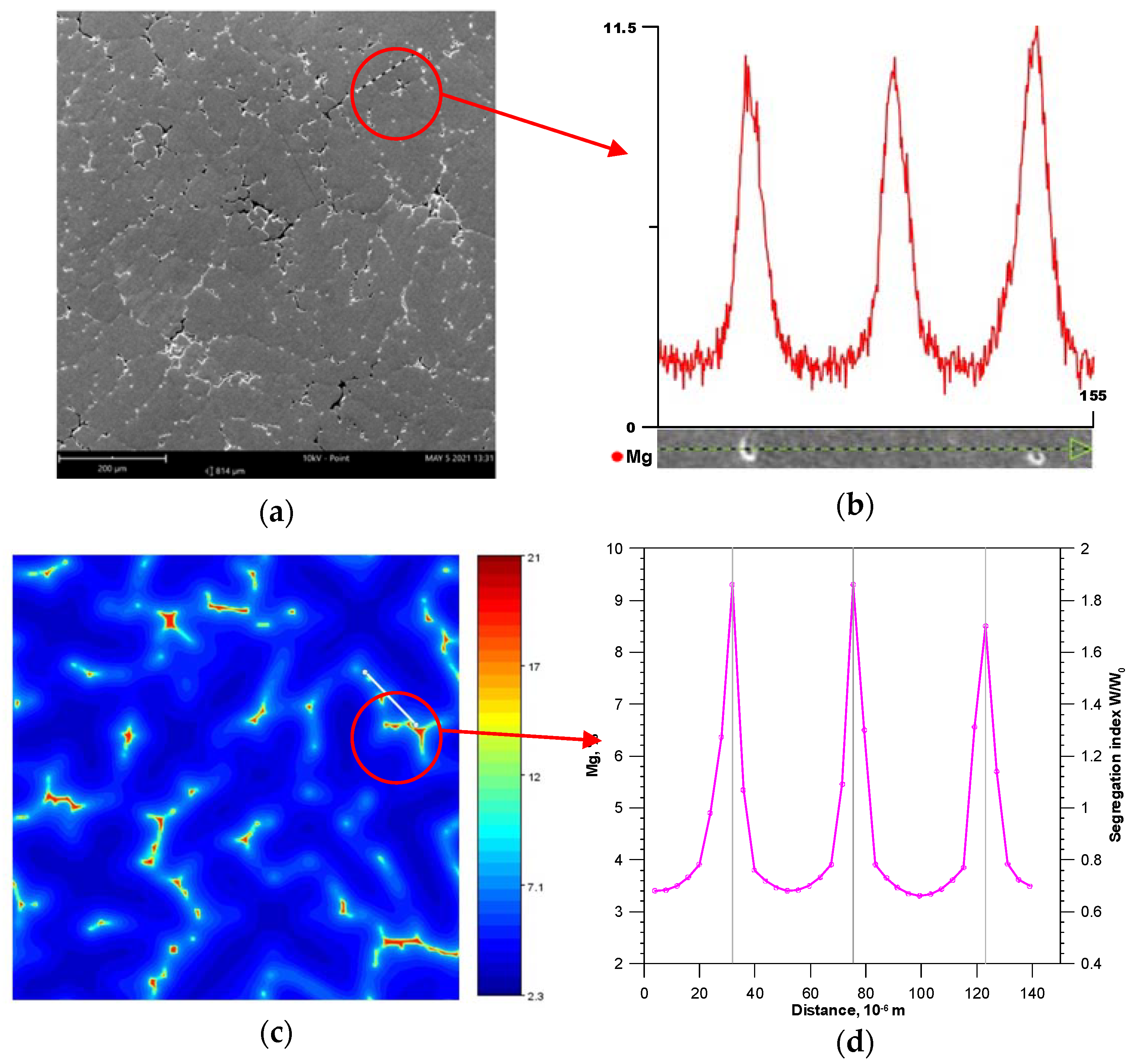
4.2. Results of Microstructural Tests
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, L.; Li, S.; Chang, X.; Zhong, H.; Fu, H. Twinned dendrite growth during Bridgman solidification. Acta Mater. 2015, 97, 269–281. [Google Scholar] [CrossRef]
- Miller, J.D.; Yuan, L.; Lee, P.D.; Pollock, T.M. Simulation of diffusion-limited lateral growth of dendrites during solidification via liquid metal cooling. Acta Mater. 2014, 69, 47–59. [Google Scholar] [CrossRef]
- Genau, A.L.; Freedman, A.C.; Ratke, L. Effect of solidification conditions on fractal dimension of dendrites. J. Cryst. Growth 2013, 363, 49–54. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Science and Engineering of Casting Solidification, 2nd ed.; Springer: New York, NY, USA, 2009; pp. 157–188. [Google Scholar]
- Wolczynski, W.; Ivanova, A.A.; Kwapisinski, P.; Olejnik, E. Structural Transformations vs. Hard Particles Motion in the Brass Ingots. Arch. Metall. Mater. 2017, 62, 2461–2467. [Google Scholar] [CrossRef] [Green Version]
- Gandin, C.A.; Desbiolles, J.L.; Rappaz, M.; Thevoz, P. A Three-Dimensional Cellular Automaton–Finite Element Model for the Prediction of Solidification Grain Structures. Metall. Mater. Trans. A 1999, 30, 3153–3165. [Google Scholar] [CrossRef]
- Wang, W.; Lee, P.D.; Mclean, M. A Model of Solidification Microstructures in Nickel-Based Superalloys: Predicting Primary Dendrite Spacing Selection. Acta Mater. 2003, 51, 2971–2987. [Google Scholar] [CrossRef]
- Zhu, M.F.; Dai, T.; Lee, S.Y.; Hong, C.P. Modeling of solutal dendritic growth with melt convection. Comput. Math. Appl. 2008, 55, 1620–1628. [Google Scholar] [CrossRef] [Green Version]
- Wie, L.; Lin, X.; Wang, M.; Huang, W. Orientation selection of equiaxed dendritic growth by three-dimensional cellular automaton model. Phys. B 2012, 407, 2471–2475. [Google Scholar]
- Zhang, X.; Zhao, J.; Jiang, H.; Zhu, M. A three-dimensional cellular automaton model for dendritic growth in multi-component alloys. Acta Mater. 2012, 60, 2249–2457. [Google Scholar] [CrossRef]
- Pineau, A.; Guillemot, G.; Tourret, D.; Karma, A.; Gandin, C.A. Growth competition between columnar dendritic grains e Cellular automaton versus phase field modeling. Acta Mater. 2018, 55, 286–301. [Google Scholar] [CrossRef]
- Gu, C.; Ridgeway, C.D.; Luo, A.A. Examination of Dendritic Growth during Solidificationof Ternary Alloysviaa Novel Quantitative 3D CellularAutomaton Model. Metall. Mater. Trans. B 2019, 50B, 123–135. [Google Scholar] [CrossRef]
- Hu, M.; Sun, C.; Fang, H.; Zhu, M. Competitive dendrite growth during directional solidification of a transparent alloy: Modeling and experiment. Eur. Phys. J. E 2020, 43, 16. [Google Scholar] [CrossRef]
- Wang, T.; Jin, J.; Zheng, X. A CA/MC model for the simulation of grain structures in solidification processes. J. Mater. Sci. 2002, 37, 2645–2650. [Google Scholar] [CrossRef]
- Beltran-Sanchez, L.; Stefanescu, D.M. Growth of Solutal Dendrites: A Cellular Automaton Model and Its Quantitative Capabilities. Metall. Mater. Trans. A 2003, 34, 367–382. [Google Scholar] [CrossRef]
- Kuangfei, W.; Shan, L.; Guofa, M.; Changyun, L.; Hengzhi, F. Simulation of microstructural evolution in directional solidification of Ti-45at.%Al alloy using cellular automaton method. China Foundry 2010, 7, 47–51. [Google Scholar]
- Dong, H.B.; Lee, P.D. Simulation of the columnar-to-equiaxed transition in directionally solidified Al–Cu alloys. Acta Mater. 2005, 53, 659–668. [Google Scholar] [CrossRef]
- Michelic, S.C.; Thuswaldner, J.M. Polydimensional modelling of dendritic growth and microsegregation in multicomponent alloys. Acta Mater. 2010, 58, 2738–2751. [Google Scholar] [CrossRef]
- Zhan, X.; Wie, Y.; Dong, Z. Cellular automaton simulation of grain growth with different orientation angles during solidification process. J. Mater. Process. Technol. 2008, 208, 1–8. [Google Scholar] [CrossRef]
- Zyska, A.; Boroń, K.; Kordas, P. Modeling of Dendritic Structure Evolution during Solidification of Al-Cu Alloy. Arch. Foundry Eng. 2018, 18, 87–92. [Google Scholar]
- Liu, L.; Pian, S.; Zhang, Z.; Bao, Y.; Li, R.; Chen, H. A cellular automaton-lattice Boltzmann method for modeling growth and settlement of the dendrites for Al-4.7%Cu solidification. Comput. Mater. Sci. 2018, 146, 9–17. [Google Scholar] [CrossRef]
- Dilthey, U.; Pavlik, V. Modeling of Casting, Welding and Advanced Solidification Processes VIII; TMS Publication: Warrendale, Poland, 1991; pp. 589–596. [Google Scholar]
- Zhu, M.F.; Hong, C.P.; Stefanescu, D.M.; Chang, Y.A. Computational Modeling of Microstructure Evolution in Solidification of Aluminum Alloys. Metall. Mater. Trans. B 2007, 38, 517–524. [Google Scholar] [CrossRef]
- Pan, S.; Zhu, M. A three-dimensional sharp interface model for the quantitative simulation of solutal dendritic growth. Acta Mater. 2010, 58, 340–352. [Google Scholar] [CrossRef]
- Yin, H.; Felicelli, S.D.; Wang, L. Simulation of a dendritic microstructure with the lattice Boltzmann and cellular automaton methods. Acta Mater. 2011, 59, 3124–3136. [Google Scholar] [CrossRef]
- Marek, M. Grid anisotropy reduction for simulation of growth processes with cellular automaton. Phys. D 2013, 253, 73–84. [Google Scholar] [CrossRef]
- Zhu, M.F.; Cao, W.; Chen, S.L.; Hong, C.P.; Chang, Y.A. Modeling of Microstructure and Microsegregation in Solidification of Multi-Component Alloys. J. Phase Equilibria Diffus. 2007, 28, 130–138. [Google Scholar] [CrossRef]
- Mingfang, Z.; Ting, D.; Sungyoon, L.; Chunpyo, H. Modeling of dendritic growth in the presence of convection. Sci. China Ser. E Eng. Mater. Sci. 2005, 48, 241–257. [Google Scholar]
- Zyska, A. Modelling of the Dendritic Structure and the Solidification Process for a Binary Alloy; Habilitation Monograph WWIPiTM P.Cz: Częstochowa, Poland, 2014; pp. 54–60. [Google Scholar]
- Udaykumar, H.S.; Kan, H.C.; Shyy, W.; Tran-Son-Tay, R. Multiphase Dynamics in Arbitrary Geometries on Fixed Cartesian Grids. J. Comput. Phys. 1997, 137, 366–405. [Google Scholar] [CrossRef]
- Udaykumar, H.S.; Mittal, R.; Shyy, W. Computation of Solid–Liquid Phase Fronts in the Sharp Interface Limit on Fixed Grids. J. Comput. Phys. 1999, 153, 535–574. [Google Scholar] [CrossRef] [Green Version]
- Liang, H.; Bin, L.; Yufeng, S.; Qingyan, X.; Zhiqiang, H.; Baicheng, L. Simulation of Magnesium Alloy AZ91D Microstructure Using Modified Cellular Automaton Method. Tsinghua Sci. Technol. 2009, 14, 307–312. [Google Scholar]
- Yan, X.; Chen, S.; Xie, F.; Chang, Y.A. Computational and experimental investigation of microsegregation in an Al-rich Al–Cu–Mg–Si quaternary alloy. Acta Mater. 2002, 50, 2199–2207. [Google Scholar] [CrossRef]
- Sasikumar, R.; Sreenivasan, R. Two dimensional simulation of dendrite morphology. Acta Metall. Mater. 2004, 42, 2381–2386. [Google Scholar] [CrossRef]
- Fraś, E. Crystallization of Metals; WNT: Warszawa, Poland, 2003; pp. 58–89. [Google Scholar]
- Ramirez, J.C.; Beckermann, C. Examination of binary alloy free dendritic growth theories with a phase-field model. Acta Mater. 2005, 53, 1721–1736. [Google Scholar] [CrossRef]




| Characteristic Quantity | Marking | DDTA Tests | The Numerical Model | Simulation Error, % |
|---|---|---|---|---|
| The temperature of the onset of solidification, °C. | TN | 627 | 629 | 0.32 |
| Temperature of maximum undercooling of the alloy, °C. | T1 | 624 | 625 | 0.16 |
| Temperature range of recalescence, °C. | δT = T3 – T1 | 1 | 1 | 0.00 |
| Maximum thermal effect of solid phase growth, °C. | T2 | 625 | 626 | 0.16 |
| The end of solidification temperature, °C. | TK | 538 | 532 | 1.12 |
| Solidification time, s | tK – tP | 31.5 | 34 | 7.94 |
| The total time of solidification and cooling to the temperature of 500 °C, s | t500–t0 | 40 | 38.5 | 3.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zyska, A. CA Modeling of Microsegregation and Growth of Equiaxed Dendrites in the Binary Al-Mg Alloy. Materials 2021, 14, 3393. https://doi.org/10.3390/ma14123393
Zyska A. CA Modeling of Microsegregation and Growth of Equiaxed Dendrites in the Binary Al-Mg Alloy. Materials. 2021; 14(12):3393. https://doi.org/10.3390/ma14123393
Chicago/Turabian StyleZyska, Andrzej. 2021. "CA Modeling of Microsegregation and Growth of Equiaxed Dendrites in the Binary Al-Mg Alloy" Materials 14, no. 12: 3393. https://doi.org/10.3390/ma14123393
APA StyleZyska, A. (2021). CA Modeling of Microsegregation and Growth of Equiaxed Dendrites in the Binary Al-Mg Alloy. Materials, 14(12), 3393. https://doi.org/10.3390/ma14123393







