Bounding the Multi-Scale Domain in Numerical Modelling and Meta-Heuristics Optimization: Application to Poroelastic Media with Damageable Cracks
Abstract
:1. Introduction
2. Description of the Micro-Scale Problem
2.1. Constitutive Equations of the Homogenized Problem
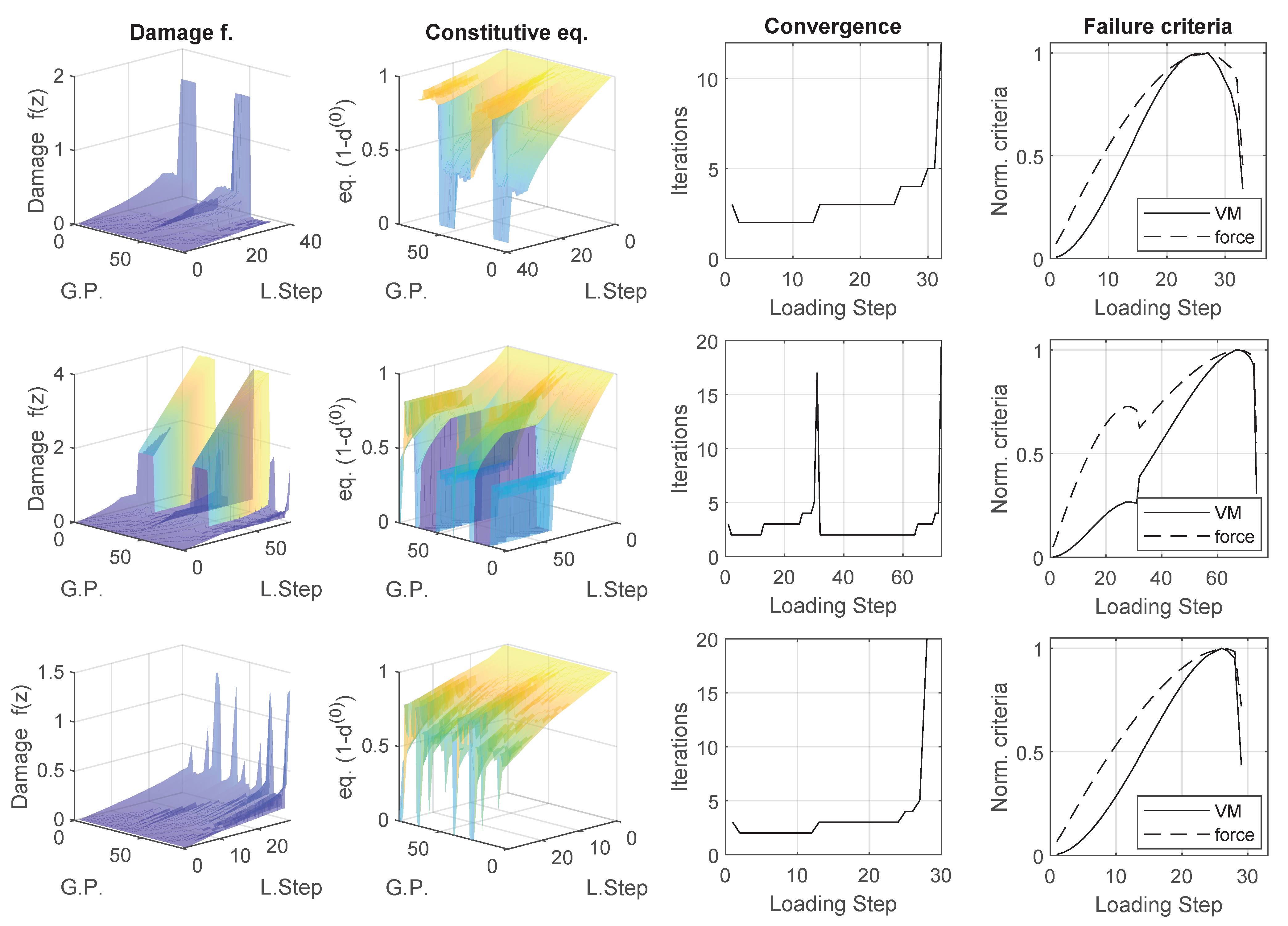
Damage
2.2. Numerical Implementation
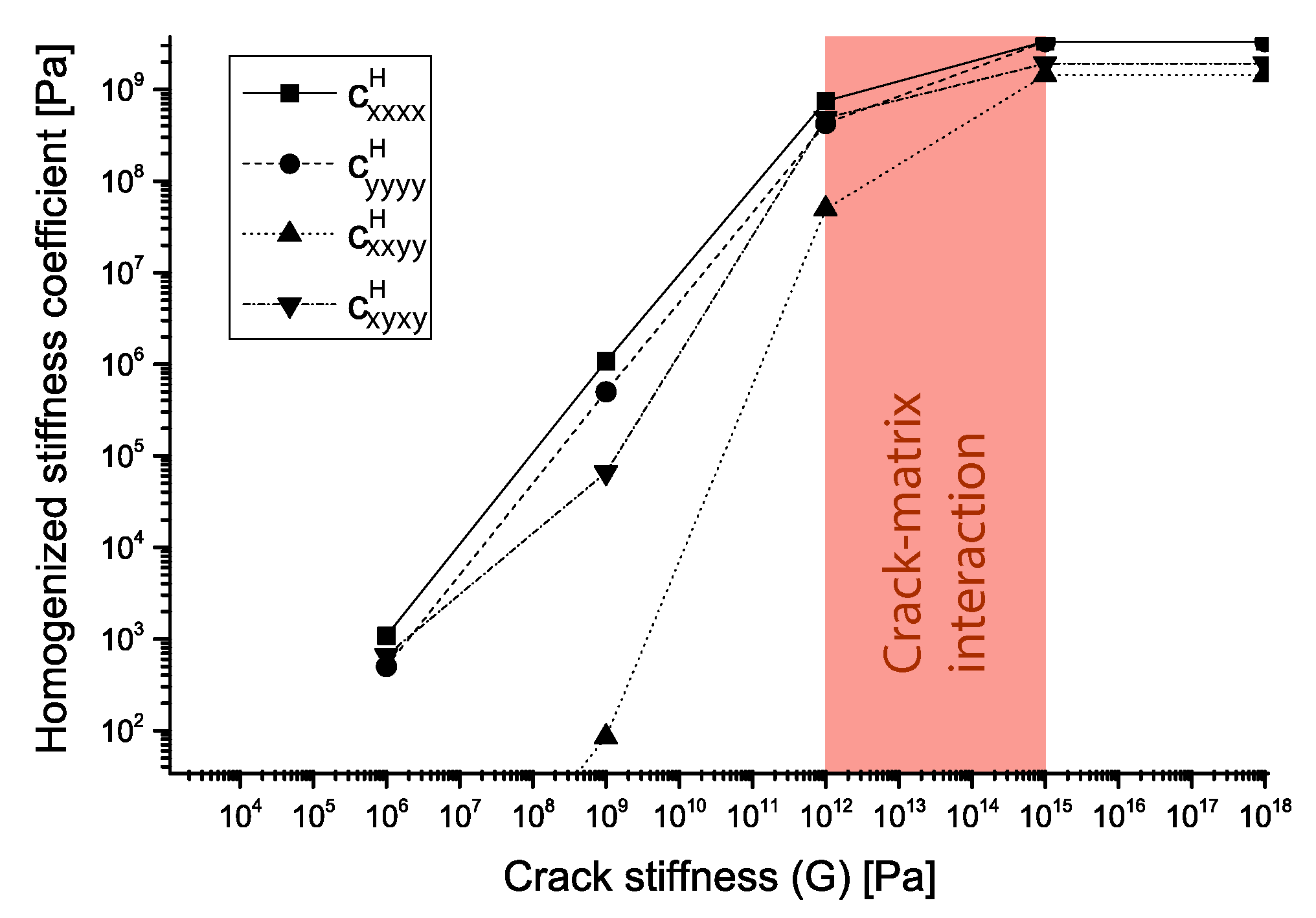
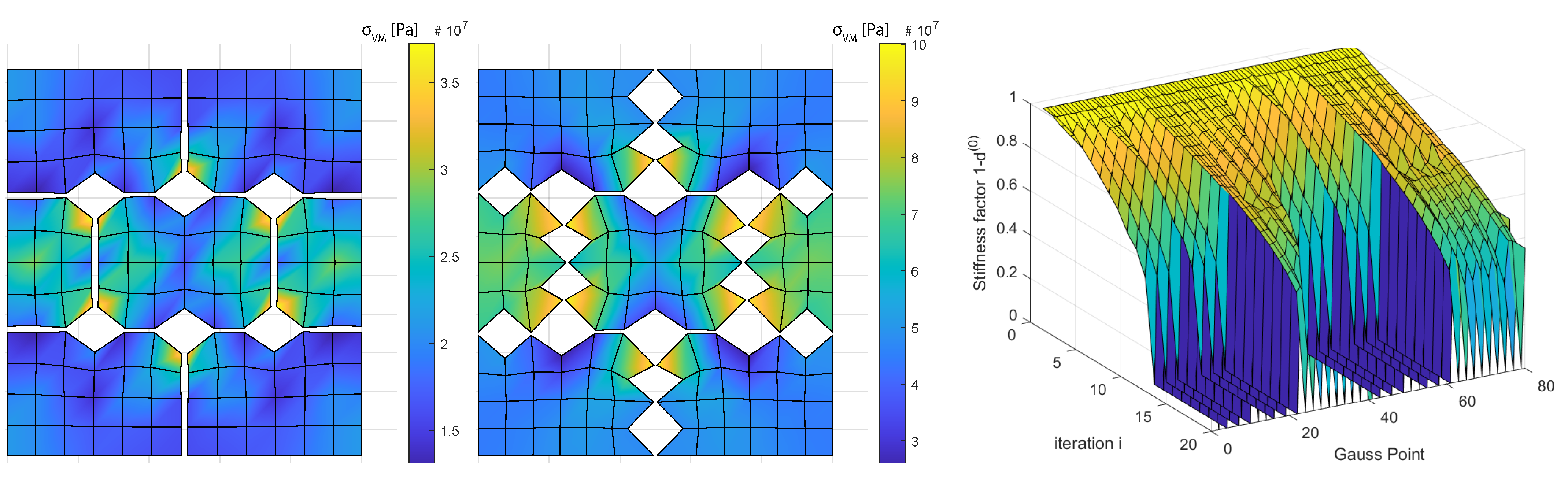
2.3. Initial Constriction of Crack Stiffness
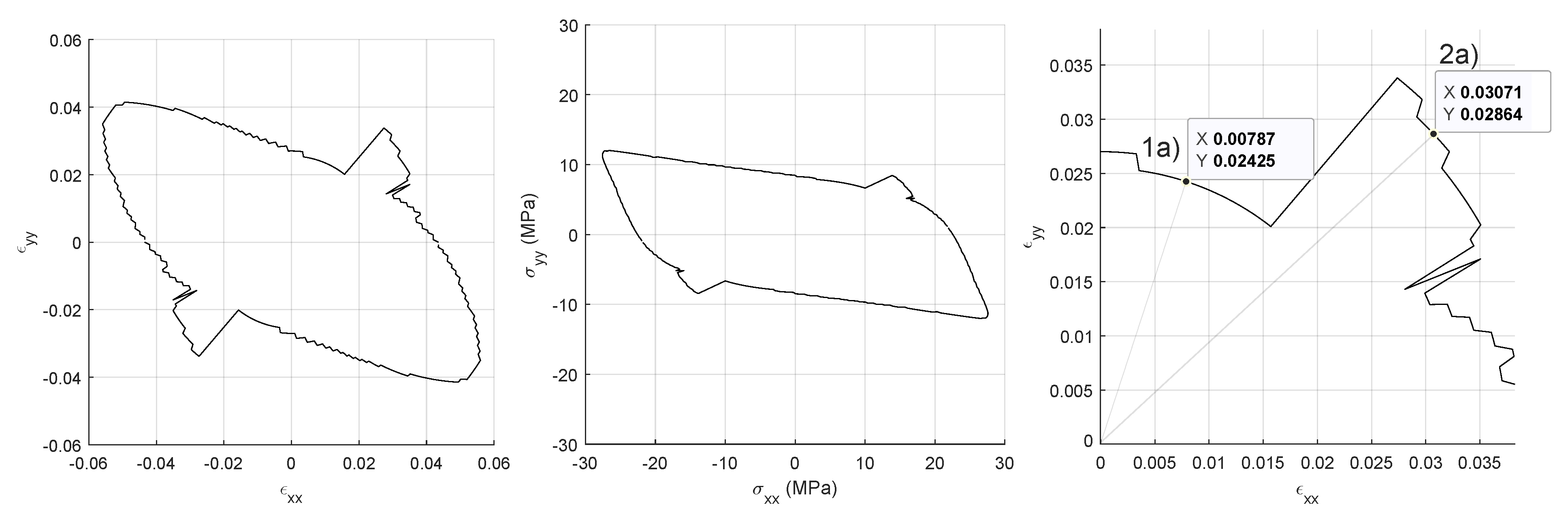
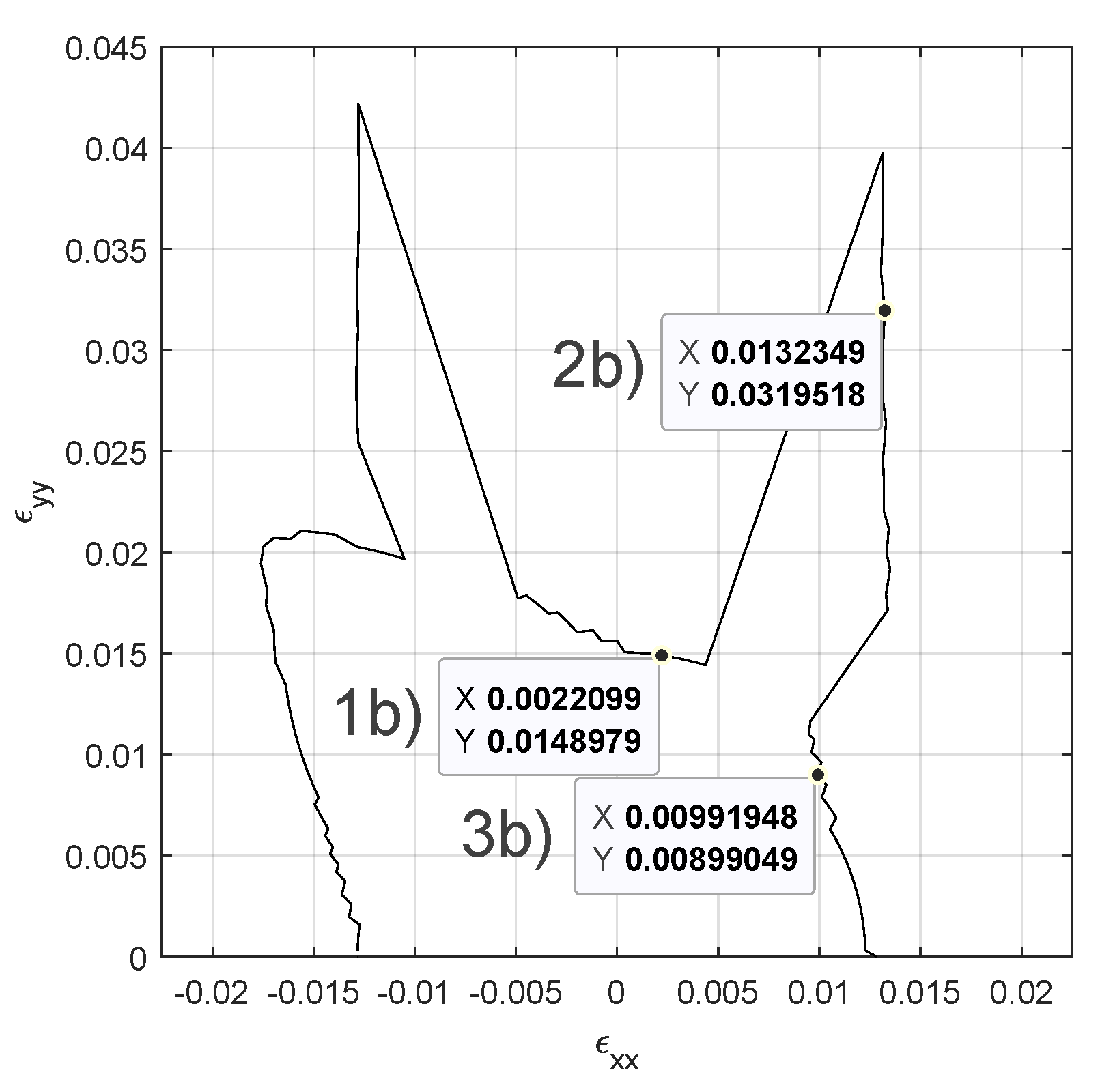
3. Failure Envelopes
3.1. Maximum Stress Failure Criterion
3.2. Von Misses Failure Criterion
3.3. Stress Ratio to Peak Failure Criterion
4. Particle Swarm Optimization
4.1. Objective Function
4.2. Increasing Swarm Size Results
4.3. Increasing Objective Function Resolution Results
4.4. Summary Particle Swarm Optimization Results
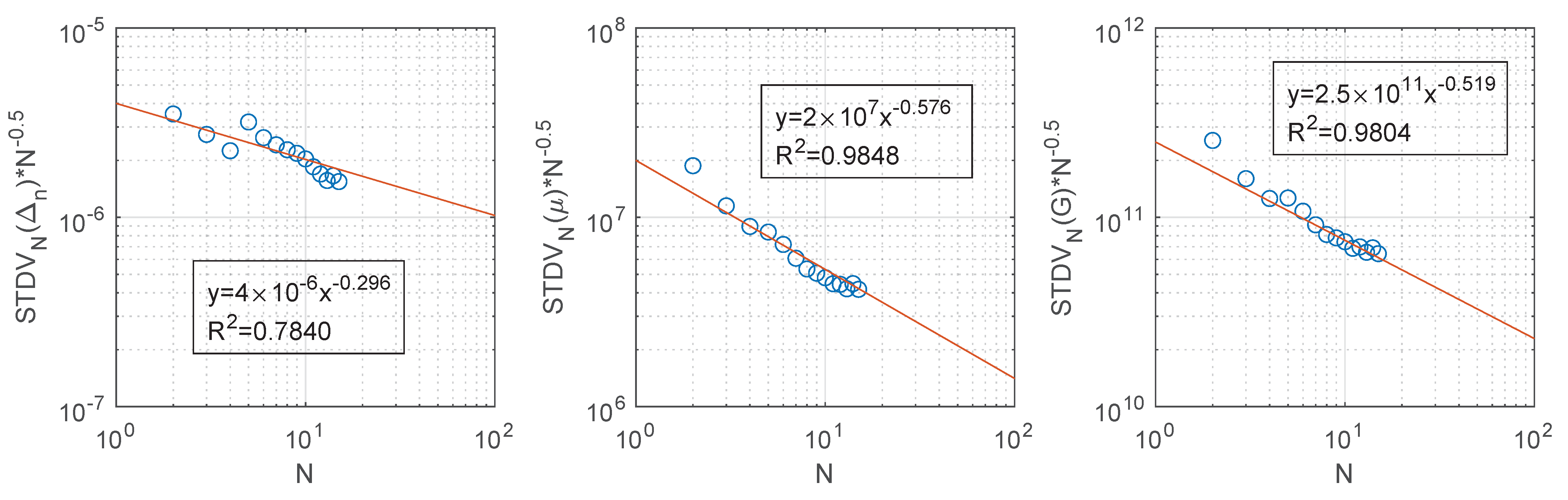
4.5. Monte-Carlo Analysis
5. Discussion
6. Conclusions
- A ratio to peak stress has shown to be a good criteria to characterize the failure of the present micro-structure.
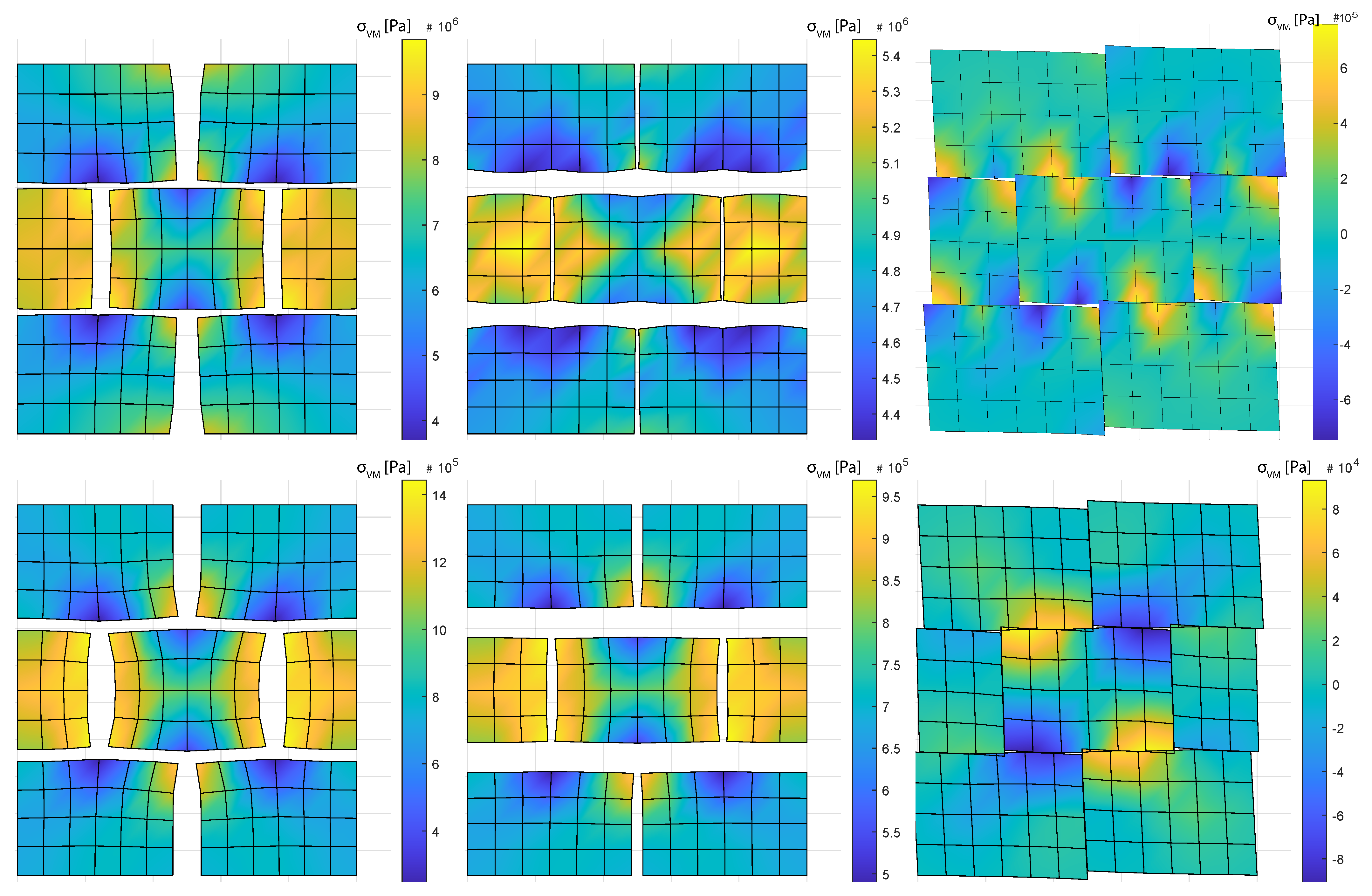
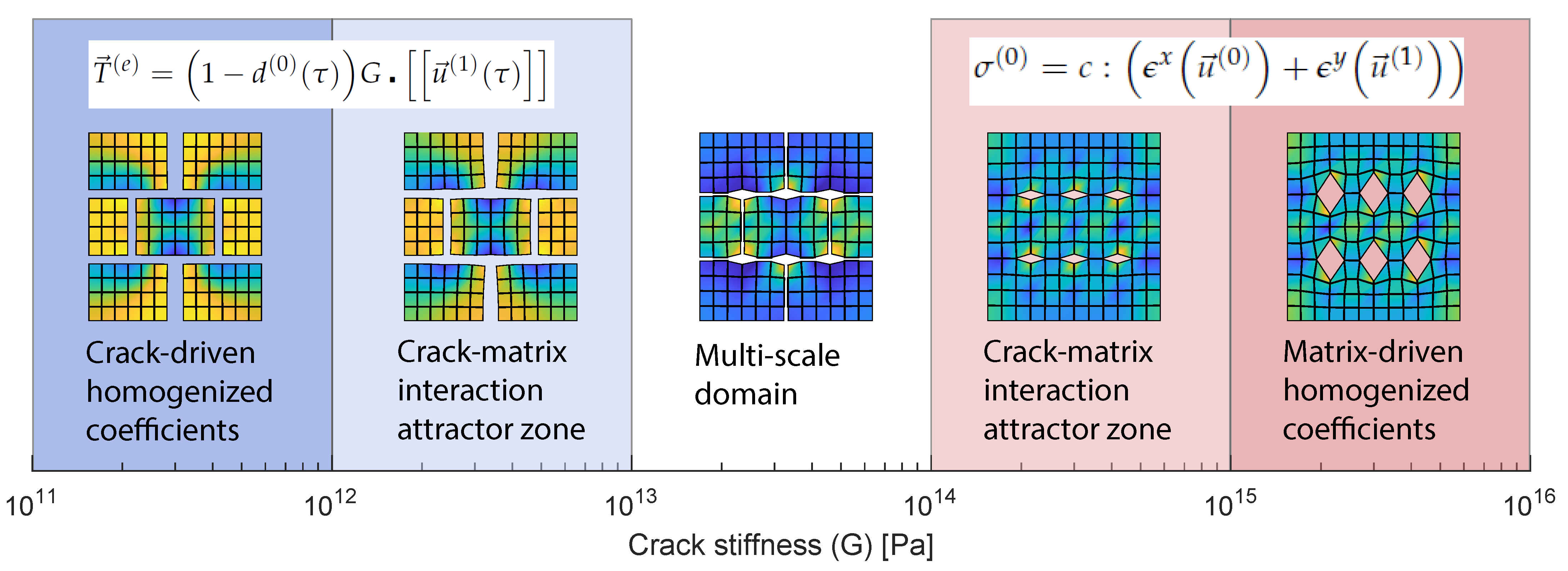
- For the initially given and elastic coefficients, the multi-scale rich micro-structure behaviour happens in the crack stiffness range ∼ Pa.
- PSO overcomes the non continuity and non differentiability of the constitutive law for a representative range of function resolutions.
- The metric best alone is able to discriminate between local and global optima.
Contribution to Science
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PDE | Partial Differential Equation |
| AI | Artificial Intelligence |
| ML | Machine Learning |
| FEM | Finite Element Model |
| PSO | Particle Swarm Optimization |
Appendix A. Convergence, Fitness and Swarm Scatter Results
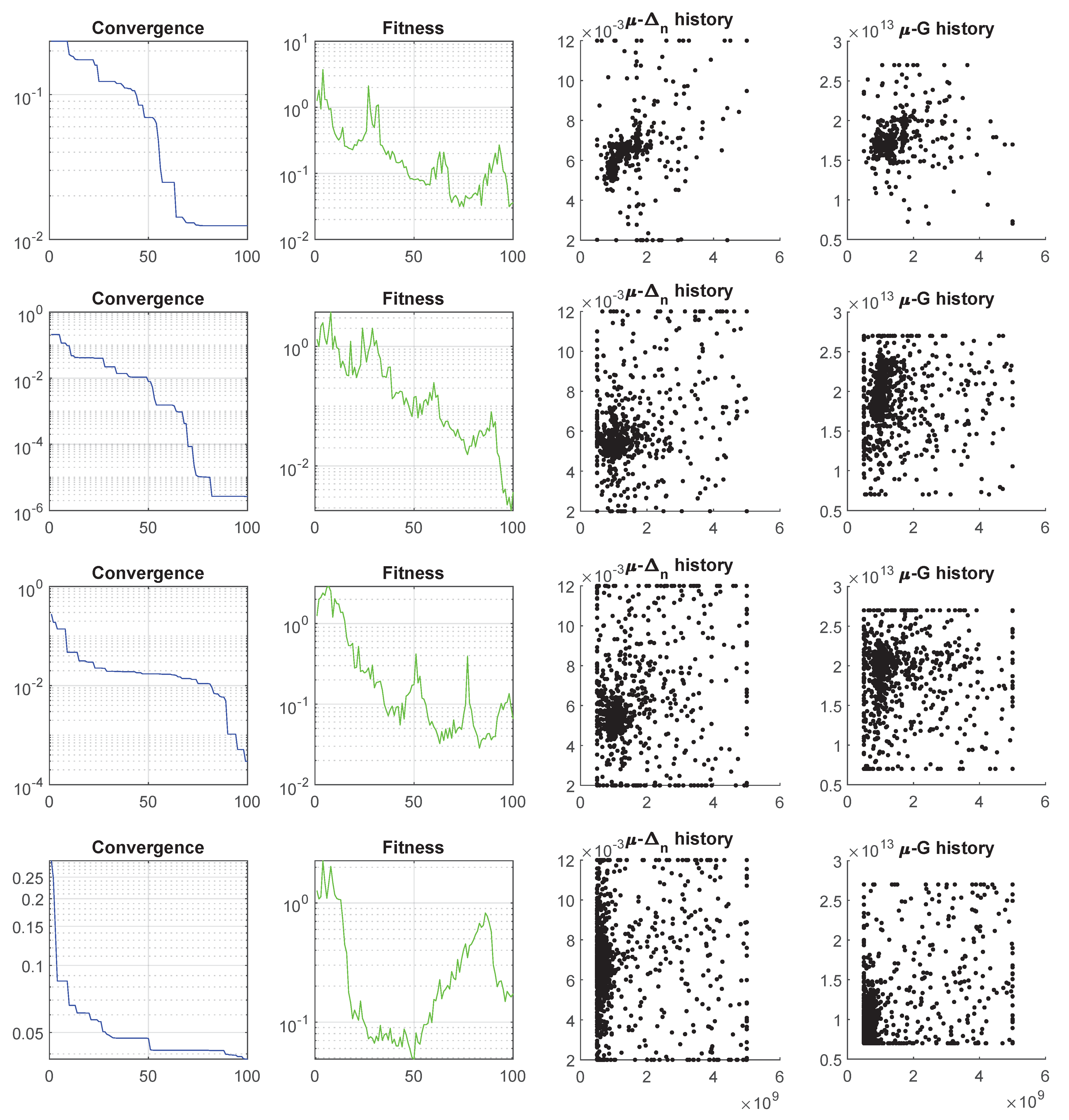
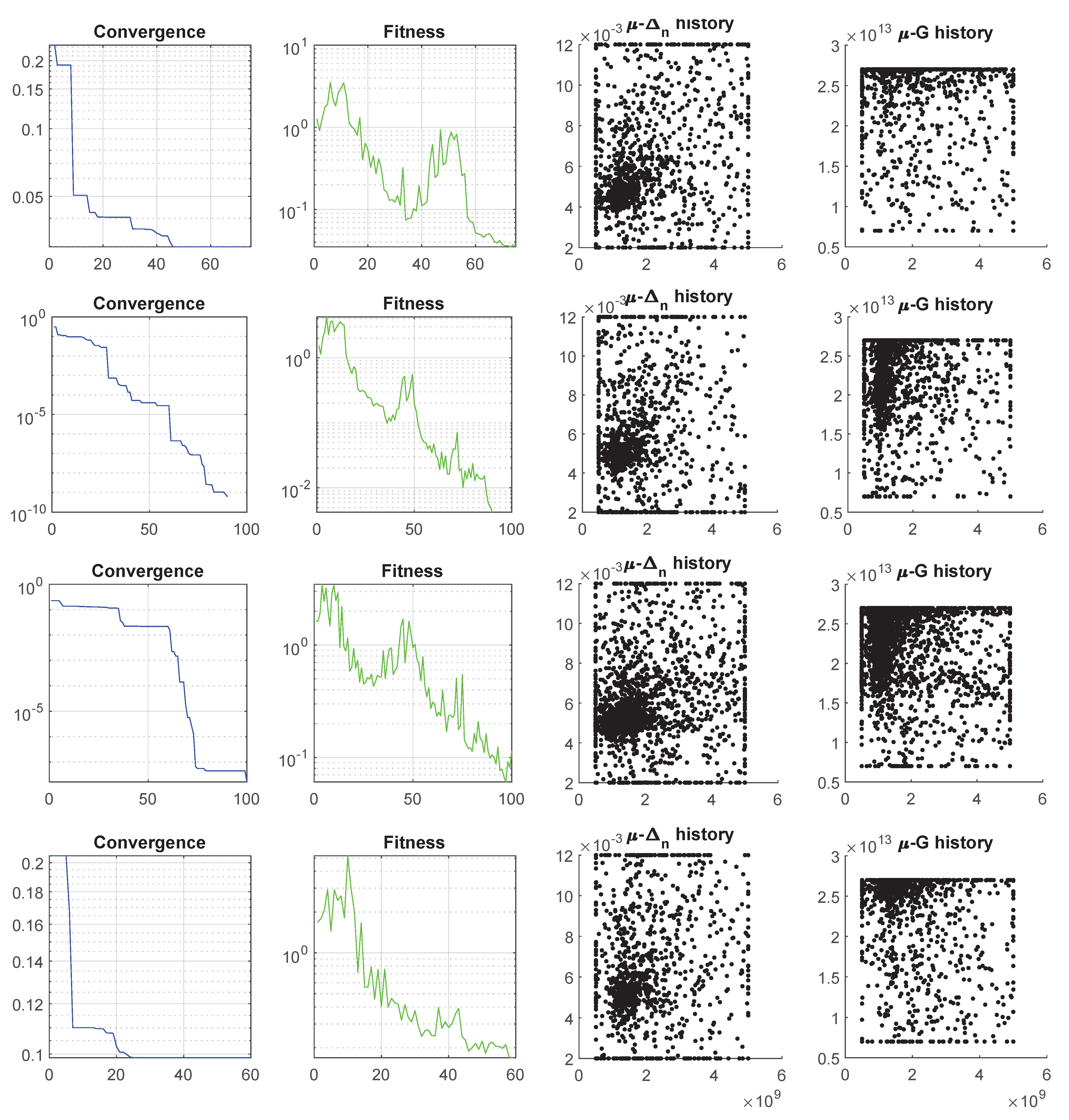
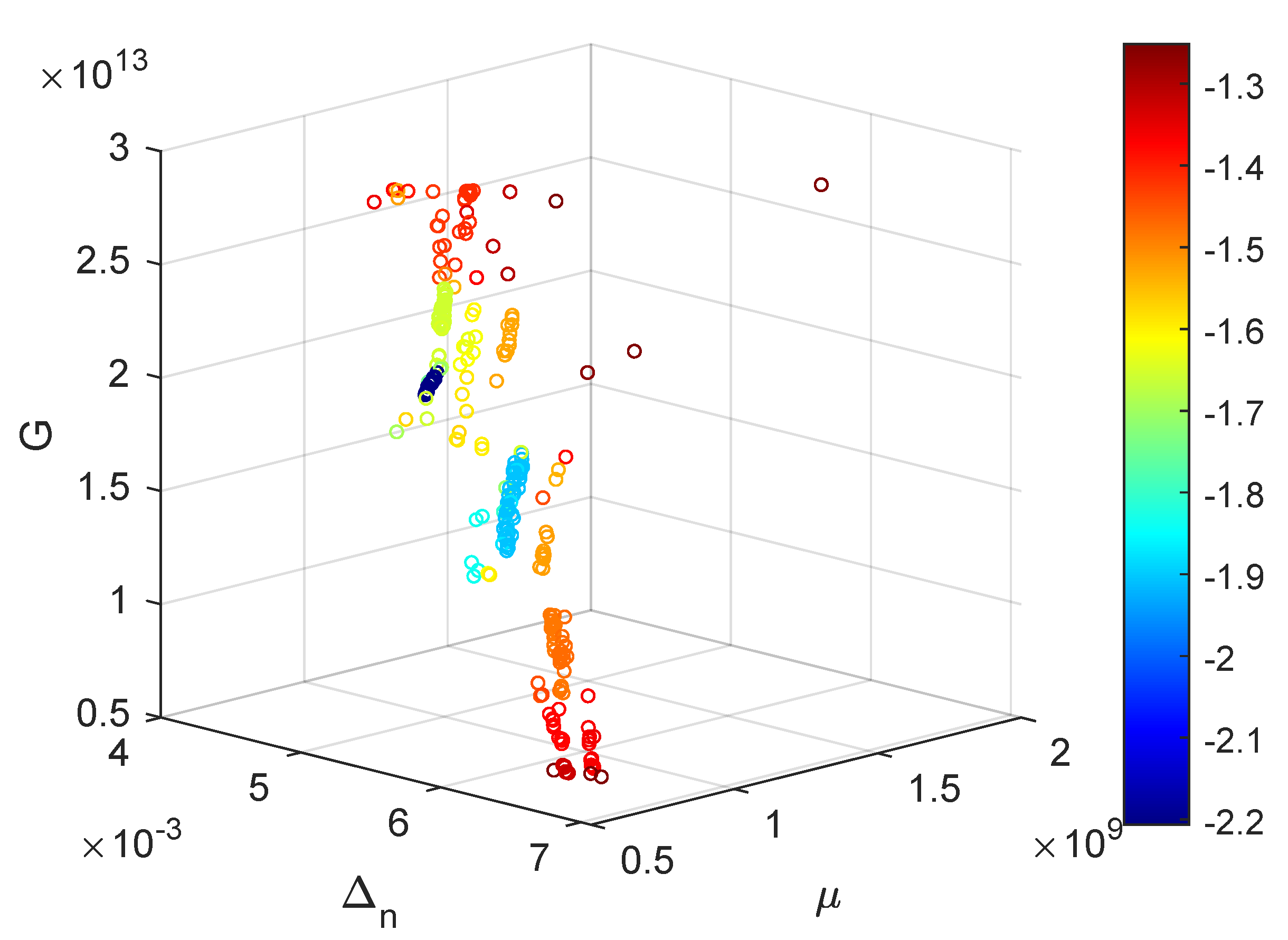
Appendix B. Convergence of Δn, μ and G Swarms


References
- Auriault, J.L. Heterogeneous medium. Is an equivalent macroscopic description possible? Int. J. Eng. Sci. 1991, 29, 785–795. [Google Scholar] [CrossRef]
- Biot, M. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Chambon, R.; Caillerie, D.; Viggiani, G. Loss of uniqueness and bifurcation vs instability: Some remarks. Rev. Fr. Génie Civ. 2004, 8, 517–535. [Google Scholar] [CrossRef]
- Papanicolau, G.; Bensoussan, A.; Lions, J.L. Asymptotic Analysis for Periodic Structures; Elsevier: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Sánchez-Palencia, E. Non-Homogeneous Media and Vibration Theory; Springer: Berlin, Germany, 1980; Volume 127, pp. 922–923. [Google Scholar]
- Arbogast, T.; Douglas, J., Jr.; Hornung, U. Derivation of the double porosity model of single phase flow via homogenization theory. SIAM J. Math. Anal. 1990, 21, 823–836. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; AMS Bookstore: New York, NY, USA, 2011; Volume 374. [Google Scholar]
- Sridhar, A.; Kouznetsova, V.; Geers, M. A general multiscale framework for the emergent effective elastodynamics of metamaterials. J. Mech. Phys. Solids 2017, 111, 414–433. [Google Scholar] [CrossRef]
- Waseem, A.; Heuzé, T.; Stainier, L.; Geers, M.; Kouznetsova, V. Model reduction in computational homogenization for transient heat conduction. Comput. Mech. 2020, 65, 249–266. [Google Scholar] [CrossRef] [Green Version]
- Auriault, J.L. Heterogeneous periodic and random media. Are the equivalent macroscopic descriptions similar? Int. J. Eng. Sci. 2011, 49, 806–808. [Google Scholar] [CrossRef]
- Stefanou, I.; Sulem, J.; Vardoulakis, I. Three-dimensional Cosserat homogenization of masonry structures: Elasticity. Acta Geotech. 2008, 3, 71–83. [Google Scholar] [CrossRef] [Green Version]
- Godio, M.; Stefanou, I.; Sab, K.; Sulem, J.; Sakji, S. A limit analysis approach based on Cosserat continuum for the evaluation of the in-plane strength of discrete media: Application to masonry. Eur. J. Mech. A Solids 2017, 66, 168–192. [Google Scholar] [CrossRef] [Green Version]
- Scholtès, L.; Donzé, F.V.; Khanal, M. Scale effects on strength of geomaterials, case study: Coal. J. Mech. Phys. Solids 2011, 59, 1131–1146. [Google Scholar] [CrossRef]
- Bertrand, F.; Cerfontaine, B.; Collin, F. A fully coupled hydro-mechanical model for the modeling of coalbed methane recovery. J. Nat. Gas Sci. Eng. 2017, 46, 307–325. [Google Scholar] [CrossRef] [Green Version]
- Valle, V.; Hedan, S.; Cosenza, P.; Fauchille, A.L.; Berdjane, M. Digital image correlation development for the study of materials including multiple crossing cracks. Exp. Mech. 2015, 55, 379–391. [Google Scholar] [CrossRef]
- Ougier-Simonin, A.; Renard, F.; Boehm, C.; Vidal-Gilbert, S. Microfracturing and microporosity in shales. Earth-Sci. Rev. 2016, 162, 198–226. [Google Scholar] [CrossRef] [Green Version]
- Arson, C. Micro-macro mechanics of damage and healing in rocks. Open Geomech. 2020, 2, 1–41. [Google Scholar] [CrossRef] [Green Version]
- Dale, M.; Miller, J.; Stepney, S. Reservoir Computing as a Model for In-Materio Computing; Springer: Cham, Switzerland, 2017; Volume 22, pp. 533–571. [Google Scholar]
- Germain, P. La méthode des puissances virtuelles en mécanique des milieux continus. J. Mec. 1973, 12, 236–274. [Google Scholar]
- Papachristos, E.; Stefanou, I. Controlling earthquake-like instabilities using artificial intelligence. arXiv 2021, arXiv:2104.13180. [Google Scholar]
- Masi, F.; Stefanou, I.; Vannucci, P.; Maffi-Berthier, V. Thermodynamics-based Artificial Neural Networks for constitutive modeling. J. Mech. Phys. Solids 2021, 147, 104277. [Google Scholar] [CrossRef]
- Lu, X.; Giovanis, D.G.; Yvonnet, J.; Papadopoulos, V.; Detrez, F.; Bai, J. A data-driven computational homogenization method based on neural networks for the nonlinear anisotropic electrical response of graphene/polymer nanocomposites. Comput. Mech. 2019, 64, 307–321. [Google Scholar] [CrossRef]
- Wang, K.; Sun, W. A multiscale multi-permeability poroplasticity model linked by recursive homogenizations and deep learning. Comput. Methods Appl. Mech. Eng. 2018, 334, 337–380. [Google Scholar] [CrossRef]
- Logarzo, H.J.; Capuano, G.; Rimoli, J.J. Smart constitutive laws: Inelastic homogenization through machine learning. Comput. Methods Appl. Mech. Eng. 2021, 373, 113482. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, C. Exploring the 3D architectures of deep material network in data-driven multiscale mechanics. J. Mech. Phys. Solids 2019, 127, 20–46. [Google Scholar] [CrossRef] [Green Version]
- Jang, D.P.; Fazily, P.; Yoon, J.W. Machine learning-based constitutive model for J2-plasticity. Int. J. Plast. 2021, 138, 102919. [Google Scholar] [CrossRef]
- Vlassis, N.N.; Sun, W. Sobolev training of thermodynamic-informed neural networks for interpretable elasto-plasticity models with level set hardening. Comput. Methods Appl. Mech. Eng. 2021, 377, 113695. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, eaaw4741. [Google Scholar] [CrossRef]
- Ye, H.; Shen, Z.; Xian, W.; Zhang, T.; Tang, S.; Li, Y. OpenFSI: A highly efficient and portable fluid–structure simulation package based on immersed-boundary method. Comput. Phys. Commun. 2020, 256, 107463. [Google Scholar] [CrossRef]
- Jokar, M.; Semperlotti, F. Finite element network analysis: A machine learning based computational framework for the simulation of physical systems. Comput. Struct. 2021, 247, 106484. [Google Scholar] [CrossRef]
- Miller, J.; Harding, S.; Tufte, G. Evolution-in-materio: Evolving computation in materials. Evol. Intell. 2014, 7, 49–67. [Google Scholar] [CrossRef]
- Beggs, J. The criticality hypothesis: How local cortical networks might optimize information processing. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2008, 366, 329–343. [Google Scholar] [CrossRef]
- Gibbons, T. Unifying Quality Metrics for Reservoir Networks; IEEE: Barcelona, Spain, 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Meier, H.; Steinmann, P.; Kuhl, E. Towards multiscale computation of confined granular media. Tech. Mech. 2008, 28, 32–42. [Google Scholar]
- de Souza Neto, E.; Blanco, P.; Sánchez, P.; Feijóo, R. An RVE-based multiscale theory of solids with micro-scale inertia and body force effects. Mech. Mater. 2015, 80, 136–144. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Sun, W.; Yuan, Z.; Fish, J. A nonlocal multiscale discrete-continuum model for predicting mechanical behavior of granular materials. Int. J. Numer. Methods Eng. 2015, 106, 129–160. [Google Scholar] [CrossRef]
- van den Eijnden, B.; Bésuelle, P.; Chambon, R.; Collin, F. A FE2 modelling approach to hydromechanical coupling in cracking-induced localization problems. Int. J. Solids Struct. 2016, 97–98, 475–488. [Google Scholar] [CrossRef]
- Desrues, J.; Argilaga, A.; Caillerie, D.; Combe, G.; Nguyen, T.; Richefeu, V.; Dal Pont, S. From discrete to continuum modelling of boundary value problems in geomechanics: An integrated FEM-DEM approach. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 919–955. [Google Scholar] [CrossRef]
- Guo, N.; Yang, Z.; Yuan, W.H.; Zhao, J. A coupled SPFEM/DEM approach for multiscale modeling of large-deformation geomechanical problems. Int. J. Numer. Anal. Methods Geomech. 2020, 45. [Google Scholar] [CrossRef]
- Argilaga, A.; Papachristos, E.; Caillerie, D.; Dal Pont, S. Homogenization of a cracked saturated porous medium: Theoretical aspects and numerical implementation. Int. J. Solids Struct. 2016, 94–95, 222–237. [Google Scholar] [CrossRef]
- Pardoen, B.; Bésuelle, P.; Dal Pont, S.; Cosenza, P.; Desrues, J. Accounting for Small-Scale Heterogeneity and Variability of Clay Rock in Homogenised Numerical Micromechanical Response and Microcracking. Rock Mech. Rock Eng. 2020, 53, 2727–2746. [Google Scholar] [CrossRef]
- Viggiani, G.; Andò, E.; Takano, D.; Santamarina, J. Laboratory X-ray Tomography: A Valuable Experimental Tool for Revealing Processes in Soils. Geotech. Test. J. 2015, 38, 61–71. [Google Scholar] [CrossRef]
- Lukić, B.; Tengattini, A.; Dufour, F.; Briffaut, M. Visualising water vapour condensation in cracked concrete with dynamic neutron radiography. Mater. Lett. 2021, 283, 128755. [Google Scholar] [CrossRef]
- Majmudar, T.; Behringer, R. Contact force measurements and stress-induced anisotropy in granular materials. Nature 2005, 435, 1079–1082. [Google Scholar] [CrossRef]
- Wiebicke, M.; Andò, E.; Herle, I.; Viggiani, G. On the metrology of interparticle contacts in sand from X-ray tomography images. Meas. Sci. Technol. 2017, 28, 124007. [Google Scholar] [CrossRef]
- Wiebicke, M.; Ando, E.; Šmilauer, V.; Herle, I.; Viggiani, G. A benchmark strategy for the experimental measurement of contact fabric. Granul. Matter 2019, 21, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Argilaga, A.; Desrues, J.; Dal Pont, S.; Combe, G.; Caillerie, D. FEMxDEM multiscale modeling: Model performance enhancement, from Newton strategy to element loop parallelization. Int. J. Numer. Methods Eng. 2018, 114, 47–65. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.Z.; Mirjalili, S.; Saremi, S.; Faris, H.; Aljarah, I. Grasshopper optimization algorithm for multi-objective optimization problems. Appl. Intell. 2018, 48. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Kennedy, J. Particle Swarm Optimization. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010; pp. 760–766. [Google Scholar]
- Royer, P.; Cherblanc, F. Homogenisation of advective–diffusive transport in poroelastic media. Mech. Res. Commun. 2010, 37, 133–136. [Google Scholar] [CrossRef] [Green Version]
- Auriault, J.L. Transport in porous media: Upscaling by multiscale asymptotic expansions. In Applied Micromechanics of Porous Materials; Springer: Vienna, Austria, 2005; pp. 3–56. [Google Scholar]
- Dascalu, C.; Bilbie, G.; Agiasofitou, E. Damage and size effects in elastic solids: A homogenization approach. Int. J. Solids Struct. 2008, 45, 409–430. [Google Scholar] [CrossRef] [Green Version]
- Marinelli, F.; Sieffert, Y.; Chambon, R. Hydromechanical modeling of an initial boundary value problem: Studies of non-uniqueness with a second gradient continuum. Int. J. Solids Struct. 2015, 54, 238–257. [Google Scholar] [CrossRef]
- Hill, R. Acceleration waves in solids. J. Mech. Phys. Solids 1962, 10, 1–16. [Google Scholar] [CrossRef]
- Rice, J.R. The Localization of Plastic Deformation; Division of Engineering, Brown University: Providence, RI, USA, 1976. [Google Scholar]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Chambon, R.; Caillerie, D.; El Hassan, N. One-dimensional localisation studied with a second grade model. Eur. J. Mech. A/Solids 1998, 17, 637–656. [Google Scholar] [CrossRef]
- Chambon, R.; Caillerie, D.; Matsuchima, T. Plastic continuum with microstructure, local second gradient theories for geomaterials: Localization studies. Int. J. Solids Struct. 2001, 38, 8503–8527. [Google Scholar] [CrossRef]
- Collin, F.; Chambon, R.; Charlier, R. A finite element method for poro mechanical modelling of geotechnical problems using local second gradient models. Int. J. Numer. Methods Eng. 2006, 65, 1749–1772. [Google Scholar] [CrossRef]
- Nova, R. Controllability of the incremental response of soil specimens subjected to arbitrary loading programmes. J. Mech. Behav. Mater. 1994, 5, 193–202. [Google Scholar] [CrossRef]





| PSO Parameter | Value |
|---|---|
| Function Tolerance | |
| Inertia Range | [ ] |
| Min. Neighbors Fraction | |
| Objective Limit | |
| Self Adjustment Weight | |
| Social Adjustment Weight |
| Sim. | Swarm Size | It. | f-Count | f(x) Res. | Best f(x) | Mean f(x) | Optimal x | Time |
|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 100 | 808 | 8 | 0.01245 | 0.03517 | [0.0056 9.4330 1.6802 ] | 42 min |
| 2 | 16 | 100 | 1616 | 8 | 0.003639 | [0.0050 9.5287 1.9847 ] | 90 min | |
| 3 | 24 | 100 | 2424 | 8 | 0.0002951 | 0.06567 | [0.0050 9.6105 2.0029 ] | 135 min |
| 4 | 32 | 100 | 3232 | 8 | 0.0379 | 0.1722 | [0.0064 6.6052 1.0255 ] | 170 min |
| 5 | 40 | 75 | 3040 | 8 | 0.02985 | 0.03623 | [0.0044 1.1140 2.6967 ] | 3 h |
| 6 | 40 | 100 | 3640 | 16 | 0.00424 | [0.0050 9.5219 1.9876 ] | 6 h | |
| 7 | 40 | 100 | 4040 | 32 | 0.1146 | [0.0050 9.6970 2.0132 ] | 14 h | |
| 8 | 40 | 59 | 2400 | 64 | 0.09868 | 0.1690 | [0.0049 1.2485 2.5521 ] | 17 h |
| Ref. x | - | - | - | - | - | - | [0.0050 9.6100 2.0000 ] | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Argilaga, A.; Papachristos, E. Bounding the Multi-Scale Domain in Numerical Modelling and Meta-Heuristics Optimization: Application to Poroelastic Media with Damageable Cracks. Materials 2021, 14, 3974. https://doi.org/10.3390/ma14143974
Argilaga A, Papachristos E. Bounding the Multi-Scale Domain in Numerical Modelling and Meta-Heuristics Optimization: Application to Poroelastic Media with Damageable Cracks. Materials. 2021; 14(14):3974. https://doi.org/10.3390/ma14143974
Chicago/Turabian StyleArgilaga, Albert, and Efthymios Papachristos. 2021. "Bounding the Multi-Scale Domain in Numerical Modelling and Meta-Heuristics Optimization: Application to Poroelastic Media with Damageable Cracks" Materials 14, no. 14: 3974. https://doi.org/10.3390/ma14143974
APA StyleArgilaga, A., & Papachristos, E. (2021). Bounding the Multi-Scale Domain in Numerical Modelling and Meta-Heuristics Optimization: Application to Poroelastic Media with Damageable Cracks. Materials, 14(14), 3974. https://doi.org/10.3390/ma14143974







