Next Article in Journal
Novel Tissue Engineering Scaffolds in the Treatment of Spinal Cord Injury—A Bibliometric Study
Previous Article in Journal
Model-Based Characterization of the Metabolism of Recombinant Adeno-Associated Virus (rAAV) Production via Human Embryonic Kidney (HEK293) Cells
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Bioengineering
Volume 12
Issue 4
10.3390/bioengineering12040346
bioengineering-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The “Cocombola Study”: A Physical Phantom Model for tDCS-Induced Electric Field Distribution

by
Matteo Guidetti
1,2,
Rosanna Ferrara
1,
Kora Montemagno
1,
Natale Vincenzo Maiorana
1,
Tommaso Bocci
1,3,
Sara Marceglia
1,
Serena Oliveri
1,3,
Anna Maria Bianchi
2,* and
Alberto Priori
1,3
1
‘Aldo Ravelli’ Research Center for Neurotechnology and Experimental Neurotherapeutics, Department of Health Sciences, University of Milan, 20142 Milan, Italy
2
Department of Electronics, Information and Bioengineering, Politecnico di Milano, Piazza Leonardo da Vinci, 32, 20133 Milan, Italy
3
III Neurology Clinic, ASST-Santi Paolo e Carlo University Hospital, 20142 Milan, Italy
*
Author to whom correspondence should be addressed.
Bioengineering 2025, 12(4), 346; https://doi.org/10.3390/bioengineering12040346
Submission received: 16 January 2025 / Revised: 7 March 2025 / Accepted: 19 March 2025 / Published: 27 March 2025
(This article belongs to the Section Biomedical Engineering and Biomaterials)
Browse Figures
Versions Notes

Abstract

Background: Transcranial direct current stimulation (tDCS)-induced electric fields (EFs) acting on brain tissues are hardly controllable. Among physical models used in neuroscience research, watermelons are known as head-like phantoms for their dielectric properties. In this study, we aimed to define an inexpensive and reliable method to qualitatively define the spatial distribution of tDCS-induced EFs based on the use of watermelons. Methods: After creating the eight cranial foramina and identifying the location of the 21 EEG scalp electrodes on the peel of a watermelon, voltage differences during stimulation were recorded in each of the 21 scalp electrode positions, one at a time, at four different depths. The recordings were graphically represented by using polar coordinates with the watermelon approximated to a perfect sphere. Results: To validate the model, we performed three experiments in well-known montages. The results obtained were in line with the expected behavior of the EFs. Conclusions: Watermelon might be a cheap and feasible phantom head model to characterize the EFs induced by tDCS and, potentially, even other non-invasive brain stimulation techniques.

1. Introduction

Transcranial direct current stimulation (tDCS) is a non-invasive brain stimulation technique that modulates brain activity through the injection of a low-intensity direct current (2–4 mA) across the scalp [1,2]. Although decades of studies have explored a wide range of clinical applications, both in healthy and pathologic subjects (for a review, see ref. [3]), showing beneficial effects with no harmful side effects [4], it is still hard to determine the treatment efficacy [5,6]. Indeed, tDCS-induced biological and behavioral effects depend upon individual anatomy (considered in a broad sense [7,8,9,10,11]) and the small electric field (EF) developed in the brain [12]. Also, tDCS-induced EF is hardly controllable [13]. Physically, the intensity and distribution of tDCS-induced EFs depend upon the characteristics of the current injected, namely temporal (e.g., waveform) and spatial (e.g., electrodes’ position) [12]. Therefore, a large number of stimulation variables play a role, and it remains a big challenge to select stimulation parameters for the best medical practices [6,14].
Computational simulations have been applied to determine the spatial–temporal distributions of the EFs within the brain [15], providing insights into the stimulation parameters to be chosen [6]. MRI-based realistic human models that incorporate complex tissue geometries [16] with dielectric properties [17,18] are currently considered the gold-standard tools [19,20]. While useful, they have limitations [21], including the accuracy and precision of MRI tissue segmentation [22], the assignment of tissue conductivities [23,24], and the numerical artifacts introduced by stair-casing error [25]. Therefore, computational predictions must be experimentally validated before a direct translation to clinical practice [6,14,21]. In the last few years, several models have been used to confirm the computational results and, in general, shape tDCS-induced EFs. Few studies have studied humans undergoing neurosurgery to record EFs induced by tDCS [26]. Although ideally in vivo recordings would be the most reliable [22], in practice, there are several factors that might mislead the recordings and interpretation—for example, the anatomical and pathophysiological characteristics of the subjects, or the technical and methodological aspects of the recording [26]. Another approach to model tDCS-induced EFs is exploiting phantom head models, i.e., models reflecting human brain biophysics (e.g., conductivity) and anatomy (e.g., weight, shape) [14], using materials with different conductivity (e.g., ceramics, clay, plastic) [27,28]. Compared to computational simulations, phantoms consider real-world influences, such as environmental noise or 3D positioning errors [28]; compared to in vivo recordings, physiological uncertainties (e.g., personal neurophysiological features) do not exist [28] and experiments are repeatable multiple times [14]. Also, phantom head models allow for real-time recordings and training in different settings [21].
Melons and watermelons have been used as head-like phantoms to improve neurophysiological [29,30,31], neurostimulation [30,32], and neuroimaging [31,33] practices. For example, watermelon as a phantom head model has been used as a control condition to identify and assess stimulus-related artifacts when recording EEG during transcranial magnetic stimulation (TMS) [29] and tDCS [34]. Similarly, it was used to ensure safety and quantify tDCS-induced noise effects in the images while performing tDCS concurrent with fMRI [33]. From a bioelectrical point of view, melon and watermelon share similar dielectric properties (or permittivity) [35], which might be a reasonable approximation of the human head. The dielectric constant of their peel is comparable to human skin, being, respectively, ε0 = 30–50 (frequency range 200 MHz–2 GHz, 24 °C—[36]) and ε0 = 40–50 (frequency range 200–500 MHz, 36 °C—[37]), and their inner pulp has a higher dielectric constant than their peel [36]. A similar physical trend is found in the human head, with gray matter and muscle in comparison to human skin [38]. Nevertheless, no previous tDCS modeling studies have been conducted on watermelon.
Under the hypothesis that watermelons may represent a non-expensive and reliable physical phantom head model for tDCS, here, we propose a method to use watermelons to qualitatively characterize the spatial distribution of tDCS-induced EF, together with an example of practical application described in the Supplementary Materials.

2. Materials and Methods

For modeling the spatial distribution of tDCS-induced EF, we propose to use a watermelon (Citrullus lanatus) whose shape (circumference around 60 cm [39]) and weight (around 4 kg [40]) are similar to the average human head. Detailed descriptions of the validation procedures are reported in the Supplementary Materials.

2.1. Watermelon Preparation

Experiments were performed in one day, to prevent fruit decay. After taking the watermelon from a room where it was stored at 24 °C, we identified the location of 21 scalp electrodes according to 10–20 conventional systems [41] to ensure a homogenous coordinate system during stimulation and recording procedures and facilitated the results description. The four anatomical landmarks used for positioning the electrodes (nasion, inion, right and left preauricular zones) were chosen by taking real measurements from a healthy volunteer. Similarly, we made eight holes (orbital, nasal, oral, ear cavities, and cranial foramen magnum) in the peel to simulate cranial foramina according to proportions taken from the same human model. Before starting the stimulation session, the weight (kg), maximum diameter (mm), temperature (°C), and resistance (kΩ) at the peel and the pulp were taken (see Supplementary Materials, Table S1). The watermelon was placed in a plastic box to electrically isolate the phantom and immersed in a few millimeters of water to simulate the electric dispersion induced by cerebrospinal fluid [42] (Figure 1A).

2.2. Recording Set Up

The signal was recorded from two self-adhesive bipolar surface Ag–AgCl electrodes (15 × 20 mm) connected to a digital oscilloscope (Tektronix TDS2024C oscilloscope—Tektronix, Inc., Johnston, IA, USA): one electrode (1.5 × 2 cm) was attached directly to the stimulating surface of tDCS electrode and considered as the reference for recording, and the other (1.5 × 2 cm) was wrapped around one end of a 48.5 cm-long and 5 mm-wide copper round bar (contact surface: 98.12 mm2), accurately covered with insulating tape. The other end of the copper wire was used as the recording area (98.12 mm2). The recording electrode was inserted in the watermelon in each of the 21 scalp electrode positions one at a time, at four depths: on the surface (Z0, roughly resembling human skin), at 33% (Z33, roughly resembling human cortex), at 66% (Z66, roughly resembling human diencephalon and midbrain), and at 100% (Z100, roughly resembling human brainstem) of the diameter of the watermelon. During stimulation, we recorded the voltage difference (ΔV) between the two recording electrodes, and EF as ΔV/Δs (Δs = distance between each recording point and the origin of the reference system). After recording, each hole was filled with saline solution [27]. No amplification, band-pass filters, or ameliorative acquisition procedures were applied. In all conditions, signal acquisition occurred when the DC stimulation intensity was maximal and steady.

2.3. Graphical Representation

To represent the results in a simple and comparable graph, we approximated the watermelon to a perfect sphere, as previously reported [43]. We calculated the 3D coordinates of each recording point E (Ex, Ey, Ez) at Z0, Z33, Z66, and Z100 by using polar coordinates (ρ, φ, θ). Then, we translated the obtained sphere model into the sphere model centered in the references for the recording system R (Rx, Ry, Rz). Finally, we calculated the distance between each recording point E (Ex, Ey, Ez) at each depth Z, and the references for the recording system R (Rx, Ry, Rz), i.e., the distance RE (see Figure 2A). EF was calculated as the ratio between the experimentally recorded ΔV (mV) and the inferred distances RE (mm). We represented ΔV and EF at each of the four recording depths as four perfect concentric spheres (Z0, Z33, Z66, Z100), on which we projected the 10–20 points from Z0 where the points were marked (see Figure 2B–D). To note, we could not register ΔV in the recording points under the stimulating pads; therefore, for these values at Z0, Z33, Z66, and Z100, we averaged the surrounding ΔV at each depth. More details are available in the Supplementary Materials.

2.4. Validation

Model validation for tDCS-induced EF distribution cannot be performed against a golden standard because each modeling strategy has limitations, and none can be used as a reference. Therefore, to evaluate the validity of the model, we relied on the testing of the method performance in known situations and assessed whether the results obtained were in line with the expected results in terms of (I) EF distribution with respect to stimulating electrode position, (II) EF gradient from surface to the internal locations, and (III) the amount of current shunted through the surface. To do so, we tested our methodology using three tDCS montages: (1) CONDITION A: monopolar montage—two anodes over simulated motor cortices (7 × 5 cm2 over C3 and C4), reference over simulated right deltoid (8 × 6 cm2 in the water) (see Figure 1B); (2) CONDITION B: bicephalic fronto–occipital montage—two anodes over simulated prefrontal cortex (5 × 5 cm2 over Fp1 and Fp2), two references over simulated occipital cortex (5 × 5 cm2 over O1 and O2) (see Figure 3A); and (3) CONDITION C: bicephalic fronto–temporal, two anodes over simulated left ventrolateral prefrontal and occipitotemporal cortex (5 × 5 cm2 over F7 and T6), references over simulated right ventrolateral prefrontal and occipitotemporal cortex (5 × 5 cm2 over F8 and T6) (see Figure 3B). DC stimulation was applied using a stimulator (2 mA, CONDITION A) or two stimulators (1.4 mA, CONDITIONs B and C) (HDCStim, Newronika, Cologno Monzese, Italy) through silicone rubber pad electrodes (1 mm thickness), with conductive gel applied between the electrodes and the peel to lower tDCS electrode resistance. For each stimulation condition, we used a watermelon (n = 3) whose shape and weight were similar to the average human head, considering that dielectric properties remain constant among them [36]. Also, we kept the temperature of the watermelon constant at around 24 °C [44] throughout the duration of the experiments.

3. Results

As for the purpose of this study, EF was measured as the ratio between the experimentally recorded ΔV (mV) and the inferred distances (mm) between each recording point E (Ex, Ey, Ez) and the origin of the recording reference system C3 (0, 0, 0). We represented ΔV and EF at each of the four recording depths as four perfect concentric spheres (Z0, Z33, Z66, Z100), on which we projected the 10–20 points from Z0 (where the points were marked). To note, we were not able to register ΔV in the recording points directly under the stimulation electrodes (C3 and C4 for CONDITON A; Fp1, Fp2, O1, and O2 for CONDITON B; F7, F8, T5, and T6 for CONDITON C) due to the presence of the stimulating pads; therefore, for these values at Z0, Z33, Z66, and Z100, we averaged the surrounding ΔV at each depth. Also, here, we report the numerical and graphical results referring only to CONDITION A, while those from CONDITION B and CONDITION C are reported in the Supplementary Materials.

3.1. CONDITION A (Monopolar Montage)

Table 1 reports values of ΔV (mV) and EF (mV/mm) for each recording point on the perfect spheres. A graphical representation of ΔV distribution shows that the difference in voltage increases with depth, with an anterior-to-posterior shift (see Figure 4, Figure 5 and Figure 6). At the surface, maximal values of ΔV were recorded in Fp2 (39,600 mV) and F7 (39,200 mV), but interestingly, Fp1 (15,800 mV) and Fpz (8080 mV) showed minimal differences in voltage. Although a similar pattern can be identified at Z33, deeper levels show a more widespread ΔV distribution. However, at Z66, it shifts more posteriorly (with CzIII, Fp1III, and Fp2III showing higher values, respectively, of 43,600 mV, 48,400 mV, and 50,400 mV), and at Z100, it concentrates around F3III (54,000 mV), CzIII (52,000 mV), and F4III (51,600 mV). Notably, Z100 presents a pattern of ΔV distribution similar to Z0 and Z33, with the lowest value recorded in FP2III (16,600 mV).
A graphical representation of EF distribution shows a tendency to be focalized in the left hemisphere, also while increasing the depth (see Figure 7, Figure 8 and Figure 9). On the surface, higher values (from 318.59 mV/mm to 484.73 mV/mm) are localized in the left fronto–parietal zone, with lower ones on the anterior (Fp1, Fpz—122.13 mV/mm and 54.79 mV/mm) and posterior (O1, Oz—204.07 mV/mm and 154.62 mV/mm) portions of the hemisphere. Although still mainly present in the anterior part of the left hemisphere (from 330.48 mV/mm to 436.55 mV/mm), the distribution is more spread at Z33, and it shifts more posteriorly with the highest values around 354.68 mV/mm at FP2II, Z66. At Z100, the distribution is lightly concentrated in the postero–lateral portion of the left hemisphere (F8III), with FP2III showing the lowest values (208.77 mV/mm).

3.2. CONDITION B (Bipolar Antero–Posterior Montage)

The Supplementary Materials report numerical and graphical representations of the CONDITION B results. Table S3 reports values of ΔV (mV) and EF (mV/mm) for each recording point on the perfect spheres. A graphical representation of ΔV distribution shows an evident pattern in which the highest values of the difference in voltage are concentrated in the anterior hemisphere. In particular, at Z0, maximal values (from 26,900 mV to 33,800 mV) amassed around the F7, F3, Fz, T4, F8, T3, C3, Cz, and C4, while at Z33, the distribution, although localized in the anterior hemisphere, is more widespread. At Z66 and Z100, a latero–lateral pattern of distribution can be identified, with maximal values in T3II (33200 mV) and T3III (33,400 mV) (see Figures S1–S3). A graphical representation of EF distribution shows the tendency to be amassed in the left postero–lateral zones, particularly at Z0 and Z100 (see Figures S4–S6). Indeed, at the surface, the maximal value was recorded at Oz (435.44 mV/mm) but high values were found also around T5 (325 mV/mm), P3 (318.35 mV/mm), and Pz (266,46 mV/mm). At Z33 and Z66, distribution is way more widespread, although still localized in the posterior hemisphere, and mainly on the left side. Interestingly, at Z100, distribution became extremely focalized at FP2III and FPzIII, with values of 253.67 mV/mm and 326.93 mV/mm.

3.3. CONDITION C (Bipolar Latero–Lateral Montage)

The Supplementary Materials report numerical and graphical representations of the CONDITION C results. Table S4 reports values of ΔV (mV) and EF (mV/mm) for each recording point on the perfect spheres. A graphical representation of ΔV distribution shows an evident pattern in which the highest values of the difference in voltage are concentrated in the left hemisphere at Z0 (T3, C3, F3, Fp1—max value 52,000 mV), tend to be more widespread at Z33 (but still more present in the left portion of the sphere), and then mass around Fp1II and Fp2II at Z66 (48,000 mV and 47,600 mV) and around FpzIII and T4III at Z100 (48,800 mV and 47,200 mV) (see Figures S7–S9). A graphical representation of EF distribution shows the tendency to be amassed in the right postero–lateral zones, particularly at Z0 and Z100 (see Figures S10–S12). Indeed, at the surface, the maximal value was recorded at P4 (643 mV/mm) but high values were found also around T4 (553.91 mV/mm), C4 (426.22 mV/mm), and O2 (423.2 mV/mm). At Z33 and Z66, distribution is far more widespread, although still localized in the posterior hemisphere, mainly on the right side. Interestingly, at Z100, distribution became extremely focalized at F7III, with values of 227.39 mV/mm.

4. Discussion

4.1. Validation Experiments

In this study, we aimed to qualitatively shape tDCS-induced EFs in a physical phantom head model (i.e., a watermelon), recording signals under three stimulation conditions that were suggested and developing significant stimulation in deep brain structures. Increasing the depth, we found that monopolar stimulation (CONDITION A) resulted in a focused EF distribution with a tendency to shift in the left-to-right direction; anterior-to-posterior stimulation (CONDITION B) created an EF distribution localized in the left parieto–occipital zones but only at the surface and the maximal depth of recording. Similarly, right-to-left stimulation (CONDITION C) showed an EF distribution amassing around the right parieto–occipital zones but only at the surface and the maximal depth of recording. It is noteworthy that CONDITION B and CONDITION C exhibited an almost perfectly symmetrical pattern of EF distribution. As watermelon might be thought of as a reasonable biophysical approximation of the human head [29], we chose to calculate EF according to the 10–20 system to simulate human brain cortical zones and record at four depths (surface, at 33% of the diameter, at 66% of the diameter, and at 100% of the diameter) to resemble anatomical head structures (respectively, human skin, human cortex, human diencephalon and midbrain, and human brainstem). In this view, our results suggest that for all conditions, EF is massively shunted by the skin. Although in line with previous knowledge [42], these results might reflect the displacement of conductive gel on the surface of the watermelon. In CONDITON A, cortical stimulation was widespread but specifically localized at the left fronto–parietal zones, and the diencephalon and brainstem could be reached by induced EF. For CONDITION B and CONDITION C, the left and right (respectively) temporo–occipital cortex were more stimulated, with surprisingly high EF values at the level of the human brainstem (more on the left for CONDITION B, and more on the right for CONDITION C), therefore suggesting a potential in stimulating the deepest cerebral zones. However, being that this is a first-of-its-kind study, our results might be compared only with the findings from computational models [45,46,47,48,49]. Previous studies have matched computational with physical results [14,21,27] but with the aim to validate in silico findings. Therefore, the authors replicated in the real world the characteristics of the simulation [14,21,27]. One should keep in mind that in this case, a frank comparison needs to be carefully considered due to the different intrinsic (e.g., computational models rely on tissue conductivities arbitrarily assigned; phantom models suffer from technical and methodological limitations of recording) and extrinsic (e.g., different study settings) characteristics of the models. The main pitfall might come from our method of signal acquisition, i.e., having the reference for recording attached directly to the stimulating surface of the tDCS electrode in C3 (CONDITION A), O1 (CONDITION B), and T6 (CONDITION C). The tDCS montage we simulated in CONDITION A (i.e., two anodes over C3 and C4; reference in extracephalic position) was suggested to induce a concentration of currents when compared to cephalic montages [45,46,49]. Although the computational results are still a matter of debate [50], our experiments suggest that CONDITION A developed a clear concentration of EF when compared with cephalic montages (CONDITION B and CONDITION C). This pattern is evident on the surface (human skin), at Z33 (human cortex), and at Z66 (human diencephalon and midbrain), but not at Z100 (human brainstem), where cephalic montages induced an almost punctual EF. Also, it was suggested that the extracephalic reference would result in a substantially greater depth of stimulation compared to cephalic configurations [45,46,47,48], although the matter remains controversial [50,51]. For example, Parazzini et al., 2013 showed that J during tDCS with an active electrode over C3 and C4 and an extracephalic reference was always higher in the midbrain, pons, and medulla than in cephalic montages [48]. These areas would roughly correspond to recordings in Z66 and Z100 in CONDITION A. Indeed, our experiments suggest that CONDITION A developed a higher E in Z66, compared to CONDITION B and CONDITION C. Also, at Z100, the monopolar montage induced weaker EF, but it was more diffuse and widespread. On the other hand, there is not much literature at present on the tDCS montages we simulated in CONDITION B (anodes over Fp1 and Fp2; references over O1 and O2) and CONDITION C (anodes over F7 and T5; references over F8 and T6). However, we applied these stimulation montages to assess the effect of stimulating electrode distance on EF distribution, with four cephalic electrodes. Our results suggest that these montages, compared to monopolar, developed lower values of EF at Z0, Z33, and Z66, but with higher and clearly localized EF at Z100. This suggests that, although globally inferior, CONDITION B and CONDITION C montages might induce a deep and focalized stimulation but only at the deepest brain levels.

4.2. General Considerations and Limitations

Determining the EF induced in the brain by tDCS is of particular concern, for both ethical and clinical implications. As watermelon might be thought of as a reasonable biophysical approximation of the human head [29], in this first-of-its-kind study, we suggest that it can be used as a cheap, feasible, and easy phantom head model to characterize the EFs induced by tDCS and, potentially, even other non-invasive brain stimulation techniques. Also, we described a methodological protocol to standardize the experiments, ensure homogenous signal recording and processing, and facilitate the translation of the results. However, several limitations must be considered. First, phantom models such as watermelons are similar but not identical to the human head, and caution is required when interpreting phantom findings. Not only EFs but also the head anatomy determine EF distribution and effects, as disclosed by a number of computational models [52,53,54,55]. For example, skull thickness and composition determine the amount of current reaching the brain [42,56]; cortical folding affects the polarity of the stimulation, creating a highly mixed pattern of directionality [57]; and cerebrospinal fluid, which dissipates the current to the deep regions [42]. Watermelon has a simpler anatomy and cannot account for human complexity. First, phantom models such as watermelons are similar, but not identical to human head and caution is required when interpreting phantom findings. Not only EFs, but also the head anatomy determines EFs distribution and effects, as disclosed by a number of computational models [52,53,54,55]. For example, skull thickness and composition determines the amount of current reaching the brain [42,56], cortical foldings affect the polarity of the stimulation creating a highly mixed pattern of directionality [57], and cerebrospinal fluid dissipates the current to the deep regions [42]. Watermelon has a far simpler anatomy, and in phantom recordings cannot account for human complexity. Second, recording errors might have occurred, as imprecisions in the measurement of potentials are unavoidable and greatly influence the estimation procedure [6,14]. For example, discrepancies in the electrode–tissue interface due to the presence of air or electrode inclination [6] or unavoidably small displacements of measurement points [28] are hurdles intrinsic to the methodology [6]. Also, the presence of measurement electrodes themselves, holes, saline solution, and/or conductive gel on the surface of the watermelon might have modified the electric conductivity and/or EF distribution, as occurs for other models and in vivo recordings [26]. Third, we calculated the value of EF according to the formula EF = ∆V/ΔS, which is an approximate average value with respect to integral calculations (EF = dV/dS). We opted for this solution first because our aim was to provide a simple and practical methodology that could be adopted also by non-expert clinicians in electrical field calculations, and, second, because we assumed that the watermelon could be considered an isotropic and homogeneous means. Finally, the decision to graphically represent the results on a perfect sphere could have slightly distorted the spatial location of the recording points in the process of approximation from the real shape of each watermelon.

5. Conclusions

Determining the EF induced in the brain by tDCS is of particular concern, for both ethical and clinical implications. In this first-of-its-kind study, we characterized tDCS-induced Es in a phantom model (i.e., a watermelon). We found that despite the physical approximations to a human head and the methodological limitations of this study, watermelon might be considered a reliable human head phantom model for the prediction of tDCS-induced EFs, which is of key importance for the study of neuromodulation. Further studies are needed to better understand whether watermelon might be considered an affordable but reliable phantom head model that is potentially useful to describe in depth the characterization of tDCS-induced EFs, now that recent advancements in technology (e.g., triboelectric nanogenerators, which transform mechanical movement into electrical energy [58]) promise to increase the feasibility and user-friendliness of neurostimulation techniques.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/bioengineering12040346/s1, Practical application (Watermelon preparation and tDCS protocols; Recording acquisition; Graphical representation; Results for CONDITION B and CONDITION C; Table S1: Physical characteristics of phantom models; Table S2: Polar (ρ, φ, θ) and cartesian (x, y, z) coordinates for recording electrodes E at each depth; Table S3: Translation of each recording electrodes E (Ex, Ey, Ez) on a sphere with origin O1 (O1x, O1y, O1z). Distance between each recording point E (Ex, Ey, Ez) at each depth Z and O1 (O1x, O1y, O1z), with ∆V recorded and EF inferred are reported; Table S4: Translation of each recording electrodes E (Ex, Ey, Ez) on a sphere with origin T6 (T6x, T6y, T6z). Distance between each recording point E (Ex, Ey, Ez) at each depth Z and T6 (T6x, T6y, T6z), with ∆V recorded and EF inferred are reported. Figure S1: Graphical representation of ΔV distribution in CONDITION B—anterior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S2: Graphical representation of ΔV distribution in CONDITION B—posterior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S3: Graphical representation of ΔV distribution in CONDITION B—superior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S4: Graphical representation of EF distribution in CONDITION B—anterior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S5: Graphical representation of EF distribution in CONDITION B—posterior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S6: Graphical representation of EF distribution in CONDITION B—superior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S7: Graphical representation of ΔV distribution in CONDITION C—anterior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S8: Graphical representation of ΔV distribution in CONDITION C—posterior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S9: Graphical representation of ΔV distribution in CONDITION C—superior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S10: Graphical representation of EF distribution in CONDITION C—anterior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S11: Graphical representation of EF distribution in CONDITION C—posterior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100. Figure S12: Graphical representation of EF distribution in CONDITION C—superior view. (A) refers to depth Z0; (B) refers to depth Z33; (C) refers to depth Z66; (D) refers to depth Z100.

Author Contributions

Conceptualization, M.G., N.V.M., A.M.B. and A.P.; methodology, M.G. and A.P.; validation, A.M.B. and A.P.; formal analysis, R.F. and K.M.; investigation, M.G. and N.V.M.; data curation, M.G., R.F. and K.M.; writing—original draft preparation, M.G., R.F., K.M., N.V.M., T.B., S.O. and A.P.; writing—review and editing, M.G., N.V.M., T.B., S.M., S.O., A.M.B. and A.P.; visualization, R.F., K.M. and N.V.M.; supervision, A.M.B. and A.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author(s).

Conflicts of Interest

S.M. and A.P. report a relationship with Newronika S.p.A. that includes equity or stocks. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results. The other authors declare no conflicts of interest.

References

  1. Thair, H.; Holloway, A.L.; Newport, R.; Smith, A.D. Transcranial Direct Current Stimulation (tDCS): A Beginner’s Guide for Design and Implementation. Front. Neurosci. 2017, 11, 641. [Google Scholar] [CrossRef]
  2. Maiorana, N.; Guidetti, M.; Dini, M.; Priori, A.; Ferrucci, R. Cerebellar tDCS as Therapy for Cerebellar Ataxias. Cerebellum 2022, 21, 755–761. [Google Scholar] [CrossRef]
  3. Lefaucheur, J.P.; Antal, A.; Ayache, S.S.; Benninger, D.H.; Brunelin, J.; Cogiamanian, F.; Cotelli, M.; De Ridder, D.; Ferrucci, R.; Langguth, B.; et al. Evidence-Based Guidelines on the Therapeutic Use of Transcranial Direct Current Stimulation (tDCS); Elsevier: Amsterdam, The Netherlands, 2017; Volume 128, pp. 56–92. [Google Scholar]
  4. Matsumoto, H.; Ugawa, Y. Adverse Events of tDCS and tACS: A Review. Clin. Neurophysiol. Pract. 2017, 2, 19–25. [Google Scholar] [CrossRef]
  5. Laakso, I.; Mikkonen, M.; Koyama, S.; Hirata, A.; Tanaka, S. Can Electric Fields Explain Inter-Individual Variability in Transcranial Direct Current Stimulation of the Motor Cortex? Sci. Rep. 2019, 9, 626. [Google Scholar] [CrossRef]
  6. Kim, D.; Jeong, J.; Jeong, S.; Kim, S.; Jun, S.C.; Chung, E. Validation of Computational Studies for Electrical Brain Stimulation with Phantom Head Experiments. Brain Stimul. 2015, 8, 914–925. [Google Scholar] [CrossRef] [PubMed]
  7. Li, L.M.; Uehara, K.; Hanakawa, T. The Contribution of Interindividual Factors to Variability of Response in Transcranial Direct Current Stimulation Studies. Front. Cell. Neurosci. 2015, 9, 181. [Google Scholar] [CrossRef]
  8. Bocci, T.; Caleo, M.; Tognazzi, S.; Francini, N.; Briscese, L.; Maffei, L.; Rossi, S.; Priori, A.; Sartucci, F. Evidence for Metaplasticity in the Human Visual Cortex. J. Neural Transm. 2014, 121, 221–231. [Google Scholar] [CrossRef]
  9. Siebner, H.R.; Lang, N.; Rizzo, V.; Nitsche, M.A.; Paulus, W.; Lemon, R.N.; Rothwell, J.C. Preconditioning of Low-Frequency Repetitive Transcranial Magnetic Stimulation with Transcranial Direct Current Stimulation: Evidence for Homeostatic Plasticity in the Human Motor Cortex. J. Neurosci. 2004, 24, 3379–3385. [Google Scholar] [CrossRef]
  10. Fridriksson, J.; Elm, J.; Stark, B.C.; Basilakos, A.; Rorden, C.; Sen, S.; George, M.S.; Gottfried, M.; Bonilha, L. BDNF Genotype and tDCS Interaction in Aphasia Treatment. Brain Stimul. 2018, 11, 1276–1281. [Google Scholar] [CrossRef]
  11. Plewnia, C.; Zwissler, B.; Längst, I.; Maurer, B.; Giel, K.; Krüger, R. Effects of Transcranial Direct Current Stimulation (tDCS) on Executive Functions: Influence of COMT Val/Met Polymorphism. Cortex 2013, 49, 1801–1807. [Google Scholar] [CrossRef]
  12. Peterchev, A.V.; Wagner, T.A.; Miranda, P.C.; Nitsche, M.A.; Paulus, W.; Lisanby, S.H.; Pascual-Leone, A.; Bikson, M. Fundamentals of Transcranial Electric and Magnetic Stimulation Dose: Definition, Selection, and Reporting Practices. Brain Stimul. 2012, 5, 435–453. [Google Scholar] [CrossRef]
  13. Datta, A.; Bansal, V.; Diaz, J.; Patel, J.; Reato, D.; Bikson, M. Gyri-Precise Head Model of Transcranial Direct Current Stimulation: Improved Spatial Focality Using a Ring Electrode versus Conventional Rectangular Pad. Brain Stimul. 2009, 2, 201–207. [Google Scholar] [CrossRef]
  14. Wang, M.; Zheng, Y.; Guan, H.; Zhang, J.; Zhang, S. Validation of Numerical Simulation for Transcranial Direct Current Stimulation with Spherical Phantom. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020. [Google Scholar] [CrossRef]
  15. Bikson, M.; Rahman, A.; Datta, A. Computational Models of Transcranial Direct Current Stimulation. Clin. EEG Neurosci. 2012, 43, 176–183. [Google Scholar] [CrossRef] [PubMed]
  16. Christ, A.; Kainz, W.; Hahn, E.G.; Honegger, K.; Zefferer, M.; Neufeld, E.; Rascher, W.; Janka, R.; Bautz, W.; Chen, J.; et al. The Virtual Family—Development of Surface-Based Anatomical Models of Two Adults and Two Children for Dosimetric Simulations. Phys. Med. Biol. 2010, 55, 23. [Google Scholar] [CrossRef] [PubMed]
  17. Gabriel, S.; Lau, R.W.; Gabriel, C. The Dielectric Properties of Biological Tissues: II. Measurements in the Frequency Range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef]
  18. Gabriel, C.; Peyman, A.; Grant, E.H. Electrical Conductivity of Tissue at Frequencies below 1 MHz. Phys. Med. Biol. 2009, 54, 4863. [Google Scholar] [CrossRef]
  19. Datta, A.; Krause, M.R.; Pilly, P.K.; Choe, J.; Zanos, T.P.; Thomas, C.; Pack, C.C. On Comparing in Vivo Intracranial Recordings in Non-Human Primates to Predictions of Optimized Transcranial Electrical Stimulation. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 1774–1777. [Google Scholar] [CrossRef]
  20. Parazzini, M.; Fiocchi, S.; Liorni, I.; Rossi, E.; Cogiamanian, F.; Vergari, M.; Priori, A.; Ravazzani, P. Modeling the Current Density Generated by Transcutaneous Spinal Direct Current Stimulation (tsDCS). Clin. Neurophysiol. 2014, 125, 2260–2270. [Google Scholar] [CrossRef] [PubMed]
  21. Morales-Quezada, L.; El-Hagrassy, M.M.; Costa, B.; McKinley, R.A.; Lv, P.; Fregni, F. Transcranial Direct Current Stimulation Optimization—From Physics-Based Computer Simulations to High-Fidelity Head Phantom Fabrication and Measurements. Front. Hum. Neurosci. 2019, 13, 388. [Google Scholar] [CrossRef]
  22. Puonti, O.; Saturnino, G.B.; Madsen, K.H.; Thielscher, A. Value and Limitations of Intracranial Recordings for Validating Electric Field Modeling for Transcranial Brain Stimulation. NeuroImage 2020, 208, 116431. [Google Scholar] [CrossRef]
  23. Saturnino, G.B.; Antunes, A.; Thielscher, A. On the Importance of Electrode Parameters for Shaping Electric Field Patterns Generated by tDCS. NeuroImage 2015, 120, 25–35. [Google Scholar] [CrossRef]
  24. Laakso, I.; Tanaka, S.; Koyama, S.; De Santis, V.; Hirata, A. Inter-Subject Variability in Electric Fields of Motor Cortical tDCS. Brain Stimul. 2015, 8, 906–913. [Google Scholar] [CrossRef]
  25. Chen, X.-L.; Benkler, S.; Chavannes, N.; De Santis, V.; Bakker, J.; van Rhoon, G.; Mosig, J.; Kuster, N. Analysis of Human Brain Exposure to Low-Frequency Magnetic Fields: A Numerical Assessment of Spatially Averaged Electric Fields and Exposure Limits. Bioelectromagnetics 2013, 34, 375–384. [Google Scholar] [CrossRef] [PubMed]
  26. Guidetti, M.; Arlotti, M.; Bocci, T.; Bianchi, A.M.; Parazzini, M.; Ferrucci, R.; Priori, A. Electric Fields Induced in the Brain by Transcranial Electric Stimulation: A Review of In Vivo Recordings. Biomedicines 2022, 10, 2333. [Google Scholar] [CrossRef]
  27. Jung, Y.J.; Kim, J.H.; Kim, D.; Im, C.H. An Image-Guided Transcranial Direct Current Stimulation System: A Pilot Phantom Study. Physiol. Meas. 2013, 34, 937. [Google Scholar] [CrossRef] [PubMed]
  28. Hunold, A.; Strohmeier, D.; Fiedler, P.; Haueisen, J. Head Phantoms for Electroencephalography and Transcranial Electric Stimulation: A Skull Material Study. Biomed. Tech. 2018, 63, 647–655. [Google Scholar] [CrossRef] [PubMed]
  29. Veniero, D.; Bortoletto, M.; Miniussi, C. TMS-EEG Co-Registration: On TMS-Induced Artifact. Clin. Neurophysiol. Off. J. Int. Fed. Clin. Neurophysiol. 2009, 120, 1392–1399. [Google Scholar] [CrossRef]
  30. Rogasch, N.C.; Thomson, R.H.; Daskalakis, Z.J.; Fitzgerald, P.B. Short-Latency Artifacts Associated with Concurrent TMS-EEG. Brain Stimul. 2013, 6, 868–876. [Google Scholar] [CrossRef]
  31. Politte, D.; Prior, F.; Ponton, C.; Nolan, T.; Larson-Prior, L. Sources of Non-Physiologic Noise in Simultaneous EEG-fMRI Data: A Phantom Study. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August—4 September 2010; pp. 5129–5132. [Google Scholar] [CrossRef]
  32. Woods, A.J.; Antal, A.; Bikson, M.; Boggio, P.S.; Brunoni, A.R.; Celnik, P.; Cohen, L.G.; Fregni, F.; Herrmann, C.S.; Kappenman, E.S.; et al. A Technical Guide to tDCS, and Related Non-Invasive Brain Stimulation Tools. Clin. Neurophysiol. 2016, 127, 1031–1048. [Google Scholar] [CrossRef]
  33. Nardo, D.; Creasey, M.; Negus, C.; Pappa, K.; Reid, A.; Josephs, O.; Callaghan, M.F.; Crinion, J.T.; Violante, I.; Moisa, M. Transcranial Direct Current Stimulation with Functional Magnetic Resonance Imaging: A Detailed Validation and Operational Guide. Wellcome Open Res. 2021, 6, 143. [Google Scholar] [CrossRef]
  34. Roy, A.; Baxter, B.; He, B. High Definition Transcranial Direct Current Stimulation Induces Both Acute and Persistent Changes in Broadband Cortical Synchronization: A Simultaneous tDCS-EEG Study. IEEE Trans. Biomed. Eng. 2014, 61, 1967. [Google Scholar] [CrossRef]
  35. Nelson, S.O. Dielectric Properties of Agricultural Products: Measurements and Applications. IEEE Trans. Electr. Insul. 1991, 26, 845–869. [Google Scholar] [CrossRef]
  36. Nelson, S.O.; Trabelsi, S.; Kays, S.J. Dielectric Spectroscopy of Melons for Potential Quality Sensing. Trans. ASABE 2008, 51, 2209–2214. [Google Scholar] [CrossRef]
  37. Sunaga, T.; Ikehira, H.; Furukawa, S.; Shinkai, H.; Kobayashi, H.; Matsumoto, Y.; Yoshitome, E.; Obata, T.; Tanada, S.; Murata, H.; et al. Measurement of the Electrical Properties of Human Skin and the Variation among Subjects with Certain Skin Conditions. Phys. Med. Biol. 2002, 47, N11. [Google Scholar] [CrossRef]
  38. Youngs, I.J.; Treen, A.S.; Fixter, G.; Holden, S. Design of Solid Broadband Human Tissue Simulant Materials. IEE Proc. Sci. Meas. Technol. 2002, 149, 323–328. [Google Scholar] [CrossRef]
  39. Lee, J.-H.; Shin, S.; Istook, C. Analysis of Human Head Shapes in the United States. Int. J. Hum. Ecol. 2006, 7, 77–83. [Google Scholar]
  40. Yoganandan, N.; Pintar, F.A.; Zhang, J.; Baisden, J.L. Physical Properties of the Human Head: Mass, Center of Gravity and Moment of Inertia. J. Biomech. 2009, 42, 1177–1192. [Google Scholar] [CrossRef]
  41. Report of the Committee on Methods of Clinical Examination in Electroencephalography: 1957. Electroencephalogr. Clin. Neurophysiol. 1958, 10, 370–375. [CrossRef]
  42. Opitz, A.; Paulus, W.; Will, S.; Antunes, A.; Thielscher, A. Determinants of the Electric Field during Transcranial Direct Current Stimulation. NeuroImage 2015, 109, 140–150. [Google Scholar] [CrossRef]
  43. Im, C.-H.; Jung, H.-H.; Choi, J.-D.; Lee, S.Y.; Jung, K.-Y. Determination of Optimal Electrode Positions for Transcranial Direct Current Stimulation (tDCS). Phys. Med. Biol. 2008, 53, N219. [Google Scholar] [CrossRef]
  44. Guo, W.; Zhu, X.; Nelson, S.O. Permittivities of Watermelon Pulp and Juice and Correlation with Quality Indicators. Int. J. Food Prop. 2013, 16, 475–484. [Google Scholar] [CrossRef]
  45. Noetscher, G.M.; Yanamadala, J.; Makarov, S.N.; Pascual-Leone, A. Comparison of Cephalic and Extracephalic Montages for Transcranial Direct Current Stimulation-a Numerical Study. IEEE Trans. Biomed. Eng. 2014, 61, 2488–2498. [Google Scholar] [CrossRef] [PubMed]
  46. Miranda, P.C.; Lomarev, M.; Hallett, M. Modeling the Current Distribution during Transcranial Direct Current Stimulation. Clin. Neurophysiol. 2006, 117, 1623–1629. [Google Scholar] [CrossRef] [PubMed]
  47. Bai, S.; Dokos, S.; Ho, K.A.; Loo, C. A Computational Modelling Study of Transcranial Direct Current Stimulation Montages Used in Depression. NeuroImage 2014, 87, 332–344. [Google Scholar] [CrossRef]
  48. Parazzini, M.; Rossi, E.; Rossi, L.; Priori, A.; Ravazzani, P.; Cogiamanian, F.; Marceglia, S.; Ardolino, G.; Barbieri, S.; Priori, A. Evaluation of the Current Density in the Brainstem during Transcranial Direct Current Stimulation with Extra-Cephalic Reference Electrode. Clin. Neurophysiol. 2013, 124, 1039–1040. [Google Scholar] [CrossRef]
  49. Mendonca, M.E.; Santana, M.B.; Baptista, A.F.; Datta, A.; Bikson, M.; Fregni, F.; Araujo, C.P. Transcranial DC Stimulation in Fibromyalgia: Optimized Cortical Target Supported by High-Resolution Computational Models. J. Pain 2011, 12, 610–617. [Google Scholar] [CrossRef]
  50. Im, C.-H.; Park, J.-H.; Shim, M.; Chang, W.H.; Kim, Y.-H. Evaluation of Local Electric Fields Generated by Transcranial Direct Current Stimulation with an Extracephalic Reference Electrode Based on Realistic 3D Body Modeling. Phys. Med. Biol. 2012, 57, 2137. [Google Scholar] [CrossRef] [PubMed]
  51. Parazzini, M.; Fiocchi, S.; Liorni, I.; Ravazzani, P. Effect of the Interindividual Variability on Computational Modeling of Transcranial Direct Current Stimulation. Comput. Intell. Neurosci. 2015, 2015, 963293. [Google Scholar] [CrossRef]
  52. Fiocchi, S.; Ravazzani, P.; Priori, A.; Parazzini, M. Cerebellar and Spinal Direct Current Stimulation in Children: Computational Modeling of the Induced Electric Field. Front. Hum. Neurosci. 2016, 10, 522. [Google Scholar] [CrossRef] [PubMed]
  53. Datta, A.; Truong, D.; Minhas, P.; Parra, L.C.; Bikson, M. Inter-Individual Variation During Transcranial Direct Current Stimulation and Normalization of Dose Using MRI-Derived Computational Models. Front. Psychiatry 2012, 3, 91. [Google Scholar] [CrossRef]
  54. Truong, D.Q.; Magerowski, G.; Blackburn, G.L.; Bikson, M.; Alonso-Alonso, M. Computational Modeling of Transcranial Direct Current Stimulation (tDCS) in Obesity: Impact of Head Fat and Dose Guidelines. NeuroImage Clin. 2013, 2, 759–766. [Google Scholar] [CrossRef]
  55. Parazzini, M.; Rossi, E.; Ferrucci, R.; Liorni, I.; Priori, A.; Ravazzani, P. Modelling the Electric Field and the Current Density Generated by Cerebellar Transcranial DC Stimulation in Humans. Clin. Neurophysiol. 2014, 125, 577–584. [Google Scholar] [CrossRef] [PubMed]
  56. Ciechanski, P.; Carlson, H.L.; Yu, S.S.; Kirton, A. Modeling Transcranial Direct-Current Stimulation-Induced Electric Fields in Children and Adults. Front Hum Neurosci 2018, 12, 268. [Google Scholar] [CrossRef] [PubMed]
  57. Huang, Y.; Liu, A.A.; Lafon, B.; Friedman, D.; Dayan, M.; Wang, X.; Bikson, M.; Doyle, W.K.; Devinsky, O.; Parra, L.C. Measurements and Models of Electric Fields in the in Vivo Human Brain during Transcranial Electric Stimulation. eLife 2017, 6, e18834. [Google Scholar] [CrossRef] [PubMed]
  58. Xu, S.; Manshaii, F.; Xiao, X.; Yin, J.; Chen, J. Triboelectric Nanogenerators for Self-Powered Neurostimulation. Nano Res. 2024, 17, 8926–8941. [Google Scholar] [CrossRef]
Bioengineering 12 00346 g001
Figure 1. (A) Watermelon with 10–20 system in plastic box with water. (B) Watermelon in CONDITION A. A = anode, C = cathode.
Figure 1. (A) Watermelon with 10–20 system in plastic box with water. (B) Watermelon in CONDITION A. A = anode, C = cathode.
Bioengineering 12 00346 g001
Bioengineering 12 00346 g002
Figure 2. (A) Approximation to a perfect sphere. Example of calculation of distance between each recording point E (Ex, Ey, Ez) at each depth Z and the origin of the reference system R. (B–D) Projection of 10–20 system recording point from the sphere Z0 to the spheres Z33, Z66, and Z100.
Figure 2. (A) Approximation to a perfect sphere. Example of calculation of distance between each recording point E (Ex, Ey, Ez) at each depth Z and the origin of the reference system R. (B–D) Projection of 10–20 system recording point from the sphere Z0 to the spheres Z33, Z66, and Z100.
Bioengineering 12 00346 g002
Bioengineering 12 00346 g003
Figure 3. (A) Watermelon in EXPERIMENTAL CONDITION B. (B) Watermelon in EXPERIMENTAL CONDITION C. A = anode; C = cathode.
Figure 3. (A) Watermelon in EXPERIMENTAL CONDITION B. (B) Watermelon in EXPERIMENTAL CONDITION C. A = anode; C = cathode.
Bioengineering 12 00346 g003
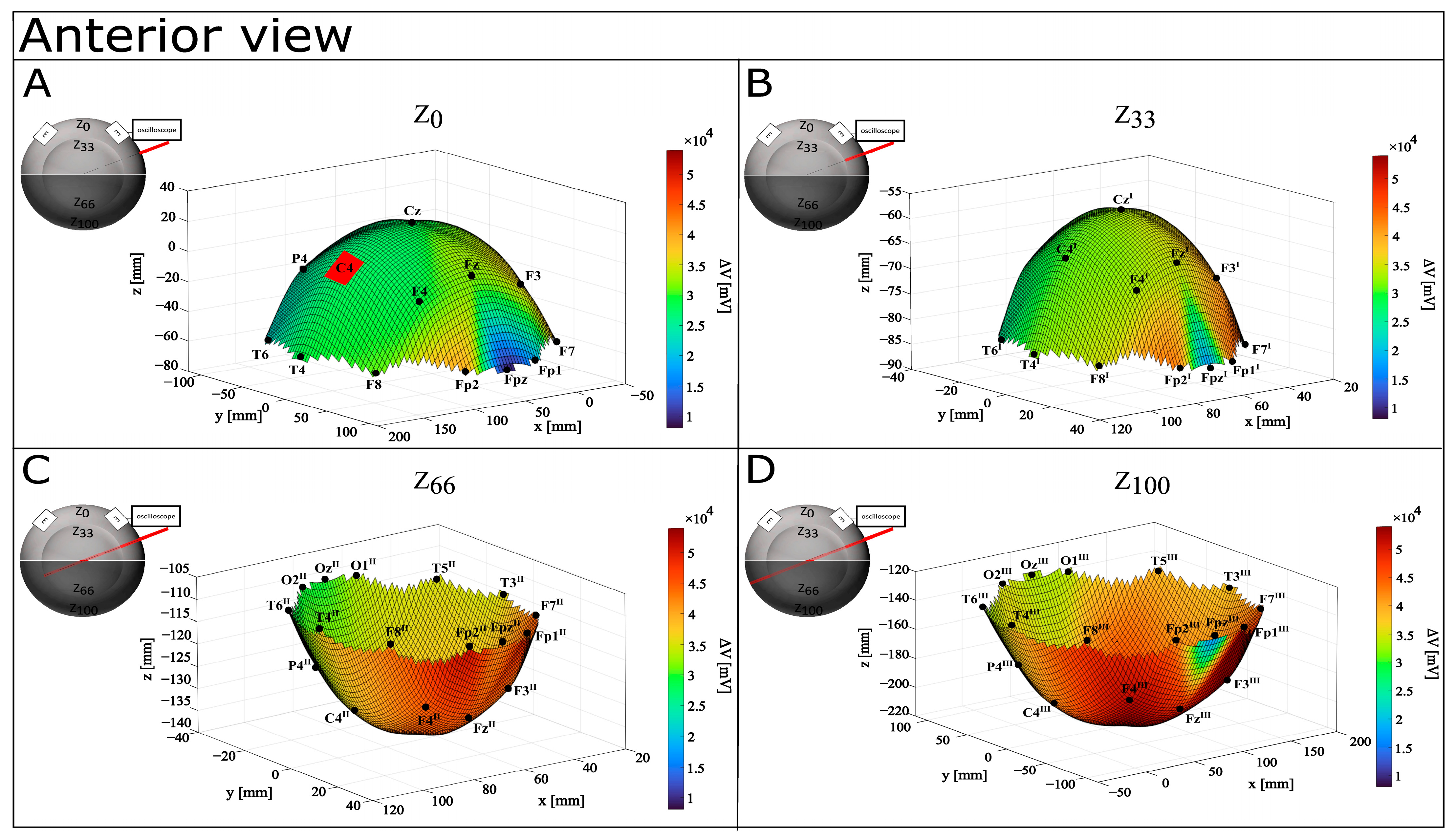
Bioengineering 12 00346 g004
Figure 4. Graphical representation of ΔV distribution in CONDITION A—anterior view. Warm colors refer to a higher value of ΔV recorded, while cool colors refer to a lower value of recorded ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Figure 4. Graphical representation of ΔV distribution in CONDITION A—anterior view. Warm colors refer to a higher value of ΔV recorded, while cool colors refer to a lower value of recorded ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Bioengineering 12 00346 g004
Bioengineering 12 00346 g005
Figure 5. Graphical representation of ΔV distribution in CONDITION A—posterior view. Warm colors refer to a higher value of recorded ΔV recorded, while cool colors refer to lower values of recorded ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Figure 5. Graphical representation of ΔV distribution in CONDITION A—posterior view. Warm colors refer to a higher value of recorded ΔV recorded, while cool colors refer to lower values of recorded ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Bioengineering 12 00346 g005
Bioengineering 12 00346 g006
Figure 6. Graphical representation of ΔV distribution in CONDITION A—superior view. Warm colors refer to a higher value of recorded ΔV, while cool colors refer to lower values of recorded ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Figure 6. Graphical representation of ΔV distribution in CONDITION A—superior view. Warm colors refer to a higher value of recorded ΔV, while cool colors refer to lower values of recorded ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Bioengineering 12 00346 g006
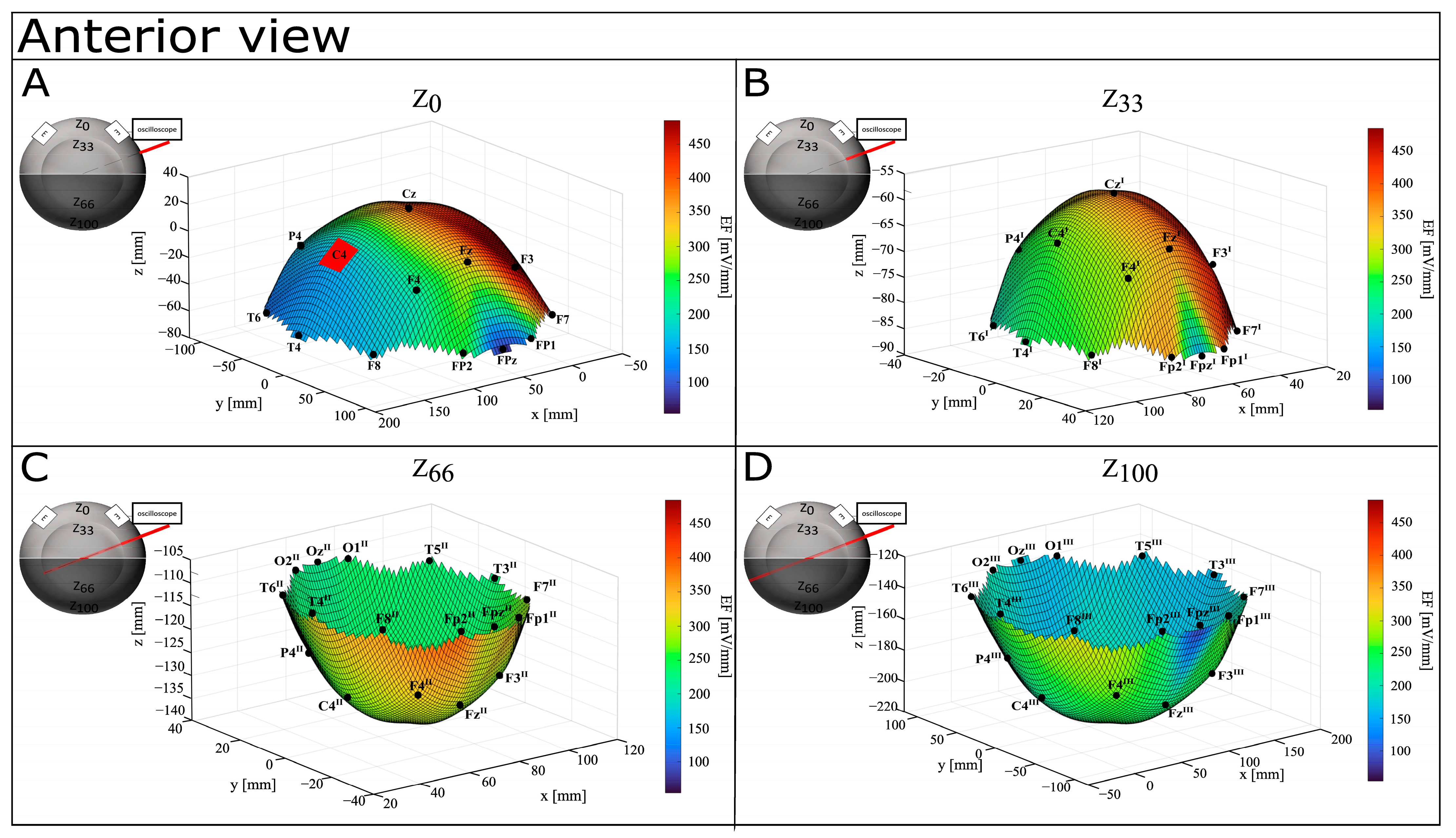
Bioengineering 12 00346 g007
Figure 7. Graphical representation of EF distribution in CONDITION A—anterior view. Warm colors refer to a higher value of calculated EF, while cool colors refer to lower values of calculated ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Figure 7. Graphical representation of EF distribution in CONDITION A—anterior view. Warm colors refer to a higher value of calculated EF, while cool colors refer to lower values of calculated ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Bioengineering 12 00346 g007
Bioengineering 12 00346 g008
Figure 8. Graphical representation of EF distribution in CONDITION A—posterior view. Warm colors refer to a higher value of calculated EF, while cool colors refer to lower values of calculated ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Figure 8. Graphical representation of EF distribution in CONDITION A—posterior view. Warm colors refer to a higher value of calculated EF, while cool colors refer to lower values of calculated ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Bioengineering 12 00346 g008
Bioengineering 12 00346 g009
Figure 9. Graphical representation of EF distribution in CONDITION A—superior view. Warm colors refer to a higher value of calculated EF, while cool colors refer to lower values of calculated ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Figure 9. Graphical representation of EF distribution in CONDITION A—superior view. Warm colors refer to a higher value of calculated EF, while cool colors refer to lower values of calculated ΔV. (A) Depth Z0; (B) depth Z33; (C) depth Z66; (D) depth Z100.
Bioengineering 12 00346 g009
Table 1. Translation of each recording electrode E (Ex, Ey, Ez) on a sphere with origin C3 (C3x, C3y, C3z). Distance between each recording point E (Ex, Ey, Ez) at each depth Z and C3 (C3x, C3y, C3z), with recorded ΔV and inferred EF reported.
Table 1. Translation of each recording electrode E (Ex, Ey, Ez) on a sphere with origin C3 (C3x, C3y, C3z). Distance between each recording point E (Ex, Ey, Ez) at each depth Z and C3 (C3x, C3y, C3z), with recorded ΔV and inferred EF reported.
Electrode Placement on SurfaceDepth ZX (mm)Y (mm)Z (mm)C3EΔV (mV)EF (mV/mm)
Fp1Z035.38108.90−60.20129.3715,800.00122.13
Z3358.9736.30−85.00109.6441,200.00375.77
Z6658.97−36.30−109.81129.8248,400.00372.82
Z10035.38−108.90−134.61176.7353,200.00301.03
FpzZ070.77114.51−60.20147.468080.0054.79
Z3370.7738.17−85.00117.0115,600.00133.32
Z6670.77−38.17−109.81136.1041,600.00305.66
Z10070.77−114.51−134.61190.3716,600.0087.20
Fp2Z0106.15108.90−60.20163.5639,600.00242.11
Z3382.5636.30−85.00123.9442,800.00345.34
Z6682.56−36.30−109.81142.1050,400.00354.68
Z100106.15−108.90−134.61203.1042,400.00208.77
F7Z0−21.8767.31−60.2092.9139,200.00421.91
Z3339.8922.44−85.0096.5440,800.00422.62
Z6639.89−22.44−109.81118.9644,000.00369.86
Z100−21.87−67.31−134.61152.0842,400.00278.80
F3Z013.5278.80−26.6484.2735,600.00484.73
Z3351.6826.27−73.8293.8639,600.00436.23
Z6651.68−26.27−121.00134.1740,400.00291.43
Z10013.52−78.80−168.17186.2154,000.00275.85
F7Z070.7770.770.00100.0832,000.00319.73
Z3370.7723.59−64.9498.9034,400.00347.82
Z6670.77−23.59−129.87149.7744,000.00293.78
Z10070.77−70.77−194.81219.0249,600.00226.47
F4Z0128.0278.80−26.64152.6729,200.00208.24
Z3389.8526.27−73.82119.2233,600.00294.73
Z6689.85−26.27−121.00152.9844,400.00286.76
Z100128.02−78.80−168.17225.5751,600.00225.01
F8Z0163.4167.31−60.20186.7031,600.00169.26
Z33101.6522.44−85.00134.3935,600.00264.90
Z66101.65−22.44−109.81151.3142,800.00282.87
Z100163.41−67.31−134.61222.1547,600.00214.27
T3Z0−43.740.00−60.2074.4130,800.00413.92
Z3332.600.00−85.0091.0432,000.00351.49
Z6632.60−0.00−109.81114.5435,200.00307.30
Z100−43.74−0.00−134.61141.5436,800.00260.00
C3Z0−0.000.000.000.00N.R. *404.08
Z3347.180.00−64.9480.27N.R. *436.54
Z6647.18−0.00−129.87138.18N.R. *275.59
Z100−0.00−0.00−194.81194.81N.R. *219.70
CzZ070.770.0022.9974.4128,000.00376.29
Z3370.770.00−57.2791.0433,200.00364.67
Z6670.770.00−137.54154.6843,600.00281.88
Z10070.770.00−217.81229.0152,000.00227.06
C4Z0141.540.000.00141.54N.R. *0.00
Z3394.360.00−64.94114.54N.R. *267.49
Z6694.360.00−129.87160.53N.R. *229.73
Z100141.540.00−194.81240.80N.R. *170.76
T4Z0185.280.00−60.20194.8129,200.00149.89
Z33108.940.00−85.00138.1832,000.00231.59
Z66108.940.00−109.81154.6836,800.00237.91
Z100185.280.00−134.61229.0138,000.00165.93
T5Z0−21.87−67.31−60.2092.9129,600.00318.59
Z3339.89−22.44−85.0096.5432,800.00339.75
Z6639.8922.44−109.81118.9634,800.00292.53
Z100−21.8767.31−134.61152.0837,600.00247.24
P3Z013.52−78.80−26.6484.2728,000.00381.25
Z3351.68−26.27−73.8293.8630,000.00330.48
Z6651.6826.27−121.00134.1736,000.00259.69
Z10013.5278.80−168.17186.2143,200.00220.68
PzZ070.77−70.770.00100.0824,400.00243.80
Z3370.77−23.59−64.9498.9027,600.00279.06
Z6670.7723.59−129.87149.7734,400.00229.68
Z10070.7770.77−194.81219.0236,700.00167.57
P4Z0128.02−78.80−26.64152.6724,000.00171.16
Z3389.85−26.27−73.82119.2227,200.00238.59
Z6689.8526.27−121.00152.9832,400.00209.26
Z100128.0278.80−168.17225.5736,800.00160.47
T6Z0163.41−67.31−60.20186.7021,600.00115.69
Z33101.65−22.44−85.00134.3924,800.00184.53
Z66101.6522.44−109.81151.3128,000.00185.06
Z100163.4167.31−134.61222.1531,600.00142.24
O1Z035.38−108.90−60.20129.3726,400.00204.07
Z3358.97−36.30−85.00109.6428,800.00262.67
Z6658.9736.30−109.81129.8233,200.00255.74
Z10035.38108.90−134.61176.7333,200.00187.86
OzZ070.77−114.51−60.20147.4622,800.00154.62
Z3370.77−38.17−85.00117.0125,200.00215.37
Z6670.7738.17−109.81136.1029,200.00214.55
Z10070.77114.51−134.61190.3733,200.00174.40
O2Z0106.15−108.90−60.20163.5622,000.00134.51
Z3382.56−36.30−85.00123.9424,400.00196.88
Z6682.5636.30−109.81142.1028,800.00202.68
Z100106.15108.90−134.61203.1034,800.00171.35
N.R. = not recordable; * values of ΔV were calculated as average of surrounding ΔVs at each depth.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Guidetti, M.; Ferrara, R.; Montemagno, K.; Maiorana, N.V.; Bocci, T.; Marceglia, S.; Oliveri, S.; Bianchi, A.M.; Priori, A. The “Cocombola Study”: A Physical Phantom Model for tDCS-Induced Electric Field Distribution. Bioengineering 2025, 12, 346. https://doi.org/10.3390/bioengineering12040346

AMA Style

Guidetti M, Ferrara R, Montemagno K, Maiorana NV, Bocci T, Marceglia S, Oliveri S, Bianchi AM, Priori A. The “Cocombola Study”: A Physical Phantom Model for tDCS-Induced Electric Field Distribution. Bioengineering. 2025; 12(4):346. https://doi.org/10.3390/bioengineering12040346

Chicago/Turabian Style

Guidetti, Matteo, Rosanna Ferrara, Kora Montemagno, Natale Vincenzo Maiorana, Tommaso Bocci, Sara Marceglia, Serena Oliveri, Anna Maria Bianchi, and Alberto Priori. 2025. "The “Cocombola Study”: A Physical Phantom Model for tDCS-Induced Electric Field Distribution" Bioengineering 12, no. 4: 346. https://doi.org/10.3390/bioengineering12040346

APA Style

Guidetti, M., Ferrara, R., Montemagno, K., Maiorana, N. V., Bocci, T., Marceglia, S., Oliveri, S., Bianchi, A. M., & Priori, A. (2025). The “Cocombola Study”: A Physical Phantom Model for tDCS-Induced Electric Field Distribution. Bioengineering, 12(4), 346. https://doi.org/10.3390/bioengineering12040346

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop