- Article
A Duplication–Divergence Hypergraph Model for Protein Complex Data
- Ruihua Zhang and
- Gesine Reinert
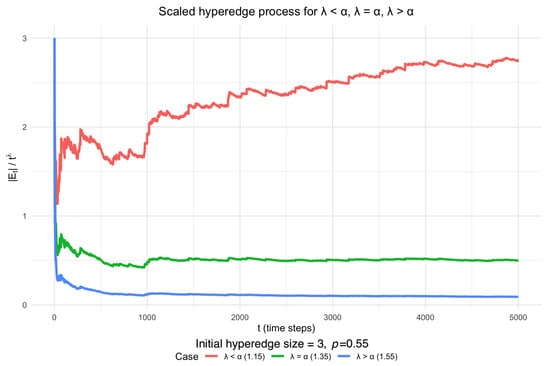
Hypergraphs, a generalisation of traditional graphs in which hyperedges may connect more than two vertices, provide a natural framework for modeling higher-order interactions in complex biological systems. In the context of protein complexes, hypergraphs capture relationships in which a single protein may participate in multiple complexes simultaneously. A fundamental question is how such protein complex hypergraphs evolve over time. Motivated by duplication–divergence–deletion models often used for protein–protein interaction networks, we propose a novel Duplication–Divergence Hypergraph (DDH) model for the evolutionary dynamics of protein complex hypergraphs. To evaluate network resilience, we simulate targeted attack strategies analogous to drug treatments or genetic knockouts that remove selected proteins and their associated hyperedges. We measure the resulting structural changes using hypergraph-based efficiency metrics, comparing synthetic networks generated by the DDH model with empirical E. coli protein complex data. This framework demonstrates closer alignment with empirical observations than standard pairwise duplication–divergence models, suggesting that hypergraphs provide a more realistic representation of protein interactions.
3 December 2025