A Simple Overview of Complex Systems and Complexity Measures
Abstract
1. Introduction
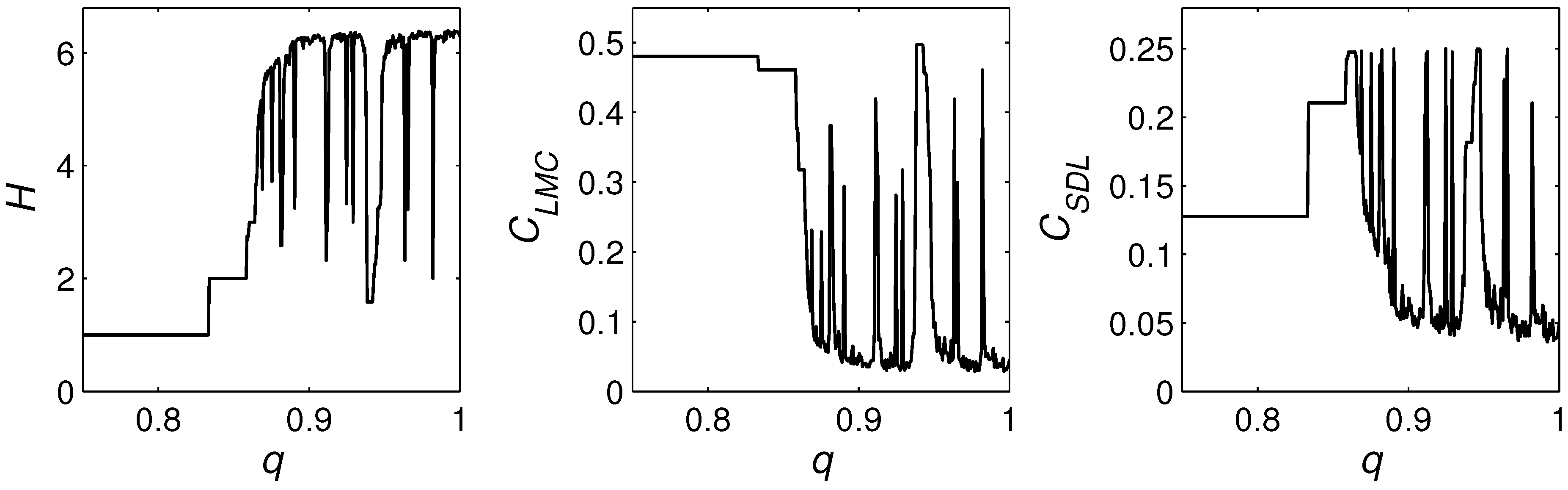
2. Complexity as Information
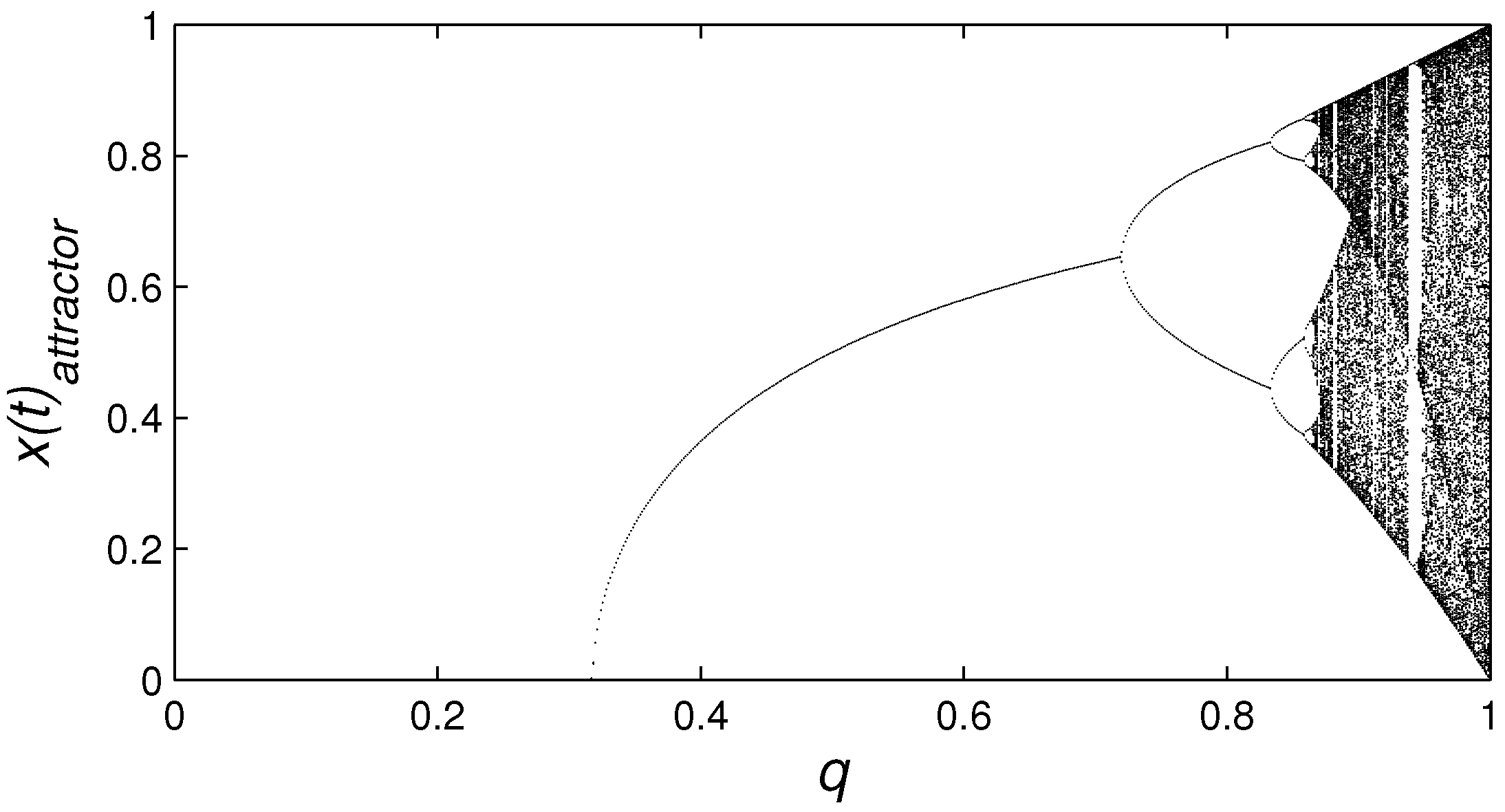
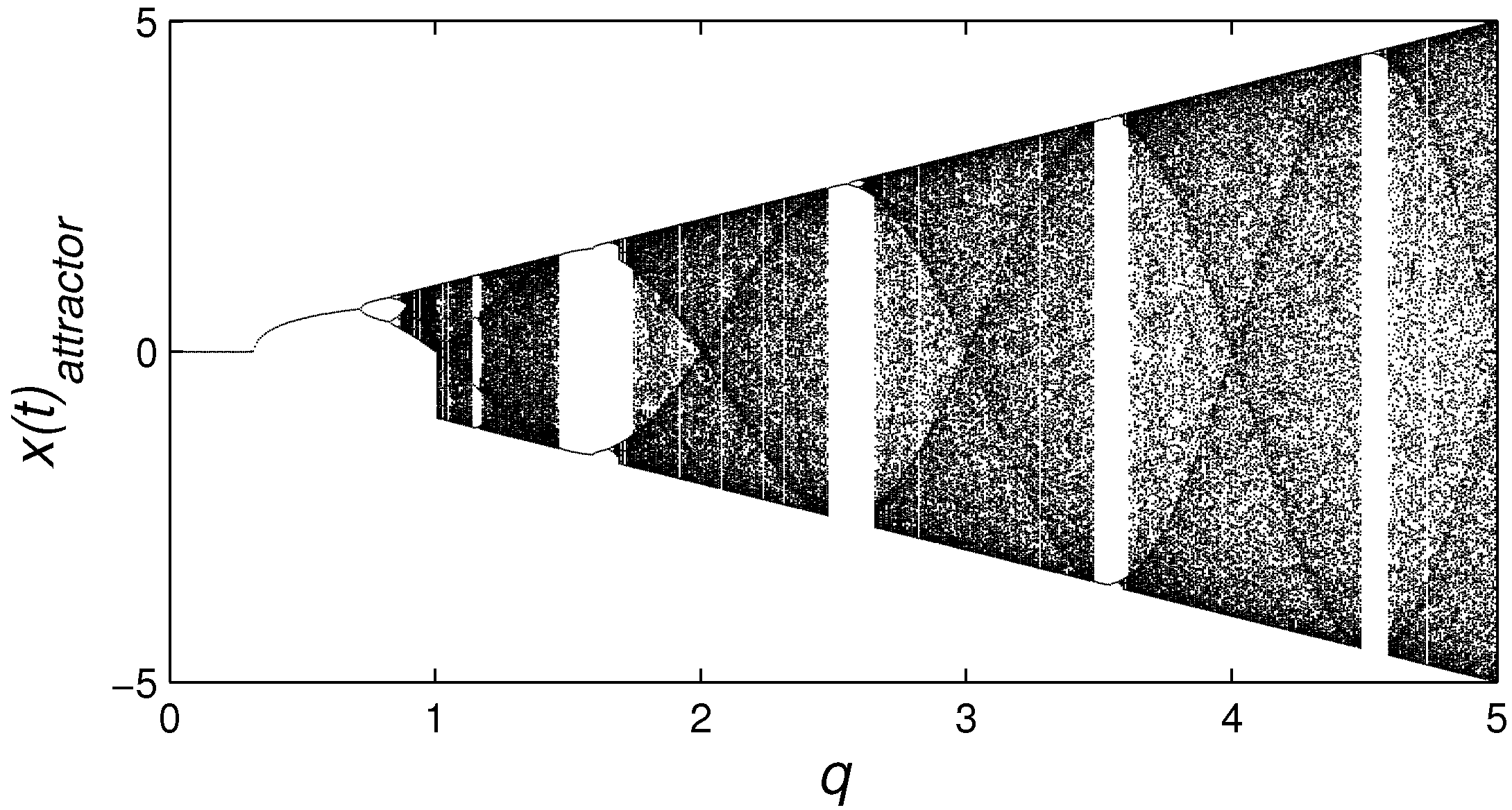
3. Complexity as Bifurcations and Chaos
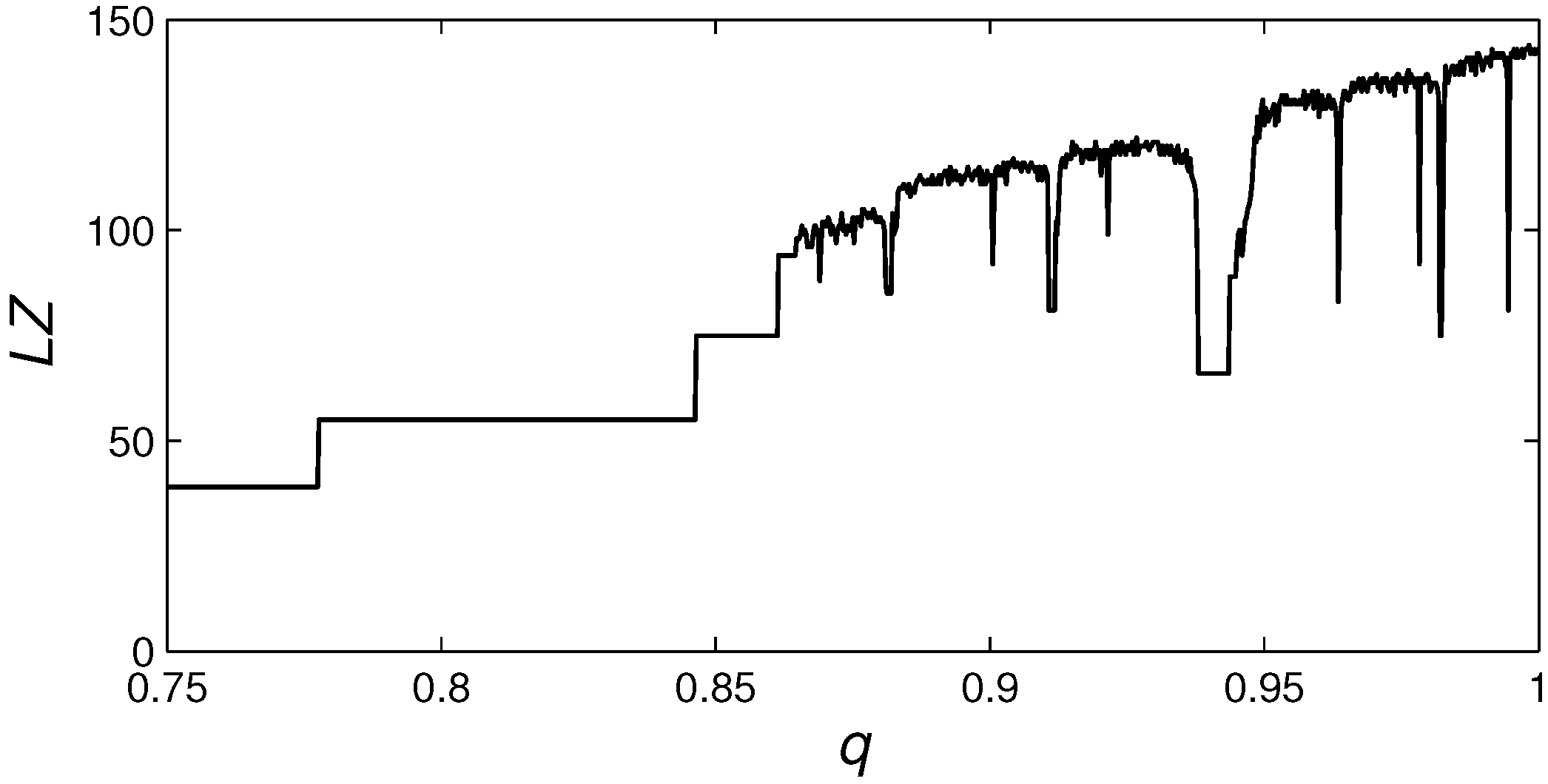
4. Complexity as Algorithm Length
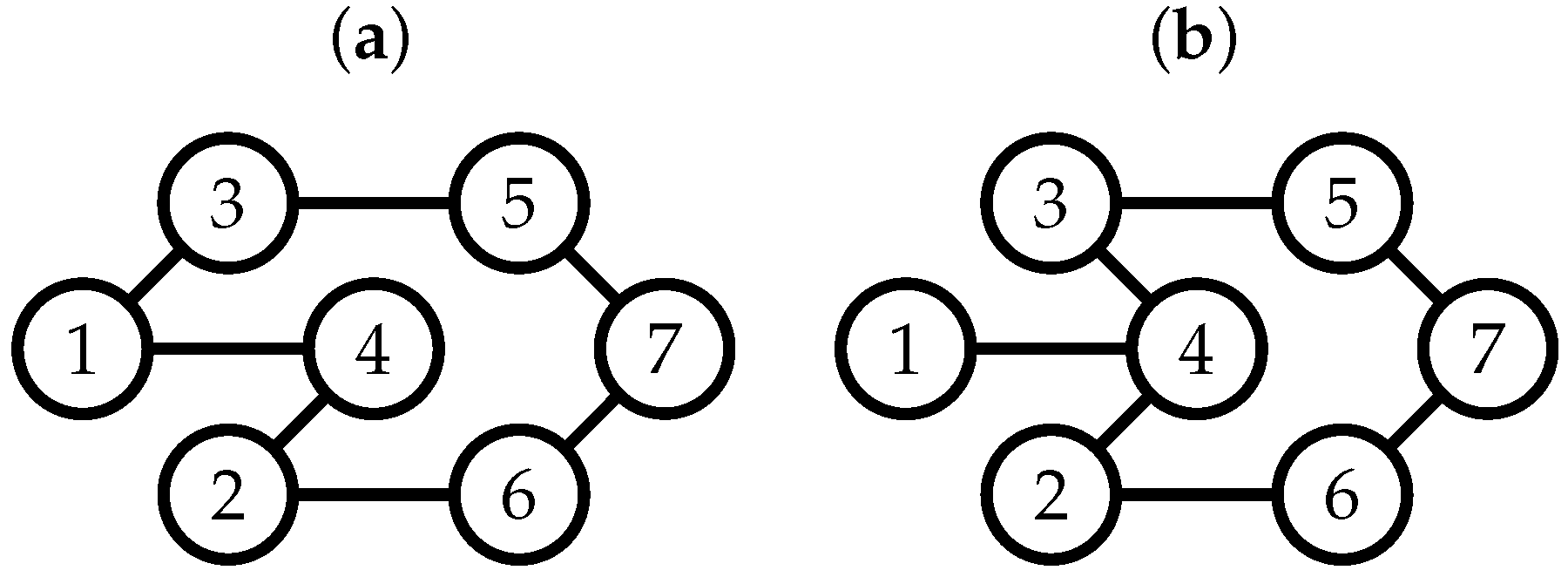
5. Complexity as Connectivity
6. Discussion and Outlook for Future Research
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Batty, M.; Torrens, P.M. Modelling and prediction in a complex world. Futures 2005, 37, 745–766. [Google Scholar] [CrossRef]
- Cumming, G.S.; Collier, J. Change and identity in complex systems. Ecol. Soc. 2005, 10, 29. [Google Scholar] [CrossRef]
- Ladyman, J.; Lambert, J.; Wiesner, K. What is a complex system? Eur. J. Philos. Sci. 2013, 3, 33–67. [Google Scholar] [CrossRef]
- Estrada, E. What is a complex system, after all? Found. Sci. 2024, 29, 1143–1170. [Google Scholar] [CrossRef]
- Riva, F.; Graco-Roza, C.; Daskalova, G.N.; Hudgins, E.J.; Lewthwaite, J.M.M.; Newman, E.A.; Ryo, M.; Mammola, S. Toward a cohesive understanding of ecological complexity. Sci. Adv. 2023, 9, eabq4207. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Guruharsha, K.G.; Rual, J.F.; Zhai, B.; Mintseris, J.; Vaidya, P.; Vaidya, N.; Beekman, C.; Wong, C.; Rhee, D.Y.; Cenaj, O.; et al. A protein complex network of Drosophila melanogaster. Cell 2011, 147, 690–703. [Google Scholar] [CrossRef] [PubMed]
- Pagani, G.A.; Aiello, M. The Power Grid as a complex network: A survey. Phys. A 2013, 392, 2688–2700. [Google Scholar] [CrossRef]
- Zanin, M.; Lillo, F. Modelling the air transport with complex networks: A short review. Eur. Phys. J.-Spec. Top. 2013, 215, 5–21. [Google Scholar] [CrossRef]
- Alvarez, N.G.; Adenso-Díaz, B.; Calzada-Infante, L. Maritime traffic as a complex network: A systematic review. Netw Spat. Econ. 2021, 21, 387–417. [Google Scholar] [CrossRef]
- Mihailovic, D.T.; Mimic, G.; Arsenic, I. Climate predictions: The chaos and complexity in climate models. Adv. Meteorol. 2014, 2014, 878249. [Google Scholar] [CrossRef]
- Brockmann, D.; Helbing, D. The hidden geometry of complex, network-driven contagion phenomena. Science 2013, 342, 1337–1342. [Google Scholar] [CrossRef]
- Fan, Y.; Ren, S.T.; Cai, H.B.; Cui, X.F. The state’s role and position in international trade: A complex network perspective. Econ. Model. 2014, 39, 71–81. [Google Scholar] [CrossRef]
- Vazza, F. On the complexity and the information content of cosmic structures. Mon. Not. Roy. Astron. Soc. 2017, 465, 4942–4955. [Google Scholar] [CrossRef]
- Silva, C.J.; Cantin, G.; Cruz, C.; Fonseca-Pinto, R.; Passadouro, R.; dos Santos, E.S.; Torres, D.F.M. Complex network model for COVID-19: Human behavior, pseudo-periodic solutions and multiple epidemic waves. J. Math. Anal. Appl. 2022, 514, 125171. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Wu, J.J.; Yuan, Q.; Zheng, Z.B. Modeling and understanding ethereum transaction records via a complex network approach. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 67, 2737–2741. [Google Scholar] [CrossRef]
- Zhao, D.; Ji, S.F.; Wang, H.P.; Jiang, L.W. How do government subsidies promote new energy vehicle diffusion in the complex network context? A three-stage evolutionary game model. Energy 2021, 230, 120899. [Google Scholar] [CrossRef] [PubMed]
- Floridi, L.; Chiriatti, M. GPT-3: Its nature, scope, limits, and consequences. Minds Mach. 2020, 30, 681–694. [Google Scholar] [CrossRef]
- Manson, S.M. Simplifying complexity: A review of complexity theory. Geoforum 2001, 32, 405–414. [Google Scholar] [CrossRef]
- Sarukkai, S. Complexity and randomness in Mathematics: Philosophical reflections on the relevance for economic modelling. J. Econ. Surv. 2011, 25, 464–480. [Google Scholar] [CrossRef]
- Turner, J.R.; Baker, R.M. Complexity theory: An overview with potential applications for the social sciences. Systems 2019, 7, 4. [Google Scholar] [CrossRef]
- Kesic, S. Complexity and biocomplexity: Overview of some historical aspects and philosophical basis. Ecol. Complex. 2024, 57, 101072. [Google Scholar] [CrossRef]
- von Bertalanffy, L. General System Theory: Foundations, Development, Applications; George Braziller: New York, NY, USA, 1969. [Google Scholar]
- Morin, E. On Complexity; Hampton Press: New York, NY, USA, 2008. [Google Scholar]
- McCauley, E.; Wilson, W.G.; de Roos, A.M. Dynamics of age-structured and spatially structured predator-prey interactions: Individual-based models and population-level formulations. Am. Nat. 1993, 142, 412. [Google Scholar] [CrossRef] [PubMed]
- Boccara, N.; Cheong, K.; Oram, M. A probabilistic automata network epidemic model with births and deaths exhibiting cyclic behaviour. J Phys.-A Math. Gen. 1994, 27, 1585. [Google Scholar] [CrossRef]
- van der Laan, J.D.; Lhotka, L.; Hogeweg, P. Sequential predation: A multi-model study. J. Theor. Biol. 1995, 174, 149–167. [Google Scholar] [CrossRef]
- Sherratt, J.A.; Eagan, B.T.; Lewis, M.A. Oscillations and chaos behind predator-prey invasion: Mathematical artifact or ecological reality? Philos. Trans. R. Soc. B-Biol. Sci. 1997, 352, 21–38. [Google Scholar] [CrossRef]
- Durrett, R. Stochastic spatial models. SIAM Rev. 1999, 41, 677. [Google Scholar] [CrossRef]
- Moreno, Y.; Pastor-Satorras, R.; Vespignani, A. Epidemic outbreaks in complex heterogeneous networks. Eur. Phys. J. B 2002, 26, 521–529. [Google Scholar] [CrossRef]
- Silva, H.A.L.R.; Monteiro, L.H.A. Self-sustained oscillations in epidemic models with infective immigrants. Ecol. Complex. 2014, 17, 40–45. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Chicago, IL, USA, 1998. [Google Scholar]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics; Waveland Press: Long Grove, IL, USA, 2009. [Google Scholar]
- von Neumann, J. Mathematical Foundations of Quantum Mechanics: New Edition; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Maruyama, K.; Nori, F.; Vedral, V. Colloquium: The physics of Maxwell’s demon and information. Rev. Mod. Phys. 2009, 81, 1. [Google Scholar] [CrossRef]
- Lopez-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Shiner, J.S.; Davison, M.; Landsberg, P.T. Simple measure for complexity. Phys. Rev. E 1999, 59, 1459. [Google Scholar] [CrossRef]
- Consolini, G.; Tozzi, R.; De Michelis, P. Complexity in the sunspot cycle. Astron. Astrophys. 2009, 506, 1381–1391. [Google Scholar] [CrossRef]
- González, C.M.; Larrondo, H.A.; Rosso, O.A. Statistical complexity measure of pseudorandom bit generators. Phys. A 2005, 354, 281–300. [Google Scholar] [CrossRef]
- Piqueira, J.R.C.; Mortoza, L.P.D. Brazilian exchange rate complexity: Financial crisis effects. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 1690–1695. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Phys. A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Yamano, T. A statistical measure of complexity with nonextensive entropy. Phys. A 2004, 340, 131–137. [Google Scholar] [CrossRef]
- Devaney, R.L. A First Course in Chaotic Dynamical Systems; Perseus Books: Cambridge, MA, USA, 1982. [Google Scholar]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Lalescu, C.C. Patterns in the sine map bifurcation diagram. arXiv 2010, arXiv:1011.6552. [Google Scholar] [CrossRef]
- Griffin, J. The Sine Map. 2013. Available online: https://people.maths.bris.ac.uk/~macpd/ads/sine.pdf (accessed on 30 April 2025).
- Zhang, Q.; Xiang, Y.; Fan, Z.H.; Bi, C. Study of universal constants of bifurcation in a chaotic sine map. In Proceedings of the 2013 Sixth International Symposium on Computational Intelligence and Design, Hangzhou, China, 28–29 October 2013; Volume 2, p. 177. [Google Scholar] [CrossRef]
- Dong, C.; Rajagopal, K.; He, S.; Jafari, S.; Sun, K. Chaotification of Sine-series maps based on the internal perturbation model. Results Phys. 2021, 31, 105010. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- May, R. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in the large: An extension of the concept of Lyapunov exponent. J. Phys. A-Math. Gen. 1997, 30, 1. [Google Scholar] [CrossRef]
- Liu, W.H.; Sun, K.H.; Zhu, C.X. A fast image encryption algorithm based on chaotic map. Opt. Lasers Eng. 2016, 84, 26–36. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Yamano, T. A statistical complexity measure with nonextensive entropy and quasi-multiplicativity. J. Math. Phys. 2004, 45, 1974–1987. [Google Scholar] [CrossRef]
- Rosso, O.A.; De Micco, L.; Larrondo, H.A.; Martín, M.T.; Plastino, A. Generalized statistical complexity measure. Int. J. Bifurc. Chaos 2010, 20, 775–785. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W. Entropy measures for biological signal analyses. Nonlinear Dyn. 2012, 68, 431–444. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of Alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Gao, J.B.; Liu, F.Y.; Zhang, J.F.; Hu, J.; Cao, Y.H. Information entropy as a basic building block of Complexity Theory. Entropy 2013, 15, 3396–3418. [Google Scholar] [CrossRef]
- Lesne, A. Shannon entropy: A rigorous notion at the crossroads between probability, information theory, dynamical systems and statistical physics. Math. Struct. Comput. Sci. 2014, 24, e240311. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Angulo, J.C.; Dehesa, J.S. A generalized complexity measure based on Rényi entropy. Eur. Phys. J. D 2014, 68, 212. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Jauregui, M.; Zunino, L.; Lenzi, E.K. Characterizing time series via complexity-entropy curves. Phys. Rev. E 2017, 95, 062106. [Google Scholar] [CrossRef]
- Amigó, J.M.; Balogh, S.G.; Hernández, S. A brief review of generalized entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef]
- Rohila, A.; Sharma, A. Phase entropy: A new complexity measure for heart rate variability. Physiol. Meas. 2019, 40, 105006. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Zhang, X.F.; Zhang, G.B. Phase permutation entropy: A complexity measure for nonlinear time series incorporating phase information. Phys. A 2021, 568, 125686. [Google Scholar] [CrossRef]
- Li, S.E.; Shang, P.J. A new complexity measure: Modified discrete generalized past entropy based on grain exponent. Chaos Solitons Fractals 2022, 157, 111928. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Shang, P.J. Distance correlation entropy and ordinal distance complexity measure: Efficient tools for complex systems. Nonlinear Dyn. 2024, 112, 1153–1172. [Google Scholar] [CrossRef]
- Das, D.; Ray, A.; Hens, C.; Ghosh, D.; Hassan, M.K.; Dabrowski, A.; Kapitaniak, T.; Dana, S.K. Complexity measure of extreme events. Chaos 2024, 34, 121104. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J.-Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Liu, L.F.; Miao, S.X.; Cheng, M.F.; Gao, X.J. Permutation entropy for random binary sequences. Entropy 2015, 17, 8207–8216. [Google Scholar] [CrossRef]
- Tsallis, C. Beyond Boltzmann–Gibbs–Shannon in Physics and elsewhere. Entropy 2019, 21, 696. [Google Scholar] [CrossRef]
- Balasis, G.; Eftaxias, K. A study of non-extensivity in the Earth’s magnetosphere. Eur. Phys. J.-Spec. Top. 2009, 174, 219–225. [Google Scholar] [CrossRef]
- Baranger, M.; Latora, V.; Rapisarda, A. Time evolution of thermodynamic entropy for conservative and dissipative chaotic maps. Chaos Solitons Fractals 2002, 13, 471–478. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Tsallis entropy index q and the complexity measure of seismicity in natural time under time reversal before the M9 Tohoku Earthquake in 2011. Entropy 2018, 20, 757. [Google Scholar] [CrossRef] [PubMed]
- Keller, S.M.; Gschwandtner, U.; Meyer, A.; Chaturvedi, M.; Roth, V.; Fuhr, P. Cognitive decline in Parkinson’s disease is associated with reduced complexity of EEG at baseline. Brain Commun. 2020, 2, fcaa207. [Google Scholar] [CrossRef]
- Wen, T.; Jiang, W. Measuring the complexity of complex network by Tsallis entropy. Phys. A 2019, 526, 121054. [Google Scholar] [CrossRef]
- Cerf, N.J.; Adami, C. Negative entropy and information in quantum mechanics. Phys. Rev. Lett. 1997, 79, 5194. [Google Scholar] [CrossRef]
- Cerf, N.J.; Adami, C. Information theory of quantum entanglement and measurement. Phys. D 1998, 120, 62–81. [Google Scholar] [CrossRef]
- Piqueira, J.R.C.; Serboncini, F.A.; Monteiro, L.H.A. Biological models: Measuring variability with classical and quantum information. J. Theor. Biol. 2006, 242, 309–313. [Google Scholar] [CrossRef] [PubMed]
- Müller-Lennert, M.; Dupuis, F.; Szehr, O.; Fehr, S.; Tomamichel, M. On quantum Rényi entropies: A new generalization and some properties. J. Math. Phys. 2013, 54, 122203. [Google Scholar] [CrossRef]
- Witten, E. A mini-introduction to information theory. Riv. Nuovo Cimento 2020, 43, 187–227. [Google Scholar] [CrossRef]
- Catalán, R.G.; Garay, J.; López-Ruiz, R. Features of the extension of a statistical measure of complexity to continuous systems. Phys. Rev. E 2002, 66, 011102. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221. [Google Scholar] [CrossRef]
- Angulo, J.C.; Antolin, J. Atomic complexity measures in position and momentum spaces. J. Chem. Phys. 2008, 128, 164109. [Google Scholar] [CrossRef] [PubMed]
- Chatzisavvas, K.C.; Psonis, V.P.; Panos, C.P.; Moustakidis, C.C. Complexity and neutron star structure. Phys. Lett. A 2009, 373, 3901–3909. [Google Scholar] [CrossRef]
- Fisher, R.A. Theory of statistical estimation. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Vignat, C.; Bercher, J.F. Analysis of signals in the Fisher-Shannon information plane. Phys. Lett. A 2003, 312, 27–33. [Google Scholar] [CrossRef]
- Rudnicki, L.; Toranzo, I.V.; Sánchez-Moreno, P.; Dehesa, J.S. Monotone measures of statistical complexity. Phys. Lett. A 2016, 380, 377–380. [Google Scholar] [CrossRef]
- Sen, K.D.; Antolín, J.; Angulo, J.C. Fisher-Shannon analysis of ionization processes and isoelectronic series. Phys. Rev. A 2007, 76, 032502. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; López-Rosa, S.; Flores-Gallegos, N. Analysis of complexity measures and information planes of selected molecules in position and momentum spaces. Phys. Chem. Chem. Phys. 2010, 12, 7108. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Dehesa, J.S.; Manzano, D.; Yáñez, R.J. Spreading lengths of Hermite polynomials. J. Comput. Appl. Math. 2010, 233, 2136–2148. [Google Scholar] [CrossRef]
- Aguiar, D.; Menezes, R.S.C.; Antonino, A.C.D.; Stosic, T.; Tarquis, A.M.; Stosic, B. Quantifying soil complexity using Fisher Shannon method on 3D X-ray computed tomography scans. Entropy 2023, 25, 1465. [Google Scholar] [CrossRef]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. Chaos: An Introduction to Dynamical Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
- Argurys, J.; Faust, G.; Haase, M.; Friedrich, R. An Exploration of Dynamical Systems and Chaos; Springer: New York, NY, USA, 2015. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology; McGraw-Hill: Toronto, ON, Canada, 1988. [Google Scholar]
- Kolmogorov, A.N.; Petrovsky, I.G.; Piskunov, N.S. Study of the diffusion equation with growth of the quantity of matter and its application to a biology problem. In Dynamics of Curved Fronts; Pelcé, P., Ed.; Academic Press: Cambridge, MA, USA, 1988; pp. 105–130. [Google Scholar] [CrossRef]
- Ross, M.C.; Hohenberg, P.C. Pattern-formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology II: Spatial Models and Biomedical Applications; Springer: New York, NY, USA, 2003. [Google Scholar]
- Malchow, H.; Petrovskii, S.V.; Venturino, E. Spatiotemporal Patterns in Ecology and Epidemiology: Theory, Models, Simulations; CRC Press: London, UK, 2008. [Google Scholar]
- Monteiro, L.H.A. Sistemas Dinâmicos Complexos; Livraria da Física: São Paulo, SP, Brazil, 2010. (In Portuguese) [Google Scholar]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. B 1952, 237, 37. [Google Scholar] [CrossRef]
- Li, T.Y.; York, J.A. Period 3 implies chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Ruelle, D. Ergodic-theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617. [Google Scholar] [CrossRef]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196. [Google Scholar] [CrossRef] [PubMed]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kuznetsov, Y. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 2004. [Google Scholar]
- Monteiro, L.H.A. Sistemas Dinâmicos; Livraria da Física: São Paulo, SP, Brazil, 2002. (In Portuguese) [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Int. J. Comput. Math. 1968, 2, 157–168. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Logical basis for information theory and probability theory. IEEE Trans. Inf. Theory 1968, 14, 662–664. [Google Scholar] [CrossRef]
- Solomonoff, R.J. A formal theory of inductive inference. Part I. Inf. Control 1964, 7, 1–22. [Google Scholar] [CrossRef]
- Solomonoff, R.J. A formal theory of inductive inference. Part II. Inf. Control 1964, 7, 224–254. [Google Scholar] [CrossRef]
- Chaitin, G.J. On the length of programs for computing finite binary sequences. J. ACM 1966, 13, 547–569. [Google Scholar] [CrossRef]
- Chaitin, G.J. Algorithmic information theory. IBM J. Res. Dev. 1977, 21, 350–359. [Google Scholar] [CrossRef]
- Wallace, C.S.; Dowe, D.L. Minimum message length and Kolmogorov complexity. Comput. J. 1999, 42, 270–283. [Google Scholar] [CrossRef]
- Zenil, H. A review of methods for estimating algorithmic complexity: Options, challenges, and new directions. Entropy 2020, 22, 612. [Google Scholar] [CrossRef]
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1937, 42, 230–265. [Google Scholar] [CrossRef]
- Martin-Delgado, M.A. Alan Turing and the origins of complexity. Arbor-Cienc. Pensam. Cult. 2013, 189, a083. [Google Scholar] [CrossRef]
- Rice, R.F.; Plaunt, J.R. Adaptive variable-length coding for efficient compression of spacecraft television data. IEEE Trans. Commun. Technol. 1971, 19, 889–897. [Google Scholar] [CrossRef]
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann: Cambridge, MA, USA, 2017. [Google Scholar]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. A universal algorithm for sequential data compression. IEEE Trans. Inf. Theory 1977, 23, 337–343. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. Compression of individual sequences via variable-rate coding. IEEE Trans. Inf. Theory 1978, 24, 530–536. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Yan, R.Q.; Gao, R.X. Complexity as a measure for machine health evaluation. IEEE Trans. Instrum. Meas. 2004, 53, 1327–1334. [Google Scholar] [CrossRef]
- Aboy, M.; Hornero, R.; Abásolo, D.; Alvarez, D. Interpretation of the Lempel-Ziv complexity measure in the context of biomedical signal analysis. IEEE Trans. Biomed. Eng. 2006, 53, 2282–2288. [Google Scholar] [CrossRef]
- Kim, K.; Lee, M. The impact of the COVID-19 pandemic on the unpredictable dynamics of the cryptocurrency market. Entropy 2021, 23, 1234. [Google Scholar] [CrossRef]
- Li, Y.X.; Geng, B.; Jiao, S.B. Dispersion entropy-based Lempel-Ziv complexity: A new metric for signal analysis. Chaos Solitons Fractals 2022, 161, 112400. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwanga, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Costa, L.D.; Rodrigues, F.A.; Travieso, G.; Boas, P.R.V. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Battiston, F.; Cencetti, G.; Iacopini, I.; Latora, V.; Lucas, M.; Patania, A.; Young, J.G.; Petri, G. Networks beyond pairwise interactions: Structure and dynamics. Phys. Rep. 2020, 874, 1–92. [Google Scholar] [CrossRef]
- Morabito, F.C.; Campolo, M.; Labate, D.; Morabito, G.; Bonanno, L.; Bramanti, A.; de Salvo, S.; Marra, A.; Bramanti, P. A longitudinal EEG study of Alzheimer’s disease progression based on a complex network approach. Int. J. Neural Syst. 2015, 25, 1550005. [Google Scholar] [CrossRef]
- Supriya, S.; Siuly, S.; Wang, H.; Zhang, Y.C. Epilepsy detection from EEG using complex network techniques: A review. IEEE Rev. Biomed. Eng. 2023, 16, 292–306. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef] [PubMed]
- Luque, B.; Lacasa, L.; Ballesteros, F.; Luque, J. Horizontal visibility graphs: Exact results for random time series. Phys. Rev. E 2009, 80, 046103. [Google Scholar] [CrossRef]
- Zhang, J.; Small, M. Complex network from pseudoperiodic time series: Topology versus dynamics. Phys. Rev. Lett. 2006, 96, 238701. [Google Scholar] [CrossRef] [PubMed]
- Campanharo, A.S.L.O.; Sirer, M.I.; Malmgren, R.D.; Ramos, F.M.; Amaral, L.A.N. Duality between time series and networks. PLoS ONE 2011, 6, e23378. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of `small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Lima-Mendez, G.; van Helden, J. The powerful law of the power law and other myths in network biology. Mol. Biosyst. 2009, 5, 1482–1493. [Google Scholar] [CrossRef]
- Willinger, W.; Alderson, D.; Doyle, J.C. Mathematics and the Internet: A source of enormous confusion and great potential. Not. Am. Math. Soc. 2009, 56, 586. [Google Scholar] [CrossRef]
- Broido, A.D.; Clauset, A. Scale-free networks are rare. Nat. Commun. 2019, 10, 1017. [Google Scholar] [CrossRef]
- Klemm, K.; Eguiluz, V.M. Growing scale-free networks with small-world behavior. Phys. Rev. E 2002, 65, 057102. [Google Scholar] [CrossRef]
- Holme, P.; Kim, B.J. Growing scale-free networks with tunable clustering. Phys. Rev. E 2002, 65, 026107. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Z.; Rong, L.L.; Wang, B.; Zhou, S.G.; Guan, J.H. Local-world evolving networks with tunable clustering. Physica A 2007, 380, 639–650. [Google Scholar] [CrossRef][Green Version]
- Boccaletti, S.; Hwang, D.U.; Latora, V. Growing hierarchical scale-free networks by means of nonhierarchical processes. Int. J. Bifurc. Chaos 2007, 17, 2447–2452. [Google Scholar] [CrossRef]
- Yang, H.X.; Wu, Z.X.; Du, W.B. Evolutionary games on scale-free networks with tunable degree distribution. EPL 2012, 99, 10006. [Google Scholar] [CrossRef]
- Colman, E.R.; Rodgers, G.J. Complex scale-free networks with tunable power-law exponent and clustering. Phys. A 2013, 392, 5501–5510. [Google Scholar] [CrossRef]
- Wang, L.; Li, G.F.; Ma, Y.H.; Yang, L. Structure properties of collaboration network with tunable clustering. Inf. Sci. 2020, 506, 37–50. [Google Scholar] [CrossRef]
- Licciardi, A.N., Jr.; Monteiro, L.H.A. A network model of social contacts with small-world and scale-free features, tunable connectivity, and geographic restrictions. Math. Biosci. Eng. 2024, 21, 4801–4813. [Google Scholar] [CrossRef]
- Sole, R.; Valverde, V. Information theory of complex networks: On evolution and architectural constraints. In Complex Networks; Springer: New York, NY, USA, 2004; Volume 650, pp. 189–207. [Google Scholar] [CrossRef]
- Wang, B.; Tang, H.W.; Guo, C.H.; Xiu, Z.L. Entropy optimization of scale-free networks’ robustness to random failures. Phys. A 2006, 363, 591–596. [Google Scholar] [CrossRef]
- Xu, X.L.; Hu, X.F.; He, X.Y. Degree dependence entropy descriptor for complex networks. Adv. Manuf. 2013, 1, 284–287. [Google Scholar] [CrossRef][Green Version]
- Zhang, Q.; Li, M.Z.; Deng, Y. A new structure entropy of complex networks based on nonextensive statistical mechanics. Int. J. Mod. Phys. C 2016, 27, 1650118. [Google Scholar] [CrossRef]
- Lei, M.L.; Liu, L.R.; Wei, D.J. An improved method for measuring the complexity in complex networks based on structure entropy. IEEE Access 2019, 7, 159190–159198. [Google Scholar] [CrossRef]
- Shakibian, H.; Charkari, N.M. Link segmentation entropy for measuring the network complexity. Soc. Netw. Anal. Min. 2022, 12, 85. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Li, M.Z.; Zhang, Q. A clustering coefficient structural entropy of complex networks. Phys. A 2024, 655, 130170. [Google Scholar] [CrossRef]
- Vafaei, N.; Sheikhi, F.; Ghasemi, A. A community-based entropic method to identify influential nodes across multiple social networks. Soc. Netw. Anal. Min. 2025, 15, 23. [Google Scholar] [CrossRef]
- Herculano-Houzel, S. The remarkable, yet not extraordinary, human brain as a scaled-up primate brain and its associated cost. Proc. Natl. Acad. Sci. USA 2012, 109, 10661–10668. [Google Scholar] [CrossRef]
- Huttenlocher, P.R. Synaptic density in human frontal cortex—Developmental changes and effects of aging. Brain Res. 1979, 163, 195–205. [Google Scholar] [CrossRef]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. arXiv 2020, arXiv:2005.14165. [Google Scholar] [CrossRef]
- Hinsch, K.; Zupanc, G.K.H. Generation and long-term persistence of new neurons in the adult zebrafish brain: A quantitative analysis. Neuroscience 2007, 146, 679–696. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monteiro, L.H.A. A Simple Overview of Complex Systems and Complexity Measures. Complexities 2025, 1, 2. https://doi.org/10.3390/complexities1010002
Monteiro LHA. A Simple Overview of Complex Systems and Complexity Measures. Complexities. 2025; 1(1):2. https://doi.org/10.3390/complexities1010002
Chicago/Turabian StyleMonteiro, Luiz H. A. 2025. "A Simple Overview of Complex Systems and Complexity Measures" Complexities 1, no. 1: 2. https://doi.org/10.3390/complexities1010002
APA StyleMonteiro, L. H. A. (2025). A Simple Overview of Complex Systems and Complexity Measures. Complexities, 1(1), 2. https://doi.org/10.3390/complexities1010002





