Reproducing Kernel Hilbert Space Approach to Multiresponse Smoothing Spline Regression Function

Abstract

In statistical analyses, especially those using a multiresponse regression model approach, a mathematical model that describes a functional relationship between more than one response variables and one or more predictor variables is often involved. The relationship between these variables is expressed by a regression function. In the multiresponse nonparametric regression (MNR) model that is part of the multiresponse regression model, estimating the regression function becomes the main problem, as there is a correlation between the responses such that it is necessary to include a symmetric weight matrix into a penalized weighted least square (PWLS) optimization during the estimation process. This is, of course, very complicated mathematically. In this study, to estimate the regression function of the MNR model, we developed a PWLS optimization method for the MNR model proposed by a previous researcher, and used a reproducing kernel Hilbert space (RKHS) approach based on a smoothing spline to obtain the solution to the developed PWLS optimization. Additionally, we determined the symmetric weight matrix and optimal smoothing parameter, and investigated the consistency of the regression function estimator. We provide an illustration of the effects of the smoothing parameters for the estimation results using simulation data. In the future, the theory generated from this study can be developed within the scope of statistical inference, especially for the purpose of testing hypotheses involving multiresponse nonparametric regression models and multiresponse semiparametric regression models, and can be used to estimate the nonparametric component of a multiresponse semiparametric regression model used to model Indonesian toddlers’ standard growth charts.

1. Introduction

A reproducing kernel Hilbert space (RKHS) theory was first introduced by Aronszajn in 1950 [1]. This theory was later developed by [1,2] to solve optimization problems in regression, especially nonparametric spline original regression. The RKHS approach was used by [3] for an M-type spline estimator. Next, Ref. [4] used the RKHS approach for a relaxed spline estimator.

There are many cases in our daily life that we have to analyze, especially cases involving the functional relationship between different variables. In statistics, to analyze the functional relationship between several variables, namely, the influence of the independent variable or predictor variable on the dependent variable or response variable, regression analysis is used. In regression analysis, it is necessary to build a mathematical model, which is commonly referred to as a regression model, and this functional relationship is expressed by a regression function. In regression analysis, there are two kinds of basic regression model approaches, namely, parametric regression models and nonparametric regression models. In general, the main problem in regression analysis whether using a parametric regression model approach or a nonparametric regression model approach is the problem of estimating the regression function. In the parametric regression model, the problem of estimating the regression function is the same as the problem of estimating the parameters of the parametric regression model where this is different from the nonparametric regression model. In nonparametric regression models, estimating the regression function is equivalent to estimating an unknown smooth function contained in a Sobolev space using smoothing techniques.

There are several frequently used smoothing techniques for estimating nonparametric regression functions, for example, local linear, local polynomial, kernel, and spline. The research results of several previous researchers have shown that smoothing techniques such as local linear, local polynomial, and kernel are highly recommended for estimating nonparametric regression functions for prediction purposes. These researchers include [5,6], who used local linear for predicting hypertension risk and predicting Mycobacterium tuberculosis numbers, respectively; Ref. [7] used local linear for determining boundary correction of nonparametric regression function; Ref. [8] used local linear for determining the bias reduction of a regression function estimate; Ref. [9] used local linear to design a standard growth chart for assessing the nutritional status of toddlers; Refs. [10,11] used local polynomial for estimating regression functions in cases of errors-in-variable and correlated errors, respectively; Refs. [12,13] used local polynomial to estimate the regression function for functional data and for finite population, respectively; Ref. [14] discussed smoothing techniques using kernel; Refs. [15,16] discussed consistency kernel regression estimation and estimating regression functions for cases of correlated errors using kernel, respectively; and Refs. [17,18] discussed estimating covariance matrix and selecting bandwidth using kernel, respectively. However, local linear, local polynomial, and kernel are highly dependent on the bandwidth in the neighborhood of the target point. Thus, if we use these local linear, local polynomial, or kernel approaches to estimate a model with fluctuating data, then we require a small bandwidth, and this results in too rough an estimation of the curve. This means that these local linear, local polynomial, and kernel approaches do not consider smoothness, only the goodness of fit. Therefore, for estimation models with fluctuating data in the sub-intervals, these local linear, local polynomial, and kernel methods are not good to use, as the results of estimation result in a large value of the mean square error (MSE). This is different from spline approaches, which consider goodness of fit and smoothness factors, as discussed by [1,19], who used splines for modeling observational data and estimating nonparametric regression functions. Furthermore, for prediction and interpretation purposes, smoothing techniques such as smoothing spline and truncated spline are better and more flexible for estimating the nonparametric regression functions [20]. Due to the flexible nature of these splines, many researchers have been interested in using and developing them in several cases. For examples, M-type splines were used by [21] to analyze variance for correlated data, and by [22] for estimating both nonparametric and semiparametric regression functions; truncated splines have been discussed by [23] to estimate mean arterial pressure for prediction purpose and by [24] to estimate blood pressure for prediction and interpretation purposes. Additionally, Ref. [25] developed truncated spline for estimating a semiparametric regression model and determining the asymptotic properties of the estimator. Furthermore, Ref. [26] discussed the flexibility of B-spline and penalties in estimating regression function; Ref. [27] discussed analyzing current status data using penalized spline; Ref. [28] analyzed the association between cortisol and ACTH hormones using bivariate spline; and Ref. [29] analyzed censored data using spline regression. In addition, Ref. [30] used both kernel and spline for estimating the regression function and selecting the optimal smoothing parameter of a uniresponse nonparametric regression (UNR) model; Refs. [31,32] developed both kernel and spline for estimating the regression function and for selecting the optimal smoothing parameter of a multiresponse nonparametric regression (MNR) model; and Ref. [33] discussed smoothing techniques, namely, kernel and spline, to estimate the coefficient of a rates model.

In regression modeling, a common problem involves more than one response variable observed at several values of predictor variables and between responses that are correlated with each other. The multiresponse nonparametric regression (MNR) model approach is appropriate for modeling the functions which represent the relationship between the response variable and predictor variable with correlated responses. In this model there is a correlation between the responses. Because of this correlation, it is necessary to construct a matrix called a weight matrix. Constructing the weight matrix is one of the things that distinguishes the MNR model approach from a classical model approach, that is, a parametric regression model or uniresponse nonparametric regression model approach. Thus, in the estimation process the regression function requires a weight matrix in the form of a symmetric matrix, especially a diagonal matrix. Furthermore, in the MNR model there are several smoothing techniques which can be used to estimate the regression function. One of these smoothing techniques is the smoothing spline approach. In recent years, studies on smoothing splines have attracted a great deal of attention and the methodology has been widely used in many areas of research, for example, for estimating regression functions of nonparametric regression models, in [34,35] used smoothing spline, mixed smoothing spline, and Fourier series; estimating regression functions were conducted by [36,37] for a semiparametric nonlinear regression model and a semiparametric regression model; and smoothing spline in an ANOVA model was discussed by [38]. Smoothing spline estimator, with its powerful and flexible properties, is one of the most popular estimators used for estimating regression function of the nonparametric regression model. Although the researchers mentioned above have previously discussed splines for estimating regression functions in many cases, none of them have used a reproducing kernel Hilbert space (RKHS) approach to estimate the regression function of the MNR model. On the other hand, even though there are studies, as mentioned above, that have used the RKHS approach for estimating regression functions, those researchers used the RKHS for estimating regression functions of single–response or uniresponse linear regression models only. This means that RKHS approaches were not used for estimating the regression function of the MNR model based on a smoothing spline estimator. In addition, although [34] used the RKHS approach to estimate the regression function of the MNR model, and also discussed it in a special case involving a simulation study; but Ref. [34] assumed that the three responses of the MNR model have the same smoothing parameter values, which in real life situation is a difficult assumption to fulfill. In addition, Ref. [34] did not discuss the consistency of the smoothing spline regression function estimator. Therefore, in this study we provide a theoretical discussion on estimating the smoothing spline regression function of the MNR model in case of unequal values of the smoothing parameters using the RKHS approach. In other words, in this study we discuss it for the more general case.

2. Materials and Methods

In this section, we briefly describe the materials and methods used according to the needs of this study, following the steps in the order in which they were carried out.

2.1. Multiresponse Nonparametric Regression Model

Suppose, given a paired observation $\left\{y_{ri},t_{ri}\right\}$ which satisfies the following multiresponse nonparametric regression (MNR) model:

$$y_{ri}=f_r\left(t_{ri}\right)+{\epsilon }_{ri},i=1,2,\dots ,n_r,r=1,2,\dots ,p$$

(1)

where $y_{ri}$ is the observation value of the response variable on the $r^{th}$ response and the $i^{th}$ observation; $f_r\left(·\right)$ represents an unknown nonparametric regression function of $r^{th}$ response which is assumed to be smooth in the sense that it is contained in a Sobolev space; $t_{ri}$ is the observation value of a predictor variable on the $r^{th}$ response and the $i^{th}$ observation; and ${\epsilon }_{ri}$ represents the value of the random error on the $r^{th}$ response and the $i^{th}$ observation, which is assumed to have zero mean and variance ${\sigma }_{ri}^2$ (heteroscedastic). In this study, we assume that the correlation between responses is ${\rho }_{rs}=\left\{\begin{array}{lll}{\rho }_r& for& r=s\\ 0& for& r\ne s\end{array}\right.$.

In general, the main problem in MNR modelling is how we estimate the MNR model, which in this case is equivalent to the problem of estimating the regression function of the MNR model. There are many smoothing techniques that can be used to estimate the MNR model presented in (1), for example, kernel, local linear, splines, and local polynomial. One of these smoothing techniques is the spline approach, in which the smoothing spline is the most flexible estimator for estimating fluctuating data on sub-intervals. The following briefly presents the estimation method using the smoothing spline estimator. Further details related to the smoothing spline estimator can be found in [20].

2.2. Smoothing Spline Estimator

In this study, we estimated the regression function, $f_r\left(t_{ri}\right)$ of the MNR model presented in (1) based on the smoothing spline estimator using the reproducing kernel Hilbert space approach, which is discussed in the following section. An estimate of the regression function of the MNR model presented in (1) can be obtained by developing the penalized weighted least squares (PWLS) optimization method proposed by [31], which is only used for the two-response nonparametric regression model with the same variance of errors, namely, the homoscedastic case. We then develop the PWLS optimization to estimate a nonparametric regression model with more than two responses, namely, the MNR model, in case of unequal variance of errors, which is called as heteroscedastic case. Hence, the estimated smoothing spline of the MNR model presented in (1) can be obtained by carrying out the following PWLS optimization:

$$\begin{array}{c}\underset{f_1,\dots ,f_p\in W_2^m\left[a_r,b_r\right]}{\min }\{N^{-1}{\left(y_{\mathbf{1}}-f_{\mathbf{1}}\right)}^T{W}_1\left(y_{\mathbf{1}}-f_{\mathbf{1}}\right)+\dots +{\left(y_{\mathit{p}}-f_{\mathit{p}}\right)}^T{W}_p\left(y_{\mathit{p}}-f_{\mathit{p}}\right)+\\ {\lambda }_1{{\displaystyle \int }}_{a_1}^{b_1}{\left(f_1^{\left(2\right)}\left(t\right)\right)}^{2}dt+\dots +{\lambda }_p{{\displaystyle \int }}_{a_p}^{b_p}{\left(f_p^{\left(2\right)}\left(t\right)\right)}^{2}dt\}\end{array}$$

(2)

where $N={{\displaystyle \sum }}_{r=1}^p{n}_r$; $W_{\mathbf{1}},\dots ,W_{\mathit{p}}$ are symmetric weight matrices, ${\lambda }_1,\dots ,{\lambda }_p$ are smoothing parameters, and $f_{\mathbf{1}},f_{\mathbf{2}},\dots ,f_p$ are unknown regression functions in a Sobolev space $W_2^m\left[a_r,b_r\right]$, where the Sobolev space $W_2^m\left[a_r,b_r\right]$ is defined as follows:

$$\begin{array}{c}{W}_2^m\left[a_r,b_r\right]=\left\{f\right|f^{\left(v\right)},v=0,1,2,\dots ,m-1\mathrm{are}\mathrm{absolutely}\mathrm{continuous}\mathrm{on}\left[a_r,b_r\right]\mathrm{and}\\ f^{\left(m\right)}\in L_2\left[a_r,b_r\right],\mathrm{where}{L}_2\left[a_r,b_r\right]\mathrm{is}\mathrm{the}\mathrm{collection}\mathrm{of}\mathrm{square}\mathrm{integrable}\mathrm{function}\mathrm{on}\\ L_2\left[a_r,b_r\right],r=1,2,\dots ,p\}\end{array}$$

Furthermore, to obtain the solution to the PWLS provided in (2), we used the reproducing kernel Hilbert space (RKHS) approach. In the following section, we provide a brief review of RKHS. Further details related to RKHS can be found in [39], a paper concerning the theory of RKHS, and in [40], a textbook which discusses the use of RKHS in probability and statistics.

2.3. Reproducing Kernel Hilbert Space

The need to reproducing kernel Hilbert space (RKHS) arises in various fields, including statistics, theory of approximation, theory of machine learning, theory of group representation, and complex analysis. In statistics, the RKHS method is often used as a method for estimating a regression function based on the smoothing spline estimator for prediction purposes. In machine learning, the RKHS method is arguably the most popular approach for dealing with nonlinearity in data. Several researchers have discussed the RKHS method; for example, Refs. [41,42] discussed the use of RKHS in Support Vector Machines (SVM) and optimization problems, respectively, and Refs. [43,44] discussed the use of RKHS in asymptotic distribution for regression and machine learning.

A Hilbert space $\mathcal{H}$ is called an RKHS on a set X over field F if the following conditions are met [1,39]:

(i)

$\mathcal{H}$ is a vector subspace of $\mathcal{F}$(X, $\mathbb{F}$), where $\mathcal{F}$(X, $\mathbb{F}$) is a vector space over $\mathbb{F}$;

(ii)

$\mathcal{H}$ is endowed with an inner product $〈,〉$, making it into a Hilbert space;

(iii)

the linear evaluation functional $E_y:\mathcal{H}\to \mathbb{F}$, defined by $E_y\left(f\right)=f\left(y\right)$, is bounded, for every $y\in$ X.

Furthermore, if $\mathcal{H}$ is an RKHS on X, then for every $y\in$ X there exists a unique vector $k_y\in \mathcal{H}$ such that for every $f\in \mathcal{H}$, $f\left(y\right)=\langle f,k_y\rangle$. This is because every bounded linear functional is provided by the inner product with a unique vector in $\mathcal{H}$. The function $k_y$ is called a reproducing kernel (RK) for point $y$. The reproducing kernel (RK) for $\mathcal{H}$ is a two–variable function defined by $K\left(x,y\right)=k_y\left(x\right)$. Hence, we have $K\left(x,y\right)=k_y\left(x\right)=\langle k_y,k_x\rangle$ and $\Vert E_y\Vert {}^2=\Vert k_y\Vert {}^2=\langle k_y,k_y\rangle =K\left(y,y\right)$.

In this study, we provide a simulation study to evaluate the performance of the proposed MNR model estimation method.

2.4. Simulation

The simulation in this study consists of a simulation to determine the optimal smoothing spline based on a generalized cross-validation (GCV) criterion to obtain the best estimated MNR model and a simulation to describe the effect of the smoothing parameters on the estimation results of the regression function of the MNR model based on minimal GCV value. We generate samples sized $n=100$ from the MNR model and provide an illustration of the effects of the smoothing parameters in order to estimate the results of the MNR model by comparing three kinds of different smoothing parameter values, namely, small, optimal, and large smoothing parameters values.

In the following section, we provide the results and discussion of this study covering estimation of the regression function of the MNR model using the RKHS approach by estimating the symmetric weight matrix and optimal smoothing parameters, a simulation study, and investigating the consistency of the smoothing spline regression function estimator.

3. Results and Discussions

The results and discussion presented in this section include estimating the regression function of the MNR model using RKHS, estimating the weight matrix, estimating the optimal smoothing parameter, investigating the consistency of the regression function estimator, a simulation study, and an application example using real data.

3.1. Estimating the Regression Function of the MNR Model Using the RKHS Approach

The MNR model presented in (1) can be expressed in matrix notation as follows:

$$y=f+\mathbf{\epsilon }$$

(3)

where $y={\left(y_{\mathbf{1}},y_{\mathbf{2}},\dots ,y_{\mathit{p}}\right)}^{\mathrm{T}}$,$f={\left(f_{\mathbf{1}},f_{\mathbf{2}},\dots ,f_{\mathit{p}}\right)}^{\mathrm{T}}$, $t={\left(t_{\mathbf{1}},t_{\mathbf{2}},\dots ,t_{\mathit{p}}\right)}^{\mathit{T}}$, $\mathsf{\epsilon }={\left({\mathsf{\epsilon }}_{\mathbf{1}},{\mathsf{\epsilon }}_{\mathbf{2}},\dots ,{\mathsf{\epsilon }}_{\mathit{p}}\right)}^{\mathrm{T}},y_{\mathit{r}}={\left(y_{r1},y_{r2},\dots ,y_{r{n}_r}\right)}^{\mathrm{T}},$ $f_{\mathit{r}}={\left(f_r\left(t_{r1}\right),f_r\left(t_{r2}\right),\dots ,f_r\left(t_{r{n}_r}\right)\right)}^{\mathrm{T}}$, $t_r={\left(t_{r1},t_{r2},\dots ,t_{r{n}_r}\right)}^T$, and ${\mathbf{\epsilon }}_{\mathit{r}}={\left({\epsilon }_{r1},{\epsilon }_{r2},\dots ,{\epsilon }_{r{n}_r}\right)}^{\mathrm{T}}$.

We assume that $\mathsf{\epsilon }$ is a zero mean random error with covariance $W^{-1}$. In this case, the covariance matrix $W^{-1}$ is a symmetrical matrix, that is, it is a diagonal matrix which can be expressed as follows:

$$W^{-1}=diag\left(W_{\mathbf{1}}^{-1},W_{\mathbf{2}}^{-1},\dots ,W_p^{-1}\right)$$

(4)

where $W_r^{\mathbf{-}\mathbf{1}}$ is an $r^{th}$-response covariance matrix of ${\mathsf{\epsilon }}_{\mathit{r}}$ for $r=1,2,\dots ,p$.

To determine the regression function of the MNR model (1) using the RKHS approach, we first express the MNR model in a general smoothing spline regression model [20]. Therefore, we can express the MNR model (1) as follows:

$$y_{ri}={\mathcal{L}}_{t_r}{f}_r+{\epsilon }_{r_i};i=1,2,\dots ,n_r;r=1,2,\dots ,p$$

(5)

where $f_r\in {\mathcal{H}}_r$ is an unknown smooth function, ${\mathcal{L}}_{t_r}\in {\mathcal{H}}_r$ is a bounded linear functional, and ${\mathcal{H}}_r$ is a Hilbert space.

Next, the Hilbert space ${\mathcal{H}}_r$ is decomposed into a direct sum of the Hilbert subspace $G_r$ and Hilbert sub space $K_r$, where $G_r$ has basis $\left\{{\alpha }_{r1},{\alpha }_{r2},\dots ,{\alpha }_{r{m}_r}\right\}$, $K_r$ has basis $\left\{{\beta }_{r1},{\beta }_{r2},\dots ,{\beta }_{r{n}_r}\right\}$, and $G_r{K}_r$ is as follows:

$${\mathcal{F}}_r=G_r\oplus K_r.$$

(6)

This implies that for $g_r\in G_r$, $z_r\in K_r$, and $r=1,2,\dots ,p$ we can express every function $f_r\in {\mathcal{F}}_r$ as follows:

$$f_r=g_r+z_r.$$

(7)

Because $\left\{{\alpha }_{r1},{\alpha }_{r2},\dots ,{\alpha }_{r{m}_r}\right\}$ is the basis of the Hilbert subspace $G_r$ and $\left\{{\beta }_{r1},{\beta }_{r2},\dots ,{\beta }_{r{n}_r}\right\}$ is the basis of the Hilbert subspace $K_r$, the function $f_r$ in (7) can be expressed as follows:

$$f_r={{\displaystyle \sum }}_{i=1}^{m_r}{b}_{ri}{\alpha }_{ri}+{{\displaystyle \sum }}_{j=1}^{n_r}{c}_{rj}{\beta }_{rj}={\alpha }_r^T{b}_r+{\mathsf{\beta }}_r^T{c}_r$$

(8)

where $r=1,2,\dots ,p$; $b_{ri},c_{rj}\in ℝ$; ${\alpha }_r={\left({\alpha }_{r1},{\alpha }_{r2},\dots ,{\alpha }_{r{m}_r}\right)}^T$; $b_r={\left(b_{r1},b_{r2},\dots ,b_{r{m}_r}\right)}^T$; ${\mathsf{\beta }}_r={\left({\beta }_{r1},{\beta }_{r2},\dots ,{\beta }_{r{n}_r}\right)}^T$; and $c_r={\left(c_{r1},c_{r2},\dots ,c_{r{n}_r}\right)}^T$.

Hence, for $r=1,2,\dots ,p$ and $i=1,2,\dots ,n_r$, we have

$$\begin{array}{cc}\hfill {\mathcal{L}}_{t_{ri}}{f}_r={\mathcal{L}}_{t_{ri}}\left(g_r+z_r\right)& ={\mathcal{L}}_{t_{ri}}\left(g_r\right)+{\mathcal{L}}_{t_{ri}}\left(z_r\right)\hfill \\ & =g_r\left(t_{ri}\right)+z_r\left(t_{ri}\right)\hfill \\ & =f_r\left(t_{ri}\right).\hfill \end{array}$$

Because ${\mathcal{L}}_{t_r}\in {\mathcal{F}}_r$ is a bounded linear functional in the Hilbert space ${\mathcal{F}}_r$, according to [20] there exists a Riesz representer ${\delta }_{ri}\in {\mathcal{F}}_r$ such that

$${\mathcal{L}}_{t_{ri}}{f}_r=\langle {\delta }_{ri},f_r\rangle =f_r\left(t_{ri}\right)$$

(9)

where $f_r\in {\mathcal{F}}_r$ and $\langle ·,·\rangle$ denote an inner product. Next, by considering Equations (8) and (9) and applying the properties of the inner product, the function $f_r\left(t_{ri}\right)$ can be written as follows:

$$\begin{array}{c}{f}_r\left(t_{ri}\right)=\langle {\delta }_{ri},{\alpha }_r^T{b}_r+{\mathsf{\beta }}_r^T{c}_r\rangle \\ =\langle {\delta }_{ri},{\alpha }_r^T{b}_r\rangle +\langle {\delta }_{ri},{\mathsf{\beta }}_r^T{c}_r\rangle \end{array}$$

(10)

Then, based on Equation (10), we can obtain the regression functions $f_r\left(t_{ri}\right)$ for $r=1,2,\dots ,p$, which are the regresion functions for the first response, the second response, …, and the p^th response, as follows:

$$\left.\begin{array}{ccc}\mathrm{For}r=1,\hfill & \mathrm{we}\mathrm{have}:f_1\left(t_{1i}\right)=\langle {\delta }_{1i},{\alpha }_1^T{b}_1\rangle +\langle {\delta }_{1i},{\mathsf{\beta }}_1^T{c}_1\rangle ,\hfill & i=1,2,\dots ,n_1\hfill \\ \mathrm{For}r=2,\hfill & \mathrm{we}\mathrm{have}:f_2\left(t_{2i}\right)=\langle {\delta }_{2i},{\alpha }_2^T{b}_2\rangle +\langle {\delta }_{2i},{\mathsf{\beta }}_2^T{c}_2\rangle ,\hfill & i=1,2,\dots ,n_2\hfill \\ & ⋮& \\ \mathrm{For}r=p,\hfill & \mathrm{we}\mathrm{have}:f_p\left(t_{pi}\right)=\langle {\delta }_{pi},{\alpha }_p^T{b}_p\rangle +\langle {\delta }_{pi},{\mathsf{\beta }}_p^T{c}_p\rangle ,\hfill & i=1,2,\dots ,n_p\hfill \end{array}\right\}$$

(11)

Hence, following Equation (11), we obtain the regression function for $i=1$ as follows:

$$f_{\mathbf{1}}\left(t_1\right)={\left(f_1\left(t_{11}\right),f_1\left(t_{12}\right),\dots ,f_1\left(t_{1n_1}\right)\right)}^T=A_{\mathbf{1}}{b}_{\mathbf{1}}+C_{\mathbf{1}}{d}_{\mathbf{1}}$$

(12)

where $b_{\mathbf{1}}={\left(b_{11},b_{12},\dots ,b_{1m_1}\right)}^T$; $d_{\mathbf{1}}={\left(d_{11},d_{12},\dots ,d_{1n_1}\right)}^T$; $A_{\mathbf{1}}=\left(\begin{array}{cc}〈{\delta }_{11},{\alpha }_{11}〉& 〈{\delta }_{11},{\alpha }_{12}〉\cdots & 〈{\delta }_{11},{\alpha }_{1m_1}〉\\ 〈{\delta }_{12},{\alpha }_{11}〉〈{\delta }_{12},{\alpha }_{12}〉\cdots & 〈{\delta }_{12},{\alpha }_{1m_1}〉\\ ⋮& ⋮& \ddots & ⋮\\ 〈{\delta }_{1n_1},{\alpha }_{11}〉〈{\delta }_{1n_1},{\alpha }_{12}〉\cdots & 〈{\delta }_{1n_1},{\alpha }_{1m_1}〉\end{array}\right)$; and $C_{\mathbf{1}}=\left(\begin{array}{c}〈{\delta }_{11},{\beta }_{11}〉〈{\delta }_{11},{\beta }_{12}〉\cdots & 〈{\delta }_{11},{\beta }_{1n_1}〉\\ 〈{\delta }_{12},{\beta }_{11}〉〈{\delta }_{12},{\beta }_{12}〉\cdots & 〈{\delta }_{12},{\beta }_{1n_1}〉\\ ⋮& ⋮& \ddots & ⋮\\ 〈{\delta }_{1n_1},{\beta }_{11}〉〈{\delta }_{1n_1},{\beta }_{12}〉\cdots & 〈{\delta }_{1n_1},{\beta }_{1n_1}〉\end{array}\right)$.

Similarly, we obtain the regression functions for $i=2,\dots ,n_1$, which are $f_{\mathbf{2}}\left(t_2\right)$, $f_{\mathbf{3}}\left(t_3\right)$, …, $f_{\mathit{p}}\left(t_p\right)$, as follows:

$$\left.\begin{array}{c}{f}_{\mathbf{2}}\left(t_2\right)={\left(f_2\left(t_{11}\right),f_2\left(t_{12}\right),\dots ,f_2\left(t_{1n_2}\right)\right)}^T=A_{\mathbf{2}}{b}_{\mathbf{2}}+C_{\mathbf{2}}{d}_{\mathbf{2}}\\ f_{\mathbf{3}}\left(t_3\right)={\left(f_3\left(t_{11}\right), f_3\left(t_{12}\right),\dots ,f_3\left(t_{1n_3}\right)\right)}^T=A_{\mathbf{3}}{b}_{\mathbf{3}}+C_{\mathbf{3}}{d}_{\mathbf{3}}\\ ⋮\\ f_{\mathit{p}}\left(t_p\right)={\left(f_p\left(t_{11}\right), f_p\left(t_{12}\right),\dots ,f_p\left(t_{1n_p}\right)\right)}^T=A_{\mathit{p}}{b}_{\mathit{p}}+C_{\mathit{p}}{d}_{\mathit{p}}\end{array}\right\}$$

(13)

Hence, based on Equations (12) and (13), we obtain the regression function $f\left(\mathrm{t}\right)$ of the MNR model as follows:

$$\begin{array}{c}f\left(t\right)={\left(f_{\mathbf{1}}\left(t_1\right),f_{\mathbf{2}}\left(t_2\right),\dots ,f_{\mathit{p}}\left(t_p\right)\right)}^T={\left({\mathbf{A}}_{\mathbf{1}}{b}_{\mathbf{1}},A_{\mathbf{2}}{b}_{\mathbf{2}},\dots ,A_{\mathit{p}}{b}_{\mathit{p}}\right)}^T+{\left(C_{\mathbf{1}}{d}_{\mathbf{1}},C_{\mathbf{2}}{d}_{\mathbf{2}},\dots ,C_{\mathit{p}}{d}_{\mathit{p}}\right)}^T\\ =diag\left(\left(A_{\mathbf{1}},A_{\mathbf{2}},\dots ,A_{\mathit{p}}\right){\left(b_{\mathbf{1}},b_{\mathbf{2}},\dots ,b_{\mathit{p}}\right)}^T\right)+\\ diag\left(\left(C_{\mathbf{1}},C_{\mathbf{2}},\dots ,C_{\mathit{p}}\right){\left(d_{\mathbf{1}},d_{\mathbf{2}},\dots ,d_{\mathit{p}}\right)}^T\right)=Ab+Cd\end{array}$$

(14)

Thus, we can express the MNR model presented in (1) in matrix notation as follows:

$$y=Ab+Cd+\mathsf{\epsilon }$$

(15)

where $A=diag\left(A_{\mathbf{1}},A_{\mathbf{2}},\dots ,A_p\right)$ is an $\left(N\times M\right)$ diagonal matrix with $N={\displaystyle \sum }_{r=1}^p{n}_r$, $M={\displaystyle \sum }_{r=1}^p{m}_r$; $b={\left(b_{\mathbf{1}}^T,b_{\mathbf{2}}^T,\dots ,b_p^T\right)}^T$ is an $\left(M\times 1\right)$ vector of parameters; $C=diag\left(C_{\mathbf{1}},C_{\mathbf{2}},\dots ,C_p\right)$ is an $\left(N\times N\right)$ diagonal matrix; and $d={\left(d_{\mathbf{1}}^T,d_{\mathbf{2}}^T,\dots ,d_p^T\right)}^T$ is an $\left(N\times 1\right)$ vector of parameters.

Now, we can determine an estimated smoothing spline regression function of the MNR model presented in (1) using the RKHS approach by taking the solution of the following optimization:

$$\underset{\begin{array}{c}{f}_r\in {\mathcal{F}}_r\\ r=1,2,\dots ,p\end{array}}{\mathrm{Min}}\{\Vert W^{\frac{1}{2}}\mathsf{\epsilon }\Vert {}^2\}=\underset{\begin{array}{c}{f}_r\in {\mathcal{F}}_r\\ r=1,2,\dots ,p\end{array}}{\mathrm{Min}}\{\Vert W^{\frac{1}{2}}\left(y-f\right)\Vert {}^2\}$$

(16)

with a constraint ${{\displaystyle \int }}_{a_r}^{b_r}{\left(f_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r<{\gamma }_r$, where ${\gamma }_r\ge 0$ and $r=1,2,\dots ,p$.

Note that determining the solution to Equation (16) is equivalent to determining the solution to the following PWLS optimization:

$$\underset{\begin{array}{c}{f}_r\in W_2^m\left[a_r,b_r\right]\\ r=1,2,\dots ,p\end{array}}{\mathrm{Min}}\left\{N^{-1}{\left(y-f\right)}^{T}W\left(y-f\right)+{{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(f_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r\right\}$$

(17)

where $N={{\displaystyle \sum }}_{r=1}^p{n}_r$;$N^{-1}{\left(y-f\right)}^{T}W\left(y-f\right)$ is a weighted least square that represents the goodness of fit, ${{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(f_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r$ represents a penalty that measures smoothness, and ${\lambda }_r,r=1,2,\dots ,p$ represents a smoothing parameter which controls the trade-off between the goodness of fit and the penalty.

Next, we decompose the penalty presented in (17) as follows:

$${{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(f_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r={\lambda }_1{{\displaystyle \int }}_{a_1}^{b_1}{\left(f_1^{\left(m\right)}\left(t_1\right)\right)}^{2}d{t}_1+\dots +{\lambda }_p{{\displaystyle \int }}_{a_p}^{b_p}{\left(f_p^{\left(m\right)}\left(t_p\right)\right)}^{2}d{t}_p$$

(18)

Because we have $\left\{\begin{array}{c}{{\displaystyle \int }}_{a_1}^{b_1}{\left(f_1^{\left(m\right)}\left(t_1\right)\right)}^{2}d{t}_1=\langle {\mathsf{\beta }}_{\mathbf{1}}^T{d}_{\mathbf{1}},{\mathsf{\beta }}_{\mathbf{1}}^T{d}_{\mathbf{1}}\rangle =d_{\mathbf{1}}^T\langle {\mathsf{\beta }}_{\mathbf{1}},{\mathsf{\beta }}_{\mathbf{1}}^T\rangle d_{\mathbf{1}}=d_{\mathbf{1}}^{\mathrm{T}}{C}_{\mathbf{1}}{d}_{\mathbf{1}}\\ {{\displaystyle \int }}_{a_2}^{b_2}{\left(f_2^{\left(m\right)}\left(t_2\right)\right)}^{2}d{t}_2=\langle {\mathsf{\beta }}_{\mathbf{2}}^T{d}_{\mathbf{2}},{\mathsf{\beta }}_{\mathbf{2}}^T{d}_{\mathbf{2}}\rangle =d_{\mathbf{2}}^T\langle {\mathsf{\beta }}_{\mathbf{2}},{\mathsf{\beta }}_{\mathbf{2}}^T\rangle d_{\mathbf{2}}=d_{\mathbf{2}}^{\mathrm{T}}{C}_{\mathbf{2}}{d}_{\mathbf{2}}\\ {{\displaystyle \int }}_{a_p}^{b_p}{\left(f_p^{\left(m\right)}\left(t_p\right)\right)}^{2}d{t}_p=\langle {\mathsf{\beta }}_{\mathit{p}}^T{d}_{\mathit{p}},{\mathsf{\beta }}_{\mathit{p}}^T{d}_{\mathit{p}}\rangle =d_p^T\langle {\mathsf{\beta }}_p,{\mathsf{\beta }}_{\mathit{p}}^T\rangle d_p=d_{\mathit{p}}^{\mathrm{T}}{C}_{\mathit{p}}{d}_p\end{array}\right.$ we are able to obtain the penalty presented in (17) or (18) as follows:

$${{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(f_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r=d^T\mathbf{Ʌ}Cd$$

(19)

where $\mathbf{Ʌ}=diag\left({\lambda }_1{I}_{n_1},{\lambda }_2{I}_{n_2},\dots ,{\lambda }_p{I}_{n_p}\right)$. Furthermore, we can write the goodness of fit component in (17) as follows:

$$N^{-1}{\left(y-f\right)}^{T}W\left(y-f\right)=N^{-1}{\left(y-Ab-Cd\right)}^{T}W\left(y-Ab-Cd\right)$$

(20)

Based on Equations (19) and (20), we can express the PWLS optimization presented in (17) as follows:

$$\begin{array}{c}\underset{b\in {ℝ}^{\mathit{p}\mathit{n}},d\in {ℝ}^{pm}}{\mathrm{Min}}\left\{Q\left(b,d\right)\right\}=\underset{b\in {ℝ}^{\mathit{p}\mathit{n}},d\in {ℝ}^{pm}}{\mathrm{Min}}\{N^{-1}{\left(y-Ab-Cd\right)}^T\times \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}W\left(y-Ab-Cd\right)+d^T\mathbf{Ʌ}Cd\}\end{array}$$

(21)

The solution to (21) can be obtained by taking the partial diferentiation $Q\left(b,d\right)$ with respect to $b$ and $d$. In this step, we obtain the estimations of $b$ and $d$ as follows:

$$\widehat{b}={\left(A^T{D}^{-\mathbf{1}}WA\right)}^{-\mathbf{1}}{A}^T{D}^{-\mathbf{1}}Wy,\mathrm{and}\widehat{d}=D^{-\mathbf{1}}W\left[I-A{\left(A^T{D}^{-\mathbf{1}}WA\right)}^{-\mathbf{1}}{A}^T{D}^{-\mathbf{1}}W\right]y$$

where $D=WC+\mathrm{N}\mathrm{Ʌ}I$.

From this step, we obtain the estimation of the smoothing spline regression function of the MNR model presented in (1) or (15) as follows:

$$\widehat{f}=A\widehat{b}+C\widehat{d}=Hy$$

(22)

where $H=A{\left(A^T{D}^{-\mathbf{1}}WA\right)}^{-\mathbf{1}}{A}^T{D}^{-\mathbf{1}}W+C{D}^{-\mathbf{1}}W\left(I-A{\left(A^T{D}^{-\mathbf{1}}WA\right)}^{-\mathbf{1}}{A}^T{D}^{-\mathbf{1}}W\right)$, $D=WC+\mathrm{N}\mathrm{Ʌ}I$, $\mathbf{Ʌ}=diag\left({\lambda }_1{I}_{n_1},{\lambda }_2{I}_{n_2},\dots ,{\lambda }_p{I}_{n_p}\right)$, $I$ is an identity matrix with dimension $N$, and $N={\displaystyle \sum }_{r=1}^p{n}_r$.

3.2. Estimating the Symmetric Weight Matrix

Based on MNR model presented in (3), the $W^{-\mathbf{1}}$ from Equation (4) is a covariance matrix of the random error $\mathsf{\epsilon }$. To obtain the estimated weight matrix $\widehat{W}$, where the weight matrix $W$ is the inverse of the covariance matrix, we first we consider a paired observation $\left\{y_{ri},t_{ri}\right\}$, $r=1,2,\dots ,p$; $i=1,2,\dots ,n_r$ which follows the MNR model presented in (3). Second, supposing that $y={\left(y_{\mathbf{1}},y_{\mathbf{2}},\dots ,y_{\mathit{p}}\right)}^T$ is a multivariate (i.e., N-variates where $N={\displaystyle \sum }_{r=1}^p{n}_r$) normally distributed random sample with mean $f$ and covariance $W^{-\mathbf{1}}$, we have the following likelihood function:

$$L\left(f,W|y\right)={{\displaystyle \prod }}_{j=1}^n\left\{\frac{1}{{\left(2\pi \right)}^{\frac{N}{2}}{\left(W^{-1}\right)}^{\frac{1}{2}}}\exp \left(-\frac{1}{2}{\left(y_j-f_j\right)}^{T}W\left(y_j-f_j\right)\right)\right\}$$

(23)

Because $N={{\displaystyle \sum }}_{r=1}^p{n}_r$ and $W=diag\left(W_{\mathbf{1}},W_{\mathbf{2}},\dots ,W_p\right)$, the likelihood function presented in (23) can be written as follows:

$$\begin{array}{cc}\hfill L\left(f,W|y\right)=& \frac{1}{{\left(2\pi \right)}^{\frac{n{n}_1}{2}}{\left(W_1^{-1}\right)}^{\frac{n}{2}}}\mathit{exp}\left(-\frac{1}{2}{\displaystyle \sum }_{j=1}^n{\left(y_{\mathbf{1}\mathit{j}}-f_{\mathbf{1}j}\right)}^T{W}_{\mathbf{1}}\left(y_{\mathbf{1}\mathit{j}}-f_{\mathbf{1}j}\right)\right)\times \hfill \\ & \frac{1}{{\left(2\pi \right)}^{\frac{n{n}_2}{2}}{\left(W_2^{-1}\right)}^{\frac{n}{2}}}\mathit{exp}\left(-\frac{1}{2}{\displaystyle \sum }_{j=1}^n{\left(y_{\mathbf{2}\mathit{j}}-f_{\mathbf{2}j}\right)}^T{W}_{\mathbf{2}}\left(y_{\mathbf{2}\mathit{j}}-f_{\mathbf{2}j}\right)\right)\times \dots \times \hfill \\ & \frac{1}{{\left(2\pi \right)}^{\frac{n{n}_p}{2}}{\left(W_p^{-1}\right)}^{\frac{n}{2}}}\exp \left(-\frac{1}{2}{\displaystyle \sum }_{j=1}^n{\left(y_{\mathit{p}\mathit{j}}-f_{pj}\right)}^T{W}_p\left(y_{\mathit{p}\mathit{j}}-f_{pj}\right)\right)\hfill \end{array}$$

(24)

Next, based on (24), the estimated weight matrix can be obtained by carrying out the following optimization:

$$\begin{array}{cc}\hfill L\left(f,W|y\right)=& \underset{W_{\mathbf{1}}}{\mathrm{Max}}\left\{\frac{1}{{\left(2\pi \right)}^{\frac{n{n}_1}{2}}{\left(W_1^{-1}\right)}^{\frac{n}{2}}}\mathit{exp}\left(-\frac{1}{2}{\displaystyle \sum }_{j=1}^n{\left(y_{\mathbf{1}\mathit{j}}-f_{\mathbf{1}j}\right)}^T{W}_{\mathbf{1}},\dots \left(y_{\mathbf{1}\mathit{j}}-f_{\mathbf{1}j}\right)\right)\right\}\times \hfill \\ & \underset{W_{\mathbf{2}}}{\mathrm{Max}}\left\{\frac{1}{{\left(2\pi \right)}^{\frac{n{n}_2}{2}}{\left(W_2^{-1}\right)}^{\frac{n}{2}}}\mathit{exp}\left(-\frac{1}{2}{\displaystyle \sum }_{j=1}^n{\left(y_{\mathbf{2}\mathit{j}}-f_{\mathbf{2}j}\right)}^T{W}_{\mathbf{2}},\dots \left(y_{\mathbf{2}\mathit{j}}-f_{\mathbf{2}j}\right)\right)\right\}\times \cdots \times \hfill \\ & \underset{W_p}{\mathrm{Max}}\left\{\frac{1}{{\left(2\pi \right)}^{\frac{n{n}_p}{2}}{\left(W_p^{-1}\right)}^{\frac{n}{2}}}\mathit{exp}\left(-\frac{1}{2}{\displaystyle \sum }_{j=1}^n{\left(y_{\mathit{p}\mathit{j}}-f_{pj}\right)}^T{W}_p\left(y_{\mathit{p}\mathit{j}}-f_{pj}\right)\right)\right\}\hfill \end{array}$$

(25)

According to [45], the maximum value of each component of the likelihood function in Equation (25) can be determined using the following equations:

$${\widehat{W}}_{\mathbf{1}}=\frac{{\hat{\mathsf{\epsilon }}}_{\mathbf{1}}{\hat{\mathsf{\epsilon }}}_{\mathbf{1}}^T}{N}=\frac{\left(y_{\mathbf{1}}-{\widehat{f}}_{\mathbf{1}}\right){\left(y_{\mathbf{1}}-{\widehat{f}}_{\mathbf{1}}\right)}^T}{N},{\widehat{W}}_{\mathbf{2}}=\frac{{\hat{\mathsf{\epsilon }}}_{\mathbf{2}}{\hat{\mathsf{\epsilon }}}_{\mathbf{2}}^T}{N}=\frac{\left(y_{\mathbf{2}}-{\widehat{f}}_{\mathbf{2}}\right){\left(y_{\mathbf{2}}-{\widehat{f}}_{\mathbf{2}}\right)}^T}{N},\dots ,{\widehat{W}}_{\mathit{p}}=\frac{{\hat{\mathsf{\epsilon }}}_p{\hat{\mathsf{\epsilon }}}_p^T}{N}=\frac{\left(y_p-{\widehat{f}}_p\right){\left(y_p-{\widehat{f}}_p\right)}^T}{N}.$$

We may express the estimated smoothing spline regression function presented in (22) as follows:

$$\widehat{f}\left(\mathbf{\lambda },{\mathsf{\sigma }}^{\mathbf{2}}\right)=H\left(\mathbf{\lambda },{\mathsf{\sigma }}^{\mathbf{2}}\right)y$$

(26)

where $\mathbf{\lambda }={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p\right)}^T$, and ${\mathsf{\sigma }}^{\mathbf{2}}={\left({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_p^2\right)}^T$.

Hence, the maximum likelihood estimator for the weight matrix $W$ is provided by:

$$\begin{array}{cc}\hfill \widehat{W}& =diag\left({\widehat{W}}_{\mathbf{1}},{\widehat{W}}_{\mathbf{2}},\dots ,{\widehat{W}}_p\right)=diag\left(\frac{\left(y_{\mathbf{1}}-{\widehat{f}}_{\mathbf{1}}\right){\left(y_{\mathbf{1}}-{\widehat{f}}_{\mathbf{1}}\right)}^T}{N},\frac{\left(y_{\mathbf{2}}-{\widehat{f}}_{\mathbf{2}}\right){\left(y_{\mathbf{2}}-{\widehat{f}}_{\mathbf{2}}\right)}^T}{N},\dots ,\frac{\left(y_p-{\widehat{f}}_p\right){\left(y_p-{\widehat{f}}_p\right)}^T}{N}\right)\hfill \\ & =diag\left(\frac{\left(I_{{\mathit{n}}_{\mathbf{1}}}-H\left({\mathbf{\lambda }}_{\mathbf{1}},{\mathbf{\sigma }}_{\mathbf{1}}^{\mathbf{2}}\right)\right)y_{\mathbf{1}}{y}_{\mathbf{1}}^T{\left(I_{{\mathit{n}}_{\mathbf{1}}}-H\left({\mathbf{\lambda }}_{\mathbf{1}},{\mathbf{\sigma }}_{\mathbf{1}}^{\mathbf{2}}\right)\right)}^T}{N},\frac{\left(I_{{\mathit{n}}_{\mathbf{1}}}-H\left({\mathbf{\lambda }}_{\mathbf{1}},{\mathbf{\sigma }}_{\mathbf{1}}^{\mathbf{2}}\right)\right)y_{\mathbf{1}}{y}_{\mathbf{1}}^T{\left(I_{{\mathit{n}}_{\mathbf{1}}}-H\left({\mathbf{\lambda }}_{\mathbf{1}},{\mathbf{\sigma }}_{\mathbf{1}}^{\mathbf{2}}\right)\right)}^T}{N},\dots ,\frac{\left(I_{{\mathit{n}}_{\mathit{p}}}-H\left({\mathbf{\lambda }}_{\mathit{p}},{\mathbf{\sigma }}_{\mathit{p}}^{\mathbf{2}}\right)\right)y_p{y}_p^T{\left(I_{{\mathit{n}}_{\mathit{p}}}-H\left({\mathbf{\lambda }}_{\mathit{p}},{\mathbf{\sigma }}_{\mathit{p}}^{\mathbf{2}}\right)\right)}^T}{N}\right).\hfill \end{array}$$

This shows that the estimated weight matrix obtained above is a symmetric matrix, specifically, a diagonal matrix the main diagonal components of which are the estimated weight matrices of the first response, second response, etc., up to the p-th response.

3.3. Estimating Optimal Smoothing Parameters

In MNR modeling, selection of the optimal smoothing parameter value λ cannot be omitted, and is crucial to obtaining a good regression function fit of the MNR model based on the smoothing spline estimator. According to [46], there are several criteria that can be used to select λ, including minimizing cross-validation (CV), generalized cross-validation (GCV), Mallows’ ${\mathrm{C}}_p$, and Akaike’s information criterion (AIC). However, according to [47], for good regression function fitting based on the spline estimator Mallows’ ${\mathrm{C}}_p$ and GCV are the most satisfactory.

In this section, we determine the optimal smoothing parameter value for good regression function fitting of the MNR model (1). Taking into account Equation (26), we may express the estimated smoothing spline regression function presented in (22) as follows:

$$\widehat{f}\left(\mathbf{\lambda },{\mathsf{\sigma }}^{\mathbf{2}}\right)=H\left(\mathbf{\lambda },{\mathsf{\sigma }}^{\mathbf{2}}\right)y$$

where $\mathbf{\lambda }={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p\right)}^T$, ${\mathsf{\sigma }}^{\mathbf{2}}={\left({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_p^2\right)}^T$. The mean squared error (MSE) of the estimated smoothing spline regression function presented in (26) is provided by

$$\begin{array}{cc}\hfill MSE& =\frac{{\left(y-\widehat{f}\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)}^{T}W\left(y-\widehat{f}\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)}{{{\displaystyle \sum }}_{r=1}^p{n}_r}=\frac{{\left(y-\widehat{f}\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)}^{T}W\left(y-\widehat{f}\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)}{N}\hfill \\ & =\frac{{\left(\left(I-H\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)y\right)}^{T}W\left(I-H\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)y}{N}\hfill \\ & =\frac{{\Vert W^{\frac{1}{2}}\left(I-H\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)y\Vert }^2}{N}\hfill \end{array}$$

Hereinafter, we define this function as follows:

$$G\left(\lambda \right)=\frac{N^{-1}{\Vert W^{\frac{1}{2}}\left(I-H\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)y\Vert }^2}{{\left(\frac{1}{N}trace\left(I_{\mathrm{N}}-H\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)\right)}^2}$$

(27)

Therefore, based on (27), we can obtain the optimal smoothing parameter value, ${\lambda }_{opt}={\left({\lambda }_{1;opt},{\lambda }_{2;opt},\dots ,{\lambda }_{p;opt}\right)}^T$, by taking the solution of the following optimization:

$$\begin{array}{cc}\hfill G_{opt}\left({\lambda }_{opt}\right)& =\underset{{\lambda }_1,\dots ,{\lambda }_p\in {ℝ}^{+}}{\mathrm{Min}}\left\{G\left(\lambda \right)\right\}\hfill \\ & =\underset{{\lambda }_1,\dots ,{\lambda }_p\in {ℝ}^{+}}{\mathrm{Min}}\left\{\frac{N^{-1}{\Vert W^{\frac{1}{2}}\left(I-H\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)y\Vert }^2}{{\left(\frac{1}{N}trace\left(I_{\mathrm{N}}-H\left(\mathbf{\lambda },{\sigma }^{\mathbf{2}}\right)\right)\right)}^2}\right\}\hfill \end{array}$$

(28)

where ${ℝ}^{+}$ represents a positive real number set and $N={\displaystyle \sum }_{r=1}^p{n}_r$.

Thus, the optimal smoothing parameter value ${\lambda }_{opt}={\left({\lambda }_{1;opt},{\lambda }_{2;opt},\dots ,{\lambda }_{p;opt}\right)}^T$ is obtained from the minimizing process of the function $G\left(\lambda \right)$ in (27). The function $G\left(\lambda \right)$ in (27) is called the generalized cross-validation function [1].

3.4. Simulation Study

In this section, we provide a simulation study for estimating the smoothing spline regression function of the MNR model, where the performance of the proposed MNR model estimation method depends on the selection of an optimal smoothing parameter value. For example, we generate samples with size $n=100$ from an MNR model, namely, a three-response nonparametric regression model, as follows:

$$\left.\begin{array}{c}{y}_{1i}=5+3\sin \left(2\pi t_{1i}^2\right)+{\epsilon }_{1i},\mathrm{for}i=1,2,\dots ,n\\ y_{2i}=3+3\sin \left(2\pi t_{1i}^2\right)+{\epsilon }_{2i},\mathrm{for}i=1,2,\dots ,n\\ y_{3i}=1+3\sin \left(2\pi t_{1i}^2\right)+{\epsilon }_{2i},\mathrm{for}i=1,2,\dots ,n\end{array}\right\}$$

(29)

where $n=100$ and with correlations ${\rho }_{12}=0.6$, ${\rho }_{13}=0.7$, ${\rho }_{23}=0.8$ and variances ${\sigma }_1^2=2$, ${\sigma }_2^2=3$, ${\sigma }_3^2=4$. Based on the results of this simulation, we obtain a minimum generalized cross-validation (GCV) value of 2.526286 and three optimal smoothing parameter values, which are ${\lambda }_{1\left(opt\right)}=2.146156\times {10}^{-7}$ (for the first response), ${\lambda }_{2\left(opt\right)}=1.084013\times {10}^{-7}$ (for the second response), and ${\lambda }_{3\left(opt\right)}=5.930101\times {10}^{-8}$ (for the third response).

Next, we present an illustration of the effects of the smoothing parameters on the estimation results of the MNR Model by comparing three kinds of different smoothing parameter values, namely, ${\lambda }_{1\left(small\right)}={10}^{-10}$, ${\lambda }_{2\left(small\right)}=2\times {10}^{-10}$, and ${\lambda }_{3\left(small\right)}=3\times {10}^{-10}$, which represent small smoothing parameter values; ${\lambda }_{1\left(opt\right)}=2.146156\times {10}^{-7}$, ${\lambda }_{2\left(opt\right)}=1.084013\times {10}^{-7}$, and ${\lambda }_{3\left(opt\right)}=5.930101\times {10}^{-8}$, which represent optimal smoothing parameter values; and ${\lambda }_{1\left(large\right)}={10}^{-5}$, ${\lambda }_{2\left(large\right)}=2\times {10}^{-5}$, and ${\lambda }_{3\left(large\right)}=3\times {10}^{-5}$, which represent large smoothing parameter values. In the following table and figures, we provide the results of this simulation study.

Table 1. Comparison estimation results of MNR Model in (29) for three kinds of smoothing parameter values.

$\mathit{n}=100$$;{\mathit{\rho }}_{12}=0.6$$;{\mathit{\rho }}_{13}=0.7$$;{\mathit{\rho }}_{23}=0.8$$;{\mathit{\sigma }}_1^2=2$$;{\mathit{\sigma }}_2^2=3$$;{\mathit{\sigma }}_3^2=4$
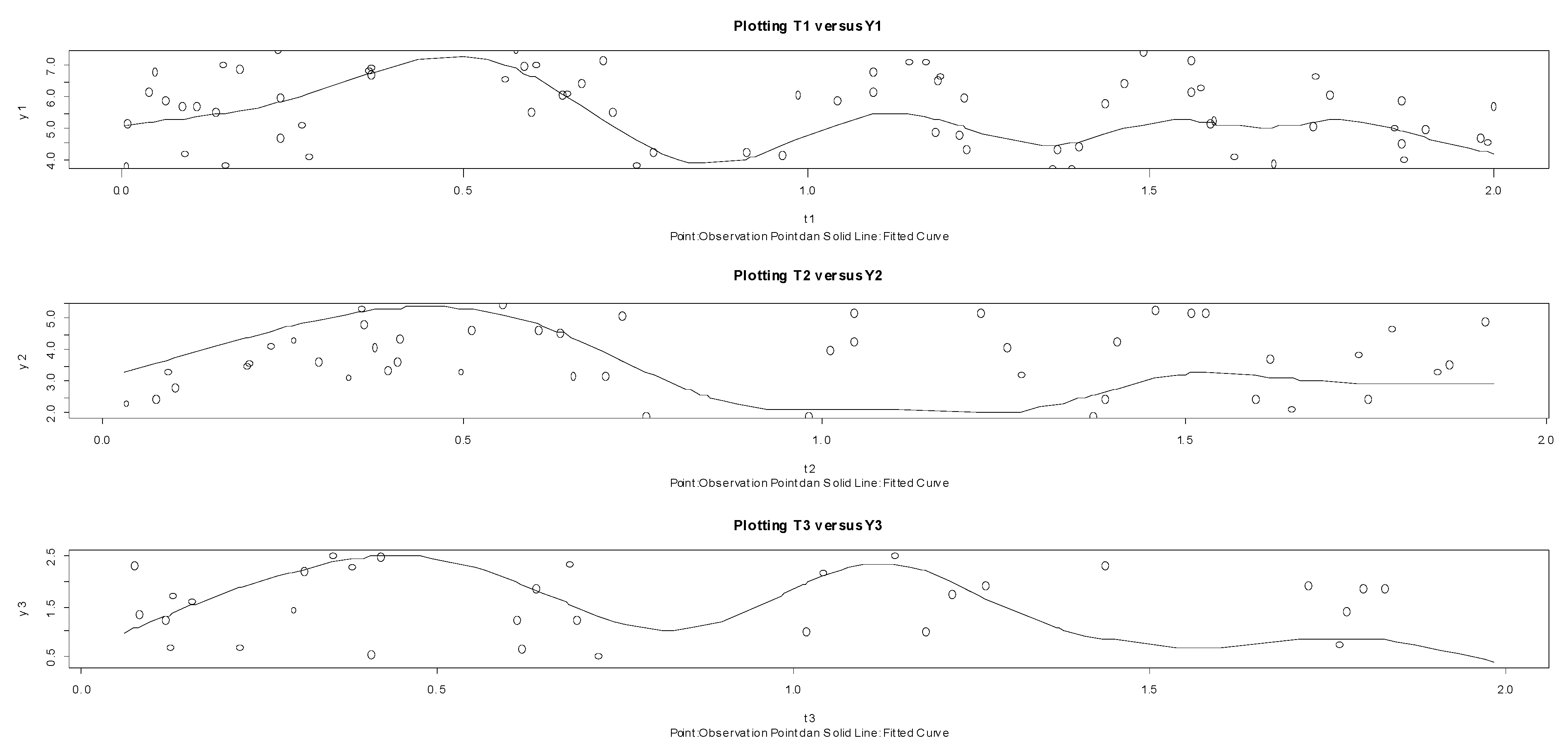
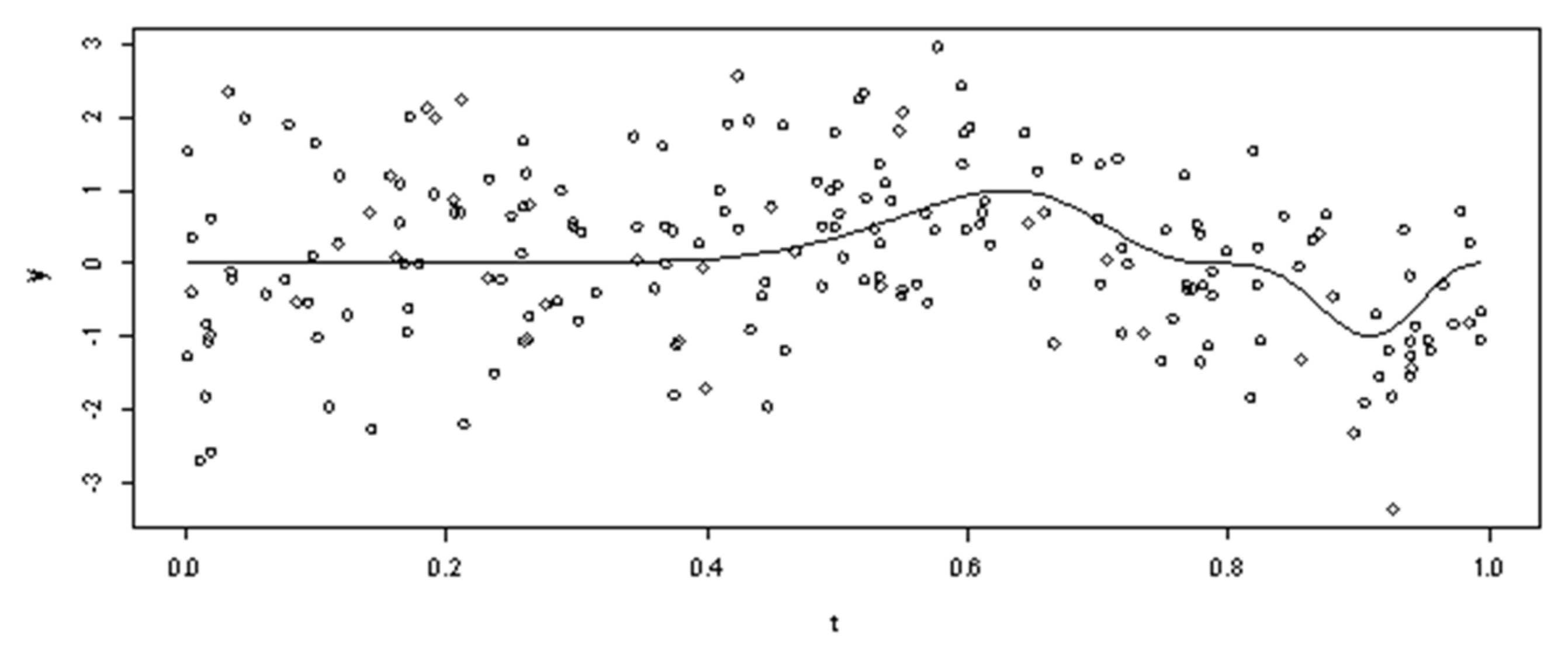
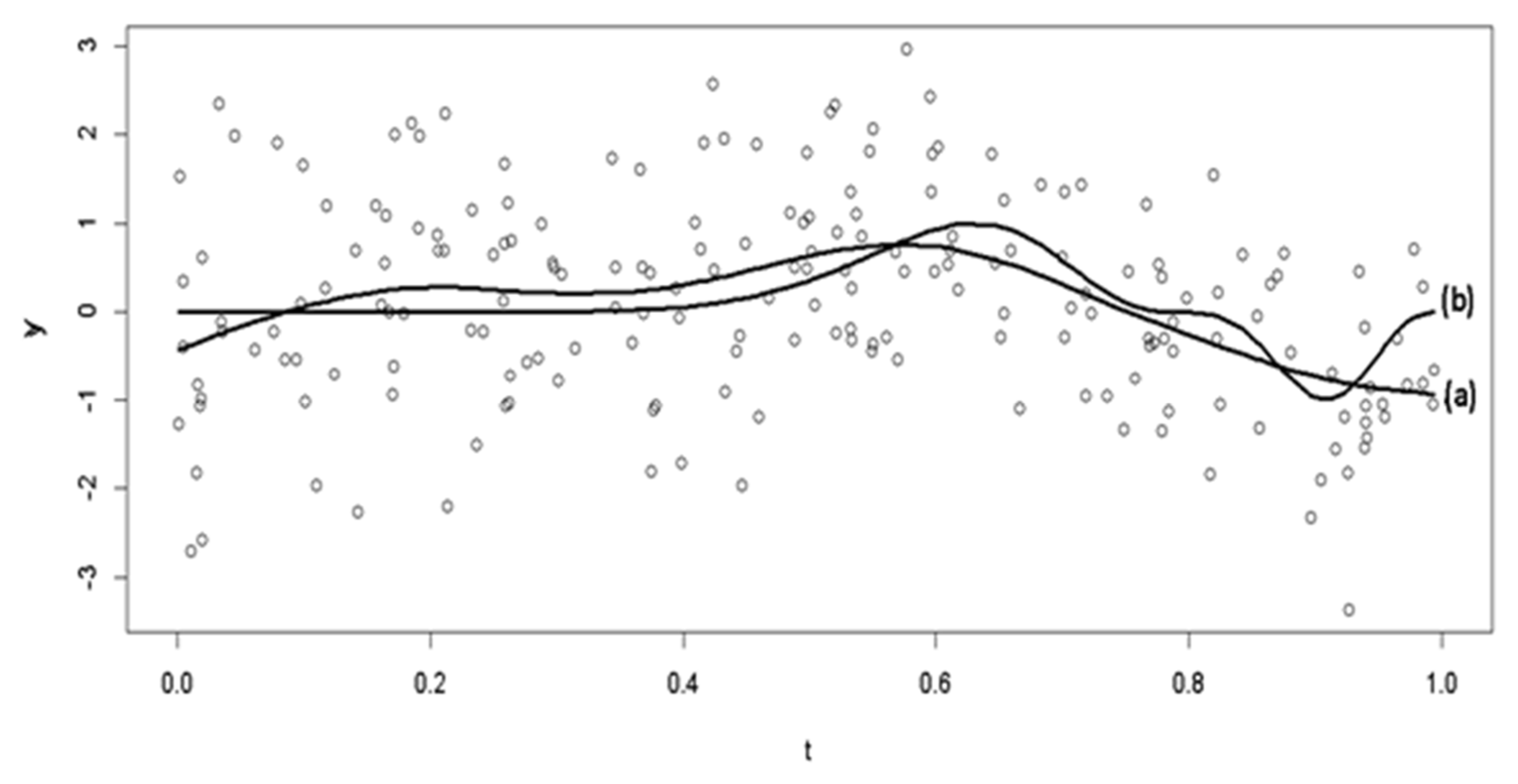
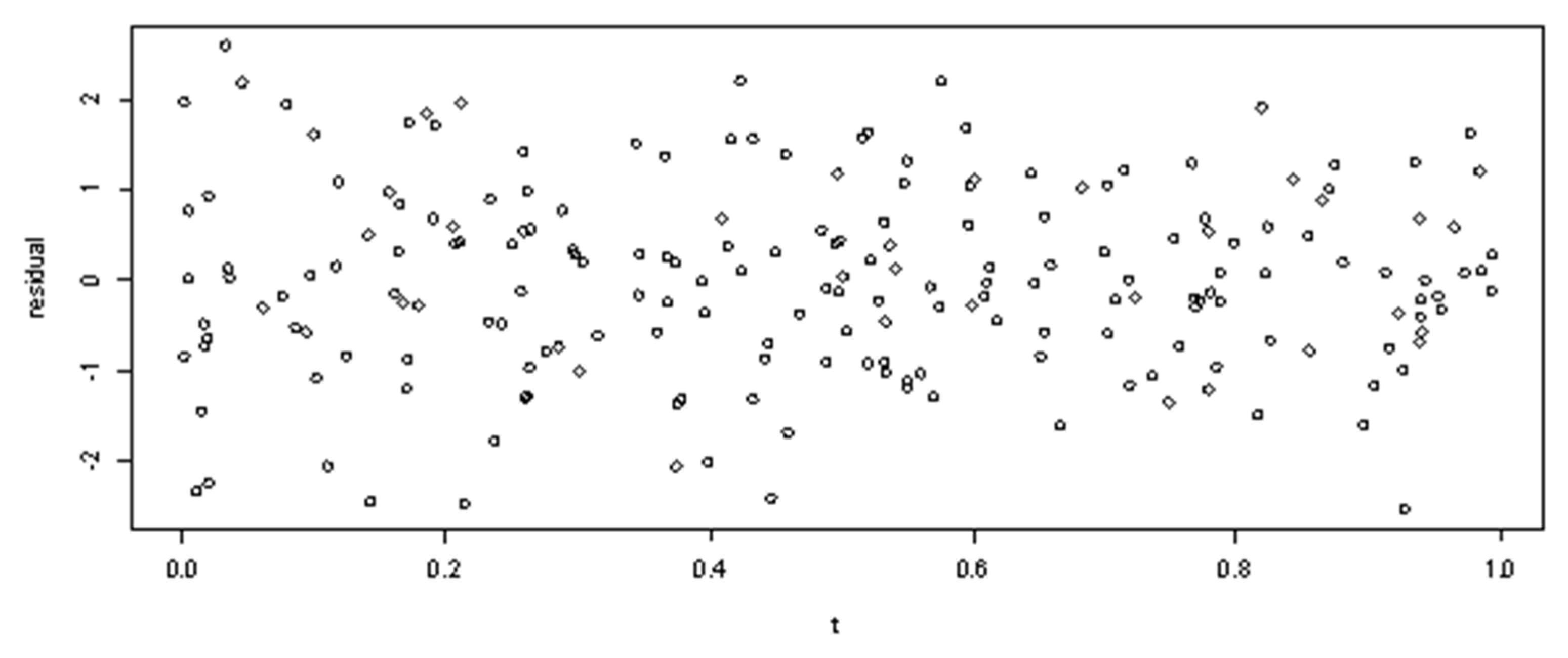
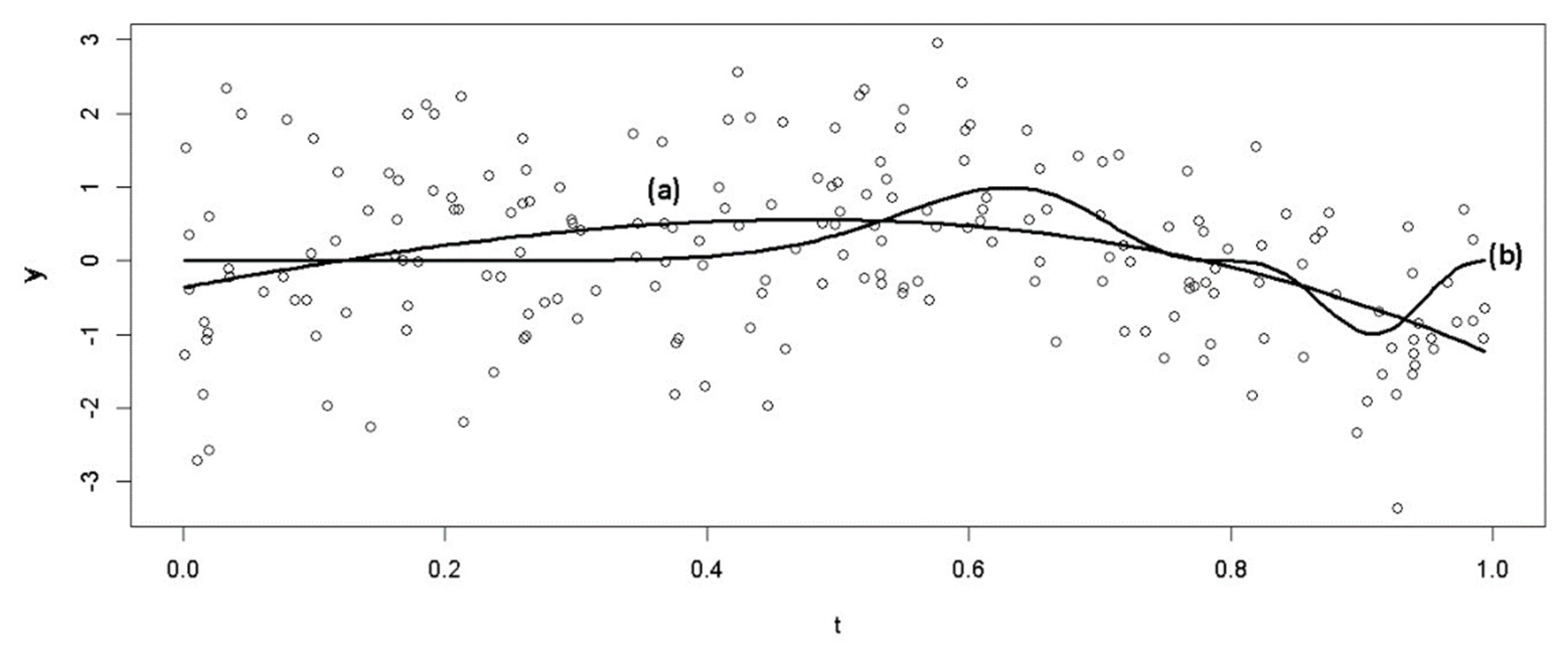
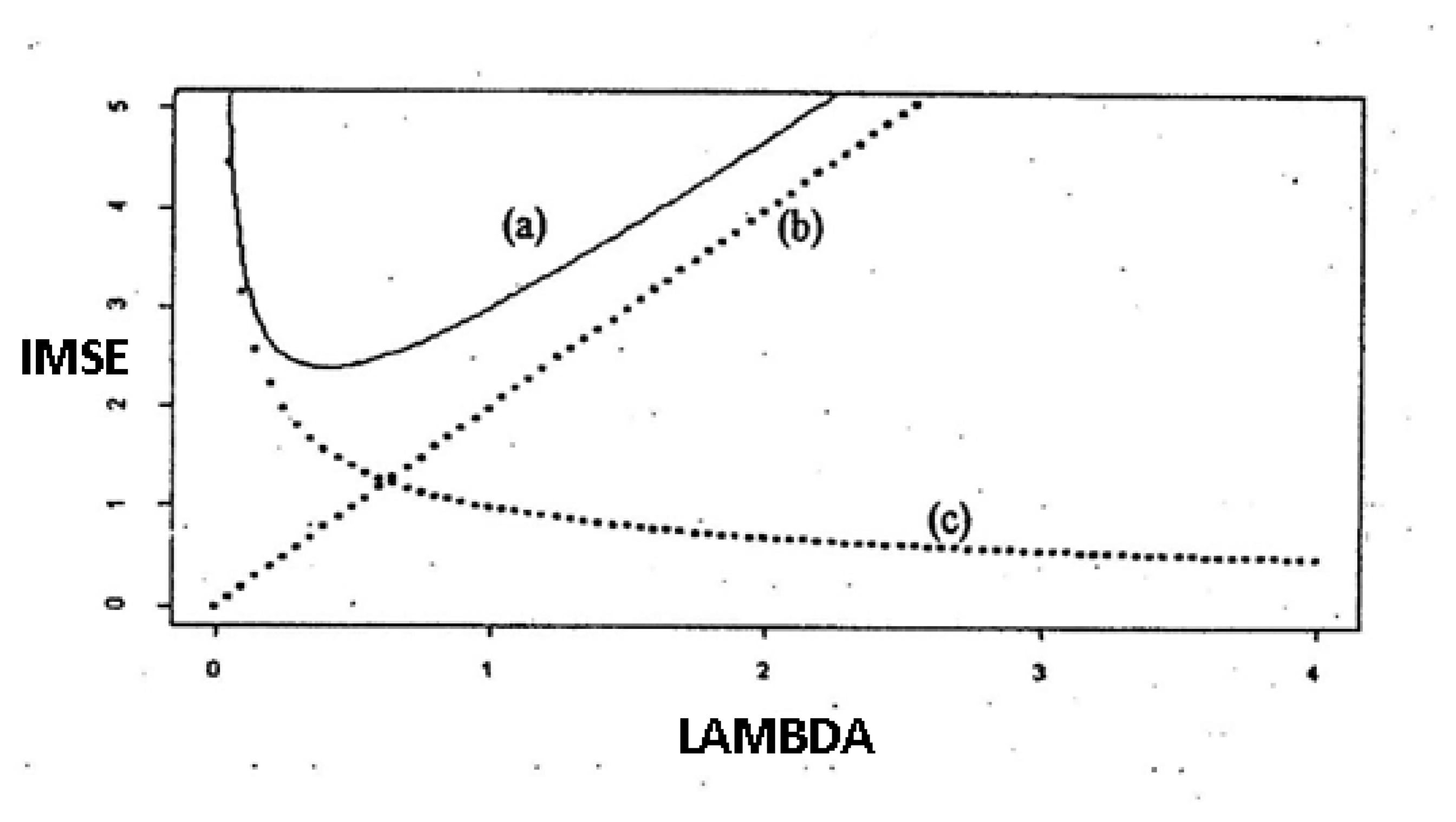
Smoothing Parameters	Minimum Values of GCV	Results of Estimation
$\left.\begin{array}{c}{\lambda }_{1\left(small\right)}={10}^{-10}\\ {\lambda }_{2\left(small\right)}=2\times {10}^{-10}\\ {\lambda }_{3\left(small\right)}=3\times {10}^{-10}\end{array}\right\}\left(SmallValues\right)$	4.763234	The estimation results are too rough.
$\left.\begin{array}{c}{\lambda }_{1\left(opt\right)}=2.146156\times {10}^{-7}\\ {\lambda }_{2\left(opt\right)}=1.084013\times {10}^{-7}\\ {\lambda }_{3\left(opt\right)}=5.930101\times {10}^{-8}\end{array}\right\}\left(OptimalValues\right)$	2.526286	The estimation results are the best.
$\left.\begin{array}{c}{\lambda }_{1\left(large\right)}={10}^{-5}\\ {\lambda }_{2\left(large\right)}=2\times {10}^{-5}\\ {\lambda }_{3\left(large\right)}=3\times {10}^{-5}\end{array}\right\}\left(LargeValues\right)$	4.617504	The estimation results are too smooth.

shows that the smoothing parameter values of $2.146156\times {10}^{-7}$, $1.084013\times {10}^{-7}$, and $5.930101\times {10}^{-8}$ are the optimal smoothing parameter values, as these smoothing parameters have the lowest GCV value (2.526286) among all the others. Thus, according to (28), these smoothing parameter values are the optimal smoothing parameters. We can write them as ${\lambda }_{1\left(opt\right)}=2.146156\times {10}^{-7}$, ${\lambda }_{2\left(opt\right)}=1.084013\times {10}^{-7}$, and ${\lambda }_{3\left(opt\right)}=5.930101\times {10}^{-8}$. The optimal smoothing parameters provide the best estimation results for the MNR model presented in (29).

The plots of the estimated regression function of the MNR model presented in (29) for the three different smoothing parameters are shown in Figure 1, Figure 2 and Figure 3.

Figure 1 shows that for all responses the small smoothing parameter values provide estimates of the regression functions of the MNR model presented in (29) that are too rough, namely, ($y_1$) for the first response, ($y_2$) for the second response, and ($y_3$) for the third response.

Figure 2 shows that the optimal smoothing parameter values provide the best estimates of the regression functions of the MNR model presented in (29) for all responses, namely, ($y_1$) for the first response, ($y_2$) for the second response, and ($y_3$) for the third response.

Figure 3 shows that for all responses the large smoothing parameter values provide estimates of the regression functions of the MNR model presented in (29) that are too smooth, namely, ($y_1$) for the first response, ($y_2$) for the second response, and ($y_3$) for the third response.

3.5. Investigating the Consistency of the Smoothing Spline Regression Function Estimator

We first investigate the asymptotic properties of the smoothing spline regression function estimator $\widehat{f}$ based on the integrated mean square error (IMSE) criterion. We develop the IMSE proposed by [14] from the uniresponse case to the multiresponse case. Suppose that we decompose the IMSE into two components, $bia{s}^2\left(\lambda \right)$ and $Var\left(\lambda \right)$, as follows:

$$IMSE\left(\lambda \right)=E{{\displaystyle \int }}_a^b\left[{\left(f\left(t\right)-\widehat{f}\left(t\right)\right)}^{T}W\left(f\left(t\right)-\widehat{f}\left(t\right)\right)\right]dt=bia{s}^2\left(\lambda \right)+Var\left(\lambda \right)$$

(30)

where $bia{s}^2\left(\lambda \right)={{\displaystyle \int }}_a^{b}E[{\left(f\left(t\right)-E\widehat{f}\left(t\right)\right)}^{T}W\left(f\left(t\right)-E\widehat{f}\left(t\right)\right)]dt,$ and $Var\left(\lambda \right)={{\displaystyle \int }}_a^{b}E\left[{\left(E\widehat{f}\left(t\right)-\widehat{f}\left(t\right)\right)}^{T}W\left(E\widehat{f}\left(t\right)-\widehat{f}\left(t\right)\right)\right]dt$. Furthermore, in order to investigate the asymptotic property of $bia{s}^2\left(\lambda \right)$, we assign the solution to PWLS optimization in the following theorem.

Theorem 1.

If $\widehat{f}\left(t\right)$is the solution that minimizes the following penalized weighted least square (PWLS):

$$N^{-1}{\left(y-g\left(t\right)\right)}^{T}W\left(y-g\left(t\right)\right)+{{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(g_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r$$

(31)

then the solution that minimizes the following penalized weighted least square (PWLS):

$$N^{-1}{\left(f\left(t\right)-g\left(t\right)\right)}^{T}W\left(f\left(t\right)-g\left(t\right)\right)+{{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(g_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r$$

(32)

is ${\widehat{g}}^{*}\left(t\right)=E\widehat{f}\left(t\right)$.

Proof of Theorem 1.

In Section 3.1, we obtained the solution to the PWLS in (31), that is, $\widehat{f}=A\widehat{b}+C\widehat{d}=Hy$, where as provided in (22), $H=A{\left(A^T{D}^{-\mathbf{1}}WA\right)}^{-\mathbf{1}}{A}^T{D}^{-\mathbf{1}}W+C{D}^{-\mathbf{1}}W\left(I-A{\left(A^T{D}^{-\mathbf{1}}WA\right)}^{-\mathbf{1}}{A}^T{D}^{-\mathbf{1}}W\right)$, $D=WC+\mathrm{N}\mathbf{Ʌ}$, $\mathbf{Ʌ}=diag\left({\lambda }_1{I}_{n_1},{\lambda }_2{I}_{n_2},\dots ,{\lambda }_p{I}_{n_p}\right)$, $N={\displaystyle \sum }_{r=1}^p{n}_r$, and $I$ is an identity matrix. Next, if we substitute $y=f\left(t\right)$ into Equation (31), we find that the value that minimizes PWLS (32) is

$${\widehat{g}}^{*}\left(t\right)=A{\left(A^T{D}^{-\mathbf{1}}WA\right)}^{-\mathbf{1}}{A}^T{D}^{-\mathbf{1}}W+C{D}^{-\mathbf{1}}W\left(I-A{\left(A^T{D}^{-\mathbf{1}}WA\right)}^{-\mathbf{1}}{A}^T{D}^{-\mathbf{1}}W\right)y=E\widehat{f}\left(t\right)$$

Thus, Theorem 1 is proved. □

Furthermore, we investigate the asymptotic property of $bia{s}^2\left(\lambda \right)$. For this purpose, we first provide the following assumptions.

Assumptions (A): 

(A1)

For every $r=1,2,\dots ,p$, $n_r=n$ and ${\lambda }_r=\lambda$.

(A2)

For every $i=1,2,\dots ,n$, $t_i=\frac{2i-1}{2n}$.

(A3)

For any continuous function $g$ and $0<{\mathrm{W}}_i=\mathrm{W}<\infty$, $i=1,2,\dots ,n$, the following statements are satisfied [48,49]:

(a)

$n^{-1}{\displaystyle \sum }_{i=1}^{n}g\left(t_i\right)\to {{\displaystyle \int }}_a^{b}g\left(t\right)dt$, as $n\to \infty$.

(b)

$n^{-1}{\displaystyle \sum }_{i=1}^n{\mathrm{W}}_{i}g\left(t_i\right)\to {{\displaystyle \int }}_a^b\mathrm{W}g\left(t\right)$dt, as $n\to \infty$.

(c)

$n^{-1}{\displaystyle \sum }_{i=1}^n{\lambda }_i{{\displaystyle \int }}_{a_i}^{b_i}{\left(g_i^{\left(m\right)}\left(t_i\right)\right)}^{2}d{t}_i\to \lambda {{\displaystyle \int }}_a^b{g}^{\left(m\right)}\left(t\right)dt$, as $n\to \infty$.

Next, given Assumptions (A), the asymptotic property of $bia{s}^2\left(\lambda \right)$ is provided in the Theorem 2.

Theorem 2.

If the Assumptions in (A) hold, then$Bia{s}^2\left(\lambda \right)\le O\left(\lambda \right)$, as $n\to \infty$.

Proof of Theorem 2.

Suppose $\widehat{g}\left(t\right)$ is the value which minimizes the following penalized weighted least square (PWLS):

$${{\displaystyle \int }}_a^b{\left(f\left(t\right)-g\left(t\right)\right)}^{T}W\left(f\left(t\right)-g\left(t\right)\right)dt+{{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(g_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r$$

then, considering the Assumptions (A), we have

$$n^{-1}{\left(f\left(t\right)-g\left(t\right)\right)}^{T}W\left(f\left(t\right)-g\left(t\right)\right)\approx {{\displaystyle \int }}_a^b{\left(f\left(t\right)-g\left(t\right)\right)}^{T}W\left(f\left(t\right)-g\left(t\right)\right)dt,\mathrm{as}n\to \infty .$$

Hence, we obtain ${\widehat{g}}^{*}\left(t\right)=E\widehat{f}\left(t\right)\approx \widehat{g}\left(t\right)$. Thus, for every $g\in W_{\mathbf{2}}^{\mathit{m}}\left[a,b\right]$ we have

$$\begin{array}{cc}\hfill Bia{s}^2\left(\lambda \right)& ={{\displaystyle \int }}_a^{b}E[{\left(f\left(t\right)-E\widehat{f}\left(t\right)\right)}^{T}W\left(f\left(t\right)-E\widehat{f}\left(t\right)\right)]dt\hfill \\ & \le {{\displaystyle \int }}_a^{b}E[{\left(f\left(t\right)-E\widehat{f}\left(t\right)\right)}^{T}W\left(f\left(t\right)-E\widehat{f}\left(t\right)\right)]dt+{\displaystyle \sum }_{\mathit{r}=\mathbf{1}}^{\mathit{p}}{\mathbf{\lambda }}_{\mathit{r}}{{\displaystyle \int }}_{\mathbf{a}}^{\mathbf{b}}{\widehat{g}}_r^{\left(m\right)}\left(t_r\right)d{t}_r\hfill \end{array}$$

Because $E\widehat{f}\left(t\right)\approx \widehat{g}\left(t\right)$, we obtain

$$Bia{s}^2\left(\lambda \right)\le {{\displaystyle \int }}_a^{b}E[{\left(f\left(t\right)-\widehat{g}\left(t\right)\right)}^{T}W\left(f\left(t\right)-\widehat{g}\left(t\right)\right)]dt+{{\displaystyle \sum }}_{\mathit{r}=\mathbf{1}}^{\mathit{p}}{\mathbf{\lambda }}_{\mathit{r}}{{\displaystyle \int }}_{\mathbf{a}}^{\mathbf{b}}{\widehat{g}}_r^{\left(m\right)}\left(t_r\right)d{t}_r$$

Thus, we have the following relationship:

$$Bia{s}^2\left(\lambda \right)\le {{\displaystyle \int }}_a^{b}E[{\left(f\left(t\right)-g\left(t\right)\right)}^{T}W\left(f\left(t\right)-g\left(t\right)\right)]dt+{{\displaystyle \sum }}_{\mathit{r}=\mathbf{1}}^{\mathit{p}}{\mathbf{\lambda }}_{\mathit{r}}{{\displaystyle \int }}_{\mathbf{a}}^{\mathbf{b}}{g}_r^{\left(m\right)}\left(t_r\right)d{t}_r$$

(33)

for every $g\in W_{\mathbf{2}}^{\mathit{m}}\left[a,b\right]$.

Because every $g\in W_{\mathbf{2}}^{\mathit{m}}\left[a,b\right]$ satisfies the relationship in (33), by taking $g\left(t\right)=f\left(t\right)$, we have

$$Bia{s}^2\left(\lambda \right)\le {{\displaystyle \sum }}_{\mathit{r}=\mathbf{1}}^{\mathit{p}}{\mathbf{\lambda }}_{\mathit{r}}{{\displaystyle \int }}_{\mathbf{a}}^{\mathbf{b}}{g}_r^{\left(m\right)}\left(t_r\right)d{t}_r=O\left(\lambda \right)\mathrm{as}n\to \infty$$

(34)

where $O\left(·\right)$ represents “big oh”. Details about “big oh” can be found in [14,50].

Thus, Theorem 2 is proved. □

Furthermore, the asymptotic property of $Var\left(\lambda \right)$ is provided in Theorem 3.

Theorem 3.

If Assumptions (A) hold and $r=1,2,\dots ,p$

, then$Var\left({\lambda }_r\right)\le O\left(\frac{1}{n{\lambda }_r^{\frac{1}{2m}}}\right)$.

Proof of Theorem 3.

To investigate the asymptotic property of $Var\left(\lambda \right)$, we first define the following function:

$$\mathbf{\omega }\left(\widehat{f},h,\alpha \right)=R\left(\widehat{f}+\alpha h\right)+{{\displaystyle \sum }}_{r=1}^p{\lambda }_r{J}_r\left(\widehat{f}+\alpha h\right)$$

where $R\left(g\right)=n^{-1}{\left(y-g\left(t\right)\right)}^{T}W\left(y-g\left(t\right)\right)$; $J_r\left(g\right)={{\displaystyle \int }}_a^b{\left[g_r^{\left(m\right)}\left(t_r\right)\right]}^{2}d{t}_r$; $h\in W_2^m\left[a,b\right]$ and $\alpha \in ℝ$.

Hence, for any $f,g\in W_2^m\left[a,b\right]$ we have

$$\begin{gathered} \mathbf{\omega }\left(\widehat{f},h,\alpha \right)=n^{-1}{\left(y-f\left(t\right)-\alpha g\left(t\right)\right)}^{T}W\left(y-f\left(t\right)-\alpha g\left(t\right)\right)+ \\ {{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(f_r^{\left(m\right)}\left(t_r\right)+\alpha g_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r \end{gathered}$$

Next, by taking the solution to $\frac{\partial \mathbf{\omega }\left(\widehat{f},h,\alpha \right)}{\partial \alpha }=\mathbf{0}$, for $\alpha =0$ we have

$$n^{-1}{\left(y-f\left(t\right)\right)}^{T}Wg\left(t\right)={{\displaystyle \sum }}_{r=1}^p{\lambda }_r{{\displaystyle \int }}_{a_r}^{b_r}{\left(f_r^{\left(m\right)}\left(t_r\right)g_r^{\left(m\right)}\left(t_r\right)\right)}^{2}d{t}_r$$

Furthermore, if ${\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n$ are the bases for the natural spline and $f_r\left(t_r\right)={{\displaystyle \sum }}_{k=1}^n{\beta }_{rk}{\gamma }_{rk}\left(t_r\right)$, $r=1,2,\dots ,p$, then according to [51] this implies that

$$\begin{array}{c}{{\displaystyle \sum }}_{j=1}^n\left(y_{rj}-{{\displaystyle \sum }}_{k=1}^n{\beta }_{rk}{\gamma }_{rk}\left(t_{rj}\right)\right){\mathrm{W}}_{rj}{g}_{rj}\left(t_{rj}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=n{\lambda }_r{\left(-1\right)}^m\left(2m-1\right)!{{\displaystyle \sum }}_{i=1}^n{g}_r\left(t_{ri}\right){{\displaystyle \sum }}_{k=1}^n{\beta }_{rk}{d}_{rik}\end{array}$$

(35)

where $d_{rik}$ is the r^th response diagonal element of matrix H in (26).

Now, because Equation (35) holds for every $g_r\in W_2^m\left[a_r,b_r\right]$, $r=1,2,\dots ,p$, it follows that determining the solution to Equation (35) is equivalent to determining the value of ${\beta }_{rk}$ that satisfies the following equation:

$$y_{ri}={{\displaystyle \sum }}_{k=1}^n\left(n{\lambda }_r{\left(-1\right)}^m\left(2m-1\right)!{\mathrm{W}}_{ri}^{-1}{d}_{rik}+{\gamma }_{rk}\left(t_{ri}\right)\right){\beta }_{rk},i=1,2,\dots ,n$$

(36)

We can express Equation (36) in matrix notation as follows:

$$y=\left(n{\lambda }_r{\left(-1\right)}^m\left(2m-1\right)!W^{-1}K+\gamma \right)\mathbf{\beta }$$

(37)

where $=\left\{{\mathbf{d}}_{rik}\right\}$, $\gamma =\left\{{\gamma }_{rk}\left(t_{ri}\right)\right\}$, $r=1,2,\dots ,p$, and $i,k=1,2,\dots ,n$.

Hence, we obtain the estimator for $\mathsf{\beta }$ in Equation (37) as follows:

$$\widehat{\mathsf{\beta }}=diag\left(\frac{1}{1+n{\lambda }_{r{\theta }_1}},\dots ,\frac{1}{1+n{\lambda }_{r{\theta }_n}}\right){\gamma }^{T}y$$

where $\{{\theta }_1,\dots ,{\theta }_n\}\in \mathcal{H}$ (here, $\mathcal{H}$ is an RKHS) and is perpendicular to $\gamma$.

Thus, the estimator for the regression function $f\left(t\right)$ can be expressed as follows:

$$\widehat{f}\left(t\right)=\gamma \left(t\right)\widehat{\mathsf{\beta }}={{\displaystyle \sum }}_{j=1}^n\frac{1}{1+n\lambda {\theta }_j}{\gamma }_j^{T}y{\gamma }_j\left(t\right)$$

(38)

Hence, for $r=1,2,\dots ,p$ Equation (38) results in

$$\begin{array}{cc}\hfill {\widehat{f}}_r\left(t_r\right)& ={\displaystyle \sum }_{j=1}^n\frac{1}{1+n{\lambda }_r{\theta }_{rj}}{\gamma }_{rj}^{T}y{\gamma }_{\mathit{r}\mathit{j}}\left(t_r\right)\hfill \\ & ={\displaystyle \sum }_{j=1}^n\frac{1}{1+n{\lambda }_r{\theta }_{rj}}{\displaystyle \sum }_{k=1}^n{\gamma }_{rj}\left(t_{rk}\right)y_{rk}{\gamma }_{rj}\left(t_{rk}\right)\hfill \end{array}$$

Thus, for $r=1,2,\dots ,p$ we have

$$\begin{array}{cc}\hfill Var\left({\widehat{f}}_r\left(t_r\right)\right)& ={\sigma }_r^2{\displaystyle \sum }_{j=1}^n\frac{{\gamma }_{rj}^2\left(t_r\right)}{{\left(1+n{\lambda }_r{\theta }_{rj}\right)}^2}{\displaystyle \sum }_{k=1}^n{\gamma }_{rj}\left(t_{rk}\right){\gamma }_{rj}\left(t_{rk}\right)W_{rk}^{-1}\hfill \\ & \le \left(\underset{1\le i\le n}{\max }\left\{W_{ri}^{-1}\right\}\right){\sigma }_r^2{\displaystyle \sum }_{j=1}^n\frac{{\gamma }_{rj}^2\left(t_r\right)}{{\left(1+n{\lambda }_r{\theta }_{rj}\right)}^2}\hfill \end{array}$$

From this step, for $r=1,2,\dots ,p$ we have

$$\begin{array}{c}Var\left({\lambda }_r\right)={{\displaystyle \int }}_{a_r}^{b_r}E\left[{\left(E{\widehat{f}}_r\left(t_r\right)-{\widehat{f}}_r\left(t_r\right)\right)}^T{W}_r\left(E{\widehat{f}}_r\left(t_r\right)-{\widehat{f}}_r\left(t_r\right)\right)\right]d{t}_r\\ \le \left(\underset{1\le i\le n}{\max }\left\{W_{ri}^{-1}\right\}\right){\sigma }_r^2{\displaystyle \sum }_{j=1}^n\frac{{\gamma }_{rj}^2\left(t_r\right)}{{\left(1+n{\lambda }_r{\theta }_{rj}\right)}^2}{{\displaystyle \int }}_{a_r}^{b_r}{\gamma }_{rj}^2\left(t_r\right)W_{r}d{t}_r\end{array}$$

In the next step, Refs. [51,52] provide an approximation for $n\to \infty$ as follows:

$$\begin{array}{c}{n}^{-1}=n^{-1}{\displaystyle \sum }_{j=1}^n{W}_{rj}{\gamma }_{rj}^2\left(t_{rj}\right)\approx {{\displaystyle \int }}_{a_r}^{b_r}{\gamma }_r^2\left(t_r\right)W_{r}d{t}_r,\mathrm{and}\\ Var\left({\lambda }_r\right)\le \left(\underset{1\le i\le n}{\max }\left\{W_{ri}^{-1}\right\}\right){\sigma }_r^2{n}^{-1}{\displaystyle \sum }_{j=1}^n\frac{1}{{\left(1+{\lambda }_r{\gamma }_j\right)}^2}.\end{array}$$

Furthermore, Ref. [51] leads to the following result:

$$Var\left({\lambda }_r\right)\le \left(\underset{1\le i\le n}{\max }\left\{W_{ri}^{-1}\right\}\right){\sigma }_r^2{n}^{-1}{{\displaystyle \sum }}_{j=1}^n\frac{1}{{\left(1+{\lambda }_r{\left(\pi j\right)}^{2m}\right)}^2}$$

Next, using integral approximation [51], for $r=1,2,\dots ,p$ we have

$$Var\left({\lambda }_r\right)\le \left(\underset{1\le i\le n}{\max }\left\{W_{ri}^{-1}\right\}\right)\frac{{\sigma }_r^2}{n\pi {\lambda }_r^{\frac{1}{2m}}}{{\displaystyle \int }}_0^{\infty }\frac{dx}{{\left(1+x^{2m}\right)}^2}=\frac{1}{n{\lambda }_r^{\frac{1}{2m}}}K\left(m,\sigma \right)=O\left(\frac{1}{n{\lambda }_r^{\frac{1}{2m}}}\right)$$

where $\left(m,\sigma \right)=\frac{{\sigma }_r^2}{\pi }\left(\underset{1\le i\le n}{\max }\left\{W_{ri}^{-1}\right\}\right){{\displaystyle \int }}_0^{\infty }\frac{dx}{{\left(1+x^{2m}\right)}^2}$. Thus, Theorem 3 is proved. □

Here, based on Theorems 2 and 3, we obtain the asymptotic property of the smoothing spline regression function estimator of the MNR model presented in (1) based on the integrated mean square error (IMSE) criterion, as follows:

$$IMSE\left(\lambda \right)=Bia{s}^2\left(\lambda \right)+Var\left(\lambda \right)\le O\left(\lambda \right)+O\left(z\right)\mathrm{as}n\to \infty$$

(39)

where $={\left({\mathbf{\lambda }}_{\mathbf{1}},{\mathbf{\lambda }}_{\mathbf{2}},\dots ,{\mathbf{\lambda }}_{\mathit{p}}\right)}^{\mathrm{T}}$ and $z={\left(\begin{array}{ccc}\frac{\mathbf{1}}{\mathit{n}{\mathbf{\lambda }}_{\mathbf{1}}^{\frac{\mathbf{1}}{\mathbf{2}\mathit{m}}}}& \frac{\mathbf{1}}{\mathit{n}{\mathbf{\lambda }}_{\mathbf{2}}^{\frac{\mathbf{1}}{\mathbf{2}\mathit{m}}}}& \begin{array}{cc}\cdots & \frac{\mathbf{1}}{\mathit{n}{\mathbf{\lambda }}_{\mathit{p}}^{\frac{\mathbf{1}}{\mathbf{2}\mathit{m}}}}\end{array}\end{array}\right)}^{\mathbf{T}}$.

The consistency of the smoothing spline regression function estimator of the MNR model presented in (1) is provided by the following theorem.

Theorem 4.

If $\widehat{f}\left(t\right)$is a smoothing spline estimator for regression function $f\left(t\right)$of the MNR model presented in (1), then $\widehat{f}\left(t\right)$is a consistent estimator for $f\left(t\right)$based on the integrated mean square error (IMSE) criterion.

Proof of Theorem 4.

Based on Equation (39), we have the following relationship:

$$IMSE\left(\lambda \right)=Bia{s}^2\left(\lambda \right)+Var\left(\lambda \right)\le O\left(\lambda \right)+O\left(z\right)\le O\left(n\lambda \right)\mathrm{as}n\to \infty .$$

Hence, according to [48], for any small positive number $\delta >0$ we have

$$\underset{n\to \infty }{\mathrm{Lim}}P\left(\left|\frac{IMSE\left(\lambda \right)}{n\lambda }\right|>\delta \right)\le \underset{n\to \infty }{\mathrm{Lim}}P\left(\left|IMSE\left(\lambda \right)\right|>\delta \right)=0.$$

(40)

Because $P\left(\left|IMSE\left(\lambda \right)\right|>\delta \right)=1-P\left(\left|IMSE\left(\lambda \right)\right|\le \delta \right)$, based on Equation (40) and applying the probability properties we have

$$\begin{array}{cc}\hfill \underset{n\to \infty }{\mathrm{Lim}}\left(1-P(\left|IMSE\left(\lambda \right)\right|\le \delta \right))=0\iff & 1-\underset{n\to \infty }{\mathrm{Lim}}P\left(\left|IMSE\left(\lambda \right)\right|\le \delta \right)=0\hfill \\ & \iff \underset{n\to \infty }{\mathrm{Lim}}P\left(\left|IMSE\left(\lambda \right)\right|\le \delta \right)=1.\hfill \end{array}$$

(41)

Equation (41) means that the smoothing spline regression function estimator of the multiresponse nonparametric regression (MNR) model is a consistent estimator based on the integrated mean square error (IMSE) criterion. Thus, Theorem 4 is proved. □

3.6. Illustration of Theorems

Suppose a paired observation $\left(y_{ri},t_{ri}\right)$ follows the multiresponse nonparametric regression (MNR) model:

$$y_{ri}=f_r\left(t_{ri}\right)+{\epsilon }_{ri},t_{ri}\in \left[0,1\right],r=1,2,\dots ,p,i=1,2,\dots ,n_r.$$

(42)

Next, for every $r=1,2,\dots ,p$, we assume $f_1=f_2=\dots =f_p=f$ and ${\epsilon }_1={\epsilon }_2=\dots ={\epsilon }_p=\epsilon$ such that $y_1=y_2=\dots =y_p=y$. Hence, we have a nonparametric regression model as follows:

$$y_i=f\left(t_i\right)+{\epsilon }_i,t_i\in \left[0,1\right],i=1,2,\dots ,n.$$

(43)

Based on the model presented in (43), we present an illustration related to the four theorems in Section 3.5 through a simulation study with sample size of $\mathit{n}=\mathbf{200}$. Based on this model, let $\mathit{f}\left(\mathit{t}\right)=\mathit{s}\mathit{i}{\mathit{n}}^{\mathbf{3}}\left(\mathbf{2}\mathbf{\pi }{\mathit{t}}^{\mathbf{3}}\right)$, where $\mathit{t}$ is generated from a uniform (0,1) distribution and $\mathbf{\epsilon }$ is generated from a standard normal distribution. The first step is to create plots of the observation values $\left(\mathit{t},\mathit{y}\right)$ and $\mathit{f}\left(\mathit{t}\right)$, as shown in Figure 4.

It can be seen from Figure 4 that there is a tendency towards $\mathit{y}$ variance inequality. For larger values of $\mathit{t}$, the $\mathit{y}$ variance tends to be larger. Next, the data model is approximated by a weighted spline with a weight of ${\mathit{w}}_{\mathit{i}}=\mathbf{1}/{\mathit{t}}_{\mathit{i}}^{\mathbf{2}}$, $i=1,2,\dots ,200$. The next step is to determine the order, number, and location of the knot points. Here, we use a weighted cubic spline model with two knot points, namely, 0.5 and 0.785. This weighted cubic spline model can be written as follows:

$$E\left(y\right)={\beta }_0+{\beta }_{1}t+{\beta }_2{t}^2+{\beta }_3{t}^3+{\beta }_4{\left(t-0.5\right)}_{+}^3+{\beta }_5{\left(t-0.785\right)}_{+}^3$$

(44)

The plot of this weighted cubic spline with two knot points is shown in Figure 5. The plots of the residuals and the estimated weighted cubic spline are shown in Figure 6.

Figure 6 shows that with weight ${\mathit{w}}_{\mathit{i}}=\mathbf{1}/{\mathit{t}}_{\mathit{i}}^{\mathbf{2}}$, the variance of the response variable y tends to be the same. Meanwhile, Figure 7 provides a residual normality plot for the weighted cubic spline model. The plot in Figure 7 shows no indication towards deviation from the normal distribution.

Next, as a comparison, we investigate a weighted cubic polynomial model with weight $w_i=1/t_i^2$, $i=1,2,\dots ,200$ for fitting the model (43). The fitting of the weighted cubic polynomial model is shown in Figure 8. From the visualization in Figure 8, it can be seen that this weighted cubic polynomial approach tends to approach the function $f\left(t\right)$ very globally. This is in contrast to the weighted cubic spline with two knot points in (44), which approaches the function $f\left(t\right)$ more locally. Thus, the weighted cubic spline model with two knot points is adequate as an approximation model for the model presented in (43).

Based on the illustration above and Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, if $\widehat{f}\left(t\right)$ is an estimator for model (43), that is, if $\widehat{f}\left(t\right)$ is the Penalized Weighted Least Squares (PWLS) solution, then ${\widehat{g}}^{*}\left(t\right)=E\left(y\right)$, from Equation (44) is an estimator for model (43) as well, such that ${\widehat{g}}^{*}\left(t\right)=E\left[\widehat{f}\left(t\right)\right]$, as provided by Theorem 1.

The plots of the asymptotic curves of $\mathit{IMSE}\left(\lambda \right)$, $\mathit{B}\mathit{i}\mathit{a}{\mathit{s}}^{\mathbf{2}}\left(\lambda \right)$, and $\mathit{Var}\left(\lambda \right)$, where $\mathit{IMSE}\left(\lambda \right)=\mathit{B}\mathit{i}\mathit{a}{\mathit{s}}^{\mathbf{2}}\left(\lambda \right)+\mathit{Var}\left(\lambda \right)$, are shown in Figure 9 [53].

Figure 9 shows that the Integrated Mean Square Error (IMSE(λ)) curve represented by curve (a) is the sum of the quadratic bias ($\mathit{B}\mathit{i}\mathit{a}{\mathit{s}}^{\mathbf{2}}\left(\lambda \right)$) curve represented by curve (b) and the variance curve ($\mathit{V}\mathit{a}\mathit{r}\left(\lambda \right)$) represented by curve (c). It can be seen from Figure 9b that $Bia{s}^2\left(\lambda \right)\le O\left(\lambda \right)$, as $n\to \infty$, that is, $\underset{n\to \infty }{\mathrm{Lim}\mathrm{Sup}}\left|\frac{Bia{s}^2\left(\lambda \right)}{\lambda }\right|<\infty$ [14,50,54]. This means that $\left|\frac{Bia{s}^2\left(\lambda \right)}{\lambda }\right|$ remains bounded, as $n\to \infty$, which is provided by Theorem 2. Furthermore, Figure 9c shows that $Var\left(\lambda \right)\le O\left(\frac{1}{n{\lambda }^{\frac{1}{2m}}}\right)$ (that is, $\underset{n\to \infty }{\mathrm{Lim}\mathrm{Sup}}\left|{\left(n{\lambda }^{\frac{1}{2m}}\right)}^{-1}/\lambda \right|<\infty$ [14,50,54]. This means that $\left|{\left(n{\lambda }^{\frac{1}{2m}}\right)}^{-1}/\lambda \right|$ remains bounded, as $n\to \infty$, which is provided by Theorem 3. Furthermore, Figure 9 shows that $IMSE\left(\lambda \right)=Bia{s}^2\left(\lambda \right)+Var\left(\lambda \right)\le O\left(n\lambda \right)$. According to [14,50,54], this means that $\underset{n\to \infty }{\mathrm{Lim}\mathrm{Sup}}\left|\frac{IMSE\left(\lambda \right)}{n\lambda }\right|<\infty$. In other words, $IMSE\left(\lambda \right)\le O\left(n\lambda \right)$ if $\left|\frac{IMSE\left(\lambda \right)}{n\lambda }\right|$ remains bounded, as $n\to \infty$. According to [14,50,54], for any small positive number $\delta >0$ we have $\underset{n\to \infty }{\mathrm{Lim}}P\left(\left|\frac{IMSE\left(\lambda \right)}{n\lambda }\right|>\delta \right)\le \underset{n\to \infty }{\mathrm{Lim}}P\left(\left|IMSE\left(\lambda \right)\right|>\delta \right)=\mathbf{0}$; hence, $\underset{n\to \infty }{\mathrm{Lim}}P\left(\left|IMSE\left(\lambda \right)\right|\le \delta \right)=1$ is consistent.

4. Conclusions

The smoothing spline estimator with the RKHS approach has good ability to estimate the MNR model, which is a nonparametric regression model where the responses are correlated with each other, because the goodness of fit and smoothness of the estimation curve is controlled by the smoothing parameter, making the estimator very suitable for prediction purposes. Therefore, selection of the optimal smoothing parameter value cannot be omitted, and is crucial to good regression function fitting of the MNR model based on smoothing spline estimator using the RKHS approach. The estimator of the smoothing spline regression function of the MNR model that we obtained is linear with respect to the observations in Equation (22), and is a consistent estimator based on the integrated mean square error (IMSE) criterion. The main influence of this study is lies in the easier estimation of a multiresponse nonparametric regression model where there is a correlation between responses using the RKHS approach based on a smoothing spline estimator. This approach is easier, and faster, and more optimal, as estimation is carried out simultaneously instead of response by response for each observation. In addition, the theory generated in this study can be used to estimate the nonparametric component of the multiresponse semiparametric regression model used to model Indonesian toddlers’ standard growth charts. In the future, the results of this study can be further developed within the scope of statistical inference, especially for the purpose of testing hypotheses involving multiresponse nonparametric regression models and multiresponse semiparametric regression models.