A Critical Review of Works Pertinent to the Einstein-Bohr Debate and Bell’s Theorem
Abstract
:1. Introduction
- The probability related work of Bell-CHSH implies that the elements of physical reality are encompassed by a finite number of elements of physical reality, such as Bertelmann’s socks [1]. Relations of the Bell-CHSH elements of reality to continua, such as time-like variables (and corresponding stochastic processes) are incompatible with the Bell-CHSH proofs. Quantum probability for measurements of entangled entities implies no such limitations.
- Quantum mechanics makes ample use of symmetry laws and merges them with the probability approach by the proper choice of variables; such proper choice of variables may easily be made also for classical probability but Bell and CHSH did not do so.
- Bell used variations of Einstein’s separation principle that do not have a solid physical basis.
- Bell and CHSH were not aware of Vorobev’s mathematical theorem [16] that was published two years before Bell’s work and presents the necessary and sufficient condition for the validity of the theorems by Bell and CHSH: the existence of a combinatorial-topological cyclicity of the involved random variables on a probability space. This necessary and sufficient condition has no direct relation to the locality conditions introduced by Bell-CHSH as the basis for their theorems.
2. The EPR Gedanken Experiment and Its EPRB Implementation
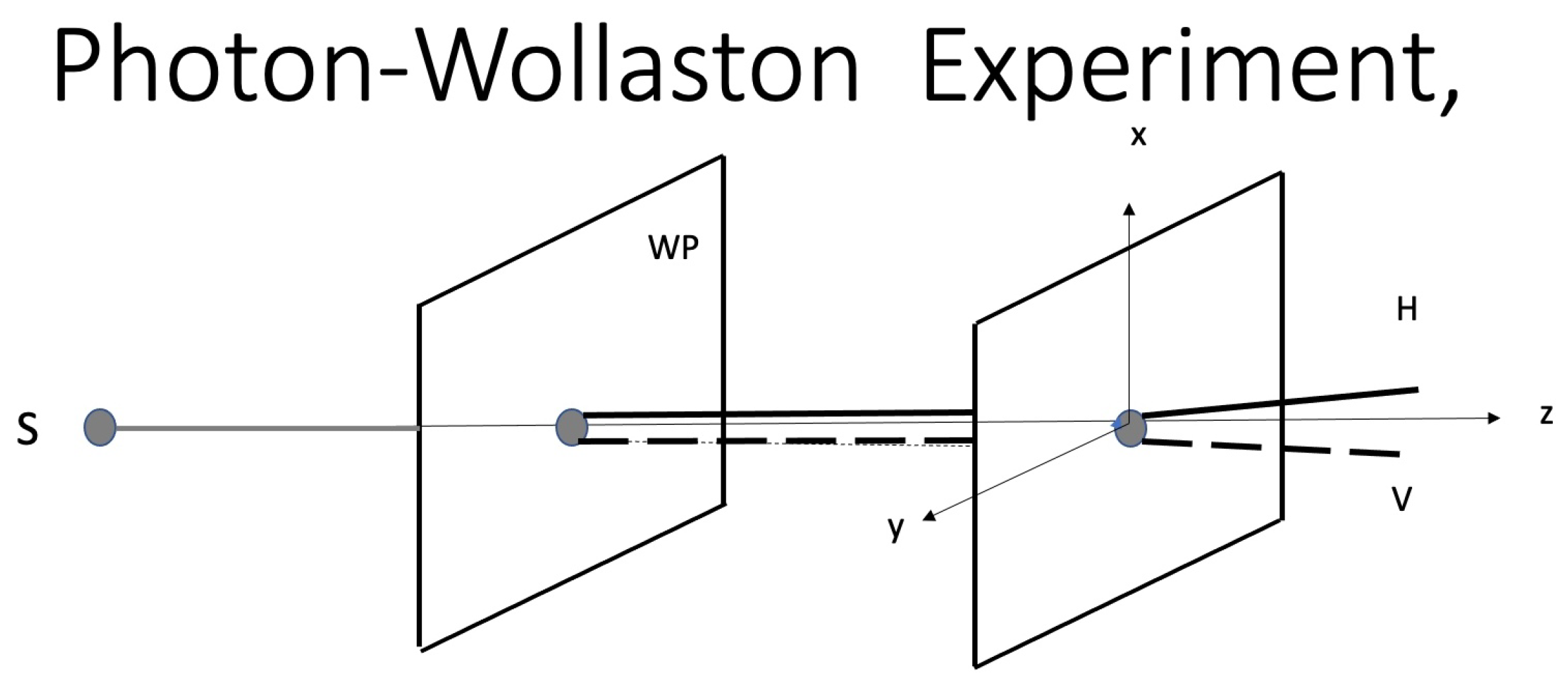
2.1. Measurements of Spin and Polarization
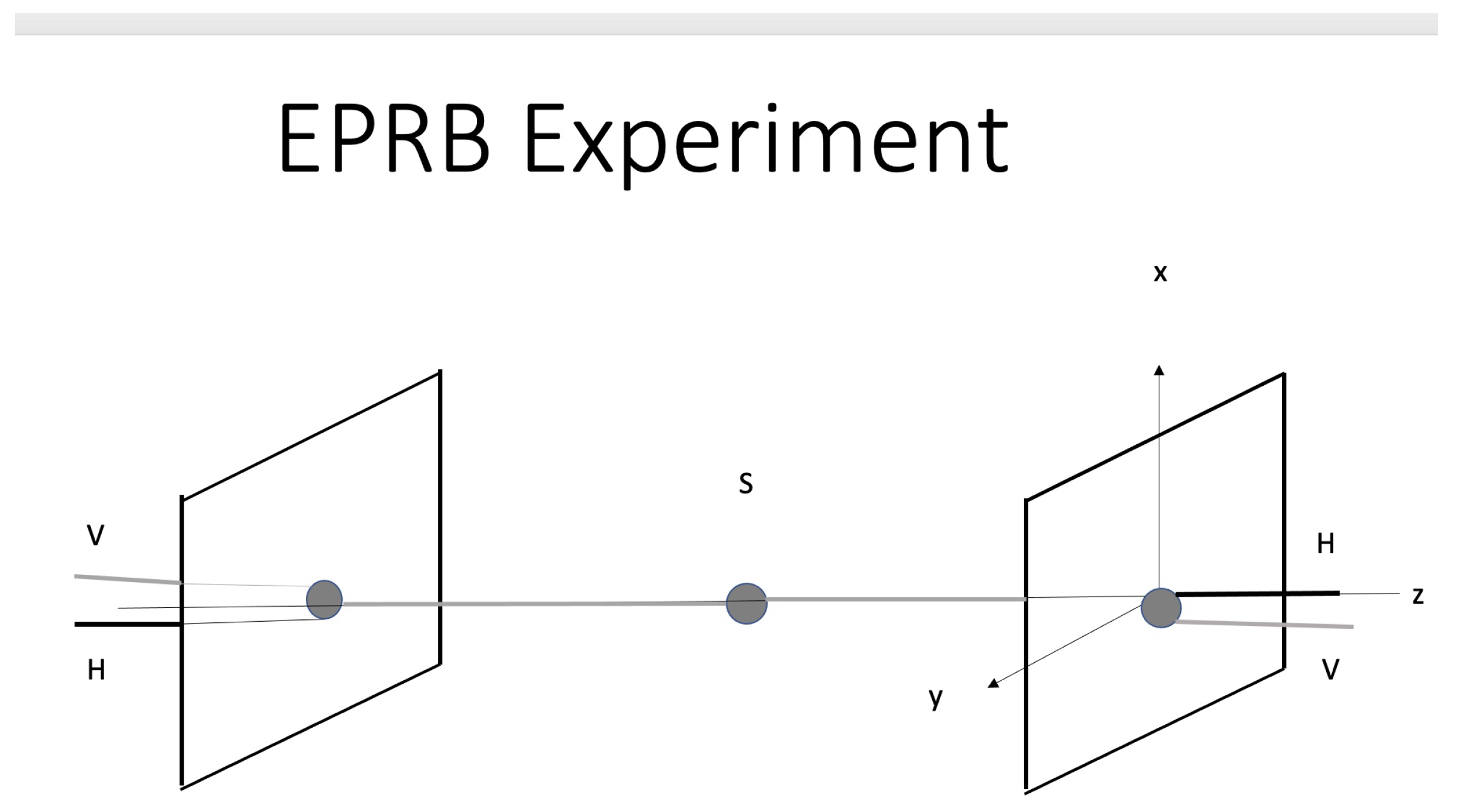
2.2. EPRB Experiments, Elements of Physical Reality and Entanglement
if, without in any way disturbing a system, we can predict with certainty...the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.
2.3. Measurements of Entangled Distant Quantum Entities
3. General Considerations for Modeling EPRB Experiments
3.1. Correlations and Einstein’s Separation Principle in Relativity
- All the laws for the elements of physical reality within the spaceships are the same and independent of the mostly constant velocities of the spaceships. They are, of course, also the same in the two stations of the EPRB experiments. In addition, physical law connects the two ships and two stations. For example, identical clocks within the two spaceships represent some of these physical laws, and their future readings are correlated in a nonlinear fashion depending on the relative velocities of the spaceships.Analogous facts, related to rotational symmetry, hold for the statistical correlations of EPRB experiments.
- Neither Alice nor Bob can give any prediction about the relative readings of their clocks as long as they have neither theoretical nor experimental knowledge about each other. Bell, CHSH and their followers demand that Alice and Bob still be able to predict the probability for the outcomes of their EPRB measurements in such a way that the outcomes have the precise correlation after merging the data taken in the two stations. This demand represents the core of what is called “the Bell game”.The fact that no one can play this game without involving nonlocal effects is taken by many as a proof for the validity of the Bell-CHSH theorems that are seen as consequence of locality assumptions. However, for the case of the two spaceships, the Bell game cannot be played either, as we know from the famous twin paradox. Nevertheless we do not suspect any non-localities or instantaneous influences at a distance in Einstein’s theory of relativity.What is overlooked by the Bell-game proponents is the fact that the data of the EPRB experiments are connected in pairs with help of an elaborate space and time system including clocks in the stations that identify and unite the two parts of the entangled pairs. EPRB experiments and their measurement results are not raw data that nature presents but are subject to symmetry laws involving our space–time system, which also determines the relevant physical variables.
- In the spaceship example, the velocity of Alice is a “gauge” variable that may be put equal to zero, thus, putting Alice at rest. The clock-reading of Bob depends on the difference of the velocity of his ship relative to Alice’s and does so in a nonlinear way. All of this follows from the invariance to the group of Lorentz transformations. If we assume that the relative clock readings of Alice and Bob depend on some absolute velocity of the spaceships, we would violate the relativistic symmetry.The symmetry governing EPRB experiments is the invariance under rotations and the EPRB experiments shown in the above figures are invariant to rotations around the z-axis. As a consequence, the Wollaston coordinates (-axis) in one given station must also be “gauge” variables that may be arbitrarily chosen. If we rotate the Wollaston of station 2 by an angle away from the x-axis, then that is the physical variable that describes the change of the statistical correlations as is well known from experiments [5] and quantum theory [18].
3.2. Classical vs. Quantum Probability: Macroscopic Configurations, Symmetries
3.2.1. General Considerations
3.2.2. Important Aspects Dealing with Observables and Random Variables
4. EPRB Models and Random Variables
4.1. Precise Bell-Type Model with Random Wollaston Orientation
- This reminds us that we are dealing with a different entangled pair (the use of a number n is also sufficient for this purpose).
- Kocher [21] has shown that the pair emissions from the source exhibit some time dependence. Therefore, for the quantitative description of such experiments the measurement times are needed.
- We also cannot exclude interactions with the measurement equipment that may depend, for example, on both the Wollaston angle and certain interaction times.
- The measurement time is needed to identify entangled pairs.
4.2. The Actual Model of Bell-CHSH
“Confusion buried deep in the formalism of very general critiques tends to rise to the surface and reveal itself when such critiques are reduced to the language of my very elementary example.”
5. Vorob’ev and Bell-CHSH-Type Theorems: Constraints for Multiple Pair Measurements
5.1. The Theorem of Vorob’ev
5.2. Theorems of Bell-CHSH and Connection to Vorob’ev’s Cyclicity
5.3. Violations of Probability Syntax by Quadruple Function-Pairs of CHSH
5.4. Are the Wollaston Angles Genuine Physical Variables?
6. Can Bell-CHSH Be Saved?
6.1. Counterfactual Reasoning
6.2. Reordering of the Elements of Reality
6.3. Listing of Imagined Triples (Another Counterfactual Idea)
6.4. Bell’s Factorization and Outcome Independence
7. Bell-Type Models Violating the Quantum Result
7.1. Larsson’s Pie Chart
7.2. The Malus Law and EPRB
7.2.1. Problems with the Double Malus Model
7.2.2. Single Malus Model
8. Why Bell-CHSH Cannot Be Saved: An Explicit Einstein-Local Counterexample
8.1. Closing Loopholes
8.2. The Bell Game
9. Consequences of Removing Bell-CHSH Constraints as Physical Constraints for EPRB Experiments
9.1. Summary of the Validity of Bell-CHSH
9.2. Consequences for the Quantum Interpretation
9.3. The Nature of Entanglement and Quantum Nonlocalities
10. A Summarizing View of Bell-CHSH
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gilder, L. The Age of Entanglement: When Quantum Physics Was Reborn; Alfred A. Knopf: New York, NY, USA, 2008. [Google Scholar]
- Hess, K. Einstein Was Right; Pan Stanford Publishing: Singapore, 2015. [Google Scholar]
- Nordén, B. Quantum entanglement: facts and fiction- how wrong was Einstein after all. QRB Discov. 2016, 49, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum mechanical description of physical reality be considered complete? Phys. Rev. 1935, 16, 777–780. [Google Scholar] [CrossRef] [Green Version]
- Kocher, C.A.; Commins, E.D. Polarization correlation of photons emitted in an atomic cascade. Phys. Rev. Lett. 1967, 18, 575–577. [Google Scholar] [CrossRef] [Green Version]
- Bell, J.S. On the Einstein Podolsky Rosen Paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef] [Green Version]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef] [Green Version]
- Aspect, A.; Dalibard, J.; Roger, J. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef] [Green Version]
- Weihs, G.; Jennewein, T.; Simon, C.; Weinfurther, H.; Zeilinger, A. A violation of Bell’s inequality under strict Einstein local conditions. Phys. Rev. Lett. 1998, 81, 5039–5043. [Google Scholar] [CrossRef] [Green Version]
- Kwiat, P.G.; Waks, E.; White, A.G.; Appelbaum, I.; Eberhard, P.H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 1999, 60, 773–776. [Google Scholar] [CrossRef] [Green Version]
- Giustina, M.; Versteegh, M.A.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.; Abellán, C. Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Phys. Rev. Lett. 2015, 115, 25401. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.; Zeilinger, A. Going beyond Bell’s theorem. In Bell’s Theorem, Quantum Theory and Conceptions of the Universe; Kafatos, M., Ed.; Kluwer Academic: Dordrecht, The Netherlands, 1989; pp. 73–76. [Google Scholar]
- Mermin, N.D. What is wrong with these elements of reality? Phys. Today 1990, 43, 9–10. [Google Scholar]
- Aschwanden, M.; Philippe, W.; Hess, K.; Barraza-Lopez, S.; Adenier, G. Local Time Dependent Instruction-set Model for the experiment of Pan et al. AIP Conf. Proc. 2006, 810, 437–445. [Google Scholar]
- Kupczynski, M. Is the Moon There if Nobody Looks: Bell Inequalities and Physical Reality. Front. Phys. 2020, 8, 1–13. [Google Scholar] [CrossRef]
- Vorob’ev, N.N. Consistent families of measures and their extension. Theory Probab. Appl. 1962, 7, 147–163. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley Series in Probability and Mathematical Statistics; Wiley: New York, NY, USA, 1968; pp. 1–9. [Google Scholar]
- Larsson, J.-A. Quantum Paradoxes, Probability Theory, and Change of Ensemble; Linkoping Studies in Science and Technology, Dissertations No. 654; Linköpings University: Linköping, Sweden, 2000. [Google Scholar]
- Hess, K.; Philipp, W. Breakdown of Bell’s theorem for certain objective local parameter spaces. Proc. Natl. Acad. Sci. USA 2004, 101, 1799–1805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hess, K. What do Bell tests Prove? A Detailed critique of Clauser-Horne-Shimony-Holt Including Counterexamples. J. Mod. Phys. 2021, 12, 1219–1236. [Google Scholar] [CrossRef]
- Kocher, C.A. Time Correlations in the Detection of Successively Emitted Photons. Ann. Phys. 1971, 65, 1–18. [Google Scholar] [CrossRef]
- Hess, K.; Philipp, W. The Bell Theorem as a Special Case of a Theorem of Bass. Found. Phys. 2005, 35, 1749–1767. [Google Scholar] [CrossRef] [Green Version]
- De Raedt, H.; Michielsen, K.; Hess, K. The Photon Identification Loophole in EPRB Experiments: computer models with single wing selection. Open Phys. 2017, 15, 713–733. [Google Scholar] [CrossRef] [Green Version]
- Leggett, A.J. The Problems of Physics; Oxford University Press: Oxford, NY, USA, 1987. [Google Scholar]
- Mermin, N.D. Reply to the comment by K. Hess and W. Philipp on “Inclusion of Time in the Theorem of Bell”. Europhys. Lett. 2004, 67, 693–694. [Google Scholar] [CrossRef]
- Mermin, N.D. What’s Wrong with this Criticism. Found. Phys. 2005, 35, 2073–2077. [Google Scholar] [CrossRef]
- Lad, F. Quantum Mysteries for No One. J. Mod. Phys. 2021, 12, 1366–1399. [Google Scholar] [CrossRef]
- Christian, J. Disproof of Bell’s Theorem; Brown Walker Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hess, K.; Philipp, W.; Aschwanden, M. What is Quantum Information? Int. J. Quantum Inf. 2006, 4, 585–625. [Google Scholar] [CrossRef]
- Hess, K.; Philipp, W. Comment on papers by Gill, and Gill, Weihs, Zeilinger and Zukowski. arXiv 2003, arXiv:quant-ph/0307092v1. [Google Scholar]
- Khrennikov, A. Has the CHSH-Inequality any relation to the EPR-Argument? Quantum Bio-Inform. 2020, 5, 87–92. [Google Scholar]
- Oaknin, D.H. Bell’s theorem revisited: geometric phases in gauge theories. Front. Phys. 2020, 8, 142–162. [Google Scholar] [CrossRef]
- Oaknin, D.H.; Hess, K. On the role of Vorob’ev cyclicities and Berry’s phase in the EPR paradox and Bell tests. arXiv 2020, arXiv:2008.02633v1. [Google Scholar]
- Rauch, D.; Handsteiner, J.; Hochrainer, A.; Gallicchio, J.; Friedman, A.S.; Leung, C.; Liu, B.; Bulla, L.; Ecker, S.; Steinlechner, F.; et al. Cosmic Bell test using random measurement settings from high-redshift quasars. Phys. Rev. Lett. 2018, 121, 080403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- The Big Bell Test Collaboration. Challenging local realism with human choices. Nature 2018, 557, 212–216. [Google Scholar] [CrossRef] [Green Version]
- Hossenfelder, S.; Palmer, T. Rethinking Superdeterminism. Front. Phys. 2020, 87, 139. [Google Scholar] [CrossRef]
- D’espagnat, B. The Quantum Theory and Reality. Sci. Am. 1979, 241, 158–181. [Google Scholar] [CrossRef]
- Hess, K.; De Raedt, H.; Michielsen, K. Analysis of Wigner’s Set Theoretical Proof for Bell-Type Inequalities. J. Mod. Phys. 2017, 8, 57–67. [Google Scholar] [CrossRef] [Green Version]
- Leggett, A.J. Nonlocal Hidden-Variable theories and Quantum Mechanics: An Incompatibility Theorem. Found. Phys. 2003, 33, 1469–1493. [Google Scholar] [CrossRef]
- Khrennikov, A. (Ed.) Foundations of Probability and Physics; World Scientific: London, UK, 2000. [Google Scholar]
- Accardi, L. Topics in quantum probability. Phys. Rep. 1981, 77, 169–192. [Google Scholar] [CrossRef]
- Jung, K. Polarization Correlation of Entangled Photons Derived without Using Non-Local Interactions. Front. Phys. 2020, 8, 170. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman lectures on Physics III; Addison-Wesley: Reading, MA, USA, 1965. [Google Scholar]
- Annila, A.; Wikström, M. Quantum Entanglement: Bell’s Inequality Trivially Violated also Classically. 2021. Available online: https://viXra.org/abs/2112.0118 (accessed on 28 December 2021).
- Pearle, P.M. Hidden-variable example based on data rejection. Phys. Rev. D 1970, 2, 1418–1425. [Google Scholar] [CrossRef]
- Hooft, G. Deterministic Quantum Mechanics: The Mathematical Equations. Front. Phys. 2020, 8, 1–12. [Google Scholar] [CrossRef]
- Bennet, C.H.; Brassard, G.; Crepeau, C.; Josca, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [Green Version]
- Hess, K. Categories of Nonlocality in EPR Theories and the Validity of Einstein’s Separation Principle as well as Bell’s Theorem. J. Mod. Phys. 2019, 10, 1209–1221. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hess, K. A Critical Review of Works Pertinent to the Einstein-Bohr Debate and Bell’s Theorem. Symmetry 2022, 14, 163. https://doi.org/10.3390/sym14010163
Hess K. A Critical Review of Works Pertinent to the Einstein-Bohr Debate and Bell’s Theorem. Symmetry. 2022; 14(1):163. https://doi.org/10.3390/sym14010163
Chicago/Turabian StyleHess, Karl. 2022. "A Critical Review of Works Pertinent to the Einstein-Bohr Debate and Bell’s Theorem" Symmetry 14, no. 1: 163. https://doi.org/10.3390/sym14010163
APA StyleHess, K. (2022). A Critical Review of Works Pertinent to the Einstein-Bohr Debate and Bell’s Theorem. Symmetry, 14(1), 163. https://doi.org/10.3390/sym14010163





