A Simple Method for Compensating Harmonic Distortion in Current Transformers: Experimental Validation
Abstract
:1. Introduction
2. Harmonic Distortion Compensation Technique
2.1. Polynomial Representation of HD
2.2. HD Compensation Technique
2.3. Simplified Approach
3. Numerical Simulations
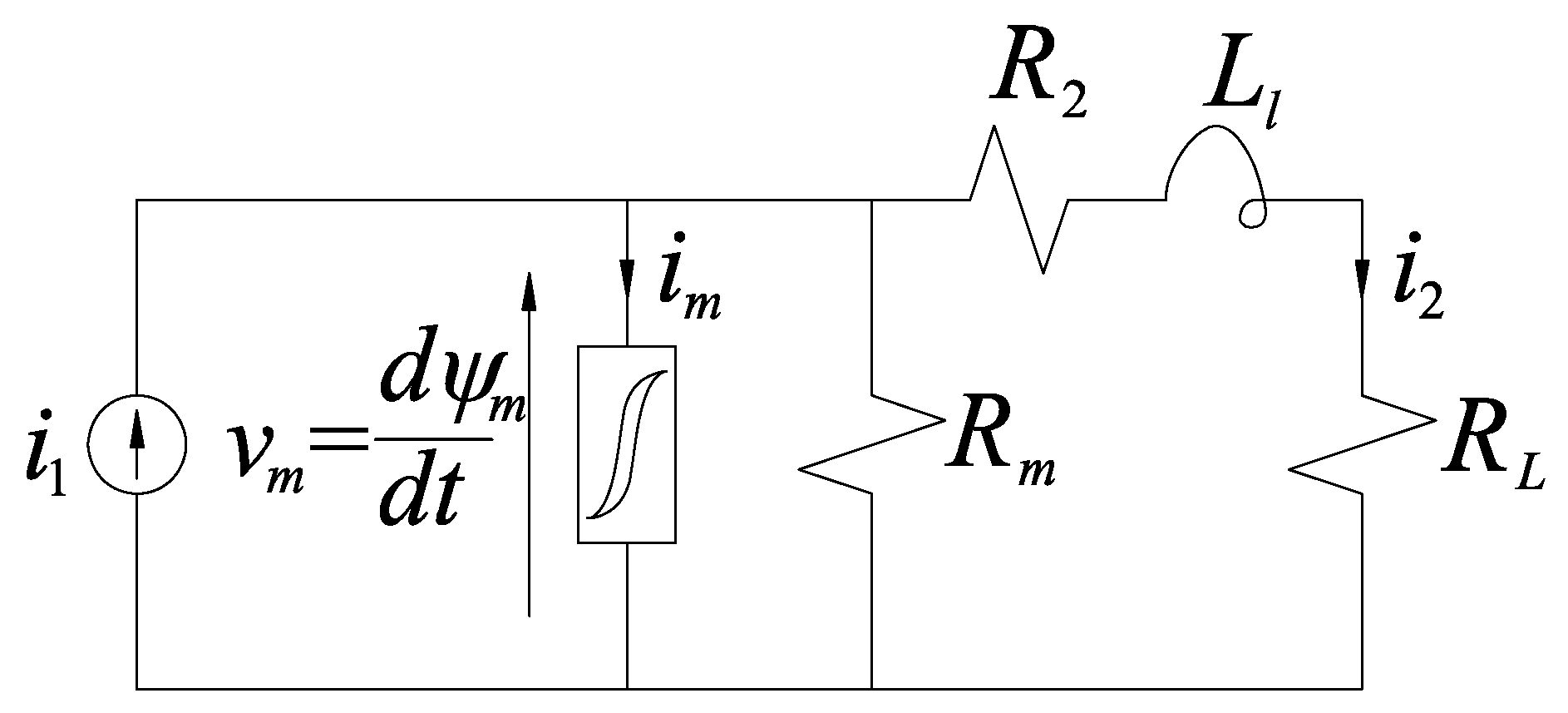
3.1. Reference Model of the CT
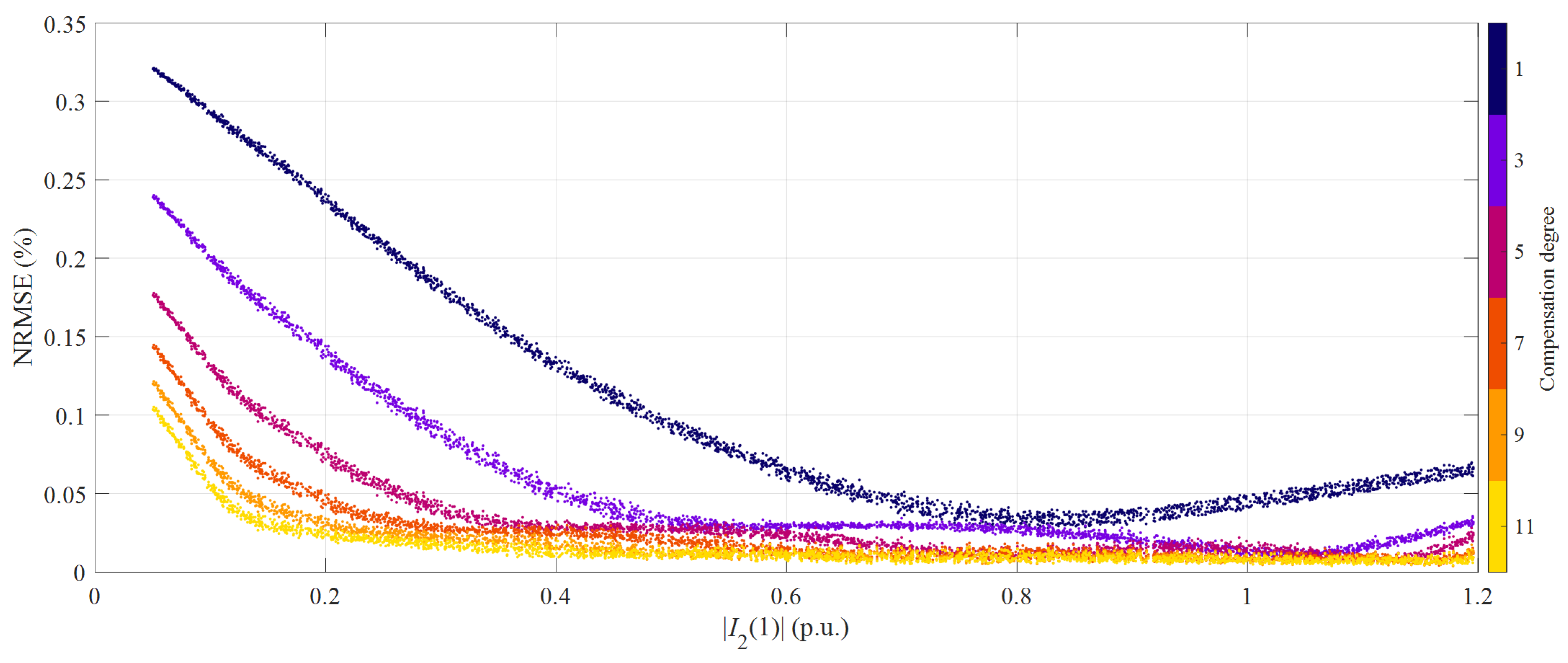
3.2. Simulation Results
4. Experimental Setup
5. Experimental Results
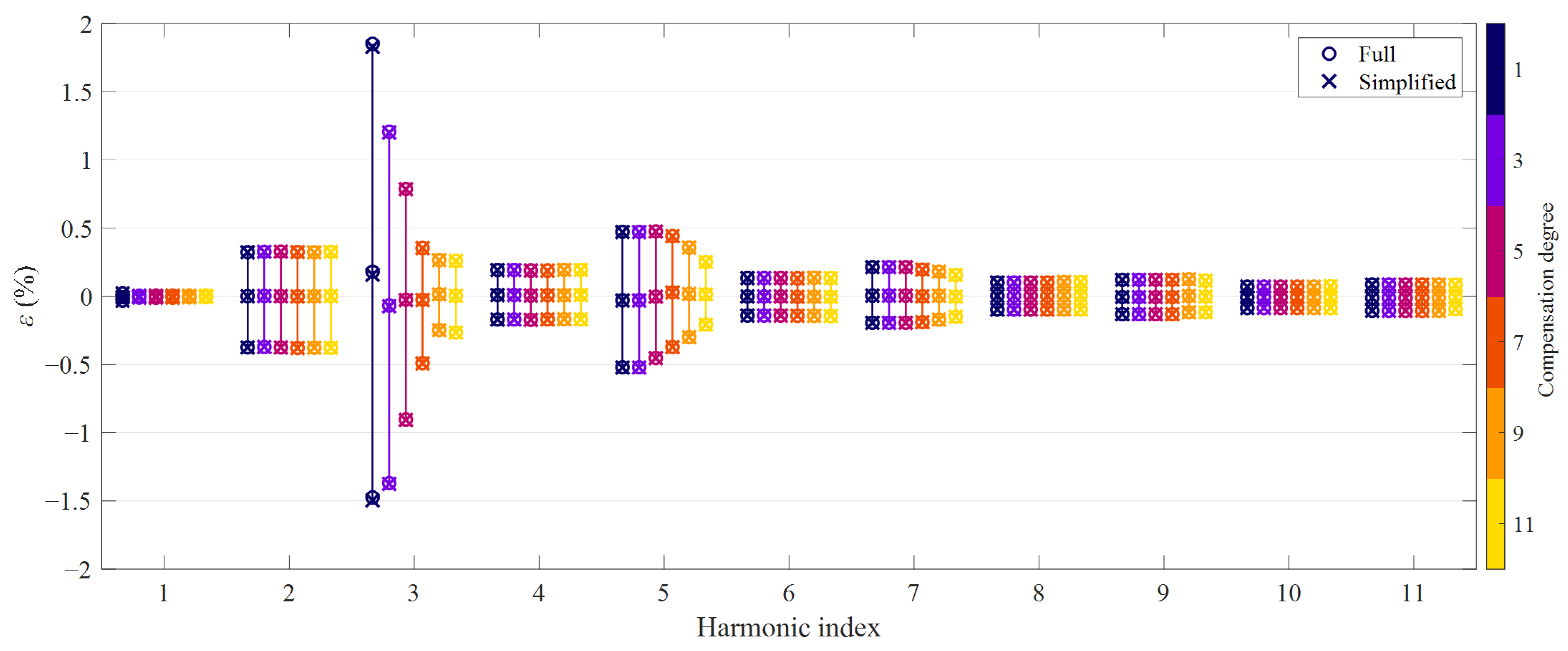
5.1. Tests on CT1
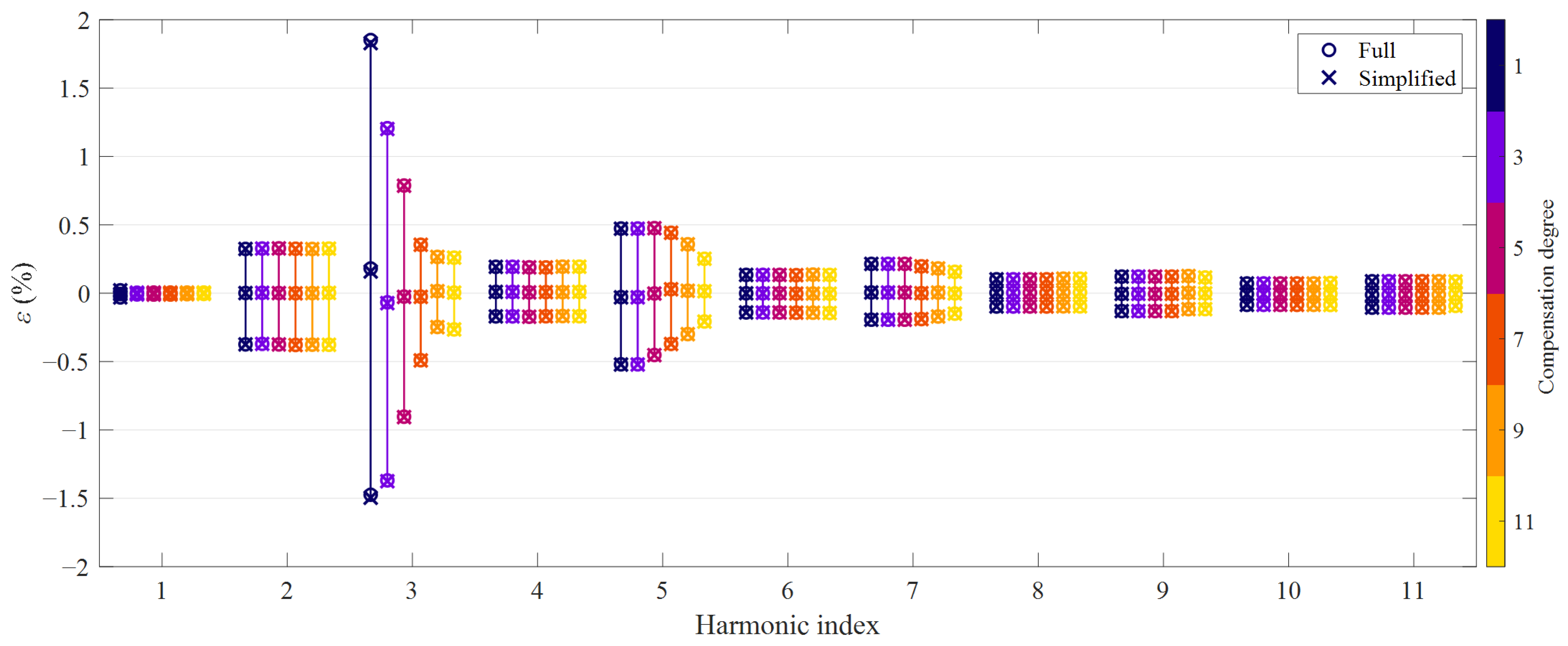
5.2. Tests on CT2
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lee, B.E.; Lee, J.; Won, S.H.; Lee, B.; Crossley, P.A.; Kang, Y.C. Saturation detection-based blocking scheme for transformer differential protection. Energies 2014, 7, 4571–4587. [Google Scholar] [CrossRef]
- Bittanti, S.; Cuzzola, F.A.; Lorito, F.; Poncia, G. Compensation of nonlinearities in a current transformer for the reconstruction of the primary current. IEEE Trans. Control Syst. Technol. 2001, 9, 565–573. [Google Scholar] [CrossRef]
- Pan, J.; Vu, K.; Hu, Y. An efficient compensation algorithm for current transformer saturation effects. IEEE Trans. Power Del. 2004, 19, 1623–1628. [Google Scholar] [CrossRef]
- Haghjoo, F.; Pak, M.H. Compensation of CT distorted secondary current waveform in online conditions. IEEE Trans. Power Del. 2016, 31, 711–720. [Google Scholar] [CrossRef]
- Montoya, F.G.; Baños, R.; Alcayde, A.; Montoya, M.G.; Manzano-Agugliaro, F. Power Quality: Scientific Collaboration Networks and Research Trends. Energies 2018, 11, 2067. [Google Scholar] [CrossRef] [Green Version]
- D’Antona, G.; Muscas, C.; Pegoraro, P.A.; Sulis, S. Harmonic source estimation in distribution systems. IEEE Trans. Instrum. Meas. 2011, 60, 3351–3359. [Google Scholar] [CrossRef]
- Cristaldi, L.; Ferrero, A. Harmonic power flow analysis for the measurement of the electric power quality. IEEE Trans. Instrum. Meas. 1995, 44, 683–685. [Google Scholar] [CrossRef]
- Granados-Lieberman, D. Global harmonic parameters for estimation of power quality indices: An approach for PMUs. Energies 2020, 13, 2337. [Google Scholar] [CrossRef]
- Castello, P.; Laurano, C.; Muscas, C.; Pegoraro, P.A.; Toscani, S.; Zanoni, M. Harmonic synchrophasors measurement algorithms with embedded compensation of voltage transformer frequency response. IEEE Trans. Instrum. Meas. 2021, 70. [Google Scholar] [CrossRef]
- IEC Standard 61869-2:2012. Instrument Transformers—Part 2: Additional Requirements for Current Transformers; IEC: Geneva, Switzerland, 2012. [Google Scholar]
- IEC Standard 61869-6:2016. Instrument Transformers—Part 6: Additional General Requirements for Low-Power Instrument Transformers; IEC: Geneva, Switzerland, 2016. [Google Scholar]
- Cataliotti, A.; Di Cara, D.; Emanuel, A.E.; Nuccio, S. A novel approach to current transformer characterization in the presence of harmonic distortion. IEEE Trans. Instrum. Meas. 2009, 58, 1446–1453. [Google Scholar] [CrossRef]
- Emanuel, A.E.; Orr, J.A. Current harmonics measurement by means of current transformers. IEEE Trans. Power Del. 2007, 22, 1318–1325. [Google Scholar] [CrossRef]
- Locci, N.; Muscas, C. Comparative analysis between active and passive current transducers in sinusoidal and distorted conditions. IEEE Trans. Instrum. Meas. 2001, 50, 123–128. [Google Scholar] [CrossRef]
- Kaczmarek, M. Measurement error of non-sinusoidal electrical power and energy caused by instrument transformers. IET Gener. Transm. Distrib. 2016, 10, 3492–3498. [Google Scholar] [CrossRef]
- Kondrath, N.; Kazimierczuk, M.K. Bandwidth of Current Transformers. IEEE Trans. Instrum. Meas. 2009, 58, 2008–2016. [Google Scholar] [CrossRef]
- Dadić, M.; Mostarac, P.; Malarić, R. Wiener filtering for real-time DSP compensation of current transformers over a wide frequency range. IEEE Trans. Instrum. Meas. 2017, 66, 3023–3031. [Google Scholar] [CrossRef]
- Gallo, D.; Landi, C.; Luiso, M. Real-time digital compensation of current transformers over a wide frequency range. IEEE Trans. Instrum. Meas. 2010, 59, 1119–1126. [Google Scholar] [CrossRef]
- Ballal, M.S.; Wath, M.G.; Suryawanshi, H.M. A novel approach for the error correction of CT in the presence of harmonic distortion. IEEE Trans. Instrum. Meas. 2019, 68, 4015–4027. [Google Scholar] [CrossRef]
- Stano, E.; Kaczmarek, M. Wideband self-calibration method of inductive CTs and verification of determined values of current and phase errors at harmonics for transformation of distorted current. Sensors 2020, 20, 2167. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, M.; Stano, E. Nonlinearity of Magnetic Core in Evaluation of Current and Phase Errors of Transformation of Higher Harmonics of Distorted Current by Inductive Current Transformers. IEEE Access 2020, 8, 118885–118898. [Google Scholar] [CrossRef]
- Collin, A.J.; Delle Femine, A.; Gallo, D.; Langella, R.; Luiso, M. Compensation of current transformers’ nonlinearities by tensor linearization. IEEE Trans. Instrum. Meas. 2019, 68, 3841–3849. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Characterization of voltage instrument transformers under nonsinusoidal conditions based on the best linear approximation. IEEE Trans. Instrum. Meas. 2018, 67, 2392–2400. [Google Scholar] [CrossRef]
- Faifer, M.; Ottoboni, R.; Prioli, M.; Toscani, S. Simplified modeling and identification of nonlinear systems under quasi-sinusoidal conditions. IEEE Trans. Instrum. Meas. 2016, 65, 1508–1515. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Prioli, M.; Toscani, S.; Zanoni, M. Definition of simplified frequency-domain Volterra models with quasi-sinusoidal input. IEEE Trans. Circuits Syst. I Reg. Papers 2018, 65, 1652–1663. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M.; Crotti, G.; Mazza, P. Overcoming frequency response measurements of voltage transformers: An approach based on quasi-sinusoidal Volterra models. IEEE Trans. Instrum. Meas. 2019, 68, 2800–2807. [Google Scholar] [CrossRef]
- Toscani, S.; Faifer, M.; Ferrero, A.M.; Laurano, C.; Ottoboni, R.; Zanoni, M. Compensating nonlinearities in voltage transformers for enhanced harmonic measurements: The Simplified Volterra Approach. IEEE Trans. Power Del. 2021, 36, 362–370. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Harmonic distortion compensation in voltage transformers for improved power quality measurements. IEEE Trans. Instrum. Meas. 2019, 58, 3823–3830. [Google Scholar] [CrossRef]
- Cataliotti, A.; Cosentino, V.; Crotti, G.; Delle Femine, A.; Di Cara, D.; Gallo, D.; Tinè, G. Compensation of nonlinearity of voltage and current instrument transformers. IEEE Trans. Instrum. Meas. 2019, 68, 1322–1332. [Google Scholar] [CrossRef]
- Laurano, C.; Toscani, S.; Zanoni, M. Improving the accuracy of current transformers through harmonic distortion compensation. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference, Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar]
- Mathews, V.J.; Sicuranza, G.L. Polynomial Signal Processing; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Mingotti, A.; Peretto, L.; Bartolomei, L.; Cavaliere, D.; Tinarelli, R. Are inductive current transformers performance really affected by actual distorted network conditions? An experimental case study. Sensors 2020, 20, 927. [Google Scholar] [CrossRef] [Green Version]
- Tellinen, J. A simple scalar model for magnetic hysteresis. IEEE Trans. Magn. 1998, 34, 2200–2206. [Google Scholar] [CrossRef]
- Cristaldi, L.; Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. A low-cost generator for testing and calibrating current transformers. IEEE Trans. Instrum. Meas. 2019, 68, 2792–2799. [Google Scholar] [CrossRef]
- Faifer, M.; Ferrero, A.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. An innovative approach to express uncertainty introduced by voltage transformers. IEEE Trans. Instrum. Meas. 2020, 69, 6696–6703. [Google Scholar] [CrossRef]


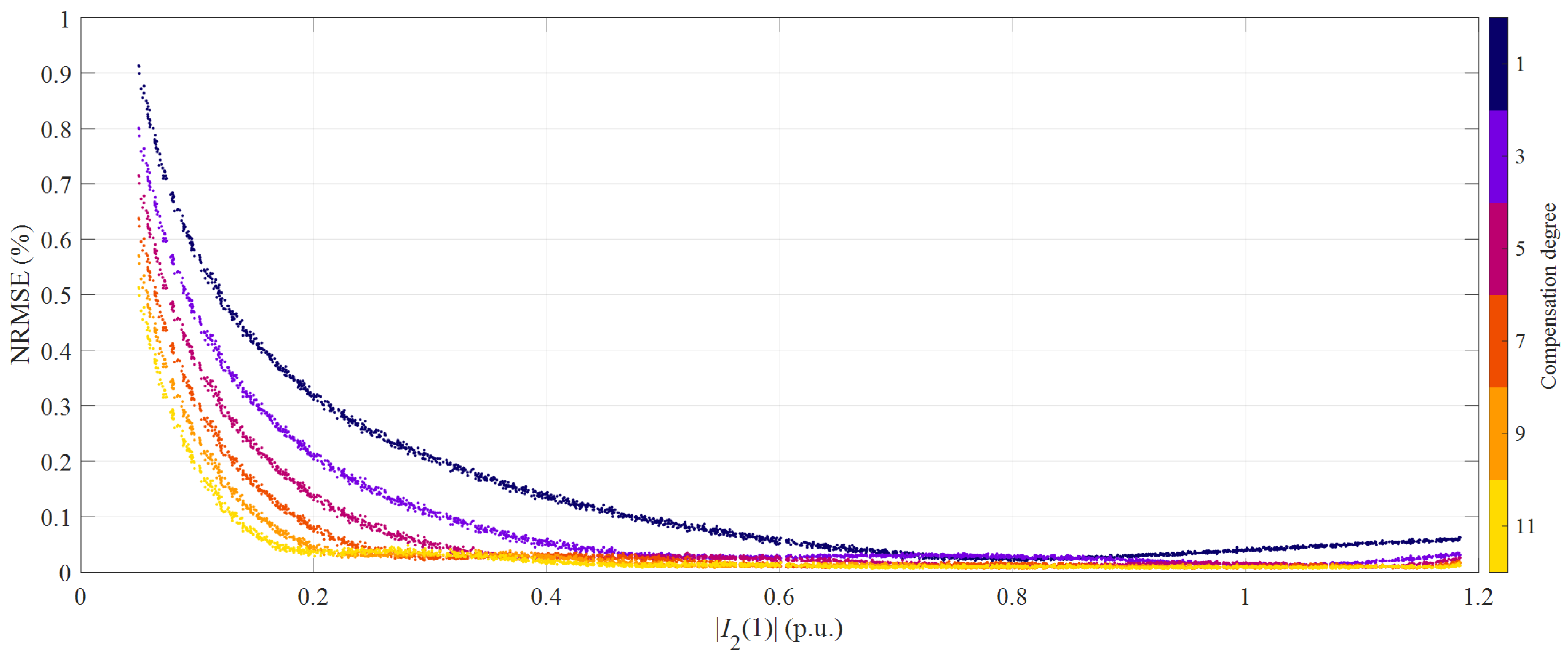
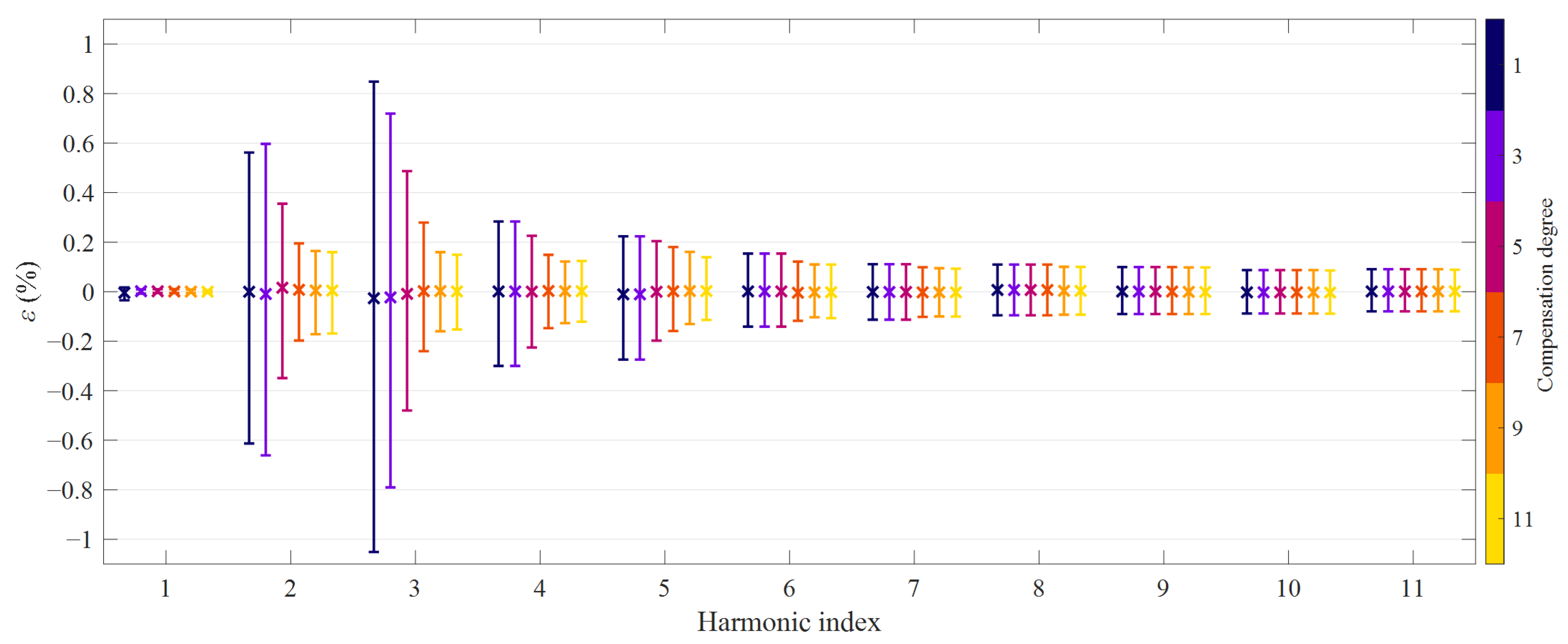
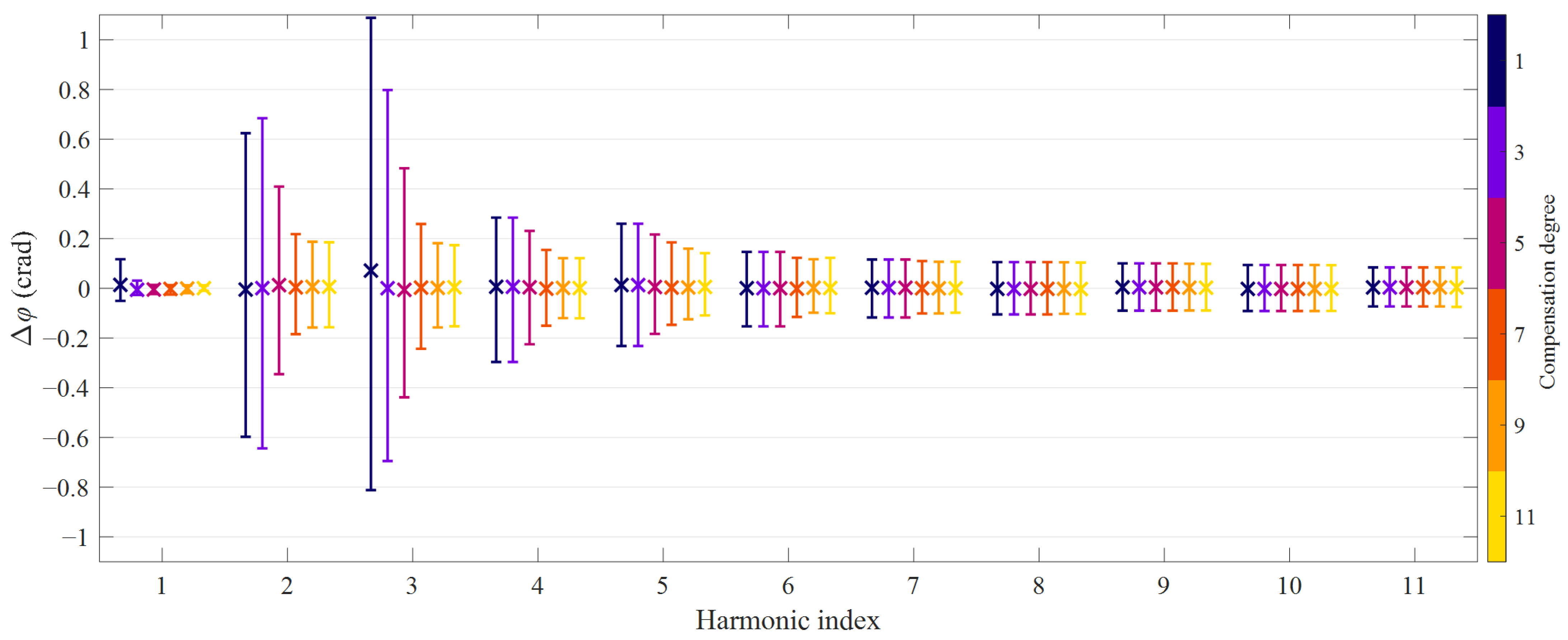

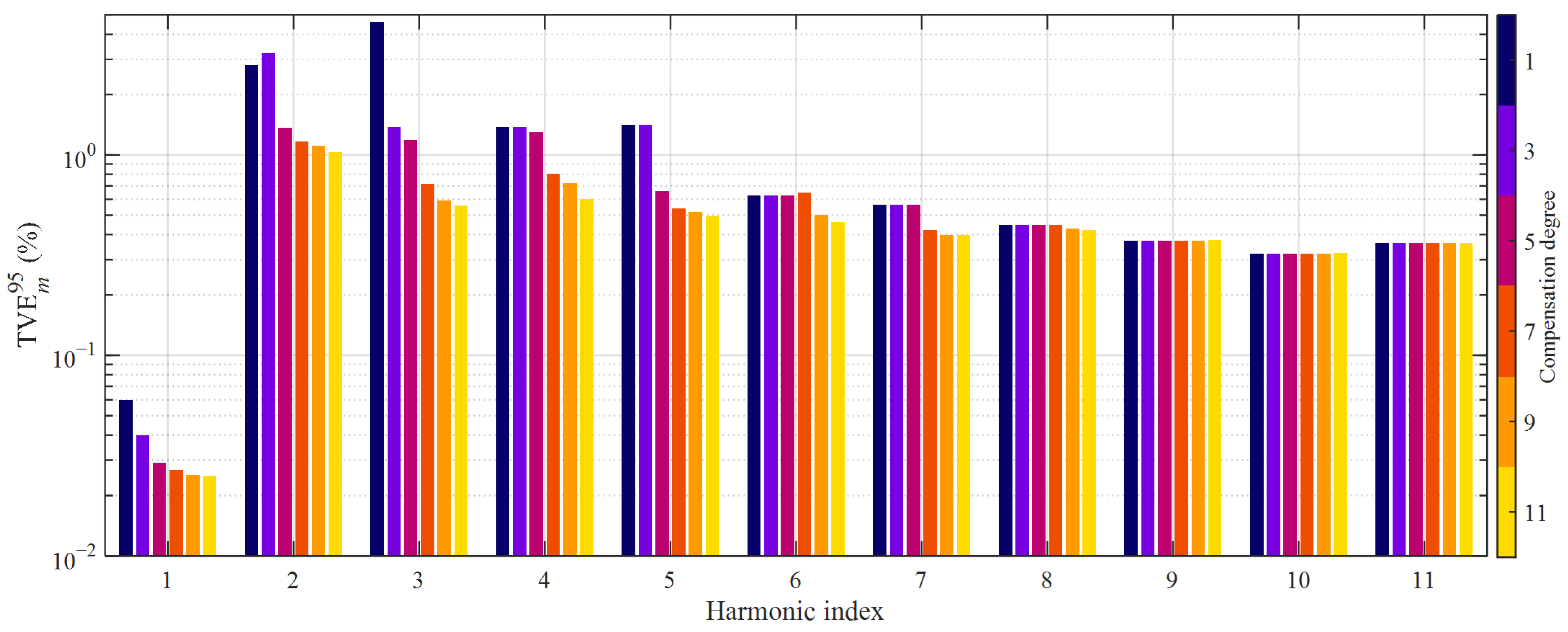
| Rm (Ω) | R2 (Ω) | Ll (μH) | RL (Ω) |
|---|---|---|---|
| 250 | 0.1 | 43 | 0.4 |
| Vmax (V) | Imax (A) | Frequency Response | THD | SNR (dB) | Voltage Gain |
|---|---|---|---|---|---|
| 200 | 43 | 0–30 kHz +0.1, −0.5 dB | <0.1% DC–30 kHz | >120 | 20 |
| I1n (A) | I2n (A) | Class | Burden (VA) |
|---|---|---|---|
| 50 | 5 | 0.5 | 10 |
| I1n (A) | I2n (A) | Class | Burden (VA) |
|---|---|---|---|
| 10 | 5 | 0.2 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laurano, C.; Toscani, S.; Zanoni, M. A Simple Method for Compensating Harmonic Distortion in Current Transformers: Experimental Validation. Sensors 2021, 21, 2907. https://doi.org/10.3390/s21092907
Laurano C, Toscani S, Zanoni M. A Simple Method for Compensating Harmonic Distortion in Current Transformers: Experimental Validation. Sensors. 2021; 21(9):2907. https://doi.org/10.3390/s21092907
Chicago/Turabian StyleLaurano, Christian, Sergio Toscani, and Michele Zanoni. 2021. "A Simple Method for Compensating Harmonic Distortion in Current Transformers: Experimental Validation" Sensors 21, no. 9: 2907. https://doi.org/10.3390/s21092907







