Nucleation and Post-Nucleation Growth in Diffusion-Controlled and Hydrodynamic Theory of Solidification
Abstract
:1. Introduction
2. Materials and Methods
2.1. Phase-Field Crystal Method
2.1.1. Thermodynamics
2.1.2. Equations of Motion (EOMs)
2.2. Numerical Methods
2.3. Materials Parameters
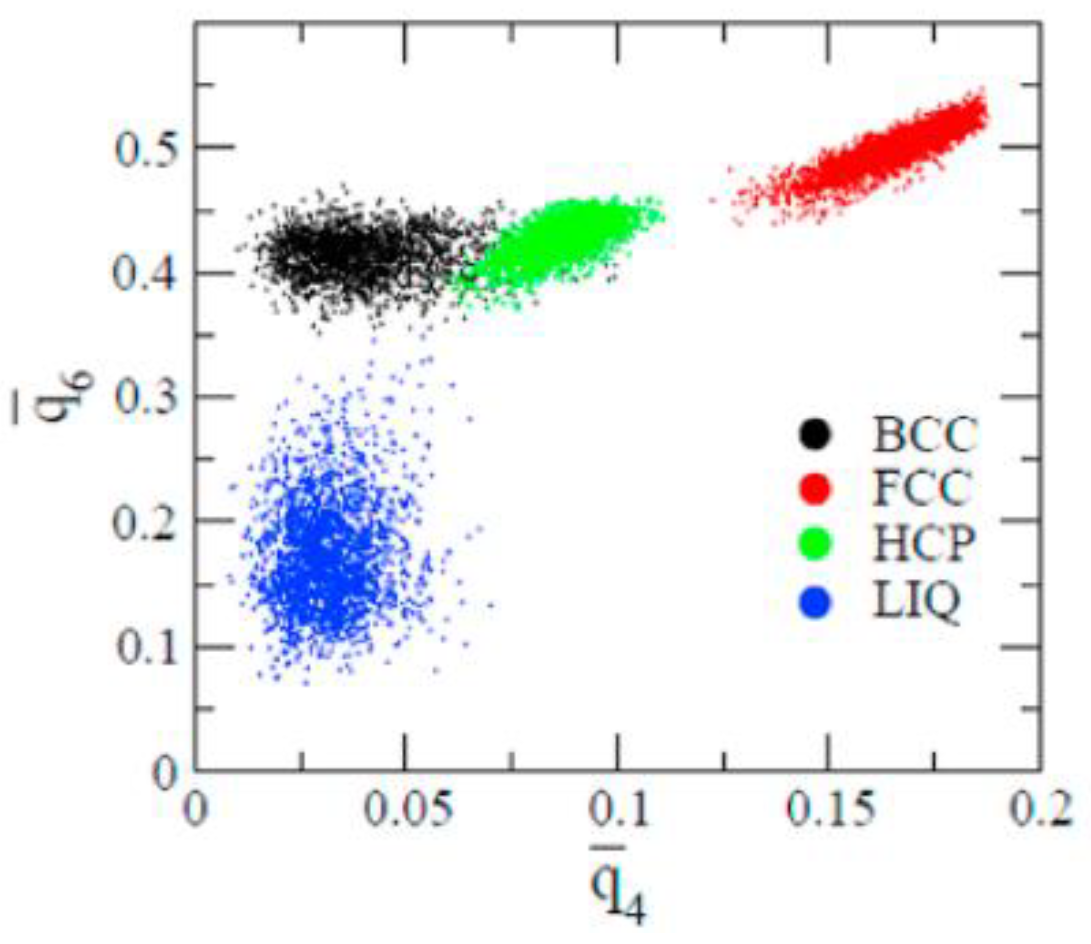
2.4. Structural Analysis
3. Results and Discussion
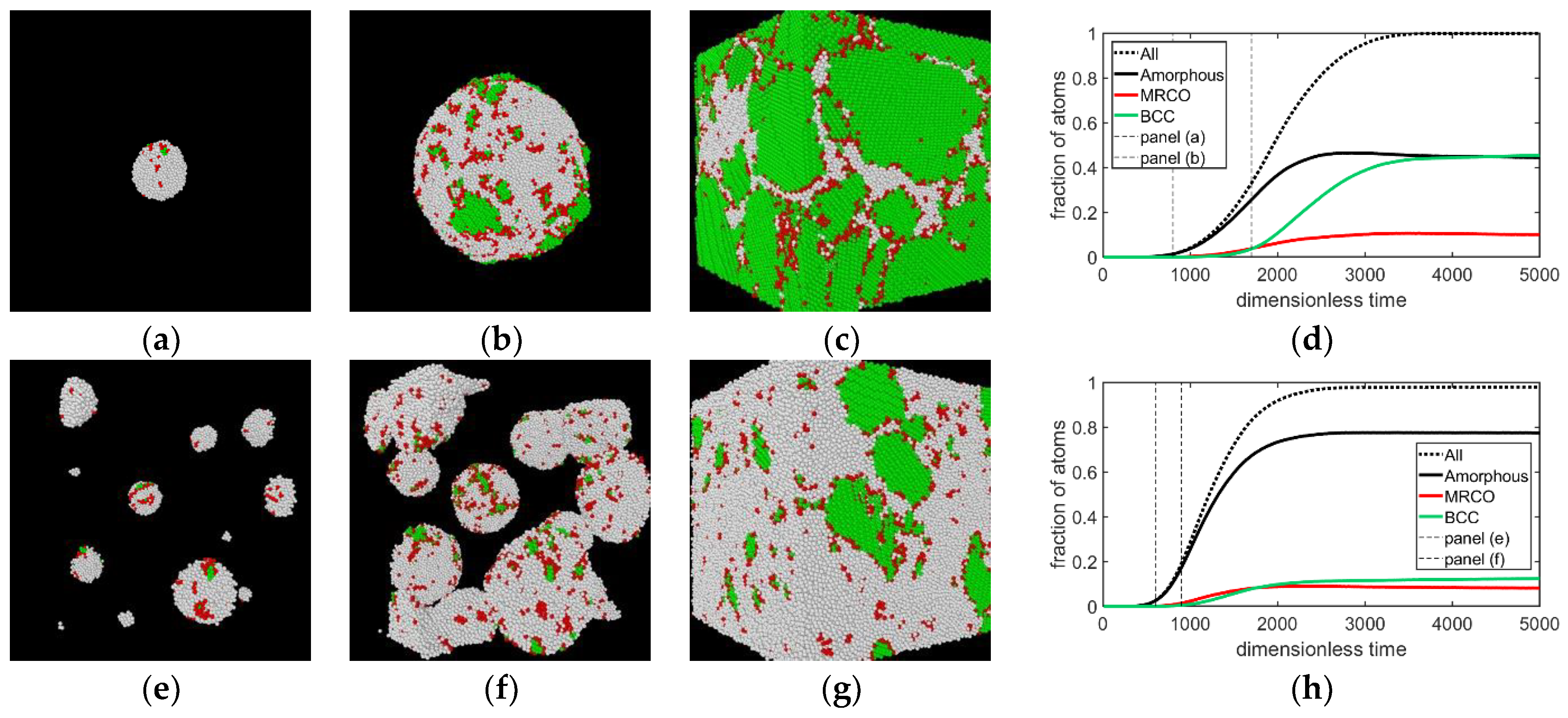
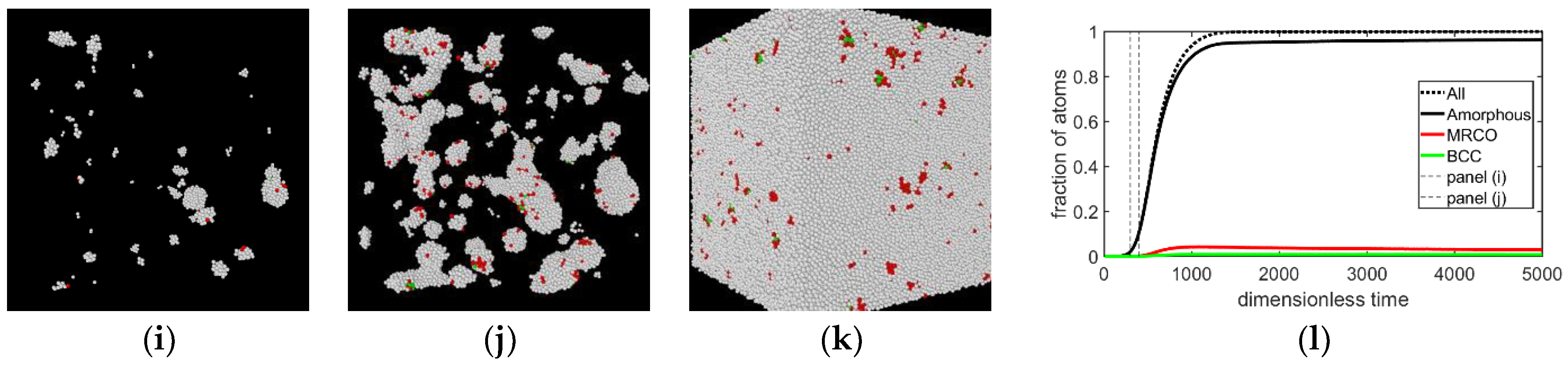
3.1. Two-Step Nucleation
3.2. Structure Evolution during Nucleation
3.3. Post-Nucleation Growth
3.4. Flat-Front Growth in the sHPFC Model
4. Conclusions
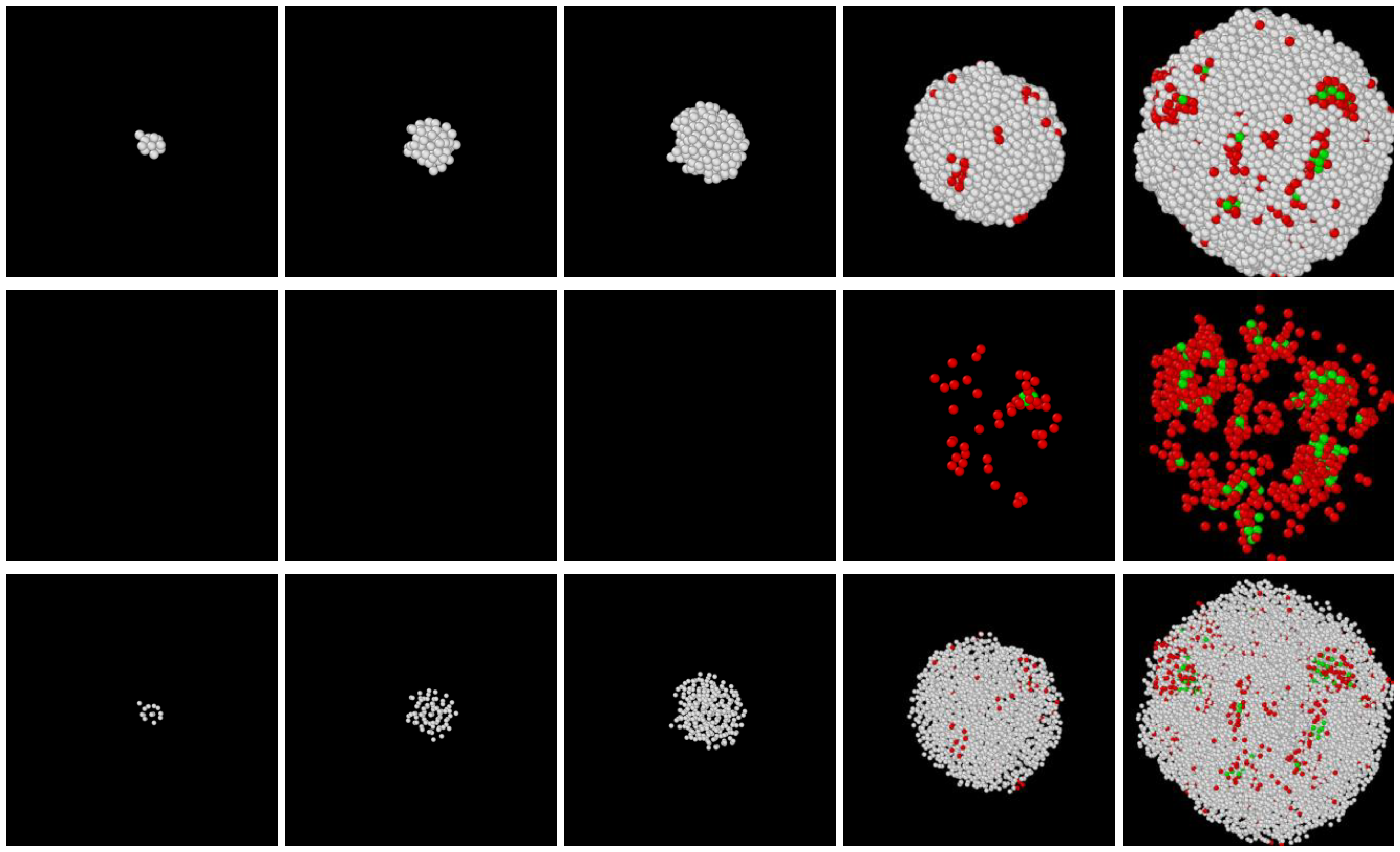
- In all three models the stable bcc phase appears via two-step nucleation.
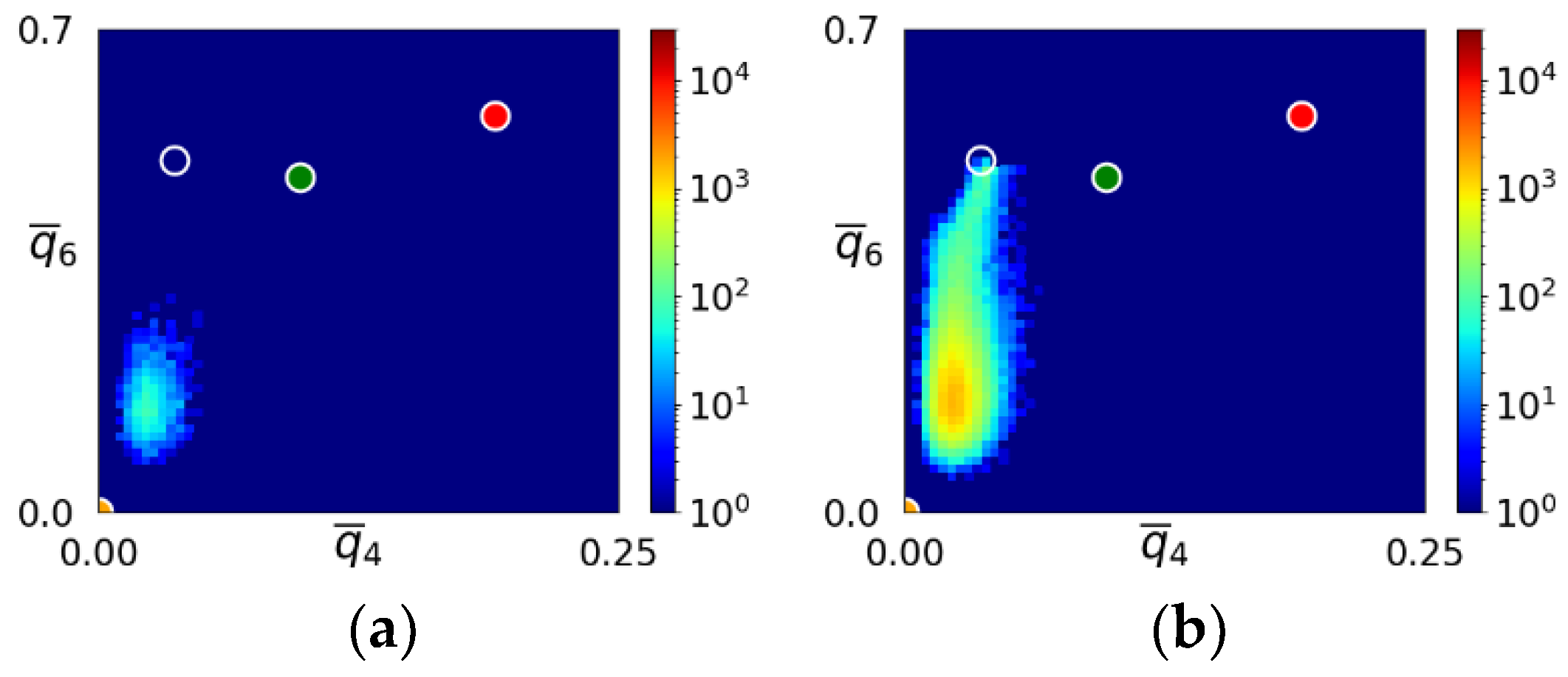
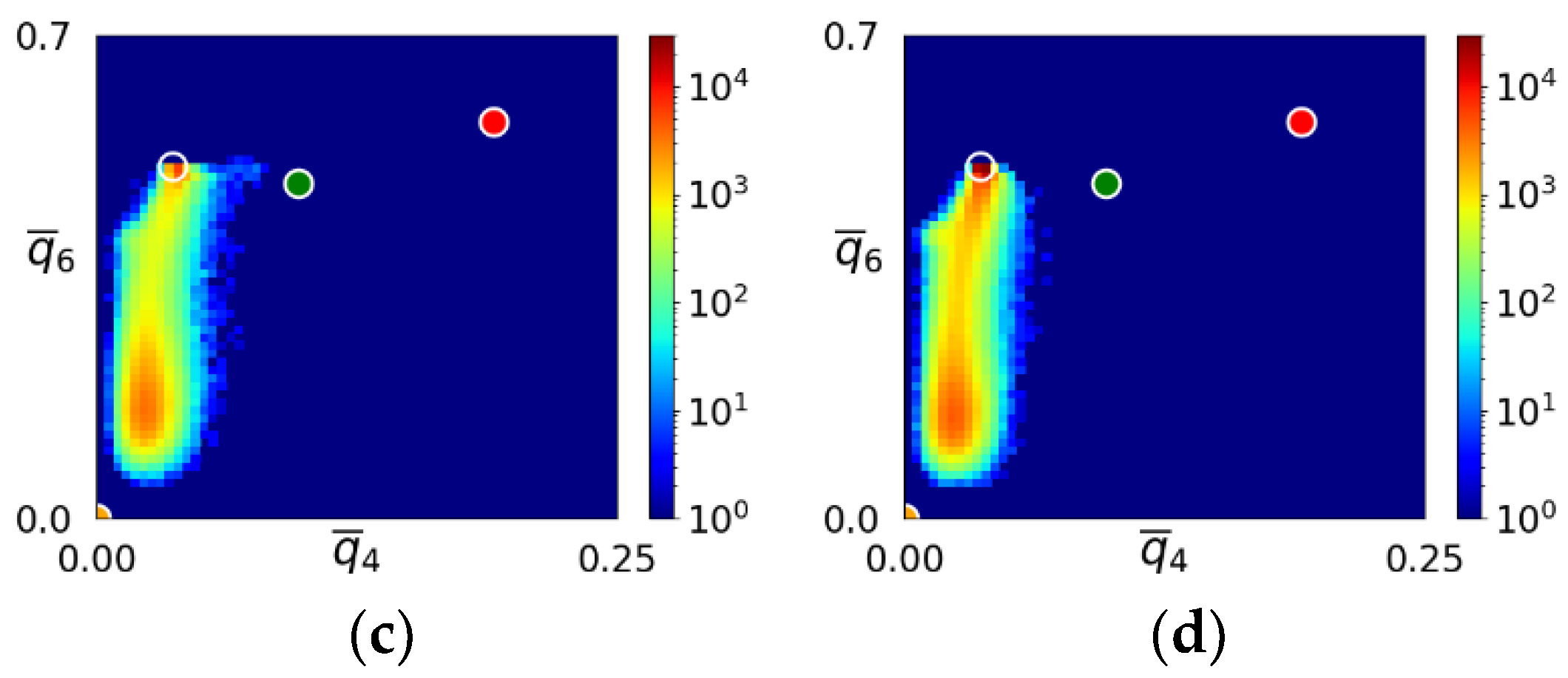
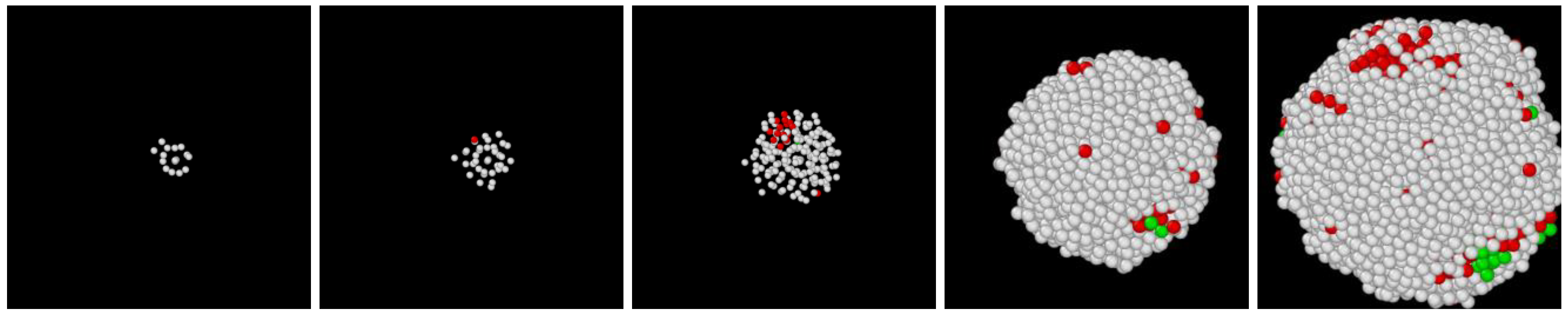
- During the early stage of nucleation, a disordered solid of liquid-like structure (0.28 > ) appears, followed by the formation of MRCO (0.28 < < 0.4), which precede the formation of the stable bcc structure.
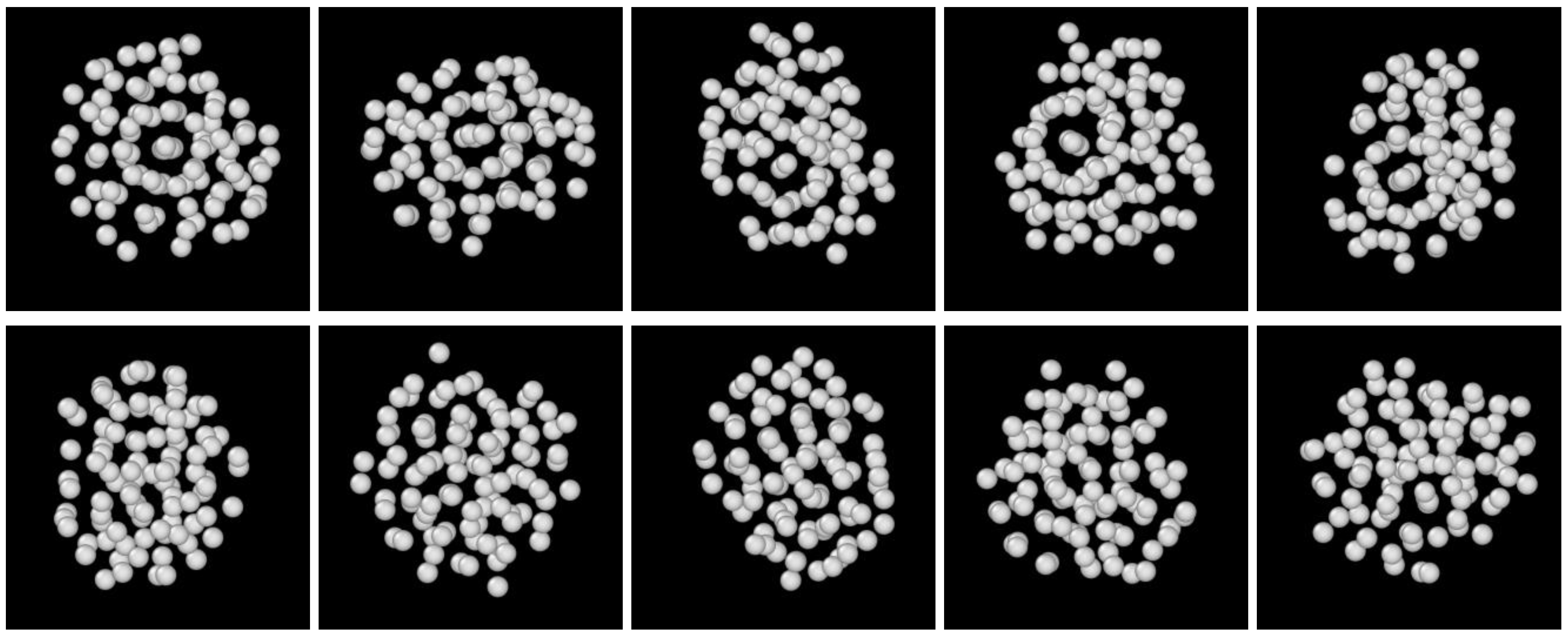
- The first appearing solid structure is ordered so that it has a concentric ring-like view from certain directions. The number of icosahedral neighborhoods is higher in this domain than in the LJ fluid. This structure may coexist with a disordered solid structure of liquid-like order. Remarkably, these two structures are not distinguished by the -based color scheme of Kawasaki and Tanaka.
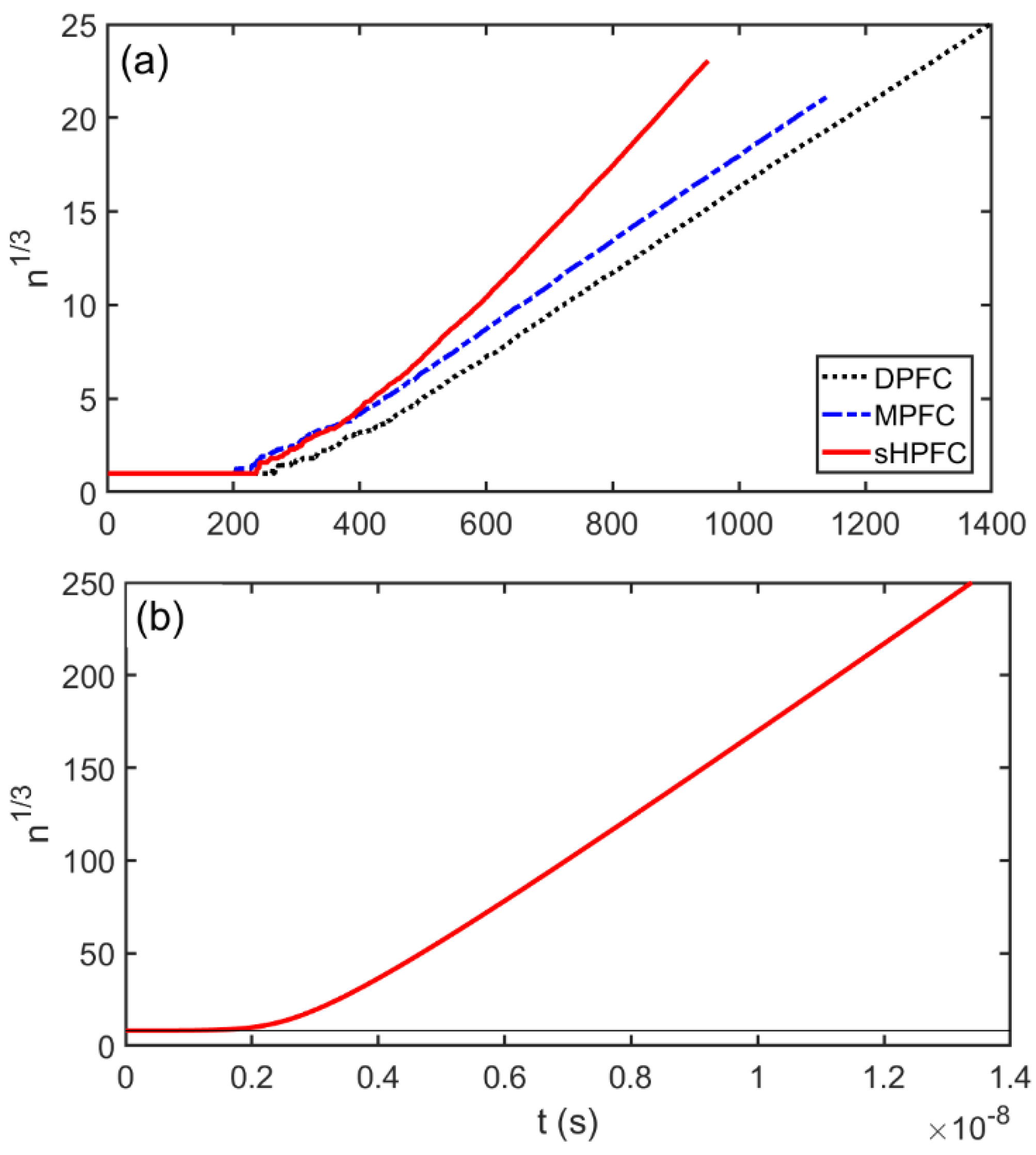
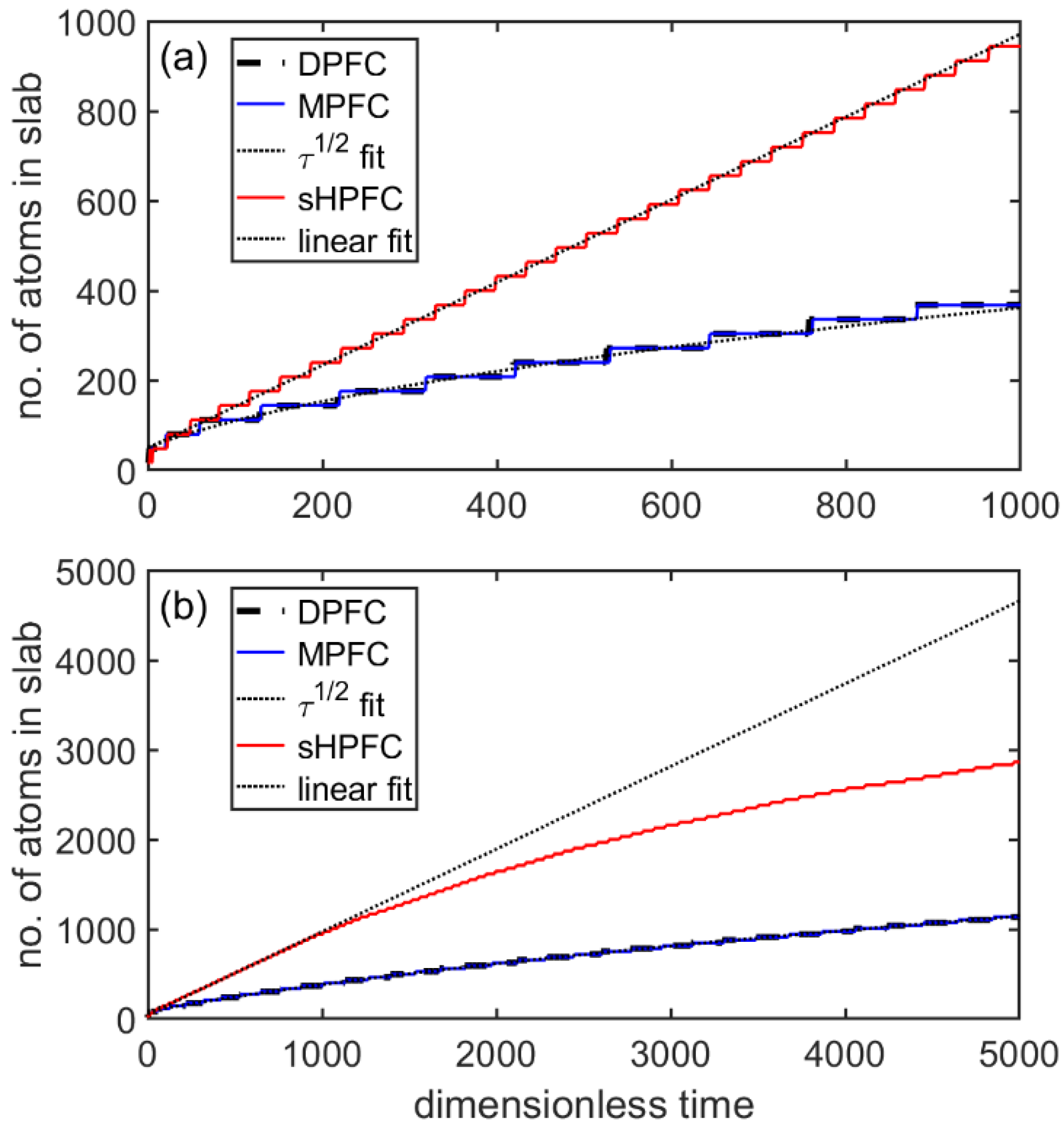
- The time dependence of grain size emerging from the post-nucleation growth was evaluated from DPFC, MPFC, and sHPFC simulations. At short times the predictions are rather similar to each other and agree reasonably well with the dependence obtained by integrating the size-dependent growth rate given by Equation (1). Differences in the growth mechanism become perceptible only on a longer time scale.
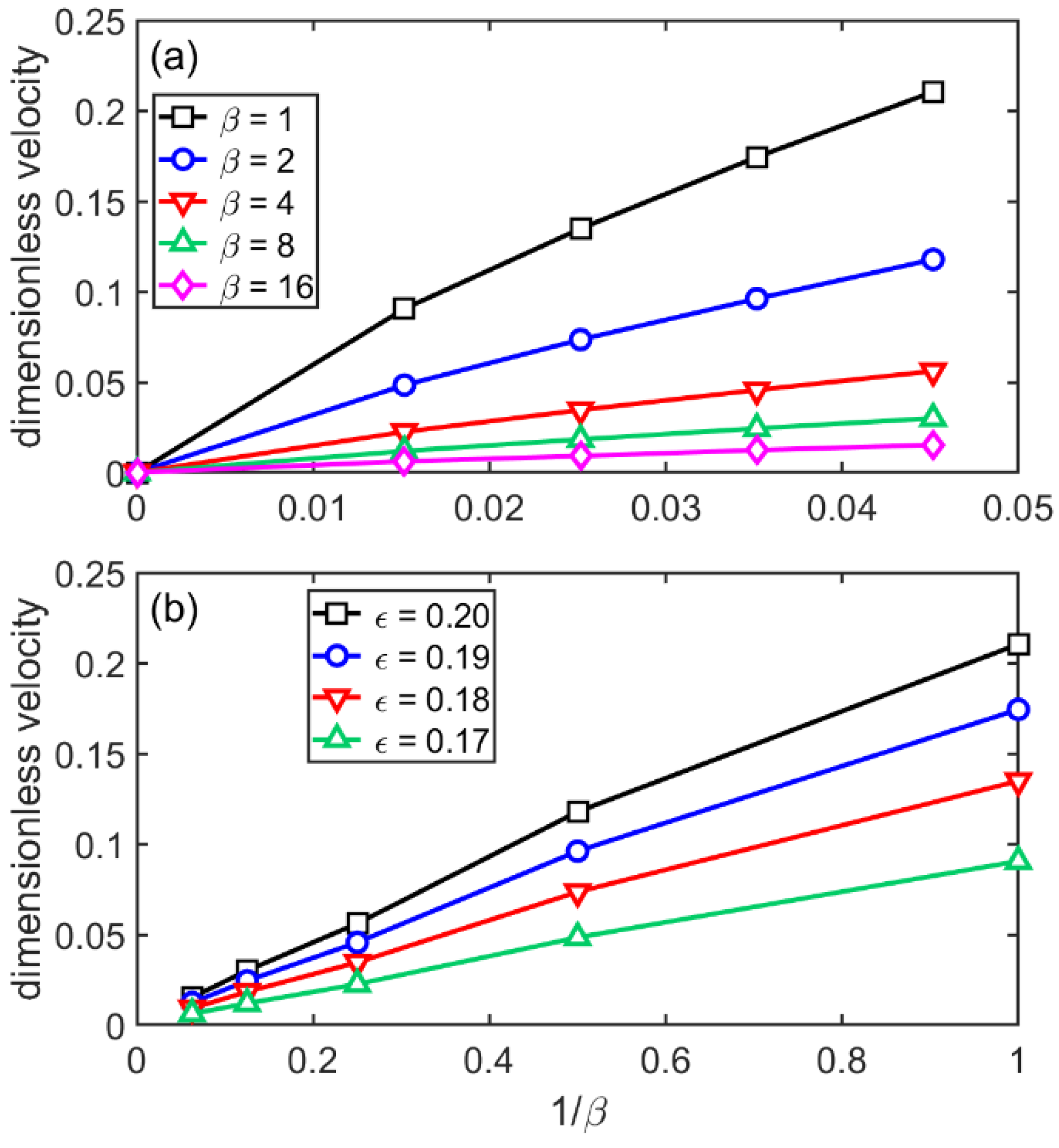
- The steady-state growth velocity the sHPFC predicts increasingly deviates downwards from a linear relationship with increasing undercooling, and it is roughly inversely proportional to the viscosity.
- Finally, we note that nucleation and the post nucleation behavior appear to be less sensitive to the mechanism of density relaxation than the kinetics of crystal growth. This is so, despite the fact that in the present studies the nucleation that took place via intermediate states preferred kinetically relative to direct bcc nucleation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herlach, D.M. Colloids as Model Systems for Metals and Alloys: A Case Study of Crystallization. Eur. Phys. J. Spec. Top. 2014, 223, 591–608. [Google Scholar] [CrossRef]
- Yethiraj, A. Tunable Colloids: Control of Colloidal Phase Transitions with Tunable Interactions. Soft Matter 2007, 3, 1099–1115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gasser, U.; Weeks, E.R.; Schofield, A.; Pusey, P.N.; Weitz, D.A. Real-Space Imaging of Nucleation and Growth in Colloidal Crystallization. Science 2001, 292, 258–262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prasad, V.; Semwogerere, D.; Weeks, E.R. Confocal Microscopy of Colloids. J. Phys. Condens. Matter 2007, 19, 113102. [Google Scholar] [CrossRef]
- Schöpe, H.J.; Bryant, G.; van Megen, W. Two-Step Crystallization Kinetics in Colloidal Hard-Sphere Systems. Phys. Rev. Lett. 2006, 96, 175701. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.H.; Liu, X.Y. How Does a Transient Amorphous Precursor Template Crystallization. J. Am. Chem. Soc. 2007, 129, 13520–13526. [Google Scholar] [CrossRef]
- Tanaka, H. Roles of Bond Orientational Ordering in Glass Transition and Crystallization. J. Phys. Condens. Matter 2011, 23, 285115. [Google Scholar] [CrossRef]
- Tan, P.; Xu, N.; Xu, L. Visualizing Kinetic Pathways of Homogeneous Nucleation in Colloidal Crystallization. Nat. Phys. 2014, 10, 73–79. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Wang, F.; Wang, Z.; Alsayed, A.M.; Zhang, Z.; Yodh, A.G.; Han, Y. Two-Step Nucleation Mechanism in Solid–Solid Phase Transitions. Nat. Mater. 2014, 14, 101–108. [Google Scholar] [CrossRef]
- Zhang, F. Nonclassical Nucleation Pathways in Protein Crystallization. J. Phys. Condens. Matter 2017, 29, 443002. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification; Trans Tech Publications: Aedermannsdorf, Switzerland, 1998. [Google Scholar]
- Dantzig, J.A.; Rappaz, M. Solidification; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Kelton, K.F.; Greer, A.L. Transient Nucleation Effect in Glass Formation. J. Non Cryst. Solids 1986, 79, 295–309. [Google Scholar] [CrossRef]
- Kelton, K.F. Crystal nucleation in liquids and glasses. Solid State Phys. 1991, 45, 75–177. [Google Scholar]
- Provatas, N.; Elder, K.R. Phase-Field Methods in Materials Science and Engineering; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010. [Google Scholar]
- Elder, K.R.; Katakowski, M.; Haataja, M.; Grant, M. Modeling Elasticity in Crystal Growth. Phys. Rev. Lett. 2002, 88, 245701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elder, K.R.; Provatas, N.; Berry, J.; Stefanovic, P.; Grant, M. Phase-Field Crystal Modeling and Classical Density Functional Theory of Freezing. Phys. Rev. B 2007, 75, 064107. [Google Scholar] [CrossRef] [Green Version]
- Emmerich, H.; Löwen, H.; Wittkowski, R.; Gruhn, T.; Tóth, G.I.; Tegze, G.; Gránásy, L. Phase-Field-Crystal Models for Condensed Matter Dynamics on Atomic Length and Diffusive Time Scales: An Overview. Adv. Phys. 2012, 61, 665–743. [Google Scholar] [CrossRef] [Green Version]
- Tóth, G.I.; Gránásy, L.; Tegze, G. Nonlinear Hydrodynamic Theory of Crystallization. J. Phys. Condens. Matter 2014, 26, 055001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Podmaniczky, F.; Tóth, G.I.; Tegze, G.; Gránásy, L. Hydrodynamic Theory of Freezing: Nucleation and Polycrystalline Growth. Phys. Rev. E 2017, 95, 052801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tegze, G.; Gránásy, L.; Tóth, G.I.; Podmaniczky, F.; Jaatinen, A.; Ala Nissila, T.; Pusztai, T. Diffusion-Controlled Anisotropic Growth of Stable and Metastable Crystal Polymorphs in the Phase-Field Crystal Model. Phys. Rev. Lett. 2009, 103, 035702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tegze, G.; Tóth, G.I.; Gránásy, L. Faceting and Branching in 2D Crystal Growth. Phys. Rev. Lett. 2011, 106, 195502. [Google Scholar] [CrossRef] [Green Version]
- Tegze, G.; Gránásy, L.; Tóth, G.I.; Douglas, J.F.; Pusztai, T. Tuning the Structure of Non-Equilibrium Soft Materials by Varying the Thermodynamic Driving Force for Crystal Ordering. Soft Matter 2011, 7, 1789–1799. [Google Scholar] [CrossRef] [Green Version]
- Backofen, R.; Voigt, A. A Phase-Field-Crystal Approach to Critical Nuclei. J. Phys. Condens. Matter 2010, 22, 364104. [Google Scholar] [CrossRef]
- Backofen, R.; Voigt, A. A Phase Field Crystal Study of Heterogeneous Nucleation–Application of the String Method. Eur. Phys. J. Special Top. 2014, 223, 497–509. [Google Scholar] [CrossRef]
- Berry, J.; Elder, K.R.; Grant, M. Simulation of an Atomistic Dynamic Field Theory for Monatomic Liquids: Freezing and Glass Formation. Phys. Rev. E 2008, 77, 061506. [Google Scholar] [CrossRef] [Green Version]
- Tóth, G.I.; Tegze, G.; Pusztai, T.; Tóth, G.; Gránásy, L. Polymorphism, Crystal Nucleation and Growth in the Phase-Field Crystal Model in 2D and 3D. J. Phys. Condens. Matter 2010, 22, 364101. [Google Scholar] [CrossRef]
- Tóth, G.I.; Pusztai, T.; Tegze, G.; Tóth, G.; Gránásy, L. Amorphous Nucleation Precursor in Highly Nonequilibrium Fluids. Phys. Rev. Lett. 2011, 107, 175702. [Google Scholar] [CrossRef] [Green Version]
- Podmaniczky, F.; Tóth, G.I.; Tegze, G.; Pusztai, T.; Gránásy, L. Phase-Field Crystal Modeling of Heteroepitaxy and Exotic Modes of Crystal Nucleation. J. Cryst. Growth 2017, 457, 24–31. [Google Scholar] [CrossRef] [Green Version]
- Gránásy, L.; Tóth, G.I.; Warren, J.A.; Podmaniczky, F.; Tegze, G.; Rátkai, L.; Pusztai, T. Phase-Field Modeling of Crystal Nucleation in Undercooled Liquids–A Review. Prog. Mater. Sci. 2020, 106, 100569. [Google Scholar] [CrossRef]
- Te Vrugt, M.; Löwen, H.; Wittkowski, R. Classical Dynamical Density Functional Theory: From Fundamentals to Applications. Adv. Phys. 2020, 69, 121–247. [Google Scholar] [CrossRef]
- Ramakrishnan, T.V.; Yussouff, M. First-Principles Order-Parameter Theory of Freezing. Phys. Rev. B 1979, 19, 2775–2794. [Google Scholar] [CrossRef]
- Van Teeffelen, S.; Backofen, R.; Voigt, A.; Löwen, H. Derivation of the Phase-Field-Crystal Model for Colloidal Solidification. Phys. Rev. E 2009, 79, 051404. [Google Scholar] [CrossRef]
- Jaatinen, A.; Ala-Nissila, T. Extended Phase Diagram of the Three-Dimensional Phase Field Crystal Model. J. Phys. Condens. Matter 2010, 22, 205402. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Pergamon: New York, NY, USA, 1959. [Google Scholar]
- Shang, B.Z.; Voulgarakis, N.K.; Chu, J.-W. Fluctuating Hydrodynamics for Multiscale Simulation of Inhomogeneous Fluids: Mapping All-Atom Molecular Dynamics to Capillary Waves. J. Chem. Phys. 2011, 135, 044111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baskaran, A.; Baskaran, A.; Lowengrub, J. Kinetic Density Functional Theory of Freezing. J. Chem. Phys. 2014, 141, 174506. [Google Scholar] [CrossRef] [Green Version]
- Heinonen, V.; Achim, C.V.; Kosterlitz, J.M.; Ying, S.-C.; Lowengrub, J.; Ala-Nissila, T. Consistent Hydrodynamics for Phase Field Crystals. Phys. Rev. Lett. 2016, 116, 024303. [Google Scholar] [CrossRef]
- Praetorius, S.; Voigt, A. A Navier-Stokes Phase-Field Crystal Model for Colloidal Suspensions. J. Chem. Phys. 2015, 142, 154904. [Google Scholar] [CrossRef] [Green Version]
- Kikkinides, E.S.; Monson, P.A. Dynamic Density Functional Theory with Hydrodynamic Interactions: Theoretical Development and Application in the Study of Phase Separation in Gas-Liquid Systems. J. Chem. Phys. 2015, 142, 094706. [Google Scholar] [CrossRef]
- Stefnovic, P.; Haataja, M.; Provatas, N. Phase-Field Crystals with Elastic Interactions. Phys. Rev. Lett. 2006, 96, 225504. [Google Scholar] [CrossRef] [Green Version]
- Galenko, P.; Danilov, D.; Lebedev, V. Phase-Field-Crystal and Swift-Hohenberg Equations with Fast Dynamics. Phys. Rev. E 2009, 72, 051110. [Google Scholar] [CrossRef]
- Russel, W.B.; Chaikin, P.M.; Zhu, J.; Meyer, W.V.; Rogers, R. Dendritic Growth of Hard Sphere Crystals. Langmuir 1997, 13, 3871–3881. [Google Scholar] [CrossRef]
- Wu, K.-A.; Karma, A. Phase-Field Crystal Modeling of Equilibrium BCC-Liquid Interfaces. Phys. Rev. B 2007, 76, 184107. [Google Scholar] [CrossRef] [Green Version]
- Jaatinen, A.; Achim, C.V.; Elder, K.R.; Ala-Nissila, T. Thermodynamics of BCC Metals in Phase-Field-Crystal Models. Phys. Rev. E 2009, 80, 031602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lechner, W.; Dellago, C. Accurate Determination of Crystal Structures Based on Averaged Local Bond Order Parameters. J. Chem. Phys. 2008, 129, 114707. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, T.; Tanaka, H. Formation of a Crystal Nucleus from Liquid. Proc. Nat. Acad. Sci. USA 2010, 107, 14036–14041. [Google Scholar] [CrossRef] [Green Version]
- Barros, K.; Klein, W. Liquid to Solid Nucleation via Onion Structure Droplets. J. Chem. Phys. 2013, 139, 174505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dzugutov, M.; Simdyakin, S.I.; Zetterling, F.H.M. Decoupling of Diffusion from Structural Relaxation and Spatial Heterogeneity in a Supercooled Simple Liquid. Phys. Rev. Lett. 2002, 89, 195701. [Google Scholar] [CrossRef] [Green Version]
- Elenius, M.; Oppelstrup, T.; Dzugutov, M. Evidence for a Simple Monatomic Ideal Glass Former: The Thermodynamic Glass Transition from a Stable Liquid Phase. J. Chem. Phys. 2010, 133, 174502. [Google Scholar] [CrossRef]
- Galenko, P.K.; Sanches, F.J.; Elder, K.R. Traveling Wave Profiles for a Crystalline Front Invading Liquid States: Analytical and Numerical Solutions. Phys. D 2015, 308, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Turnbull, D. Formation of Crystal Nuclei in Liquid Metals. J. Appl. Phys. 1950, 21, 1022–1028. [Google Scholar] [CrossRef]
- Ankudinov, A.; Galenko, P.K. Growth of Different Faces in a Body Centered Cubic Lattice: A Case of the Phase-Field-Crystal modeling. J. Cryst. Growth 2020, 539, 125608. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podmaniczky, F.; Gránásy, L. Nucleation and Post-Nucleation Growth in Diffusion-Controlled and Hydrodynamic Theory of Solidification. Crystals 2021, 11, 437. https://doi.org/10.3390/cryst11040437
Podmaniczky F, Gránásy L. Nucleation and Post-Nucleation Growth in Diffusion-Controlled and Hydrodynamic Theory of Solidification. Crystals. 2021; 11(4):437. https://doi.org/10.3390/cryst11040437
Chicago/Turabian StylePodmaniczky, Frigyes, and László Gránásy. 2021. "Nucleation and Post-Nucleation Growth in Diffusion-Controlled and Hydrodynamic Theory of Solidification" Crystals 11, no. 4: 437. https://doi.org/10.3390/cryst11040437
APA StylePodmaniczky, F., & Gránásy, L. (2021). Nucleation and Post-Nucleation Growth in Diffusion-Controlled and Hydrodynamic Theory of Solidification. Crystals, 11(4), 437. https://doi.org/10.3390/cryst11040437





