Evaluation of the Performance of Published Point Defect Parameter Sets in Cone and Body Phase of a 300 mm Czochralski Silicon Crystal
Abstract
:1. Introduction
2. Growth Experiment
3. Numerical Model
3.1. Heat Transfer and Phase Boundaries
3.2. Point Defects
3.2.1. Governing Equations
3.2.2. Numerical Aspects
3.3. Considered Parameter Sets
3.4. Thermal Stresses
4. Results and Discussion
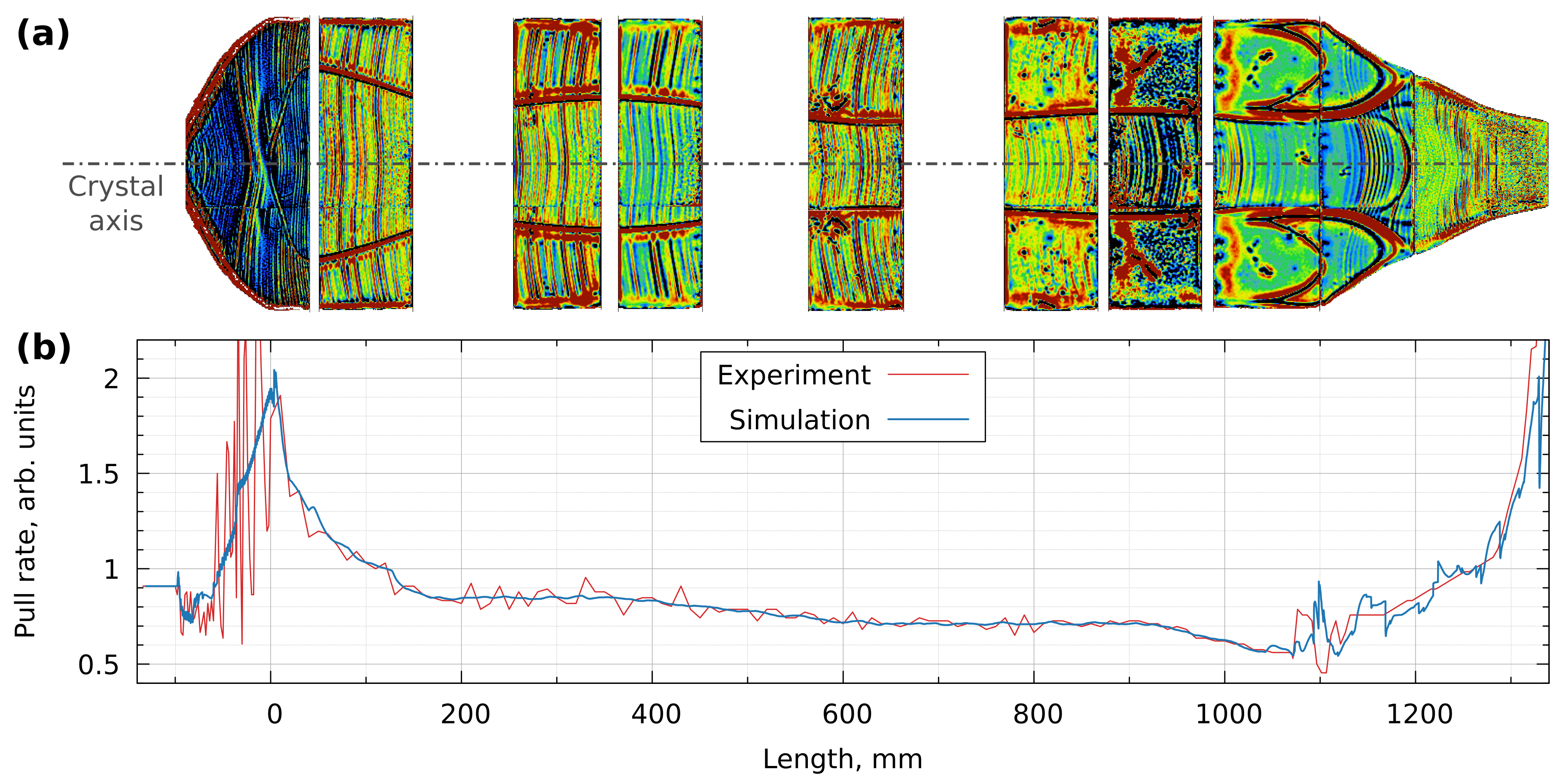
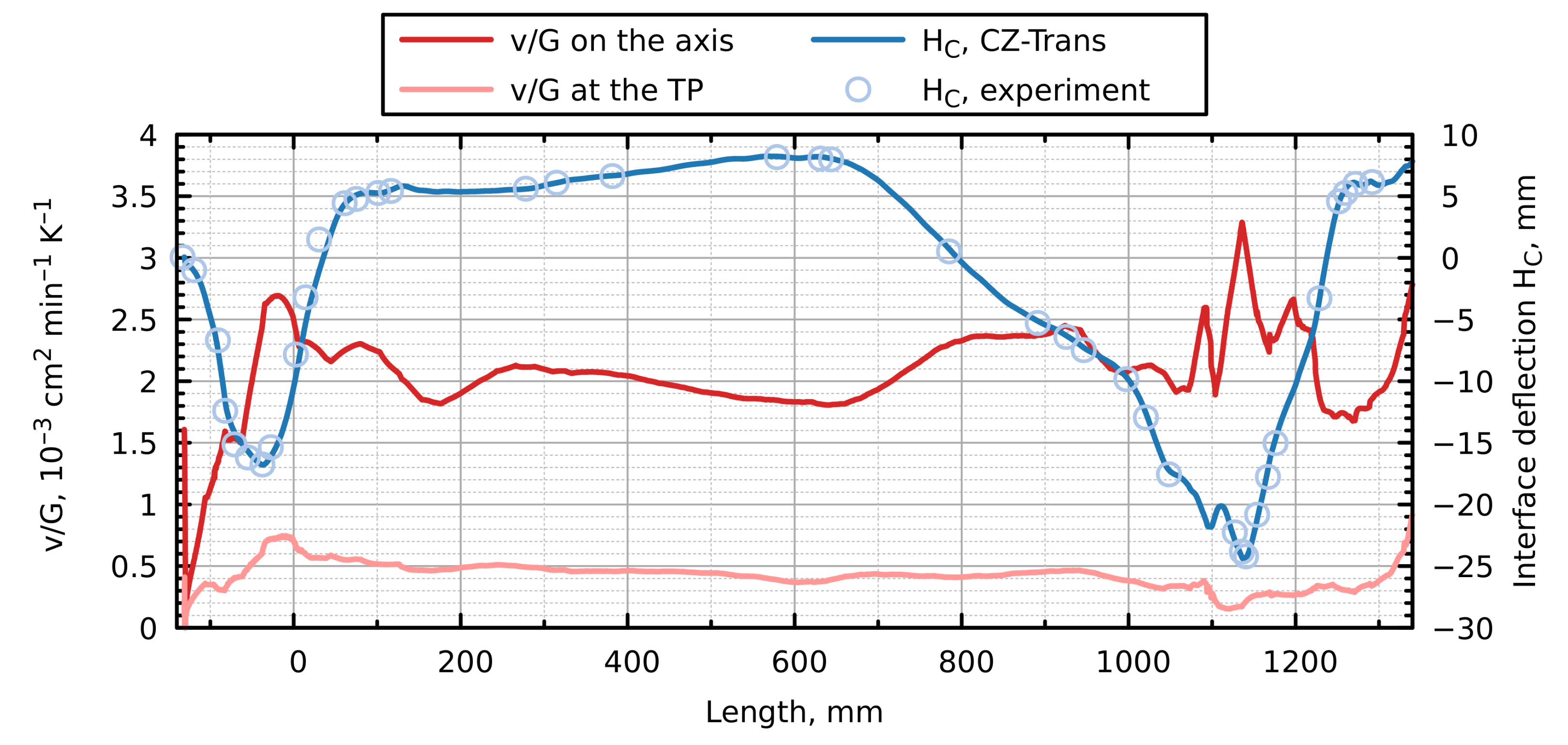
4.1. Heat Transfer and Phase Boundaries
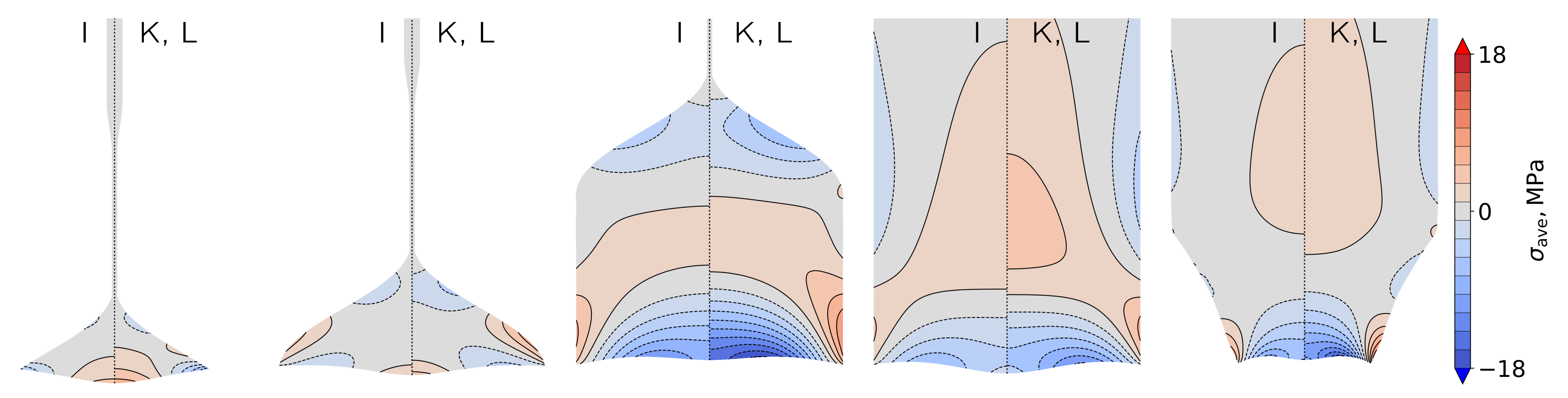
4.2. Thermal Stresses
4.3. Point Defects
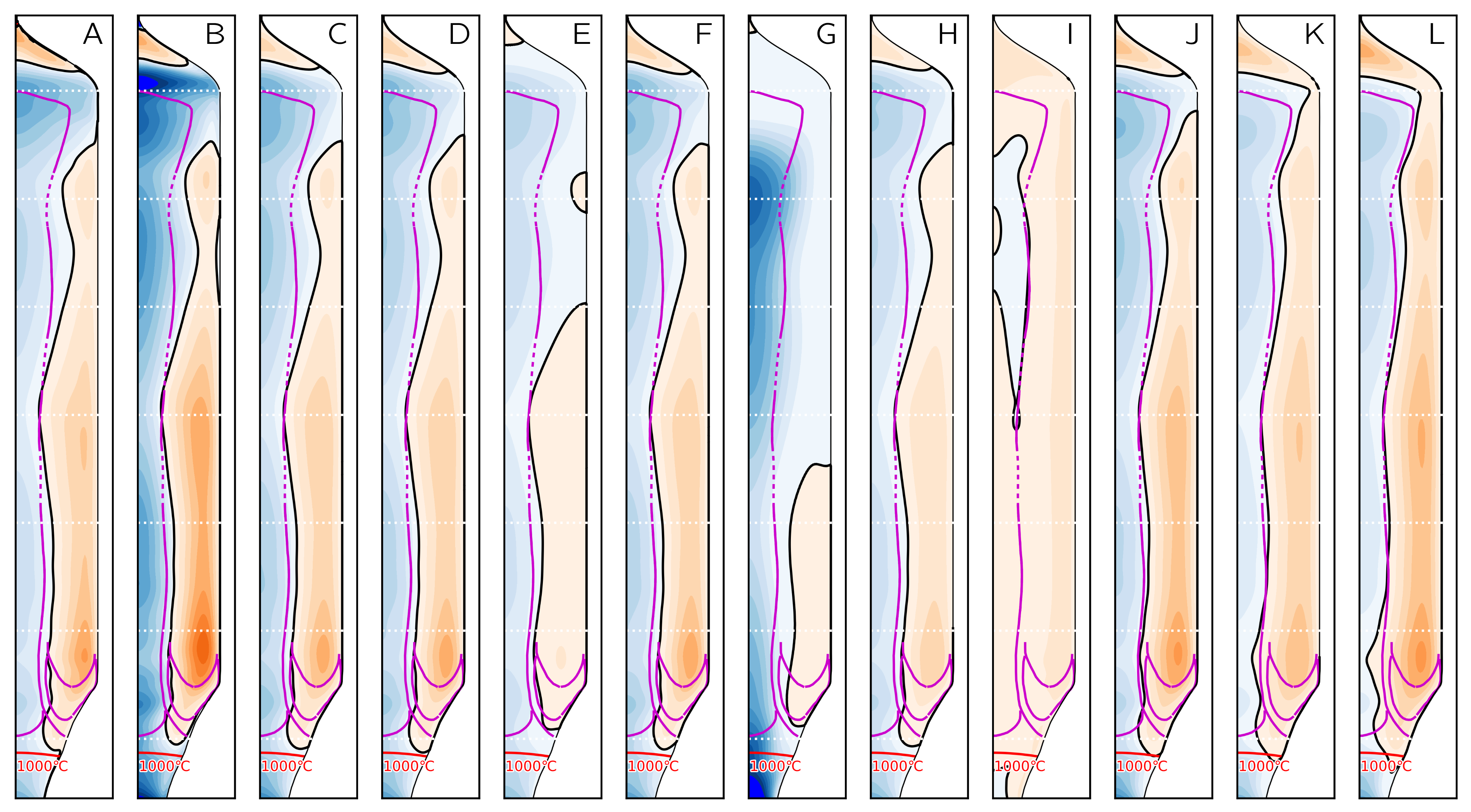
4.3.1. Overview
4.3.2. Original PD Parameters
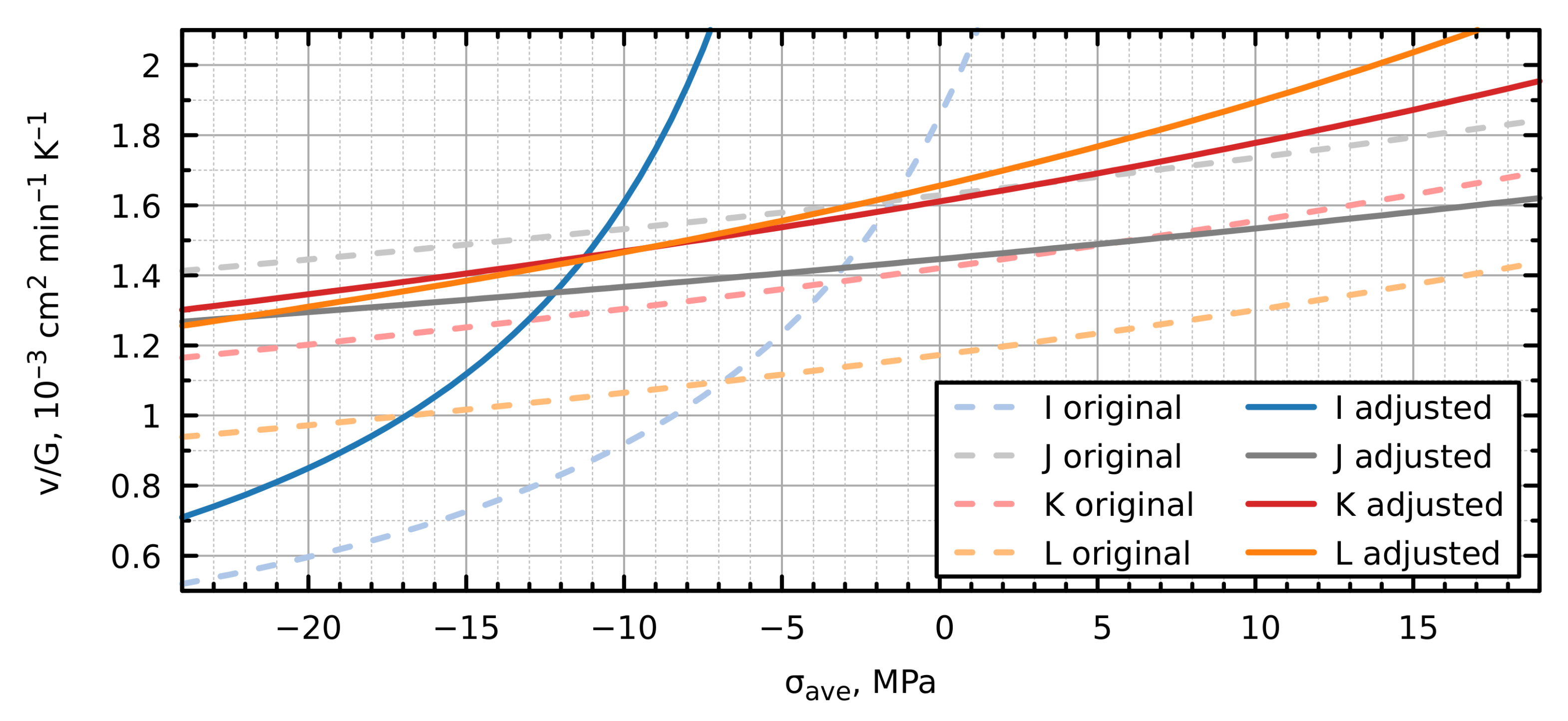
4.3.3. Adjusted PD Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BC | Boundary condition |
| FEM | Finite element method |
| I | Self-interstitials |
| IVB | I-V boundary |
| LPS | Lateral photovoltage scanning |
| MP | Melting point |
| µ-PCD | Microwave photoconductivity decay |
| PD | Point defects |
| TP | Triple point |
| V | Vacancies |
References
- Voronkov, V.V. The mechanism of swirl defects formation in silicon. J. Cryst. Growth 1982, 59, 625–643. [Google Scholar] [CrossRef]
- Dornberger, E.; von Ammon, W. The dependence of ring-like distributed stacking faults on the axial temperature gradient of growing Czochralski silicon crystals. J. Electrochem. Soc. 1996, 143, 1648–1653. [Google Scholar] [CrossRef]
- Dornberger, E.; von Ammon, W.; Virbulis, J.; Hanna, B.; Sinno, T. Modeling of transient point defect dynamics in Czochralski silicon crystals. J. Cryst. Growth 2001, 230, 291–299. [Google Scholar] [CrossRef]
- Sinno, T.; Brown, R.A.; von Ammon, W.; Dornberger, E. Point defect dynamics and the oxidation-induced stacking-fault ring in Czochralski-grown silicon crystals. J. Electrochem. Soc. 1998, 145, 302–318. [Google Scholar] [CrossRef]
- Woo, H.S.; Jeong, J.H.; Kang, I.S. Optimization of surface temperature distribution for control of point defects in the silicon single crystal. J. Cryst. Growth 2003, 247, 320–332. [Google Scholar] [CrossRef]
- Dupret, F.; Nicodème, P.; Ryckmans, Y.; Wouters, P.; Crochet, M.J. Global modelling of heat transfer in crystal growth furnaces. Int. J. Heat Mass Transf. 1990, 33, 1849–1871. [Google Scholar] [CrossRef]
- Dornberger, E.; von Ammon, W.; den Bogaert, N.V.; Dupret, F. Transient computer simulation of a CZ crystal growth process. J. Cryst. Growth 1996, 166, 452–457. [Google Scholar] [CrossRef]
- Den Bogaert, N.V.; Dupret, F. Dynamic global simulation of the Czochralski process I. Principles of the method. J. Cryst. Growth 1997, 171, 65–76. [Google Scholar] [CrossRef]
- Brown, R.A.; Maroudas, D.; Sinno, T. Modelling point defect dynamics in the crystal growth of silicon. J. Cryst. Growth 1994, 137, 12–25. [Google Scholar] [CrossRef]
- Van Goethem, N.; de Potter, A.; Van den Bogaert, N.; Dupret, F. Dynamic prediction of point defects in Czochralski silicon growth. An attempt to reconcile experimental defect diffusion coefficients with the V/G criterion. J. Phys. Chem. Solids 2008, 69, 320–324. [Google Scholar] [CrossRef]
- Von Ammon, W.; Sattler, A.; Kissinger, G. Springer handbook of electronic and photonic materials. In Springer Handbook of Electronic and Photonic Materials; Kasap, S., Capper, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Chapter 5. Defects in Monocrystalline Silicon; pp. 111–132. [Google Scholar] [CrossRef]
- Tanahashi, K.; Inoue, N. Non-equilibrium thermodynamic analysis on the behaviour of point defects in growing silicon crystals: Effects of stress. J. Mater. Sci. Mater. Electron. 1999, 10, 359–363. [Google Scholar] [CrossRef]
- Tanahashi, K.; Kikuchi, M.; Higashino, T.; Inoue, N.; Mizokawa, Y. Concentration of point defects in growing CZ silicon crystal under the internal stresses: Effects of impurity doping and thermal stress. Phys. B Condens. Matter 1999, 273-274, 493–496. [Google Scholar] [CrossRef]
- Sattler, A.; von Ammon, W.; Weber, M.; Haeckl, W.; Schmidt, H. Semiconductor Wafers of Silicon and Method for their Production. U.S. Patent 8,043,427, 25 October 2011. [Google Scholar]
- Vanhellemont, J. Intrinsic point defect incorporation in silicon single crystals grown from a melt, revisited. J. Appl. Phys. 2011, 110, 063519. [Google Scholar] [CrossRef]
- Vanhellemont, J. On the impact of stress on intrinsic defect formation during single crystal silicon growth. Phys. B Condens. Matter 2012, 407, 3009–3012. [Google Scholar] [CrossRef]
- Vanhellemont, J.; Kamiyama, E.; Sueoka, K. Silicon single crystal growth from a melt: On the impact of dopants on the v/G criterion. ECS J. Solid State Sci. Technol. 2013, 2, P166–P179. [Google Scholar] [CrossRef]
- Nakamura, K.; Suewaka, R.; Ko, B. Experimental study of the impact of stress on the point defect incorporation during silicon growth. ECS Solid State Lett. 2014, 3, N5–N7. [Google Scholar] [CrossRef]
- Sueoka, K.; Kamiyama, E.; Vanhellemont, J.; Nakamura, K. Impact of Plane Thermal Stress near the Melt/Solid Interface on the v/G Criterion for Defect-Free Large Diameter Single Crystal Si Growth. ECS Solid State Lett. 2014, 3, P69–P72. [Google Scholar] [CrossRef]
- Kamiyama, E.; Abe, Y.; Banba, H.; Saito, H.; Maeda, S.; Kuliev, A.; Iizuka, M.; Mukaiyama, Y.; Sueoka, K. Impact of anisotropic thermal stress on behavior of grown-in defects during Si crystal growth from a melt. ECS J. Solid State Sci. Technol. 2016, 5, P553–P555. [Google Scholar] [CrossRef]
- Mukaiyama, Y.; Sueoka, K.; Maeda, S.; Iizuka, M.; Mamedov, V.M. Numerical analysis of effect of thermal stress depending on pulling rate on behavior of intrinsic point defects in large-diameter Si crystal grown by Czochralski method. J. Cryst. Growth 2020, 531, 125334. [Google Scholar] [CrossRef]
- Sueoka, K.; Mukaiyama, Y.; Maeda, S.; Iizuka, M.; Mamedov, V.M. Computer simulation of concentration distribution of intrinsic point defect valid for all pulling conditions in large-diameter Czochralski Si crystal growth. ECS J. Solid State Sci. Technol. 2019, 8, P228–P238. [Google Scholar] [CrossRef]
- Suewaka, R.; Nakamura, K. Effect of thermal stress on point defect behavior during single crystal Si growth. Jpn. J. Appl. Phys. 2019, 59, 015502. [Google Scholar] [CrossRef]
- Brown, R.A.; Wang, Z.; Mori, T. Engineering analysis of microdefect formation during silicon crystal growth. J. Cryst. Growth 2001, 225, 97–109. [Google Scholar] [CrossRef]
- Kulkarni, M.S. Defect dynamics in the presence of oxygen in growing Czochralski silicon crystals. J. Cryst. Growth 2007, 303, 438–448. [Google Scholar] [CrossRef]
- Nishimoto, M.; Nakamura, K.; Hourai, M.; Ono, T.; Sugimura, W.; Motooka, T. Determination of physical properties for point defects during CZ silicon crystal growth by high-precision thermal simulations. J. Jpn. Inst. Met. Mater. 2011, 75, 657–664. [Google Scholar] [CrossRef]
- Sabanskis, A.; Bergfelds, K.; Muiznieks, A.; Schröck, T.; Krauze, A. Crystal shape 2D modeling for transient CZ silicon crystal growth. J. Cryst. Growth 2013, 377, 9–16. [Google Scholar] [CrossRef]
- Sabanskis, A.; Virbulis, J. Modelling of thermal field and point defect dynamics during silicon single crystal growth using CZ technique. J. Cryst. Growth 2019, 519, 7–13. [Google Scholar] [CrossRef]
- Abe, T.; Takahashi, T. Intrinsic point defect behavior in silicon crystals during growth from the melt: A model derived from experimental results. J. Cryst. Growth 2011, 334, 16–36. [Google Scholar] [CrossRef]
- Bergfelds, K.; Sabanskis, A.; Virbulis, J. Validation of mathematical model for CZ process using small-scale laboratory crystal growth furnace. IOP Conf. Ser. Mater. Sci. Eng. 2018, 355, 012004. [Google Scholar] [CrossRef]
- Arndt, D.; Bangerth, W.; Davydov, D.; Heister, T.; Heltai, L.; Kronbichler, M.; Maier, M.; Pelteret, J.P.; Turcksin, B.; Wells, D. The deal.II library, version 8.5. J. Numer. Math. 2017, 25, 137–145. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Voronkov, V.V.; Falster, R. Gigantic uphill drift of vacancies and self-interstitials in silicon. Mater. Sci. Eng. B 2009, 159–160, 138–141. [Google Scholar] [CrossRef]
- Oh, H.J.; Wang, J.H.; Yoo, H.D. Comparison of numerical simulation and experiment for the OiSF-ring diameter in czochralski-grown silicon crystal. J. Korean Cryst. Growth Cryst. Technol. 2000, 10, 356–361. [Google Scholar]
- Wang, J.H.; Oh, H.J.; Yoo, H.D. Numerical analysis for the dynamics of the oxidation-induced stacking fault in czochralski-grown silicon crystals. Korean J. Chem. Eng. 2001, 18, 81–87. [Google Scholar] [CrossRef]
- Nakamura, K.; Saishoji, T.; Tomioka, J. Simulation of the point defect diffusion and growth condition for defect free Cz silicon crystal. Electrochem. Soc. Proc. 2002, PV 2002-2, 554–566. [Google Scholar]
- Vanhellemont, J.; Kamiyama, E.; Nakamura, K.; Śpiewak, P.; Sueoka, K. Impacts of thermal stress and doping on intrinsic point defect properties and clustering during single crystal silicon and germanium growth from a melt. J. Cryst. Growth 2017, 474, 96–103. [Google Scholar] [CrossRef]
- Dornberger, E. Prediction of OSF Ring Dynamics and Grown-In Voids in Czochralski Silicon Crystals. Ph.D. Thesis, Université Catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 1997. [Google Scholar] [CrossRef]
- Rudevics, A.; Muiznieks, A.; Riemann, H.; Luedge, A.; Ratnieks, G.; von Ammon, W. Numerical study and comparisons with experimental data for transient behaviour of phase boundaries during industrial FZ process for silicon crystal growth. J. Cryst. Growth 2005, 275, e561–e565. [Google Scholar] [CrossRef]
- Software Package CGSim. Available online: https://www.str-soft.com/software/cgsim/ (accessed on 12 March 2021).
- Nakamura, K.; Saishoji, T.; Tomioka, J. Simulation of point defect distributions in silicon crystals during melt-growth. J. Cryst. Growth 2000, 210, 49–53. [Google Scholar] [CrossRef]
- Kulkarni, M.S. Lateral incorporation of vacancies in Czochralski silicon crystals. J. Cryst. Growth 2008, 310, 3183–3191. [Google Scholar] [CrossRef]
- Sinno, T. A bottom-up multiscale view of point-defect aggregation in silicon. J. Cryst. Growth 2007, 303, 5–11. [Google Scholar] [CrossRef]
- Nishimoto, M.; Sueoka, K.; Motooka, T. First-principles calculation for interfacial energy of void defect in CZ silicon crystal. J. Jpn. Inst. Met. Mater. 2011, 75, 640–644. [Google Scholar] [CrossRef]


| Parameter Set | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|
| A | 2000-Nakamura | [41] | I | 1.040 × 104 | 2.4 | 1.060 × 1022 | 2.4 | |
| V | 2.140 | 1.4 | 5.290 × 1022 | 2.6 | ||||
| B | 2001-Wang | [34,35] | I | 2.101 × 10−1 | 0.907 | 3.945 × 1026 | 3.943 | −3.66 |
| V | 1.000 × 10−4 | 0.489 | 2.675 × 1023 | 2.848 | −2.66 | |||
| C | 2002-Nakamura | [36] | I | 2.459 × 10−1 | 0.9 | 6.284 × 1026 | 4.05 | −1.01 |
| V | 3.513 × 10−4 | 0.3 | 3.951 × 1026 | 3.94 | 0.0 | |||
| D | 2007-Kulkarni-I | [25,42] | I | 1.950 × 10−1 | 0.9 | 6.176 × 1026 | 4 | |
| V | 6.262 × 10−4 | 0.4 | 7.520 × 1026 | 4 | ||||
| E | 2007-Kulkarni-II | [25,42] | I | 4.000 × 10−3 | 0.3 | 4.725 × 1027 | 4.3492 | |
| V | 2.000 × 10−3 | 0.38 | 1.200 × 1027 | 4.12 | ||||
| F | 2007-Sinno | [43] | I | 2.370 × 10−1 | 0.937 | 6.365 × 1026 | 4.0 | |
| V | 7.870 × 10−4 | 0.457 | 9.931 × 1025 | 3.7 | ||||
| G | 2009-Voronkov | [33] | I | 3.667 × 10−3 | 0.2 | 1.884 × 109 | 4.95 | 4.5 |
| V | 1.876 × 10−3 | 0.38 | 2.967 × 1026 | 3.95 | 29 | |||
| H | 2011-Nishimoto | [26,44] | I | 2.590 | 1.18 | 5.992 × 1025 | 3.77 | |
| V | 9.918 × 10−4 | 0.4 | 1.400 × 1026 | 3.84 | ||||
| I | 2013-Vanhellemont-s | [17] | I | 3.800 × 10−2 | 0.88 | 6.400 × 1025 | 3.68 | |
| V | 1.200 × 10−3 | 0.45 | 2.580 × 1026 | 3.88 | ||||
| J | 2014-Nakamura-s | [18] | I | 2.459 × 10−1 | 0.9 | 6.284 × 1026 | 4.05 | −1.01 |
| V | 3.513 × 10−4 | 0.3 | 3.951 × 1026 | 3.94 | 0.0 | |||
| K | 2016-Kamiyama-s | [20,26] | I | 2.590 | 1.18 | 5.992 × 1025 | 3.77 | |
| V | 9.918 × 10−4 | 0.4 | 1.400 × 1026 | 3.84 | ||||
| L | 2019-Mukaiyama-s | [21,22] | I | 2.459 × 10−1 | 0.9 | 6.284 × 1026 | 4.05 | |
| V | 3.442 × 10−4 | 0.3 | 4.030 × 1026 | 3.94 | ||||
| Set | |||||||
|---|---|---|---|---|---|---|---|
| I | V | I | V | I | V | ||
| A | 6.898 | 1.390 | 7.030 | 8.850 | 1.819 | 48.495 | 12.303 |
| B | 4.070 | 0.034 | 6.348 | 8.111 | 1.762 | 25.839 | 0.280 |
| C | 5.000 | 0.445 | 4.840 | 6.490 | 1.650 | 24.200 | 2.888 |
| D | 3.964 | 0.398 | 6.712 | 8.172 | 1.461 | 26.603 | 3.256 |
| E | 5.067 | 1.460 | 4.635 | 5.707 | 1.071 | 23.489 | 8.334 |
| F | 3.734 | 0.338 | 6.917 | 8.520 | 1.602 | 25.831 | 2.881 |
| G | 9.250 | 1.370 | 2.950 | 4.550 | 1.600 | 27.288 | 6.234 |
| H | 7.656 | 0.631 | 3.174 | 4.580 | 1.406 | 24.300 | 2.890 |
| I | 0.887 | 0.541 | 6.301 | 6.407 | 0.106 | 5.587 | 3.467 |
| J | 5.000 | 0.445 | 4.840 | 6.490 | 1.650 | 24.200 | 2.888 |
| K | 7.656 | 0.631 | 3.174 | 4.580 | 1.406 | 24.300 | 2.890 |
| L | 5.000 | 0.436 | 4.840 | 6.620 | 1.780 | 24.200 | 2.886 |
| Parameter Set | E | |||||
|---|---|---|---|---|---|---|
| I | V | |||||
| I | 2013-Vanhellemont-s | 100 | 4.66 | 0.25 | −0.070 | 0.160 |
| J | 2014-Nakamura-s | 139.7 | 4.66 | 0.225 | −0.070 | 0.154 |
| K | 2016-Kamiyama-s | 166 | 4.66 | 0.217 | −0.0694 | 0.3069 |
| L | 2019-Mukaiyama-s | 165 | 4.66 | 0.217 | −0.0694 | 0.3069 |
| Parameter Set | Scale | orig. | adj. | ||
|---|---|---|---|---|---|
| A | 2000-Nakamura | 0.037 | 1.038 | 1.22 | 1.50 |
| B | 2001-Wang | −0.1802 | 0.835 | 2.51 | 1.31 |
| C | 2002-Nakamura | −0.056 | 0.946 | 1.63 | 1.32 |
| D | 2007-Kulkarni-I | −0.0322 | 0.968 | 1.57 | 1.32 |
| E | 2007-Kulkarni-II | −0.031 | 0.969 | 1.47 | 1.24 |
| F | 2007-Sinno | −0.0041 | 0.996 | 1.35 | 1.32 |
| G | 2009-Voronkov | −0.6635 | 0.515 | 2.32 | 1.23 |
| H | 2011-Nishimoto | −0.014 | 0.986 | 1.42 | 1.36 |
| I | 2013-Vanhellemont-s | 0.0134 | 1.013 | 0.60 | 0.85 |
| J | 2014-Nakamura-s | −0.0306 | 0.970 | 1.45 | 1.29 |
| K | 2016-Kamiyama-s | 0.0356 | 1.036 | 1.20 | 1.35 |
| L | 2019-Mukaiyama-s | 0.0795 | 1.083 | 0.97 | 1.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabanskis, A.; Plāte, M.; Sattler, A.; Miller, A.; Virbulis, J. Evaluation of the Performance of Published Point Defect Parameter Sets in Cone and Body Phase of a 300 mm Czochralski Silicon Crystal. Crystals 2021, 11, 460. https://doi.org/10.3390/cryst11050460
Sabanskis A, Plāte M, Sattler A, Miller A, Virbulis J. Evaluation of the Performance of Published Point Defect Parameter Sets in Cone and Body Phase of a 300 mm Czochralski Silicon Crystal. Crystals. 2021; 11(5):460. https://doi.org/10.3390/cryst11050460
Chicago/Turabian StyleSabanskis, Andrejs, Matīss Plāte, Andreas Sattler, Alfred Miller, and Jānis Virbulis. 2021. "Evaluation of the Performance of Published Point Defect Parameter Sets in Cone and Body Phase of a 300 mm Czochralski Silicon Crystal" Crystals 11, no. 5: 460. https://doi.org/10.3390/cryst11050460
APA StyleSabanskis, A., Plāte, M., Sattler, A., Miller, A., & Virbulis, J. (2021). Evaluation of the Performance of Published Point Defect Parameter Sets in Cone and Body Phase of a 300 mm Czochralski Silicon Crystal. Crystals, 11(5), 460. https://doi.org/10.3390/cryst11050460








