A Multi-Dimensional Construction Safety Risk Optimization Model
Abstract
:1. Introduction
2. Safety Risk Assessment Practices in the Construction Industry
2.1. Safety Risk Parameters
| Risk Parameter | Reference |
|---|---|
| Probability | [14,16,17,18,19,29,31,35,36,38,40,41,42,43,44] |
| Severity | [14,16,17,18,19,29,31,35,36,38,40,41,42,43,44] |
| Frequency/Exposure | [14,16,19,35,36,41,43] |
| Detection | [16,17,19,29,38,41,43] |
| Expenses | [42] |
| Safety barriers | [18] |
| Safety climate | [18] |
| Accident percentage | [42] |
| Safety level | [42] |
| Hazard criticality | [31] |
| Sensitivity to the failure of barriers | [16] |
| Sensitivity to the poor safety climate | [16] |
| Sensitivity to poor site safety conditions | [16] |
| Sensitivity to bad environmental conditions | [16] |
| Worsening factor | [19] |
| Sensitivity | [44] |
| Reference | Project Cost | Project Duration | Company Reputation | Environment | Society |
|---|---|---|---|---|---|
| [46] | ✓ | ||||
| [47] | ✓ | ||||
| [48] | ✓ | ✓ | |||
| [20] | ✓ | ✓ | ✓ | ✓ | |
| [26] | ✓ | ✓ | ✓ | ✓ | |
| [28] | ✓ | ✓ | |||
| [36] | ✓ | ||||
| [49] | ✓ | ✓ | |||
| [38] | ✓ | ✓ | ✓ | ✓ | |
| [39] | ✓ | ✓ | |||
| [50] | ✓ | ✓ | ✓ | ||
| [51] | ✓ | ✓ | |||
| [16] | ✓ | ||||
| [19] | ✓ | ✓ | ✓ | ✓ | |
| [21] | ✓ | ✓ | ✓ | ✓ | |
| [15] | ✓ | ✓ | |||
| [52] | ✓ | ||||
| [53] | ✓ | ✓ | |||
| [54] | ✓ | ✓ | ✓ |
2.2. Multi-Dimensional Safety Risk Assessment Approaches
2.3. Research Gap
- Current research indicates that OHS risks impact not only the workers’ physical integrity but also the environment, society, reputation of the company, duration of projects, and costs (Table 2). However, a complete risk assessment approach that addresses all these issues is lacking. In this context, current risk assessment models require enhancements to incorporate these factors.
- The literature highlights the limits of approaches such as TOPSIS and AHP, which have been employed in recent years to assess OHS hazards. AI-based optimization techniques can significantly enhance the identification of optimal options by presenting broader solution spaces. Consequently, integrating AI-driven methodologies emerges as a significant domain for consideration in risk assessment procedures.
- The current literature reveals that comprehensive risk assessment methods are inadequate to reduce risk scores and precautionary costs for each work item in building projects. Such models should provide more comprehensive and cohesive strategies for reducing risks and costs. Developing models that optimize risks and costs for each work item is essential to improving the effectiveness of risk management practices.
2.4. Aims and Objectives
3. Model Development and Research Methodology
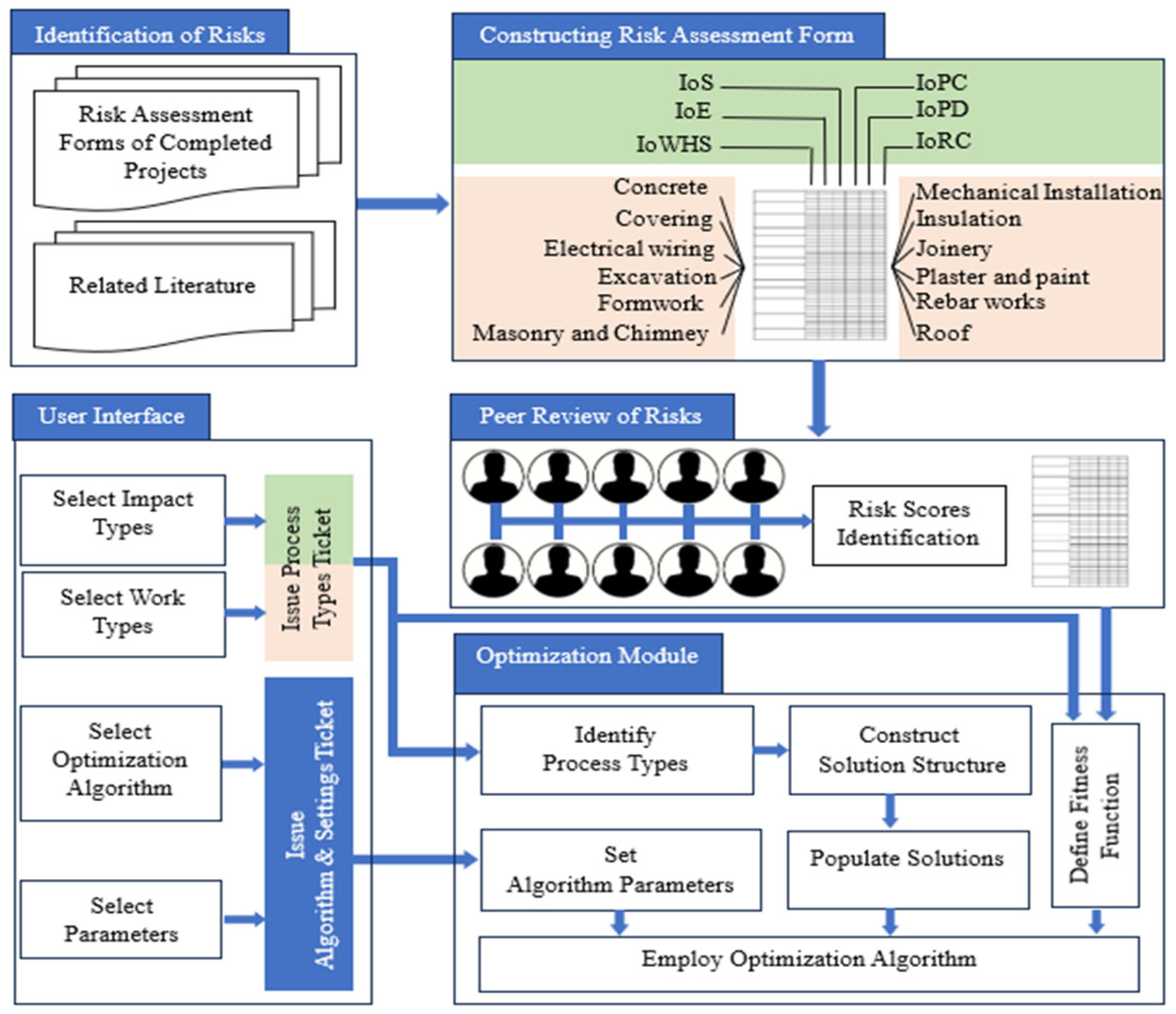
3.1. Identification of Risks
3.2. Constructing Risk Assessment Form
3.3. Peer-Review of Risks
3.4. Optimization Module and User Interface
3.4.1. Implementation of the Genetic Algorithm
3.4.2. User Interface
3.5. Case Study
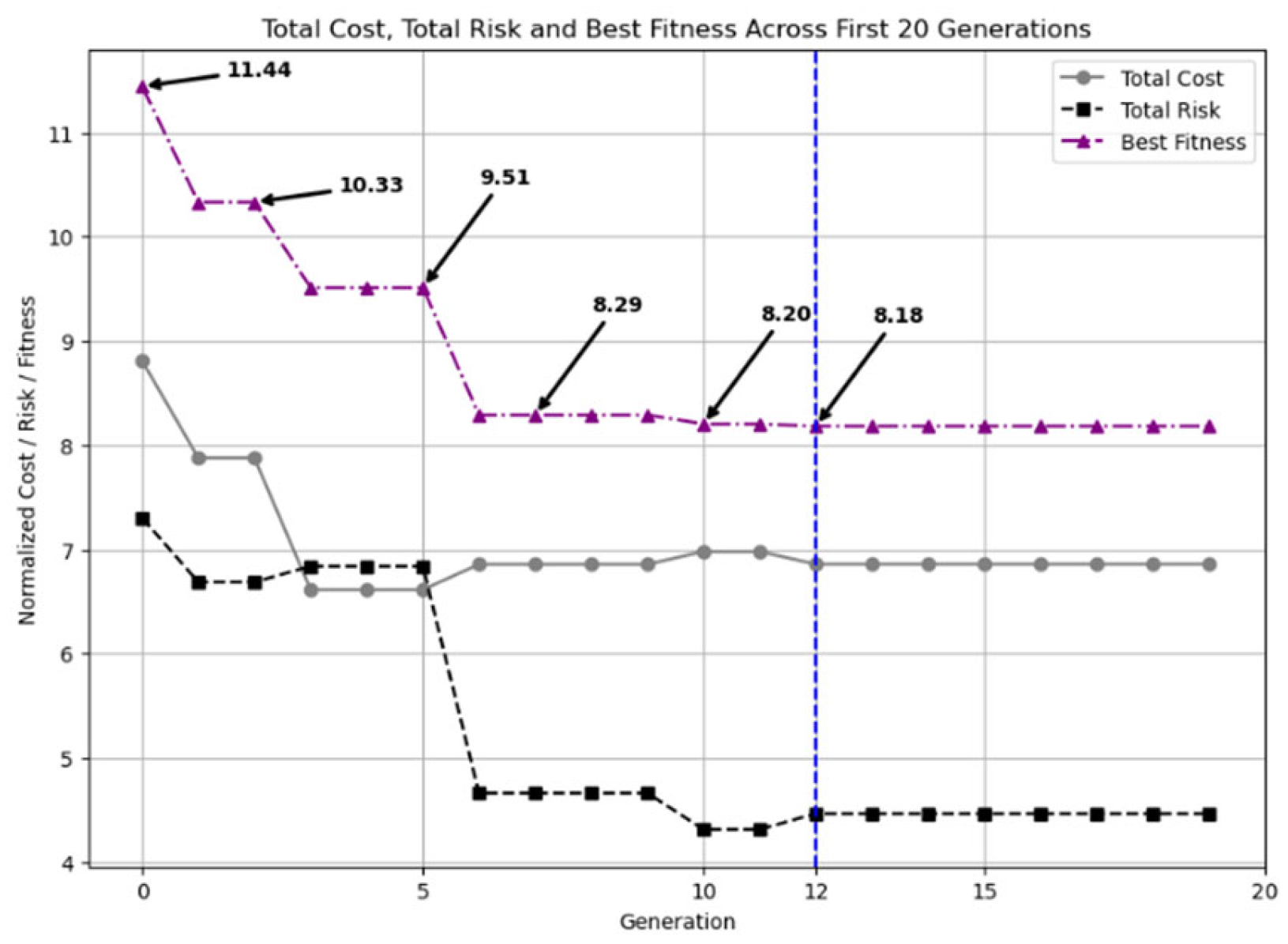
4. Results and Discussion
5. Implications
6. Limitations and Future Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gürcanlı, G.E. İnşaat Sektöründe Gerçekleşen Ölüm ve Yaralanmaların Analizi. Mesleki Sağlık ve Güvenlik Derg. 2013, 13, 20–29. [Google Scholar]
- Birhane, G.E.; Yang, L.; Geng, J.; Zhu, J. Causes of Construction Injuries: A Review. Int. J. Occup. Saf. Ergon. 2022, 28, 343–353. [Google Scholar] [CrossRef] [PubMed]
- Ayduran, A.C.; Olcay, Z.F. Investigation of The Effects of Construction Sector Employees on The Occupational Health and Safety Culture Levels and Safe Behaviors. Ergonomi 2022, 5, 108–119. [Google Scholar] [CrossRef]
- Özkılıç, Ö. İş Sağlığı, Güvenliği ve Çevresel Etki Risk Değerlendirmesi; Tisk Yayınları: Ankara, Türkiye, 2005. [Google Scholar]
- Murat, B.; Motorcu, A.R.; Kayır, Y. İş Sağlığı ve Güvenliği Faaliyetlerinde Yapay Zeka ve Uzman Sistem Uygulamalarının Değerlendirilmesi. In Proceedings of the 5th International Engineering and Technology Management Congress, Istanbul, Türkiye, 24–25 April 2021; Volume 1, sa.5. pp. 240–248. [Google Scholar]
- Awolusi, I.; Marks, E.; Hainen, A.; Alzarrad, A. Incident Analysis and Prediction of Safety Performance on Construction Sites. Civileng 2022, 3, 669–686. [Google Scholar] [CrossRef]
- Bağıran, H.E.; Erçetin, R. Risk Assessment Application with FMEA Method in Universal and CNC Controlled Lathe Machines. Eur. J. Sci. Technol. 2022, 38, 24–31. [Google Scholar] [CrossRef]
- Doğan, F.; Şimşek, S. COVID-19 Pandemisinin, Yaşam Kalitesine, İşletmelerin İş Sağlığı ve Güvenliği Uygulamalarına Etkileri: İstanbul Ikitelli Organize Sanayi Örneği. J. Bus. Res. 2022, 14, 2290–2308. [Google Scholar] [CrossRef]
- Xu, J.; Cheung, C.; Manu, P.; Ejohwomu, O.; Too, J. Implementing Safety Leading Indicators in Construction: Toward a Proactive Approach to Safety Management. Saf. Sci. 2023, 157, 105929. [Google Scholar] [CrossRef]
- Ak, Ş.; Zorluer, İ. İnşaat Sektöründeki İş Kazalarının Hata Ağacı Analizi Ile Değerlendirilmesi. Tek. Dergi 2022, 33, 12817–12846. [Google Scholar] [CrossRef]
- Tian, H.; Zhang, S.; Garg, H.; Liu, X. An Extended SECA-GDM Method Considering Flexible Linguistic Scale Optimization and Its Application in Occupational Health and Safety Risk Assessment. Alexandria Eng. J. 2024, 88, 317–330. [Google Scholar] [CrossRef]
- Topal, S.; Atasoylu, E. A Fuzzy Risk Assessment Model for Small Scale Construction Work. Sustainability 2022, 14, 4442. [Google Scholar] [CrossRef]
- Ning, X.; Qi, J.; Wu, C. A Quantitative Safety Risk Assessment Model for Construction Site Layout Planning. Saf. Sci. 2018, 104, 246–259. [Google Scholar] [CrossRef]
- Toktaş, P.; Can, G.F.; İle, K.-M.Y.; Nmasi, S. Şantiyelerin İş Sağlığı ve Güvenliği Açısından Risk Düzeylerine Göre Kemira-M Yöntemi Ile Sıralanması. Ergonomics 2018, 1, 123–136. [Google Scholar]
- Sekhavati, E.; Jalilzadeh Yengejeh, R. Assessment Optimization of Safety and Health Risks Using Fuzzy TOPSIS Technique (Case Study: Construction Sites in the South of Iran). J. Environ. Health Sustain. Dev. 2021, 6, 1494–1506. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Zhang, X. Developing a Holistic Occupational Health and Safety Risk Assessment Model: An Application to a Case of Sustainable Construction Project. J. Clean. Prod. 2021, 291, 125934. [Google Scholar] [CrossRef]
- Durmaz, E.D.; Gölcük, İ. Entropi Tabanlı TOPSIS-Sort Ile Iş Güvenliği Risklerinin Sınıflandırılması. J. Turkish Oper. Manag. 2023, 1, 1550–1563. [Google Scholar] [CrossRef]
- Pinto, A. QRAM a Qualitative Occupational Safety Risk Assessment Model for the Construction Industry That Incorporate Uncertainties by the Use of Fuzzy Sets. Saf. Sci. 2014, 63, 57–76. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Durdyev, S.; Sadeghi, H.; Mahdiyar, A.; Hosseini, M.R.; Banihashemi, S.; Martek, I. Towards Enhancement in Reliability and Safety of Construction Projects: Developing a Hybrid Multi-Dimensional Fuzzy-Based Approach. Eng. Constr. Archit. Manag. 2023, 30, 2255–2279. [Google Scholar] [CrossRef]
- Elsebaei, M.; Elnawawy, O.; Ahmed, A.; Othman, E. Causes and Impacts of Site Accidents in the Egyptian Construction Industry. Int. J. Constr. Manag. 2022, 22, 2659–2670. [Google Scholar] [CrossRef]
- Rostamzadeh, S.; Abouhossein, A.; Chalak, M.H.; Vosoughi, S.; Norouzi, R. An Integrated DEMATEL–ANP Approach for Identification and Prioritization of Factors Affecting Fall from Height Accidents in the Construction Industry. Int. J. Occup. Saf. Ergon. 2023, 29, 474–483. [Google Scholar] [CrossRef]
- Garzia, F. New Security Risk Assessment and Genetic Algorithms Based Methods to Optimize Risk Reduction Countermeasures for Cultural Heritage Sites. Int. J. Comput. Methods Exp. Meas. 2023, 11, 45–54. [Google Scholar] [CrossRef]
- Papazoglou, I.A.; Aneziris, O.N.; Bellamy, L.J.; Ale, B.J.M.; Oh, J. Multi-Hazard Multi-Person Quantitative Occupational Risk Model and Risk Management. Reliab. Eng. Syst. Saf. 2017, 167, 310–326. [Google Scholar] [CrossRef]
- Mukilan, K.; Rameshbabu, C.; Velumani, P. A Modified Particle Swarm Optimization for Risk Assessment and Claim Management in Engineering Procurement Construction Projects. Mater. Today Proc. 2021, 42, 786–794. [Google Scholar] [CrossRef]
- Omle, I.; Askar, A.H.; Kovács, E. Optimizing the Design of Container House Walls Using Argon and Recycled Plastic Materials. Buildings 2024, 14, 3944. [Google Scholar] [CrossRef]
- Guo, S.; Li, J.; He, J.; Luo, W.; Chen, B. A Modified Risk Matrix Method for Behavioral Risk Evaluation in the Construction Industry. J. Asian Archit. Build. Eng. 2022, 21, 1053–1066. [Google Scholar] [CrossRef]
- Ahmed, T.; Hoque, A.S.M.; Lekha Chitra, K.; Ahmed, S. Integrated Approach for Occupational Health and Safety (OHS) Risk Assessment: An Empirical (Case) Study in Small Enterprises. Saf. Sci. 2023, 164, 106143. [Google Scholar] [CrossRef]
- Gürcanlı, G.E.; Bilir, S.; Sevim, M. Activity Based Risk Assessment and Safety Cost Estimation for Residential Building Construction Projects. Saf. Sci. 2015, 80, 1–12. [Google Scholar] [CrossRef]
- Mard, H.R.S.A.; Estiri, A.; Hadadi, P.; Mard, M.S.A. Occupational Risk Assessment in the Construction Industry in Iran. Int. J. Occup. Saf. Ergon. 2017, 23, 570–577. [Google Scholar] [CrossRef]
- Zermane, A.; Zahirasri, M.; Tohir, M.; Rafee, M. Risk Assessment of Fatal Accidents Due to Work at Heights Activities Using Fault Tree Analysis: Case Study in Malaysia. Saf. Sci. 2022, 151, 105724. [Google Scholar] [CrossRef]
- Sanni-Anibire, M.O.; Mahmoud, A.S.; Hassanain, M.A.; Salami, B.A. A Risk Assessment Approach for Enhancing Construction Safety Performance. Saf. Sci. 2020, 121, 15–29. [Google Scholar] [CrossRef]
- Cheng, L.; Cao, D. Evolution Model and Quantitative Assessment of Risk Network in Housing Construction Accidents. Eng. Constr. Archit. Manag. 2024, 31, 227–246. [Google Scholar] [CrossRef]
- Ikpesu, J.E.; Okeke, G.N.; Ogbolime, M.C. Identification of Hazards and Risk Assessment in Construction Site. Direct Res. J. Public Health Environ. Technol. 2024, 9, 144–157. [Google Scholar]
- Zolfagharian, S.; Irizarry, J.; Ressang, A.; Nourbakhsh, M.; Gheisari, M. Automated Safety Planning Approach for Residential Construction Sites in Malaysia. Int. J. Constr. Manag. 2014, 14, 134–147. [Google Scholar] [CrossRef]
- Gul, M.; Celik, E. Fuzzy Rule-Based Fine–Kinney Risk Assessment Approach for Rail Transportation Systems. Hum. Ecol. Risk Assess. An Int. J. 2018, 24, 1786–1812. [Google Scholar] [CrossRef]
- Ilbahar, E.; Karaşan, A.; Cebi, S.; Kahraman, C. A Novel Approach to Risk Assessment for Occupational Health and Safety Using Pythagorean Fuzzy AHP & Fuzzy Inference System. Saf. Sci. 2018, 103, 124–136. [Google Scholar] [CrossRef]
- Ak, M.F.; Yucesan, M.; Gul, M. Occupational Health, Safety and Environmental Risk Assessment in Textile Production Industry through a Bayesian BWM-VIKOR Approach. Stoch. Environ. Res. Risk Assess. 2022, 36, 629–642. [Google Scholar] [CrossRef]
- Khan, M.W.; Ali, Y.; De Felice, F.; Petrillo, A. Occupational Health and Safety in Construction Industry in Pakistan Using Modified-SIRA Method. Saf. Sci. 2019, 118, 109–118. [Google Scholar] [CrossRef]
- Liu, R.; Mou, X.; Liu, H.-C. Occupational Health and Safety Risk Assessment Based on Combination Weighting and Uncertain Linguistic Information: Method Development and Application to a Construction Project. IISE Trans. Occup. Ergon. Hum. Factors 2020, 8, 175–186. [Google Scholar] [CrossRef]
- Lu, Y.; Gong, P.; Tang, Y.; Sun, S.; Li, Q. BIM-Integrated Construction Safety Risk Assessment at the Design Stage of Building Projects. Autom. Constr. 2021, 124, 103553. [Google Scholar] [CrossRef]
- Karasan, A.; Ilbahar, E.; Cebi, S.; Kahraman, C. A New Risk Assessment Approach: Safety and Critical E Ff Ect Analysis (SCEA) and Its Extension with Pythagorean Fuzzy Sets. Saf. Sci. 2018, 108, 173–187. [Google Scholar] [CrossRef]
- Debnath, J.; Biswas, A.; Sivan, P.; Sen, K.N.; Sahu, S. Fuzzy Inference Model for Assessing Occupational Risks in Construction Sites. Int. J. Ind. Ergon. 2016, 55, 114–128. [Google Scholar] [CrossRef]
- Sadeghi, H.; Mohandes, S.R.; Hosseini, M.R.; Banihashemi, S.; Mahdiyar, A.; Abdullah, A. Developing an Ensemble Predictive Safety Risk Assessment Model: Case of Malaysian Construction Projects. Int. J. Environ. Res. Public Health 2020, 17, 8395. [Google Scholar] [CrossRef] [PubMed]
- Yao, H.; She, J.; Zhou, Y. Risk Assessment of Construction Safety Accidents Based on Association Rule Mining and Bayesian Network. J. Intell. Constr. 2024, 2, 9180015. [Google Scholar] [CrossRef]
- Ouédraogo, A.; Groso, A.; Meyer, T. Risk Analysis in Research Environment—Part I: Modeling Lab Criticity Index Using Improved Risk Priority Number. Saf. Sci. 2011, 49, 778–784. [Google Scholar] [CrossRef]
- Aminbakhsh, S.; Gündüz, M.; Sönmez, R. Safety Risk Assessment Using Analytic Hierarchy Process (AHP) during Planning and Budgeting of Construction Projects. J. Saf. Res. 2013, 46, 99–105. [Google Scholar] [CrossRef]
- Amiri, M.; Ardeshir, A.; Fazel Zarandi, M.H. Fuzzy Probabilistic Expert System for Occupational Hazard Assessment in Construction. Saf. Sci. 2017, 93, 16–28. [Google Scholar] [CrossRef]
- Dharmapalan, V.; Gambatese, J.A.; Fradella, J.; Moghaddam Vahed, A. Quantification and Assessment of Safety Risk in the Design of Multistory Buildings. J. Constr. Eng. Manag. 2015, 141, 04014090. [Google Scholar] [CrossRef]
- Junjia, Y.; Alias, A.H.; Haron, N.A.; Abu Bakar, N. Identification and Analysis of Hoisting Safety Risk Factors for IBS Construction Based on the AcciMap and Cases Study. Heliyon 2024, 10, e23587. [Google Scholar] [CrossRef]
- Mete, S.; Serin, F.; Oz, N.E.; Gul, M. A Decision-Support System Based on Pythagorean Fuzzy VIKOR for Occupational Risk Assessment of a Natural Gas Pipeline Construction. J. Nat. Gas Sci. Eng. 2019, 71, 102979. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Zhang, X. Towards the Development of a Comprehensive Hybrid Fuzzy-Based Occupational Risk Assessment Model for Construction Workers. Saf. Sci. 2019, 115, 294–309. [Google Scholar] [CrossRef]
- Sui, Y.; Ding, R.; Wang, H. A Novel Approach for Occupational Health and Safety and Environment Risk Assessment for Nuclear Power Plant Construction Project. J. Clean. Prod. 2020, 258, 120945. [Google Scholar] [CrossRef]
- Sun, Y.; Fang, D.; Wang, S.; Dai, M.; Lv, X. Safety Risk Identification and Assessment for Beijing Olympic Venues Construction. J. Manag. Eng. 2008, 24, 40–47. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Chen, C. Fuzzy Comprehensive Bayesian Network-Based Safety Risk Assessment for Metro Construction Projects. Tunn. Undergr. Sp. Technol. 2017, 70, 330–342. [Google Scholar] [CrossRef]
- Yüksel, İ.; Dagdeviren, M. Using the Analytic Network Process (ANP) in a SWOT Analysis—A Case Study for a Textile Firm. Inf. Sci. (Ny). 2007, 177, 3364–3382. [Google Scholar] [CrossRef]
- Bayazıt, Ö. A New Methodology in Multiple Criteria Decision-Making Systems: Analitic Network Process (ANP) and an Application. Ankara Üniversitesi SSF Derg. 2002, 57, 15–34. [Google Scholar]
- Liu, H.; Tsai, Y. A Fuzzy Risk Assessment Approach for Occupational Hazards in the Construction Industry. Saf. Sci. 2012, 50, 1067–1078. [Google Scholar] [CrossRef]
- Koulinas, G.K.; Marhavilas, P.K.; Demesouka, O.E.; Vavatsikos, A.P.; Koulouriotis, D.E. Risk Analysis and Assessment in the Worksites Using the Fuzzy-Analytical Hierarchy Process and a Quantitative Technique—A Case Study for the Greek Construction Sector. Saf. Sci. 2019, 112, 96–104. [Google Scholar] [CrossRef]
- Chalos, P. Managing Cost in Today’s Manufacturing Environment; Prentice Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Gebre, S.L.; Cattrysse, D.; Alemayehu, E.; Van Orshoven, J. Multi-Criteria Decision Making Methods to Address Rural Land Allocation Problems: A Systematic Review. Int. Soil Water Conserv. Res. 2021, 9, 490–501. [Google Scholar] [CrossRef]
- Abu Taha, R.; Daim, T. Multi-Criteria Applications in Renewable Energy Analysis, a Literature Review. In Research and Technology Management in the Electricity Industry; Springer: London, UK, 2013; pp. 17–30. [Google Scholar]
- Wheeler, J.; Páez, M.A.; Guillén-Gosálbez, G.; Mele, F.D. Combining Multi-Attribute Decision-Making Methods with Multi-Objective Optimization in the Design of Biomass Supply Chains. Comput. Chem. Eng. 2018, 113, 11–31. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Z.; Lee, K.; Owens, E.; Boufadel, M.C.; An, C.; Taylor, E. Decision Support Tools for Oil Spill Response (OSR-DSTs): Approaches, Challenges, and Future Research Perspectives. Mar. Pollut. Bull. 2021, 167, 112313. [Google Scholar] [CrossRef]
- Atlas, M. Çok Amaçlı Programlama Çözüm Tekni̇kleri̇ni̇n Sınıflandırılması. Anadolu Üni̇versi̇tesi̇ Sos. Bi̇li̇mler Dergi̇si̇ 2008, 8, 47–68. [Google Scholar]
- Tsoukalas, V.D.; Fragiadakis, N.G. Prediction of Occupational Risk in the Shipbuilding Industry Using Multivariable Linear Regression and Genetic Algorithm Analysis. Saf. Sci. 2016, 83, 12–22. [Google Scholar] [CrossRef]
- Ak, M.F. Comparison of Risk Assessment Methods within the Scope of Occupational Safety in the Construction Sector. Eur. J. Sci. Technol. 2020, 18, 272–282. [Google Scholar] [CrossRef]
- Abbasianjahromi, H.; Aghakarimi, M. Safety Performance Prediction and Modification Strategies for Construction Projects via Machine Learning Techniques. Eng. Constr. Archit. Manag. 2021, 30, 1146–1164. [Google Scholar] [CrossRef]
- Ayhan, B.U.; Tokdemir, O.B. Predicting the Outcome of Construction Incidents. Saf. Sci. 2019, 113, 91–104. [Google Scholar] [CrossRef]
- Kedong, Y.; Zhou, S.; Xu, T. Research on Optimization of Index System Design and Its Inspection Method. Mar. Econ. Manag. 2019, 2, 1–28. [Google Scholar] [CrossRef]
- Roberti, F.; Oberegger, U.F.; Lucchi, E.; Troi, A. Energy Retrofit and Conservation of a Historic Building Using Multi-Objective Optimization and an Analytic Hierarchy Process. Energy Build. 2017, 138, 1–10. [Google Scholar] [CrossRef]
- Alkaissy, M.; Arashpour, M.; Ashuri, B.; Bai, Y.; Hosseini, R. Safety Management in Construction: 20 Years of Risk Modeling. Saf. Sci. 2020, 129, 104805. [Google Scholar] [CrossRef]
- Coşkun, A. Yapay Zeka Optimizasyon Teknikleri: Literatür Değerlendirmesi. Fırat Üniversitesi Doğu Anadolu Bölgesi Araştırmaları Dergisi Doğu Anadolu Bölgesi Araştırmaları 2007, 2, 142–146. [Google Scholar]
- Atalay, M.Ç.E. Büyük Veri Analizinde Yapay Zeka ve Makine Öğrenmesi Uygulamaları. Mehmet Akif Ersoy Üniversitesi Sos. Bilim. Enstitüsü Derg. 2017, 9, 155–172. [Google Scholar]
- Ojha, M.; Singh, K.P.; Chakraborty, P.; Verma, S. A Review of Multi-Objective Optimisation and Decision Making Using Evolutionary Algorithms. Int. J. Bio-Inspired Comput. 2019, 14, 69. [Google Scholar] [CrossRef]
- Yang, X.-S. Introduction to Algorithms for Data Mining and Machine Learning; Academic Press: London, UK, 2019. [Google Scholar]
- Rout, B.; Sikdar, B. Hazard Identification, Risk Assessment, and Control Measures as an Effective Tool of Occupational Health Assessment of Hazardous Process in an Iron Ore Pelletizing Industry. Indian J. Occup. Environ. Med. 2017, 21, 56. [Google Scholar] [CrossRef] [PubMed]
- Forteza, F.J.; Carretero-Gómez, J.M.; Sesé, A. Occupational Risks, Accidents on Sites and Economic Performance of Construction Firms. Saf. Sci. 2017, 94, 61–76. [Google Scholar] [CrossRef]
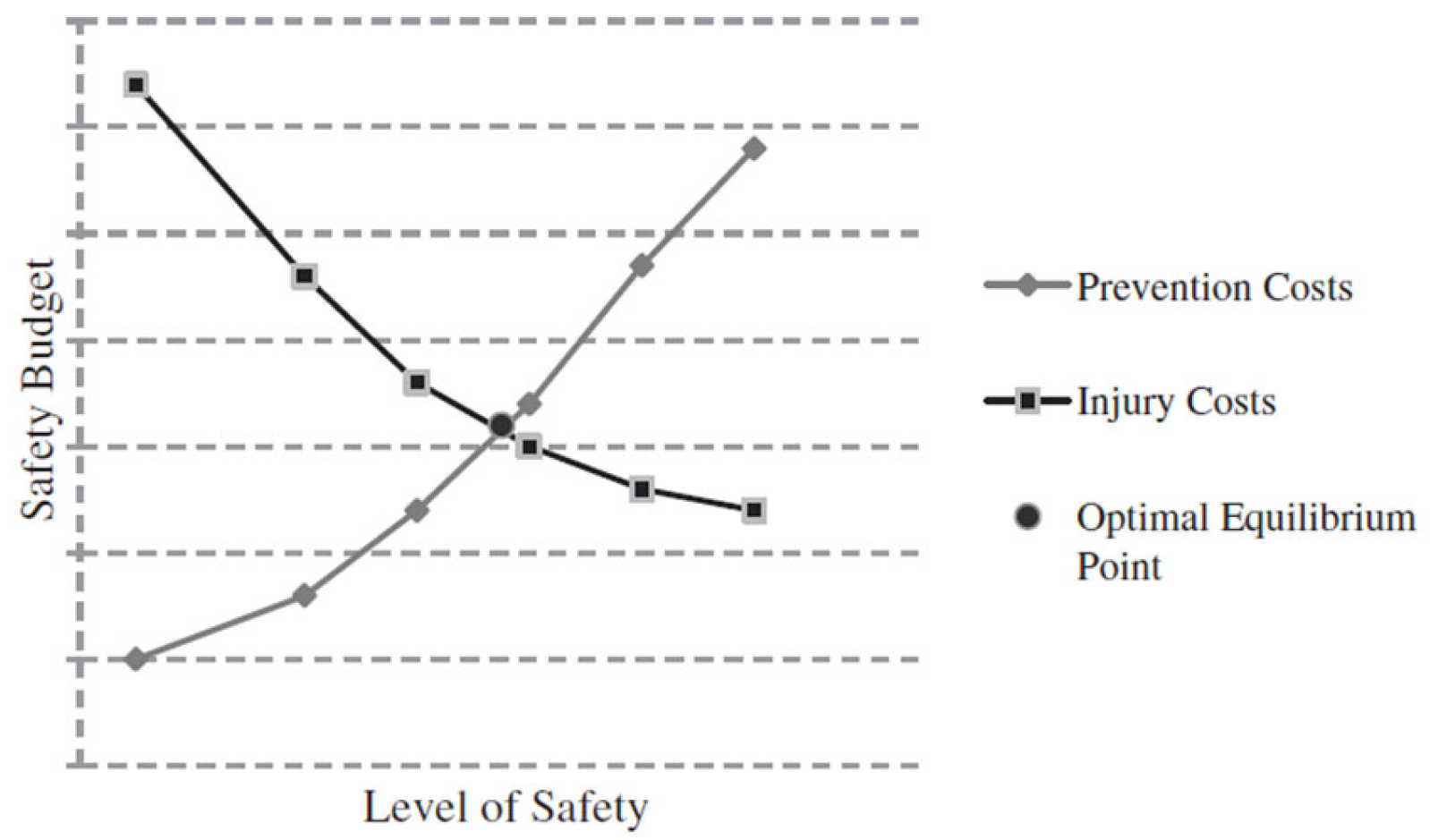
- Ma, Y.; Zhao, Q.; Xi, M. Decision-Makings in Safety Investment: An Opportunity Cost Perspective. Saf. Sci. 2016, 83, 31–39. [Google Scholar] [CrossRef]
- Ghousi, R.; Khanzadi, M.; Atashgah, K.M.; Branch, Q. A Flexible Method of Building Construction Safety Risk Assessment and Investigating Financial. Int. J. Optim. Civ. Eng. 2018, 8, 433–452. [Google Scholar]
- Azadeh-Fard, N.; Schuh, A.; Rashedi, E.; Camelio, J.A. Risk Assessment of Occupational Injuries Using Accident Severity Grade. Saf. Sci. 2015, 76, 160–167. [Google Scholar] [CrossRef]
- Al-Anbari, S.; Khalina, A.; Alnuaimi, A.; Normariah, A.; Yahya, A. Risk Assessment of Safety and Health (RASH) for Building Construction. Process Saf. Environ. Prot. 2015, 94, 149–158. [Google Scholar] [CrossRef]



| Parameter | Description | Parameter | Description |
|---|---|---|---|
| P | Degree to which the risk is likely to materialize | IoPD | Impact of occupational accidents on project duration |
| IoWHS | Impact of risk on workers health | IoPC | The impact of cost increases such as lawsuits that may be filed against construction companies affected by accidents, compensation paid to the family of the injured worker |
| IoE | Impact of fire, explosion, or vehicle accidents on the environment or bystanders in situations | ||
| IoS | Moral impact of accidents on society in companies, victims’ families and colleagues, or society in general | IoRC | The impact of media coverage of accidents or accusations made by victims or their families |
| Work Items | Hazards/Risks | Precautions |
|---|---|---|
| Concrete | Concrete mixer hits workers, concrete mixer hits surrounding structures/vehicles, electric shock, fall from height | Having a marker person on the field, insulated gloves, warning signs, and safety rope systems |
| Covering | Material falls, improper use of hand tools, electric shock, the air well remains open | Railing systems, building cover systems, protective goggles, warning signs, insulated gloves, closing of air well |
| Electrical wiring | Electric shock, fire risk | Insulated gloves, warning signs |
| Excavation | Fall from height, construction equipment hitting people and objects, entering dangerous areas, electric shock, the vehicle overturned at the excavation site, workers were trapped under the cave-in, inhalation of dust, occupational accidents due to machine malfunctions, improper use of hand tools, hitting the power transmission lines | Railing systems, protective goggles, warning signs, insulated gloves, closing of air well, security area curtains, having a marker person on the field, safety lane, dust mask |
| Formwork | Splattered materials hitting workers, material fall, improper use of hand tools, fall from height | Railing systems, safety rope systems, protective goggles, security area curtains, safety lane |
| Masonry andchimney | Fall from height, material fall, the air well remaining open, improper use of hand tools, electric shock, inhalation of dust, object getting into the eye | Railing systems, safety rope systems, protective goggles, warning signs, insulated gloves, closing of shaft gaps, building cover systems, dust mask |
| Mechanical installation | Falling through elevator shafts, improper use of hand tools, dust getting into the eye, inhalation of dust, material fall, electric shock, the air well remains open | Railing systems, safety rope systems, protective goggles, warning signs, insulated gloves, building cover systems, closing of air well, dust mask |
| Insulation | Fall from height, material fall, improper use of hand tools, electric shock, the air well remains open | Railing systems, safety rope systems, protective goggles, warning signs, insulated gloves, building cover systems, closing of air well, dust mask |
| Joinery | Fall from height, electric shock, improper use of hand tools, material fall, the air well remains open | Railing systems, safety rope systems, protective goggles, warning signs, insulated gloves, closing of air well, building cover systems |
| Plaster and paint | Improper use of hand tools falls from height, material falls, inhalation of dust, objects getting into the eye, poisoning, the air well remaining open | Railing systems, safety rope systems, protective goggles, warning signs, building cover systems, closing of air well, dust mask |
| Rebar works | Improper use of hand tools, electric shock, fall from height | Railing systems, safety rope systems, protective goggles, warning signs, insulated gloves |
| Roof | Fall from height, material fall, improper use of hand tools, electric shock, the air well remains open | Railing systems, safety rope systems, building cover systems, protective goggles, insulated gloves, warning signs, closing of air well |
| Roofing Activities | P | IoWHS | IoE | IoS | IoPC | IoPD | IoRC |
|---|---|---|---|---|---|---|---|
| Fall from height (No precautions) | … | … | … | … | … | … | … |
| Fall from height (Railing systems) | … | … | … | … | … | … | … |
| Fall from height (Safety rope systems) | … | … | … | … | … | … | … |
| Material fall (No precautions) | … | … | … | … | … | … | … |
| Material fall (Railing systems) | … | … | … | … | … | … | … |
| Material fall (Building cover systems) | … | … | … | … | … | … | … |
| Improper use of hand tools (No precautions) | … | … | … | … | … | … | … |
| Improper use of hand tools (Protective goggles) | … | … | … | … | … | … | … |
| Electric shock (No precautions) | … | … | … | … | … | … | … |
| Electric shock (Insulated gloves) | … | … | … | … | … | … | … |
| Electric shock (Warning signs) | … | … | … | … | … | … | … |
| Falling of materials through open shaft voids (No precautions) | … | … | … | … | … | … | … |
| Falling of materials through open shaft voids (Closing of air well) | … | … | … | … | … | … | … |
| Position | Professional Experience (Years) | Experience in Risk Assessment (Years) | Education |
|---|---|---|---|
| Academician | 50 | 20 | Doctoral Degree |
| 15 | 10 | Doctoral Degree | |
| 17 | 10 | Doctoral Degree | |
| Occupational Safety Expert | 17 | 7 | Master’s Degree |
| 5 | 5 | Master’s Degree | |
| 7 | 5 | Master’s Degree | |
| 8 | 5 | Master’s Degree | |
| 10 | 5 | Master’s Degree | |
| 7 | 5 | Bachelor’s Degree | |
| Civil Engineer | 20 | 20 | Master’s Degree |
| Parameter | Optimization Algorithms | |||
|---|---|---|---|---|
| GA | B-ABC | B-FA | B-FPA | |
| Population size | 50 | 50 | 50 | 50 |
| Number of generations | 150 | 150 | 150 | 150 |
| Elit count | 1 | -- | -- | -- |
| Crossover probability | 1 | -- | -- | -- |
| Mutation probability | 0.2 | -- | -- | -- |
| Scout probability | -- | 0.4 | -- | -- |
| Switch probability | -- | -- | -- | 0.5 |
| Phi | -- | -- | -- | 0.9 |
| Initial Gamma | -- | -- | 1 | -- |
| Beta | -- | -- | 0.7 | -- |
| Precautionary Status | Risk Scores | Total Cost ($) | ||||||
|---|---|---|---|---|---|---|---|---|
| IoWHS | IoE | IoS | IoPC | IoPD | IoRC | Total | ||
| No precautions | 986 | 748 | 711 | 726 | 700 | 780 | 4651 | 0 |
| Proposed model | 467 | 257 | 287 | 266 | 270 | 275 | 1822 | 29,178.89 |
| All precautions | 325 | 162 | 188 | 178 | 173 | 181 | 1207 | 51,734.08 |
| IoWHS | IoWHS, IoE | IoWHS, IoS | IoWHS, IoPC | IoWHS, IoPD | IoWHS, IoRC | IoWHS, IoPC, IoPD | IoWHS, IoE, IoS, IoRC | All Parameters | |
|---|---|---|---|---|---|---|---|---|---|
| Total Risk Score | 462 | 714 | 746 | 733 | 737 | 742 | 1003 | 1286 | 1822 |
| Total Cost ($) | 29,179.47 | 29,179.47 | 29,179.47 | 29,179.89 | 29,179.89 | 29,179.89 | 29,179.89 | 29,179.89 | 29,179.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aydinli, S.; Alboga, Ö.; Oral, M.; Erdiş, E. A Multi-Dimensional Construction Safety Risk Optimization Model. Buildings 2025, 15, 985. https://doi.org/10.3390/buildings15060985
Aydinli S, Alboga Ö, Oral M, Erdiş E. A Multi-Dimensional Construction Safety Risk Optimization Model. Buildings. 2025; 15(6):985. https://doi.org/10.3390/buildings15060985
Chicago/Turabian StyleAydinli, Serkan, Özge Alboga, Mustafa Oral, and Ercan Erdiş. 2025. "A Multi-Dimensional Construction Safety Risk Optimization Model" Buildings 15, no. 6: 985. https://doi.org/10.3390/buildings15060985
APA StyleAydinli, S., Alboga, Ö., Oral, M., & Erdiş, E. (2025). A Multi-Dimensional Construction Safety Risk Optimization Model. Buildings, 15(6), 985. https://doi.org/10.3390/buildings15060985






