Observations on the Relationship between Crash Frequency and Traffic Flow

Abstract

This work analyzes the relationship between crash frequency N (crashes per hour) and exposure Q (cars per hour) on the macroscopic level of a whole city. As exposure, the traffic flow is used here. Therefore, it analyzes a large crash database of the city of Berlin, Germany, together with a novel traffic flow database. Both data display a strong weekly pattern, and, if taken together, show that the relationship $N\left(Q\right)$ is not a linear one. When Q is small, N grows like a second-order polynomial, while at large Q there is a tendency towards saturation, leading to an S-shaped relationship. Although visible in all data from all crashes, the data for the severe crashes display a less prominent saturation. As a by-product, the analysis performed here also demonstrates that the crash frequencies follow a negative binomial distribution, where both parameters of the distribution depend on the hour of the week, and, presumably, on the traffic state in this hour. The work presented in this paper aims at giving the reader a better understanding on how crash rates depend on exposure.

1. Motivation

Recent years have seen some progress when it comes to the availability and analysis of crash data [1,2,3], or [4]. This has triggered new work and new methods, most notably from machine learning that have the potential to improve knowledge, models, and, ultimately, also the state of traffic safety.

In many cases, road safety work consists of identifying crash blackspots, determining corrective measures, implementing them, and later evaluating them. A reasonable definition of a road accident blackspot will involve the number of crashes per unit of exposure. This paper deals with the problem of modeling the relationship between crash rates and exposure. A better understanding of this relationship allows traffic safety management targeting hazardous locations more clearly based on risk and not merely on crash frequency.

Traditionally, one approach in this context is the development of crash prediction models. They estimate the impact of several variables $x_{j·}$ on crash frequencies. This is done by applying models of the type [5,6,7,8,9]:

$$N_i={\beta }_0{(Q_i/Q_0)}^{{\beta }_1}exp\left({\mu }_i\right)={\beta }_0{(Q_i/Q_0)}^{{\beta }_1}exp\left(\sum _{j=2}^n{\beta }_j{x}_{ji}+\zeta \right),$$

(1)

where $N_i$ is the crash frequency at a certain instance i (time, place,…), $Q_i$ is an exposure variable, $Q_0$ is a baseline flow, ${\mu }_i$ is the mean value of the crash rate, the $x_{ij}$ are factors thought to influence the crash frequency, and the ${\beta }_j$ are coefficients that quantify the strength of each factor. Moreover, there is a gamma-distributed noise term $\zeta$ here where exp$\left(\zeta \right)$ has mean one and variance $\gamma$.

The crash frequencies themselves are then found as a realization of a stochastic process with a negative binomial distribution (NBD) with a mean $\mu$ and variance ${\sigma }^2$:   

$${\sigma }^2=\mu +\gamma {\mu }^2.$$

(2)

The parameter $\gamma$ describes how much the NBD deviates from a Poisson distribution, with $\gamma =0$ for a Poisson distribution.

The exposure variable, which in the following will be mainly the traffic flow, is difficult to include properly in traffic safety analyses. This is due to the fact that crashes are rare events, and that more often than not, a measurement of the exposure is not available at the site and time of the crash. If available, it is often only in the form of an average over a day, and very often from travel demand models instead of directly measured. Similar difficulties plague the other data source of exposure, which is the one that stems from travel surveys. In many cases, they are averages over large spatial areas (as in travel survey data) although attempts exist to integrate traffic flow with more detail [10,11,12,13]. However, it might be speculated that crash probabilities depend strongly on the traffic state itself, with traffic flow being one of the major influencing variable [14,15].

Especially of interest is the relationship between the crash frequency N when displayed versus the traffic flow Q, see [14]. Note that often not N itself is displayed as a function of Q, the crash rate $\rho$ is used instead:

$$\rho \left(Q\right)={\displaystyle \frac{N\left(Q\right)}{Q}}.$$

(3)

The crash rate is the ratio between an average crash frequency and the corresponding average traffic flow, leading to a continuous variable. As is demonstrated in Section 3.1, another interpretation is to use the discrete number of crashes in one hour and the associated traffic flow in this hour, which leads to a mixture between a discrete and a continuous distribution. (A similar approach can be found in [16], they have used the mileage on the x-axis.)

Some thoughts about the relationship between $N\left(Q\right)$ and $\rho \left(Q\right)$ are in order. It is very likely that the crash rate does not vanish as a function of Q, even for very small exposure Q we expect that the crash rate does not drop to zero, and the results of this work will lend additional credibility to this idea. So:

$$N\left(Q\right)\propto Q\iff \rho \left(Q\right)\propto {\rho }_0\mathrm{for}Q\to 0.$$

(4)

For freeway traffic, a good deal of results for $N\left(Q\right)$ and $\rho \left(Q\right)$ are available. The most commonly used model has a roughly U-shaped form for $\rho \left(Q\right)$, where crash rates are rather large for small and large flows and have a minimum for intermediate flows. e.g., the work [17,18] claims:

$$\rho \left(Q\right)=c_1{Q}^{-{\beta }_1}+c_2{Q}_2^{\beta }.$$

(5)

where the exponent ${\beta }_1$ is around 1, and ${\beta }_2$ is between 1 and 2. Note that it is assumed that the flow values are normalized to a constant flow so that the units drop out. The first term is for single-vehicle crashes, while the second term describes multi-car crashes. Ceder also observed that one should discern free traffic from congested traffic; this, however, raises the question of how to do this properly based on hourly values. Furthermore, a recent meta-analysis [19] that used 118 studies come to a similar conclusion, albeit with different exponents ${\beta }_1,{\beta }_2$.

Similar results exist [15,20,21] or the German study [22], sometimes more symmetric second-order polynomial relationships $\rho \left(Q\right)\propto c_1{(Q-Q_c)}^2+c_0$ have been used to describe the data. The approach of [23] is a bit different since it displays crash rate as a function of a novel indicator that is difficult to translate into traffic flow or volume/capacity ratios. Note as an oddity that one of the earliest models on this topic [24] proposed an inverse U-shaped relationship, which is once again a second-order polynomial; this time, the crash rate is being small for small flow and large flows, which were in this case AADT values (AADT = annual average daily traffic). However, Veh’s data are also consistent with the assumption that the crash rate is constant, or a weakly increasing function of exposition.

In essence, it could be stated that currently there is no univocal picture about the relationship $\rho \left(Q\right)$ for freeway data; for a more complete overview see [25]. Note, however, that at least the idea of a diverging crash rate for $Q\to 0$ might be questionable; however, this is not the topic of this work.

Results are different when looking at the relationship between $\rho$ and AADT as an exposure variable. In this case, crash rates increase with Q, eventually again as a power-law $\rho \left(Q\right)\propto Q^{\beta }$ [26].

Very little work has been done so far that looks at the relationship $N\left(Q\right)$ on the basis for a whole city, with notable exceptions of [27] with a more theoretical approach, and [28] trying to test this theory without having real flow data available, and the recent work on a network-based macroscopic safety diagram [29].

The hypothesis behind this work was the assumption that at least the crash frequency that involves two cars should be a second-order polynomial function of the traffic flow [30]. A similar idea is also proposed in [27,31]. Therefore, a reasonable model for the crash frequency in a city is a combination of single-car crashes (which can be assumed to be proportional to the number of vehicles around Q) and an interaction term proportional to $Q^2$. This interaction term is due to a naive assumption that if vehicles move independently of each other, then there is a probability proportional to $Q^2$ that they meet:

$$N={\alpha }_{1}Q+{\alpha }_2{Q}^2$$

(6)

Note that it is not easy to bring Equation (6) in line with Equation (1): the latter one is tailored towards the use of generalized linear models (GLM) with a logarithmic link function, and by exchanging $Q^{{\beta }_1}$ with ${\alpha }_{1}Q+{\alpha }_2{Q}^2$, the very character of this model is changed into something that no longer can be treated as GLM with a logarithmic link function.

However, this work deals only with the prefactor and ignores $exp\left({\mu }_i\right)$, so a GLM and its generalization GAM (generalized additive model) can still be used, but in most cases with the identity as the link function.

As a final remark, note that models with a power-law term as in Equation (1) are not in line with the assumption in Equation (4) that the crash rate becomes constant for small exposure. However, when looking closely into [17,18], then Equation (5) function might be modified to avoid the divergence at $Q\to 0$ by modifying the first term in the equation into $c_1{(Q+b)}^{-{\beta }_1}$.

2. The Data

This paper uses two types of data. The first one is a large crash database that contains all crashes reported by the Berlin police in the city of Berlin, Germany, during the years 2001–2019. The data are de-identified, i.e., they do not contain numberplates or names of the crash participants or any other information that can be used to identify them. Furthermore, for the subset of data used in the work reported here, the crash-time has been aggregated to the hour.

Note that common practice in Berlin is different from other German federal states since even a lot of property damage only (PDO) crashes are reported in the database. However, even here the analyst must be aware of the fact that these numbers are biased due to the under-reporting of small crashes. For this paper, only some part of the data in this database has been used, see below for a more detailed description.

The second set of data stems from the Traffic4cast competition [32]. It contains de-identified data from most of the days of 2018 in Berlin, where the speeds and the number of probes of a certain vehicle fleet have been recorded. Since such a data set is a bit unusual, it has been complemented by two other de-identified data sets so that comparisons between the different data could be performed that are interesting in their own right. These are the annual hourly count data from 28 detection sites, which have been provided by the German Federal Highway Research Institute (BASt) and data from the latest travel survey in Germany named Mobility in Deutschland (MiD) [33].

2.1. The Crash Database

The crash database has been provided by the Berlin police, and it is not publicly available. It contains for each crash i about $60\times n_i$ variables (some redundant), where $n_i$ is the number of people involved in the crash. Here, only the time $t_i$, the severity, and the vehicle types have been used. Time is described with minutes’ resolution; however, it is good not to use these numbers to this precision since preference for multiples of 15 min can be observed (see also [3]). The severity of each crash is described by the number of lightly injured, the number of severely injured, the number of fatalities, and the damage.

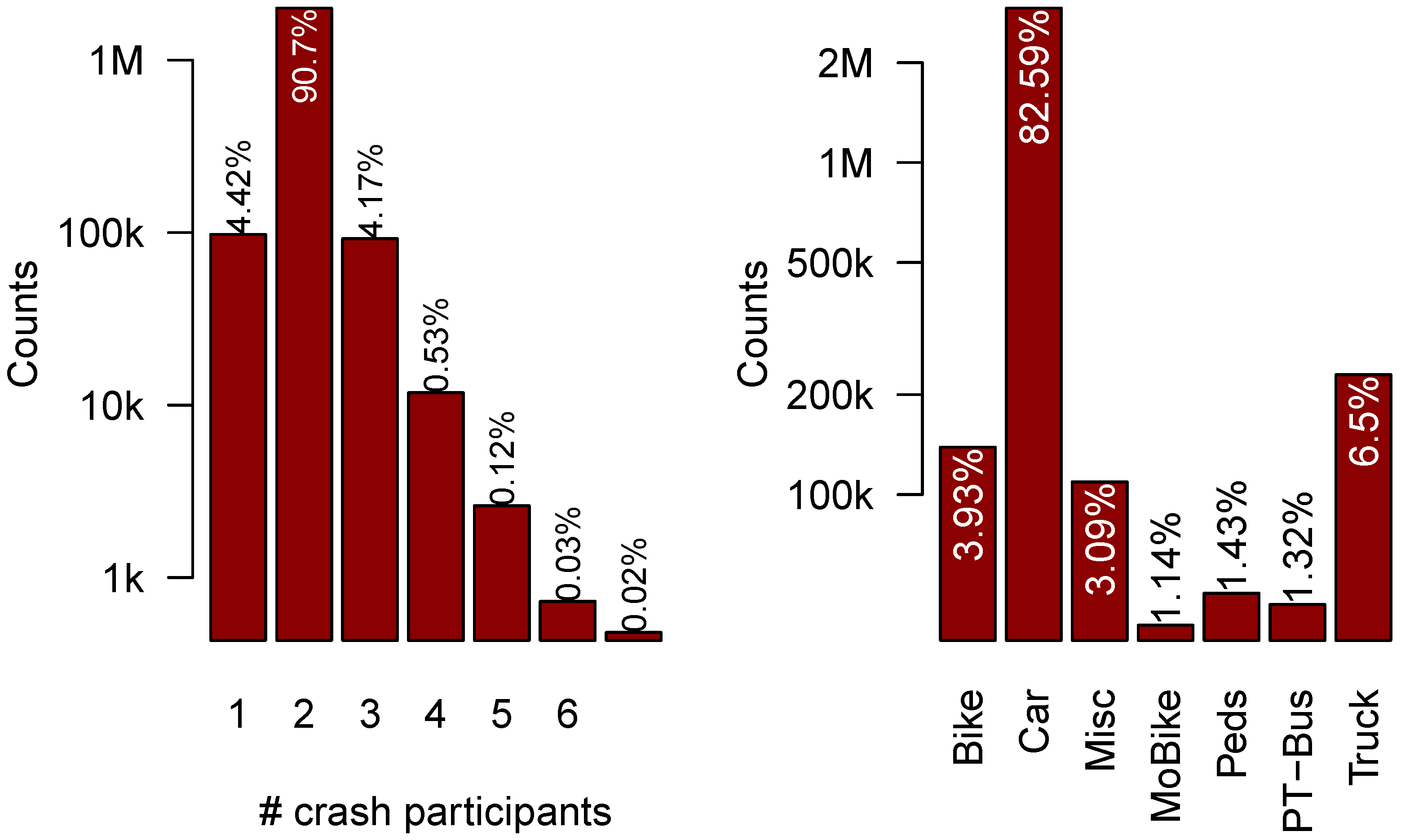
In the following, only severe (crashes with injured or killed participants) and non-severe PDO crashes will be distinguished. The database contains 1,888,038 crashes, and what is important for the analysis below: most of all crashes are between two cars, as can be seen in Figure 1.

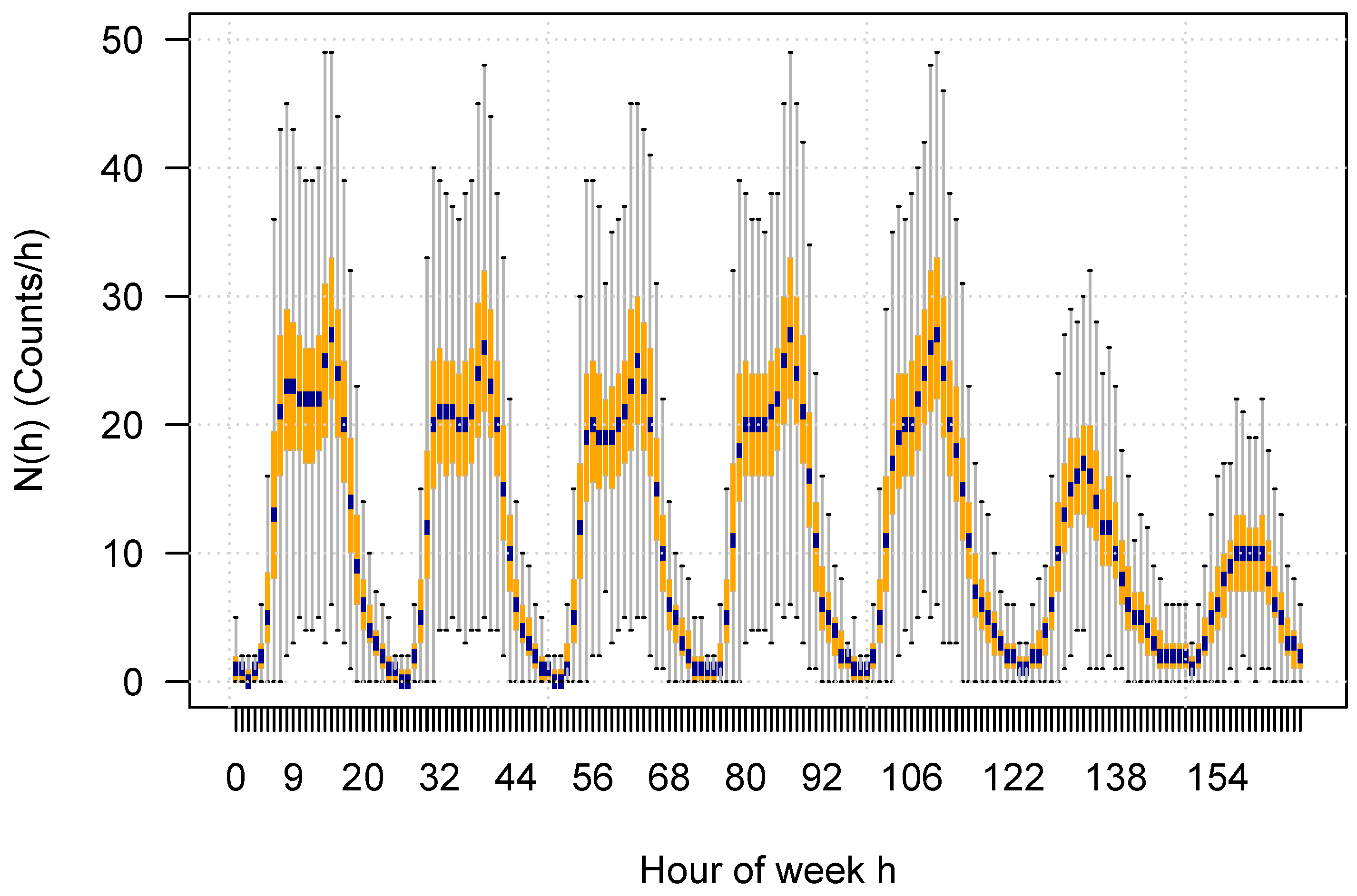
For this study, the timestamps of all crashes of the database have been rounded down to the nearest full hour and translated to the corresponding hour of the week (0–167). Since the data set spans 19 years, each hour occurs 992 times in the data set, resulting in 992 crash numbers for every hour of the week h. Therefore, for each hour of the week, the distribution of counts can be determined directly. The results are displayed in Figure 2 as a boxplot, and they display a strong weekly pattern. Very similar results have been reported recently by [34].

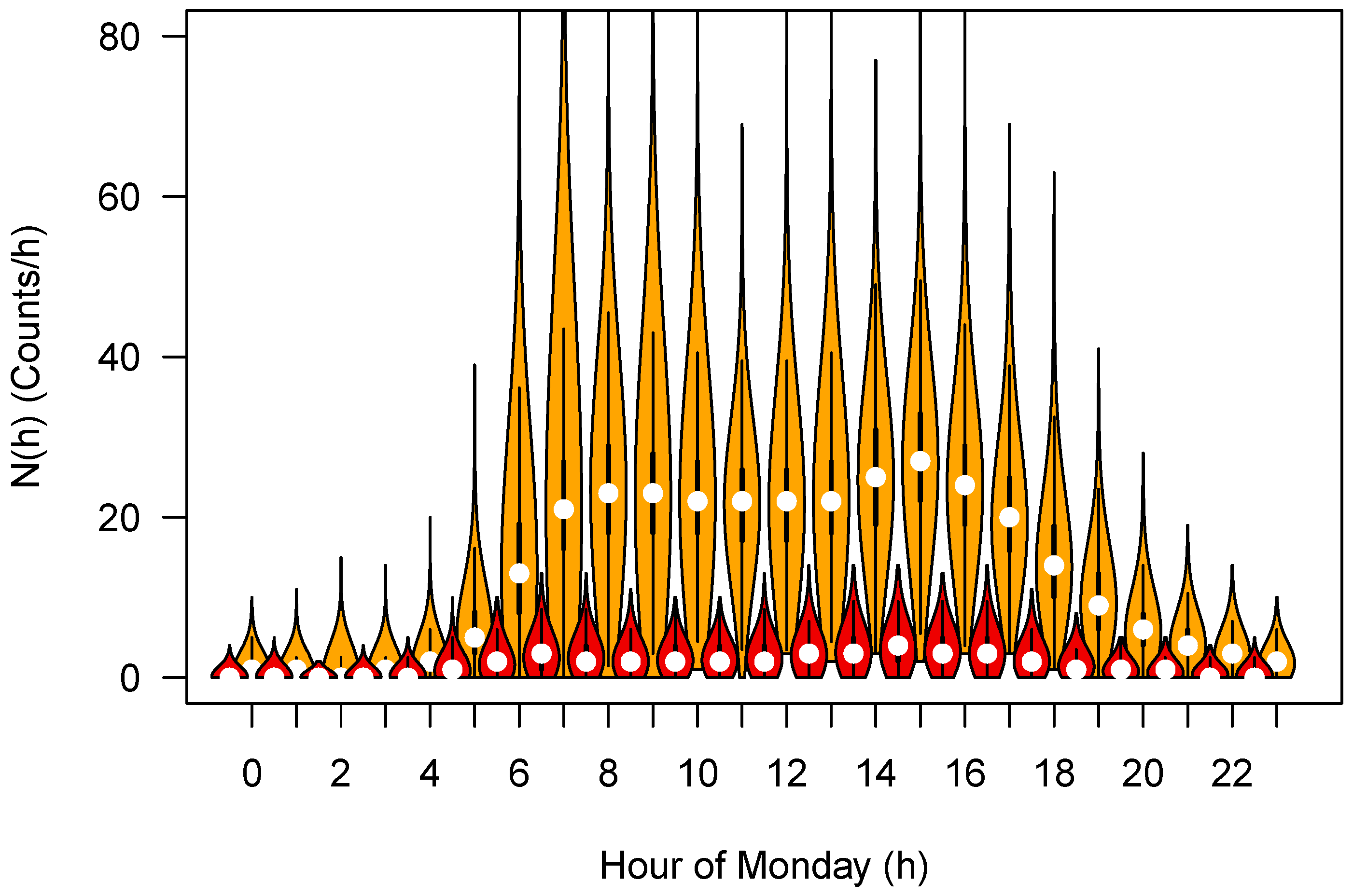
The Figure 3 displays this result for the Monday only as a violin plot so that the shape of the distributions can be seen more clearly. Moreover, the distribution of severe crashes has been included in this Figure as well.

2.2. The Distribution of the Crash Frequency

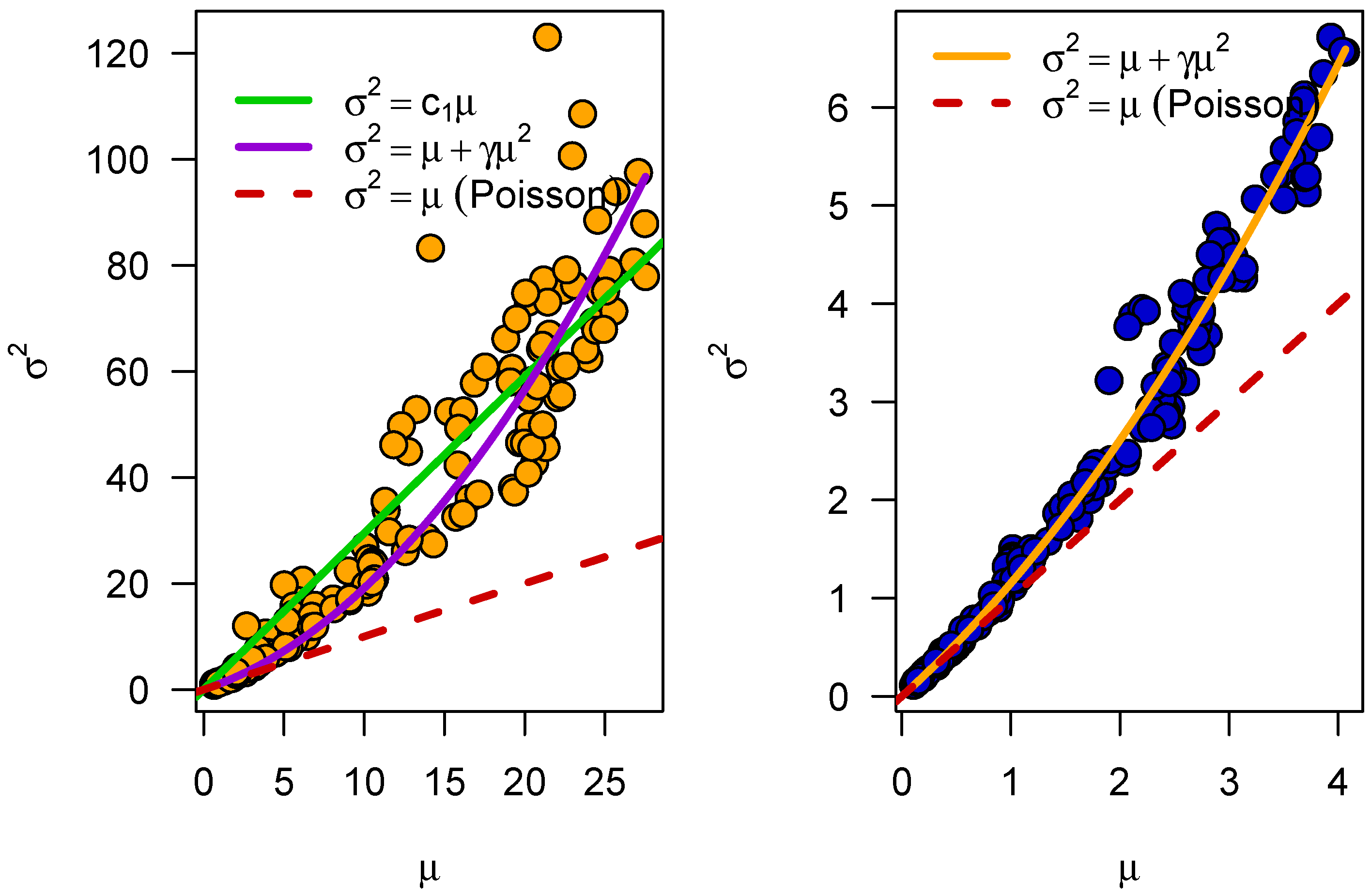
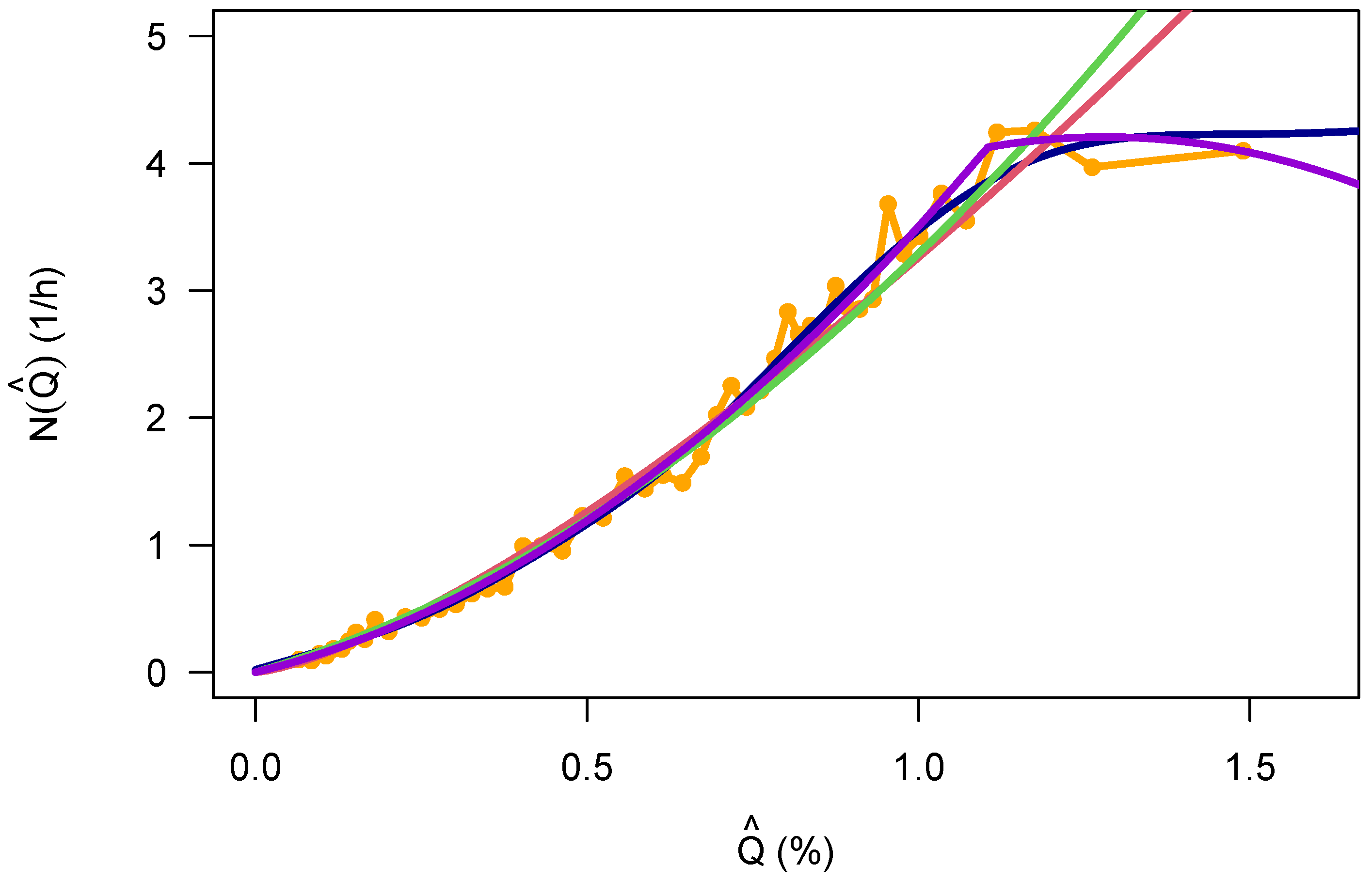
Most likely, the individual distributions in each hour are following an NBD. This can be tested by plotting their variance ${\sigma }^2$ against their mean value $\mu$. An NBD displays then a second-order polynomial relationship between $\mu$ and ${\sigma }^2$ as stated already in Equation (2), where the parameter $\gamma$ specifies the deviation of the distribution from a Poisson distribution. The results can be seen in Figure 4. Figure 4 shows that the data follow an NBD. Also, the same analysis has been performed for severe crashes only. Various fits to this cloud of data-points have been included in this Figure as well demonstrating that the assumption of the NBD fits these data quite well. All fits are done with R’s lm() function [35], which executes a linear least-squares fit to these data. The fit for the severe crashes is even better (larger $R^2$), leading to two different estimates for the $\gamma$ variable. For all crashes, $\gamma$ is estimated as $\gamma =0.091\pm 0.003$, while it is larger for the severe crashes with $\gamma =0.153\pm 0.003$. All fits are highly significant, with p-values for the parameters well below $p<{10}^{-10}$, and $R^2$-values above 0.93.

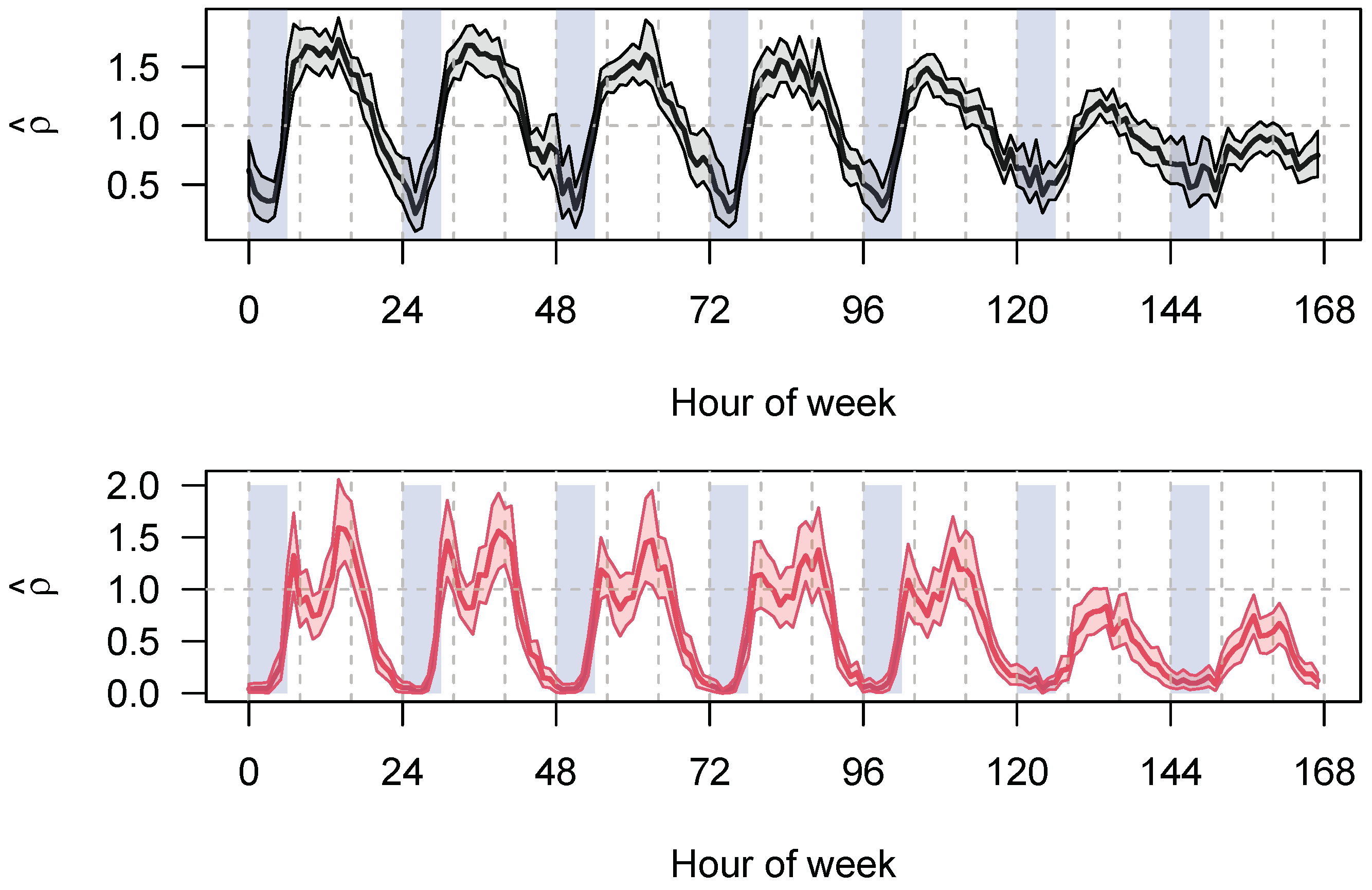
Furthermore, the distribution of each hour of the week can be fitted directly with an NBD. From this, it can be stated that not only $\mu$ depends on the hour of the week (and presumably, on the traffic state during this hour), the same is true for $\gamma$ as well, see Figure 5. We have found little work showing such a relationship between $\gamma$ and the traffic state; in [36] it is shown that their parameter $k=1/\gamma$ depends on the length of a road section and that they have not found a dependence of k on AADT.

2.3. The Traffic Flow Data

The traffic flow data are from the Traffic4cast challenge (T4C), where scientists were asked to find the best possible prediction of the traffic state in a city. Traffic state is defined as the speed and flow pattern $v_{i,j}\left(t\right)$, $q_{i,j}\left(t\right)$ of the cars of a large vehicle fleet, resulting from about ${10}^{11}$ probe vehicle data. The index $i,j$ is running from 0 to $436\times 495$ respectively, while the time t is aggregated to five minutes intervals. Each $i,j$ refers to a specific $100\times 100\mathrm{m}$ box, where the boxes cover the whole area of Berlin. Note that the data have been aggregated so that in each of the spatial boxes an 8-bit number $\{0,\dots ,255\}$ results for the flows $q_{i,j}\left(t\right)$, and the speeds $v_{i,j}\left(t\right)$.

Altogether, data of 273 days from the training-set have been used here, and have been aggregated into hourly values as well for the analysis here. Note that neither the flow nor the speed values can be related to ”real” numbers, they are in a complicated manner scaled variables. Nevertheless, especially the aggregated flow values $Q\left(t\right)={\sum }_{i,j}{q}_{i,j}$ have been used, they should be proportional to the real traffic flow in the city.

When doing the same aggregation as with the crash data (and taking care of the fact that the timestamps of the training data set are in UTC, Coordinated Universal Time), a similar plot as in Figure 2 is obtained in Figure 6.

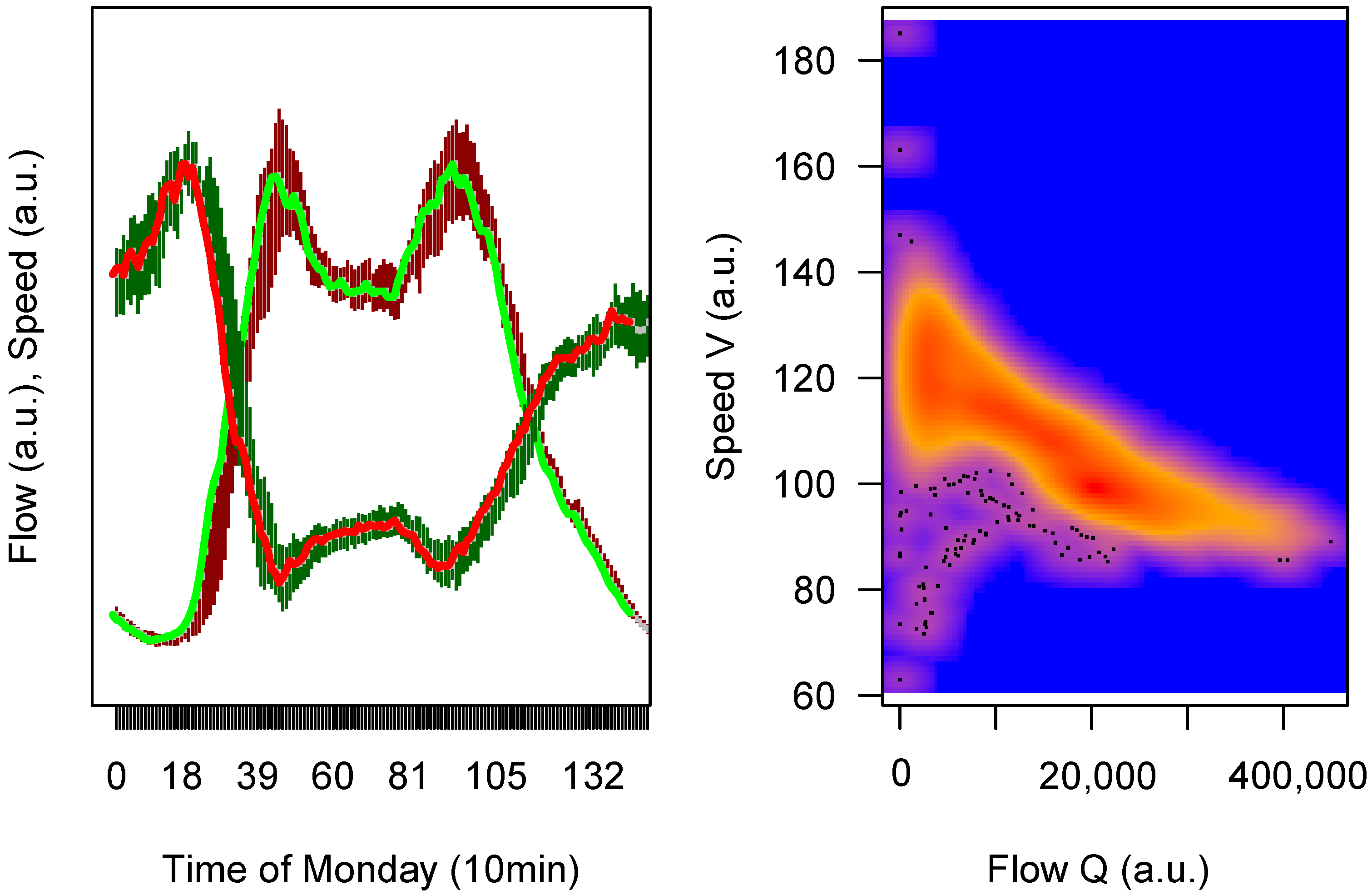
Again, a zoom-in of the flow data is provided in Figure 7; moreover, the aggregated speed data have been drawn there as well, and a fundamental diagram (which is a so-called macroscopic fundamental diagram [37]) to demonstrate that these data display a reasonable behavior [29].

2.4. Supplemental Traffic Flow Data

Since this data set is unusual, it is compared to other data sets that describe the weekly pattern of demand for transport. As already mentioned, two of them have been used here: the annual hourly count data from 28 detection sites in Berlin [38], which have been provided by the BASt, and data from the latest version of Germany’s travel survey MiD.

The BASt data [38] are hourly counts for every hour of 2018, 12 of them are located on federal roads through Berlin, the other 16 are located on the freeways in Berlin. They count only motorized traffic (several types are recognized, here only the total count is used), and since they are installed on major roads only, there might be a certain tendency toward large demand values, which might be different from the T4C data set. To match the T4C data, and to ease later analyses, each weekly demand curve $Q\left(h\right)$ where h being the hour of the week, has been scaled to yield $\widehat{Q}\left(h\right)$ so that its sum is one:

$$\widehat{Q}\left(h\right)={\displaystyle \frac{Q\left(h\right)}{{\sum }_{h=0}^{167}Q\left(h\right)}}$$

(7)

Subsequently, these scaled curves for the different sites have been added to get an aggregated traffic demand curve for this data, they are named LOOP in the following. This normalization has also been performed for all the other weekly demand patterns, to easily compare them with each other.

The MiD data set is different (the data can be obtained from [39]), since it is from a travel survey conducted in 2016 and 2017. Altogether 960,619 trips have been collected for the MiD. They are distributed over all of Germany, and considerable efforts have been undertaken to make it a representative sample of the mobility of the German population. For the purpose here, all trips for large cities have been picked, which yields 172,761 trips in total, of which 73,696 belong to motorized traffic. Furthermore, trips with travel-speeds larger than 150 km/h have been eliminated, which left 58,525 trips in the final data set.

Each trip in this data set is described by 116 variables, of which only the starting time, the trip duration, the trip distance, and an expansion factor have been used. The expansion factor assigns a weight to each trip so that the MiD data are in line with the kilometers traveled in Germany.

They have been counted according to the starting time of the trip, and have been again aggregated to the number of trips per hour of the week (named MiD-Q in the following). Moreover, each trip has been multiplied either by its trip duration (named MiD-T) or by its trip-length (MiD-X) to yield an alternative exposure measure for inclusion into the analysis.

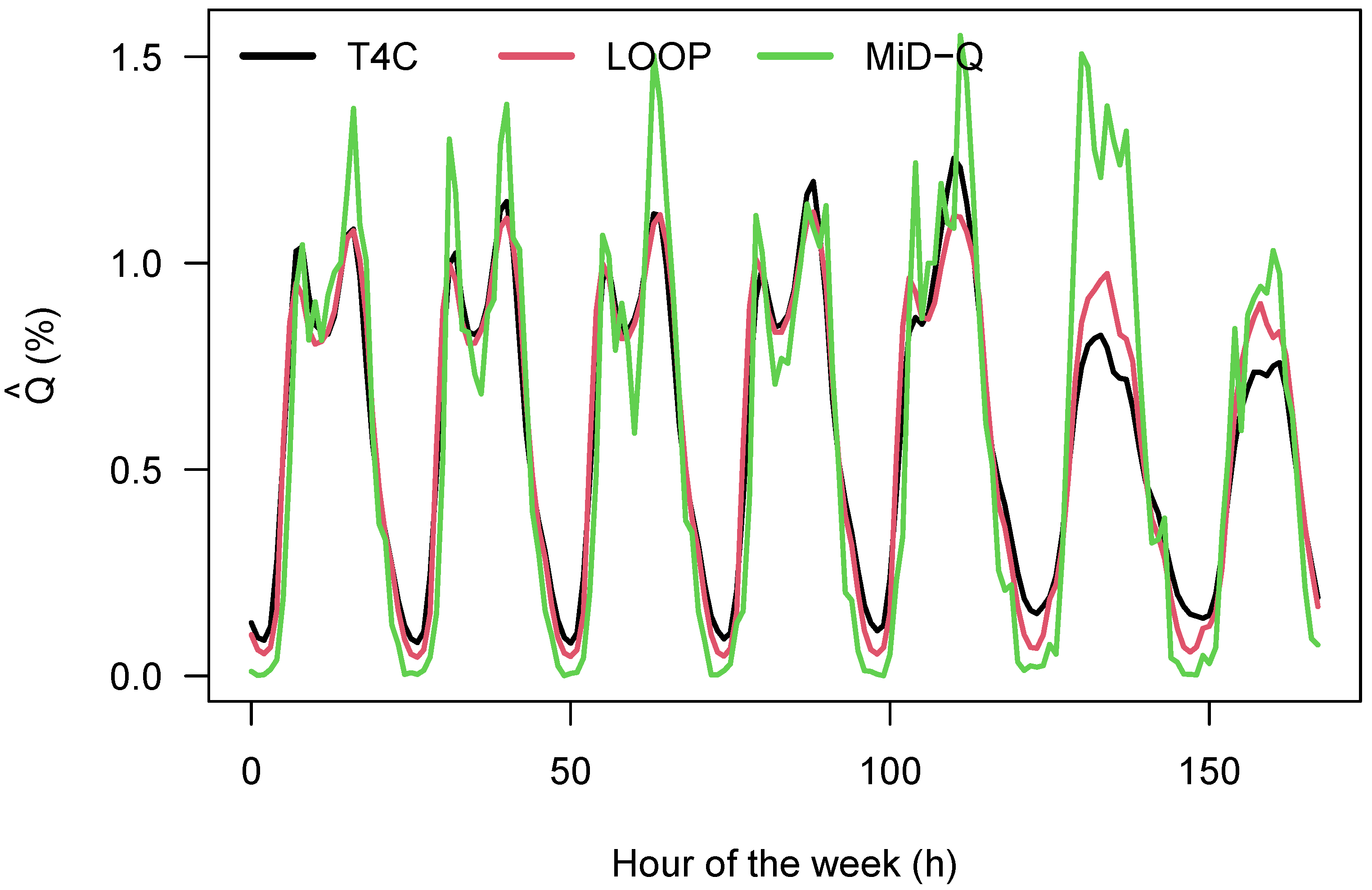
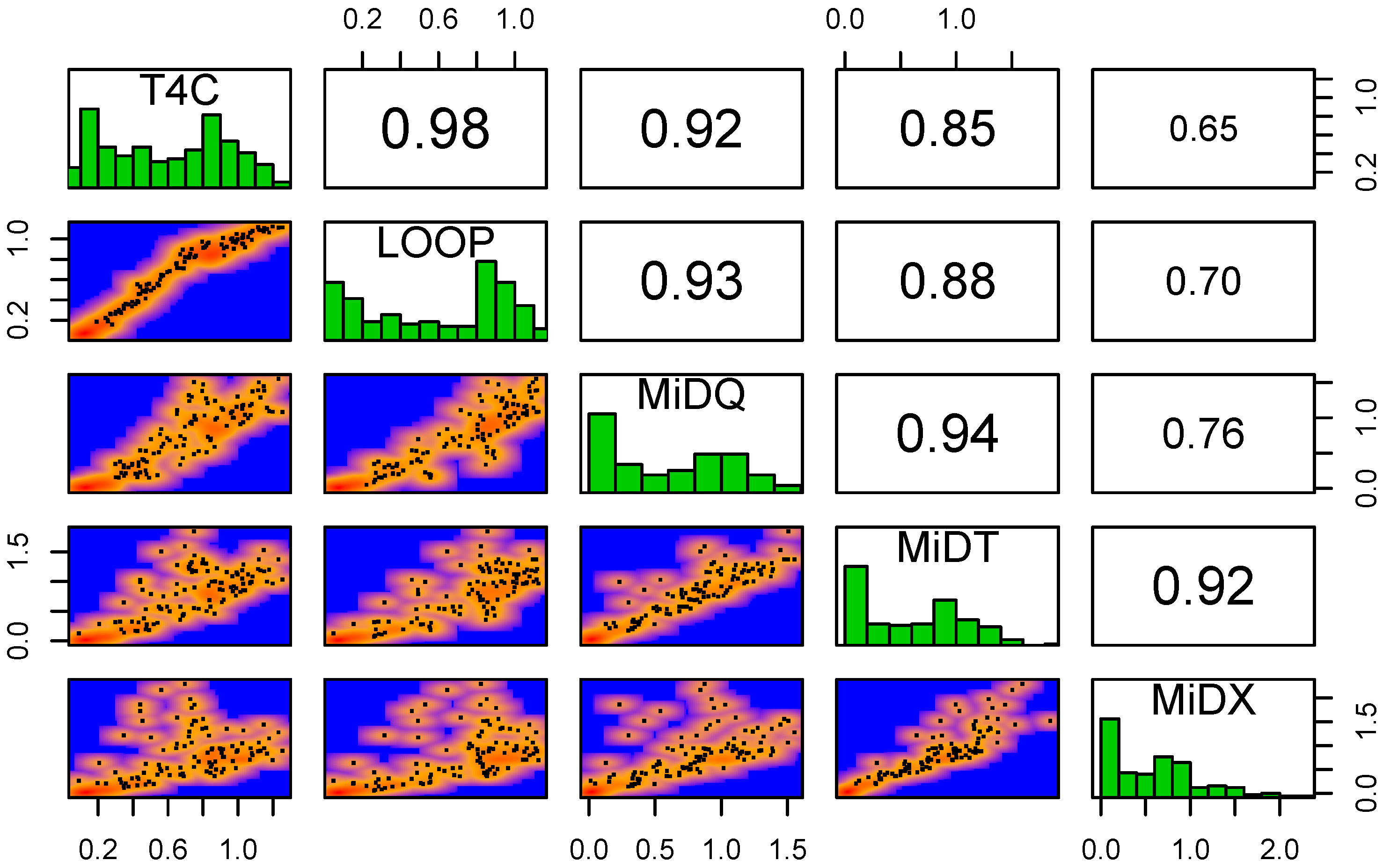
There are similarities between the flow patterns from the three sources, and this is at least satisfactorily given how very different they are. The correlation between them is between 0.65 for the worst pair (T4C and MiD-X) and 0.98 for the best pair (LOOP and T4C). See also the pairwise comparison below for more details. This correlation improves considerably if long trips (distance larger than 40 km, duration longer than 90 min) are excluded from the MiD data, but this has not been done in the following.

The MiD-T and MiD-X data are noisier than the MiD-Q data, which points to problems with the sampling, especially long trips that do not happen that often and may have an under-sampling issue, but also short trips may not have been faithfully recorded by the respondents.

Figure 8 displays the weekly normalized pattern of the T4C, the LOOP, and the MiD-Q data, respectively. As can be seen from Figure 8, there are differences between them: the MiD data display more pronounced weekly patterns, and the Saturdays and Sundays have too much traffic when compared to the T4C and LOOP data, but also when compared to the working days. Especially the small demand at night in the MiD data might be due to a sampling or under-reporting effect, for the excess on weekends, there is no explanation right now. However, this is a known effect [40] and is therefore not a bug in the analysis done here.

The difference between the T4C and the LOOP data is more subtle: in essence, the pattern of the LOOP data is more pronounced (in most cases), this can be attributed to the fact that they are samples from roads with considerable demand, while the T4C data are samples over the whole Berlin road transport system. This sampling of the T4C data may tend to smooth out large amplitudes when compared to the LOOP data.

Figure 9 provides a more complete characterization of the correlation between the five different exposure data.

3. On Crashes and Cars

To investigate the relationship between the crash frequency and the traffic flow, there are two possibilities to relate them to each other with the data sets at hand. The first one and most convincing one is, for the data from 2018, to plot for each hour of the year where the T4C traffic flow data are available (these are 6552 of the 8760 possible ones) the corresponding crash frequency. The second one is to plot only the aggregated data against each other, i.e., the crash data for each hour of the week from the years 2001–2019 against the weekly flow data from 2018. The results are similar, but not identical. The aggregated approach will tend to smooth out extreme values and therefore yield a less noisy, but also a less clear signal.

There is a third approach: to sample from all crash data for each hour of 2018 where flow data are available one data set from the crash data that has the same hour of the week. This has been done as well; however, the results are not displayed here since they are almost the same as the data for 2018.

3.1. The 2018 Data

In Figure 10 and Figure 11, the 2018 data are analyzed. For each hour where the traffic flow Q is present, there is also the crash frequency N in this hour. To aggregate the data, the flow values have been summarized into bins with an equal number of Q-values (in this case, 50 bins for the Q-values have been chosen, resulting in 131 $(Q,N)$-pairs for each bin). This leads to bins on the Q-axis that have different widths. Then, for each bin, the mean value of the N-values can be computed and displayed in Figure 10 as an orange line overlaid on the distribution of $(Q,N)$-values in the background as a greyscale density plot, where darker grey means higher density. Three models have been estimated for these data, which is the power-law of Equation (1) (which yields an exponent of ${\beta }_1=1.50\pm 0.01$), the proposed second-order polynomial model of Equation (6), and a GAM-fit (Generalized Additive Model) [41,42]. Especially at small flows, all these models give roughly the same results. They differ at large values of the traffic flow: the empirical curve, as well as the GAM-model, show a tendency towards saturation, while the two other models do not. Note, that the GAM-fit overlaps with the empirically determined curve very nicely, which adds credibility to this result. Note, too, that almost all results for the fitted models are statistically highly significant and pretty much comparable to each other, where the GAM-model has the smallest AIC (Akaike Information Criterion), but not by very much. Therefore, from the visual appearance, one may favor the GAM-model, since it describes especially the saturation part better. Statistics, however, is not that clear; the AIC values differ just by just 1% between the best and the worst model. This is due to the fact that the data for large demand are rare, and therefore statistics gets weak there. Some of the fit results are summarized in

Table 1. Results of the fits of the three models displayed in Figure 10.

Model	Link	R Function	AIC	Parameters (All $\mathit{p}<2\times {10}^{-16}$)
power	log	gam	35,129	$23.57Q^{1.50}$
polynomial	id	glm.nb	35,186	$7.43Q+16.65Q^2$
gam	id	gam	34,821	$12.25+2.99s\left(Q\right)$

.

To learn more about the relationship between N and $\widehat{Q}$, in Figure 11 the crash rate $\rho$ has been analyzed as well. Here, two data-points with $\rho$-values larger than 200 have been eliminated, and then two different models have been applied to these data. (Please note that the hyperbola visible in Figure 11 are a consequence of the discreteness of N.) Especially the aggregated data (average $\rho$ in each of the $\widehat{Q}$-bins, the red points in Figure 11) suggests that $\rho (\widehat{Q})$ consists of two different branches: for $\widehat{Q}<Q_c$, where $Q_c\approx 0.9$, a linearly increasing relationship seems an appropriate description of the data presented, while for $\widehat{Q}\ge Q_c$ another linear decreasing relationship fits the data well.

$$\rho (\widehat{Q})=\left\{\begin{array}{cc}{c}_0+c_1\widehat{Q}\hfill & \widehat{Q}<Q_c\hfill \\ c_2+c_3(\widehat{Q}-Q_c)\hfill & \widehat{Q}\ge Q_c\mathrm{with}{c}_2=c_0+c_1{\widehat{Q}}_c\hfill \end{array}\right.$$

(8)

Note, from comparing this bi-linear fit (the green curve) to the averaged data (red points) in Figure 11, the left branch might be described a bit better by a power-law (the blue curve in Figure 11):

$$\rho (\widehat{Q})=\left\{\begin{array}{cc}{c}_0+c_1{\widehat{Q}}^{\beta }:\hfill & \widehat{Q}<Q_c\hfill \\ c_2+c_3(\widehat{Q}-Q_c)\hfill & \widehat{Q}\ge Q_c\mathrm{with}{c}_2=c_0+c_1{\widehat{Q}}_c^{\beta }\hfill \end{array}\right.$$

(9)

It turns out that $\beta =1.60\pm 0.11$; in this case, the fits have been performed with a non-linear regression (the function ‘nls()’ from R [35]) because of the need to fit the point $Q_c$ where the two branches meet as well, which changes the fit into a non-linear one.

Therefore, the relationship between N and $\widehat{Q}$ might be something like:

$$N(\widehat{Q})=\left\{\begin{array}{cc}{c}_0\widehat{Q}+c_1{\widehat{Q}}^{\beta +1}\hfill & \widehat{Q}<Q_c\hfill \\ c_2\widehat{Q}+c_3\widehat{Q}(\widehat{Q}-Q_c)\hfill & \widehat{Q}\ge Q_c\hfill \end{array}\right.$$

(10)

Note that $c_2=c_0{\widehat{Q}}_c+c_1{\widehat{Q}}_c^{\beta +1}$ is needed for a continuous function, and where $\beta =1$ might occur.

In Figure 12 and Figure 13, a similar behavior is to be seen for the severe crashes. However, the saturation does not look as convincing as for all crashes, and the crash rate is better approximated by the bi-linear model Equation (8)-the non-linear fit does not converge properly for Equation (9).

In Figure 13, four curves have been plotted on top of the data (orange line): the power-law model Equation (1), the second-order polynomial model Equation (6), the GAM-model (blue), and finally, the $Q·\rho \left(Q\right)$ curve (violet) where the parameters of $\rho \left(Q\right)$ have been estimated by the non-linear fit to Equation (8) which means that $\beta =1$.

Nevertheless, it can be stated that the models with saturation do better describe the data for large values of the traffic flow.

An additional observation, which is mentioned here in passing, is the dependence of the crash frequency N on speed V. The data suggest that N decreases as a function of speed. Note, however, that there is a very strong negative correlation between speed and flow as is apparent from Figure 7 and is well-known from traffic flow theories. It is not clear to us how to properly disentangle the two to get a pure dependence of crash frequency on speed.

3.1.1. Weekly Curves of the Crash Rate

A different view of these data can be constructed by analyzing the crash rate Equation (3) as a function of the hour of the week, which is done in Figure 14.

Once more, the curves have been normalized so that it is easier to compare them with each other. Although the survey data show the well-known effect that the risk is larger during the night (from midnight to 3 a.m.) [43,44,45], the traffic flow data display a completely different behavior. Risk is lower during the night, except for the nights at weekends, and it is higher during the busy times of the day. The amplitude of the safety index is, however, smaller for the flow data, and this seems, at least, reasonable. The difference in $\rho$ for the survey data is most likely too strong.

In fact, looking at the flow curves themselves in Figure 8 it could be seen that the survey data have a smaller value during the night, resulting in larger than indicated by flow data risk at night. Part of this result can be traced to the fact that the survey data have passenger traffic only, so at least the business and freight traffic is missing. However, the share of crashes with trucks is not much different during the night, only the accident costs per crash are much larger during these night hours (results not shown), the latter being a well-known result.

In Figure 15, the crash rate is plotted only for the T4C data, but this time for all crashes as well as for the severe crashes. Note that there is one difference between the two curves: while the risk index $\widehat{\rho }$ is almost flat between 8 and 16 o’clock for all the crashes, the risk index for the severe crashes still display the double peak structure also visible in the crash data as well as in the traffic flow data.

The amplitude, i.e., the ratio between the smallest and the largest crash rate is roughly a factor of 4, and this is what has been reported in other research, so it seems that at least the range is in line with the results from other research.

3.1.2. A Remaining Pattern

Since there are models at hand (the bi-linear one is used in the following), it is interesting to see whether there is any weekly pattern left if the actual crash frequency is divided by the expected crash frequency $\widehat{N}$ according to the model. This number will be called prediction index ${\Lambda }$ in the following and is defined as:

$${\Lambda }={\displaystyle \frac{N}{\widehat{N}}}$$

(11)

The resulting pattern in Figure 16 looks similar to the risk index $\rho$, but has a smaller amplitude. Therefore, the model in Equation (10) explains at least some of the variability of the weekly pattern in the crash numbers. Nevertheless, it is surprising that ${\Lambda }$ displays so much of the weekly pattern of $N\left(h\right)$ and $Q\left(h\right)$.

4. Summary and Conclusions

This work has analyzed several databases that allowed mapping the crash frequency to the number of vehicles on travel as an exposure variable, on a weekly basis with an aggregation time of one hour. From this, it was possible to find a parameterized form of the distribution of the crashes itself, the dependence of its parameters on the week of the hour (and therefore on the traffic state), and the relationship between the crash frequency and the exposure. The data indicate that the crash frequency saturates with larger traffic flow (which is also related to an increase in congestion).

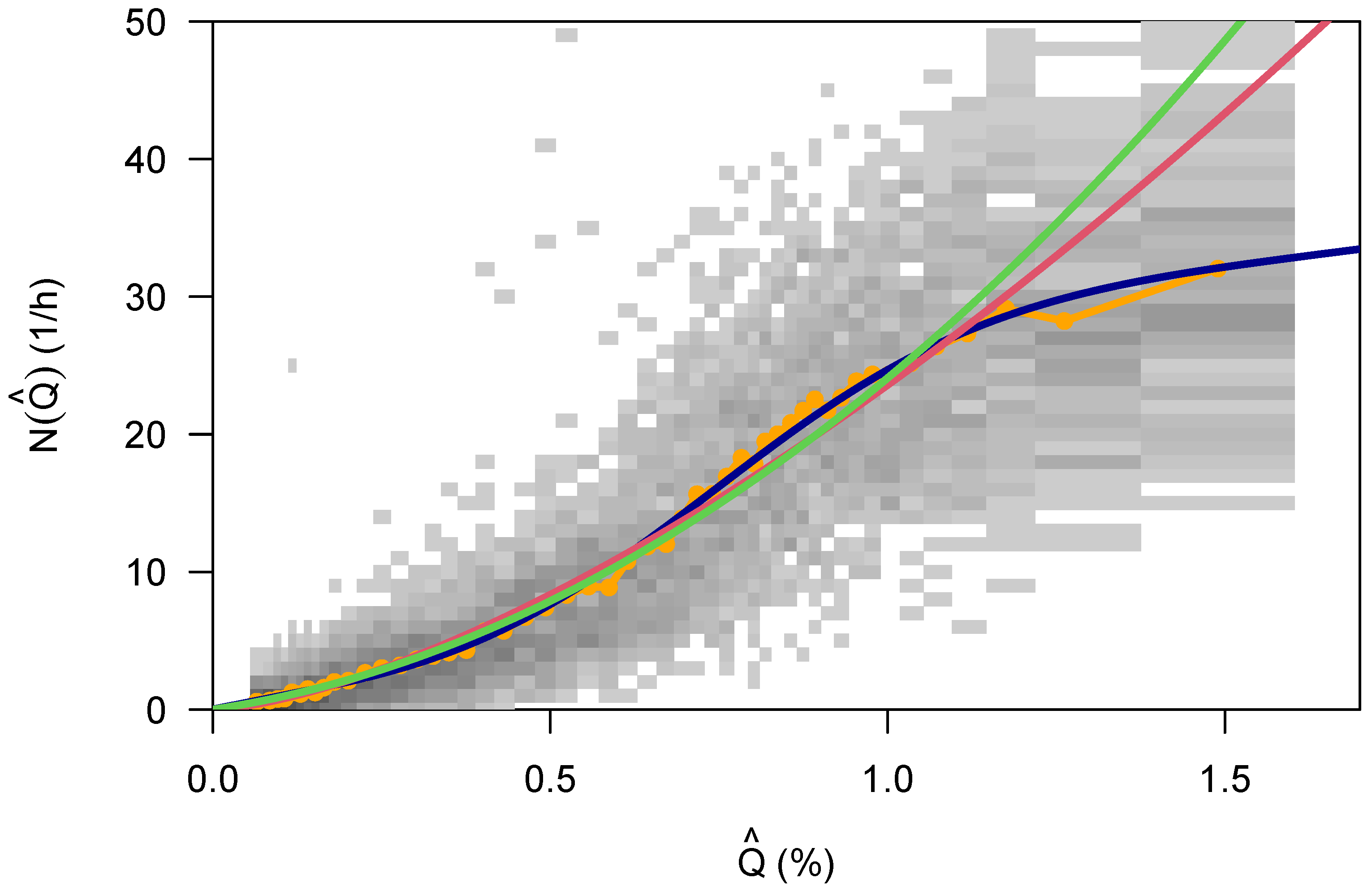
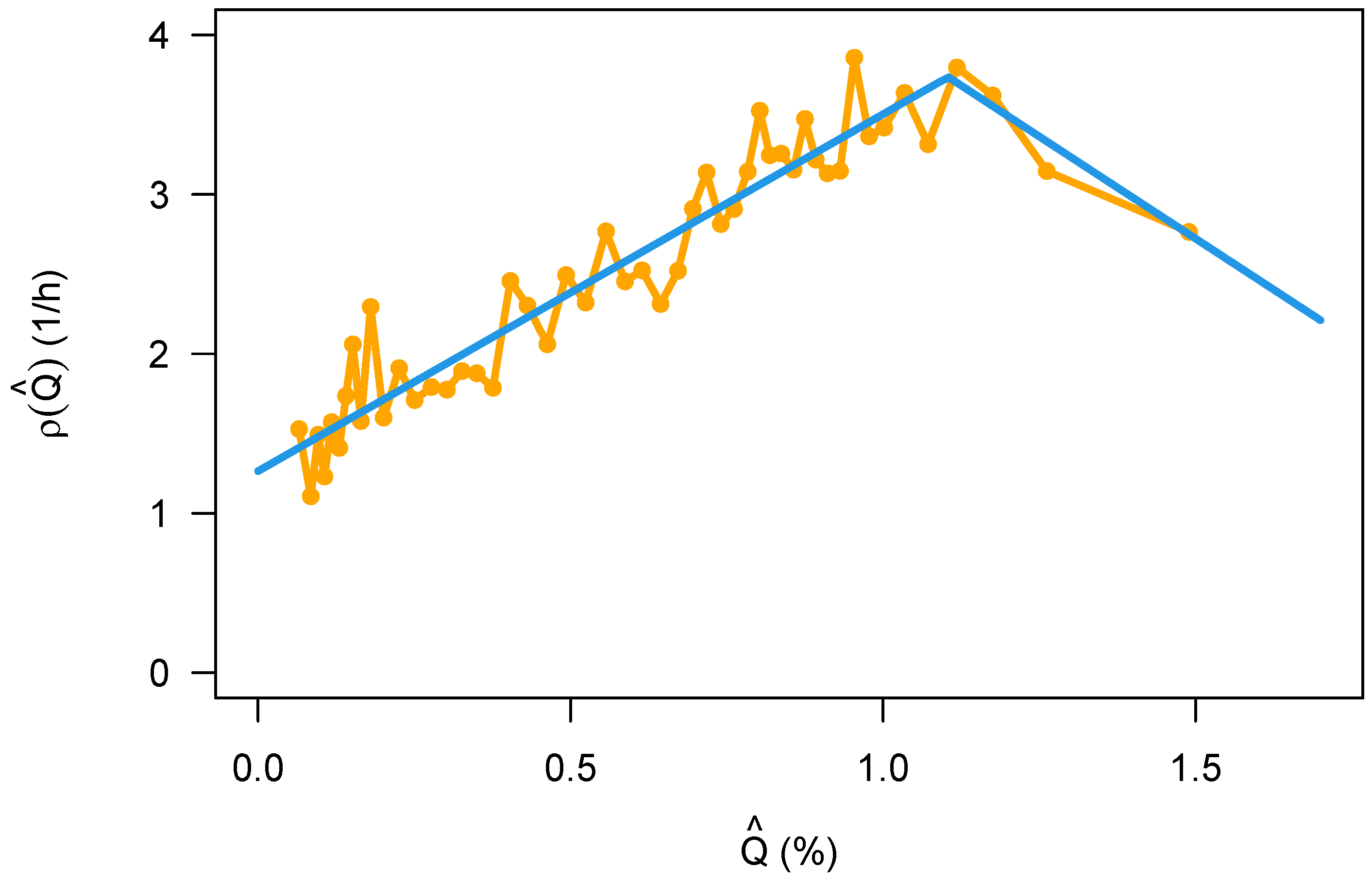
The crash rate as a function of traffic flow displays an interesting bi-linear relationship that has a maximum at about $\widehat{Q}\approx 1$ (Equation (8)). This is similar to the inverse “U” that has been reported already in Veh’s work [24], and it may have a connection to the theory proposed in [27]. For small values of the traffic flow, this is suspiciously close to the naive approach Equation (6), and this is at least satisfactorily since there is a simple mechanistic model available for this kind of relationship. If, however, the more complicated model in Equation (9) turns out to be a better description, then the question might be asked where the additional ${\widehat{Q}}^{0.6}$ comes from (the exponent was $\beta =1.60\pm 0.11$, 0.6 larger than 1).

These results suggest that the simple power-law model that comes with the traditional approach to road safety modeling (Equation (1)) is not in line with the results presented here. However, these results are also not in line with most of the results from research on freeway traffic. There is, however, a certain similarity with what has been proposed in [27].

The most surprising and conflicting result of this research is that the crash rate in the city of Berlin seems to be smaller during the night hours, so traveling is safer than it is during the day. If this is true in fact and not a glitch in the data or the data analysis, then a simple explanation might be that driving during the day with its much stronger traffic is more demanding, causing a higher error rate. However, this is for sure not the whole story behind since the crash rate from 8 a.m. to 6 p.m. for all the crashes (but not for the severe crashes, they still do display the double peak structure) is more or less constant within the analysis performed here, while the traffic flow changes considerably over this time.

Several things might have gone wrong with the approach presented here. First is that it is not clear that the traffic flows determined from the T4C database are a good measure of the real traffic flow, and whether this traffic flow is a good proxy for the exposure of cars to crashes. Or, for that matter, that there is a simple linear relationship between traffic flow and exposure. On the other hand, the comparisons to the loop data and the MiD data indicate that the usage of those data is an interesting investigation. In addition, as can be seen especially from Figure 8 and Figure 9, the survey data (MiD data in this case) seem to have issues of their own, which only might become visible in comparisons as the ones done here. Nevertheless, a recommendation for future research is to watch out more closely for the role of the traffic state in general on crash probability. Here, the traffic state is understood as the combination of flow and speed and maybe other variables as well that may influence traffic safety.

It will be interesting to see whether similar results can be found in other circumstances, or whether these results are just an oddity of research in traffic safety.

Another direction of research is related to the dependence of crash frequency on speed, or much better, its dependency on the two-dimensional description of the traffic state by flow and speed $(Q,V)$, respectively, the fundamental diagram. For freeways, some steps have been done already in this direction [15]. However, this is difficult since such a proposed relationship $N(Q,V)$ cannot be formulated as a simple function, since there are values of $(Q,V)$ that are never realized in real traffic.