Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry
Abstract
1. Introduction
2. Results
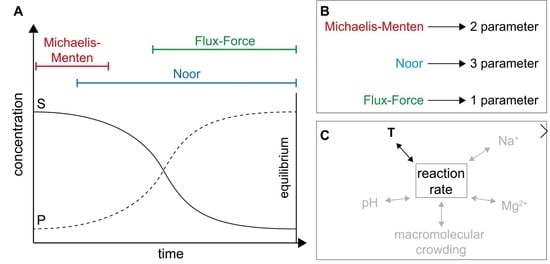
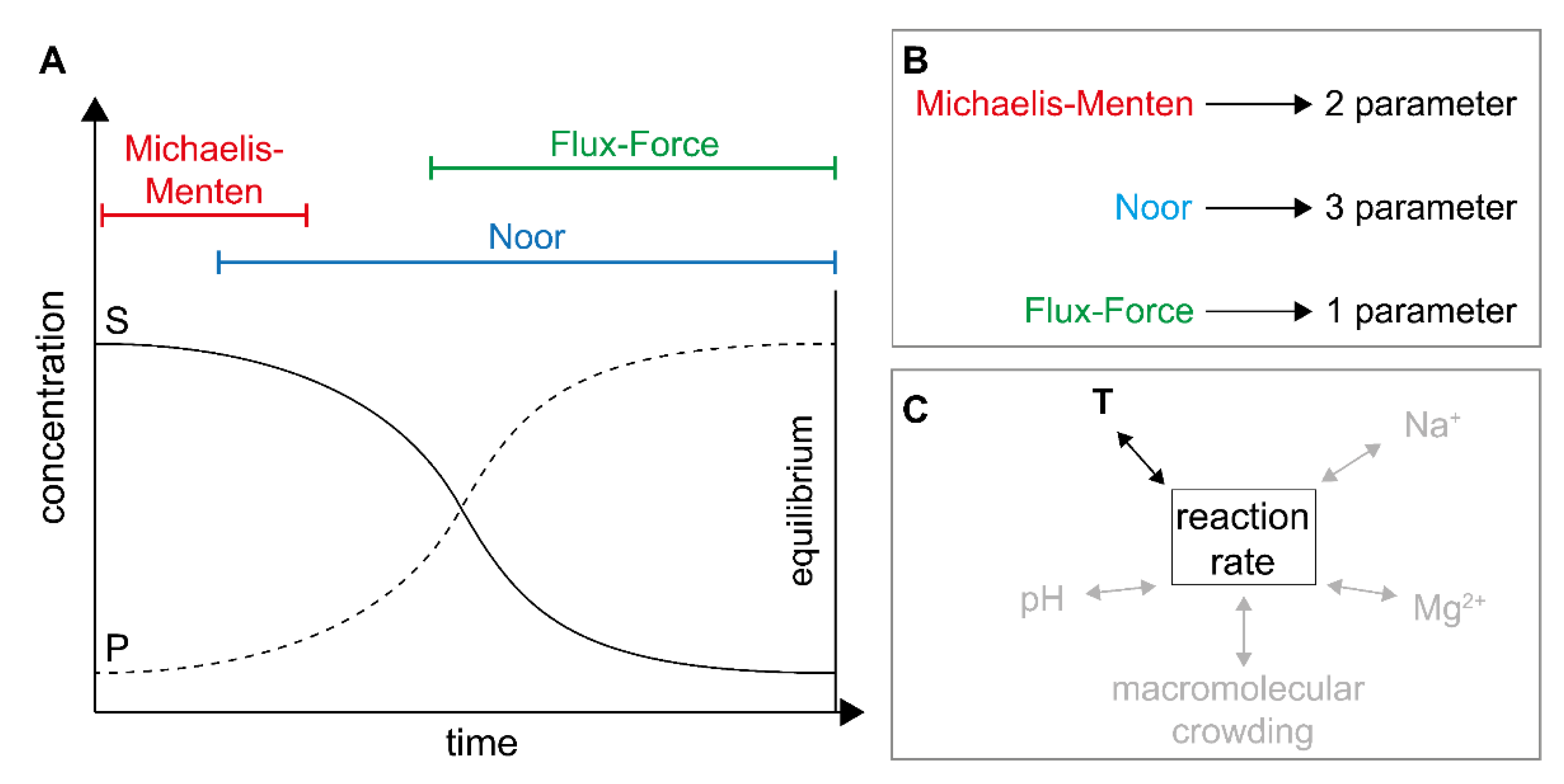
2.1. Definitions and Specifications
2.2. Application of Irreversible Thermodynamics for Kinetic Evaluation
2.3. ITC Results
2.4. Kinetic Analyses
3. Discussion
3.1. Thermodynamic Data for Reaction 2
3.2. Validation of Kinetic Models by the New Calorimetric Data
3.3. Temperature Dependency of the Kinetics of Reaction 2
3.4. Temperature Dependency of Reaction 9
4. Materials and Methods
4.1. Chemicals
4.2. Sample Preparation for ITC Measurement
4.3. ITC Measurements
4.3.1. Reaction 2 (Phosphoglucose Isomerase Reaction)
4.3.2. Reaction 9 (Enolase Reaction)
4.4. Determination of Reaction Enthalpy and Equilibrium Constant
4.5. Kinetic Investigations
4.6. Statistics
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ITC | isothermal titration calorimetry |
| G6P | glucose-6-phosphate |
| F6P | fructose-6-phosphate |
| 2PG | 2-phosphoglycerate |
| PEP | phosphoenolpyruvate |
| PGI | phosphoglucose isomerase |
References
- Brown, A.J. XXXVI.—Enzyme action. J. Chem. Soc. Perkin 1 1902, 81, 373–388. [Google Scholar] [CrossRef]
- Henri, V. Lois Générales De L’action Des Diastases; Librairie Scientifique A.: Hermann, MO, USA, 1903. [Google Scholar]
- Henri, V. Théorie Générale De L’action De Quelques Diastases; Gauthier-Villars: Paris, France, 1902. [Google Scholar]
- Michaelis, L.; Menton, M.L. Kinetik der Invertinwirkung. Biochem. Z. 1913, 49, 333. [Google Scholar]
- Miller, W.G.; Alberty, R.A. Kinetics of the reversible Michaelis-Menten mechanism and the applicability of the steady-state approximation. J. Am. Chem. Soc. 1958, 80, 5146–5151. [Google Scholar] [CrossRef]
- Paul, S.; Gangopadhyay, G. Power law kinetics in reversible enzyme-catalyzed reaction due to diffusion. J. Chem. Phys. 2003, 119, 3501–3508. [Google Scholar] [CrossRef]
- Voet, D.; Voet, J.G. Biochemistry, 4th ed.; W. Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Cornish-Bowden, A.; Cardenas, M.L. Information transfer in metabolic pathways. Effects of irreversible steps in computer models. Eur. J. Biochem. 2001, 268, 6616–6624. [Google Scholar] [CrossRef]
- Noor, E.; Flamholz, A.; Liebermeister, W.; Bar-Even, A.; Milo, R. A note on the kinetics of enzyme action: A decomposition that highlights thermodynamic effects. FEBS Lett. 2013, 587, 2772–2777. [Google Scholar] [CrossRef]
- Cornish-Bowden, A. Fundamentals of Enzyme Kinetics; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Imperial, S.; Centelles, J.J. Enzyme Kinetic Equations of Irreversible and Reversible Reactions in Metabolism. J. Biosci. Med. 2014, 2, 24–29. [Google Scholar] [CrossRef]
- Rohwer, J.M.; Postma, P.W.; Kholodenko, B.N.; Westerhoff, H.V. Implications of macromolecular crowding for signal transduction and metabolite channeling. Proc. Natl. Acad. Sci. USA 1998, 95, 10547–10552. [Google Scholar] [CrossRef]
- Smith, W.G. In Vivo Kinetics and the Reversible Michaelis-Menten Model. J. Chem. Educ. 1992, 69, 981–984. [Google Scholar] [CrossRef]
- Hoh, C.Y.; CordRuwisch, R. A practical kinetic model that considers endproduct inhibition in anaerobic digestion processes by including the equilibrium constant. Biotechnol. Bioeng. 1996, 51, 597–604. [Google Scholar] [CrossRef]
- Keleti, T. Two rules of enzyme kinetics for reversible Michaelis-Menten mechanisms. FEBS Lett. 1986, 208, 109–112. [Google Scholar] [CrossRef]
- Lee, L.W.; Yin, L.; Zhu, X.M.; Ao, P. Generic enzymatic rate equation under living conditions. J. Biol. Syst. 2007, 15, 495–514. [Google Scholar] [CrossRef]
- Brooks, S.P.J.; Storey, K.B. A kinetic description of sequential, reversible, Michaelis-Menten reactions: Practical application of theory to metabolic pathways. Mol. Cell. Biochem. 1992, 115, 43–48. [Google Scholar] [CrossRef]
- Cha, S. A Simple Method for Derivation of Rate Equations for Enzyme-catalyzed Reactions under the Rapid Equilibrium Assumption or Combined Assumptions of Equilibrium and Steady State. J. Biol. Chem. 1968, 243, 820–825. [Google Scholar]
- Zadvornyy, O.A.; Boyd, E.S.; Posewitz, M.C.; Zorin, N.A.; Peters, J.W. Biochemical and structural characterization of enolase from Chloroflexus aurantiacus: Evidence for a thermophilic origin. Front. Bioeng. Biotechnol. 2015, 3, 74. [Google Scholar] [CrossRef]
- Pancholi, V.; Fischetti, V.A. Alpha-enolase, a novel strong plasmin(ogen) binding protein on the surface of pathogenic streptococci. J. Biol. Chem. 1998, 273, 14503–14515. [Google Scholar] [CrossRef]
- Wold, F.; Ballou, C.E. Studies on the enzyme enolase II. kinetic studies. J. Biol. Chem. 1957, 227, 313–328. [Google Scholar]
- Westhead, E.W.; Malmstrom, B.G. The chemical kinetics of the enolase reaction with special reference to the use of mixed solvents. J. Biol. Chem. 1957, 228, 655–671. [Google Scholar] [PubMed]
- Kornblatt, M.J.; Musil, R. The Inhibition of Yeast Enolase by Li+ and Na+. Arch. Biochem. Biophys. 1990, 277, 301–305. [Google Scholar] [CrossRef]
- Dyson, J.E.; Noltmann, E.A. The effect of pH and temperature on the kinetic parameters of phosphoglucose isomerase. Participation of histidine and lysine in a proposed dual function mechanism. J. Biol. Chem. 1968, 243, 1401–1414. [Google Scholar]
- Zera, A.J. Temperature-dependent kinetic variation among phosphoglucose isomerase allozymes from the whing-polymorphic water strider, Limnoporus Canaliculatus. Mol. Biol. Evol. 1987, 4, 266–285. [Google Scholar]
- Grosch, J.H.; Wagner, D.; Nistelkas, V.; Spiess, A.C. Thermodynamic activity-based intrinsic enzyme kinetic sheds light on enzyme-solvent interactions. Biotechnol. Prog. 2017, 33, 96–103. [Google Scholar] [CrossRef]
- Pleiss, J. Thermodynamic activity-based interpretation of enzyme kinetics. Trends Biotechnol. 2017, 35, 379–382. [Google Scholar] [CrossRef]
- Gopal, S.M.; Klumpers, F.; Herrmann, C.; Schafer, L.V. Solvent effects on ligand binding to a serine protease. Phys. Chem. Chem. Phys. 2017, 19, 10753–10766. [Google Scholar] [CrossRef]
- Knierbein, M.; Wangler, A.; Luong, T.Q.; Winter, R.; Held, C.; Sadowski, G. Combined co-solvent and pressure effect on kinetics of a peptide hydrolysis: An activity-based approach. Phys. Chem. Chem. Phys. 2019, 21, 22224–22229. [Google Scholar] [CrossRef]
- Wangler, A.; Held, C.; Sadowski, G. Thermodynamic activity-based solvent design for bioreactors. Trends Biotechnol. 2019, 37, 1038–1041. [Google Scholar] [CrossRef] [PubMed]
- Lonhienne, T.G.; Winzor, D.J. A potential role for isothermal calorimetry in studies of the effects of thermodynamic non-ideality in enzyme-catalyzed reactions. J. Mol. Recognit. 2004, 17, 351–361. [Google Scholar] [CrossRef]
- van Eunen, K.; Bakker, B.M. The importance and challenges of in vivo-like enzyme kinetics. Perspect. Sci. 2014, 1, 126–130. [Google Scholar] [CrossRef]
- Beard, D.A.; Qian, H. Relationship between thermodynamic driving force and one-way fluxes in reversible processes. PLoS ONE 2007, 2, e144. [Google Scholar] [CrossRef]
- Maskow, T.; Paufler, S. What does calorimetry and thermodynamics of living cells tell us? Methods 2015, 76, 3–10. [Google Scholar] [CrossRef]
- Todd, M.J.; Gomez, J. Enzyme kinetics determined using calorimetry: A general assay for enzyme activity? Anal. Biochem. 2001, 296, 179–187. [Google Scholar] [CrossRef]
- Westerhoff, H.V. Thermodynamics and Control. of Biological Free-Energy Transduction; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Stitt, M. Control of sucrose synthesis: Estimation of free energy changes, investigation of the contribution of equilibrium and non-equilibrium reactions, and estimation of elasticities and flux control coefficients. In Techniques and New Developments in Photosynthesis Research; Springer: Berlin, Germany, 1989; pp. 365–391. [Google Scholar]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. für Phys. Chem. 1889, 4U, 226–248. [Google Scholar]
- Mazzei, L.; Ciurli, S.; Zambelli, B. Hot Biological Catalysis: Isothermal Titration Calorimetry to Characterize Enzymatic Reactions. J. Vis. Exp. 2014, 86, 8. [Google Scholar] [CrossRef] [PubMed]
- Vogel, K.; Greinert, T.; Harms, H.; Sadowski, G.; Held, C.; Maskow, T. Influence of cytosolic conditions on the reaction equilibrium and the reaction enthalpy of the enolase reaction accessed by calorimetry and van ‘t HOFF. Biochim. Biophys. Gen. Subj. 2020, 1864, 129675. [Google Scholar] [CrossRef] [PubMed]
- Tewari, Y.B.; Steckler, D.K.; Goldberg, R.N. Thermodynamics of isomerization reactions involving sugar phosphates. J. Biol. Chem. 1988, 263, 3664–3669. [Google Scholar]
- Hoffmann, P.; Held, C.; Maskow, T.; Sadowski, G. A thermodynamic investigation of the glucose-6-phosphate isomerization. Biophys. Chem. 2014, 195, 22–31. [Google Scholar] [CrossRef]
- Hines, M.C.; Wolfe, R.G. Phosphoglucose isomerase. 2. Influence of pH on kinetic parameters. Biochemistry 1963, 2, 770–775. [Google Scholar] [CrossRef]
- Ruijter, G.J.G.; Visser, J. Characterization of Aspergillus niger phosphoglucose isomerase. Use for quantitative determination of erythrose 4-phosphate. Biochimie 1999, 81, 267–272. [Google Scholar] [CrossRef]
- Staples, J.F.; Suarez, R.K. Honeybee flight muscle phosphoglucose isomerase: Matching enzyme capacities to flux requirements at a near-equilibrium reaction. J. Exp. Biol. 1997, 200, 1247–1254. [Google Scholar]
- Holt, A.; Wold, F. The isolation and characterization of rabbit muscle enolase. J. Biol. Chem. 1961, 236, 3227–3231. [Google Scholar] [PubMed]
- Lowry, O.H.; Passonneau, J.V. The relationships between substrates ad enzymes of glycolysis in brain. J. Biol. Chem. 1964, 239, 31–42. [Google Scholar] [PubMed]
- Vinarov, D.A.; Nowak, T. pH Dependence of the reaction catalyzed by yeast Mg−enolase. Biochemistry. 1998, 37, 15238–15246. [Google Scholar] [CrossRef]
- Stuart, C.C.P. A study of temperature-coeffcients and van ‘t Hoff’s rule. KNAW Proc. 1912, 14, 1159–1173. [Google Scholar]
- Sangwan, R.S.; Singh, R. Characterization of amyloplastic phosphohexose isomerase from immature wheat (Triticum aestivum L.) endosperm. Indian J. Biochem. Biophys. 1990, 27, 23–27. [Google Scholar]
- Westhead, E.W.; McLain, G. A purification of brewers’ and baker’s yeast enolase yielding a single active component. J. Biol. Chem. 1964, 239, 2464–2468. [Google Scholar]
- Schurig, H.; Rutkat, K.; Rachel, R.; Jaenicke, R. Octameric enolase from the hyperthermophilic baxcterium Thermotoga maritima—purification, characterization, and image processing. Protein Sci. 1995, 4, 228–236. [Google Scholar] [CrossRef]
- Hansen, L.D.; Transtrum, M.K.; Quinn, C.; Demarse, N. Enzyme-catalyzed and binding reaction kinetics determined by titration calorimetry. Biochim. Biophys. Gen. Subj. 2016, 1860, 957–966. [Google Scholar] [CrossRef]





| Symbol | Property | Unit |
|---|---|---|
| A | pre-exponential factor | s−1 |
| activity of component | - | |
| concentration of component | mol kg−1 | |
| concentration of component at time 0 | mol kg−1 | |
| equilibrium concentration of component | mol kg−1 | |
| product concentration | mol kg−1 | |
| substrate concentration | mol kg−1 | |
| activation energy | J mol−1 | |
| Gibbs energy of biochemical reaction | J mol−1 | |
| standard Gibbs energy of biochemical reaction | J mol−1 | |
| enthalpy of biochemical reaction | J mol−1 | |
| J | flux | mol L−1 s−1 |
| thermodynamic equilibrium constant of biochemical reaction | - | |
| apparent equilibrium-molality ratio of biochemical reaction | −/mol kg−1 | |
| kinetic constant of reaction | s−1 | |
| Michaelis constant for substrate/product | mol kg−1 | |
| activity-coefficient ratio of biochemical reaction | −/mol kg−1 | |
| L | phenomenological coefficient/kinetic parameter | s−1 |
| m | mass | kg |
| P | heat production rate | W |
| Q | heat | J |
| universal gas constant (8.314 J mol−1 K−1) | J mol−1 K−1 | |
| r | reaction rate | mol L−1 s−1 |
| maximum reaction rate | mol L−1 s−1 | |
| temperature | K | |
| α | correlation factor | mol kg−1 s−1 |
| Λ | kinetic parameter | s−1 |
| thermodynamic driving force | - | |
| rational activity coefficient of component on molality base | - |
| Buffer | |
|---|---|
| HEPES | 9.7 ± 0.3 |
| Potassium phosphate | 9.6 ± 0.2 |
| MOPS | 11.1 ± 0.5 |
| Reaction 2 | Reaction 9 [40] | |||||
|---|---|---|---|---|---|---|
| Temperature (K) | Q (mJ) | Q (mJ) | ||||
| 298.15 | 7.63 ± 0.14 | 0.285 | 10.3 ± 0.2 | 8.15 ± 0.72 | 239.4 | 2.4 ± 0.2 |
| 305.15 | 7.63 ± 0.07 | 0.318 | 10.6 ± 0.1 | 7.85 ± 0.17 | 245.9 | 2.4 ± 0.1 |
| 310.15 | 7.86 ± 0.33 | 0.343 | 11.1 ± 0.5 | 7.64 ± 0.22 | 251.3 | 2.4 ± 0.1 |
| Temperature (K) | Reaction 2 | Reaction 9 | ||
|---|---|---|---|---|
(µmol kg−1s−1) | (mmol kg−1) | (ms−1) | (mmol kg−1) | |
| 298.15 | 7.03 ± 0.58 | 4.35 ± 0.64 | 0.34 ± 0.01 | 10.2 ± 0.92 |
| 305.15 | 10.30 ± 0.88 | 3.41 ± 0.39 | 0.44 ± 0.13 | 13.8 ± 3.35 |
| 310.15 | 13.21 ± 1.20 | 3.26 ± 0.09 | 0.57 ± 0.03 | 16.5 ± 0.48 |
| Temperature (K) | Reaction 2 | Reaction 9 |
|---|---|---|
| L Value (s−1) | L Value (s−1) | |
| 298.15 | 217.18 ± 14.27 | 10.13 ± 0.65 |
| 305.15 | 358.80 ± 17.29 | 14.57 ± 3.20 |
| 310.15 | 518.44 ± 43.84 | 20.37 ± 1.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogel, K.; Greinert, T.; Reichard, M.; Held, C.; Harms, H.; Maskow, T. Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry. Int. J. Mol. Sci. 2020, 21, 8341. https://doi.org/10.3390/ijms21218341
Vogel K, Greinert T, Reichard M, Held C, Harms H, Maskow T. Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry. International Journal of Molecular Sciences. 2020; 21(21):8341. https://doi.org/10.3390/ijms21218341
Chicago/Turabian StyleVogel, Kristina, Thorsten Greinert, Monique Reichard, Christoph Held, Hauke Harms, and Thomas Maskow. 2020. "Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry" International Journal of Molecular Sciences 21, no. 21: 8341. https://doi.org/10.3390/ijms21218341
APA StyleVogel, K., Greinert, T., Reichard, M., Held, C., Harms, H., & Maskow, T. (2020). Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry. International Journal of Molecular Sciences, 21(21), 8341. https://doi.org/10.3390/ijms21218341