Evaluation of Osmotic Dehydration Process in Plant Tissue with Low-Field Magnetic Resonance Imaging Enhanced with Paramagnetic Ions
Abstract
:1. Introduction
2. Materials and Methods
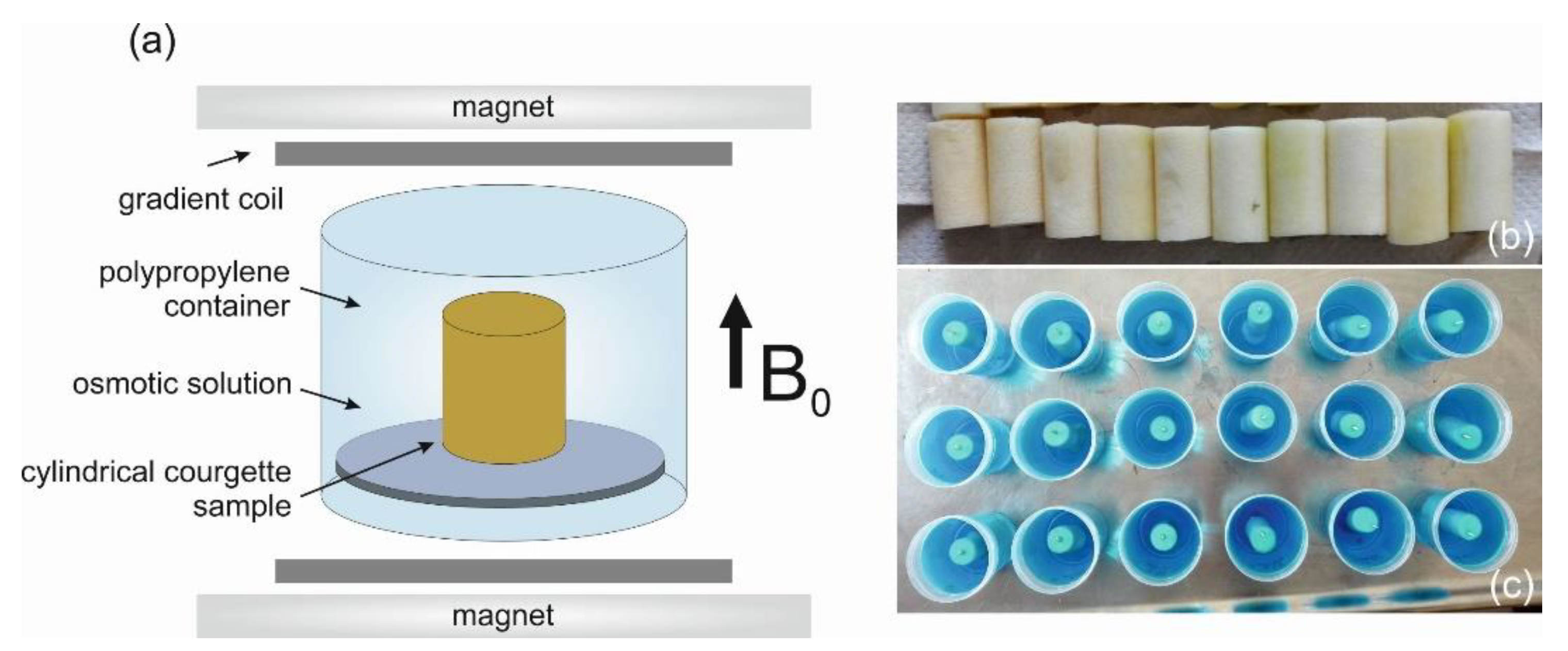
2.1. Sample Preparation
2.2. Osmotic Solution Preparation
2.3. Osmotic Dehydration
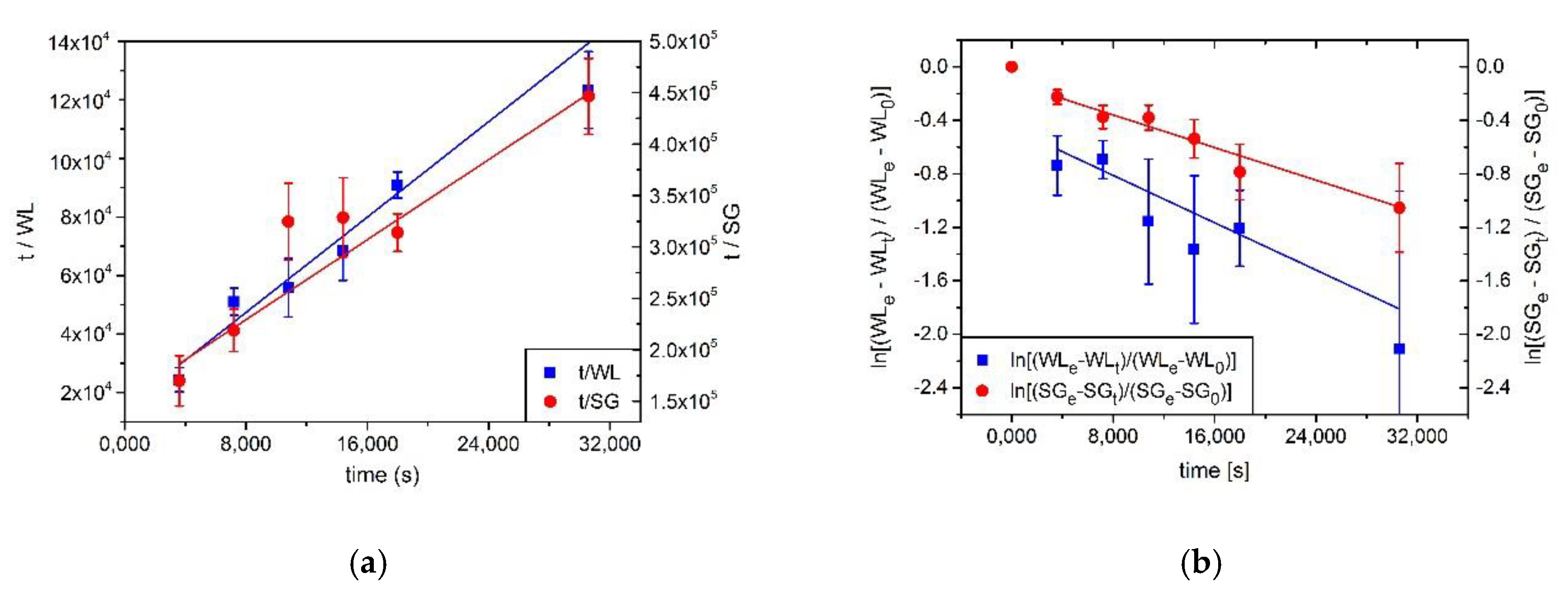
2.4. Mass Transfer Modelling
2.5. Magnetic Resonance Imaging
2.5.1. MRI Protocol
2.5.2. Contrast Agent
2.6. Image Analysis
3. Results
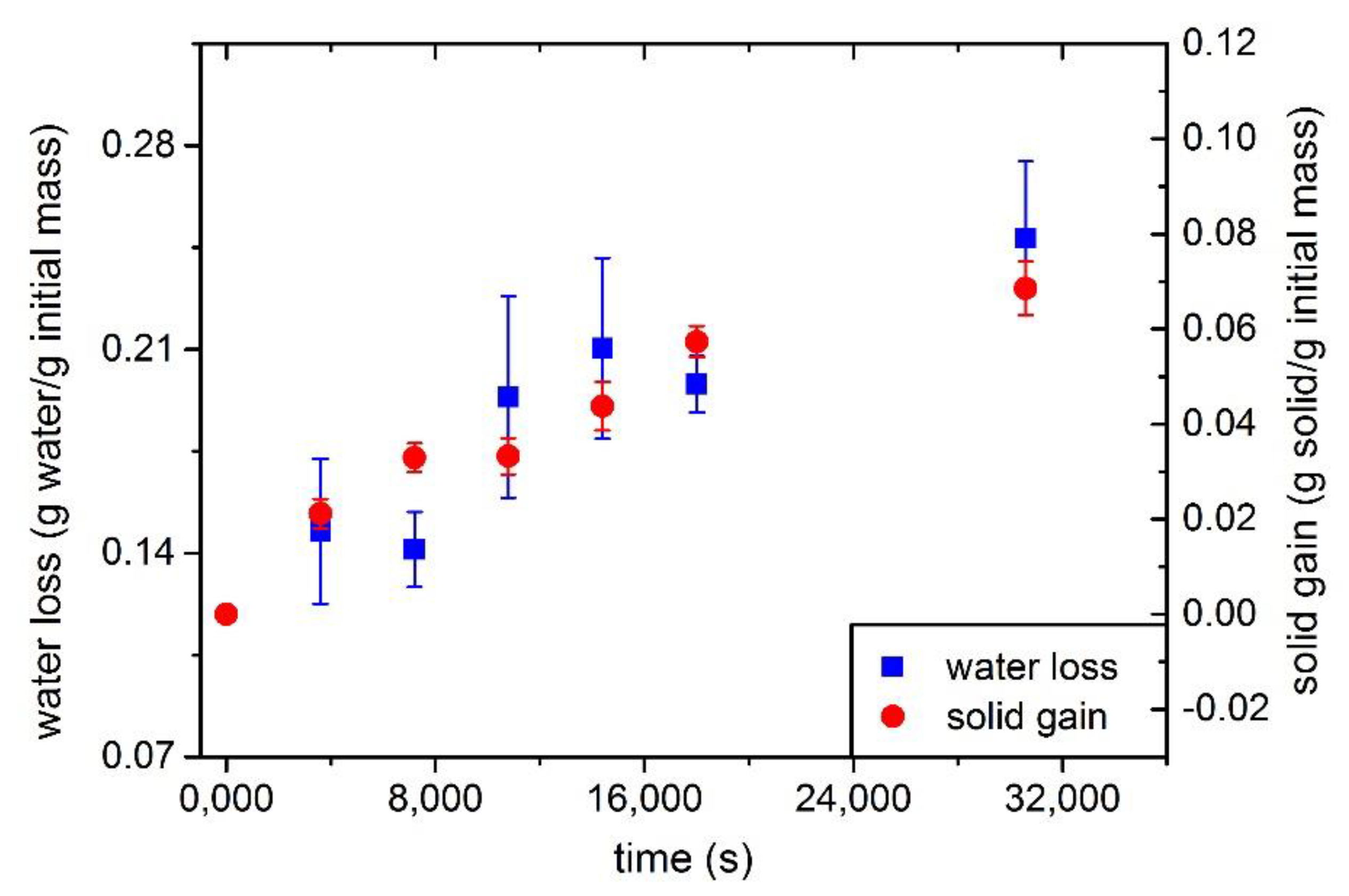
3.1. Determination of WL, SG and Diffusion Coefficient
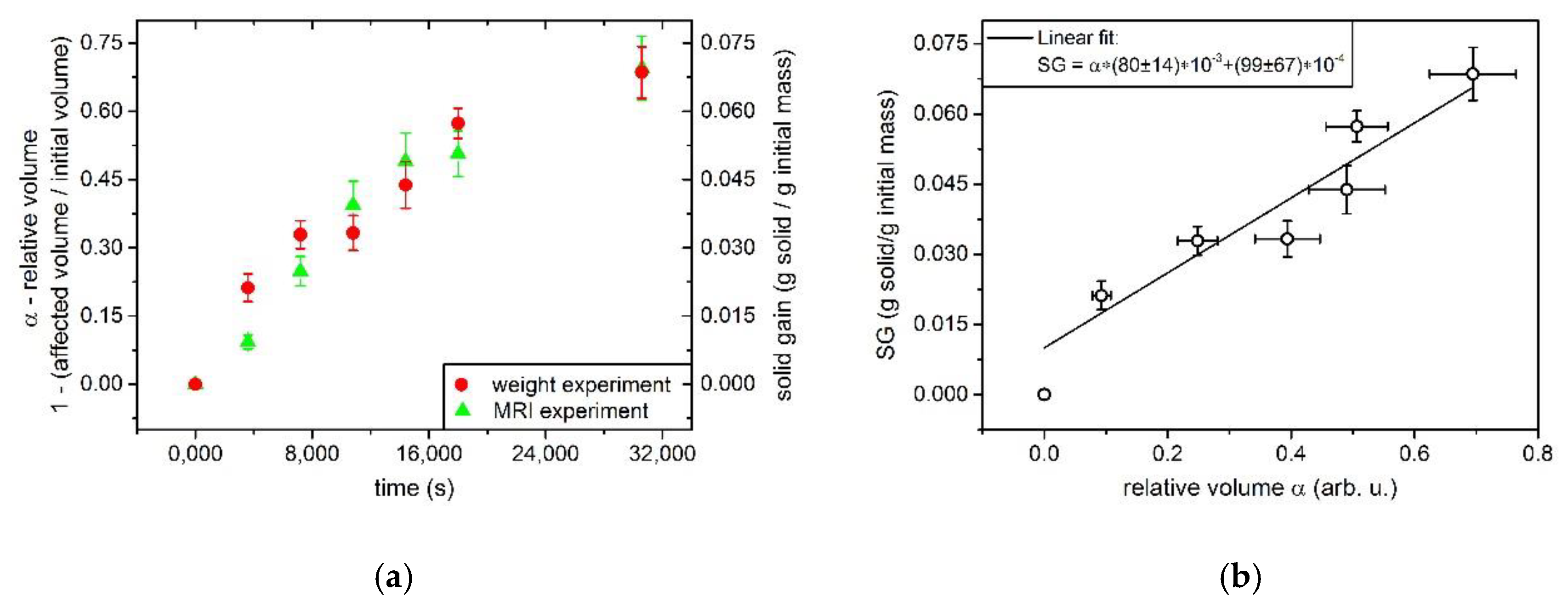
3.2. Determination MRI Data Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Muñiz-Becera, S.; Mendez-Lagunas, L.L.; Rodriguez-Ramirez, J. Solute Transfer in Osmotic Dehydration of Vegetable Foods: A Review. J. Food Sci. 2017, 82, 2251–2259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramya, V.; Jain, N.K. A Review on Osmotic Dehydration of Fruits and Vegetables: An Integrated Approach. J. Food Process Eng. 2017, 40, e12440. [Google Scholar] [CrossRef]
- Ciurzyńska, A.; Kowalska, H.; Czajkowska, K.; Lenart, A. Osmotic dehydration in production of sustainable and healthy food. Trends Food Sci. Technol. 2016, 50, 186–192. [Google Scholar] [CrossRef]
- Rastogi, N.K.; Raghavarao, K.S.M.S.; Niranjan, K.; Knorr, D. Recent developments in osmotic dehydration: Methods to enhance mass transfer. Trends Food Sci. Technol. 2002, 13, 48–59. [Google Scholar] [CrossRef]
- Kowalska, H.; Lenart, A.; Leszczyk, D. The effect of blanching and freezing on osmotic dehydration of pumpkin. J. Food Eng. 2008, 86, 30–38. [Google Scholar] [CrossRef]
- Mayor, L.; Pissarra, J.; Sereno, A.M. Microstructural changes during osmotic dehydration of parenchymatic pumpkin tissue. J. Food Eng. 2008, 85, 326–339. [Google Scholar] [CrossRef]
- Duce, S.L.; Carpenter, T.A.; Hall, L.D. Nuclear magnetic resonance imaging of fresh and frozen courgettes. J. Food Eng. 1992, 16, 165–172. [Google Scholar] [CrossRef]
- Rossi, G.; Socciarelli, S.; Aromolo, R.; Ciampa, A.; Beni, C. The effects of mineral and organic fertilizers on zucchini (Cucurbita pepo L.) investigated by the multiparameters analyses and magnetic resonance imaging (MRI). Agrochimica 2016, 60, 275–287. [Google Scholar]
- Evans, S.D.; Brambilla, A.; Lane, D.M.; Torreggiani, D.; Hall, L.D. Magnetic resonance imaging of strawberry (Fragaria vesca) slices during osmotic dehydration and air drying. LWT-Food Sci. Technol. 2002, 35, 177–184. [Google Scholar] [CrossRef]
- Derossi, A.; De Pilli, T.; Severini, C.; McCarthy, M.J. Mass transfer during osmotic dehydration of apples. J. Food Eng. 2008, 86, 519–528. [Google Scholar] [CrossRef]
- Brücher, E.; Tircsó, G.; Baranyai, Z.; Kovács, Z.; Sherry, A.D. Stability and Toxicity of Contrast Agents. In The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, 2nd ed.; Merbach, A.E., Helm, L., Tóth, É., Eds.; Wiley: New York, NY, USA, 2013; pp. 157–208. [Google Scholar] [CrossRef] [Green Version]
- Falade, K.O.; Igbeka, J.C.; Ayanwuyi, F.A. Kinetics of mass transfer, and colour changes during osmotic dehydration of watermelon. J. Food Eng. 2007, 80, 979–985. [Google Scholar] [CrossRef]
- Azuara, E.; Beristain, C.I.; Gutierrez, G.F. A method for continuous kinetic evaluation of osmotic dehydration. LWT-Food Sci. Technol. 1998, 31, 317–321. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: London, UK, 1975; pp. 69–88. [Google Scholar]
- Hamedi, F.; Mohebbi, M.; Shahidi, F.; Azarpazhooh, E. Ultra-sound-assisted osmotic treatment of model food impregnated with pomegranate Peel phenolic compounds: Mass transfer, texture, and phenolic evaluations. Food Bioprocess Technol. 2018, 11, 1061–1074. [Google Scholar] [CrossRef]
- Suchanek, M.; Cieślar, K.; Pałasz, T.; Suchanek, K.; Dohnalik, T.; Olejniczak, Z. Magnetic resonance imaging at low magnetic field using hyperpolarized 3He gas. Acta Phys. Pol. A 2005, 107, 491–506. [Google Scholar] [CrossRef]
- Suchanek, M.; Olejniczak, Z. Visualization of fluid flow pathways in wood by low-field 1H and 3He contrast MRI. Int. J. Multiph. Flow 2015, 72, 83–87. [Google Scholar] [CrossRef]
- Koenig, S.H.; Baglin, C.R.; Brown, D., 3rd; Brewer, C.F. Magnetic field dependence of solvent proton relaxation induced by Gd3+ and Mn2+ complexes. Magn. Reson. Med. 1984, 1, 496–501. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Mazonakis, M.; Damilakis, J.; Maris, T.; Prassopoulos, P.; Gourtsoyiannis, N. Comparison of Two Volumetric Techniques for Estimating Liver Volume Using Magnetic Resonance Imaging. J. Magn. Reson. Imaging 2002, 15, 557–563. [Google Scholar] [CrossRef]
- Chandra, R.; Rusinek, H. Tissue volume determinations from brain MRI images: A phantom study. In Medical Imaging V: Image Processing; International Society for Optics and Photonics: Bellingham, WA, USA, 1991; Volume 1445, pp. 133–144. [Google Scholar] [CrossRef]
- Zúñiga, R.N.; Pedreschi, F. Study of the Pseudo-equilibrium during Osmotic Dehydration of Apples and Its Effect on the Estimation of Water and Sucrose Effective Diffusivity Coefficients. Food Bioprocess Technol. 2012, 5, 2717–2727. [Google Scholar] [CrossRef]
- Mayor, L.; Moreira, R.; Chenlo, F.; Sereno, A.M. Water sorption isotherms of fresh and partially osmotic dehydrated pumpkin parenchyma and seeds at several temperatures. Eur. Food Res. Technol. 2005, 220, 163–167. [Google Scholar] [CrossRef]
- Mayor, L.; Delgado, J.M.P.Q.; Vázquez Da Silva, M.; Sereno, A.M.; Gonçalves, M.P. Effect of Temperature and Volume Changes on Effective Diffusivities of Sucrose and NaCl during Osmotic Dehydration of Vegetable Tissue. Defect Diffus. Forum 2008, 273, 138–143. [Google Scholar] [CrossRef]
- Lech, K.; Michalska, A.; Wojdylo, A.; Nowicka, P.; Figiel, A. The Influence of the Osmotic Dehydration Process on Physicochemical Properties of Osmotic Solution. Molecules 2017, 22, 2246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borde, A.; Bergstrand, A.; Gunnarsson, C.; Larsson, A. Osmotic-driven mass transport of water: Impact on the adhesiveness of hydrophilic polymers. J. Colloid Interface Sci. 2010, 3, 255–260. [Google Scholar] [CrossRef] [PubMed]

| Parameters from (Water Loss) | Parameters from (Solid Gain) | |
|---|---|---|
| Pearson′s correlation coefficient | 0.980 | 0.952 |
| Slope | 3.54 ± 0.32 | 9.5 ± 1.8 |
| Intercept | 19,000 ± 5300 | 167,000 ± 29,000 |
| S1 | (1.9 ± 0.5) × 10−4 | - |
| WLe | 0.28 ± 0.03 | - |
| S2 | - | (0.57 ± 0.14) × 10−4 |
| SGe | - | 0.11 ± 0.02 |
| Parameters from | ||
|---|---|---|
| Pearson’s correlation coefficient | −0.884 | −0.966 |
| Slope | (−6.09 ± 0.90) × 10−5 | (−3.38 ± 0.30) × 10−5 |
| Intercept | −0.30 ± 0.14 | −0.071 ± 0.045 |
| De(WL) (m2/s) | (2.91 ± 0.47) × 10−9 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suchanek, M.; Olejniczak, Z. Evaluation of Osmotic Dehydration Process in Plant Tissue with Low-Field Magnetic Resonance Imaging Enhanced with Paramagnetic Ions. Processes 2020, 8, 887. https://doi.org/10.3390/pr8080887
Suchanek M, Olejniczak Z. Evaluation of Osmotic Dehydration Process in Plant Tissue with Low-Field Magnetic Resonance Imaging Enhanced with Paramagnetic Ions. Processes. 2020; 8(8):887. https://doi.org/10.3390/pr8080887
Chicago/Turabian StyleSuchanek, Mateusz, and Zbigniew Olejniczak. 2020. "Evaluation of Osmotic Dehydration Process in Plant Tissue with Low-Field Magnetic Resonance Imaging Enhanced with Paramagnetic Ions" Processes 8, no. 8: 887. https://doi.org/10.3390/pr8080887
APA StyleSuchanek, M., & Olejniczak, Z. (2020). Evaluation of Osmotic Dehydration Process in Plant Tissue with Low-Field Magnetic Resonance Imaging Enhanced with Paramagnetic Ions. Processes, 8(8), 887. https://doi.org/10.3390/pr8080887






