Hyperspectral Image Classification Based on Spectral and Spatial Information Using Multi-Scale ResNet
Abstract
Featured Application
Abstract
1. Introduction
- To reduce the correlation between HSI spectral bands and the amount of computation, the principle component analysis (PCA) method is used to preprocess the HSI data.
- Spatial and spectral features are combined ahead of feeding into the classification model.
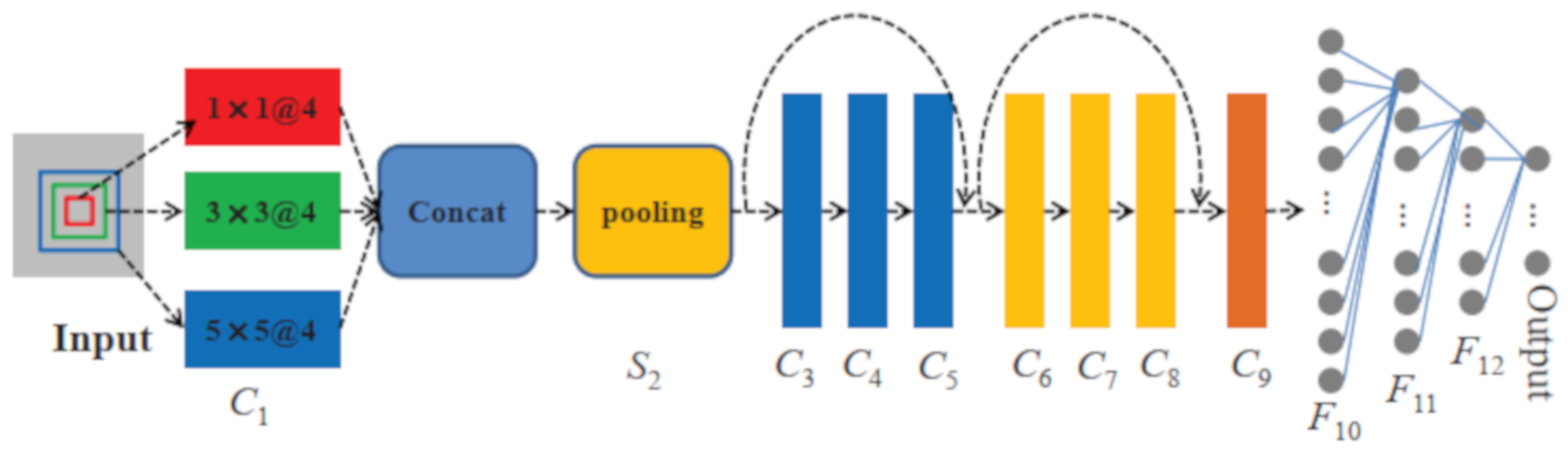
- To fully extract the most important information and reduce the risk of overfitting, multi-scale kernels are applied to the first convolutional layer.
- To protect the integrity of information and deepen the network, residual blocks are added to the network.
2. Related Works
2.1. CNN for Classification
2.2. Hyperspectral Image Classification
3. The Proposed Method
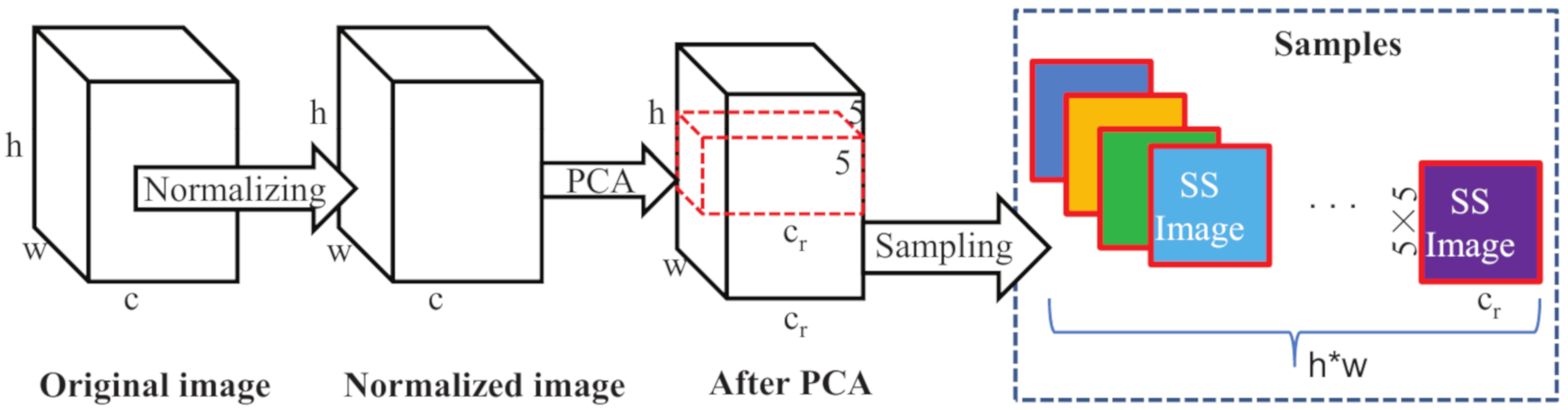
3.1. Data Preprocessing
- After PCA is conducted, we assume that a labelled pixel at location of is selected as a sample, and labeled as the class of .
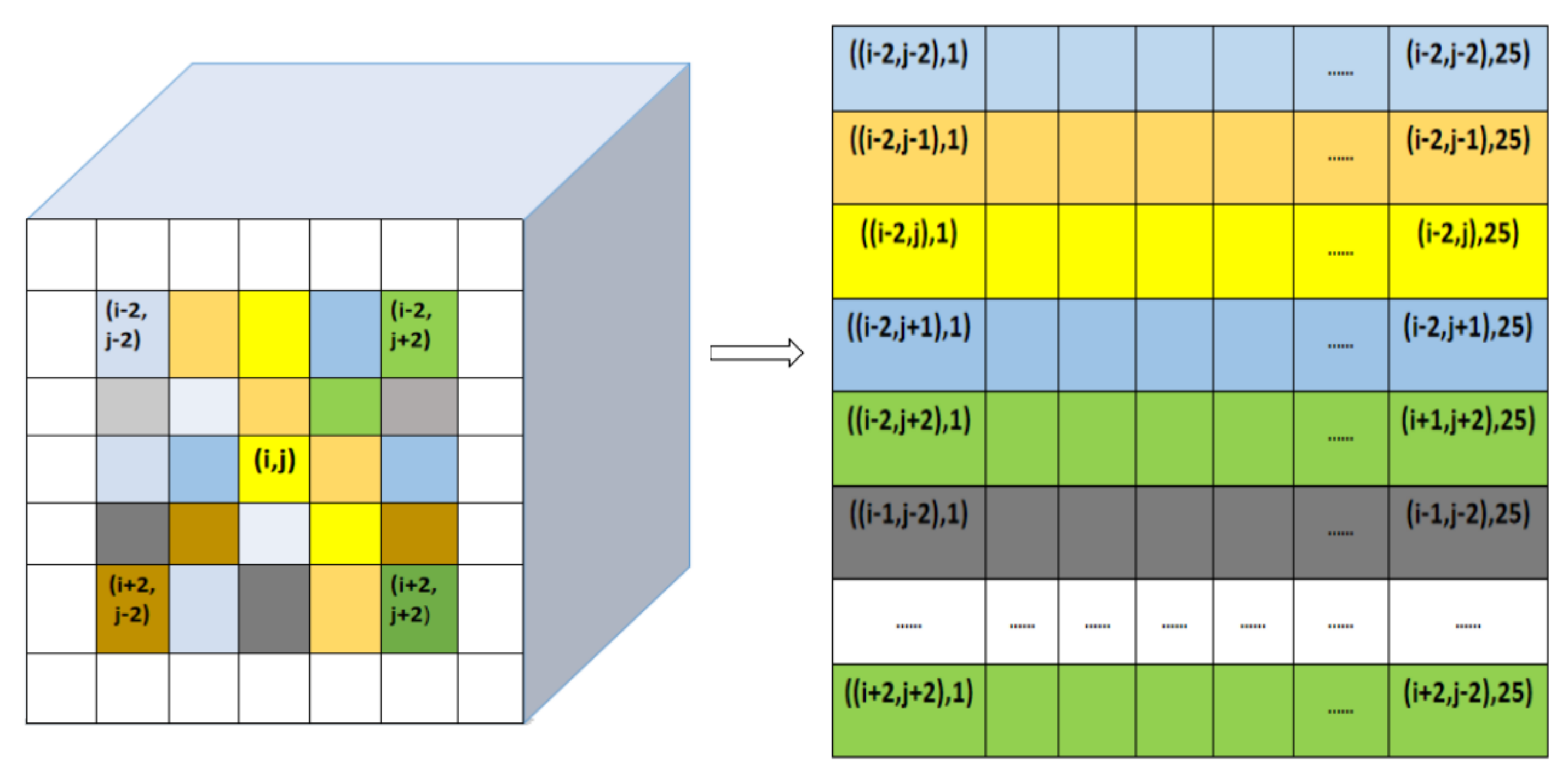
- Then, we center on pixel , increase the rows and columns from to respectively, and capture an area of to form a three-dimensional cube of .
- Finally, the three-dimensional cube is unfolded by extracting the spectral band values of each pixel to form a row vector from left to right and from top to bottom, thus a image is formed as shown in Figure 2, which combine spectral and spatial information as an input, denoted as . A sample of , an SS Image, is formed as .
- Repeat steps (1–3), and we can form the dataset .
3.2. Network Architecture
3.3. Loss Function
4. Experiment Results and Analysis
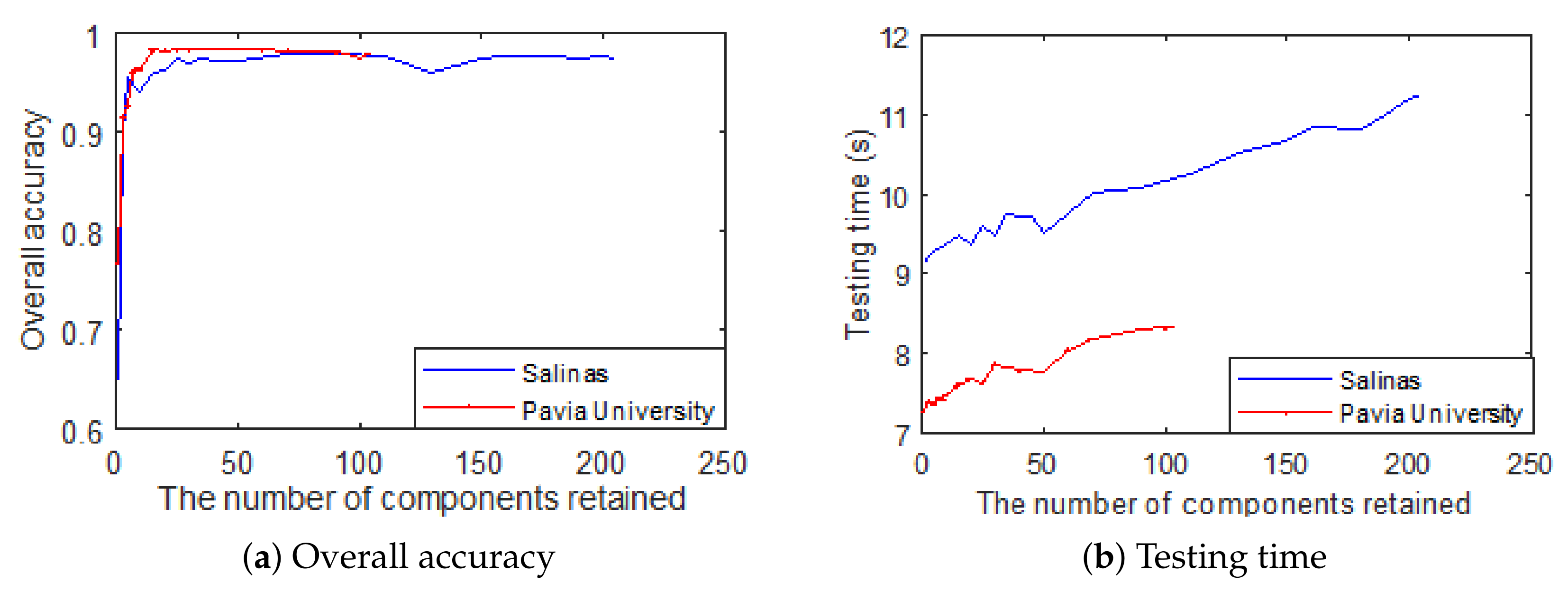
4.1. How Many Components Should Be Remained?
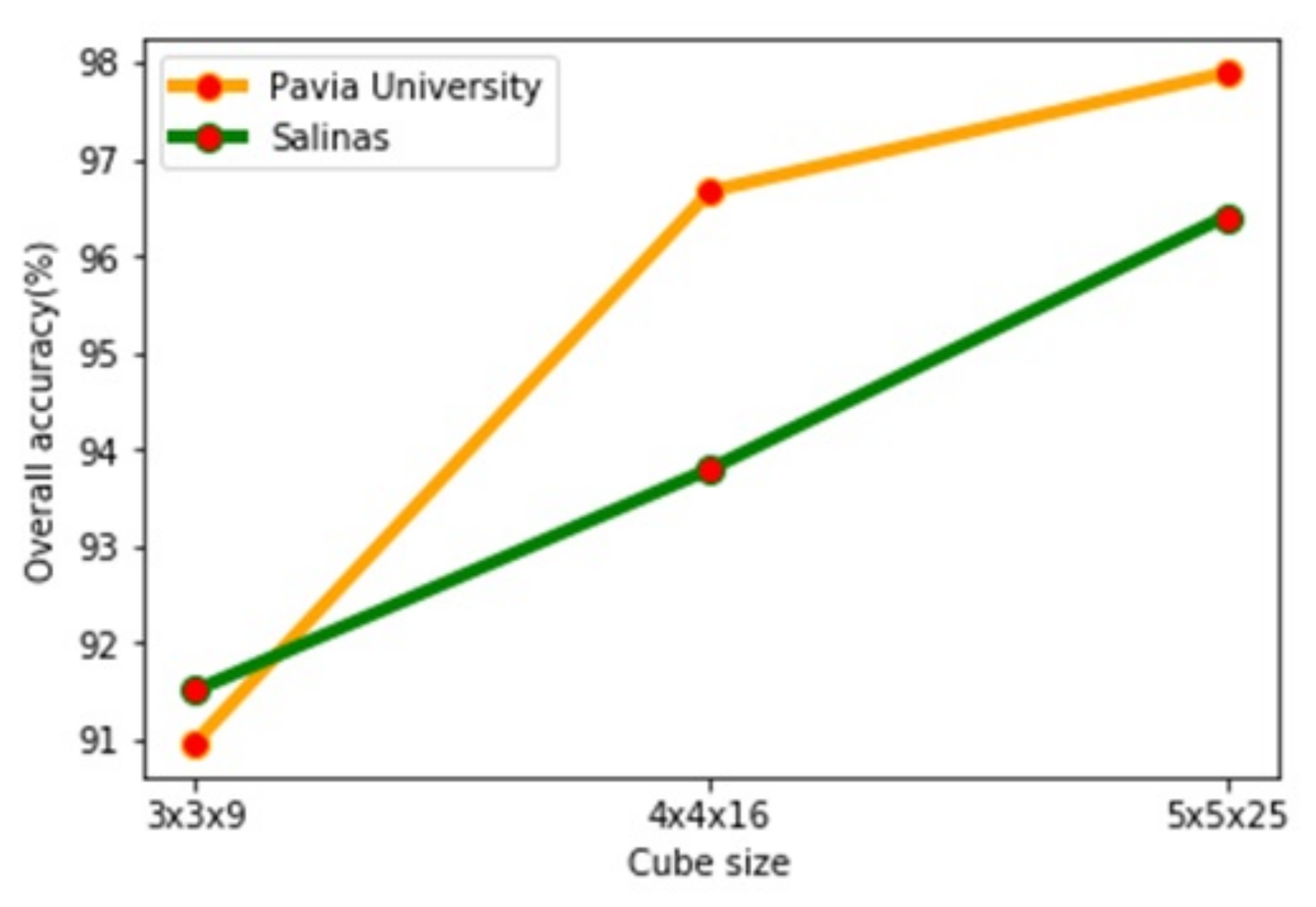
4.2. The Effect of the Cube Size
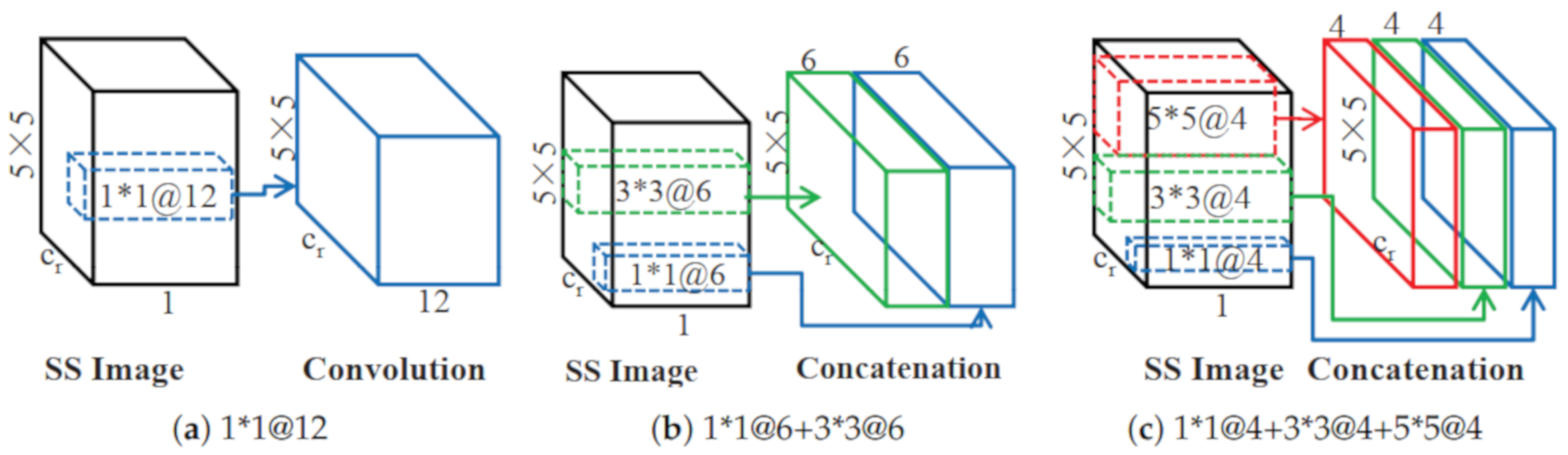
4.3. How the Multi-Scale Affects the Classification
4.4. The Performance of Classification on the Salinas and Pavia University Datasets
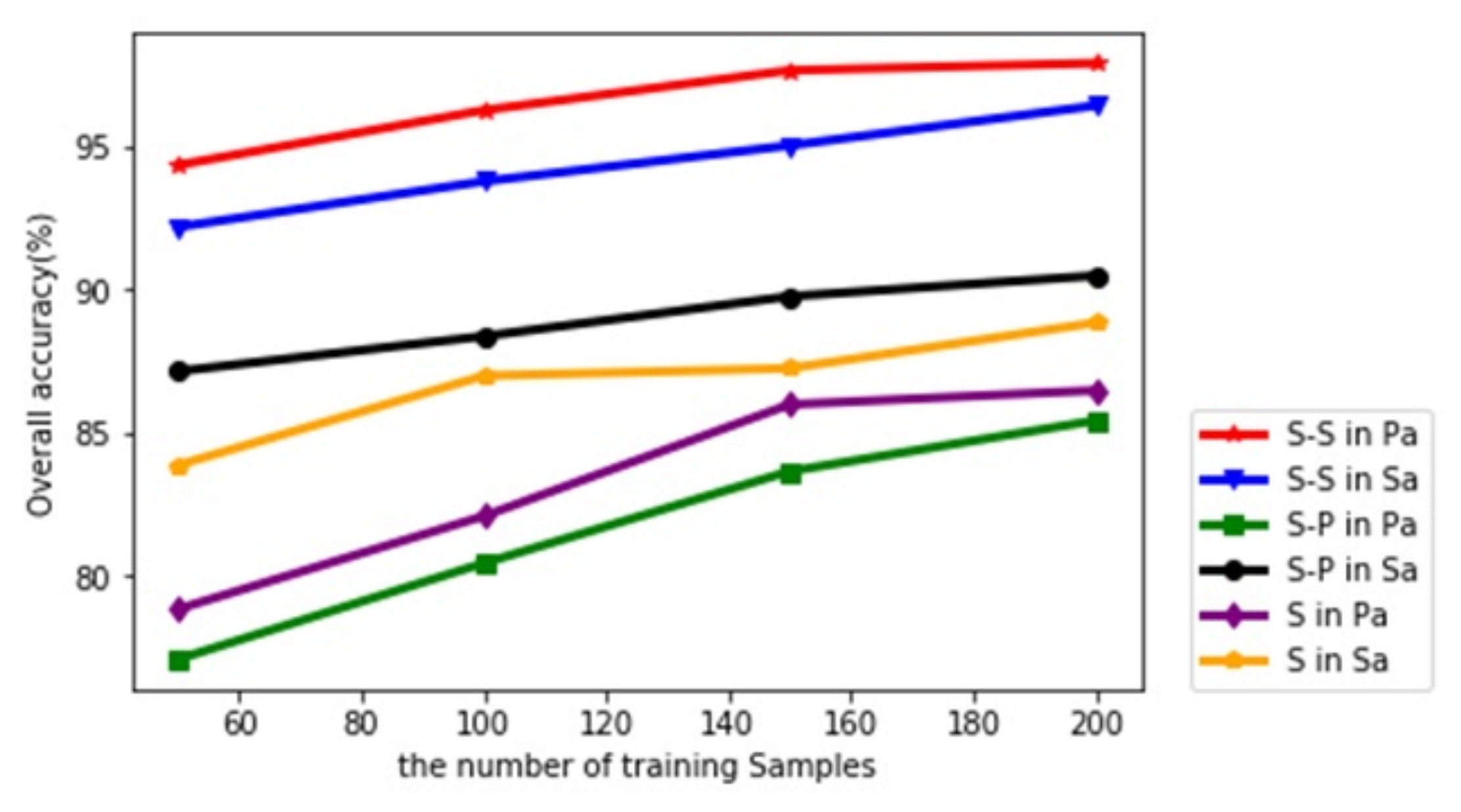
4.5. The Influence between the Number of Training Samples and the Classification
4.6. Comparison of other Proposed Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HSI | Hyperspectral Image |
| PCA | Principle Component Analysis |
| CNN | Convolutional Neural Network |
References
- Bioucas-Dias, J.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral-Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in Hyperspectral Image Classification: Earth Monitoring with Statistical Learning Methods. IEEE Signal Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef]
- Blanzieri, E.; Melgani, F. Nearest Neighbor Classification of Remote Sensing Images with the Maximal Margin Principle. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1804–1811. [Google Scholar] [CrossRef]
- Yang, X.; Hong, H.; You, Z.; Cheng, F. Spectral and Image Integrated Analysis of Hyperspectral Data for Waxy Corn Seed Variety Classification. Sensors 2015, 15, 15578–15594. [Google Scholar] [CrossRef]
- Rutlidge, H.T.; Reedy, B.J. Classification of heterogeneous solids using infrared hyperspectral imaging. Appl. Spectrosc. 2009, 63, 172. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Support vector machines for classification of hyperspectral remote-sensing images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 1, pp. 506–508. [Google Scholar] [CrossRef]
- Archibald, R.; Fann, G. Feature Selection and Classification of Hyperspectral Images with Support Vector Machines. IEEE Geosci. Remote Sens. Lett. 2007, 4, 674–677. [Google Scholar] [CrossRef]
- Wei, L.; Chen, C.; Su, H.; Qian, D. Local Binary Patterns and Extreme Learning Machine for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar]
- Gurram, P.; Kwon, H. Sparse Kernel-Based Ensemble Learning with Fully Optimized Kernel Parameters for Hyperspectral Classification Problems. IEEE Trans. Geosci. Remote Sens. 2013, 51, 787–802. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, T.; Jia, X.; Benediktsson, J.A.; Chanussot, J. Nonlinear Multiple Kernel Learning with Multiple-Structure-Element Extended Morphological Profiles for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3235–3247. [Google Scholar] [CrossRef]
- Morsier, F.D.; Borgeaud, M.; Gass, V.; Thiran, J.P.; Tuia, D. Kernel Low-Rank and Sparse Graph for Unsupervised and Semi-Supervised Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3410–3420. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Z.; Li, J.; Plaza, A.; Yuan, Y. Probabilistic-Kernel Collaborative Representation for Spatial-Spectral Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2371–2384. [Google Scholar] [CrossRef]
- Wang, Q.; Gu, Y.; Tuia, D. Discriminative Multiple Kernel Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3912–3927. [Google Scholar] [CrossRef]
- Guo, B.; Gunn, S.R.; Damper, R.; Nelson, J. Customizing kernel functions for SVM-based hyperspectral image classification. IEEE Trans. Image Process. 2008, 17, 622–629. [Google Scholar] [CrossRef]
- Yang, L.; Min, W.; Yang, S.; Rui, Z.; Zhang, P. Sparse Spatio-Spectral LapSVM With Semisupervised Kernel Propagation for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2046–2054. [Google Scholar] [CrossRef]
- Roscher, R.; Waske, B. Shapelet-Based Sparse Representation for Landcover Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1623–1634. [Google Scholar] [CrossRef]
- Zehtabian, A.; Ghassemian, H. Automatic Object-Based Hyperspectral Image Classification Using Complex Diffusions and a New Distance Metric. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4106–4114. [Google Scholar] [CrossRef]
- Jia, S.; Jie, H.; Yao, X.; Shen, L.; Li, Q. Gabor Cube Selection Based Multitask Joint Sparse Representation for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3174–3187. [Google Scholar] [CrossRef]
- Xia, J.; Chanussot, J.; Du, P.; He, X. Rotation-Based Support Vector Machine Ensemble in Classification of Hyperspectral Data With Limited Training Samples. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1519–1531. [Google Scholar] [CrossRef]
- Zhong, Z.; Fan, B.; Ding, K.; Li, H.; Xiang, S.; Pan, C. Efficient Multiple Feature Fusion With Hashing for Hyperspectral Imagery Classification: A Comparative Study. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4461–4478. [Google Scholar] [CrossRef]
- Xia, J.; Bombrun, L.; Adali, T.; Berthoumieu, Y.; Germain, C. Spectral-Spatial Classification of Hyperspectral Images Using ICA and Edge-Preserving Filter via an Ensemble Strategy. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4971–4982. [Google Scholar] [CrossRef]
- Jia, S.; Deng, B.; Zhu, J.; Jia, X.; Li, Q. Superpixel-Based Multitask Learning Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2575–2588. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Hu, W.; Yangyu, H.; Li, W.; Fan, Z.; Hengchao, L. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Contextual Deep CNN Based Hyperspectral Classification. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3322–3325. [Google Scholar]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep Learning Classification of Land Cover and Crop Types Using Remote Sensing Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral-spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Ying, L.; Zhang, H.; Qiang, S. Spectral-spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar]
- Zhang, M.; Li, W.; Du, Q. Diverse Region-Based CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef]
- Yang, L.; Leon, B.; Yoshua, B.; Patrick, H. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. arXiv 2016, arXiv:1602.07261. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]
- Xue, Z.; Du, P.; Su, H. Harmonic Analysis for Hyperspectral Image Classification Integrated With PSO Optimized SVM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2131–2146. [Google Scholar] [CrossRef]
- Ratle, F.; Camps-Valls, G.; Weston, J. Semisupervised Neural Networks for Efficient Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2271–2282. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Ran, L.; Yanning, Z.; Wei, W.; Qilin, Z. A Hyperspectral Image Classification Framework with Spatial Pixel Pair Features. Sensors 2017, 17, 2421. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-Based Edge-Preserving Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A Superpixelwise PCA Approach for Unsupervised Feature Extraction of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1–13. [Google Scholar] [CrossRef]
- Wei, L.; Wu, G. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2016, 55, 844–853. [Google Scholar]
- Lee, H.; Kwon, H. Going Deeper with Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]



| No. | Classes | Total Samples | Training Samples |
|---|---|---|---|
| 1 | Asphalt | 6631 | 200 |
| 2 | Meadows | 18,649 | 200 |
| 3 | Gravel | 2099 | 200 |
| 4 | Trees | 3064 | 200 |
| 5 | Painted metal sheets | 1345 | 200 |
| 6 | Bare Soil | 5029 | 200 |
| 7 | Bitumen | 1330 | 200 |
| 8 | Self-blocking bricks | 3682 | 200 |
| 9 | Shadows | 947 | 200 |
| Total | 42776 | 1800 |
| No. | Classes | Total Samples | Train Samples |
|---|---|---|---|
| 1 | Brocoli green weeds 1 | 2009 | 200 |
| 2 | Brocoli green weeds 2 | 3726 | 200 |
| 3 | Fallow | 1976 | 200 |
| 4 | Fallow rough plow | 1394 | 200 |
| 5 | Fallow smooth | 2678 | 200 |
| 6 | Stubble | 3959 | 200 |
| 7 | Celery | 3579 | 200 |
| 8 | Grapes untrained | 11,271 | 200 |
| 9 | Soil vinyard develop | 6203 | 200 |
| 10 | Corn senesced green weeds | 3278 | 200 |
| 11 | Lettuce romaine 4wk | 1068 | 200 |
| 12 | Lettuce romaine 5wk | 1927 | 200 |
| 13 | Lettuce romaine 6wk | 916 | 200 |
| 14 | Lettuce romaine 7wk | 1070 | 200 |
| 15 | Vinyard untrained | 7268 | 200 |
| 16 | Vinyard vertical trellis | 1807 | 200 |
| Total | 54,129 | 3200 |
| Datasets | Kernels | Training Time | Testing Time | OA | AA | Kappa |
|---|---|---|---|---|---|---|
| Pavia University | 1*1@12 | 26.40 | 7.32 | 0.963604 | 0.956682 | 0.951763 |
| 3*3@12 | 26.15 | 7.23 | 0.978551 | 0.97294 | 0.971562 | |
| 5*5@12 | 26.23 | 7.30 | 0.97834 | 0.966848 | 0.971356 | |
| 1*1@6+3*3@6 | 26.93 | 7.45 | 0.978551 | 0.97294 | 0.971562 | |
| 3*3@6+5*5@6 | 26.84 | 7.48 | 0.978995 | 0.968616 | 0.972227 | |
| 1*1@4+3*3@4+5*5@4 | 27.57 | 7.49 | 0.986153 | 0.983208 | 0.981648 | |
| Salinas | 1*1@12 | 25.96 | 8.95 | 0.957255 | 0.982387 | 0.952307 |
| 3*3@12 | 26.13 | 9.04 | 0.965719 | 0.982829 | 0.961777 | |
| 5*5@12 | 26.12 | 9.27 | 0.964592 | 0.983698 | 0.96056 | |
| 1*1@6+3*3@6 | 26.63 | 9.17 | 0.971393 | 0.986391 | 0.968131 | |
| 3*3@6+5*5@6 | 27.04 | 9.28 | 0.974165 | 0.98662 | 0.971259 | |
| 1*1@4+3*3@4+5*5@4 | 27.61 | 9.53 | 0.975608 | 0.986853 | 0.972731 |
| Class | Spectral | Spectral + PCA | Spectral-Spatial + PCA |
|---|---|---|---|
| 1 | 96.17 | 99.75 | 100.00 |
| 2 | 99.81 | 99.87 | 100.00 |
| 3 | 99.75 | 96.96 | 100.00 |
| 4 | 99.21 | 99.21 | 99.93 |
| 5 | 98.36 | 98.32 | 98.58 |
| 6 | 99.77 | 99.70 | 100.00 |
| 7 | 99.64 | 99.61 | 99.80 |
| 8 | 70.00 | 87.19 | 91.40 |
| 9 | 99.03 | 99.15 | 99.97 |
| 10 | 93.90 | 92.01 | 97.28 |
| 11 | 95.97 | 98.97 | 99.81 |
| 12 | 99.74 | 96.16 | 99.95 |
| 13 | 98.47 | 99.56 | 99.67 |
| 14 | 98.97 | 96.92 | 98.97 |
| 15 | 70.50 | 57,31 | 88.80 |
| 16 | 99.11 | 99.28 | 99.78 |
| OA | 88.84 | 90.48 | 96.41 |
| AA | 93.73 | 91.15 | 98.09 |
| Kappa | 87.61 | 89.38 | 96.01 |
| Time (s) | 2.3799 | 1.3771 | 5.0755 |
| Class | Spectral | Spectral + PCA | Spectral-Spatial + PCA |
|---|---|---|---|
| 1 | 83.74 | 81.81 | 97.45 |
| 2 | 85.81 | 83.67 | 98.47 |
| 3 | 80.32 | 77.23 | 97.33 |
| 4 | 95.43 | 93.37 | 98.43 |
| 5 | 99.78 | 99.48 | 100.00 |
| 6 | 84.67 | 87.55 | 98.91 |
| 7 | 94.43 | 90.90 | 99.47 |
| 8 | 82.16 | 85.17 | 92.42 |
| 9 | 100.00 | 99.89 | 99.89 |
| OA | 86.48 | 85.43 | 97.89 |
| AA | 84.19 | 83.58 | 95.57 |
| Kappa | 82.46 | 81.18 | 97.22 |
| Time (s) | 1.3992 | 1.0734 | 4.2585 |
| Datasets | Methods | Numbers of Training Samples | |||
|---|---|---|---|---|---|
| 50 | 100 | 150 | 200 | ||
| Salinas | CNN [26] | 89.20 | 89.58 | 89.60 | 89.72 |
| CNN-PPF [46] | 92.15 | 93.88 | 93.84 | 94.80 | |
| CD-CNN [47] | 82.74 | 98.58 | - | 95.42 | |
| Proposed method | 92.18 | 93.77 | 95.02 | 96.41 | |
| Pavia University | CNN [26] | 86.39 | 88.53 | 90.89 | 92.27 |
| CNN-PPF [46] | 88.14 | 93.35 | 94.97 | 96.48 | |
| CD-CNN [47] | 92.19 | 93.35 | - | 96.73 | |
| Proposed method | 94.34 | 96.25 | 97.64 | 97.89 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.-Y.; Xia, Q.-M.; Yan, J.-W.; Xuan, S.-Q.; Su, J.-H.; Yang, C.-F. Hyperspectral Image Classification Based on Spectral and Spatial Information Using Multi-Scale ResNet. Appl. Sci. 2019, 9, 4890. https://doi.org/10.3390/app9224890
Wang Z-Y, Xia Q-M, Yan J-W, Xuan S-Q, Su J-H, Yang C-F. Hyperspectral Image Classification Based on Spectral and Spatial Information Using Multi-Scale ResNet. Applied Sciences. 2019; 9(22):4890. https://doi.org/10.3390/app9224890
Chicago/Turabian StyleWang, Zong-Yue, Qi-Ming Xia, Jing-Wen Yan, Shu-Qi Xuan, Jin-He Su, and Cheng-Fu Yang. 2019. "Hyperspectral Image Classification Based on Spectral and Spatial Information Using Multi-Scale ResNet" Applied Sciences 9, no. 22: 4890. https://doi.org/10.3390/app9224890
APA StyleWang, Z.-Y., Xia, Q.-M., Yan, J.-W., Xuan, S.-Q., Su, J.-H., & Yang, C.-F. (2019). Hyperspectral Image Classification Based on Spectral and Spatial Information Using Multi-Scale ResNet. Applied Sciences, 9(22), 4890. https://doi.org/10.3390/app9224890






