An Analytical Technique to Solve the System of Nonlinear Fractional Partial Differential Equations

Abstract

The Kortweg–de Vries equations play an important role to model different physical phenomena in nature. In this research article, we have investigated the analytical solution to system of nonlinear fractional Kortweg–de Vries, partial differential equations. The Caputo operator is used to define fractional derivatives. Some illustrative examples are considered to check the validity and accuracy of the proposed method. The obtained results have shown the best agreement with the exact solution for the problems. The solution graphs are in full support to confirm the authenticity of the present method.

1. Introduction

In the study of nonlinear dispersive waves, Kortweg–de Vries (KdV) is an important class of differential equations. This class is derived by two great scientists Kortweg and de Vries in 1895 for describing long wave propagation on shallow water. Although KdV equations are studied from a decade, its physical behavior is still curious. The phenomena described by Russell can be expressed by the KdV equation successfully [1]. This equation plays an important role in various fields of science and technology, so a lot of research work has been devoted for this study [2]. Numerous physical problems in different fields of mechanics, biology, hydrodynamics and plasma physics are successfully modelled by a nonlinear coupled system of Partial Differential Equations (PDEs).

In nonlinear PDEs, the nonlinear term is completely responsible for the study of any physical problem [3]. The exact solution of nonlinear PDEs may not be calculated easily, therefore various analytical and numerical techniques have been suggested for the solution of such types of equations. The well-known analytical approaches for the solution of coupled systems of differential equations are iterative methods, perturbation methods and homotopy based methods, etc. Each approach has its own merits and demerits. Some approaches for the solution of coupled system of differential equations have been discussed successfully in [2].

Generalized Hirota–Satsuma coupled KdV equations have been solved, using the modified decomposition method [4]. An exact approach has been suggested for the solution of coupled KdV, using the homogenous balance method [5]. By using the differential transform method, the analytical solutions of coupled KdV have been studied in [6]. The homotopy analysis method have been described in [7] for solving KdV equations. The exact solution of KdV has been investigated in [8] using the variational iteration method. The analytical solution for a generalized coupled system of Zakharov–Kuznetsov and KdV equations have been obtained in [9] using the modified extended tanh method.

In 1980, George Adomian has introduced a new mathematical technique, known as the adomian decomposition method (ADM) to solve nonlinear differential equations [10]. Similarly, another powerful technique for solving PDEs discovered by Pierre-Simon Laplace is known as the Laplace transform method, which transforms the original differential equations into an algebraic expression [11]. Among all these methods, the Laplace Adomian Decompostion Method (LADM) is an efficient analytical method to solve nonlinear fractional partial differential equations. LADM is the combination of two powerful techniques, Laplace transform and the Adomian Decomposition Method. Furthermore, the proposed method has no requirement of predefined size declaration like Runge–Kutta methods. Therefore, this technique is considered to be ideal for those equations that represent nonlinear models. Compared to other analytical techniques, LADM have less numbers of parameters; therefore, LADM is a perfect technique, requiring no discretization and linearization [12]. Non-linear Coupled PDE’s and non-linear Blasius flow equation using Laplace decompostion method [13,14]. A comparison between the LADM and ADM for the analysis of FPDEs is discussed in [15]. The Kundu–Eckhaus Equation deals in the quantum field theory, and the analytical solution of this nonlinear PDEs has been derived in [10] using LADM. The multi-step Laplace Adomian decomposition method has been described in [16] for nonlinear fractional differential equations. Analysis of the fractional order smoke model has been studied successfully by using LADM [17]. Such as Fractional Order Epidemic Model of a Vector Born Disease [18], Multi dimensional of Navier–Stokes equation [19] and third-order dispersive FPDE’s using LADM [20]. Motivated from the above studies, in this paper, we applied LADM to solve the system of fractional KdV equations [21].

2. Definitions and Preliminary Concepts

Definition 1.

R-L fractional integral

$$I_x^{\gamma }g\left(x\right)=\left\{\begin{array}{cc}g\left(x\right),\hfill & if\gamma =0,\hfill \\ \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}{\int }_0^x{(x-\upsilon )}^{\gamma -1}g\left(\upsilon \right)d\upsilon \hfill & if\gamma >0,\hfill \end{array}\right.$$

where Γ denote the gamma function defined by

$$\mathsf{\Gamma }\left(\omega \right)={\int }_0^{\infty }{e}^{-x}{x}^{\omega -1}dx\omega \in \mathbb{C}.$$

In this study, Caputo et al. [22] suggested a revised fractional derivative operator in order to overcome inconsistency measured in the Riemann–Liouville derivative [23]. The above mathematical statement described the Caputo fractional derivative operator of initial and boundary conditions for fractional as well as integer order derivatives.

Definition 2.

The Caputo operator of order γ for fractional derivative is given by the following mathematical expression for $n\in \mathbb{N}$, $x>0$, $g\in {\mathbb{C}}_t$, $t\ge -1$:

$$D^{\gamma }g\left(x\right)=\frac{{\partial }^{\gamma }g\left(x\right)}{\partial t^{\gamma }}=\left\{\begin{array}{cc}{I}^{n-\gamma }\left[\frac{{\partial }^{\gamma }g\left(x\right)}{\partial t^{\gamma }}\right],\hfill & ifn-1<\gamma \le n,n\in \mathbb{N},\hfill \\ \frac{{\partial }^{\gamma }g\left(x\right)}{\partial t^{\gamma }}.\hfill \end{array}\right.$$

Hence, we require the subsequent properties given in the next Lemma.

Lemma 1.

If $n-1<\gamma \le n$ with $n\in \mathbb{N}$ and $g\in {\mathbb{C}}_t$ with $t\ge -1,$ then

$$\begin{array}{c}{I}^{\gamma }{I}^{a}g\left(x\right)=I^{\gamma +a}g\left(x\right),a,\gamma \ge 0.\hfill \\ I^{\gamma }{x}^{\lambda }=\frac{\mathsf{\Gamma }(\lambda +1)}{\mathsf{\Gamma }(\gamma +\lambda +1)}{x}^{\gamma +\lambda },\gamma >0,\lambda >-1,x>0.\hfill \\ I^{\gamma }{D}^{\gamma }g\left(x\right)=g\left(x\right)-\sum _{k=0}^{n-1}{g}^{\left(k\right)}\left(0^{+}\right)\frac{x^k}{k!},\mathrm{for}x>0,n-1<\gamma \le n.\hfill \end{array}$$

In the current study, the Caputo operator is reasonable as other fractional derivative operators have certain disadvantages. Further information about fractional derivatives are found in [24].

Definition 3.

The Laplace transform of $h\left(t\right),$$t>0$ is defined by

$$H\left(s\right)=\mathcal{L}\left[h\left(t\right)\right]={\int }_0^{\infty }{e}^{-st}h\left(t\right)dt.$$

Definition 4.

The Laplace transform in term of convolution is given by

$$\mathcal{L}[h_1\ast h_2]=\mathcal{L}\left[h_1\left(t\right)\right]\ast \mathcal{L}\left[h_2\left(t\right)\right].$$

Here, $h_1\ast h_2$, define the convolution between $h_1$ and $h_2$,

$$(h_1\ast h_2)t={\int }_0^{\tau }{h}_1\left(\tau \right)h_2(t-\tau )dt.$$

Fractional derivative in terms of Laplace transform is

$$\mathcal{L}\left(D_t^{\gamma }h\left(t\right)\right)=s^{\gamma }\mathit{H}\left(\mathit{s}\right)-\sum _{k=0}^{n-1}{s}^{\gamma -1-k}{h}^{\left(k\right)}\left(0\right),n-1<\gamma <n,$$

where $H\left(s\right)$ is the Laplace transform of $h\left(t\right)$.

Definition 5.

The Mittag–Leffler function, $E_{\gamma }\left(p\right)$ for $\gamma >0$ is represented as

$$E_{\gamma }\left(p\right)=\sum _{n=0}^{\infty }\frac{p^n}{\mathsf{\Gamma }\left(\gamma n+1\right)}\gamma >0,p\in \mathbb{C}.$$

Theorem 1.

Here, we will study the convergence analysis in the same manner as [25] of the LADM applied to the fractional-order Kortweg–de Vries. Let us consider the Hilbert space H which may define by $H=L^2\left((\alpha ,\beta )X[0,T]\right)$ the set of applications:

$$u:(\alpha ,\beta )X[0,T]\to with{\int }_{(\alpha ,\beta )X[0,T]}{u}^2(x,s)dsd\theta <+\infty .$$

Now, we consider the fractional-order Kortweg–de Vries in the above assumptions and let us denote

$$L\left(u\right)=\frac{{\partial }^{\gamma }u}{\partial t^{\gamma }}.$$

Then, the fractional dispersive PDE becomes in an operator form

$$L\left(u\right)=-\phi \frac{\partial \nu (x,t)}{\partial x}-w\frac{{\partial }^3\nu (x,t)}{\partial x^3}.$$

The LADM is convergence, if the following two hypotheses are satisfied:

$$\left(H1\right)(L\left(u\right)-L\left(v\right),u-v)\ge k\Vert u-v{\Vert }^2;k>0,\forall u,vϵH.$$

$H\left(2\right)$ may be $M>0$, and there exists a constant $C\left(M\right)>0$ such that, for $u,vϵH$ with $\Vert u\Vert \le M$, $\Vert v\Vert \le M$, we have $\left(L\right(u)-L(v),u-v)\le C\left(M\right)\Vert u-v\Vert \Vert w\Vert$ for every $wϵH$.

3. Idea of Fractional Laplace–Adomian Decomposition Method

In this section, the Laplace–Adomian Decomposition Method is discussed for the solution of FPDEs:

$$D^{\gamma }u(x_1,t_1)+Lu(x_1,t_1)+Nu(x_1,t_1)=q(x_1,t_1),x_1,t_1\ge 0,m-1<\gamma <m,$$

(1)

where $D^{\gamma }=\frac{{\partial }^{\gamma }}{\partial t_1^{\gamma }}$ the Caputo Operator $\gamma ,m\in \mathbb{N}$, where L and N are linear and nonlinear functions, q is the source function.

The initial condition is

$$u(x_1,0)=k\left(x_1\right),0<\gamma \le 1,t_1>0.$$

(2)

Applying the Laplace transform to Equation (1), we have

$$\mathcal{L}\left[D^{\gamma }u(x_1,t_1)\right]+\mathcal{L}\left[Lu(x_1,t_1)+Nu(x_1,t_1)\right]=\mathcal{L}\left[q(x_1,t_1)\right],$$

(3)

and using the differentiation property of Laplace transform, we get

$$s^{\gamma }\mathcal{L}\left[u(x_1,t_1)\right]-s^{\gamma -1}u(x_1,0)=\mathcal{L}\left[q(x_1,t_1)\right]-\mathcal{L}\left[Lu(x_1,t_1)+Nu(x_1,t_1)\right],$$

$$\mathcal{L}\left[u(x_1,t_1)\right]=\frac{k\left(x_1\right)}{s}+\frac{1}{s^{\gamma }}\mathcal{L}\left[q(x_1,t_1)\right]-\frac{1}{s^{\gamma }}\mathcal{L}\left[Lu(x_1,t_1)+Nu(x_1,t_1)\right].$$

(4)

The LADM solution $u(x_1,t_1)$ is represented by the following infinite series

$$u(x_1,t_1)=\sum _{j=0}^{\infty }{u}_j(x_1,t_1),$$

(5)

and the nonlinear terms (if any) in the problem are defined by the infinite series of Adomian polynomials,

$$Nu(x_1,t_1)=\sum _{j=0}^{\infty }{A}_j,$$

(6)

$$A_j=\frac{1}{j!}{\left[\frac{d^j}{d{\lambda }^j}\left[N\sum _{j=0}^{\infty }\left({\lambda }^j{u}_j\right)\right]\right]}_{\lambda =0},j=0,1,2...$$

(7)

Substituting Equations (5) and (6) into Equation (4), we get

$$\mathcal{L}\left[\sum _{j=0}^{\infty }u(x_1,t_1)\right]=\frac{k\left(x_1\right)}{s}+\frac{1}{s^{\gamma }}\mathcal{L}\left[q(x_1,t_1)\right]-\frac{1}{s^{\gamma }}\mathcal{L}\left[M\sum _{j=0}^{\infty }{u}_j(x_1,t_1)+\sum _{j=0}^{\infty }{A}_j\right].$$

(8)

Applying the linearity of the Laplace transform,

$$\mathcal{L}\left[u_0(x_1,t_1)\right]=\frac{u(x_1,0)}{s}+\frac{1}{s^{\gamma }}\mathcal{L}\left[q(x_1,t_1)\right]=k(x_1,s),$$

$$\mathcal{L}\left[u_1(x_1,t_1)\right]=-\frac{1}{s^{\gamma }}\mathcal{L}\left[L{u}_0(x_1,t_1)+A_0\right].$$

Generally, we can write

$$\mathcal{L}\left[u_{j+1}(x_1,t_1)\right]=-\frac{1}{s^{\gamma }}\mathcal{L}\left[L{u}_j(x_1,t_1)+A_j\right],j\ge 1.$$

(9)

Applying the inverse Laplace transform, in Equation (9)

$$u_0(x_1,t_1)=k(x_1,t_1)$$

$$u_{j+1}(x_1,t_1)=-{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[L{u}_j(x_1,t_1)+A_j\right]\right].$$

(10)

4. Results

Example 1.

Consider the nonlinear KdV system of time-fractional order

$$\begin{array}{c}\frac{{\partial }^{\gamma }u}{\partial t_1^{\gamma }}=-a\frac{{\partial }^{3}u}{\partial x_1^3}-6au\frac{\partial u}{\partial x_1}+6v\frac{\partial v}{\partial x_1},\hfill \\ \frac{{\partial }^{\gamma }v}{\partial t_1^{\gamma }}=-a\frac{{\partial }^{3}v}{\partial x_1^3}-3au\frac{\partial v}{\partial x_1},0<\gamma <1,\hfill \end{array}$$

(11)

with initial condition

$$u(x_1,0)={\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}),v(x_1,0)=\sqrt{\frac{a}{2}}{\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}).$$

(12)

For $\gamma =1$, the exact solutions of the KdV system Equation (11) are given by

$$\begin{array}{c}u(x_1,t_1)={\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}-\frac{a{\eta }^3{t}_1}{2}),\hfill \\ v(x_1,t_1)=\sqrt{\frac{a}{2}}{\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}-\frac{a{\eta }^3{t}_1}{2}),\hfill \end{array}$$

(13)

where the constant a is a wave velocity and η,α are arbitrary constants.

Taking Laplace transform of Equation (11),

$$\mathcal{L}\left[\frac{{\partial }^{\gamma }u}{\partial t_1^{\gamma }}\right]=\mathcal{L}\left[-a\frac{{\partial }^{3}u}{\partial x_1^3}-6au\frac{\partial u}{\partial x_1}+6v\frac{\partial v}{\partial x_1}\right],$$

$$\mathcal{L}\left[\frac{{\partial }^{\gamma }v}{\partial t_1^{\gamma }}\right]=\mathcal{L}\left[-a\frac{{\partial }^{3}v}{\partial x_1^3}-3au\frac{\partial v}{\partial x_1}\right],$$

$$s^{\gamma }\mathcal{L}\left[u(x_1,t_1)\right]-s^{\gamma -1}\left[u(x_1,0)\right]=\mathcal{L}\left[-a\frac{{\partial }^{3}u}{\partial x_1^3}-6au\frac{\partial u}{\partial x_1}+6v\frac{\partial v}{\partial x_1}\right],$$

$$s^{\gamma }\mathcal{L}\left[v(x_1,t_1)\right]-s^{\gamma -1}\left[v(x_1,0)\right]=\mathcal{L}\left[-a\frac{{\partial }^{3}v}{\partial x_1^3}-3au\frac{\partial v}{\partial x_1}\right].$$

Applying inverse Laplace transform

$$\begin{array}{c}u(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{u(x_1,0)}{s}+\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^{3}u}{\partial x_1^3}-6au\frac{\partial u}{\partial x_1}+6v\frac{\partial v}{\partial x_1}\right]\right],\hfill \\ v(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{v(x_1,0)}{s}+\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^{3}v}{\partial x_1^3}-3au\frac{\partial v}{\partial x_1}\right]\right],\hfill \end{array}$$

$$\begin{array}{c}u(x_1,t_1)={\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^{3}u}{\partial x_1^3}-6au\frac{\partial u}{\partial x_1}+6v\frac{\partial v}{\partial x_1}\right]\right],\hfill \\ v(x_1,t_1)=\sqrt{\frac{a}{2}}{\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^{3}v}{\partial x_1^3}-3au\frac{\partial v}{\partial x_1}\right]\right].\hfill \end{array}$$

Using the ADM procedure, we get

$$\begin{array}{c}\sum _{j=0}^{\infty }{u}_j(x_1,t_1)={\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})\hfill \\ +{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\sum _{j=0}^{\infty }\frac{{\partial }^3{u}_j}{\partial x_1^3}-6a\sum _{j=0}^{\infty }{A}_j(u,u_{x_1})+6\sum _{j=0}^{\infty }{B}_j(v,v_{x_1})\right]\right],\hfill \end{array}$$

$$\sum _{j=0}^{\infty }{v}_j(x_1,t_1)=\sqrt{\frac{a}{2}}{\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\sum _{j=0}^{\infty }\frac{{\partial }^3{v}_j}{\partial x_1^3}-3a\sum _{j=0}^{\infty }{C}_j(u,v_{x_1})\right]\right],$$

where $A_j(u,u_{x_1})$, $B_j(v,v_{x_1})$ and $C_j(u,v_{x_1})$ are Adomian polynomials, represent nonlinear terms in above equations. The components of the above Adomian polynomials are given below:

$$\begin{array}{c}{A}_0(u,u_{x_1})=u_0\frac{\partial u_0}{\partial x_1},\hfill \\ A_1(u,u_{x_1})=u_0\frac{\partial u_1}{\partial x_1}+u_1\frac{\partial u_0}{\partial x_1},\hfill \\ A_2(u,u_{x_1})=u_0\frac{\partial u_2}{\partial x_1}+u_1\frac{\partial u_1}{\partial x_1}+u_2\frac{\partial u_0}{\partial x_1}.\hfill \end{array}$$

$$\begin{array}{c}{B}_0(v,v_{x_1})=v_0\frac{\partial v_0}{\partial x_1},\hfill \\ B_1(v,v_{x_1})=v_0\frac{\partial v_1}{\partial x_1}+v_1\frac{\partial v_0}{\partial x_1},\hfill \\ B_2(v,v_{x_1})=v_0\frac{\partial v_2}{\partial x_1}+v_1\frac{\partial v_1}{\partial x_1}+v_2\frac{\partial v_0}{\partial x_1}.\hfill \end{array}$$

$$\begin{array}{c}{C}_0(u,v_{x_1})=u_0\frac{\partial v_0}{\partial x_1},\hfill \\ C_1(u,v_{x_1})=u_0\frac{\partial v_1}{\partial x_1}+u_1\frac{\partial v_0}{\partial x_1},\hfill \\ C_2(u,v_{x_1})=u_0\frac{\partial v_2}{\partial x_1}+u_1\frac{\partial v_1}{\partial x_1}+u_2\frac{\partial v_0}{\partial x_1}.\hfill \end{array}$$

$$\begin{array}{c}{u}_0(x_1,t_1)={\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}),\hfill \\ v_0(x_1,t_1)=\sqrt{\frac{a}{2}}{\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}),\hfill \end{array}$$

(14)

$$u_{j+1}(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\sum _{j=0}^{\infty }\frac{{\partial }^3{u}_j}{\partial x_1^3}-6a\sum _{j=0}^{\infty }{A}_j(u,u_{x_1})+6\sum _{j=0}^{\infty }{B}_j(v,v_{x_1})\right]\right],$$

$$v_{j+1}(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\sum _{j=0}^{\infty }\frac{{\partial }^3{v}_j}{\partial x_1^3}-3a\sum _{j=0}^{\infty }{C}_j(u,v_{x_1})\right]\right],$$

for $j=0,1,2,..$

$$\begin{array}{c}{u}_1(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^3{u}_0}{\partial x_1^3}-6a{u}_0\frac{\partial u_0}{\partial x_1}+6v_0\frac{\partial v_0}{\partial x_1}\right]\right],\hfill \\ u_1(x_1,t_1)={\eta }^{5}atanh(\frac{\alpha }{2}+\frac{\eta x_1}{2})sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}){\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma +1}}\right]\hfill \\ ={\eta }^{5}atanh(\frac{\alpha }{2}+\frac{\eta x_1}{2})sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})\frac{t_1^{\gamma }}{\mathsf{\Gamma }(\gamma +1)},\hfill \\ v_1(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^3{v}_0}{\partial x_1^3}-3a{u}_0\frac{\partial v_0}{\partial x_1}\right]\right],\hfill \\ v_1(x_1,t_1)=\frac{{\eta }^5{a}^{\frac{3}{2}}}{\sqrt{2}}tanh(\frac{\alpha }{2}+\frac{\eta x_1}{2})sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}){\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma +1}}\right]\hfill \\ =\frac{{\eta }^5{a}^{\frac{3}{2}}}{\sqrt{2}}tanh(\frac{\alpha }{2}+\frac{\eta x_1}{2})sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})\frac{t_1^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}.\hfill \end{array}$$

(15)

The subsequent terms are

$$\begin{array}{c}{u}_2(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^3{u}_1}{\partial x_1^3}-6a{u}_0\frac{\partial u_1}{\partial x_1}-6a{u}_1\frac{\partial u_0}{\partial x_1}+6v_0\frac{\partial v_1}{\partial x_1}+6v_1\frac{\partial v_0}{\partial x_1}\right]\right],\hfill \\ =\frac{{\eta }^8{a}^2}{2}[2cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})-3]sec{h}^4(\frac{\alpha }{2}+\frac{\eta x_1}{2})\frac{t_1^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)},\hfill \\ v_2(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^3{v}_1}{\partial x_1^3}-3a{u}_0\frac{\partial v_1}{\partial x_1}-3a{u}_1\frac{\partial v_0}{\partial x_1}\right]\right],\hfill \\ =\frac{{\eta }^5{a}^{\frac{5}{2}}\sqrt{2}}{4}[2cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})-3]sec{h}^4(\frac{\alpha }{2}+\frac{\eta x_1}{2})\frac{t_1^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}.\hfill \\ u_3(x_1,t_1)={\mathcal{L}}^{-1}[\frac{1}{s^{\gamma }}\mathcal{L}[-a\frac{{\partial }^3{u}_2}{\partial x_1^3}-6a{u}_0\frac{\partial u_2}{\partial x_1}-6a{u}_1\frac{\partial u_1}{\partial x_1}-6a{u}_2\frac{\partial u_0}{\partial x_1}\hfill \\ +6v_0\frac{\partial v_2}{\partial x_1}+6v_1\frac{\partial v_1}{\partial x_1}+6v_2\frac{\partial v_0}{\partial x_1}\left]\right],\hfill \\ =\frac{sinh(\frac{\alpha }{2}+\frac{\eta x_1}{2})t_1^{3\gamma }{a}^3{\eta }^4}{2\mathsf{\Gamma }(3\gamma +1)\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^7(\frac{\alpha }{2}+\frac{\eta x_1}{2})}{[2\mathsf{\Gamma }(\gamma +1)}^{2}cos{h}^4(\frac{\alpha }{2}+\frac{\eta x_1}{2})\hfill \\ -18\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+6\mathsf{\Gamma }(2\gamma +1)cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+18\mathsf{\Gamma }{(\gamma +1)}^2-9\mathsf{\Gamma }(2\gamma +1)]\hfill \\ v_3(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-a\frac{{\partial }^3{v}_2}{\partial x_1^3}-3a{u}_0\frac{\partial v_2}{\partial x_1}-3a{u}_1\frac{\partial v_1}{\partial x_1}-3a{u}_2\frac{\partial v_0}{\partial x_1}\right]\right],\hfill \\ =\frac{\sqrt{2}sinh(\frac{\alpha }{2}+\frac{\eta x_1}{2})t_1^{3\gamma }{a}^{\frac{7}{2}}{\eta }^{11}}{4\mathsf{\Gamma }(3\gamma +1)\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^7(\frac{\alpha }{2}+\frac{\eta x_1}{2})}{[2\mathsf{\Gamma }(\gamma +1)}^{2}cos{h}^4(\frac{\alpha }{2}+\frac{\eta x_1}{2})\hfill \\ -18\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+6\mathsf{\Gamma }(2\gamma +1)cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+18\mathsf{\Gamma }{(\gamma +1)}^2-9\mathsf{\Gamma }(2\gamma +1)].\hfill \end{array}$$

(16)

The LADM solution for Example 1 is

$$u(x_1,t_1)=u_0(x_1,t_1)+u_1(x_1,t_1)+u_2(x_1,t_1)+u_3(x_1,t_1)+...,$$

$$v(x_1,t_1)=v_0(x_1,t_1)+v_1(x_1,t_1)+v_2(x_1,t_1)+v_3(x_1,t_1)+...,$$

$$\begin{array}{c}u(x_1,t_1)={\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+{\eta }^{5}atanh(\frac{\alpha }{2}+\frac{\eta x_1}{2})sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})\frac{t_1^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}\hfill \\ +\frac{{\eta }^8{a}^2}{2}[2cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})-3]sec{h}^4(\frac{\alpha }{2}+\frac{\eta x_1}{2})\frac{t_1^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}\hfill \\ +\frac{sinh(\frac{\alpha }{2}+\frac{\eta x_1}{2})t_1^{3\gamma }{a}^3{\eta }^4}{2\mathsf{\Gamma }(3\gamma +1)\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^7(\frac{\alpha }{2}+\frac{\eta x_1}{2})}{[2\mathsf{\Gamma }(\gamma +1)}^{2}cos{h}^4(\frac{\alpha }{2}+\frac{\eta x_1}{2})\hfill \\ -18\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+6\mathsf{\Gamma }(2\gamma +1)cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})\hfill \\ +18\mathsf{\Gamma }{(\gamma +1)}^2-9\mathsf{\Gamma }(2\gamma +1)]+...,\hfill \end{array}$$

$$\begin{array}{c}v(x_1,t_1)=\sqrt{\frac{a}{2}}{\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+\frac{{\eta }^5{a}^{\frac{3}{2}}}{\sqrt{2}}tanh(\frac{\alpha }{2}+\frac{\eta x_1}{2})sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})\frac{t_1^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}\hfill \\ +\frac{{\eta }^8{a}^2}{2}[2cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})-3]sec{h}^4(\frac{\alpha }{2}+\frac{\eta x_1}{2})\frac{t_1^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}\hfill \\ +\frac{\sqrt{2}sinh(\frac{\alpha }{2}+\frac{\eta x_1}{2})t_1^{3\gamma }{a}^{\frac{7}{2}}{\eta }^{11}}{4\mathsf{\Gamma }(3\gamma +1)\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^7(\frac{\alpha }{2}+\frac{\eta x_1}{2})}{[2\mathsf{\Gamma }(\gamma +1)}^{2}cos{h}^4(\frac{\alpha }{2}+\frac{\eta x_1}{2})\hfill \\ -18\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})+6\mathsf{\Gamma }(2\gamma +1)cos{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2})\hfill \\ +18\mathsf{\Gamma }{(\gamma +1)}^2-9\mathsf{\Gamma }(2\gamma +1)]+...,\hfill \end{array}$$

For $\gamma =1$, the exact solutions of the KdV system Equation (11) are given by

$$\begin{array}{c}u(x_1,t_1)={\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}-\frac{a{\eta }^3{t}_1}{2}),\hfill \\ v(x_1,t_1)=\sqrt{\frac{a}{2}}{\eta }^{2}sec{h}^2(\frac{\alpha }{2}+\frac{\eta x_1}{2}-\frac{a{\eta }^3{t}_1}{2}).\hfill \end{array}$$

(17)

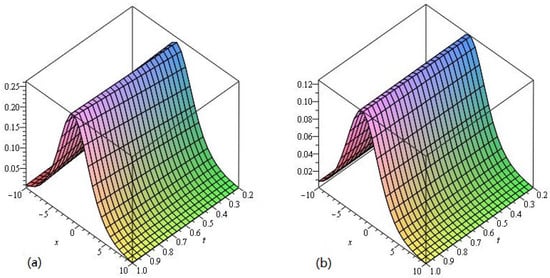
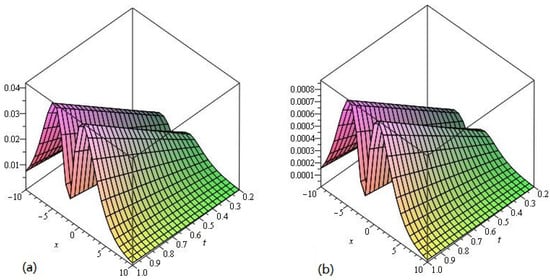
The numerical values of Example 1 show the accuracy and efficiency of the LADM at different values of $x_1,t_1$ in

Table 1. Solution of LADM for different values of $\gamma$ when $\eta =0.001$ and Absolute Error (AE) of Example 1.

LADM		$\mathit{\gamma }=0.55$		$\mathit{\gamma }=1$		Ex($\mathit{\gamma }=1$)		AE
${\mathit{x}}_{\mathbf{1}}$	${\mathit{t}}_{\mathbf{1}}$	${\mathit{u}}_{\mathit{LADM}}$	${\mathit{v}}_{\mathit{LADM}}$	${\mathit{u}}_{\mathit{LADM}}$	${\mathit{v}}_{\mathit{LADM}}$	${\mathit{u}}_{\mathit{EX}}$	${\mathit{v}}_{\mathit{EX}}$	${\mathit{u}}_{\mathit{EX}}-{\mathit{u}}_{\mathit{app}}$	${\mathit{v}}_{\mathit{EX}}-{\mathit{v}}_{\mathit{app}}$
−10	0.1	0.017635	0.002788	0.017654	0.002791	0.017661	0.002791	7.449 $\times {10}^{-6}$	4.928 $\times {10}^{-7}$
	0.3	0.017613	0.002785	0.017637	0.002789	0.017659	0.002787	2.238 $\times {10}^{-5}$	1.478 $\times {10}^{-6}$
	0.5	0.017597	0.002783	0.017620	0.002786	0.017657	0.002784	3.727 $\times {10}^{-5}$	2.464 $\times {10}^{-6}$
0	0.1	0.196755	0.031107	0.196657	0.031093	0.196617	0.031096	3.975 $\times {10}^{-5}$	2.629 $\times {10}^{-6}$
	0.3	0.196875	0.031123	0.196748	0.031106	0.196628	0.031114	1.192 $\times {10}^{-4}$	7.889 $\times {10}^{-6}$
	0.5	0.196961	0.031135	0.196839	0.031118	0.196640	0.031131	1.987 $\times {10}^{-4}$	1.314 $\times {10}^{-5}$
10	0.1	0.002470	0.000390	0.002467	0.000390	0.002466	0.000390	1.073 $\times {10}^{-6}$	7.100 $\times {10}^{-8}$
	0.3	0.002473	0.000390	0.002470	0.000390	0.002466	0.000390	3.221 $\times {10}^{-6}$	2.131 $\times {10}^{-7}$
	0.5	0.002475	0.000391	0.002472	0.000390	0.002467	0.000391	5.368 $\times {10}^{-6}$	3.552 $\times {10}^{-7}$

. In Figure 1 and Figure 2 and Table 1, we consider fixed values $a=\eta =0.5$, $\alpha =1$ and fixed order $\gamma =1$ for piecewise approximation values of $x_1,t_1$ in the domain $-10\le x_1\le 10$ and $0.20\le t_1\le 1$. Figure 1a,b represent the graphs of LADM solution at $\gamma =1$, and error graphs a and b at $\gamma =1$ in Figure 2 respectively of Example 1. It is clear from the Figure 1a,b that LADM solutions are in good agreement with the exact solution of the problems. There is a small difference from the solutions graph of the problem because the solution of the fractional-order problems creates a little deviation from the solution at the integer order problem. The a and b in Figure 2 show the variation of the error for different values of the variables $x_1$ and $t_1$.

Example 2.

Consider the nonlinear dispersive long wave system of time fractional order

$$\begin{array}{c}\frac{{\partial }^{\gamma }u}{\partial t_1^{\gamma }}=-\frac{\partial v}{\partial x_1}-\frac{1}{2}\frac{\partial u^2}{\partial x_1},\hfill \\ \frac{{\partial }^{\gamma }v}{\partial t_1^{\gamma }}=-\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}-\frac{\partial uv}{\partial x_1},0<\gamma <1,\hfill \end{array}$$

(18)

with initial condition

$$u(x_1,0)=a[tanh(\frac{\eta }{2}+\frac{a{x}_1}{2})+1],v(x_1,0)=-1+\frac{1}{2}{a}^{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2}).$$

(19)

Taking Laplace transform of Equation (17),

$$\mathcal{L}\left[\frac{{\partial }^{\gamma }u}{\partial t_1^{\gamma }}\right]=\mathcal{L}\left[-\frac{\partial v}{\partial x_1}-\frac{1}{2}\frac{\partial u^2}{\partial x_1}\right],$$

$$\mathcal{L}\left[\frac{{\partial }^{\gamma }v}{\partial t_1^{\gamma }}\right]=\mathcal{L}\left[-\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}-\frac{\partial uv}{\partial x_1}\right],$$

$$\begin{array}{c}{s}^{\gamma }\mathcal{L}\left[u(x_1,t_1)\right]-s^{\gamma -1}\left[u(x_1,0)\right]=\mathcal{L}\left[-\frac{\partial v}{\partial x_1}-\frac{1}{2}\frac{\partial u^2}{\partial x_1}\right],\hfill \\ s^{\gamma }\mathcal{L}\left[v(x_1,t_1)\right]-s^{\gamma -1}\left[v(x_1,0)\right]=\mathcal{L}\left[-\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}-\frac{\partial uv}{\partial x_1}\right].\hfill \end{array}$$

Applying inverse Laplace transform

$$\begin{array}{c}u(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{u(x_1,0)}{s}+\frac{1}{s^{\gamma }}\mathcal{L}\left[-\frac{\partial v}{\partial x_1}-\frac{1}{2}\frac{\partial u^2}{\partial x_1}\right]\right],\hfill \\ v(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{v(x_1,0)}{s}+\frac{1}{s^{\gamma }}\mathcal{L}\left[-\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}-\frac{\partial uv}{\partial x_1}\right]\right],\hfill \end{array}$$

$$\begin{array}{c}u(x_1,t_1)=a[tanh(\frac{\eta }{2}+\frac{a{x}_1}{2})+1]+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\frac{\partial v}{\partial x_1}-\frac{1}{2}\frac{\partial u^2}{\partial x_1}\right]\right],\hfill \\ v(x_1,t_1)=-1+\frac{1}{2}{a}^{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}-\frac{\partial uv}{\partial x_1}\right]\right].\hfill \end{array}$$

Using the ADM procedure, we get

$$\begin{array}{c}\sum _{j=0}^{\infty }{u}_j(x_1,t_1)=a[tanh(\frac{\eta }{2}+\frac{a{x}_1}{2})+1]\hfill \\ +{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\sum _{j=0}^{\infty }\frac{\partial v_j}{\partial x_1}-\frac{1}{2}\sum _{j=0}^{\infty }\frac{\partial u_j^2}{\partial x_1}\right]\right],\hfill \end{array}$$

$$\begin{array}{c}\sum _{j=0}^{\infty }{v}_j(x_1,t_1)=-1+\frac{1}{2}{a}^{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})\hfill \\ +{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\sum _{j=0}^{\infty }\frac{\partial u_j}{\partial x_1}-\sum _{j=0}^{\infty }\frac{{\partial }^3{u}_j}{\partial x_1^3}-\sum _{j=0}^{\infty }{A}_j{(u,v)}_{x_1}\right]\right],\hfill \end{array}$$

where $A_j{(u,v)}_{x_1}$ is Adomian polynomials, representing nonlinear terms in the above equations. The components of the above Adomian polynomials are given below

$$\begin{array}{c}{u}_0(x_1,t_1)=a[tanh(\frac{\eta }{2}+\frac{a{x}_1}{2})+1],\hfill \\ v_0(x_1,t_1)=-1+\frac{1}{2}{a}^{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2}),\hfill \end{array}$$

(20)

$$u_{j+1}(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\sum _{j=0}^{\infty }\frac{\partial v_j}{\partial x_1}-\frac{1}{2}\sum _{j=0}^{\infty }\frac{\partial u_j^2}{\partial x_1}\right]\right],$$

$$v_{j+1}(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\sum _{j=0}^{\infty }\frac{\partial u_j}{\partial x_1}-\sum _{j=0}^{\infty }\frac{{\partial }^3{u}_j}{\partial x_1^3}-\sum _{j=0}^{\infty }{A}_j{(u,v)}_{x_1}\right]\right],$$

for $j=0,1,2,..$

$$\begin{array}{c}{u}_1(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\frac{\partial v_0}{\partial x_1}-\frac{1}{2}\frac{\partial {u_0}^2}{\partial x_1}\right]\right],\hfill \\ u_1(x_1,t_1)=-\frac{a^3}{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2}){\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma +1}}\right]\hfill \\ =-\frac{a^2}{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t^{\gamma }}{\mathsf{\Gamma }(\gamma +1)},\hfill \\ v_1(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\frac{\partial u_0}{\partial x_1}-\frac{{\partial }^3{u}_0}{\partial {x_1}^3}-\frac{\partial \left(u_0{v}_0\right)}{\partial x_1}\right]\right],\hfill \\ v_1(x_1,t_1)=\frac{a^4}{2}sinh(\frac{\eta }{2}+\frac{a{x}_1}{2})sec{h}^3(\frac{\eta }{2}+\frac{a{x}_1}{2}){\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma +1}}\right]\hfill \\ =\frac{a^3}{2}sinh(\frac{\eta }{2}+\frac{a{x}_1}{2})sec{h}^3(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t_1^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}.\hfill \end{array}$$

(21)

The subsequent terms are

$$\begin{array}{c}{u}_2(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\frac{\partial v_1}{\partial x_1}-\frac{1}{2}\frac{\partial {u_1}^2}{\partial x_1}\right]\right],\hfill \\ =-\frac{a^5}{4}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}+\frac{3a^5}{4}sin{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})sec{h}^4(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}\hfill \\ +\frac{a^7}{4}sinh(\frac{\eta }{2}+\frac{a{x}_1}{2})sec{h}^5(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{\mathsf{\Gamma }(2\gamma +1)t^{3\gamma }}{\mathsf{\Gamma }(3\gamma +1)\mathsf{\Gamma }{(\gamma +1)}^2}\hfill \\ v_2(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[-\frac{\partial u_1}{\partial x_1}-\frac{{\partial }^3{u}_1}{\partial {x_1}^3}-\frac{\partial \left(u_0{v}_1\right)}{\partial x_1}-\frac{\partial \left(u_1{v}_0\right)}{\partial x_1}\right]\right],\hfill \\ =\frac{a^6}{4}[2cos{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})-3]sec{h}^4(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t_1^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}.\hfill \end{array}$$

(22)

The LADM solution for Example 2 is

$$u(x_1,t_1)=u_0(x_1,t_1)+u_1(x_1,t_1)+u_2(x_1,t_1)+u_3(x_1,t_1)+...,$$

$$v(x_1,t_1)=v_0(x_1,t_1)+v_1(x_1,t_1)+v_2(x_1,t_1)+v_3(x_1,t_1)+...,$$

$$\begin{array}{c}u(x_1,t_1)=a[tanh(\frac{\eta }{2}+\frac{a{x}_1}{2})+1]-\frac{a^3}{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}\hfill \\ -\frac{a^5}{4}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}+\frac{3a^5}{4}sin{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})sec{h}^4(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}\hfill \\ +\frac{a^7}{4}sinh(\frac{\eta }{2}+\frac{a{x}_1}{2})sec{h}^5(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{\mathsf{\Gamma }(2\gamma +1)t^{3\gamma }}{\mathsf{\Gamma }(3\gamma +1)\mathsf{\Gamma }{(\gamma +1)}^2}+...,\hfill \end{array}$$

$$\begin{array}{c}v(x_1,t_1)=-1+\frac{1}{2}{a}^{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})+\frac{a^4}{2}sinh(\frac{\eta }{2}+\frac{a{x}_1}{2})sec{h}^3(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t_1^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}\hfill \\ \frac{a^6}{4}[2cos{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2})-3]sec{h}^4(\frac{\eta }{2}+\frac{a{x}_1}{2})\frac{t_1^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}+...,\hfill \end{array}$$

For $\gamma =1$, the exact solutions of the KdV system Equation (17) are given by

$$\begin{array}{c}u(x_1,t_1)=a[tanh(\frac{\eta }{2}+\frac{a{x}_1}{2}-\frac{a^2{t}_1}{2})+1],\hfill \\ v(x_1,t_1)=-1+\frac{1}{2}{a}^{2}sec{h}^2(\frac{\eta }{2}+\frac{a{x}_1}{2}-\frac{a^2{t}_1}{2}),\hfill \end{array}$$

(23)

where a,η are arbitrary constants.

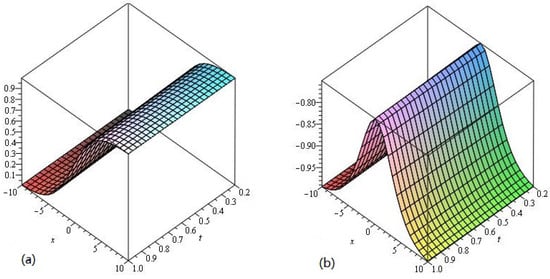
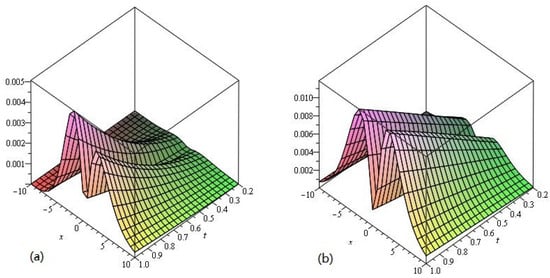
Similarly, the numerical values of the Example 2 show the accuracy and efficiency of the LADM at different values of $x_1,t_1$ in

Table 2. Solution of LADM for different value of $\gamma$ when $\eta =0.001$ and Absolute Error of Example 2.

LADM		$\mathit{\gamma }=0.55$		$\mathit{\gamma }=1$		Ex($\mathit{\gamma }=1$)		AE
${\mathit{x}}_{\mathbf{1}}$	${\mathit{t}}_{\mathbf{1}}$	${\mathit{u}}_{\mathit{LADM}}$	${\mathit{v}}_{\mathit{LADM}}$	${\mathit{u}}_{\mathit{LADM}}$	${\mathit{v}}_{\mathit{LADM}}$	${\mathit{u}}_{\mathit{EX}}$	${\mathit{v}}_{\mathit{EX}}$	${\mathit{u}}_{\mathit{EX}}-{\mathit{u}}_{\mathit{app}}$	${\mathit{v}}_{\mathit{EX}}-{\mathit{v}}_{\mathit{app}}$
−10	0.1	0.010173	−0.98953	0.010718	−0.98926	0.010718	−0.98939	1.210 $\times {10}^{-7}$	1.312 $\times {10}^{-4}$
	0.3	0.009571	−0.98982	0.010200	−0.98951	0.010201	−0.98990	6.351 $\times {10}^{-7}$	3.848 $\times {10}^{-4}$
	0.5	0.009181	−0.99001	0.009707	−0.98975	0.009708	−0.99038	5.301 $\times {10}^{-7}$	6.274 $\times {10}^{-4}$
0	0.1	0.603381	−0.76294	0.616554	−0.76429	0.616566	−0.76358	1.230 $\times {10}^{-5}$	7.041 $\times {10}^{-4}$
	0.3	0.586890	−0.76158	0.604564	−0.76297	0.604679	−0.76095	1.141 $\times {10}^{-4}$	2.015 $\times {10}^{-3}$
	0.5	0.574744	−0.76081	0.592339	−0.76177	0.592666	−0.75858	3.267 $\times {10}^{-4}$	3.188 $\times {10}^{-3}$
10	0.1	0.995627	−0.99577	0.995829	−0.99589	0.995827	−0.99584	2.502 $\times {10}^{-6}$	5.088 $\times {10}^{-5}$
	0.3	0.995404	−0.99562	0.995636	−0.99579	0.995614	−0.99563	2.271 $\times {10}^{-5}$	1.566 $\times {10}^{-4}$
	0.5	0.995261	−0.99550	0.995454	−0.99567	0.995390	−0.99541	6.364 $\times {10}^{-5}$	2.680 $\times {10}^{-4}$

. In Figure 3 and Figure 4 and Table 2, we consider fixed values $a=\eta =0.5$, $\alpha =1$ and fixed order $\gamma =1$ for piecewise approximation values of $x_1,t_1$ in the domain $-10\le x_1\le 10$ and $0.20\le t_1\le 1$. The a and b in Figure 3 represent the graphs of LADM solution at $\gamma =1$, and error graphs a and b at $\gamma =1$ in Figure 4, respectively, of Example 2. It is clear from the Figure 3a,b that LADM solutions are in good agreement with the exact solution of the problems. The small difference from the solutions graph of the problem because the solution of the fractional-order problems creates a little deviation from the solution at integer order problems. The a and b in Figure 4 show the variation of the error for different values of the variables $x_1$ and $t_1$.

Example 3.

Consider the nonlinear KdV of time-fractional order as given in [26]:

$$\begin{array}{c}\frac{{\partial }^{\gamma }u}{\partial t_1^{\gamma }}=6u\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3},0<\gamma <1,\hfill \end{array}$$

(24)

with initial condition

$$u(x_1,0)=-2sec{h}^2\left(x_1\right).$$

(25)

Taking Laplace transform of Equation (24),

$$\mathcal{L}\left[\frac{{\partial }^{\gamma }u}{\partial t_1^{\gamma }}\right]=\mathcal{L}\left[6u\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}\right],$$

$$s^{\gamma }\mathcal{L}\left[u(x_1,t_1)\right]-s^{\gamma -1}\left[u(x_1,0)\right]=\mathcal{L}\left[6u\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}\right],$$

Applying inverse Laplace transform

$$\begin{array}{c}u(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{u(x_1,0)}{s}+\frac{1}{s^{\gamma }}\mathcal{L}\left[6u\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}\right]\right],\hfill \end{array}$$

$$\begin{array}{c}u(x_1,t_1)=-2sec{h}^2\left(x_1\right)+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[6u\frac{\partial u}{\partial x_1}-\frac{{\partial }^{3}u}{\partial x_1^3}\right]\right].\hfill \end{array}$$

Using ADM procedure, we get

$$\begin{array}{c}\sum _{j=0}^{\infty }{u}_j(x_1,t_1)=-2sec{h}^2\left(x_1\right)+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[6\sum _{j=0}^{\infty }{D}_j(u,u_{x_1})-\sum _{j=0}^{\infty }\frac{{\partial }^3{u}_j}{\partial x_1^3}\right]\right],\hfill \end{array}$$

where $D_j(u,u_{x_1})$ are Adomian polynomials, representing nonlinear terms in the above equations. The components of above Adomian polynomials are given below:

$$\begin{array}{c}{D}_0(u,u_{x_1})=u_0\frac{\partial u_0}{\partial x_1},\hfill \\ D_1(u,u_{x_1})=u_0\frac{\partial u_1}{\partial x_1}+u_1\frac{\partial u_0}{\partial x_1},\hfill \\ D_2(u,u_{x_1})=u_0\frac{\partial u_2}{\partial x_1}+u_1\frac{\partial u_1}{\partial x_1}+u_2\frac{\partial u_0}{\partial x_1},\hfill \end{array}$$

$$\begin{array}{c}{u}_0(x_1,t_1)=-2sec{h}^2\left(x_1\right),\hfill \end{array}$$

(26)

$$\begin{array}{c}\sum _{j=0}^{\infty }{u}_j(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[6\sum _{j=0}^{\infty }{D}_j(u,u_{x_1})-\sum _{j=0}^{\infty }\frac{{\partial }^3{u}_j}{\partial x_1^3}\right]\right],\hfill \end{array}$$

for $j=0,1,2,..$

$$\begin{array}{c}{u}_1(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[6u_0\frac{\partial u_0}{\partial x_1}-\frac{{\partial }^3{u}_0}{\partial x_1^3}\right]\right],\hfill \\ u_1(x_1,t_1)=-16sec{h}^2\left(x_1\right)tan{h}^2\left(x_1\right){\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma +1}}\right]\hfill \\ =-16sec{h}^2\left(x_1\right)tan{h}^2\left(x_1\right)\frac{t_1^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}.\hfill \end{array}$$

(27)

The subsequent terms are

$$\begin{array}{c}{u}_2(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[6u_0\frac{\partial u_1}{\partial x_1}+6u_1\frac{\partial u_0}{\partial x_1}-\frac{{\partial }^3{u}_1}{\partial x_1^3}\right]\right],\hfill \\ u_2(x_1,t_1)=-64sec{h}^4\left(x_1\right)(-3+2cos{h}^2\left(x_1\right))\frac{t^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)},\hfill \\ u_3(x_1,t_1)={\mathcal{L}}^{-1}\left[\frac{1}{s^{\gamma }}\mathcal{L}\left[6u_0\frac{\partial u_2}{\partial x_1}+6u_1\frac{\partial u_1}{\partial x_1}+6u_2\frac{\partial u_0}{\partial x_1}-\frac{{\partial }^3{u}_1}{\partial x_1^3}\right]\right],\hfill \\ u_3(x_1,t_1)=-512sec{h}^{6}tanh\left(x_1\right)(-18\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^2+18\mathsf{\Gamma }{(\gamma +1)}^2+2\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^4\hfill \\ +6\mathsf{\Gamma }(2\gamma +1)cos{h}^2-9\mathsf{\Gamma }(2\gamma +1))\frac{t^{3\gamma }}{\mathsf{\Gamma }{(\gamma +1)}^2\mathsf{\Gamma }(3\gamma +1)}.\hfill \end{array}$$

(28)

The LADM solution for Example 3 is

$$u(x_1,t_1)=u_0(x_1,t_1)+u_1(x_1,t_1)+u_2(x_1,t_1)+u_3(x_1,t_1)+...,$$

$$\begin{array}{c}u(x_1,t_1)=-2sec{h}^2\left(x_1\right)-16sec{h}^2\left(x_1\right)tan{h}^2\left(x_1\right)\frac{t_1^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}-64sec{h}^4\left(x_1\right)(-3+2cos{h}^2\left(x_1\right))\hfill \\ \frac{t^{2\gamma }}{\mathsf{\Gamma }(2\gamma +1)}-512sec{h}^{6}tanh\left(x_1\right)(-18\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^2+18\mathsf{\Gamma }{(\gamma +1)}^2+2\mathsf{\Gamma }{(\gamma +1)}^{2}cos{h}^4\hfill \\ +6\mathsf{\Gamma }(2\gamma +1)cos{h}^2-9\mathsf{\Gamma }(2\gamma +1))\frac{t^{3\gamma }}{\mathsf{\Gamma }{(\gamma +1)}^2\mathsf{\Gamma }(3\gamma +1)}.\hfill \end{array}$$

The exact solution of $u(x_1,t_1)$ is in a closed form as

$$u(x_1,t_1)=-2sec{h}^2(x_1-4t_1).$$

(29)

5. Conclusions

In this research article, we applied the Laplace–Adomian Decomposition Method for the solution of the fractional KdV type system of partial differential equations. The fractional derivatives are represented by the Caputo operator. The results of the proposed method are obtained for both fractional and integer order problems successfully. The solutions of fractional order problems are convergent to the integer order problem as fractional order approaches to integer order. Moreover, the behavior of the method is explained through graphs of different numerical examples. The analysis has confirmed that the results obtained by this method are in good contact with the exact solutions for the problems.