Energy Criterion for Attachment and Detachment in Viscoelastic Adhesive Contacts

Abstract

Adhesion plays a crucial role across a wide range of natural systems and technological applications. High adhesion is typically observed in contacts involving highly deformable materials, which are generally viscoelastic in nature. Although some of the key concepts explored in this work—such as the application of energy-based criteria to viscoelastic adhesive contacts—have been addressed in earlier studies, including the seminal work by Greenwood and Johnson, these approaches relied on considerably more complex analytical methods. In this paper, we build on those foundational insights and present a significantly simplified and more accessible formulation by employing the Method of Dimensionality Reduction (MDR). We propose that the processes of adhesive crack propagation and viscoelastic material relaxation occur on well-separated timescales, which allows the use of a Griffith-like energy balance criterion even in viscoelastic systems. This MDR-based energetic approach not only provides conceptual clarity but also enables the straightforward analytical treatment of a wide range of practical problems, including arbitrary loading scenarios. The theory naturally explains the different effective works of adhesion during attachment and detachment and offers a unified, first-principles framework for analyzing and designing soft adhesive systems.

1. Introduction

The classic theory of adhesion of parabolic elastic solids by Johnson, Kendall and Roberts (JKR) [1,2,3] is based on the principle of virtual work, stating that a mechanical system is in equilibrium if any small perturbation does not change the energy of the system. This energetic criterion was first applied to the equilibrium of cracks in brittle elastic bodies by Griffith [4,5]. Johnson, Kendall and Roberts realized that the boundary of an adhesive contact is equivalent to the Griffith crack and applied the same criterion of energy balance to adhesive contacts. When applied to cracks or adhesive contacts, this criterion means that the tip of a crack is in equilibrium if the elastic energy released due to a small increase in the crack is equal to the work of adhesion needed to create new free surfaces. In its pure form, the energy balance criterion is applicable only to elastic bodies. However, the criterion is so simple and attractive that it is used also in considering the propagation of cracks (or, equivalently, adhesive contacts) in dissipative media. One introduces a modified “effective separation energy”, which is needed not only for the creation of new surfaces but also for performing work against dissipative forces (due to viscosity, plasticity, etc.). For example, Barquins and Maugis postulated the existence of an effective work of adhesion depending on the crack propagation velocity [6]. Energetic analysis of viscoelastic adhesive contacts was provided by Greenwood and Johnson in their seminal 1981 work [7]. Their approach, based on fracture mechanics and viscoelastic crack modeling, demonstrated that effective work of adhesion depends on the time-dependent material response and differs between attachment and detachment. The analysis of viscoelastic crack propagation by Greenwood and Johnson [7] was based in large part on the theoretical framework developed earlier by Schapery [8], who provided a general formulation for crack initiation and growth in viscoelastic media.

In 2021, Popov suggested how the energetic criterion can be applied to viscoelastic contacts in a rigorous way, without the introduction of any empirical effective work of adhesion [9], formulated in the framework of the Method of Dimensionality Reduction (MDR). While this formulation significantly simplifies analysis using MDR, it reaches conclusions that are conceptually aligned with those of Greenwood and Johnson. As the MDR maps the true three-dimensional contact problem onto a contact with viscoelastic foundation, it makes the main ideas especially simple and, much more importantly, allows the simple consideration of arbitrary loading scenarios. The proposed energetic criterion was based on the observation that the process of crack opening is mediated by very fast processes involving the short-ranged adhesive potential and the material’s glass modulus, while the dissipative properties of the material affect the contact on a longer timescale. This allows the energy balance to be applied to attachment and detachment with only slight modifications of the classic JKR theory. This approach promises to be a powerful first-principles tool for analyzing viscoelastic adhesive contacts but is not without limitations. First and foremost, it is based on the assumption that adhesive interaction has a purely conservative character (i.e., the viscoelasticity is related exclusively to the volume of the medium but not to the surface forces). In [9], this property is characterized as “non-entropic surface interaction”. Secondly, only the limiting case of adhesive contacts with very short-ranged adhesive forces is considered (smaller than any other characteristic dimension of the contact), which is characterized as “JKR-type adhesion” as opposed to the DMT-type adhesion [10,11] with long-rage adhesive interactions.

In the present paper, we describe the energetic criterion formulated in [9] in more detail and apply it to quasistatic adhesive contacts of viscoelastic bodies. As a working example of viscoelastic material, we consider the “standard viscoelastic body” [12]. Throughout our analysis, we use the Method of Dimensionality Reduction, which is described in [13]. This allows for a much simpler formulation and flexible extension of the theory than in the work of [14], who arrived at similar conclusions using the much more complex methods of classic contact mechanics.

In addition to its theoretical importance, understanding viscoelastic adhesion has far-reaching practical implications in a variety of application areas. These include soft robotics, where reversible and programmable adhesion is critical; biomedical adhesives, such as skin patches and tissue scaffolds; and microelectronics, where controlled adhesion is essential for material integration at small scales.

2. Basics of the Method of Dimensionality Reduction

2.1. Elastic Non-Adhesive Contacts

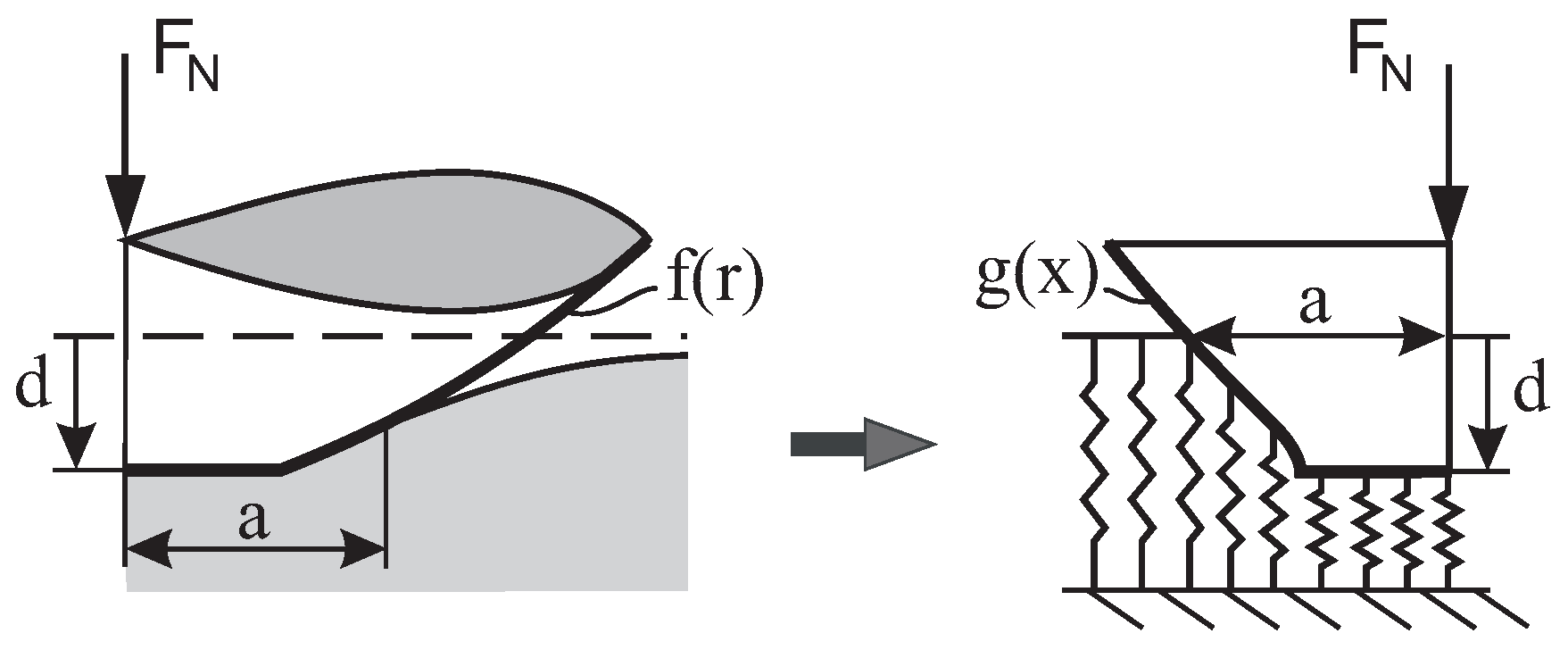
Solving an axially symmetric three-dimensional contact problem of two elastic bodies with the Method of Dimensionality Reduction (MDR) involves the following steps [13] (see also Figure 1). First, the shapes of the contacting bodies are reduced to the gap function $\tilde{z}=f(r)$, and this profile is transformed into a plane profile $g(x)$ via an Abel transformation:

$$g(x)=\left|x\right|{\displaystyle \underset{0}{\overset{\left|x\right|}{\int }}\frac{f^{\prime }(r)}{\sqrt{x^2-r^2}}\mathrm{d}r}$$

(1)

The profile $g(x)$ is then pushed by an indentation depth $d$ into a one-dimensional elastic foundation, a series of springs with spacing $\Delta x$ and stiffness

$$\Delta k_z=E^{*}\Delta x,$$

(2)

where the effective elastic modulus $E^{*}$ is defined as

$${\displaystyle \frac{1}{E^{*}}}={\displaystyle \frac{1-{\nu }_1^2}{E_1}}+{\displaystyle \frac{1-{\nu }_2^2}{E_2}}.$$

(3)

where $E_1$ and $E_2$ are Young’s moduli, and ${\nu }_1$ and ${\nu }_2$ are the Poisson numbers of the contacting bodies.

The vertical displacement of a spring at the position $x$ and the corresponding spring force are given by the equations

$$u_z(x)=d-g(x),$$

(4)

$$\Delta F_N=E^{*}\Delta x\cdot u_z(x)=E^{*}\Delta x(d-g(x)).$$

(5)

The contact radius $a$ is determined from the condition

$$u_z(a)=d-g(a)=0$$

(6)

and the total normal force is given by the summation (or integration) of the spring forces (5)

$$F_N=2{\displaystyle \underset{0}{\overset{a}{\int }}{E}^{*}(d-g(x))\mathrm{d}x}.$$

(7)

In [8], it is proved that the relationships between the normal force $F_N$, the indentation depth $d$ and the contact radius $a$ given by Equations (6) and (7) exactly coincide with those of the initial three-dimensional contact problem.

2.2. Elastic Adhesive Contacts

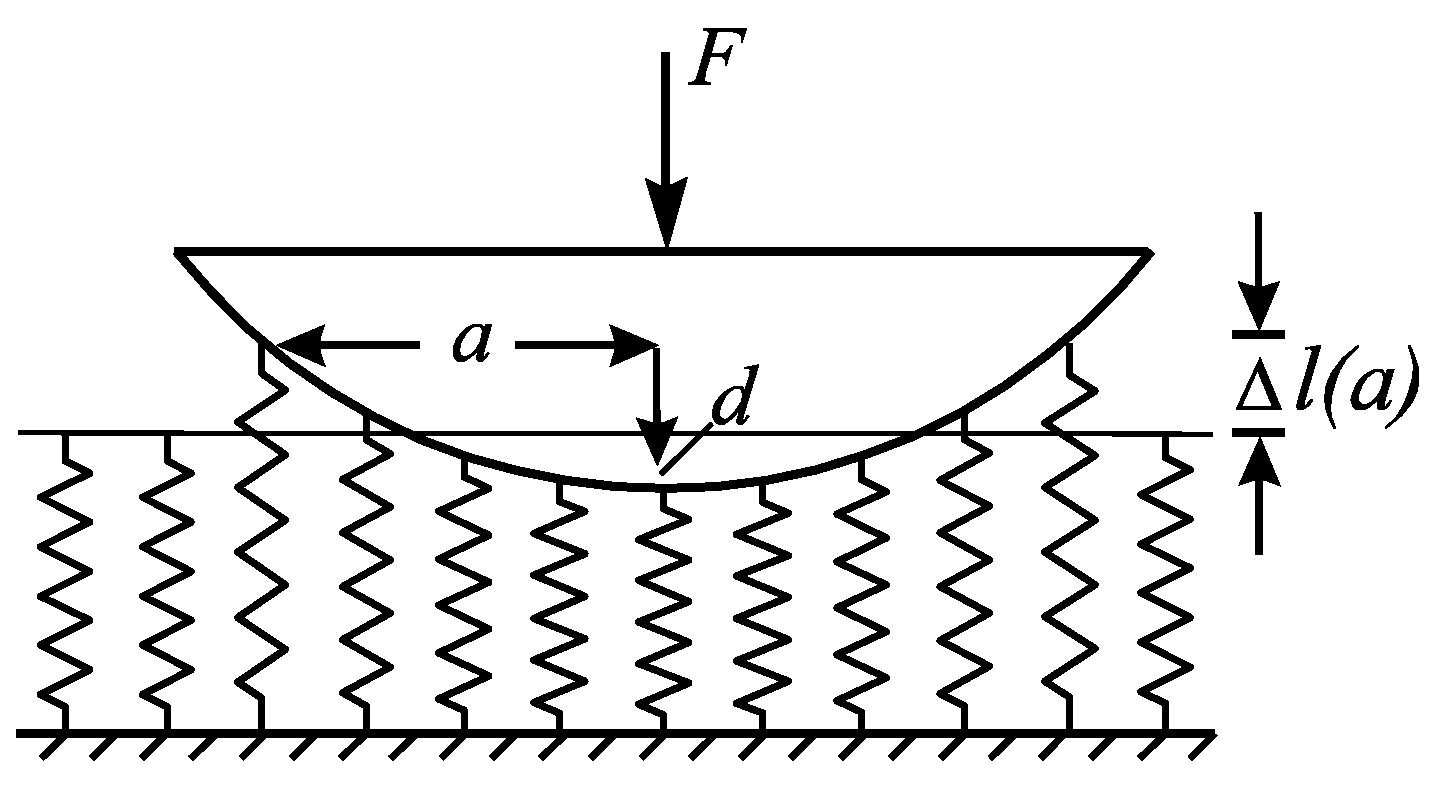
The adhesive contact between two elastic bodies is solved using exactly the same transformation (1) and procedural steps as in the non-adhesive case. The only modification lies in the criterion used to determine the extent of the contact area (i.e., the position of the contact boundary). Rather than applying Equation (6), we consider the following process. The indenter is first pressed into the elastic foundation and then gradually lifted. It is assumed that all springs initially in contact remain attached to the indenter, maintaining a constant contact radius during retraction. In this scenario, the outermost springs bear the maximum tensile load (Figure 2). When their elongation reaches a critical value,

$$\Delta l_c(a)=\sqrt{{\displaystyle \frac{2\pi a\Delta \gamma }{E^{*}}}},$$

(8)

they detach. $\Delta \gamma$ is here the specific work of adhesion. This detachment rule is known as the Heß criterion [15,16] {XE “rule of Hess”}. The resulting condition for the contact boundary is expressed as

$$u_z(a)=d-g(a)=-\Delta l_c(a)=\sqrt{{\displaystyle \frac{2\pi a\Delta \gamma }{E^{*}}}}.$$

(9)

Both the relationship between the indentation depth and contact radius given by (9) and the normal force given by (7) reproduce the solution by Johnson, Kendall and Roberts [1].

The rule of Heß, Equation (8), can be derived using the principle of virtual work. According to this principle, the system is in equilibrium when the energy does not change due to small variations in its generalized coordinates. Applied to the boundary of an adhesive contact, it means that the change in the elastic energy due to a small reduction in the contact radius from $a$ to $a-\Delta x$ is equal to the change in the surface energy $2\pi a\Delta x\Delta \gamma$, needed to create new surfaces. Since the MDR maps the relationship of force to displacement exactly, the elastic energy is also reproduced exactly. The change in the elastic energy can, therefore, be calculated directly in the MDR model. Due to the detachment of two springs on the left and right edges of the contact, the relaxed elastic energy is $2\Delta k\Delta l_c^2/2=E^{*}\Delta x\Delta l_c^2$. Balancing the changes in the elastic energy and the work of adhesion $2\pi a\Delta x\Delta \gamma$ gives

$$2\pi a\Delta x\Delta \gamma =E^{*}\Delta x\Delta l^2$$

(10)

which results in (8).

Note that criterion (8) has to be checked both for the springs that are in contact (if their elongation is larger than the critical one, they detach) and for the springs immediately outside the contact (if their coming into contact produces elongation less than is critical, then they must jump into contact). Thus, the boundary of an adhesive contact can propagate in both directions until it reaches the equilibrium state.

2.3. Viscoelastic Non-Adhesive Contacts

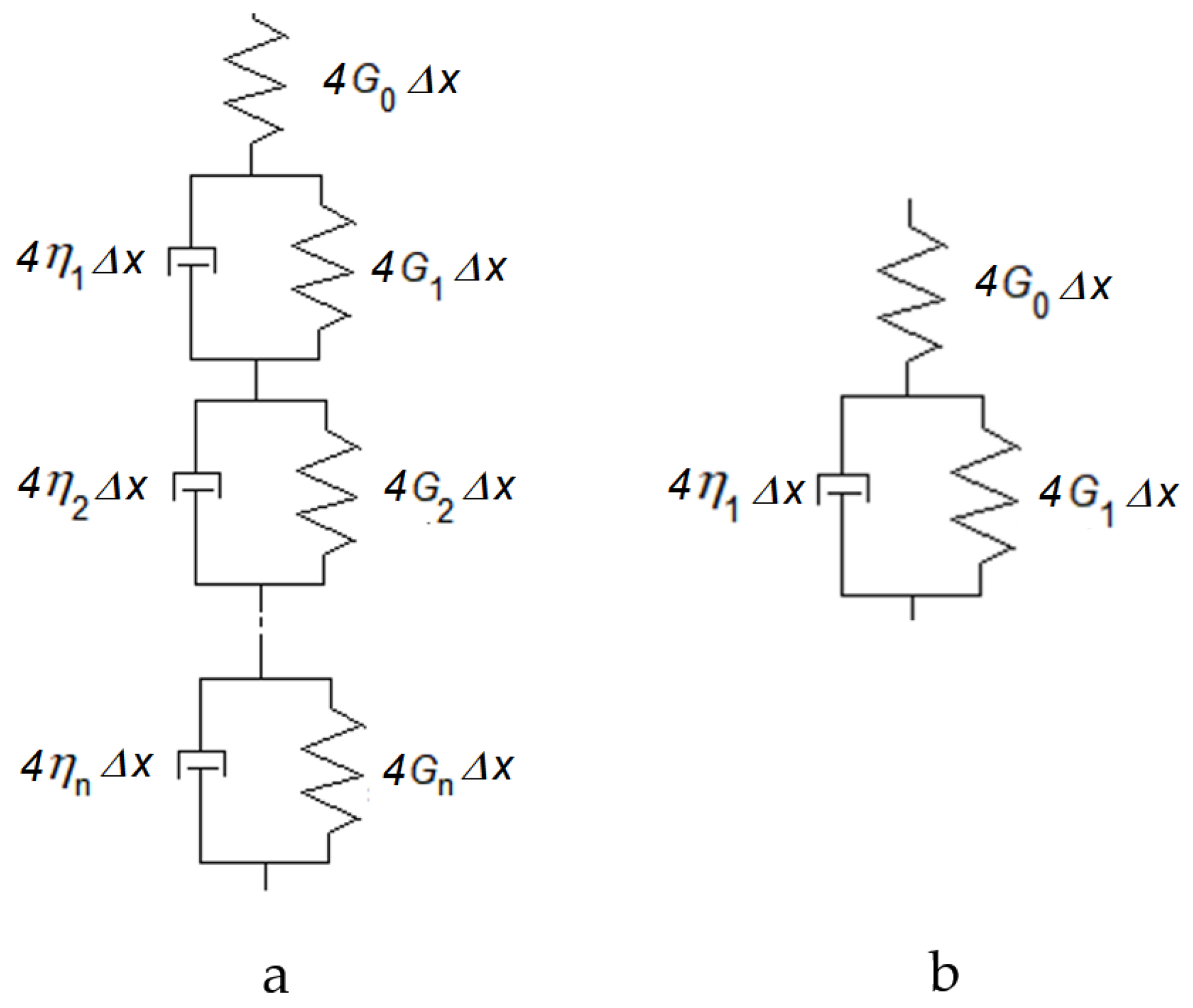
The Method of Dimensionality Reduction can also be applied to viscoelastic contacts by replacing the spring elements with corresponding rheological elements, as defined in [17]. Linear rheology can always be represented by a generalized creep element consisting of a number of Kelvin elements connected in series. In the case of an incompressible medium $E^{*}=4G$, where $G$ is the shear modulus. Correspondingly, the generalized creep elements consist of springs with stiffness $4G_i$ and a damping constant $4{\eta }_i$, where ${\eta }_i$ is dynamic viscosity (Figure 3a).

It has been shown [17] that the indentation of the MDR-transformed profile $g(x)$ into a viscoelastic foundation exactly replicates the original three-dimensional contact problem for a viscoelastic medium with the corresponding rheological properties. For qualitative analysis, a commonly used model is the “standard viscoelastic element”, which consists of a purely elastic spring (representing the glass modulus) in parallel with a Kelvin–Voigt element, as illustrated in Figure 3b. This simplified model will also serve as the basis for much of the subsequent analysis in this paper.

3. Energetic Criterion for Viscoelastic Adhesive Contacts

The general approach closely parallels that used for elastic adhesive contact. However, in the case of viscoelastic materials, each spring in the elastic foundation is replaced by a corresponding creep element, as depicted in Figure 3a. When the body is lifted, the element located at the edge of the contact undergoes an elongation $\Delta l$. This total elongation is composed of the individual deformations of all the sub-elements within the creep element: $\Delta l=\Delta l_0+\Delta l_1+\dots +\Delta l_n+\dots$, where $\Delta l_0$ is the elongation of spring $G_0$, $\Delta l_1$ is the elongation of the Kelvin element $(G_1,{\eta }_1)$, and so on.

The core concept behind applying the energy criterion to viscoelastic bodies lies in recognizing the different relaxation timescales within a rheological element. When the system is deformed, elastic energy is stored across all components of the viscoelastic element. Upon detachment from the indenter, only the energy stored in the purely elastic spring, $G_0$, associated with the glass modulus, can relax instantaneously and contribute to the formation of new surfaces, i.e., perform the work of adhesion. In contrast, the energy stored in the Kelvin elements relaxes more slowly and cannot be utilized during the brief moment of detachment, which occurs at the molecular level and is effectively instantaneous from a macroscopic perspective. Consequently, the material’s immediate response is governed by its glass modulus, making the detachment process effectively conservative.

This justifies the application of the energy balance criterion, where the quickly releasable elastic energy, $2\cdot \left(4G_0\right)\Delta x\Delta l_0^2/2$, is equated to the specific work of adhesion, $2\pi a\cdot \Delta x\cdot \Delta \gamma$:

$$2\pi a\cdot \Delta x\cdot \Delta \gamma =\left(4G_0\right)\Delta x\Delta l_0^2,$$

(11)

which has exactly the same form as the detachment criterion (10) for the elastic case, with the only difference being that $G_0$ is now the glass modulus of the medium and $\Delta l_0$ is only part of the total elongation. Note that we consider here the case of energetic interfaces; thus, we assume that $\Delta \gamma$ is a well-defined material parameter that does not depend on the velocity of detachment. Solving Equation (11) with respect to $\Delta l_0$ gives

$$\Delta l_0=\sqrt{{\displaystyle \frac{\pi a\Delta \gamma }{2G_0}}}.$$

(12)

This criterion does not depend on the rheology of the medium. However, how large the elongation part $\Delta l_0$ is does depend on the rheology and on the loading history.

4. Quasistatic Indentation and Detachment

In the following, we consider a displacement-controlled quasistatic indentation of a rigid parabolic indenter $f(r)=r^2/(2R)$ into a viscoelastic half-space described with the “standard viscoelastic model” with a stiff spring $G_0$ and Kelvin element $G_1,{\eta }_1$ (Figure 3b). The corresponding MDR profile is, in this case, according to Equation (1), given by

$$g(x)={\displaystyle \frac{x^2}{R}}.$$

(13)

4.1. Indentation Phase

At the first touch, an adhesive neck will appear by propagation of the boundary of adhesive contact. As the initial length of all rheological elements is zero and during the attachment process only the spring $G_0$ is instantly deformed, the boundary of adhesive contact propagates until the following condition is fulfilled:

$${\displaystyle \frac{a^2}{R}}=\sqrt{{\displaystyle \frac{\pi a\Delta \gamma }{2G_0}}}.$$

(14)

Thus, the initial contact radius is given by the following equation:

$$a={\left({\displaystyle \frac{\pi R^2\Delta \gamma }{2G_0}}\right)}^{1/3}.$$

(15)

Associated with this instant attachment is an instant drop in force by

$$\Delta F_{N,\mathrm{instant}}=-8G_0{\displaystyle \underset{0}{\overset{a}{\int }}\frac{x^2}{R}\mathrm{d}x}=-{\displaystyle \frac{8G_0}{3R}}{a}^3=-{\displaystyle \frac{4}{3}}\pi R\Delta \gamma .$$

(16)

However, as soon as the springs are stretched, this force begins to relax. At the end of the relaxation process, the stiffness of each rheological element is $4{\displaystyle \frac{G_0{G}_1}{G_0+G_1}}\Delta x$, and the normal force is equal to

$$\Delta F_{N,\mathrm{relaxed}}=-8{\displaystyle \frac{G_0{G}_1}{G_0+G_1}}{\displaystyle \underset{0}{\overset{a}{\int }}\frac{x^2}{R}\mathrm{d}x}=-{\displaystyle \frac{4}{3}}\pi R\Delta \gamma {\displaystyle \frac{G_1}{G_0+G_1}}=-{\displaystyle \frac{4}{3}}\pi R\Delta {\gamma }_{eff,1}$$

(17)

with

$$\Delta {\gamma }_{eff,1}=\Delta \gamma {\displaystyle \frac{G_1}{G_0+G_1}}\ll \Delta \gamma .$$

(18)

Thus, the quasistatic value of the normal force appearing after the initial touch is given by the usual JKR equation but with an effective work of adhesion given by Equation (18).

Consider now an arbitrary indentation $d$. Now, the condition for the boundary of an adhesive contact takes the following form:

$$d-{\displaystyle \frac{a^2}{R}}=-\sqrt{{\displaystyle \frac{\pi a\Delta \gamma }{2G_0}}}=-\sqrt{{\displaystyle \frac{\pi a\Delta {\gamma }_{eff,1}}{2\frac{G_0{G}_1}{G_0+G_1}}}}$$

(19)

and the force in the relaxed state is give by

$$F_{N,\mathrm{relaxed}}=8{\displaystyle \frac{G_0{G}_1}{G_0+G_1}}{\displaystyle \underset{0}{\overset{a}{\int }}\left(d-\frac{x^2}{R}\right)\mathrm{d}x}=8{\displaystyle \frac{G_0{G}_1}{G_0+G_1}}\left(da-{\displaystyle \frac{a^3}{3R}}\right).$$

(20)

These two equations exactly coincide with the JKR equations with replacements

$$E^{*}\to 4{\displaystyle \frac{G_0{G}_1}{G_0+G_1}}, \Delta \gamma \to \Delta {\gamma }_{eff,1}=\Delta \gamma {\displaystyle \frac{G_1}{G_0+G_1}}.$$

(21)

Thus, during the indentation phase, the contact is characterized by a soft (relaxed) elastic modulus and a very low effective work of adhesion (suppressed by the factor $G_1/(G_0+G_1)$).

4.2. Detachment Phase

A very important difference from the elastic case is that, due to the relaxation, the edge springs during the indentation phase are not in a critical state. Thus, if the indentation is stopped and the indenter is quasistatically lifted, the stiff springs $G_0$ have first to achieve the critical elongation (12) before the detachment process starts. During this phase, the contact size remains constant. This is the well-known “sticking zone” [18,19].

The detachment starts when the elongation of spring $G_0$ reaches the critical value $\Delta l_0$ given by (12). At this moment, the elongation of spring $G_1$ will be $\Delta l_1=(G_0/G_1)\Delta l_0$. Thus, the whole elongation of the rheological element will be

$$\Delta l={\displaystyle \frac{G_0+G_1}{G_1}}\Delta l_0.$$

(22)

The condition for the contact radius thus reads

$$d-{\displaystyle \frac{a^2}{R}}=-{\displaystyle \frac{G_0+G_1}{G_1}}\Delta l_0=-{\displaystyle \frac{G_0+G_1}{G_1}}\sqrt{{\displaystyle \frac{\pi a\Delta \gamma }{2G_0}}}=-\sqrt{{\displaystyle \frac{\pi a\Delta {\gamma }_{eff,2}}{2\frac{G_0{G}_1}{\left(G_0+G_1\right)}}}}$$

(23)

with

$$\Delta {\gamma }_{eff,2}=\Delta \gamma {\displaystyle \frac{\left(G_0+G_1\right)}{G_1}}.$$

(24)

For elements at position $x$, we have the following equations for the vertical displacement of the whole element and the force:

$$u_z(x)=d-{\displaystyle \frac{x^2}{R}}, \Delta F(x)={\displaystyle \frac{G_0{G}_1}{G_0+G_1}}{u}_z(x)={\displaystyle \frac{G_0{G}_1}{G_0+G_1}}\left(d-{\displaystyle \frac{x^2}{R}}\right)$$

(25)

and for the total normal force

$$F_N={\displaystyle \frac{G_0{G}_1}{G_0+G_1}}{\displaystyle \underset{0}{\overset{a}{\int }}\left(d-\frac{x^2}{R}\right)\mathrm{d}x}={\displaystyle \frac{G_0{G}_1}{G_0+G_1}}\left(da-{\displaystyle \frac{a^3}{3R}}\right)$$

(26)

Equations (23) and (26) are exactly equivalent to the JKR theory with replacements

$$E^{*}\to 4{\displaystyle \frac{G_0{G}_1}{G_0+G_1}}, \Delta \gamma \to \Delta {\gamma }_{eff,2}=\Delta \gamma {\displaystyle \frac{G_0+G_1}{G_1}}.$$

(27)

Thus, during the detachment phase, the contact is characterized by a soft (relaxed) elastic modulus and a very high effective work of adhesion (enhanced by factor $(G_0+G_1)/G_1$), which was found by de Gennes using other arguments [20].

5. Limits of Applicability of the Energy Criterion

An essential assumption for the applicability of the energetic criterion described in this paper is timescale separation—elastic detachment is a quick process, while the subsequent viscous relaxation a slow one. The physical substantiation of the scale separation is the short range of adhesive forces, which is assumed to be much smaller than any other dimension of the contact problem. In real systems, the range of adhesive force might be small but finite, and this will impose some restrictions on the applicability of the above theory. For this sake, we must consider the three-dimensional shape of the adhesive gap. This gap is different for the indentation and the pull-off phases.

5.1. Gap Shape During the Indentation Phase

During the indentation phase, the elongation of the last spring in contact is given by Equation (12), while the next spring (outside the contact) has zero elongation. Thus, at the boundary of adhesive contact, there is a jump in vertical displacement

$$\Delta u_z(a)=\sqrt{{\displaystyle \frac{\pi a\Delta \gamma }{2G_0}}}.$$

(28)

According to the rules of the Method of Dimensionality Reduction, the displacement of the surface outside the contact in the original three-dimensional contact problem is given by Equation (7) (Equation (2.14) in [7])

$$u_{z,3\mathrm{D}}={\displaystyle \frac{2}{\pi }}{\displaystyle \underset{0}{\overset{r}{\int }}\frac{u_z(x)}{\sqrt{r^2-x^2}}\mathrm{d}x}$$

(29)

A jump of $\Delta u_z(a)$ at point $x=a$ leads to an asymptotic form of a gap

$$u_{z,3\mathrm{D}}={\displaystyle \frac{2}{\pi }}\Delta u_z(a){\displaystyle \underset{a}{\overset{r}{\int }}\frac{1}{\sqrt{r^2-x^2}}\mathrm{d}x}\approx {\displaystyle \frac{2}{\pi }}\Delta u_z(a)\sqrt{2{\displaystyle \frac{r-a}{a}}}.$$

(30)

With jump (28), this equation becomes

$$u_{z,3\mathrm{D}}\approx 2\sqrt{{\displaystyle \frac{\Delta \gamma }{\pi G_0}}\left(r-a\right)}.$$

(31)

The process of detachment is completed when the distance between the surfaces of the gap becomes $2h$, where $h$ is the characteristic interaction range of adhesive forces:

$$2\sqrt{{\displaystyle \frac{\Delta \gamma }{\pi G_0}}\left(r-a\right)}\approx 2h.$$

(32)

Thus, to complete detachment, the tip of the crack should advance by the distance

$$\Delta r\approx {\displaystyle \frac{\pi G_0{h}^2}{\Delta \gamma }}.$$

(33)

If the propagation velocity of the boundary of adhesive contact is $v$, this happens during time

$$\Delta t\approx {\displaystyle \frac{\Delta r}{v}}\approx {\displaystyle \frac{\pi G_0{h}^2}{v\Delta \gamma }}.$$

(34)

Detachment can be considered “instant” if this time is much smaller than the relaxation time $\tau$ of the elastomer:

$${\displaystyle \frac{\pi G_0{h}^2}{v\Delta \gamma }}\ll \tau .$$

(35)

Hence, the velocity must be larger than

$$v\gg v_{c,1}={\displaystyle \frac{\pi G_0{h}^2}{\tau \Delta \gamma }}.$$

(36)

5.2. Gap Shape During the Detachment Phase

In the detachment phase, the jump of the elongation of the boundary element is given by Equation (22):

$$\Delta l={\displaystyle \frac{G_0+G_1}{G_1}}\sqrt{{\displaystyle \frac{\pi a\Delta \gamma }{2G_0}}}.$$

(37)

Thus, criterion (32) takes the form

$$2{\displaystyle \frac{G_0+G_1}{G_1}}\sqrt{{\displaystyle \frac{\Delta \gamma }{\pi G_0}}\left(r-a\right)}\approx 2h$$

(38)

and the velocity condition (36) is replaced by

$$v\gg v_{c,2}={\displaystyle \frac{\pi G_0{h}^2}{\tau \Delta \gamma }}{\left({\displaystyle \frac{G_1}{G_0+G_1}}\right)}^2.$$

(39)

Using the values $G_0={10}^9\mathrm{Pa}$, $G_1={10}^7 \mathrm{Pa}$, $h={10}^{-9} \mathrm{m}$, $\tau ={10}^{-3} \mathrm{s}$, and $\Delta \gamma ={10}^{-2} {\mathrm{J}/\mathrm{m}}^2$ for estimation, we obtain the following estimations for the critical velocities:

$$v_{c,1}\approx 3\cdot {10}^{-4} \mathrm{m}/\mathrm{s}, v_{c,2}\approx 3\cdot {10}^{-8} \mathrm{m}/\mathrm{s}.$$

(40)

Thus, the almost arbitrary pull-off velocities used in the experiment guarantee the scale separation at the pull-off stage. During the indentation phase, more detailed consideration might be necessary, depending on the rheology (relaxation time).

6. Discussion

We have shown how (and when) a purely energetic criterion can be used to determine detachment and attachment conditions in adhesive contact with a viscoelastic body. Under the restrictions described in Section 5, two timescales can be identified: the time of detachment and the time of relaxation of the elastomer. If the time of detachment is much smaller than the time of relaxation, it can be considered to be nearly instant. In this case, only the part of elastic energy that is stored in the stiff spring $G_0$, characterizing the instant rigidity of the body, is available for the creation of surface energy. We have shown that if the indenter is now pressed into the medium and pulled-off “quasistatically”, which means slowly enough for complete relaxation of the medium but quickly enough so that no relaxation occurs during the detachment process, then the force–displacement relationship and the force–contact radius relationship can be found analytically. They are given by Equations (19) and (20) for indentation and by Equations (23) and (26) for detachment. By reversing the direction of motion (from indentation to pull-off), the contact radius remains constant until a critical condition is achieved, which leads to the appearance of the “sticking zone”.

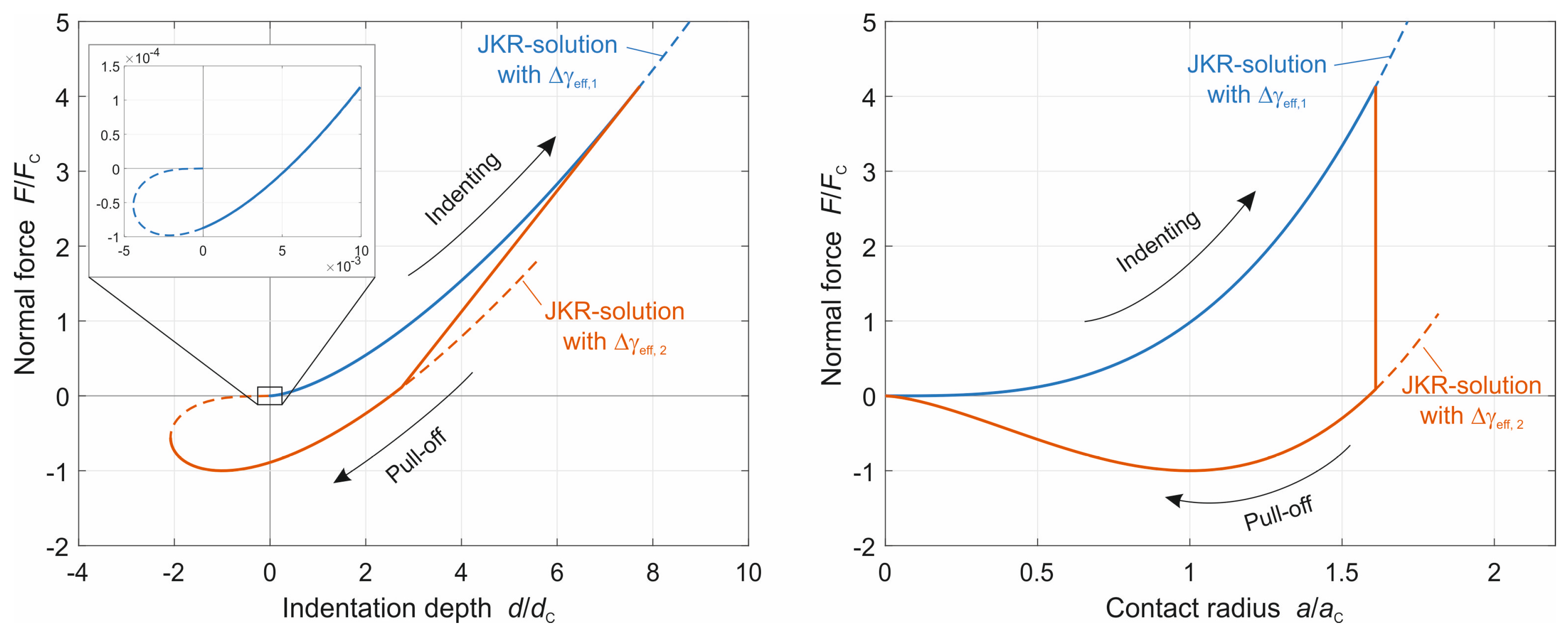
These results are illustrated in Figure 4. Both the indentation and detachment processes are described by the JKR theory, but indentation only has very low effective adhesive energy, given by (21), and detachment has very high effective separation energy, given by (27). In both cases, the small (relaxed) elastic modulus must be used. The force, the indentation depth and the contact radius in Figure 4 are normalized by

$$F_c={\displaystyle \frac{3}{2}}\pi R\Delta {\gamma }_{eff,2}, d_c={\left({\displaystyle \frac{3{\pi }^2\Delta {\gamma }_{eff,2}^{2}R}{1024{\left(\frac{G_0{G}_1}{G_0+G_1}\right)}^2}}\right)}^{1/3}, a_c={\left({\displaystyle \frac{9\pi \Delta {\gamma }_{eff,2}{R}^2}{32\left(\frac{G_0{G}_1}{G_0+G_1}\right)}}\right)}^{1/3}.$$

(41)

It is often believed that if the indentation and detachment occur very slowly, then the viscoelastic medium can be considered a soft elastic body. This is true only partially; the elastic response at a quasistatic deformation is given both during indentation and pull-off by the relaxed modulus. However, the detachment criterion is different. This is due to the fact that the process of detachment is always quick (nearly instant), even at quasistatic deformation. This leads to pronounced adhesive hysteresis, in complete agreement with the overwhelming experimental evidence. We do not provide here any comparison with experiments but mention that the curves in Figure 4 are strikingly similar to much of the experimental data (see e.g., [21,22]). In particular, all experimental studies show that the indentation process is related to a very small effective work of adhesion, which is several orders of magnitude smaller than the effective work of adhesion observed during the detachment phase.

Enhancement of the effective surface energy during the pull-off phase by factor $\sim G_0/G_1$, as compared with the thermodynamic value, was obtained earlier [14,23,24] without using the MDR but with methods and arguments that are ultimately equivalent to those presented here.

In an earlier work, the difference in the work of adhesion at attachment and detachment was related to the friction of the boundary line of adhesive contact [25]. The approach described in this paper sheds a completely new light on the physical origin of two different works of adhesion. In particular, from paper [25], it remains unclear why the experimentally observed work of adhesion at indentation is orders of magnitude smaller than that at detachment. The approach of the present paper gives a simple explanation to this fundamental experimental fact.

Here, we considered only quasistatic indentation and detachment. The formulated energetic criterion allows arbitrary loading scenarios within the same framework to be considered.

The concept of effective surface energy used in this work is closely related to similar notions in fracture mechanics, where viscoelastic dissipation is commonly treated through energy release rates that incorporate time-dependent effects. The present formulation builds directly on this tradition by offering a simplified, yet rigorous, energetic criterion grounded in the Method of Dimensionality Reduction. Unlike previous approaches, which often required numerical inversion of hereditary integrals, the current method permits straightforward analytical treatment, thus broadening the practical applicability of the rate-dependent adhesion concept.

7. Conclusions

We have shown how the energetic criterion (Griffith criterion) can be applied in an exact and straightforward way to adhesive contacts of viscoelastic bodies. The limits of applicability of the energetic criterion have been analyzed, showing that the restrictions are stronger during the indentation phase than during the detachment phase. The formulated procedure is applicable to arbitrary loading scenarios. In the present paper, only quasistatic indentation and detachment have been considered. It has been shown that both indentation and detachment are described by the JKR theory, but indentation with an effective work of adhesion is suppressed by factor $\sim G_1/G_0$, and detachment with an effective work of adhesion is enhanced by factor $\sim G_0/G_1$. Due to the strong suppression of effective energy, indentation occurs almost as if there were no adhesion (almost pure Hertz). Reversing the direction of motion leads first to a sticking zone, followed by a JKR dependence with a very high effective work of adhesion. These results coincide with the earlier results obtained by Barthel with other analytical methods [24].

Beyond providing analytical tractability, the method offers a clear conceptual insight into why hysteresis arises in viscoelastic adhesive contacts—namely, the delayed relaxation of energy stored in dissipative elements. These results also align closely with experimental observations, particularly the pronounced asymmetry in effective adhesion energy between the approach and retraction phases.

The theoretical framework presented here is not only of academic interest but also relevant for the design and analysis of soft adhesive systems in practical applications, such as biomedical adhesives, flexible electronics and soft robotics. The simplicity and generality of the MDR-based energetic criterion opens the door to systematic studies of more complex loading scenarios and geometries. In this study, we have focused on the ultimate quasistatic limit of adhesive contact. A detailed analysis of adhesion under finite separation rates will be presented in a forthcoming paper. In the general case, the adhesive force is expected to depend not only on the loading history but also, in particular, on the maximum indentation depth—an effect that has been consistently observed in experiments [26]. Further work at finite velocities could also impact the broader problem of oscillation effects on adhesive contacts [27] and the interrelation between adhesion and friction [28].