Abstract
The study of the conditions under which a stratified shear flow becomes turbulent is important, as turbulence is the source of mixing and dissipation in the atmosphere and can significantly influence the momentum and temperature structure of the atmospheric circulation. This study investigates the asymmetric Holmboe instability, which is the instability of a parallel shear flow of a stably stratified atmosphere with two layers of homogeneous but different density, where the interface of the two layers is not in the middle of the shear region, but at some height above it. We calculate the evolution of small-amplitude, three-dimensional perturbations around this background flow for various values of the Richardson number and of the non-dimensional asymmetry height. Instability is found for all values of the Richardson number and the asymmetry height with the most unstable modes being counter-propagating waves in the plane of the flow with differing wave speeds. The eastward propagating mode is found to have a larger scale and faster growth in comparison to the westward propagating mode. Both the scale and the growth rate of the most unstable waves were found to decrease with the Richardson number, while an increase in asymmetry was found to increase the scale and the growth rate of the most unstable eastward wave.
1. Introduction
Stratified shear instability dominates small-scale mixing in the atmosphere. It is the primary source of turbulence in the nocturnal atmospheric boundary layer, playing a critical role in the dispersion of atmospheric pollutants, and it also contributes to momentum and thermal mixing aloft as it is involved in many phenomena such as breaking of gravity waves and clear air turbulence. Therefore, it is important to achieve a thorough understanding of the mechanisms underlying shear instability [1].
There are three major categories of stratified shear instability. The first is Kelvin–Helmholtz instability, occurring in cases of weak stratification [2]. In this case, instability leads to the formation of stationary, meandering structures. In these structures, the denser air masses lie above the lighter ones, resulting in gravitational collapse and the generation of turbulence and mixing. The second is Taylor–Caulfield instability that occurs in cases of a stratified atmosphere with multiple layers of constant density separated by sharp density gradients [3]. The third is Holmboe instability that occurs in cases of strong stratification and is the subject of this study. Holmboe instability differs significantly from the Kelvin–Helmholtz type. The structures that form have a lower growth rate compared to those in Kelvin–Helmholtz instability and are not stationary—rather, they propagate in the direction of the flow with well-defined phase velocities, forming wave-like structures with sharp edges along the interface between the two atmospheric layers [4]. These cusp-like edges are sites of intermittent turbulence and mixing.
To analytically investigate the initial stage of the evolution of Holmboe instability, previous studies considered a simplified setting in which there are two atmospheric layers of different densities with a shear region in between the interface of the two layers [5]. When this interface is at the midpoint of the shear region, the incipient instability is termed symmetric Holmboe instability, and when it is located at a certain height above the center of the shear region, it is termed asymmetric. The evolution of planar perturbations in both the symmetric and asymmetric cases was examined in previous papers, which found a pair of exponentially growing waves propagating in opposite directions [5]. In this work, we extend these results by considering the stability of the stratified shear flow with respect to three-dimensional perturbations. We thoroughly investigate the characteristics of instability as a function of the bulk Richardson number and the asymmetry height, compare our results with the previously obtained results regarding growth of planar perturbations, and highlight the differences in comparison to the symmetric case.
2. Stability Analysis of an Asymmetric Layered Fluid
We consider two atmospheric layers of different densities with a zonal shear flow between them, as illustrated in Figure 1.
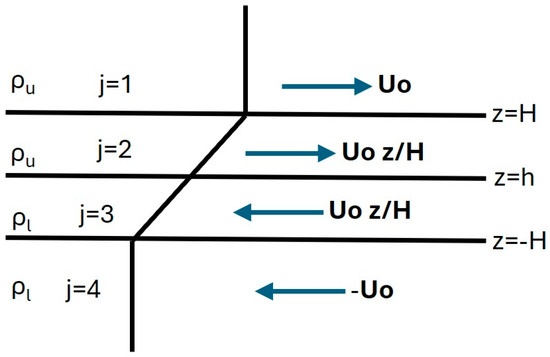
Figure 1.
Profile of velocity and density in the case of asymmetric Holmboe instability.
Thus, the wind speed and the density are given by
Notice that the density layer interface is at a height above the center of the shear region, with the special case of symmetric instability occurring for . This state, with a pressure field that balances gravity hydrostatically, is an equilibrium state for an inviscid and incompressible atmosphere. To investigate the stability of this equilibrium, we consider small perturbations in both velocity and pressure. The velocity field in the four regions of the flow shown in Figure 1 is thus expressed as
where ,, and ; the perturbations are denoted with primed functions; and denotes the small amplitude of these perturbations. The pressure in the four regions is given by
where is the background pressure, and .
The dimensionless linear equations governing the evolution of perturbations are
where the tildes denote non-dimensional variables, , , , , and , with being the relative density difference of the two layers. The equations have been non-dimensionalized assuming the depth of the layer as the length scale, the difference in wind speed as the velocity scale, the advection time as the time scale, the mean density as the density scale, and as the pressure scale. When the relative density difference is small, we can approximate the mean density as homogeneous . This is the Boussinesq approximation that is typically employed in the studies of Holmboe instability.
At the interfaces between the different regions occurring at and at , the kinematic condition requires continuity of vertical velocity
while continuity of pressure requires
where is the non-dimensional Richardson number.
Taking advantage of the continuity equation and after algebraic manipulations, we can reduce the number of equations to two for the evolution of vorticity and vertical velocity :
where is the non-dimensional Laplacian. Due to the temporal and spatial homogeneity of the base flow, the solution can be expanded on a Fourier basis:
Thus, the above yields a fourth-order polynomial equation for the frequency for each of the plane waves. The stability of the equilibrium depends on the complex roots of the polynomial , which are functions of the Richardson number, the dimensionless asymmetry height , and the plane wave characteristics, which can be described by the wavenumber magnitude and the angle that the constant phase lines form with the plane of the flow. The equilibrium is unstable if the imaginary part of the roots is negative as the perturbations grow exponentially with the growth rate . Additionally, the perturbations propagate with a phase velocity given by . The perturbations that are expected to dominate the flow are the waves with the largest growth rate, , as these modes will grow faster than all others and will have the largest amplitude after a short time.
3. Characteristics of the Unstable Waves
Figure 2 shows the phase velocity and the growth rate of the two unstable modes as functions of the wavenumber magnitude and the angle in the case of and . We observe exponentially growing waves that are propagating eastward (top panels) and westward (bottom panels), as indicated by their nonzero phase velocity. The eastward propagating wave has a slightly lower phase speed compared to the westward one and also has a larger scale as the growth rate is maximized over lower wavenumbers. We also observe that there is a range of large wavenumbers where the flow is stable with respect to planar perturbations but is unstable with respect to three-dimensional perturbations. For example, for the flow is stable with respect to planar eastward propagating perturbations but is unstable with respect to three-dimensional perturbations. As a result, we expect the smaller-scale waves appearing in the flow to be three-dimensional. However, the most unstable perturbations lie in the plane of the flow, with the maximum growth rate occurring at for both eastward and westward propagating modes, and the most unstable perturbation is the eastward propagating mode.
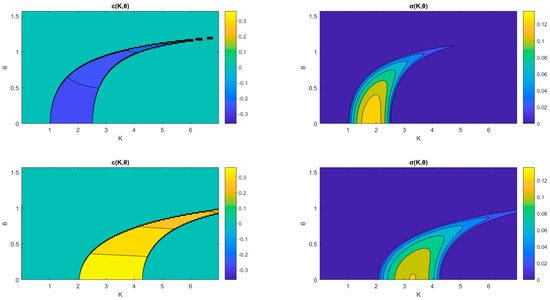
Figure 2.
The phase velocity (left) and the exponential growth rate (right) for the eastward propagating mode (top panels) and the westward propagating mode (lower panels) as functions of the wavenumber magnitude and angle for and .
For higher Richardson numbers and larger values of , we observe similar characteristics for instability, with the most unstable perturbations being traveling waves confined to the plane of the flow. What changes, however, is the growth rate and the scale of the most unstable disturbances. The scale separation between the eastward and the westward propagating modes increases with both and , while the most unstable mode is always the eastward propagating wave. Figure 3 shows the maximum growth rate of this mode, , as a function of the Richardson number for two different values of . We observe that the maximum growth rate decreases with an increasing Richardson number and monotonically increases with the asymmetry height. Thus, instability develops more slowly under stronger stratification but more rapidly under asymmetric flows. Furthermore, Figure 4 presents the wavenumber for which the maximum growth rate is attained as a function of for two values of . It is evident that the wavenumber increases monotonically with the Richardson number, while it decreases with . This means that under stronger stratification, the dominant perturbations have smaller spatial scales, whereas greater asymmetry leads to larger-scale disturbances being observed compared to the symmetric configuration.
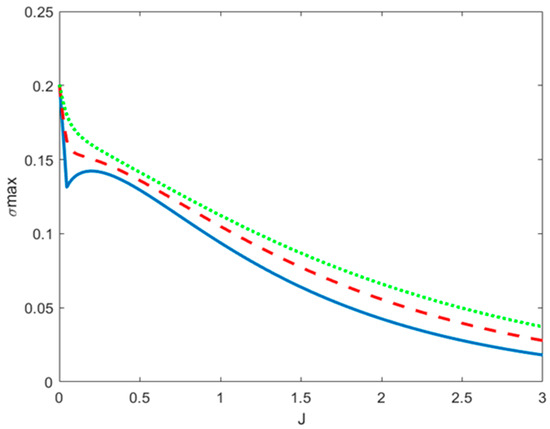
Figure 3.
Maximum exponential growth rate as a function of the Richardson number for (solid line), (dashed line), and (dotted line).
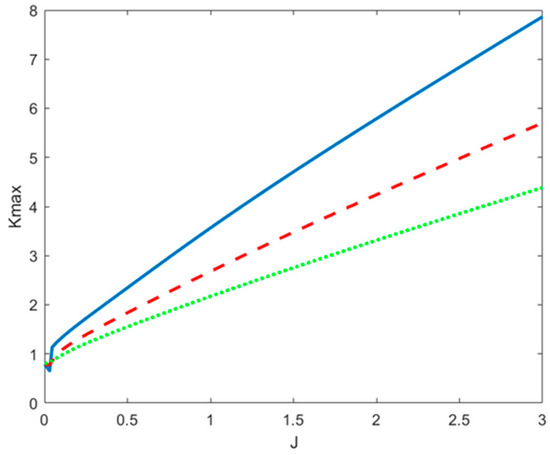
Figure 4.
Wavenumber of the perturbation corresponding to the maximum growth rate, , as a function of the Richardson number for (solid line), (dashed line), and (dotted line).
4. Conclusions
In this study, the asymmetric Holmboe instability was investigated—namely, the instability of a parallel shear flow in a stably stratified atmosphere consisting of two layers of different densities, where the interface separating the two fluids is located at a height above the center of the shear region rather than at its midpoint. We analytically computed the solutions that describe the evolution of small disturbances around the equilibrium state of an ideal, incompressible fluid. It was found that for moderate stratification, two planar counter-propagating waves are expected to develop in the plane of the flow, with the eastward propagating wave having a larger scale compared to its westward propagating counterpart and growing at a faster rate. Additionally, the emergence of three-dimensional waves with smaller scales is possible although less likely due to their lower growth rates. Under stronger stratification, the expected planar eastward propagating wave exhibits a smaller scale and grows more slowly. Finally, increasing the asymmetry leads to two-dimensional waves of larger scale compared to the symmetric case, which also grow faster.
Author Contributions
Conceptualization, N.A.B.; methodology, G.M. and N.A.B.; validation, G.M.; formal analysis, G.M.; investigation, G.M.; writing—original draft preparation, G.M.; writing—review and editing, N.A.B.; visualization, G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; pp. 124–250. [Google Scholar]
- Swinney, H.L. Hydrodynamic instabilities and the transition to turbulence. Prog. Theor. Phys. Suppl. 1978, 64, 164–175. [Google Scholar] [CrossRef][Green Version]
- Caulfield, C.P. Multiple linear instability of stratified shear flow. J. Fluid Mech. 1994, 258, 255–285. [Google Scholar] [CrossRef]
- Smyth, W.D.; Peltier, W.R. The transition between Kelvin–Helmholtz and Holmboe instability. J. Atmos. Sci. 1989, 46, 3698–3720. [Google Scholar] [CrossRef]
- Haigh, S.P.; Lawrence, G.A. Symmetric and nonsymmetric Holmboe instabilities in an inviscid flow. Phys. Fluids 1999, 11, 1459–1468. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).