Intelligent Optimal Strategy for Balancing Safety–Quality–Efficiency–Cost in Massive Concrete Construction
Abstract
:1. Introduction
2. Research Framework and Mathematical Model
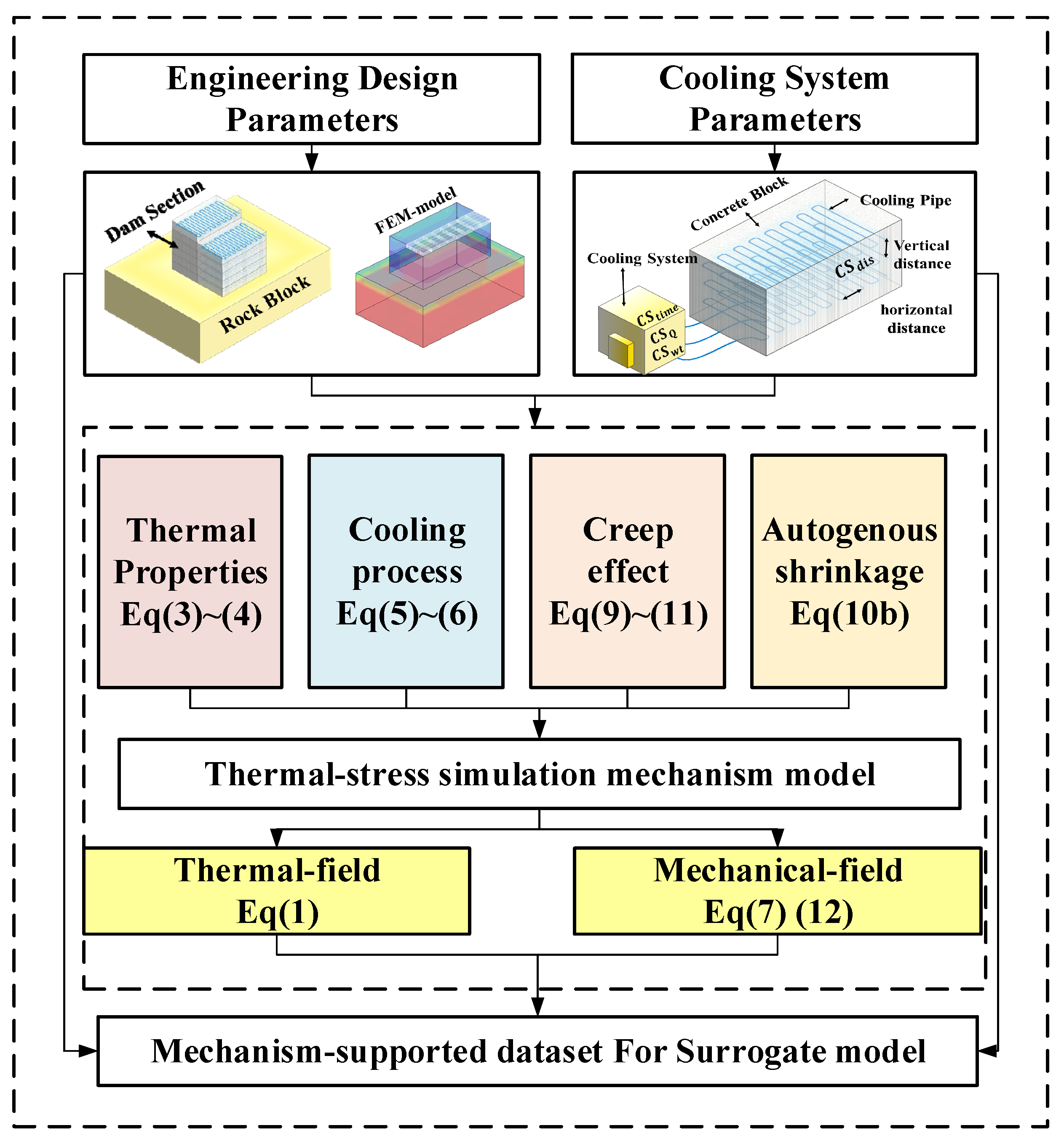
2.1. Research Framework
2.2. Mathematical Model
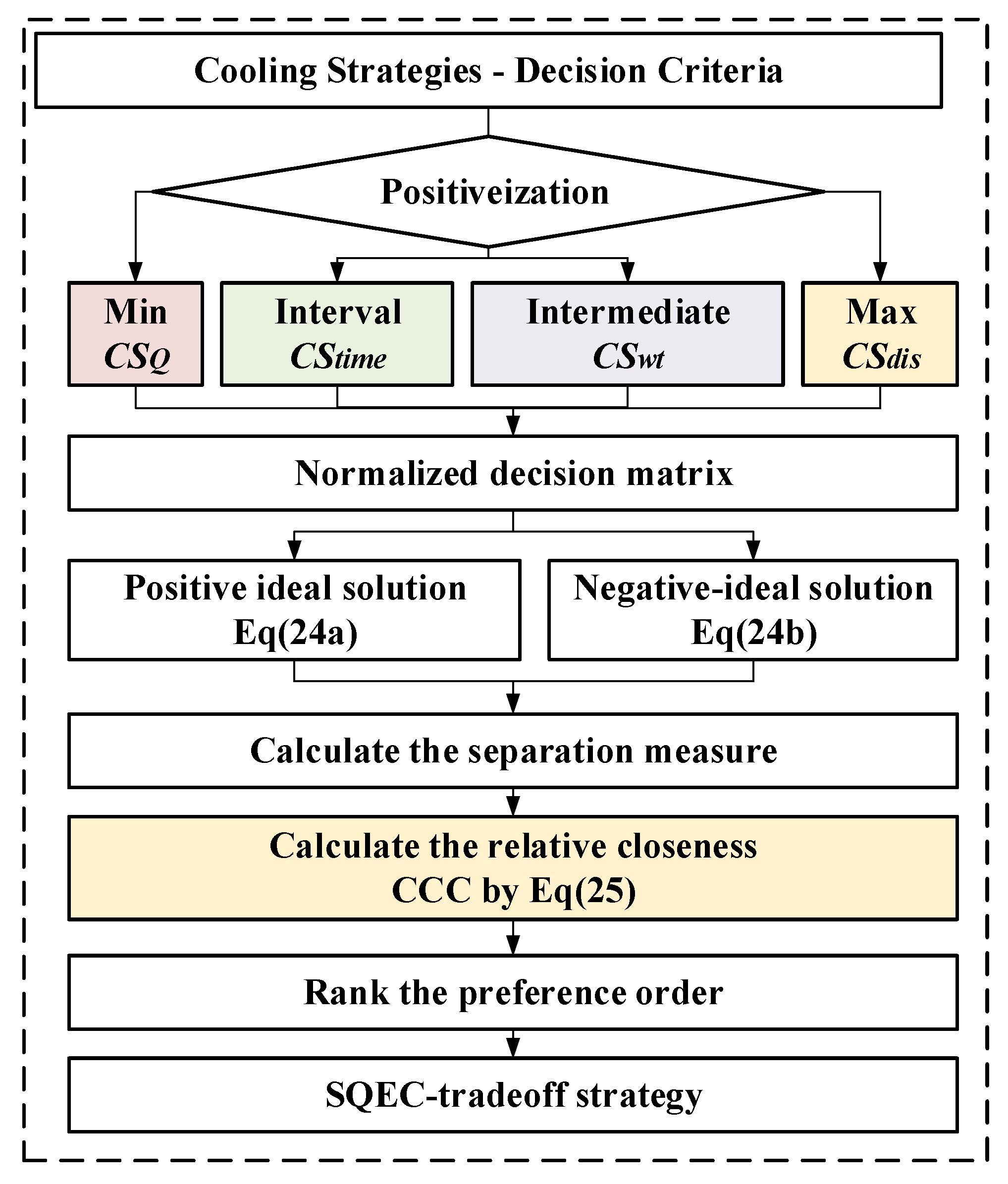
- In practical engineering projects, water pipe spacing is considered a maximum indicator, where increased spacing leads to lower costs due to reduced expenses on materials, labor, and space. This is especially significant in dam construction, where the costs of transporting, storing, and placing water pipes on the dam are extensive.
- Cooling water flow rate is viewed as a minimum indicator, with smaller flow rates providing greater benefits. High-powered pumps are required to achieve high-flow cooling water, generating additional energy consumption, particularly during the construction of dams, where limited space and height differences in the water system require specialized design considerations.
- Cooling water temperature is regarded as an intermediate-type indicator due to its effect on the temperature gradient around the cooling water pipe. If the water temperature is too low, it can result in a large temperature gradient, which increases the risk of cracking around the water pipe [7]. Conversely, high water temperature in the cooling water pipe affects cooling efficiency, and controlling cooling water temperature often requires high power compressors. Compressors are energy-intensive devices that incur high cooling costs, particularly when the external ambient temperature is significantly higher than the target temperature.
- Cooling time is classified as an interval-type indicator. Prolonged cooling times can lead to increased costs, while too-short cooling times can result in incomplete hydration heat release of concrete, leading to temperature recovery issues later on [54], which ultimately has a detrimental effect on the structure. Typically, around 60–80% of the heat of hydration is released after around 28 days of concrete age, with more than 90% released when the design age of 90 days is reached. Therefore, cooling time needs to correspond with the design strength attainment of the concrete material, with the cooling time being determined by a surrogate model.
3. Implementation of SQEC-TSOM
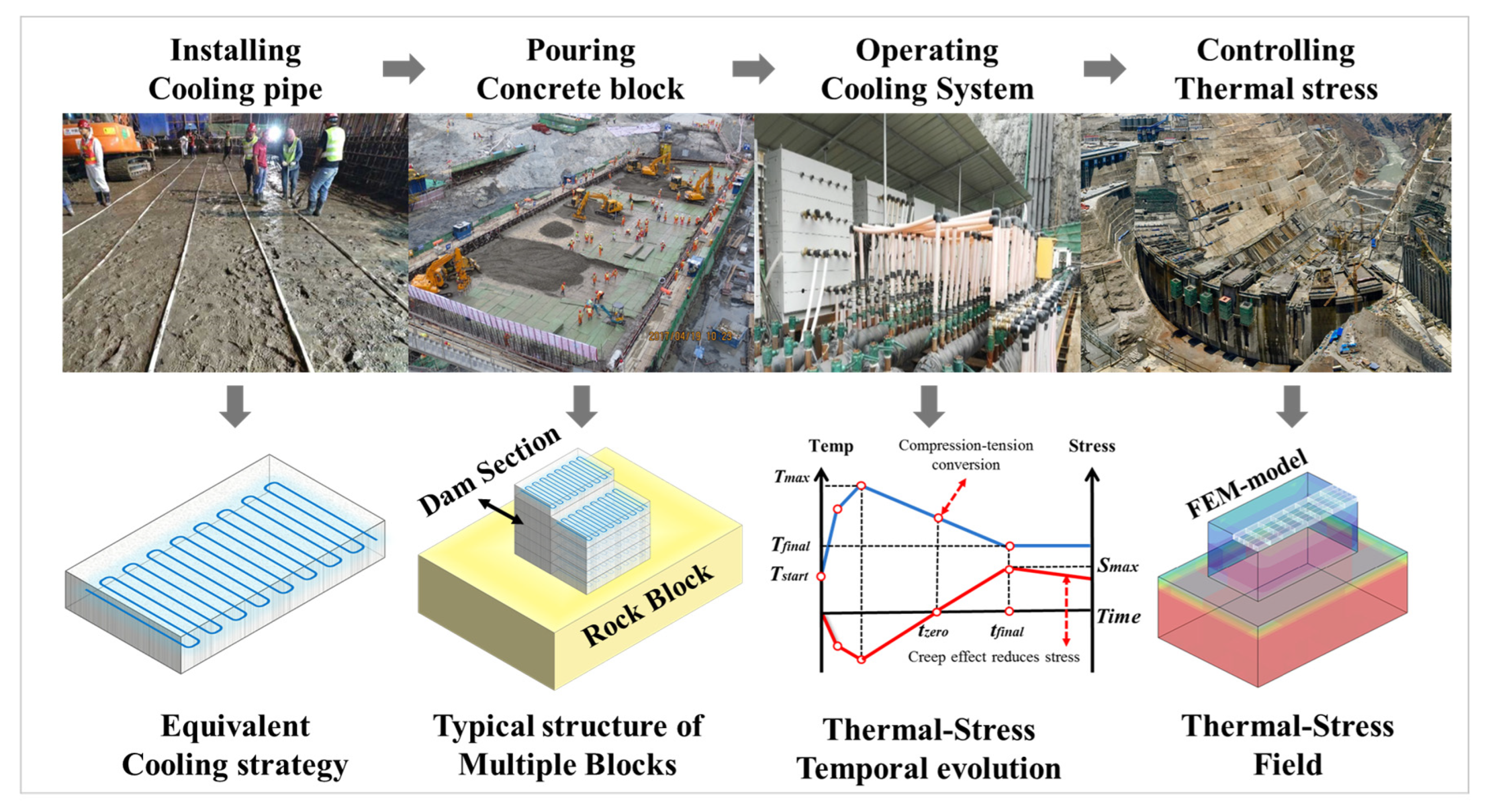
3.1. Implementation of TSMM
3.1.1. Temperature Field Simulations
Heat Conduction
Thermal Properties of Materials
Cooling System Simulation
3.1.2. Stress Field Simulation
3.1.3. Safety Performance Assessment
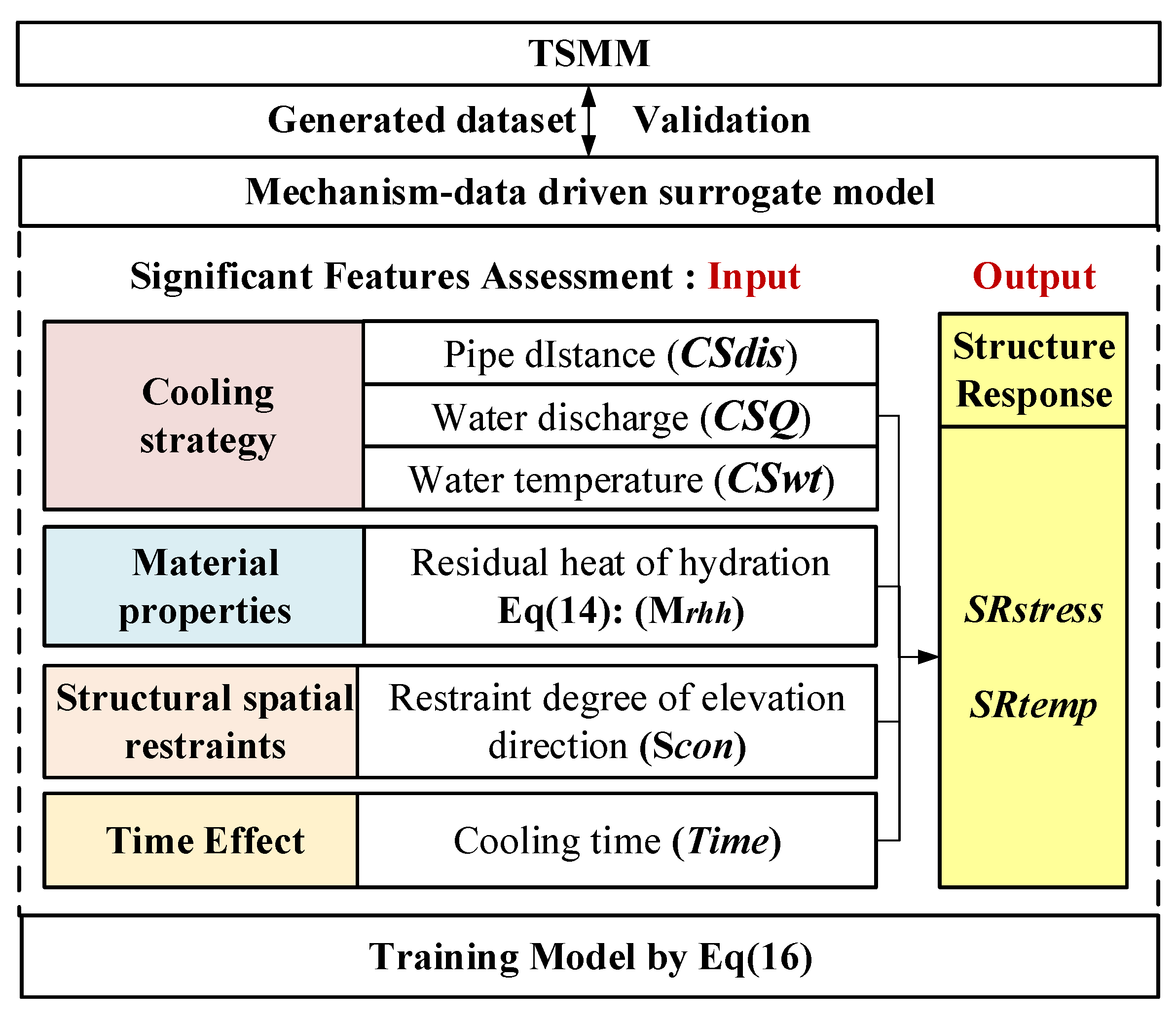
3.2. Implementation of MD-SM
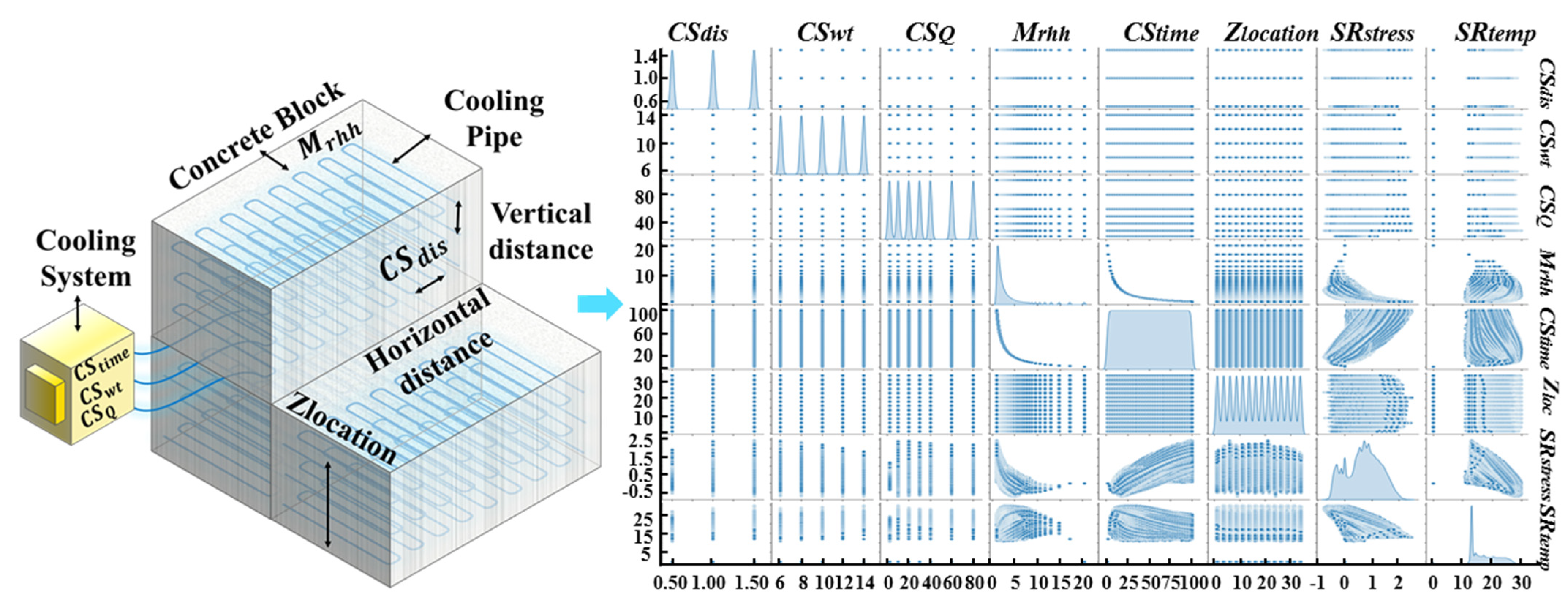
3.2.1. Selection of Important Features
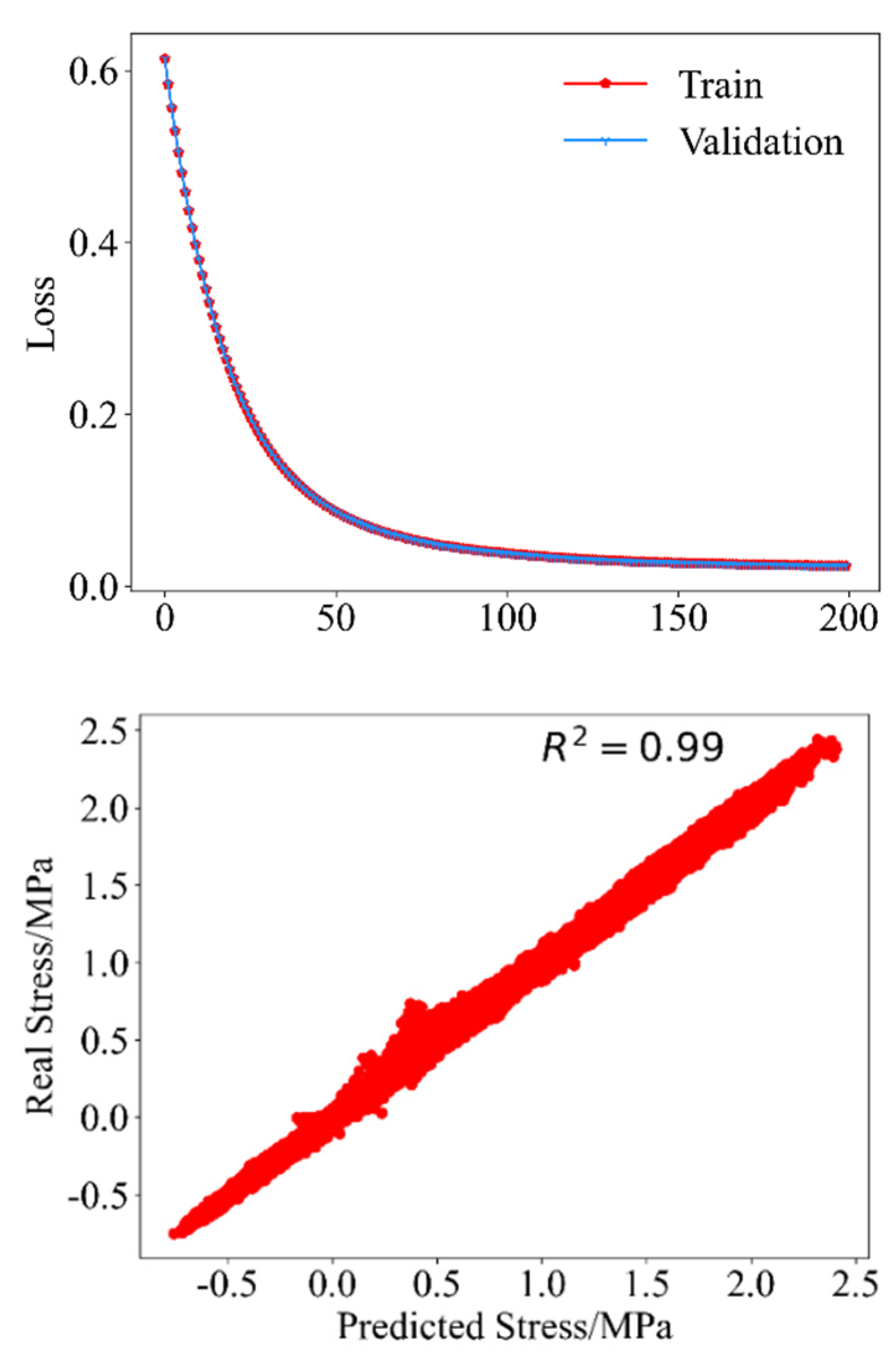
3.2.2. Surrogate Model Selection and Training
3.2.3. Assessment of Surrogate Models
3.2.4. Datasets and Model Training
3.3. Implementation of IOM
3.3.1. Objective Function
3.3.2. Constraints
3.3.3. Algorithm Process of NSGA2
3.4. Implementation of MCDM
4. Case Study
4.1. TSSM of Arch Dam
4.1.1. Mechanistic Model Based on Actual Engineering
4.1.2. Calculation Parameters Configuration
4.1.3. TSSM Validation
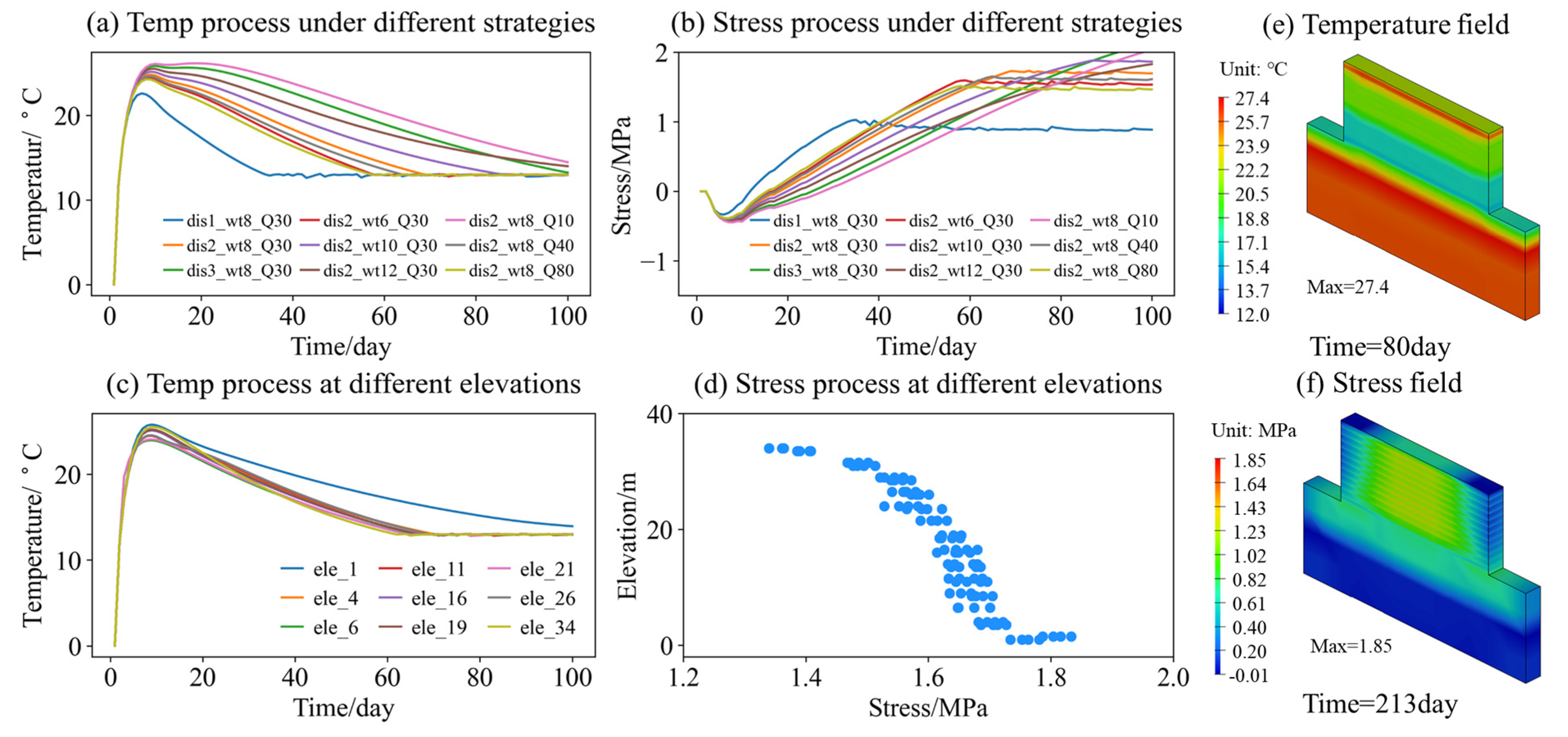
Temperature Response Under Different Cooling Strategies
Stress Response Under Different Cooling Strategies
Temperature and Stress Response at Different Elevations Under the Same Cooling Strategy
Structural Space Temperature and Stress Response
4.2. Surrogate Model for Arch Dams
4.2.1. Dataset Generation
4.2.2. Model Training
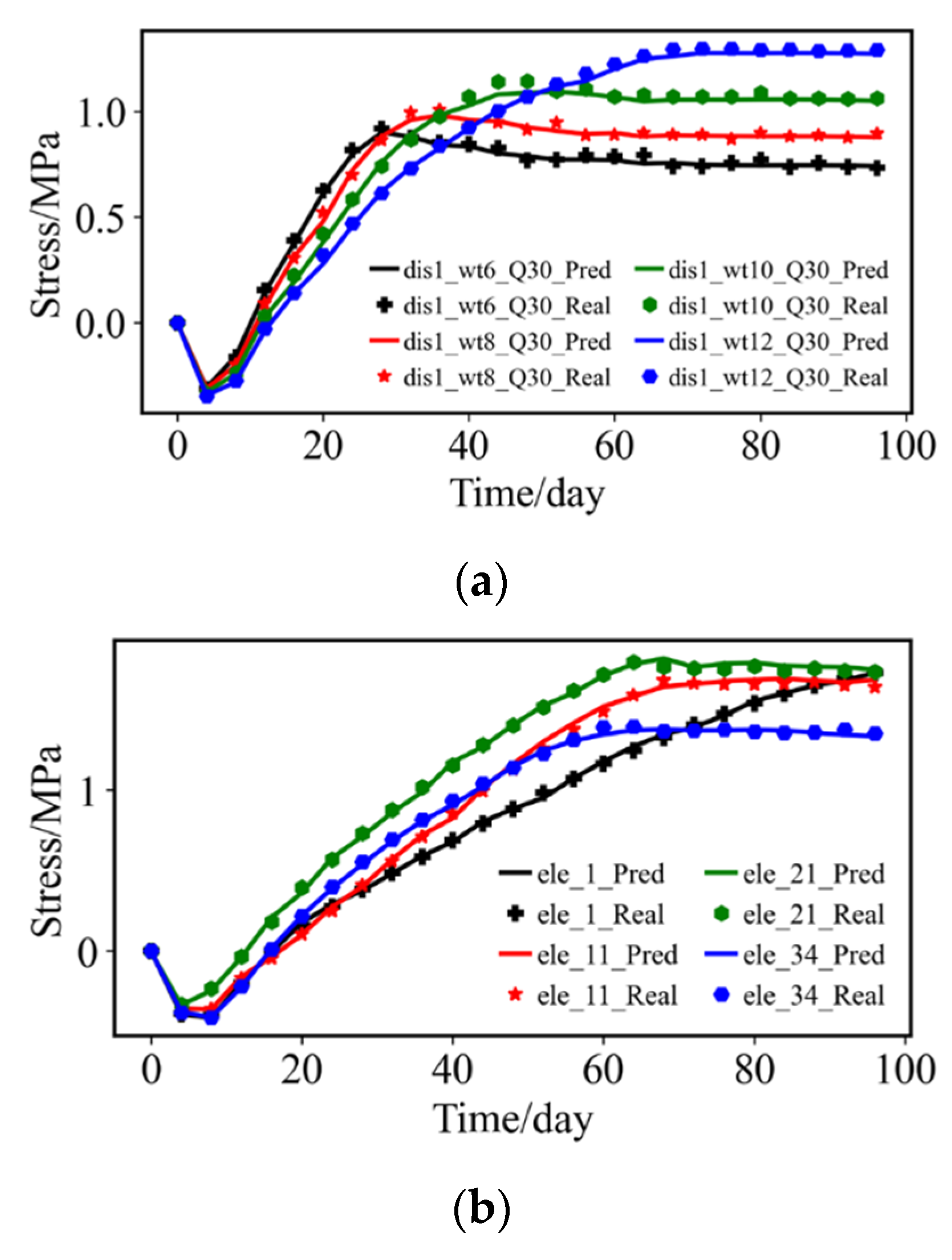
4.2.3. Model Validation
4.2.4. Model Interpretability
4.2.5. Comparative Discussion of Surrogate Model and Mechanism Model
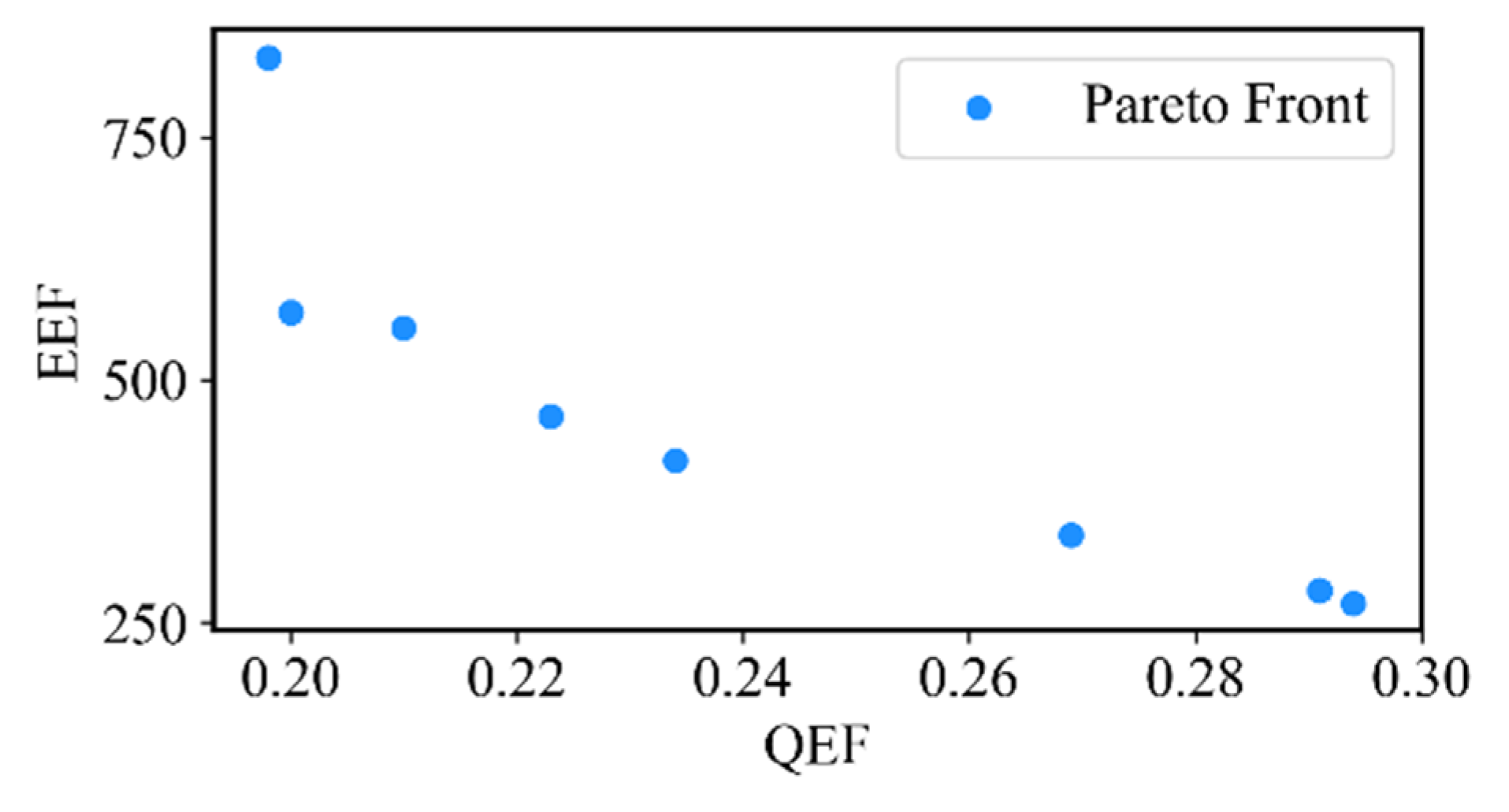
4.3. Optimization Model
4.4. Decision Model
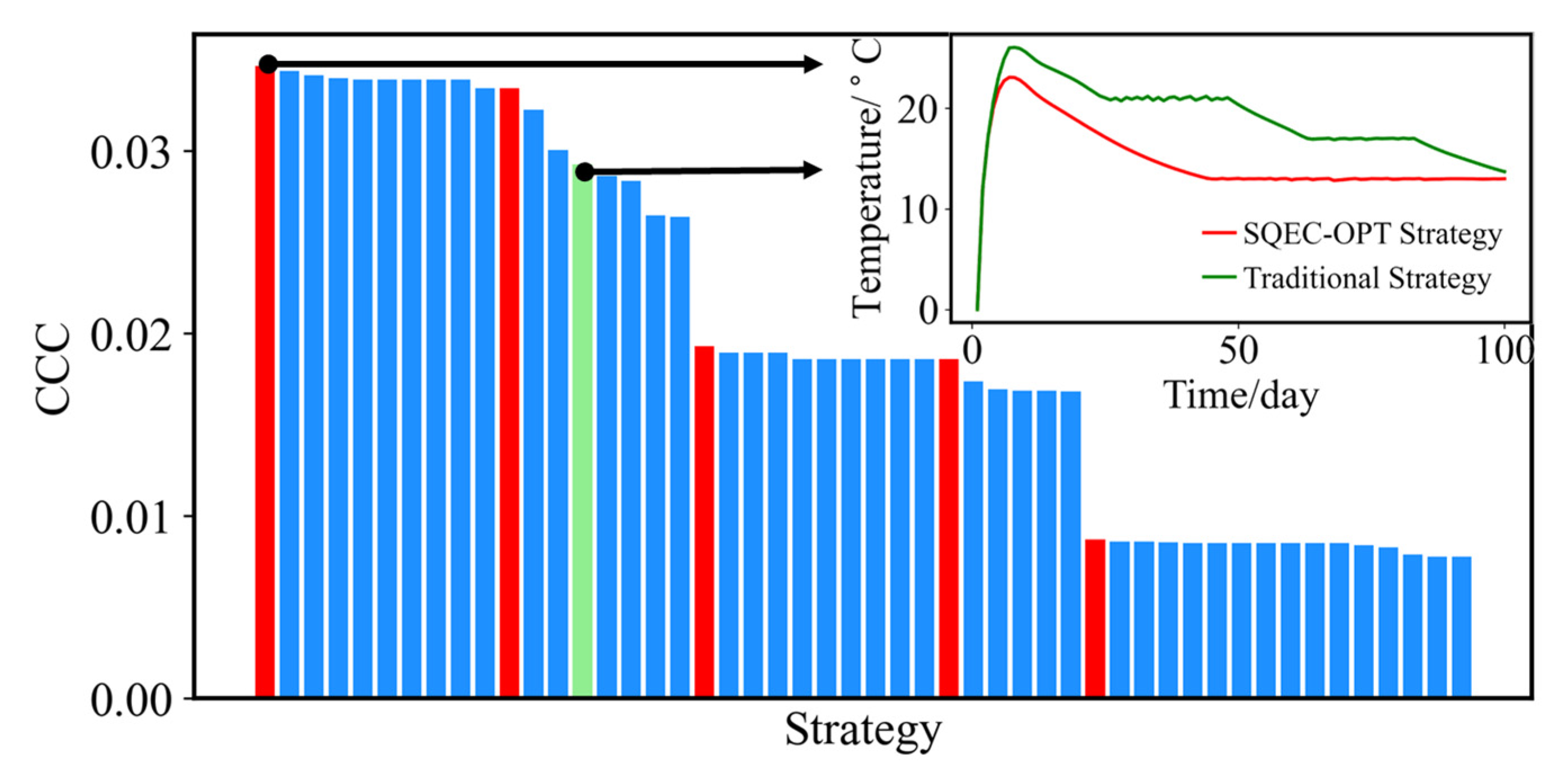
4.4.1. Strategy Comparison
4.4.2. Optimization Strategy Versus Traditional Strategy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | Greek Symbols |
| TSMM | Thermal Stress Simulation Mechanism Model |
| MD-SM | mechanism data-driven surrogate model |
| IOM | multi-objective optimization model (IOM). |
| SEF | structural safety evaluation function |
| QEF | material quality evaluation function |
| EEF | cooling efficiency evaluation function |
| SEQC-TSOM | the Safety–Quality–Efficiency–Cost–Balance Thermal Stress Management Strategy Intelligent Optimization Method |
| the current step stress increment | |
| the current step strain increment | |
| elastic strain increment | |
| creep strain increment | |
| temperature strain increment. | |
| autogenous shrinkage increment. | |
| current time-step equivalent elastic modulus | |
| coefficient matrix | |
| final elastic modulus | |
| , | material-dependent constants |
| creep produced under unit stress | |
| , , , | creep parameters |
| equivalent elastic matrix. | |
| concrete splitting strength | |
| structural stress level | |
| safety factor | |
| design tensile strength of concrete | |
| equivalent age | |
| final degree of hydration | |
| initial degree of hydration | |
| R | ideal gas constant, equal to 8.314 J/(mol∙K) |
| apparent activation energy of concrete | |
| heat emitted per unit volume per unit time | |
| surface temperature | |
| surface heat dissipation coefficient | |
| air temperature | |
| heat of hydration function | |
| final adiabatic temperature rise | |
| and | hydration heat dissipation coefficient of concrete |
| cooling effect function | |
| cooling water temperature | |
| fitting coefficients, which are related to the thermal properties of concrete, the length of the water pipe and the flow rate through the water | |
| thermal conductivity of concrete | |
| length of the cooling water pipe | |
| specific heat | |
| density | |
| flow rate of water | |
| the ratio of the equivalent thermal conductivity coefficient to the thermal conductivity coefficient, | |
| vertical spacing | |
| horizontal spacing | |
| equivalent cooling diameter | |
| residual heat of hydration of the material | |
| maximum temperature | |
| final temperature | |
| loss function | |
| regularization term | |
| RMSE | root-mean-square error |
| R2 | coefficient of determination |
| spacing of cooling water pipes | |
| water temperature | |
| water flow rate | |
| the indicator in the strategy | |
| positive ideal solution | |
| negative ideal solution | |
| cooling comprehensive cost index | |
| weight occupied by the jth indicator |
References
- Bofang, Z. Thermal Stresses and Temperature Control of Mass Concrete; Elsevier Inc.: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- ACI Committee. ACI 207.2R-07 Report on Thermal and Volume Change Effects on Cracking of Mass Concrete; ACI Committee: Farmington Hills, MI, USA, 2007. [Google Scholar]
- Pesavento, F.; Knoppik, A.; Smilauer, V.; Briffaut, M.; Rossi, P. Numerical Modelling. Thermal Cracking of Massive Concrete Structures. State of the Art Report of the RILEM Technical Committee 254-CMS; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- ACI Committee. ACI 231 Report on Early-Age Cracking: Causes, Measurement, and Mitigation; ACI Committee: Farmington Hills, MI, USA, 2010. [Google Scholar]
- Li, Y.; Nie, L.; Wang, B. A numerical simulation of the temperature cracking propagation process when pouring mass concrete. Autom. Constr. 2014, 37, 203–210. [Google Scholar] [CrossRef]
- Tasri, A.; Susilawati, A. Effect of cooling water temperature and space between cooling pipes of post-cooling system on temperature and thermal stress in mass concrete. J. Build. Eng. 2019, 24, 100731. [Google Scholar] [CrossRef]
- Tasri, A.; Susilawati, A. Effect of material of post-cooling pipes on temperature and thermal stress in mass concrete. Structures 2019, 20, 204–212. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Lothenbach, B.; Kulik, D.A.; Matschei, T.; Balonis, M.; Baquerizo, L.; Dilnesa, B.; Miron, G.D.; Myers, R.J. Cemdata18: A chemical thermodynamic database for hydrated Portland cements and alkali-activated materials. Cem. Concr. Res. 2019, 115, 472–506. [Google Scholar] [CrossRef]
- Wang, L.; Yang, H.; Dong, Y.; Chen, E.; Tang, S. Environmental evaluation, hydration, pore structure, volume deformation and abrasion resistance of low heat Portland (LHP) cement-based materials. J. Clean. Prod. 2018, 203, 540–558. [Google Scholar] [CrossRef]
- Maruyama, I.; Lura, P. Properties of early-age concrete relevant to cracking in massive concrete. Cem. Concr. Res. 2019, 123, 105770. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, Y.; Li, Q.; Ma, R. Restrained cracking failure behavior of concrete due to temperature and shrinkage. Constr. Build. Mater. 2020, 244, 118318. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Nguyen, V.; Lura, P.; Dao, V.T. Temperature-stress testing machine—A state-of-the-art design and its unique applications in concrete research. Cem. Concr. Compos. 2019, 102, 28–38. [Google Scholar] [CrossRef]
- Xin, J.; Zhang, G.; Liu, Y.; Wang, Z.; Wu, Z. Evaluation of behavior and cracking potential of early-age cementitious systems using uniaxial restraint tests: A review. Constr. Build. Mater. 2020, 231, 117146. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Q.; Hu, Y.; Ma, R. Double Feedback Control Method for Determining Early-Age Restrained Creep of Concrete Using a Temperature Stress Testing Machine. Materials 2018, 11, 1079. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, Y.; Ma, R.; Wang, J.; Li, Q. Concrete thermal failure criteria, test method, and mechanism: A review. Constr. Build. Mater. 2021, 283, 122762. [Google Scholar] [CrossRef]
- Keshavarzi, B.; Kim, Y.R. A dissipated pseudo strain energy-based failure criterion for thermal cracking and its verification using thermal stress restrained specimen tests. Constr. Build. Mater. 2020, 233, 117199. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, G.; Huang, S.; Rao, R.; Hu, C. Experimental and finite element investigations on the temperature field of a massive bridge pier caused by the hydration heat of concrete. Constr. Build. Mater. 2018, 192, 240–252. [Google Scholar] [CrossRef]
- Hu, Y.; Zuo, Z.; Li, Q.; Duan, Y. Boolean-Based Surface Procedure for the External Heat Transfer Analysis of Dams during Construction. Math. Probl. Eng. 2013, 2013, 175616. [Google Scholar] [CrossRef]
- Conceição, J.; Faria, R.; Azenha, M.; Miranda, M. A new method based on equivalent surfaces for simulation of the post-cooling in concrete arch dams during construction. Eng. Struct. 2020, 209, 109976. [Google Scholar] [CrossRef]
- Ding, J.; Chen, S. Simulation and feedback analysis of the temperature field in massive concrete structures containing cooling pipes. Appl. Therm. Eng. 2013, 61, 554–562. [Google Scholar] [CrossRef]
- Tatin, M.; Briffaut, M.; Dufour, F.; Simon, A.; Fabre, J.-P. Statistical modelling of thermal displacements for concrete dams: Influence of water temperature profile and dam thickness profile. Eng. Struct. 2018, 165, 63–75. [Google Scholar] [CrossRef]
- Santillán, D.; Salete, E.; Toledo, M. A methodology for the assessment of the effect of climate change on the thermal-strain–stress behaviour of structures. Eng. Struct. 2015, 92, 123–141. [Google Scholar] [CrossRef]
- Bažant, Z.P. Prediction of concrete creep and shrinkage: Past, present and future. Nucl. Eng. Des. 2001, 203, 27–38. [Google Scholar] [CrossRef]
- Rasoolinejad, M.; Rahimi-Aghdam, S.; Bažant, Z.P. Prediction of autogenous shrinkage in concrete from material composition or strength calibrated by a large database, as update to model B4. Mater. Struct. Mater. Constr. 2019, 52, 33. [Google Scholar] [CrossRef]
- Zuo, Z.; Hu, Y.; Li, Q.; Zhang, L. Data Mining of the Thermal Performance of Cool-Pipes in Massive Concrete via In Situ Monitoring. Math. Probl. Eng. 2014, 2014, 985659. [Google Scholar] [CrossRef]
- Bofang, Z.; Jianbo, C. Finite Element Analysis of Effect of Pipe Cooling in Concrete Dams. J. Constr. Eng. Manag. 1989, 115, 487–498. [Google Scholar] [CrossRef]
- Cheng, J.; Li, T.C.; Liu, X.; Zhao, L.H. A 3D discrete FEM iterative algorithm for solving the water pipe cooling problems of massive concrete structures. Int. J. Numer. Anal. Methods Géoméch. 2016, 40, 487–508. [Google Scholar] [CrossRef]
- Yang, J.; Hu, Y.; Zuo, Z.; Jin, F.; Li, Q. Thermal analysis of mass concrete embedded with double-layer staggered heterogeneous cooling water pipes. Appl. Therm. Eng. 2012, 35, 145–156. [Google Scholar] [CrossRef]
- Zhong, R.; Hou, G.-P.; Qiang, S. An improved composite element method for the simulation of temperature field in massive concrete with embedded cooling pipe. Appl. Therm. Eng. 2017, 124, 1409–1417. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Chang, X.; Zhou, W.; Cheng, Y.; Duan, Y. Precise simulation analysis of the thermal field in mass concrete with a pipe water cooling system. Appl. Therm. Eng. 2015, 78, 449–459. [Google Scholar] [CrossRef]
- ACI 207.4R-20: Report on Cooling and Insulating Systems for Mass Concrete. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal.aspx?m=details&id=51729338 (accessed on 9 May 2023).
- Azenha, M.; Kanavaris, F.; Schlicke, D.; Jędrzejewska, A.; Benboudjema, F.; Honorio, T.; Šmilauer, V.; Serra, C.; Forth, J.; Riding, K.; et al. Recommendations of RILEM TC 287-CCS: Thermo-chemo-mechanical modelling of massive concrete structures towards cracking risk assessment. Mater. Struct. 2021, 54, 135. [Google Scholar] [CrossRef]
- Kheradmand, M.; Azenha, M.; Vicente, R.; de Aguiar, J.L. An innovative approach for temperature control of massive concrete structures at early ages based on post-cooling: Proof of concept. J. Build. Eng. 2020, 32, 101832. [Google Scholar] [CrossRef]
- Lu, X.; Chen, B.; Tian, B.; Li, Y.; Lv, C.; Xiong, B. A new method for hydraulic mass concrete temperature control: Design and experiment. Constr. Build. Mater. 2021, 302, 124167. [Google Scholar] [CrossRef]
- Kang, F.; Wu, Y.; Li, J.; Li, H. Dynamic parameter inverse analysis of concrete dams based on Jaya algorithm with Gaussian processes surrogate model. Adv. Eng. Inform. 2021, 49, 101348. [Google Scholar] [CrossRef]
- Lin, C.; Li, T.; Chen, S.; Yuan, L.; van Gelder, P.; Yorke-Smith, N. Long-term viscoelastic deformation monitoring of a concrete dam: A multi-output surrogate model approach for parameter identification. Eng. Struct. 2022, 266, 114553. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Mahdavi, G. Generalized uncertainty in surrogate models for concrete strength prediction. Eng. Appl. Artif. Intell. 2023, 122, 106155. [Google Scholar] [CrossRef]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting concrete compressive strength using hybrid ensembling of surrogate machine learning models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Esteghamati, M.Z.; Flint, M.M. Do all roads lead to Rome? A comparison of knowledge-based, data-driven, and physics-based surrogate models for performance-based early design. Eng. Struct. 2023, 286, 116098. [Google Scholar] [CrossRef]
- Alavipour, S.R.; Arditi, D. Time-cost tradeoff analysis with minimized project financing cost. Autom. Constr. 2019, 98, 110–121. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P.; Elamrousy, K.M.; González-Cruz, M.C. Non-linear time-cost trade-off models of activity crashing: Application to construction scheduling and project compression with fast-tracking. Autom. Constr. 2019, 97, 229–240. [Google Scholar] [CrossRef]
- Ghoddousi, P.; Eshtehardian, E.; Jooybanpour, S.; Javanmardi, A. Multi-mode resource-constrained discrete time–cost-resource optimization in project scheduling using non-dominated sorting genetic algorithm. Autom. Constr. 2013, 30, 216–227. [Google Scholar] [CrossRef]
- Salmasnia, A.; Mokhtari, H.; Abadi, I.N.K. A robust scheduling of projects with time, cost, and quality considerations. Int. J. Adv. Manuf. Technol. 2012, 60, 631–642. [Google Scholar] [CrossRef]
- Monghasemi, S.; Nikoo, M.R.; Fasaee, M.A.K.; Adamowski, J. A novel multi criteria decision making model for optimizing time–cost–quality trade-off problems in construction projects. Expert Syst. Appl. 2015, 42, 3089–3104. [Google Scholar] [CrossRef]
- Mungle, S.; Benyoucef, L.; Son, Y.-J.; Tiwari, M. A fuzzy clustering-based genetic algorithm approach for time–cost–quality trade-off problems: A case study of highway construction project. Eng. Appl. Artif. Intell. 2013, 26, 1953–1966. [Google Scholar] [CrossRef]
- Zhang, H.; Xing, F. Fuzzy-multi-objective particle swarm optimization for time–cost–quality tradeoff in construction. Autom. Constr. 2010, 19, 1067–1075. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Alamry, E. Swarm Intelligence: Principles, Advances, and Applications; CRC Press, Inc.: Boca Raton, FL, USA, 2015. [Google Scholar]
- Mirjalili, S.; Dong, J.S. Multi-Objective Optimization using Artificial Intelligence Techniques; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J. From evolutionary computation to the evolution of things. Nature 2015, 521, 476–482. [Google Scholar] [CrossRef]
- Shih, H.-S. TOPSIS Basics. In TOPSIS and its Extensions: A Distance-Based MCDM Approach; Springer International Publishing: Cham, Switzerland, 2022; pp. 17–31. [Google Scholar] [CrossRef]
- Li, Q.; Liang, G.; Hu, Y.; Zuo, Z. Numerical Analysis on Temperature Rise of a Concrete Arch Dam after Sealing Based on Measured Data. Math. Probl. Eng. 2014, 2014, 602818. [Google Scholar] [CrossRef]
- Gao, X.; Li, Q.; Liu, Z.; Zheng, J.; Wei, K.; Tan, Y.; Yang, N.; Liu, C.; Lu, Y.; Hu, Y. Modelling the Strength and Fracture Parameters of Dam Gallery Concrete Considering Ambient Temperature and Humidity. Buildings 2022, 12, 168. [Google Scholar] [CrossRef]
- Mi, Z.; Hu, Y.; Li, Q.; Gao, X.; Yin, T. Maturity model for fracture properties of concrete considering coupling effect of curing temperature and humidity. Constr. Build. Mater. 2019, 196, 1–13. [Google Scholar] [CrossRef]
- Mi, Z.; Hu, Y.; Li, Q.; Zhu, H. Elevated temperature inversion phenomenon in fracture properties of concrete and its application to maturity model. Eng. Fract. Mech. 2018, 199, 294–307. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y. Hybrid machine learning model and Shapley additive explanations for compressive strength of sustainable concrete. Constr. Build. Mater. 2022, 330, 127298. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Liang, M.; Chang, Z.; He, S.; Chen, Y.; Gan, Y.; Schlangen, E.; Šavija, B. Predicting early-age stress evolution in restrained concrete by thermo-chemo-mechanical model and active ensemble learning. Comput. Civ. Infrastruct. Eng. 2022, 37, 1809–1833. [Google Scholar] [CrossRef]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost algorithm-based prediction of concrete electrical resistivity for structural health monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 2017, 4766–4775. [Google Scholar]
- Wang, Y.; Wang, B.-C.; Li, H.-X.; Yen, G.G. Incorporating Objective Function Information Into the Feasibility Rule for Constrained Evolutionary Optimization. IEEE Trans. Cybern. 2016, 46, 2938–2952. [Google Scholar] [CrossRef]





| Strategies | Type of Indicator | Characteristics of Indicators |
|---|---|---|
| Maximization | Greater spacing between water pipes results in lower costs. | |
| Minimization | Lower flow rates yield higher benefits. | |
| Interval type | The ideal cooling time corresponds to the release of 70% to 90% of the heat of hydration from the concrete. | |
| Intermediate | The ideal water temperature should be maintained at a certain value, both to avoid cracking due to excessive gradients and to avoid temperatures too high to reach the target temperature and thus cost. |
| Name/Type | Concrete | Rock |
|---|---|---|
| Modulus of elasticity/GPa | 44 | 26 |
| Poisson’s ratio | 0.215 | 0.25 |
| Coefficient of linear expansion/(10−6/°C) | 4.94 | 6.79 |
| Density/(kg/m3) | 2663 | 2500 |
| Specific heat capacity/(KJ/(kg°C) | 0.86 | 0.85 |
| Adiabatic temperature rise θ/°C | 26.0 | - |
| Exothermic coefficient of hydration/m | 0.39 | - |
| Thermal conductivity/(W/(m°C)) | 2.02 | 2.14 |
| Tensile strength/MPa | 3.98 | - |
| Parameter Name | Value | |
|---|---|---|
| Cooling System | Pipe spacing/m | 0.5–1.5 |
| Water flow/(m3/d) | 2.0–80.0 | |
| Water temperature/°C | 6.0–14.0 | |
| Temperature conditions | Rock temperature/°C | 25.9 |
| Casting temperature/°C | 12.0 | |
| Target temperature/°C | 13.0 | |
| Ambient temperature/°C | From statistical averages | |
| Construction schedule | Pouring interval/d | 7 |
| Calculate time/d | 213 | |
| Strategy (ID) | CSdis (/m) | CSwt (/°C) | CSQ/(m3/d) | Cstime (/Day) | CCC |
|---|---|---|---|---|---|
| S8 | 0.6 | 9.80 | 32.46 | 56.9 | 0.035 |
| S44 | 0.6 | 9.05 | 32.49 | 56.9 | 0.033 |
| S49 | 1.5 | 8.00 | 30.00 | 90.0 | 0.029 |
| S3 | 0.6 | 12.34 | 47.91 | 83.2 | 0.019 |
| S23 | 0.5 | 12.34 | 47.92 | 83.2 | 0.019 |
| S27 | 0.7 | 6.21 | 67.93 | 28.3 | 0.009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, R.; Zhang, F.; Li, Q.; Hu, Y.; Liu, Z.; Tan, Y.; Zhang, Q. Intelligent Optimal Strategy for Balancing Safety–Quality–Efficiency–Cost in Massive Concrete Construction. Intell. Infrastruct. Constr. 2025, 1, 2. https://doi.org/10.3390/iic1010002
Ma R, Zhang F, Li Q, Hu Y, Liu Z, Tan Y, Zhang Q. Intelligent Optimal Strategy for Balancing Safety–Quality–Efficiency–Cost in Massive Concrete Construction. Intelligent Infrastructure and Construction. 2025; 1(1):2. https://doi.org/10.3390/iic1010002
Chicago/Turabian StyleMa, Rui, Fengqiang Zhang, Qingbin Li, Yu Hu, Zhaolin Liu, Yaosheng Tan, and Qinglong Zhang. 2025. "Intelligent Optimal Strategy for Balancing Safety–Quality–Efficiency–Cost in Massive Concrete Construction" Intelligent Infrastructure and Construction 1, no. 1: 2. https://doi.org/10.3390/iic1010002
APA StyleMa, R., Zhang, F., Li, Q., Hu, Y., Liu, Z., Tan, Y., & Zhang, Q. (2025). Intelligent Optimal Strategy for Balancing Safety–Quality–Efficiency–Cost in Massive Concrete Construction. Intelligent Infrastructure and Construction, 1(1), 2. https://doi.org/10.3390/iic1010002






