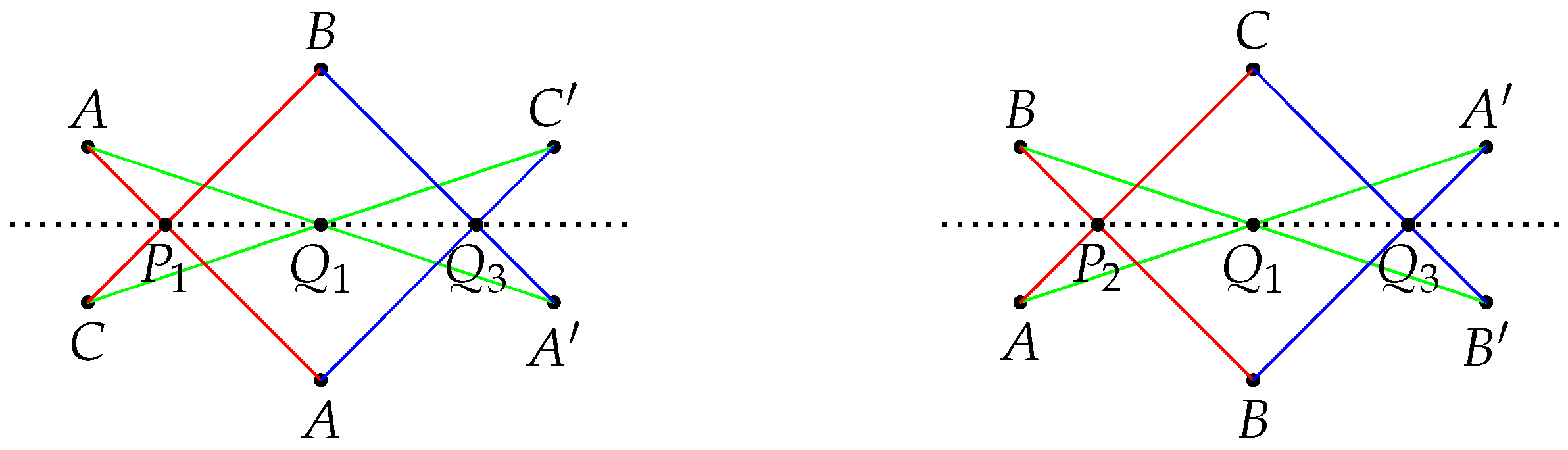1. Introduction
Historically, the Kiepert hyperbola was introduced by Ludwig Kiepert [
1] in 1869 along with solving Lemoine’s problem [
2]. The question published by Lemoine asks about the following construction problem: Given one vertex of each of the equilateral triangles placed on the sides of a triangle, construct the original triangle (Wikipedia [
2,
3]). Kiepert solved the problem and generalized to a construction in which the equilateral triangles on the sides of the original triangle were replaced by isosceles triangles. For example, denoting the base angle of the isosceles triangles by
, Kiepert showed that the lines connecting the vertices of the given triangle and the corresponding peaks of the isosceles triangles concur. By varying
, the locus of the points of concurrence gives a rectangular hyperbola known as a Kiepert hyperbola. This hyperbola contains many interesting points, usually called
triangle centers, in reference to the original triangle. In the case of Lemoine’s problem, this corresponds to
and the point of concurrence is called the First Fermat point
which arises as an interesting optimization problem [
4]. For
, the point of concurrence is the centroid
M of the reference triangle, and for
one gets the second Fermat point
. As an analogue of Lemoine’s problem and in the setting of Yiu’s problem, we may pose the following question: Given a Kiepert hyperbola, one of the two Fermat points and one vertex of the reference triangle, construct the other two vertices of the reference triangle. The question is answered directly by the main results of our note.
For a scalene triangle , let (resp. ) be its first (resp. second) Fermat point. The Kiepert hyperbola we need here is the unique conic passing through the five points and . Since it is well known that must also pass through the centroid M of , it is convenient to construct from the five points and M. We will call the reference triangle of . Yiu’s problem is stated as follows. The orientation of the triangles may be flipped for different configurations, but this situation can be understood better in a more general setting such as in the proof of Proposition 1 or in its corollaries.
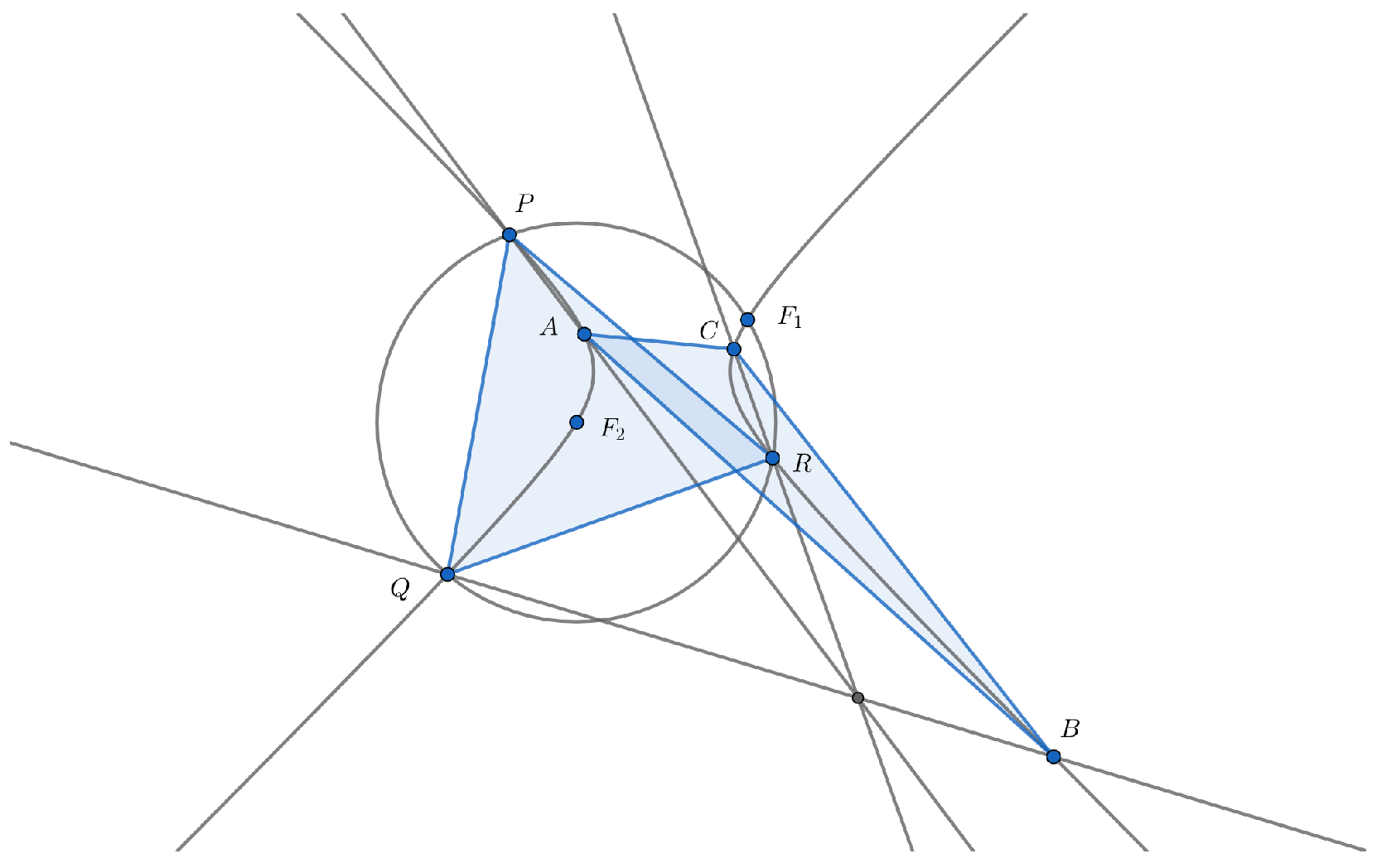
Theorem 1. Let be a Kiepert hyperbola with reference triangle Let (resp. ) be the circle centered at (resp. ) with radius . The circle (resp. ) intersects at three points (resp. ) other than (resp. ). Then one has (see Figure 1) (a) Triangle (resp. ) is equilateral;
(b) Triangle (resp. ) is triply perspective with triangle , in the sense that meet at a common point ; meet at a common point ; meet at a common point (resp. meet at a common point ; meet at a common point ; meet at a common point ); and moreover
(c) The three perspectors in (b) are collinear in a line that also passes through the three perspectors constructed from the triangle
The author first learned Paul Yiu’s problem in July 2018 from the Mathoverflow website ([
5]; See also [
6]), where Dao Thanh Oai posted and promoted Yiu’s problem. According to Dao, this result is comparable to the case of Morley triangles or Napoleon triangles, and Dao placed a great importance to this construction as Kiepert hyperbola is a very special conic which passes through many triangle centers. The author established the truth of all the statements in Yiu’s problem in November 2018, using analytic method with the help of computer algebra system, SAGE. The idea of this method involves a direct computation by introducing the slope variable
, where
is the second Fermat point. By elimination,
m will need to satisfy a cubic equation
. Then by manipulations with symmetric functions on the roots of
, one can prove all the statements of the problem. In this note, we tried to solve the problem using synthetic methods as much as possible. The statements in Theorem 2 allow one to see the general situation more transparently. Once the uniqueness of the construction is verified, this can be used to reconstruct the reference triangle, assuming that the Kiepert hyperbola, one of the two Fermat points, and one of the vertices of the reference triangle are given.
2. Preliminaries
We gather some definitions and known facts here. These are to be referred to only when necessary. The results from Lemma 1 to Proposition 1 and its corollaries may be classical, but it is not easy to sieve through the results (cf. [
7,
8,
9,
10]) to get what we need here; therefore, we provide direct proofs.
The first Fermat point (or the first isogonic center) of a triangle is constructed by erecting an equilateral triangle from the outside of each side of the triangle: The lines joining each outer vertex to the opposite vertex of the triangle concur at .
Similarly, the second Fermat point (or the second isogonic center) of a triangle is constructed by erecting an equilateral triangle from the inside of each side of the triangle.
The Nine Point Circle (or the Feuerbach circle) for a triangle is the circle that passes through the following nine points: the midpoint of each side of the triangle, the foot of each altitude, and the midpoint of the line segment from each vertex of the triangle to the orthocenter.
The Kiepert hyperbola defined in the beginning of the introduction is a rectangular hyperbola (meaning that the asymptotes are perpendicular to each other). It is known that for a triangle inscribed in a rectangular hyperbola, the orthocenter of the triangle lies on the rectangular hyperbola.
A version of the Feuerbach Conic Theorem we will use is the following: Let
be a triangle inscribed in a rectangular hyperbola. Then the Feuerbach circle of
passes through the center of the rectangular hyperbola. Furthermore, the center of the Kiepert hyperbola associated with
is midway between the two Fermat points (isogonic centers) ([
11,
12]).
Any two conics are related by a projective collineation and a projective correlation: Any three distinct points on the first conic can be made to correspond to any three distinct points of the second (Ex.4 on page 79 of [
13], or Theorem 6.4.1 of [
14]).
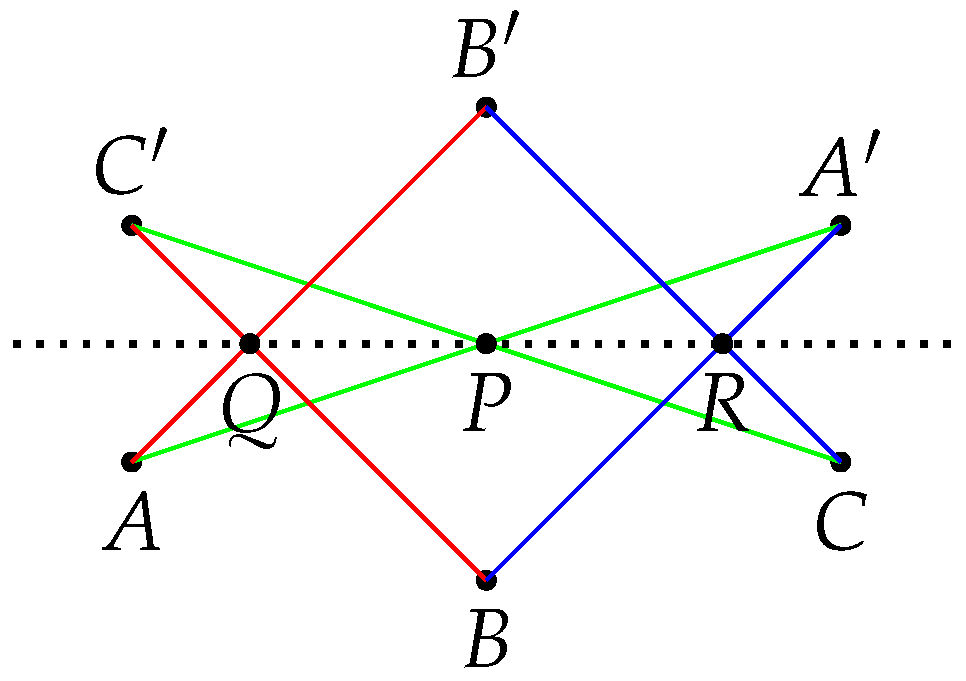
Lemma 1. Let and be two triangles inscribed in a conic such that is perspective with with perspector P, and is perspective with with perspector Q. Then there exists R in line such that is perspective with with perspector R.
Proof. The existence of
R such that
is perspective with
is guaranteed since it is well known that doubly perspective implies triply perspective. It suffices to show that the three perspectors
are collinear. Applying Pascal’s theorem (see
Figure 2) to the ordered lists
and
shows that
and
P are collinear. □
Definition 1. Let be a triangle inscribed in a conic . Let the line tangent to at A meet line at P, the line tangent to at B meet line at Q, and the line tangent to at C meet line at R. Then by a limiting case of Pascal’s theorem, it can be shown that are collinear. We call this line the Hessian line of with respect to (cf. p.130 of [15]). Lemma 2. Let and be two triply perspective triangles inscribed in a conic. Then the line passing through the three perspectors (see Lemma 1) coincides with the Hessian line of with respect to the conic.
Proof. Let the tangent line at
A (resp.
B) meet line
(resp. line
) at
(resp.
). Let
be perspective with
(resp.
) of perspector
(resp.
). Applying Pascal’s theorem (see
Figure 3) to the ordered lists
and
(resp.
and
) shows that
(resp.
) lies on line
. Hence lines
and
coincide. □
The following statement is simple and useful; it may have been known to A. Cayley (1851) in his article on triply perspective triangles inscribed in a conic, published in the Philosophical Transactions of the Royal Society. As the author has not found a specific reference, we state the result here and provide a proof.
Proposition 1. Two inscribed triangles on a conic are triply perspective if and only if they share the same Hessian line.
Proof. The necessity follows from Lemma 2. To prove the other implication, assume that two inscribed triangles and on a conic share the same Hessian line. We now prove that they are triply perspective.
By 2.6, we can apply a projective collineation and a projective correlation such that the result gives an equilateral triangle (still using the same letters) on a circle. In this case, the Hessian line is the line at infinity. Since and share the Hessian line, the Hessian line for is also the line at infinity. It follows that the triangle is also an equilateral triangle. It is clear now that the two triangles are triply perspective when the vertices are denoted with different orientations. Mapping back by the inverse collineation and correlation, we conclude that the original triangles are triply perspective. □
Corollary 1. Let and be two inscribed triangles on a conic and let L be the Hessian line of If and are perspective with a perspector Then the two triangles are triply perspective.
Proof. As in the proof of Proposition 1, we may assume that both triangles lie on a circle, and is equilateral. Now the Hessian line L is the line at infinity, and the condition shows that both triangles are perspective at a point at infinity. This forces to be three parallel lines, and we obtain an equilateral triangle on the same circle with a different orientation. Clearly the two triangles are triply perspective. □
Corollary 2. Let be three inscribed triangles on a conic and let L be the Hessian line of Assume that is perspective with (resp. ) of a perspector (resp. Then is triply perspective with , i.e., they are reverse triply perspective.
Proof. In the proof of Corollary 1, has a different orientation with respect to the equilateral triangles and on a circle. Thus and have the same orientation. It follows that is triply perspective with □
3. Proof of Theorem 1
Part (a) of Theorem 1 follows immediately from a more general result, stated as Proposition 2, by taking
to be the Kiepert hyperbola
associated with the reference triangle
and
and
to be the two Fermat points of
The formulation of this result was inspired by a comment made by Elias M. Hagos [
16] on 8 February 2021, upon his reading of the preprint of this note.
Proposition 2. Given a rectangular hyperbola of center O, let be a pair of antipodal points on i.e., O is the midpoint of the segment Assume that the circle centered at of radius intersects at (other than ). Then the triangle is equilateral.
Proof. By construction,
lie on a circle of center
and radius
. Since
is a rectangular conic containing the points
, we can apply Feuerbach’s theorem (2.5) to the triangles
and
which are inscribed in
. Let
be the midpoints of
respectively, and let
be the midpoints of
, respectively. Note that by construction,
where
O is both the center of the rectangular hyperbola
and the midpoint of
By Feuerbach’s theorem applied to the four triangles and the conic
with center
O, it follows that
and
where the last statement follows from the first three. Now, since
is the circumcenter of
, the points
are perpendicular feet from
to the sides of the triangle
. Pythagorean Theorem shows now that
is equilateral. □
Now, we reverse the process by looking at the following
model in Theorem 2, starting with
and an equilateral triangle
. Theorem 2 would conclude the rest of the statements in Theorem 1, provided that we can show that the candidate triangles
yield all generic triangles
with
as the two Fermat points (see
Figure 4, where
is labeled
).
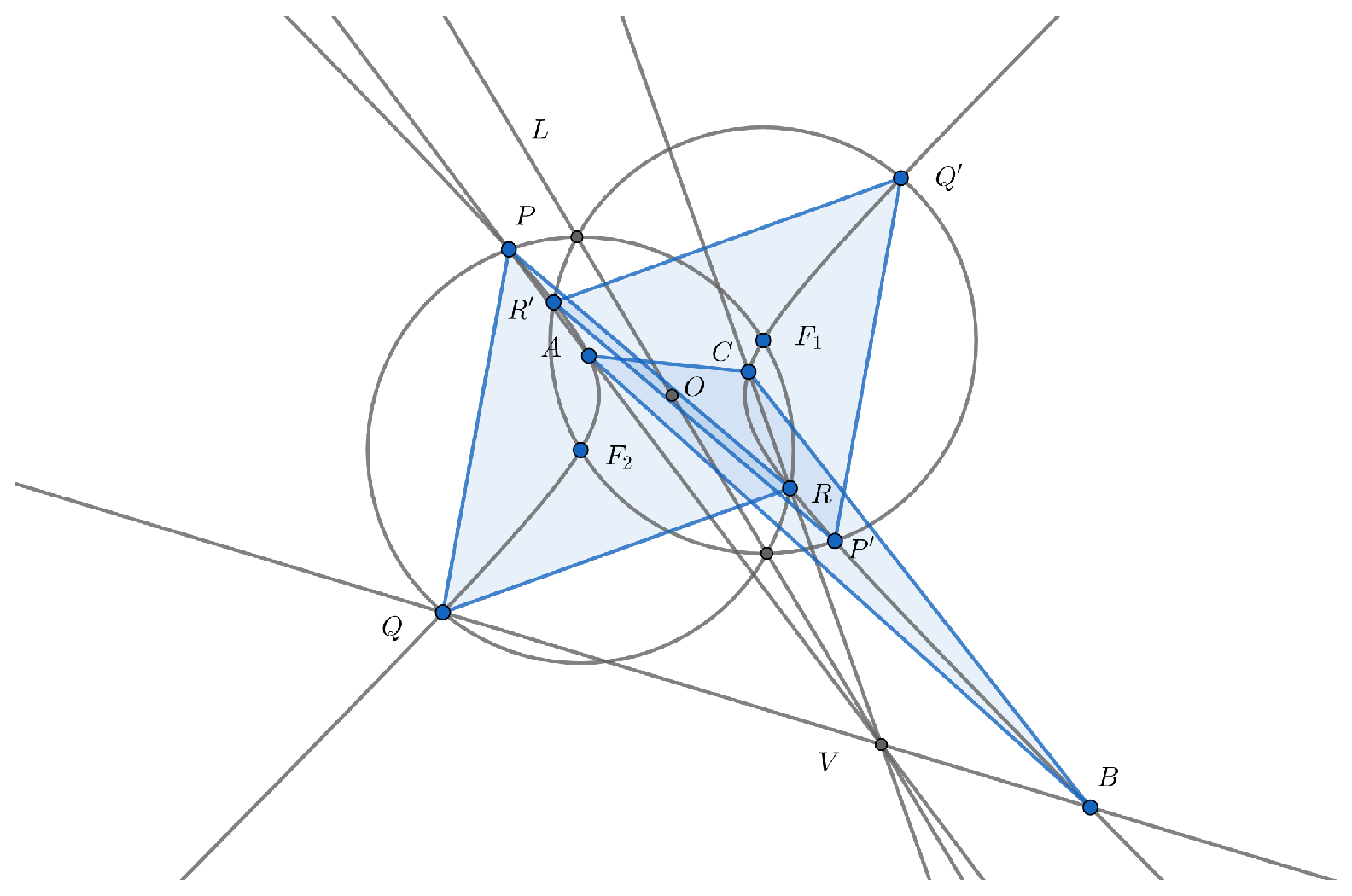
Theorem 2. Let and let (resp. ) be a circle centered at (resp. ) with radius . Let be an equilateral triangle inscribed in and let (an equilateral triangle inscribed in ) be the reflection of with respect to the center of Then
(a) The two triangles and are triply perspective with perspectors consisting of and the two intersection points of circles and . Consequently, the perspectors lie on the radical axis L of and .
(b) There is a unique conic passing through and .
(c) For any point , let be the other point of intersection of the line and . Define and in a similar way. Then is triply perspective with , and the other two perspectors lie on L. Similarly, is triply perspective with (i.e. one needs to reverse the orientation).
(d) Let be the triangle constructed in (c). Then is the Kiepert hyperbola through the two Fermat points and with respect to the reference triangle .
(e) For two distinct triangles and constructed as in (c), is triply perspective with . Both and are triply perspective with .
Proof. (a) It is clear that and intersect at and L is the line with equation The result follows by angle chasing and symmetry, noting that the cord joining the two intersection points above is of length corresponding to a circular angle of
(b) Denoting
P (using a rational parameterization of circle
) by
and turning counterclockwise
successively, we have
and
Then the unique conic
through
has the equation
and it is evident that
also passes through
which are the reflection of
with respect to the origin.
(c) By the result of (a) and Lemma 2, we know that L is the Hessian line of triangle with respect to the conic Now by the construction of triangle is perspective with with perspector hence by Corollary 1, the two triangles are triply perspective with the other two perspectors lying on Since triangle is triply perspective with both and it follows from (a) and Corollary 2 that is triply perspective with (i.e. one needs to reverse the orientation).
(d) This can be checked by a computer algebra system using the parameterization and equation given in (b).
(e) This follows from Corollary 2. □
Now it is plausible that the model in Theorem 2 should yield all generic triangles (i.e. ) up to similarity. For example, the degree of freedom is two: one from the choice of P (the position of the equilateral triangle), and one from the choice of V (the position of a perspector on L). This matches the degree of freedom for a generic triangle up to similarity. However, without further justification of the degree-of-freedom argument, the mere statement of Theorem 2 is not enough to conclude the proof of Theorem 1. For example, what if instead of the triangle in there exists another triangle in with the same Fermat points If this were the case, then we could not say anything about the triply perspective property. To address this ambiguity, we need to explain why the construction in Theorem 2 allows us to recover any general scalene triangle as a reference triangle on the Kiepert hyperbola. To do this, we verify that the equilateral triangle from the model and the reference triangle on the Kiepert hyperbola share the same Hessian line. Since we already know that the Hessian line of the equilateral triangle is which is the perpendicular bisector of it remains to check that if we start with any generic triangle with its associated Kiepert hyperbola, the Hessian line of this triangle must be the perpendicular bisector of the segment joining the two Fermat points of We check this directly as follows.
Hessian Line for a Generic Reference Triangle
Here we consider the generic case for
(corresponding to
in the statement of Theorem 2). Without loss of generality, let
We compute the two Fermat points and the Kiepert hyperbola
as follows:
and
We verify directly that the tangent line at
A intersects line
at
And similarly, the tangent line at
C intersects line
at
Note that line
is the Hessian line associated with triangle
By checking the slopes of line
and line
we see that they are perpendicular to each other. Furthermore, the common intersection of line
and line
is
which is the midpoint of
Hence the Hessian line
of
is the perpendicular bisector of
It follows that the Hessian line associated with
and
agree, being the perpendicular bisector of
This concludes the proof of Theorem 1.
In the spirit of Lemoine’s problem, we may ask how to recover the reference triangle used to construct the Kiepert hyperbola. To this end, we have the following result.
Corollary 3. Given a Kiepert hyperbola , one of the two Fermat points and a vertex of the reference triangle on , we can recover the other two vertices of the reference triangle.
Proof. Note that the center
O of
can be constructed by using 2.5. Reflecting one Fermat point with respect to
O gives another Fermat point. With
and the two Fermat points, we follow the construction as in the statements of Theorem 2 and the proof for (a) of Theorem 1 to get an equilateral triangle
. Note also that the reference triangle
plays the same role as
in Theorem 2. Using a construction similar to (c) of Theorem 2, join any vertex of
, say
P, with a vertex of the reference triangle, say
A; let line
intersect
L at a point
V (See
Figure 4). Then follow the steps in (c) to recover
B and
C. □