On the Relation Between a Locus and Poncelet’s Closure Theorem

Abstract

This article contains a synthetic proof of the following proposition: consider a conic $c_1$ and its variable chord $AB$, which subtends a right angle at a given point P. Then, the foot E of the perpendicular dropped from P onto the line $AB$ lies on a certain circle (the line being the limiting case of the circle). To prove this proposition, we show how Poncelet’s closure theorem for quadrilaterals can be derived by elementary projective considerations only (without any computations, either in Cartesian or projective coordinates). Finally, the limiting case of the proposition, where the point P lies on the conic, is also mentioned. The problem can then be reduced to Frégier’s theorem and may represent a slightly different perspective on this theorem.

1. Introduction

This paper deals with a synthetic justification of a problem, which states that the locus of points constructed by a certain procedure is always a circle or a line. We call this problem “motivational”. In the process of solving it, we will encounter several other theorems that are interesting in themselves and are closely related to what we might call the “projective generalization of the bicentric quadrilateral” (a quadrilateral that can be inscribed in and circumscribed about circles). In particular, we will prove Poncelet’s closure theorem for $n=4$ in an elementary way.

The formulation of the motivational problem (M) is shown below.

Problem M. 

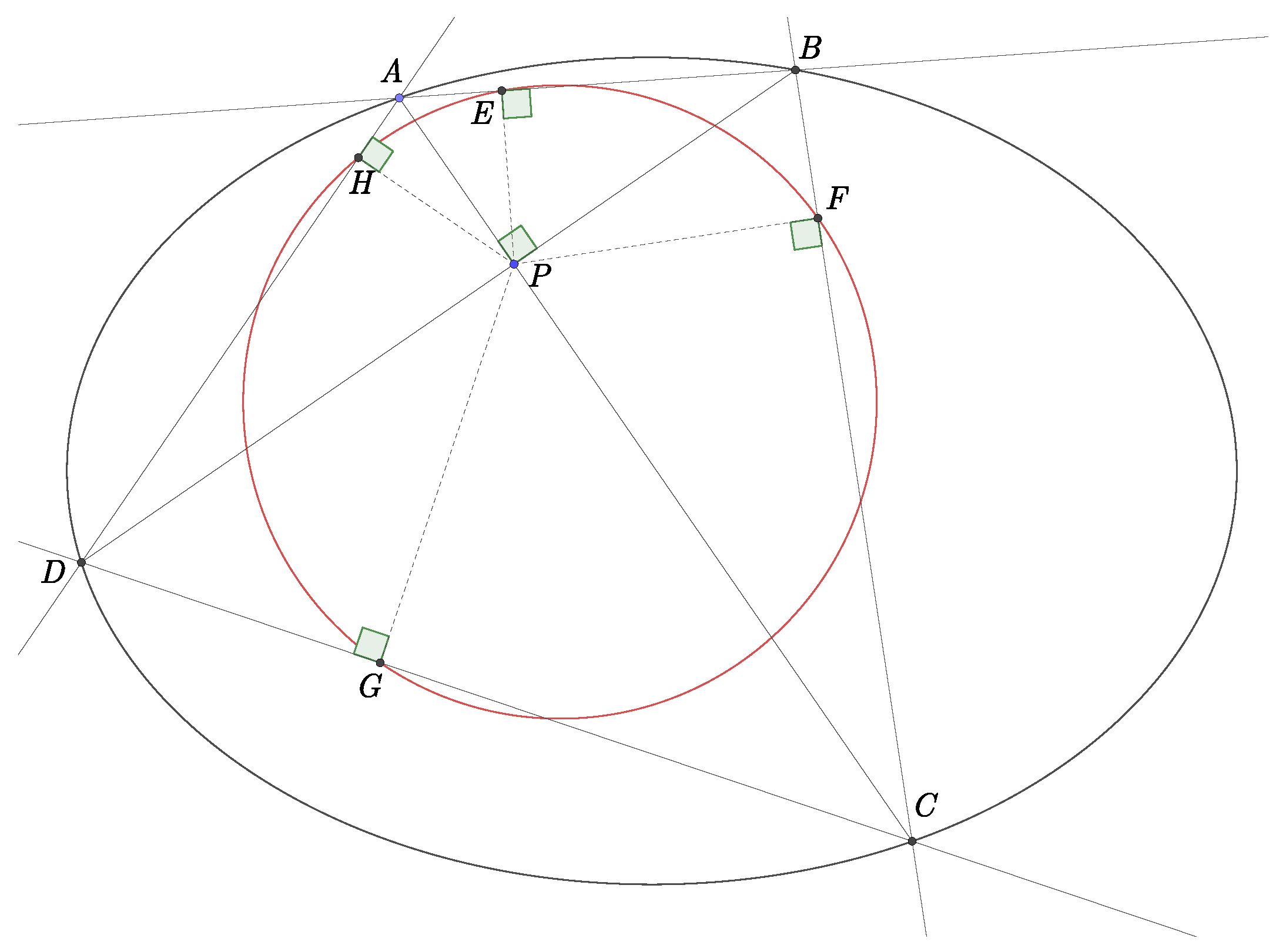
Consider an arbitrary conic $c_1$ in the plane. Let us choose an arbitrary point P and construct two perpendicular lines m and n passing through P (Figure 1). Let the line m intersect the conic at two points, A and C, and the line n intersect the conic at two points, B and D. Denote by E the foot of the perpendicular from the point P to the line $AB$. Now, rotate the perpendicular lines m and n about the point P. The locus of the point E is a circle k (or a line in special cases). Denote by $F,G,$ and H the feet of the perpendiculars from the point P to the lines $BC$, $CD$, and $DA$. These points also lie on the circle k. Prove it.

The author noticed this property of conics in GeoGebra by chance many years ago. It is probable that this was not a new observation, since special cases of problem M (i.e., a special position of the point P for a particular conic) are traceable on the internet as exercises in analytic geometry, e.g., https://math.stackexchange.com/questions/1528265/foot-of-perpendicular-on-a-chord-of-a-conic (accessed on 14 November 2015) and https://www.doubtnut.com/qna/142211 (accessed on 3 December 2017). In [1], a proof of problem M is based on computational elimination using the Grobner basis. However, the significance of that paper for our purposes (i.e., for obtaining a synthetic proof) lies in something else: in [1], it is shown by computer computation that the envelope of the lines $AB$ ($BC$, $CD$, $EF$) is a conic. At the very end, there is a remark that the fact that the envelope of the lines is a conic with focus at the point P implies that the locus of feet E of perpendiculars lies on the auxiliary circle of the conic. This is the first step of the synthetic proof, which is presented in the following pages.

To prove problem M, we use several theorems, most of which are stated in the relevant literature. This paper would be much shorter if their proofs were replaced with references. Specifically, we prove Poncelet’s closure theorem for $n=4$, which was published and proved for arbitrary $n>2$ by the French mathematician Jean-Victor Poncelet in 1822. The proof presented here has a twofold meaning—(1) the proof is elementary, using only basic projective reasoning and avoiding any computation; (2) this paper is complete after including the proof. The reader does not need to look for external sources to understand the logic chain.

The following considerations are divided into three sections: the “Solution Procedure”, the “Proof of Theorem M”, and the “Conclusions”. In the first section, we gradually state the theorems that will be used in the synthetic solution of problem M. In the next section, we summarize all the theorems in a logical chain leading to the complete proof of problem M. Finally, in the Conclusions, we mention a question related to the solution.

2. Solution Procedure

First, let us mention an elementary theorem.

Theorem 1. 

Consider an arbitrary quadrilateral $ABCD$ whose diagonals $AC$ and $BD$ are perpendicular and intersect at the point P. Construct the feet of the perpendiculars from the point P to the sides $AB$, $BC$, $CD$, and $DA$ and denote them by E, F, G, and H. Then, the quadrilateral $EFGH$ can be inscribed in a circle k (Figure 2).

Proof. 

As the opposite angles are right, the quadrilaterals $PEAH$ and $PEBF$ are cyclic. Therefore,

$$\measuredangle HEF=\measuredangle HEP+\measuredangle PEF=\measuredangle HAP+\measuredangle PBF=\measuredangle DAP+\measuredangle PBC$$

By analogy, we arrive at the equalities

$$\measuredangle HGF=\measuredangle HGP+\measuredangle PGF=\measuredangle HDP+\measuredangle PCF=\measuredangle ADP+\measuredangle PCB$$

So,

$$\measuredangle HEF+\measuredangle HGF=\measuredangle DAP+\measuredangle PBC+\measuredangle ADP+\measuredangle PCB$$

$$=(\measuredangle ADP+\measuredangle DAP)+(\measuredangle PCB+\measuredangle PBC)={90}^{\circ }+{90}^{\circ }={180}^{\circ }$$

and the quadrilateral EFGH is cyclic. □

Now, let us recall a well-known fact (see, e.g., [2]).

Fact 1. 

Consider an arbitrary conic $c_2$ with foci $F_1$ and $F_2$, inscribed in quadrilateral $ABCD$. Then, the oriented magnitudes of angles subtended by opposite segments (e.g., $AD$ and $BC$) at the focus (e.g., $F_1$) are equal (Figure 3). Written symbolically,

$$\measuredangle A{F}_{1}D\equiv \measuredangle B{F}_{1}Cmod{180}^{\circ }$$

The theorem below can be understood as a generalization of a property inherent to the bicentric quadrilateral.

Theorem 2. 

Consider the conic $c_1$ circumscribed about the quadrilateral $ABCD$ and the conic $c_2$ inscribed in this quadrilateral. Let P be the intersection of the diagonals $AC$ and $BD$. Then, the polar of the point P with respect to the conic $c_1$ is identical to its polar with respect to the conic $c_2$ (Figure 4).

Proof. 

Let I, J, K, and L be the points of contact of the conic $c_2$ with the lines $AB$, $BC$, $CD$, and $DA$ of the quadrilateral. Let $X_1$ be the intersection of the lines $AB$ and $CD$, let $X_2$ be the intersection of the lines $BC$ and $AD$, let $Y_1$ be the intersection of the lines $IJ$ and $LK$, and let $Y_2$ be the intersection of $JK$ and $IL$ (Figure 4). Let us first recall some facts [3,4]:

–

The diagonals $AC$, $IK$, $BD$, and $LJ$ intersect at a common point P (a consequence of Brianchon’s theorem).

–

The triangle $P{Y}_1{Y}_2$ is self-polar with respect to $c_2$, and the triangle $P{X}_1{X}_2$ is self-polar with respect to $c_1$.

–

For the proof, it suffices to show that the line $Y_1{Y}_2$ (the polar of P with respect to $c_2$) is identical to the line $X_1{X}_2$ (the polar of P with respect to $c_1$).

The lines $Y_2{Y}_1$, $LK$, $Y_{1}P$, and $IJ$ intersect at $Y_1$, and the cross-ratio of the lengths of the segments on any line that intersects them is $-1$. The polar of the line $Y_2{Y}_1$ with respect to the conic $c_2$ is the point P, the polar of the line $LK$ is D, the polar of the line $Y_{1}P$ is $Y_2$, and the polar of the line $IJ$ is B. Therefore, the points $Y_2$, D, P, and B are collinear, and the cross-ratio $(BD,P{Y}_2)=-1$. By analogy, the points A, P, C, and $Y_1$ are collinear, and $(AC,P{Y}_1)=-1$.

Since the line $X_1{X}_2$ is the polar of the point P with respect to $c_1$, the intersections $Y_1^{\prime }$ and $Y_2^{\prime }$ of the lines $AC$ and $X_1{X}_2$ and $BD$ and $X_1{X}_2$, respectively, fulfill $(AC,P{Y}_1^{\prime })=-1$ and $(BD,P{Y}_2^{\prime })=-1$. Hence, $Y_1^{\prime }=Y_1$ and $Y_2^{\prime }=Y_2$, and the lines $X_1{X}_2$ and $Y_1{Y}_2$ are identical. □

We now prove Poncelet’s closure theorem for quadrilateral. We first state this theorem in a general version and then give a formulation of it for $n=4$, which is in a certain way adapted for our purposes.

• Poncelet’s closure theorem (general version). Let $c_1$ and $c_2$ be two plane conics. If, for a given $n>2$, there exists at least one n-sided polygon that is simultaneously inscribed in $c_1$ and circumscribed about $c_2$, then there are infinitely many of them. Each point of $c_1$ or $c_2$ is a vertex or tangency (respectively) of one such polygon.

Theorem 3 

(Poncelet’s closure theorem for quadrilateral, adapted). Consider a conic $c_1$ that is circumscribed about a given quadrilateral $ABCD$ and a conic $c_2$ that is inscribed in it. Let P be the intersection of the diagonals $AC$ and $BD$. From any point $A_1$ on the conic $c_1$, let us draw a tangent to the conic $c_2$. Let this tangent intersect $c_1$ at another point $B_1$. From the point $B_1$, let us draw another tangent to $c_2$ that intersects $c_1$ at another point $C_1$. In the same way, let us construct the point $D_1$. Then, the line $A_1{D}_1$ is tangent to $c_2$. This means that conic $c_2$ is inscribed in the quadrilateral $A_1{B}_1{C}_1{D}_1$, and the intersection of the diagonals $A_1{C}_1$ and $B_1{D}_1$ is again point P.

Proof. 

We distinguish three cases:

(a)

The point P lying inside the conic $c_1$;

(b)

The point P lying outside conic $c_1$ but inside the conic $c_2$;

(c)

The point P lying outside both conics $c_1$ and $c_2$.

Proof of case (a). Since the point P lies inside the conic $c_1$, its polar p does not intersect it. Consider an arbitrary projective mapping of the plane that sends the polar p to infinity (i.e., it becomes the ideal line). The image of the conic $c_1$ is an ellipse $c_1^{\prime }$ (since it has no intersection with the ideal line), the image of the conic $c_2$ is $c_2^{\prime }$, and the image of the point P is a point S. Because the polar of the point S is common to both conics and lies at infinity, it is the center of both conics $c_1^{\prime }$ and $c_2^{\prime }$. Next, let us apply an affinity that converts the ellipse $c_1^{\prime }$ into a circle, which we also denote as $c_1^{\prime }$.

We have obtained the following (Figure 5): a circle $c_1^{\prime }$ is circumscribed about a quadrilateral $ABCD$ whose diagonals pass through the center S of the circle and whose sides are tangent to a certain conic $c_2^{\prime }$, the conic and the circle being concentric. Since the diagonals pass through the center S, the quadrilateral $ABCD$ is a rectangle, or, in other words, the tangents $AB$, $BC$, $CD$, and $DA$ make right angles. However, this means that the circle $c_1^{\prime }$ is a director circle (or orthoptic circle) for the conic $c_2^{\prime }$. It is well known that from any point $A_1^{\prime }$ of the circle, one can successively construct the points $B_1$, $C_1$, and $D_1$ such that the rectangle $A_1{B}_1{C}_1{D}_1$ has the properties required in the assignment of Theorem 3. Thus, the original conics $c_1$ and $c_2$ also have the required property. There are several synthetic or very simple analytic proofs that the orthoptic curve for a conic is a circle or line (see, e.g., http://users.math.uoc.gr/~pamfilos/eGallery/problems/Director.html, accessed on 1 January 2016. or [5] and [6], p. 5).

Proof of case (b). Let us consider the dual image $c_3$ of the conic $c_1$ with respect to the conic $c_2$ (Figure 6). The image of the quadrilateral $ABCD$ is the quadrilateral $IJKL$ inscribed in the conic $c_2$ and tangent to the conic $c_3$, whose diagonals intersect at the point P (see the proof of Theorem 2). Now, the theorem to be proved is equivalent to the statement that from every point $A_1^{\prime }\in c_2$, one can construct a quadrilateral $A_1^{\prime }{B}_1^{\prime }{C}_1^{\prime }{D}_1^{\prime }$ inscribed in the conic $c_2$ and tangent to the conic $c_3$. But this is the case (a) since the point P lies inside the conic $c_2$.

Proof of case (c). First, we send a line through the point P, which does not intersect the conic $c_1$, to infinity. The conic $c_1$ thus becomes an ellipse, which we then adjust to a circle by a suitable affinity.

The tangents from the ideal point P to the circle are parallel, so the diameter of the circle lies on the polar p, and the tangents make right angles with the polar. For the same reason, the diameter and the center of the conic $c_2$ must lie on the polar p. Since this diameter makes right angles with the tangents, there are only two possibilities:

• The foci of the conic $c_2$ lie on the polar.
• The conic is an ellipse, and the foci are axially symmetric with respect to the polar.

For the first possibility, we proceed as described below.

We have a quadrilateral $ABCD$ whose diagonals $AC$ and $BD$ are parallel, as they intersect at the ideal point P, and which can be circumscribed by the circle $c_1$. On the polar p, passing through the center of the circle and perpendicular to the diagonals, lie the foci $F_1$ and $F_2$ of the conic $c_2$. In our case, we assume an ellipse. The reasoning for a parabola or a hyperbola would be identical. The conic is tangent to the sides of the quadrilateral (Figure 7). The angle bisector of $DAB$ passes through the center $F^{\prime }$ of the arc $BD$ and is identical to the angle bisector $F_{1}A{F}_2$ (Poncelet’s first theorem). Thus, the line $F_1{F}_2$ passes through the center of the circle $c_1$ and the angle bisector of $F_{1}A{F}_2$, and the line $F_1{F}_2$ and the circle $c_1$ intersect at the same point $F^{\prime }$. But this means that $c_1$ is the Apollonius circle for the triangle $F_{1}A{F}_2$. In other words, the points A, B, C, and D lie on the same Apollonius circle for the points $F_1$ and $F_2$.

Now, let us choose two points $A_1$ and $C_1$, symmetrical with respect to the polar p and lying on the circle $c_1$. Let the tangents drawn from these points to the conic intersect at the points $B_1$ and $D_1$ (Figure 7). Given the reflectional symmetry, the quadrilateral $A_1{B}_1{C}_1{D}_1$ is inscribed in a circle $c_1^{\prime }$. Following from the previous paragraph, $c_1^{\prime }$ is the Apollonius circle for the triangle $F_1{A}_1{F}_2$. Since different Apollonius circles for two fixed points $F_1$ and $F_2$ do not intersect, we have $c_1^{\prime }=c_1$. Moreover, due to reflectional symmetry, the diagonals $A_1{C}_1$ and $B_1{D}_1$ intersect again at the ideal point P. The theorem is proved for this case.

The procedure for the case where the foci do not lie on the polar is described below.

As before, the angle bisector of $F_{1}A{F}_2$ is identical to the angle bisector of $BAD$ (Figure 8). Let $F^{\prime }$ be the intersection of this bisector with the polar p. The polar is the perpendicular bisector of the segment $F_1{F}_2$. The quadrilateral $C{F}_{1}A{F}_2$ is cyclic since it is symmetric with respect to the polar. At the same time, the point $F^{\prime }$ lies on the circle circumscribed about this quadrilateral. As this point also lies on the circle $c_1$, both circles have three points C, A, and $F’$ in common, so they are identical, and points $F_1$ and $F_2$ lie on the circle $c_1$.

Let us now choose two points $A_1\in c_1$, $C_1\in c_1$, symmetrical with respect to the polar, and draw from them tangents to the ellipse $c_2$. Let us denote their intersections by $B_1$ and $D_1$ (Figure 8). From the preceding procedure it is clear that the circle $c_1^{\prime }$ circumscribed about the quadrilateral $A_1{B}_1{C}_1{D}_1$ passes through the points $F_1$ and $F_2$. Since the points $F_1$, $F_2$, $A_1$, and $C_1$ lie on the circle $c_1$, it follows that $c_1^{\prime }=c_1$, and the diagonals $A_1{C}_1$ and $B_1{D}_1$ intersect again at the ideal point P.

All cases are covered and the proof of Theorem 3 is complete. □

3. Proof of Theorem M

Let us recall this theorem once again.

Problem M. 

Consider an arbitrary conic $c_1$ in the plane. Let us choose an arbitrary point P and construct two perpendicular lines m and n passing through P (Figure 9). Let the line m intersect the conic at two points, A and C, and the line n intersect the conic at two points, B and D. Denote by E the foot of the perpendicular from the point P to the line $AB$. Now, rotate the perpendicular lines m and n about the point P. The locus of the point E is a circle k (or a line in special cases). Denote by $F,G,$ and H the feet of the perpendiculars from the point P to the lines $BC$, $CD$, and $DA$. These points also lie on the circle k. Prove it.

Proof. 

If a point E is to be determined, the line m intersects the conic at one point. The same holds for the line n. But the conic and the line have, in general, two intersections, so we can assume the existence of a quadrilateral $ABCD$ inscribed in the conic $c_1$, whose diagonals intersect at the point P and are perpendicular.

According to Theorem 1, the quadrilateral $EFGH$ can be inscribed in a circle. In this auxiliary circle, the focus P and the tangents $AB$, $BC$, $CD$, and $DA$ uniquely determine the conic $c_2$. The second focus is symmetric to P with respect to the center of the circle k. If P lies inside the circle, $c_2$ is an ellipse; if outside, it is a hyperbola.

According to Theorem 3, from each point $A_1$ of the conic $c_1$, we can construct the quadrilateral $A_1{B}_1{C}_1{D}_1$, which is tangent to the conic $c_2$. At the same time, the diagonals $A_1{C}_1$ and $B_1{D}_1$ intersect at the point P. Moreover, the point P is now the focus of the conic $c_2$.

However, as the diagonals of the quadrilateral intersect at the focus of the inscribed conic, they make a right angle. This is because on the one hand,

$$\measuredangle APD=\measuredangle CPB,$$

which is a consequence of the fact that $AC$ and $BD$ are diagonals, and on the other hand, according to Fact 1,

$$\measuredangle APD\equiv \measuredangle BPCmod{180}^{\circ },$$

which is a consequence of the fact that the point P is the focus of the conic, so the angles are oriented.

Hence,

$$\measuredangle CPB\equiv \measuredangle BPCmod{180}^{\circ },$$

and this equation is satisfied only if the angle is right.

Finally, the feet of the perpendiculars dropped from the point P to the sides of the quadrilateral $A_1{B}_1{C}_1{D}_1$ lie on the auxiliary circle of the conic $c_2$. □

• Remark—Frégier’s theorem 

The proof presented above does not work in one special case: when the point P lies on the conic $c_1$. In such a case, Poncelet’s Theorem cannot be used, at least not in the form proved in this paper.

The proposition that the locus of the point E is a circle is then completely equivalent to the proposition that the lines $AB$ pass through a fixed point Y. This point is called Frégier’s point, which was discussed in 1815 [7,8].

Here, we try to prove this theorem as a limit case of the already proved problem M when the point P lies inside the conic $c_1$.

• Frégier’s theorem 

Given a conic $c_1$ and a point O on $c_1$, the hypotenuses of right-angled triangles inscribed in $c_1$ and having a common right-angle vertex O intersect at one point Y, the Fregiér’s point to O with respect to $c_1$.

Proof. 

Consider any point P inside the conic $c_1$. Without loss of generality, let the conic be an ellipse. Next, let us choose an arbitrary point O on $c_1$. For any point P, the quadrilateral $ABCD$ is defined, and the tangent conic $c_2$ is defined as well. Now, let us move the point P arbitrarily close to the point O. Let

$$\underset{P\to O}{\lim }C=\underset{P\to O}{\lim }D=\underset{P\to O}{\lim }P=O$$

Hence,

$$\underset{P\to O}{\lim }H=\underset{P\to O}{\lim }G=\underset{P\to O}{\lim }F=O$$

Based on limit considerations, the “quadrilateral” $ABO$ has a tangent conic that has a focus at $P=O$ and passes through the points $H=G=F=O$. Since the focal point P lies on the conic, it must be a degenerate conic, a line segment, and the foci are its two extreme points. Thus, the degenerate ellipse $c_2^{\prime }$, segment $OY$, is tangent to the sides of the triangle $ABO$ (see Figure 10), which means that the extreme point Y lies on the line $AB$. However, since for any point P inside the conic $c_1$, the conic $c_2$ is tangent to all lines $AB$ (constructed according to the given algorithm), it can be proved using a continuity argument that the same property must hold for the degenerate conic $c_2^{\prime }$. But this means that the line segment $OY$ is “tangent” to all triangles $OAB$. In other words, all lines $AB$ pass through the fixed point Y.

The proof that the feet of the perpendiculars dropped from the point O lie on the circle with diameter $OY$ is left to the reader. □

The author is aware that the above proof is not completely rigorous. It could probably be improved but at the expense of length. The reader can find a standard proof of Frégier’s theorem in [8].

4. Conclusions

In this article, a synthetic proof was presented that the locus constructed according to the procedure given in the introduction is always a circle or a line. In doing so, we proved Poncelet’s closure theorem for a quadrilateral using only elementary projective considerations.

Let us mention a question related to the topic of this article. The synthetic proof presented above says nothing about whether the locus under consideration is a circle or a line. In the former case, the conic $c_2$ is an ellipse or hyperbola; in the latter case, $c_2$ is a parabola. Analytical calculations show that a line comes out only in the case of an equilateral hyperbola (see [1]). Is there a purely synthetic proof for this fact?

There are other ways to generalize the problem addressed here. However, it is uncertain whether such generalizations are amenable to synthetic investigation. Problem M presented here is interesting precisely for the simplicity of the search locus, which can be justified based on (relatively) elementary arguments.