Thermal Management and Optimization of Large-Scale Metal Hydride Reactors for Shipboard Hydrogen Storage and Transport

Abstract

Hydrogen storage is vital to the development of renewables, especially in low-infrastructure countries. Metal hydrides offer a small but safe solid-state candidate for hydrogen storage at medium pressures and near-ambient temperature, yet large-scale applications face heat-management challenges. In this article, we numerically analyze examples of two large-scale lanthanum pentanickel (LaNi₅)-based metal hydride reactor configurations with shell-and-tube heat exchangers. This research studies two large-scale shell-and-tube metal hydride reactor configurations: a tube-side cooling reactor with hydride powder packed in the shell and coolant flowing through internal tubes, and a shell-side cooling reactor using annular hydride pellets with coolant circulating through the shell. The thermal and kinetic performance of these large-scale reactors was simulated using COMSOL Multiphysics (version 6.1) and analyzed under different geometries and operating conditions typical of industrial scales. The tube-side solution provided 90% hydrogen absorption in 1500–2000 s at 30 bar, while the shell-side solution reached the same level of absorption in 430 s at 10 bar. Results show that tube-side cooling has higher storage, while shell-side cooling improves heat removal and kinetics. For energy and maritime transport applications, these findings reveal optimization insights for large-scale, efficient hydrogen storage systems.

1. Introduction

According to the U.S. Energy Information Administration, 79% of U.S. energy consumption is attributable to petroleum, natural gas, or coal [1]. The annual increase in energy demands, combined with a finite supply of fossil fuels, has made the pursuit of renewable and sustainable energy sources a key area of research [2]. One of these clean energy sources is hydrogen fuel cell technology, a sophisticated yet zero-emission and low-carbon-emitting technique for generating electricity [3]. Hydrogen has the potential to produce fuel while emitting water vapor and warm air only, which is a better alternative to combustion by-products, has a high efficiency rate of 40–60%, and is suitable for grid-scale and backup power as its fuel cells can operate in a continuum [4].

With the advancement of technology, this renewable energy system is gaining popularity due to its high efficiency and reduced equipment requirements. However, there are still challenges that hinder its widespread use, making it a popular topic among researchers worldwide [5,6]. Within the United States, a notable example is Alaska, a state known for its abundant fossil fuel resources while continually exploring green energy options to reduce its carbon emissions. Alaska, leveraging its geology, has a long history of hydroelectric and geothermal energy generation and is now considering hydrogen fuel cell technology as a potential solution for remote communities [7]. On the global stage, Japan is a country heavily invested in using hydrogen as a fuel to achieve carbon neutrality by 2050 [8].

Like other technological initiatives under the current wave of renewable energy research, using hydrogen as a fuel has transportation and storage challenges that need to be addressed for it to reach its true potential. Hydrogen has a low volumetric energy density, but its high diffusion capacity requires innovative storage machinery to improve its storage capacity and enhance security. That said, the expansion of a robust infrastructure for hydrogen storage and distribution, including pipelines, remains a significant obstacle today [9]. Over the years, thorough exploration into the subject identified the use of hydrides as a method of storing hydrogen at near-ambient temperatures that does not require large pressurization [10]. Evidence suggests that this method has proven successful for storing hydrogen at lower pressures and near-ambient temperatures [11]. They also have a minimal risk of accidental leaks; however, some drawbacks remain. The major issue identified was the amount of heat produced during hydrogen absorption. As metal hydrides have a very slow heat transfer rate, they need to be equipped with more efficient heat transmission techniques during design and optimization [5,12].

Metal hydride reactors are limited in their capacity to absorb hydrogen quickly due to the presence of hot spots formed during the exothermic reaction [13]. Recent research indicates that external cooling jackets, embedded fins, and other optimized tube bundles as well as various shell geometries (circular, polygonal and conical) are important in mitigating thermal non-uniformities [14,15]. To speed up and safeguard hydrogen charging, phase-change materials (PCM) and high-conductivity fillers are employed to minimize thermal spikes [16,17]. Experimental and numerical investigations consistently demonstrate that combining these techniques can decrease peak temperatures, reduce hotspots, and enhance reaction uniformity, which is crucial for large-diameter and maritime MH reactors [18,19].

Vigorous research and applications of metal hydrides are present in current literature, but most of them are presented on small-scale models. Most these investigations have been restricted to laboratory-scale reactors, usually with diameters below 100 mm. A few recent studies investigating the modular design of a metal hydride reactor for large-scale hydrogen storage applications have also emerged [4,12,20]. Due to the worldwide transition towards hydrogen commercialization, significant demand has emerged for large-capacity metal hydride reactors capable of gas storage and release at the industrial scale and for maritime carriers. Such a requirement is of particular importance in ship-based hydrogen transport, where metal hydride beds could provide a thermally stable, safe method for transporting hydrogen from coastal hydrogen plants in Alaska to the continental United States, Japan, and South Korea. This solution eliminates the need for cryogenic infrastructure and lowers the energy wastage on long-distance ship loadings. While the potential is substantial, there is a paucity of studies on the thermal behavior and optimization of large-diameter (≈1 m) hydride reactors under operational conditions which are relevant to marine logistics.

This work extends the information base on hydrogen storage by constructing a model for a large-scale (≈1 m diameter) metal hydride reactor suitable for ship-based hydrogen transportation, and by integrating and comparing two shell-and-tube heat exchanger designs to improve thermal characteristics [21]. The results of this study are expected to support future Alaska-to-Asia hydrogen export networks and strengthen the technical foundations of a global hydrogen economy.

Recent IMO technology-readiness assessments and interim hydrogen fuel guidelines further confirm the growing regulatory and industrial momentum toward marine hydrogen transport systems, reinforcing the relevance of the large-scale hydride reactor concepts examined in this study [22,23].

2. Theoretical Framework and Governing Models

The following research investigates the use of two potential heat exchangers, each with a 1 m diameter. The first scenario involves packing the shell-side of the reactor with $\mathrm{L}\mathrm{a}\mathrm{N}{\mathrm{i}}_5$ metal hydride powder with a cooling fluid flowing through the tubes. The second scenario involves packing the tubes with annular $\mathrm{L}\mathrm{a}\mathrm{N}{\mathrm{i}}_5$ pellets and cooling fluid flowing through the shell-side of the heat exchanger. For both scenarios, seawater was selected as the cooling fluid due to its abundance and ease of access in coastal regions. The cooling water temperature was 10 °C. The thermal properties of the seawater are described in

Table 1. Thermal properties of seawater at 10 °C [24,25].

⍴ (kg/m3)	Cp (kJ/kgK)	µ (Pa s)	k (W/(m K))	Pr
1027	4.003	0.00139	0.587	9.52

.

2.1. Model Assumptions

To simulate the transient heat and mass transfer processes within the large-scale reactor, a multi-physical numerical model was utilized in COMSOL Multiphysics. The following assumptions were made to govern the equations:

-

The metal hydride bed is treated as a homogeneous and isotropic porous medium.

-

Local thermal equilibrium (LTE) exists between the solid metal hydride powder and the hydrogen gas.

-

The radiative heat transfer within the bed is negligible due to the moderate operating temperatures.

-

The thermophysical properties of the metal hydride (density, specific heat, thermal conductivity) are assumed constant during the absorption process.

-

The volumetric heat capacity of the hydrogen gas is assumed to be negligible compared to that of the solid metal hydride bed.

2.2. Metal Hydride Hydrogenation Reaction

To accurately describe the reaction occurring between hydrogen and the chosen metal hydride in a reactor, several key equations must be considered. Equation (1) represents the reaction between the metal hydride and hydrogen. The enthalpy term ($\mathsf{\Delta }$) is significant in this case, and as this reaction generates a considerable amount of heat, effective heat transfer techniques must be implemented [26,27].

$$M+{\displaystyle \frac{x}{2}}{H}_2\leftrightarrow M{H}_x+\mathsf{\Delta }H$$

(1)

2.3. Thermodynamic and Kinetic Models

There are further equations that can be used to model this process accurately. The equilibrium pressure can be demonstrated using the Van’t Hoff equation:

$$ln(P_{eq})={\displaystyle \frac{\mathsf{\Delta }H}{RT}}-{\displaystyle \frac{\mathsf{\Delta }S}{R}}$$

(2)

The mass balance for the hydrogen gas flowing through the porous media is described by the continuity equation:

$$\varphi {\displaystyle \frac{\partial {\rho }_{MH}}{\partial t}}+\nabla ·\left({\rho }_{MH}u\right)=-S_m$$

(3)

where $\varphi$ is the porosity, u is the Darcy velocity vector, and $S_m$ is the mass course term corresponding to the hydrogen absorbed by the metal alloy. The flow of hydrogen gas through the packed bed is governed by Darcy’s Law, which relates the fluid velocity to the pressure gradient:

$$u=-{\displaystyle \frac{K}{\mu }}\nabla P$$

(4)

where K is the permeability of the metal hydride and $\mu$ is the viscosity of hydrogen gas. The temperature distribution in the metal hydride bed is governed by the energy conservation equation:

$${\rho }_{MH}{C}_{{p,}_{MH}}{\displaystyle \frac{\partial T}{\partial t}}=k_{MH}{\nabla }^{2}T+S_M{H}_r$$

(5)

where $C_{p,MH}$ is the specific heat, k_MH is the thermal conductivity, and $H_r$ is the enthalpy of reaction.

The reaction rate can be denoted by the following equation:

$${\displaystyle \frac{dF}{dt}}=C_{a}exp(-{\displaystyle \frac{E_a}{RT}})ln({\displaystyle \frac{P}{P_{eq}}})(1-F)$$

(6)

In the rate of reaction formula, $C_a$ is the hydriding constant, $E_a$ is the activation energy, P is the supply pressure, and F is the rate of reaction.

3. Tube Side Cooling Heat Exchanger Design and Simulation

3.1. Geometry and Modeling Approach

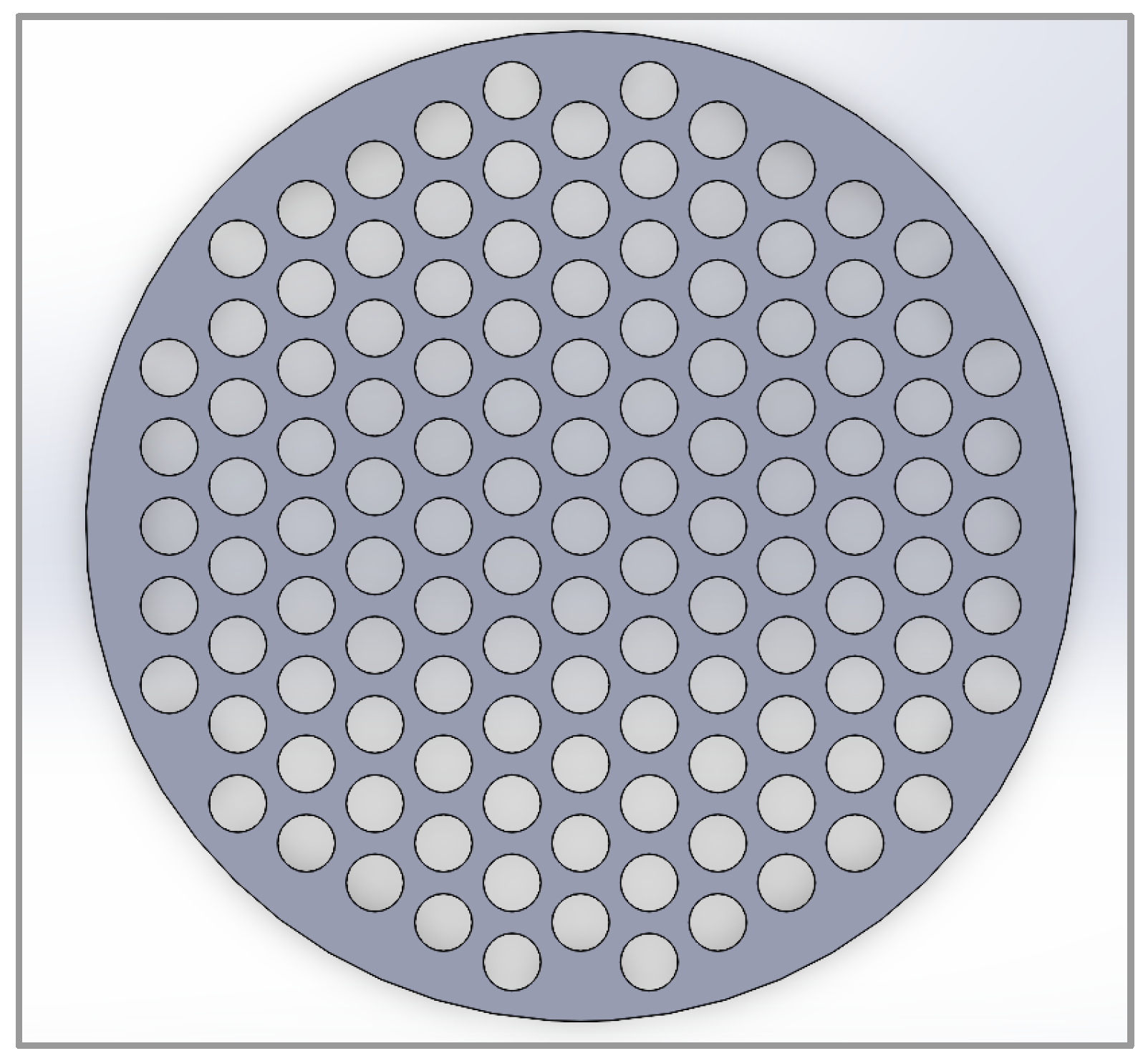
When creating the reactor geometry in COMSOL, one-quarter of the total reactor was utilized. Since each quarter is identical, simulating one section should yield results equivalent to modeling the complete reactor, while significantly reducing computational time [28,29,30,31]. The model was designed to allow easy modifications of variables for testing multiple reactors. In this article, the variables that will be varied are the inner tube diameter and the tube spacing. The geometry for each reactor was initially sketched in SolidWorks 2023 and then imported into COMSOL. This made testing different reactors efficient as the software provided capability to design tube bundles with a triangular pitch ($T$) and different diameters (D) that could be varied as required.

To ensure numerical accuracy, a grid independence study was conducted by systematically refining the computational mesh using COMSOL’s predefined element size sequences. Different mesh levels were examined, and the transient solution was evaluated at t = 3000 s using the hotspot temperature difference (ΔT = T_hotspot − T_initial) as a representative metric. The adopted mesh yielded ΔT = 40.33 K, while the immediately coarser mesh produced ΔT = 40.23 K, corresponding to a relative difference of approximately 0.25%. Further mesh refinement resulted in negligible changes relative to the additional computational cost. Based on this convergence behavior, the selected mesh was deemed grid-independent and was used for all subsequent simulations.

Model verification in this study is conducted through literature-based validation and physical consistency checks, as direct experimental validation at the present reactor scale (1 m diameter) is currently unavailable in the open literature and beyond the scope of this work. The numerical framework is based on conservation equations and LaNi₅ hydrogen absorption kinetics that have been experimentally characterized and validated in prior small-scale studies, and subsequently adopted in numerous numerical and reactor-scale investigations for comparative and scale-up analyses [2,4,13,14]. In addition, the model reproduces physically consistent trends, including hotspot formation under insufficient heat removal and sensitivity of absorption time to cooling tube distribution, supporting its suitability for comparative reactor design evaluation.

3.2. Tube Side Cooling Heat Transfer Coefficient

To determine the tube-side heat transfer coefficient, the Dittus-Boelter equation was used, as seen below.

$$N{u}_D=0.023R{e_D}^{0.8}P{r}^{0.4}=\left(hD\right)/k$$

(7)

$$R{e}_D=\left(4\mathsf{ṁ}\right)/\left(\pi D\mu \right)$$

(8)

3.3. Volumetric Occupancy of LaNi₅ in Reactor Core

For the first simulation, the tube diameter remained the same, but the triangular pitch and number of tubes varied, allowing the comparison of reaction times for reactors containing varying amounts of $LaN{i}_5$ powder. The heat transfer coefficient was kept consistent for each trial (3768 $\mathrm{W}{\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$). For this case, the Reynolds number was determined using ṁ = 5.36 kg/s, D = 0.06 m, and μ = 0.00139 Pa·s. The resulting Reynolds number ($R{e}_D$) was 81,829. With a Prandtl number of $Pr$ = 9.52 and a seawater thermal conductivity of $k$ = 0.587 $\mathrm{W}{\mathrm{m}}^{-1}{\mathrm{K}}^{-1}$, the Nusselt number and heat transfer coefficient obtained were 385.2 and 3768 $\mathrm{W}{\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$, respectively. Each reactor had the same diameter, cooling tube diameter, and mass flow rate. The reactor specifications are listed in

Table 2. Reactor Specifications.

Reactor Outer Diameter (m)	Cooling Tube Diameter (m)	Mass Flow Rate (kg/s)
1	0.06	5.36

. The initial reactor configurations tested are listed in

Table 3. Initial reactor configurations.

Reactor Number	Number of Cooling Tubes	Volume Occupied by LaNi5 (%)	Triangular Pitch (m)
1	73	66.24	0.105
2	85	60.70	0.100
3	97	55.15	0.089
4	109	49.60	0.087
5	121	44.05	0.083
6	139	35.73	0.076

, the operating and kinetic parameters governing the hydrogen absorption process in LaNi₅ are summarized in

Table 4. (a). Operating and kinetic parameters for ${\mathrm{H}}_2$ and $\mathrm{L}\mathrm{a}\mathrm{N}{\mathrm{i}}_5$ powder [31,32,33,34]. (b). Thermophysical properties of ${\mathrm{H}}_2$ and $\mathrm{L}\mathrm{a}\mathrm{N}{\mathrm{i}}_5$ powder [31,32,33,34].

a
Symbol	Parameter	Value
$C_a$	LaNi5 hydriding constant	59.187 ${\mathrm{s}}^{-1}$
$\mathsf{\Delta }S$	Reaction entropy	−105 $\mathrm{J}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}{\mathrm{K}}^{-1}$
$E_a$	Activation energy	21,179.6 $\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l}{\mathrm{H}}_2$
$H_r$	Enthalpy of reaction	−30,100 $\mathrm{J}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}$
$M{W}_{H2}$	Hydrogen molecular weight	2 $\mathrm{g}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}$
$P$	Hydrogen supply pressure	30 $\mathrm{b}\mathrm{a}\mathrm{r}$
$P_0$	Atmospheric pressure	1 $\mathrm{a}\mathrm{t}\mathrm{m}$
$R$	Universal gas constant	8.314 $\mathrm{J}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}{\mathrm{K}}^{-1}$
b
Symbol	Parameter	Value
$M{W}_{H2}$	Hydrogen molecular weight	2 $\mathrm{g}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}$
$\varphi$	LaNi5 porosity	0.5
$wt\mathrm{\%}$	Maximum weight percent H2 stored	1.3%
$C_{p,MH}$	LaNi5 specific heat	419 $\mathrm{J}\mathrm{k}{\mathrm{g}}^{-1}{\mathrm{K}}^{-1}$
$k_{MH}$	LaNi5 thermal conductivity	1.087 $\mathrm{W}{\mathrm{m}}^{-1}{\mathrm{K}}^{-1}$
${\rho }_{MH}$	LaNi5 density	8400 $\mathrm{k}\mathrm{g}{\mathrm{m}}^{-3}$
K	LaNi5 permeability	$1\times 10^{-7}{\mathrm{m}}^2$

a, and the thermophysical properties of H₂ and LaNi₅ powder are listed in Table 4b. Low hydrogen supply pressure in these simulations led to poor cooling times; therefore, the supply pressure was set to 30 bar, similar to that used in other larger-scale metal hydride reactors [28]. The aluminum tube thickness must be at least 4 mm [29] to withstand a pressure of 60 bar, twice the operating pressure.

For all reactor configurations, the cooling fluid velocity should be in the range 0.5–2 m/s [30]. The initial reactor configurations had a cooling fluid mass flow rate of 5.36 kg/s, or 1.85 m/s, which fell within the desired range. The reactor length in this instance was limited.

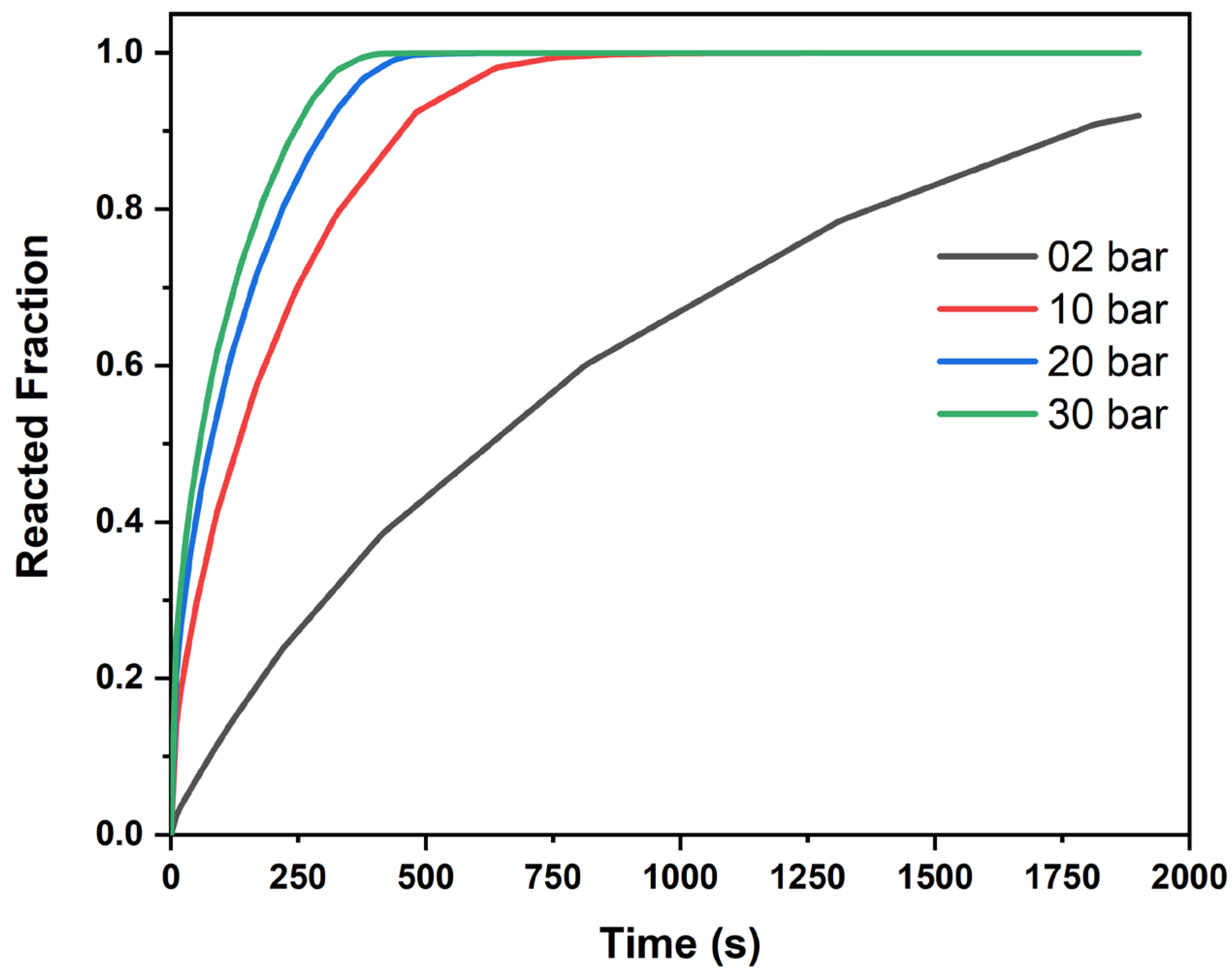
The hydrogen charging time is defined as the time it takes for the supplied hydrogen to be absorbed by 90% of the metal hydride material. This is also referred to as the “90% cooling time”. The results in Figure 1 highlight the importance of tube spacing relative to other factors. For example, reactor 2 (n = 85) resulted in a 90% cooling time of 3720 s, whereas reactor 3 (n = 97) could not reach a 90% reacted fraction within the 5000 s heat transfer simulation. Although reactor 3 incorporated a larger volume for cooling, it exhibited a poorer cooling performance due to the formation of hotspots around its outer region.

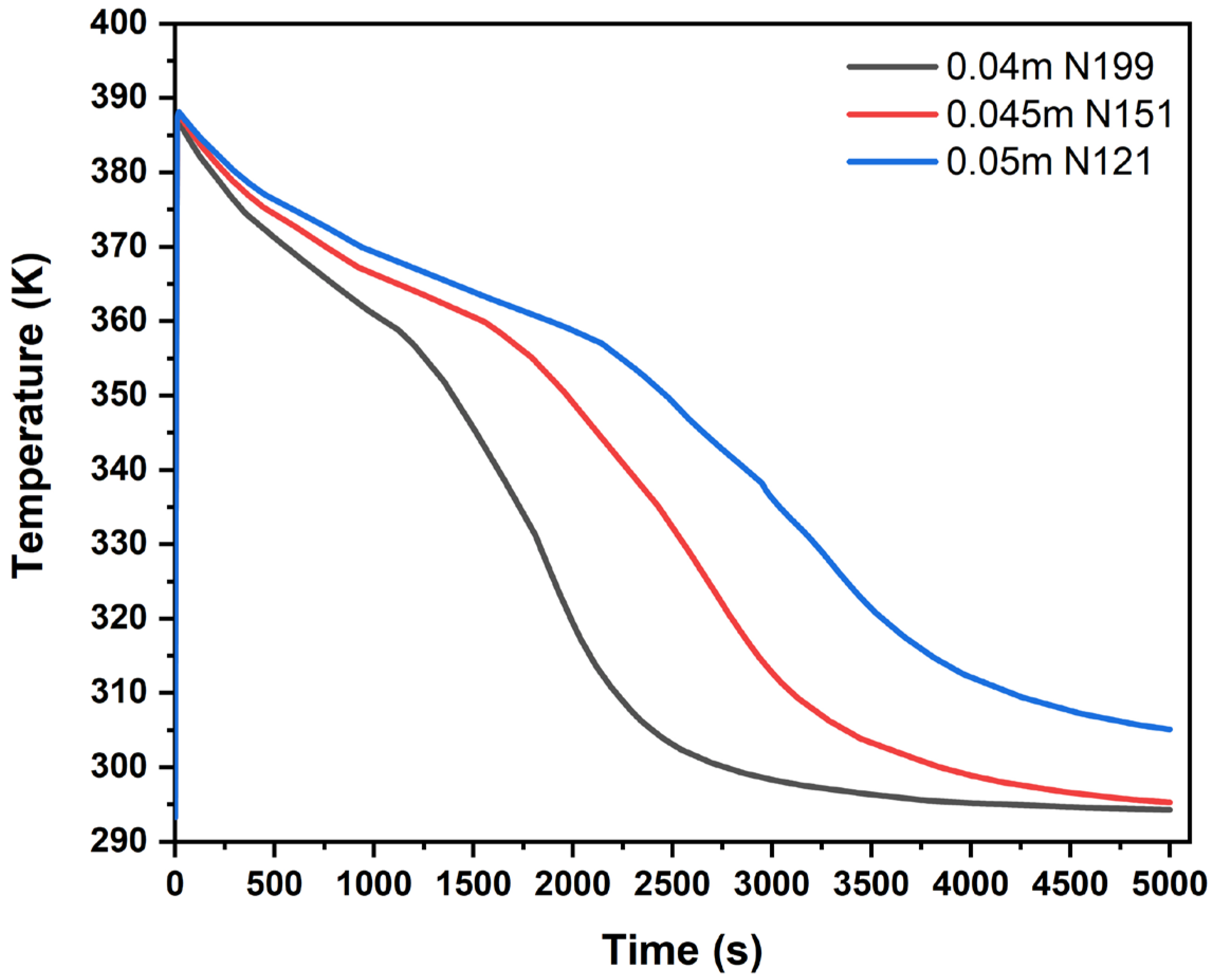
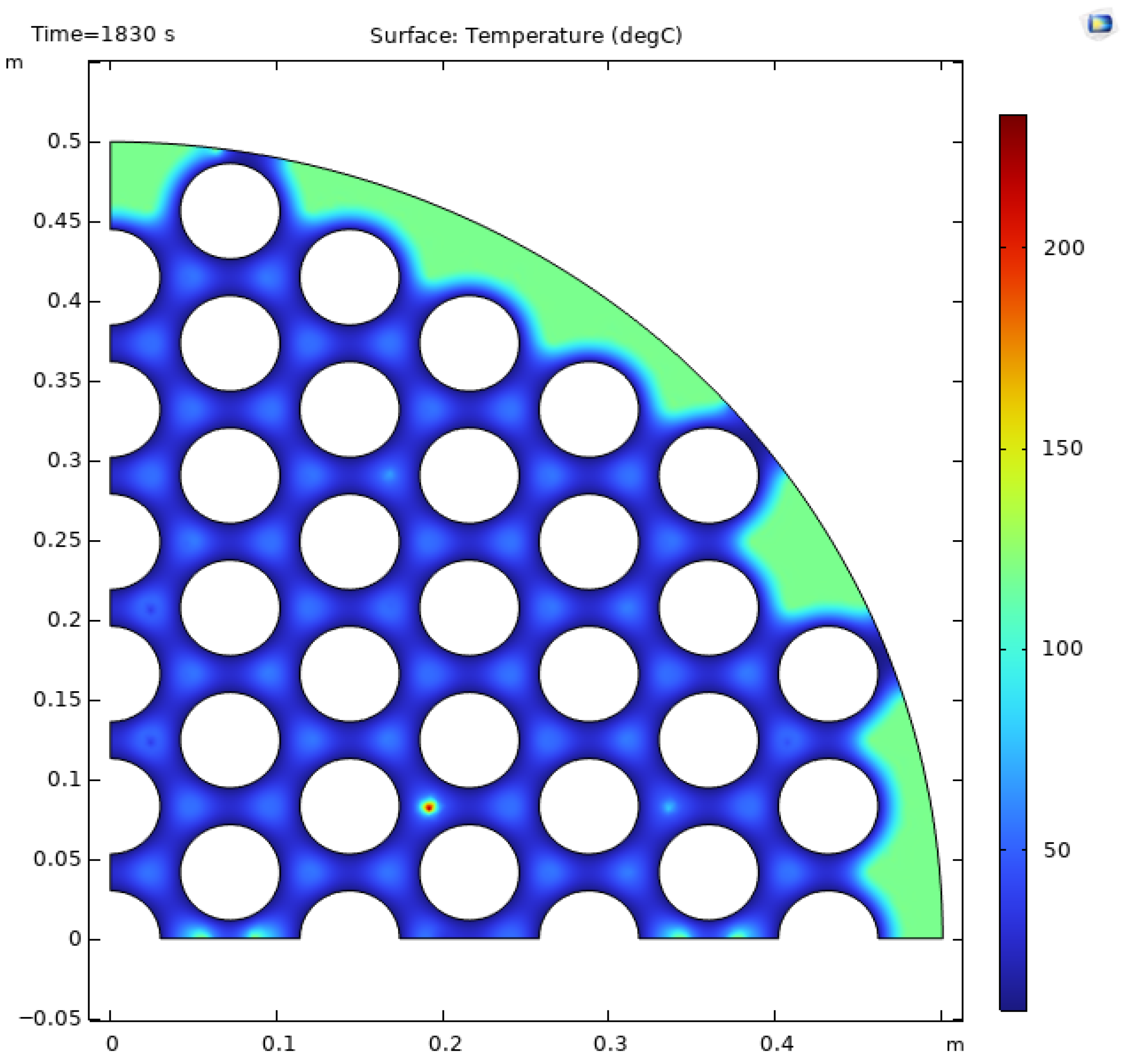
This same trend is observed between reactors 5 and 6 (n = 121 and n = 139, respectively). Reactor 5 reached a 90% cooling time of 1830 s, where reactor 6 required 3330 s to reach the same level of hydrogen absorption. These findings showed that the tube spacing and count are important, but it is equally important to ensure equal distribution of the cooling tubes around the outside of the reactor. 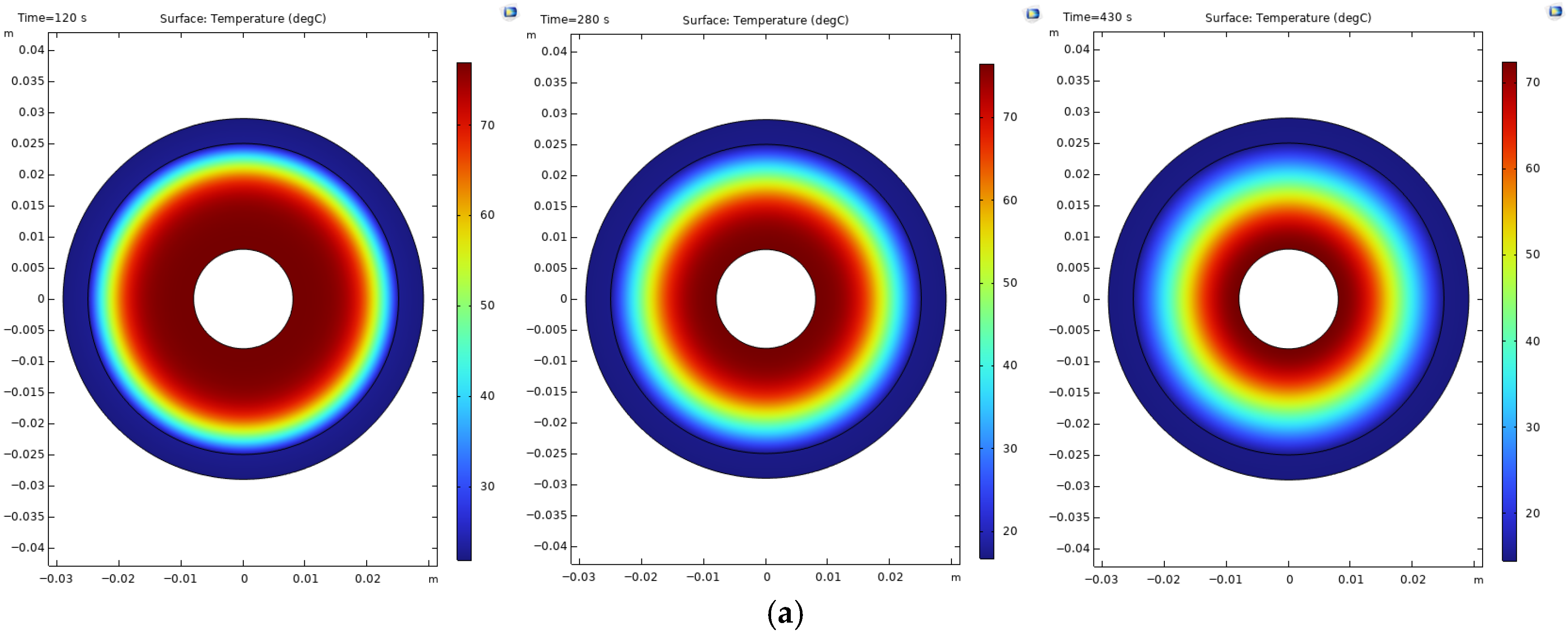Reactor 5 (Figure 2) illustrates minimal hotspot formation around the outside of the reactor compared to the reactors with a poor cooling time, such as reactors 3 and 6.

The presence of hotspots on the hydride bed is an indication of uneven temperature distribution. These zones of localized high temperature can hamper the hydrogen absorption kinetics, produce thermal stress concentrations, and, with prolonged cycling, deteriorate materials and reduce the mechanical integrity of the reactor shell. Hence, optimized tube spacing and balanced cooling distribution are essential measures to ameliorate hotspot temperatures and to achieve thermal uniformity, structural reliability, and safe operation of large-scale metal hydride reactors.

Overall, four of the six reactor configurations, reactors 2, 4, 5, and 6, achieved 90% cooling within the 5000 s simulation window. Reactor 2 displayed a 90% cooling time of 3720 s, highlighting a favorable balance between storage capacity and heat removal. From these simulations, maintaining a metal hydride storage volume of approximately 55–60% appears reasonable. However, the arrangement of and the number of cooling tubes require further optimization to minimize temperature non-uniformity and enhance overall reactor performance.

Figure 1 shows the reacted fraction for each tube configuration. Increasing the number of tubes initially results in a faster rate of reaction as expected, but as previously mentioned, the tube spacing and diameter must be optimized for 90% of the reaction to be completed. When the metal hydride bed is not evenly cooled, the reaction rate significantly decreases after reaching 80%. This effect is evident in Figure 3 with the 139-tube reactor (reactor 6). A large portion of the metal hydride absorbs hydrogen within 1000 s (approximately 82%), yet the remaining 8% requires 2000 s due to insufficient cooling. The hot spots in this reactor are shown in Figure 3.

3.4. Optimization via Variable Tube Diameter and Spacing

After these initial simulations, other reactors were tested with metal hydride storage volume between 55–60%, by varying the outer tube diameter ($D$) and triangular pitch ($T$) for each test. The reactor geometries in

Table 5. Reactor configurations for varying tube diameters.

Reactor Number	Number of Cooling Tubes	Volume Occupied by LaNi5 (%)	Triangular Pitch (m)	Tube Diameter (m)	h $\mathbf{\left(}\mathbf{W}{\mathbf{m}}^{\mathbf{-}\mathbf{2}}{\mathbf{K}}^{\mathbf{-}\mathbf{1}}\mathbf{\right)}$
7	199	54.15	0.0656	0.040	4088
8	151	57.58	0.0755	0.045	4081
9	121	59.30	0.0840	0.050	3906

were simulated in this test:

The flow velocity from the first set of simulations was maintained for these simulations (~1.85 m/s). Due to the changing diameter of the cooling tubes, the mass flow rate for each reactor differed, impacting the heat transfer coefficient of the cooling fluid.

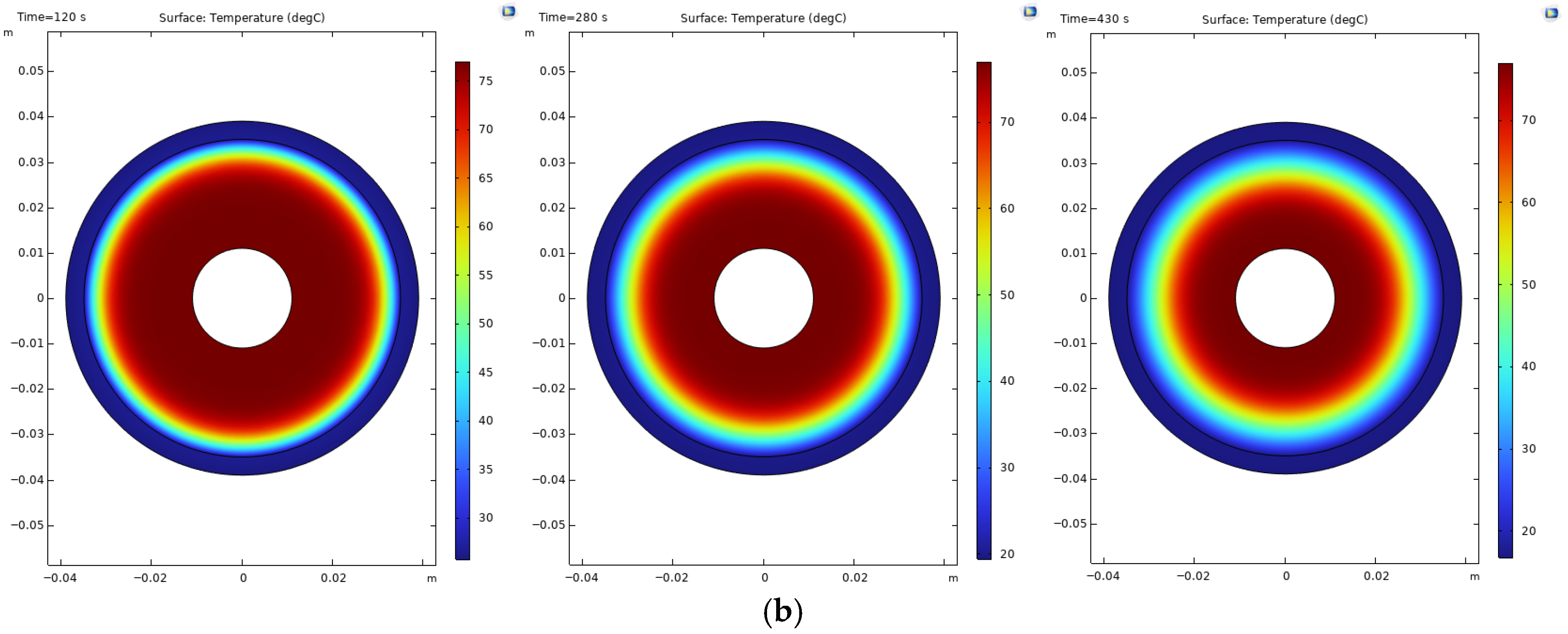
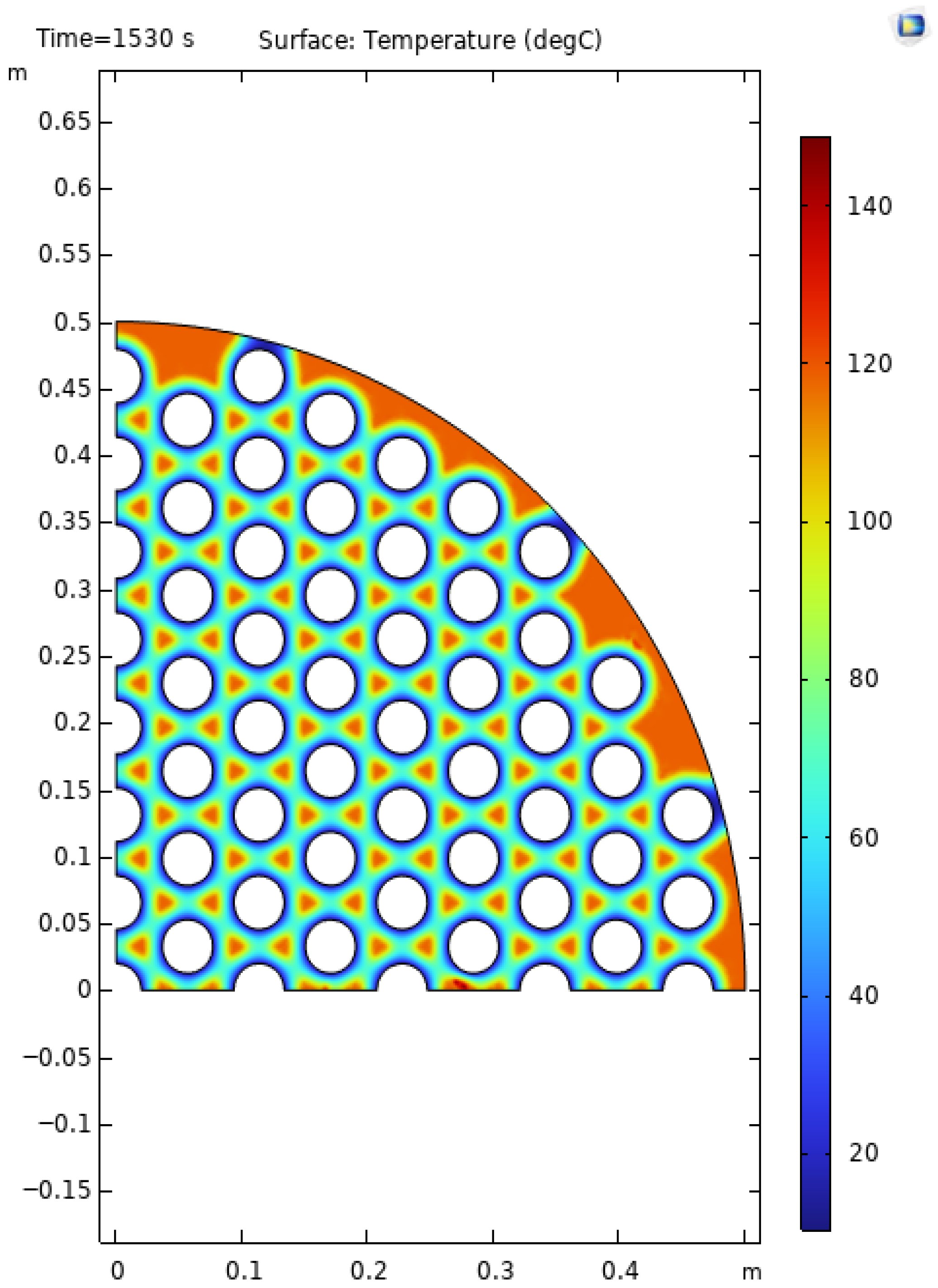
The simulations of reactors 7–9 (Figure 4) showed that when the tube spacing adequately cools the outer portion of the reactor, the number of cooling tubes becomes the main factor to reach 90% reaction completion. Reactors 7, 8, and 9 achieved 90% reaction completion in 1540 s, 2110 s, and 2730 s, respectively. Reactor 9, like reactor 5, had the same number of cooling tubes but a smaller tube diameter and a slightly increased spacing between tubes. This tube spacing was increased from 8.3 cm to 8.4 cm. The primary purpose of this reactor test was to determine if reactor 5, which had the best cooling time from the previous experiment, was effectively utilizing the area for cooling fluid. Reactor 9 did show a slower cooling time by roughly 15 min but had a metal hydride storage percent volume of nearly 60% compared to 44% in reactor 5. Reactors 7 and 8 were modelled to maintain the volume occupied by the metal hydride and to assess how much the cooling time could be extended by adding more cooling tubes. Reactor 7 had a significant decrease in cooling time but also utilized 199 cooling tubes compared to reactors 5 and 9. Figure 5 shows the temperature distribution for reactors 7 and 8. All the reactors tested still contained hotspots around the reactor exterior, regardless of the tube bundle configuration. The tube spacing is determined to ensure that over 90% of the metal hydride powder is in contact with the cooling fluid. This allows the tube diameter and number of tubes to be adjusted to achieve the desired 90% cooling time. If cooling time is a critical reactor design factor, a higher tube count is typically selected, despite the increased reactor complexity. Conversely, if cooling times between 1800 and 3600 s are deemed acceptable, the tube count can be reduced to simplify the reactor design. In this scenario, tube spacing must be carefully optimized to minimize hotspots within the reactor. Future design considerations may include implementing one or more of the following:

1.

External cooling jacket: This might effectively eliminate the hotspots around the outer portion of the reactor.

2.

Circular tube bundle: This would help ensure that the cooling effects reach 90–100% of the metal hydride powder.

3.

Changing reactor shell geometry: A polygonal shape might better utilize storage space by better fitting the shape of the tube bundle.

3.5. Pressure Drop in Tube-Side Cooling

3.5.1. Pressure Loss Equations

Total pressure loss through the heat exchanger can be defined by the following equation [30]:

$$\mathsf{\Delta }{P}_{tot}=\mathsf{\Delta }{P}_T+\mathsf{\Delta }{P}_{Ni}+\mathsf{\Delta }{P}_{No}$$

(9)

where $\mathsf{\Delta }{P}_T$ is the pressure loss through the cooling tube, $\mathsf{\Delta }{P}_{Ni}$ is the pressure loss through the inlet nozzle, and $\mathsf{\Delta }{P}_{No}$ is the pressure loss through the outlet nozzle. Each of these terms can be calculated using the following three equations:

$$\mathsf{\Delta }{P}_T=0.5\left({w_T}^2\rho \right)n_P\left[\right(fL)/d_i+4]$$

(10)

where the friction factor $f=0.216/R{e}^{0.2}$

$$\mathsf{\Delta }{P}_{Ni}=\left({w_T}^2\rho \right)/2$$

(11)

$$\mathsf{\Delta }{P}_{No}=0.25{w_{No}}^2\rho$$

(12)

At this point, it is vital to note that the length of the cooling tubes was limited by the phase change of the cooling fluid. Therefore, it was important to ensure that the heat produced by the metal hydride powder during absorption was removed by the circulating seawater without boiling. This was achieved using the enthalpy of hydrogen reaction for lanthanum-nickel alloy and calculating the total mass of hydrogen absorbed from 0 s to the peak temperature point ($\mathsf{\Delta }$t). This time was very brief (approximately 30 s), as shown in Figure 6. The heat generated during this period was denoted by $Q_{abs,\mathsf{\Delta }t}$. To ensure that the seawater removed this generated heat, the following formula was used:

$${ Q}_{abs,dt}={\displaystyle \frac{\Delta H m_{H_2}}{dt}}<\mathsf{ṁ}{C}_p(T_{out}-T_{in})N_{tube}$$

(13)

where $C_P=4.003 \mathrm{k}\mathrm{J}\mathrm{k}{\mathrm{g}}^{-1}{\mathrm{K}}^{-1}, T_{out}=100 °\mathrm{C}, and T_{in}=10 °\mathrm{C}$.

Mass flow rate and tube count are both dependent on the reactor being analyzed. The total mass of hydrogen stored can be denoted by the following equation:

$${ m}_{H_2}={\rho }_{MH}{A}_{MH}LF(wt\%)$$

(14)

All the variables, except the tube length (L), are known and can be adjusted to ensure that $T_{out}$ does not surpass 100 °C. Using the preceding formulas with the reactor that had the shortest cooling time, it was observed that the phase change of the cooling fluid would be of little concern. To exceed an outlet temperature of 100 °C, the tube length would need to be over 70 m, which is significantly longer than any practical heat exchanger. To determine pressure loss throughout the cooling tubes, the cooling tube length was set to 4 m [35]. Using Equations (9)–(12) to calculate pressure loss for each reactor configuration, the total pressure drop ranged from 10.7 kPa to 13.5 kPa. Reactor 7, which achieved the best cooling time in the previous section, had a total pressure loss of 12.86 kPa. Changing the configuration did not appear to significantly affect total pressure loss.

3.5.2. Thermal Limitations in Tube Geometry Design

It was challenging to adequately space the cooling tubes throughout the reactor using a triangular pitch configuration, with hotspots present along the reactor’s outer region in each configuration. Further optimization could be achieved by adopting a tube configuration that provides a more uniform bed temperature distribution and by increasing the number of cooling fluid passes to better utilize the seawater.

3.6. System-Level Storage Capacity

To evaluate maritime relevance, the volumetric hydrogen density was calculated for the 4 m reactor length (V = 3.14 m³). The tube-side cooling design (Reactor 9) achieves a storage capacity of 206 kg H₂, corresponding to a volumetric density of 65.6 kg-H₂/m³. This is highly significant for shipboard applications, as it approaches the density of liquid hydrogen (71 kg/m³) without requiring cryogenic infrastructure.

4. Shell–Side Cooling with Embedded Hydride Pellets

For the COMSOL simulations, a 2-dimensional model was utilized. To simplify the model and reduce the computational time, a single metal hydride tube was analyzed for each configuration.

4.1. Modelling Strategy and Geometry

The second reactor stored compacted metal hydride pellets in the embedded tubes and used cooling fluid in the shell-side for cooling. For these simulations, the volume occupied by the metal hydride was initially fixed, and the cooling time for the fixed volume was maximized. It was considered that the volume might need adjustment if the results show a rapid cooling time.

Design considerations included ensuring that the cross-sectional velocity of the cooling fluid remained between 0.5–2 m/s [30] when determining the tube sizing and spacing. Manufacturing considerations for each reactor configuration were also noted. To maximize hydrogen storage volume, either large pellets for larger-diameter tubes or a significant number of smaller tubes in the bundle are required. For example, one possible configuration for the tube bundle would be a 0.03 m-diameter (Metal Hydride) MH pellet with 0.051 m spacing between tubes. The criteria for cross-sectional flow velocity were met; however, this configuration contained 313 metal hydride tubes and occupied only 26.17% of the reactor volume with metal hydride pellets (Figure 7).

Importantly, there is a change in the thermal properties of LaNi₅ powder when it is compacted into a pellet; the thermal conductivity increases, while the permeability and porosity decrease. LaNi₅ powder has an effective thermal conductivity, permeability, and porosity of 1.087 $\mathrm{W}{\mathrm{m}}^{-1}{\mathrm{K}}^{-1}$, $1\times 10^{-7}$ ${\mathrm{m}}^2$, and 0.5, respectively. On the other hand, the annular metal hydride pellet for these simulations has an effective thermal conductivity, permeability, and porosity of 5 $\mathrm{W}{\mathrm{m}}^{-1}{\mathrm{K}}^{-1}$, $3\times 10^{-14}$ ${\mathrm{m}}^2$, and 0.22, respectively [36].

4.2. Shell-Side Heat Transfer Coefficient

To accurately estimate the shell-side heat transfer coefficient, reactions and relations present in the current literature were used [30]. These equations were valid for a shell-and-tube heat exchanger with specified baffle spacing (B) and triangular pitch (T). The applicable heat exchanger is shown in Figure 8. The recommended flow velocity for liquids ranges from 0.5–2 m/s [30]. The first step is to find the flow cross-section $a_{cross}$, which is given by

$${ a}_{cross}=D_{i}B(1-d_0/T)\mathrm{or} a_{cross}=B(D_i-n_{acr}{d}_0)$$

(15)

where $n_{acr}=D_i/T.$

Once this value is determined, the flow velocity $w_{cross}$ for the cross-stream is determined:

$${ w}_{cross}=V_{shell}/\left({3600a}_{cross}\right)$$

(16)

The next step is the calculation of the Reynolds number and resulting Nusselt number:

$$Re={(w}_{cross}{d}_0)/\nu$$

(17)

$$Nu=0.196{Re}^{0.6}P{r}^{0.3}=\left(hD\right)/k$$

(18)

As seen from the equations above, the heat transfer coefficient varies depending on the flow throughput ($V_{shell}$), tube diameter ($D$), and triangular pitch ($T$). To achieve the shortest cooling time, these parameters were set to ensure the heat transfer coefficient was maximized.

4.3. COMSOL Simulation Results

Effect of Supply Pressure on Cooling Time

The first reactor tested had tubes with an inner diameter of 50 mm and a tube thickness of 4 mm. The hole in the center of the metal hydride pellet had a diameter of 16 mm. Tube spacing was set to 70 mm, with a total of 121 tubes. The volume occupied by the metal hydride pellets equaled 27.15% of the total reactor volume, excluding the shell thickness. The layout of this tube bundle is shown in Figure 9. The flow throughput was set to 350 ${\mathrm{m}}^3/\mathrm{h}$, resulting in a crossflow velocity ($w_{cross}$) of 1.178 m/s when the baffle spacing ($B$) was set to 200 mm. This configuration gives a heat transfer coefficient of 2769 $\mathrm{W}{\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$.

Initially, the supply pressure was set to 30 bar, resulting in a 90% cooling time of 240 s, indicating that a high supply pressure may not be necessary in this shell-and-tube configuration. Given the rapid cooling time shown, other reactors were tested with the same tube configuration, but at lower hydrogen supply pressures to determine whether effective cooling could be maintained at reduced pressures. The other three simulations had supply pressures of 2 bar, 10 bar, and 20 bar, respectively. When the supply pressure was decreased to 2 bar, the 90% cooling time was 1780 s; at 10 bar, 450 s; and at 20 bar, 300 s. These cooling times are shown in Figure 10.

Since hydrogen supply pressure could be reasonably lowered while still maintaining acceptable cooling times, further simulations used a supply pressure of 10 bar. The following configurations varied tube diameters and tube counts, while maintaining a flow throughput of 350 ${\mathrm{m}}^3/\mathrm{h}$ and a crossflow velocity within the desired range of 0.5–2 m/s [30].

When evaluating possible tube bundle configurations, the heat transfer coefficient decreased with increasing tube diameter. The first configuration tested had a pellet diameter of 0.05 m, like the reactor previously tested under varying supply pressures. The only difference was the number of tubes, which also affected the heat transfer coefficient on the outside of the cooling tube. As shown in

Table 6. Reactor configurations with varying tube diameter and tube count.

	Tube Inner Diameter (m)	Hole Diameter (m)	Triangular Pitch (m)	Tube Count	Wcross (m/s)	h (W/m2-K))
Reactor 1	0.05	0.016	0.07	163	1.89	3677
Reactor 2	0.06	0.019	0.082	121	1.9	3459
Reactor 3	0.07	0.022	0.098	85	1.56	2942

, increasing the tube count and decreasing the tube spacing increased both the crossflow velocity and the heat transfer coefficient. Therefore, if manufacturing with many metal hydride tubes is feasible, it is best to maximize the tube count and minimize the tube spacing while keeping the crossflow velocity within the desired range. This configuration displayed a 90% cooling time of 430 s, compared to 450 s for the previous reactor with equal-diameter tubes. In addition to the slight increase in cooling time, the metal hydride volume increased with the addition of 42 tubes. Figure 11 shows the reaction times for the other two configurations. The right side of the figure denotes pellet diameter and tube count. With a pellet diameter of 0.06 m and 121 storage tubes, the 90% cooling time was 585 s. When the pellet diameter increased to 0.07 m and the tube count decreased to 85, the 90% cooling time decreased to 785 s. The percentage volume occupied by metal hydride for reactors 1, 2 and 3 was 36.58%, 39.19%, and 29.48%, respectively. There is little benefit in increasing the pellet diameter to 0.07 m, as there is limited room to increase the tube count while maintaining the crossflow velocity below 2 m/s. Reactor 2 stores slightly less metal hydride than reactor 1 and has a longer cooling time, but it reduces the tube count by 42. If the tube count is not a limiting factor during manufacturing, reactor 1 would be the better option.

Figure 12a,b illustrates that at 430 s, when Reactor 1 had reached 90% conversion, Reactor 3 had achieved only about 70% completion, as reflected in the corresponding temperature distributions (temperatures in °C).

4.4. Shell-Side Pressure Loss Evaluation

Friction Factors and Loss Components

The total pressure loss $\mathsf{\Delta }{P}_{tot}$ can be determined using the following equations [32]:

$$\mathsf{\Delta }{P}_{tot}=\mathsf{\Delta }{P}_w+\mathsf{\Delta }{P}_{cr}+\mathsf{\Delta }{P}_n$$

(19)

$$\mathsf{\Delta }{P}_w=\left(BF\right)n_B⍴{w_w}^2$$

(20)

$$\mathsf{\Delta }{P}_{cr}=\left(BF\right)(n_B+1)f{n}_{cross}{w_{cr}}^2(\rho /2)$$

(21)

In this case, the Bell friction factor was found to be $f_B=2.68R{e}^{-0.182}$ [37].

$$\mathsf{\Delta }{P}_n=\left({w_n}^2\rho \right)/2$$

(22)

In the above equations, $\mathsf{\Delta }{P}_w$ is the pressure loss from the baffle window, $\mathsf{\Delta }{P}_{cr}$ is the pressure loss from the flow across the MH tubes, and $\mathsf{\Delta }{P}_n$ is the pressure loss from the shell-side inlet. Pressure loss depends on specific geometrical parameters, such as baffle spacing, the number of baffles, and the baffle window area. The baffle window area is illustrated in Figure 13, including the area occupied by the tube space.

As with the tube-side cooling heat exchanger, it is important to ensure that the cooling fluid will not change phases as it passes through the heat exchanger. Equations (9) and (10) were used to determine the maximum heat exchanger length, with the flow rate held at 350 ${\mathrm{m}}^3/\mathrm{h}$, corresponding to a mass flow rate of 99.85 kg/s. This means the maximum heat absorbed by the circulating cooling fluid was 35.97 kW. Using reactor 3, which had an outer MH tube diameter of 0.058 m and 163 cooling tubes, the heat generated during the first 30 s (until the bed temperature peaked) was roughly 35.76 kW when the tube length was set to 7.7 m. However, at this length, the cooling fluid would be close to changing phases. To ensure that the cooling fluid only absorbs enough heat to reach 80 °C, the maximum reactor length would be 6 m. Like the tube-side cooling reactors discussed earlier, the reactor length can be set to 4 m to satisfy both criteria: maintaining one phase and keeping the reactor length-to-diameter ratio reasonable ($3\le L/D_s\le 5)$ [37]. At this point, with the reactor length determined, the pressure loss through the heat exchanger was calculated using Equations (14)–(17) for the three shell-side cooling reactors with varying tube diameters.

For reactor 1, the total pressure loss was 48.6 kPa. Reactors 2 and 3 had a total pressure loss of 43.7 kPa and 31.7 kPa, respectively. The most significant pressure loss for each of the three reactors occurred in the crossflow section, followed by the pressure loss across the baffle window.

5. Conclusions

This paper numerically evaluated two large-scale LaNi₅ metal hydride reactors (nearly 1 m in diameter) for hydrogen storage and transport on ships. Thermal and kinetic behaviors were analyzed in COMSOL Multiphysics for simulation under different shapes and pressures. In the tube-side cooling reactor, which packed the shell with LaNi₅ powder and circulated coolant through an internal tube, approximately 55–60% of the reactor volume was occupied by hydride. A 90% reacted fraction required an approximate 30 bar supply pressure; lower pressures led to poor kinetics and heat removal, resulting in hot spots. The shell-side cooling structure (compacted with annular LaNi₅ pellets, with coolant circulating in the shell) provided better thermal uniformity, faster absorption times, and a lower risk of failure. At 10 bar, the 90% cooling time was 430 s, indicating thermal-transport limitations rather than pressure constraints above 20 bar. However, the packing fraction of hydrides (25–40%) and pressure losses were higher, hence the maximum effective reactor length is only ~6 m.

Based on the numerical analysis of absorption kinetics and thermal behavior, both designs demonstrate potential as viable candidates. The tube-side reactor maximizes storage capacity, while the shell-side reactor offers superior heat management at lower pressures.

Further validation at larger scales—potentially involving 0.5–1 m prototype reactors—will be essential for confirming the thermally controlled absorption behavior predicted by this model. Although developing such prototypes lies beyond the near-term scope of this work, future experimental efforts in the field would offer a critical foundation for assessing the performance of conventional LaNi₅ and high-conductivity composite hydrides under marine-relevant operating conditions. While the present work focuses on thermal performance at the 1 m scale, subsequent studies will examine material degradation, vessel integrity, leak mitigation, manufacturing tolerances, pellet durability, and long-term maintenance requirements to ensure safe and reliable shipboard hydrogen storage systems that can be scaled effectively.

Although the shell-side reactor configuration exhibits a lower hydride packing fraction than the core design, its faster absorption kinetics and lower operating pressures may offer practical advantages for marine hydrogen transport applications, particularly where rapid turnaround and enhanced safety margins are required.