Development of a Mechanical Vehicle Battery Module Simulation Model Combined with Short Circuit Detection
Abstract
1. Introduction
2. Method
2.1. Experiments
2.2. Simulation
2.3. Cell and Module Under Study
3. Validated Cell Model
3.1. Mechanical Testing of Pouch Cells
3.2. FE Model of Pouch Cell
3.3. Virtual Short Circuit Detection
4. LIB Module
4.1. FE Model Module
4.2. Mechanical Tests of Battery Modules
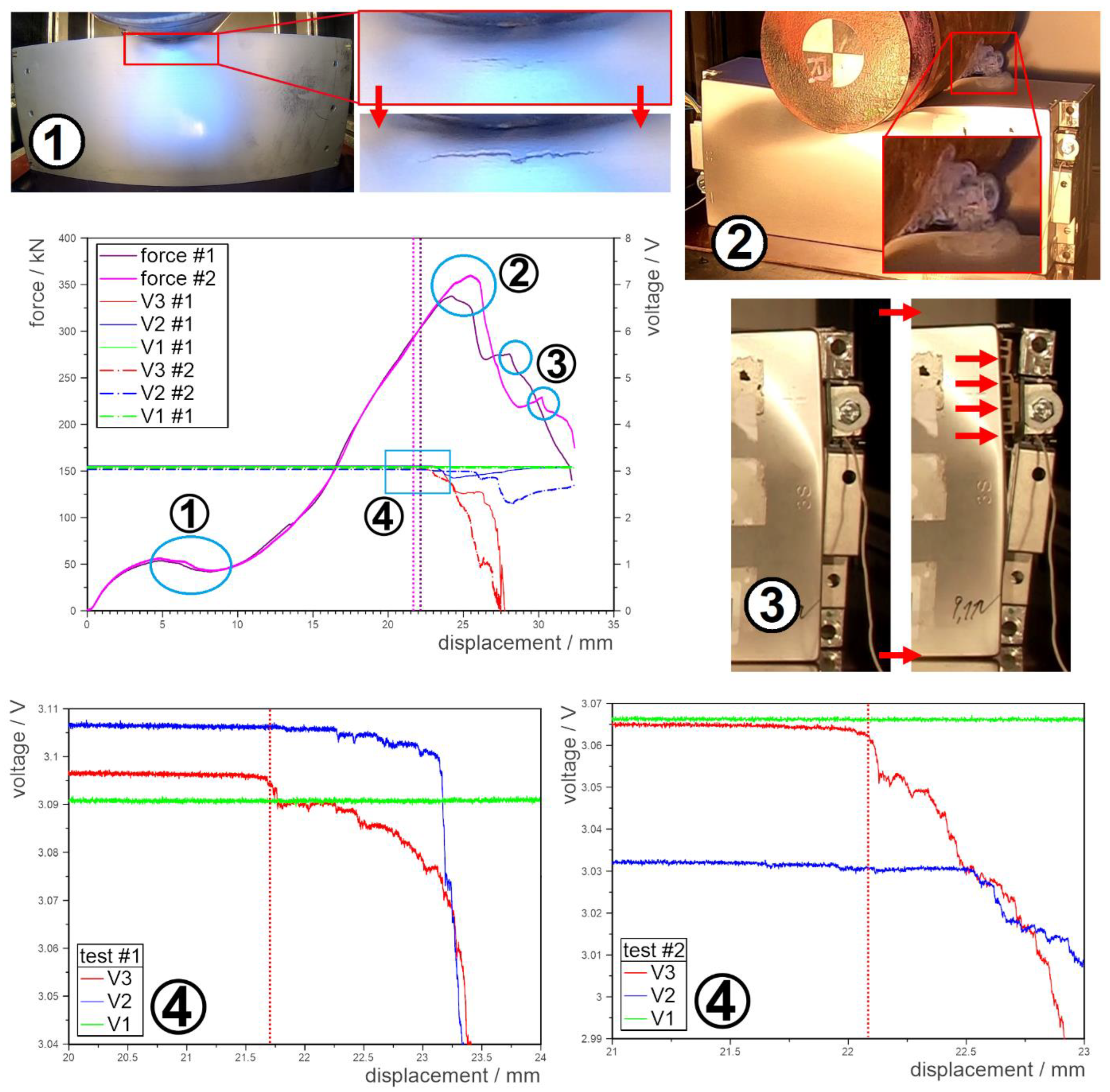
5. Generation of Validation Data
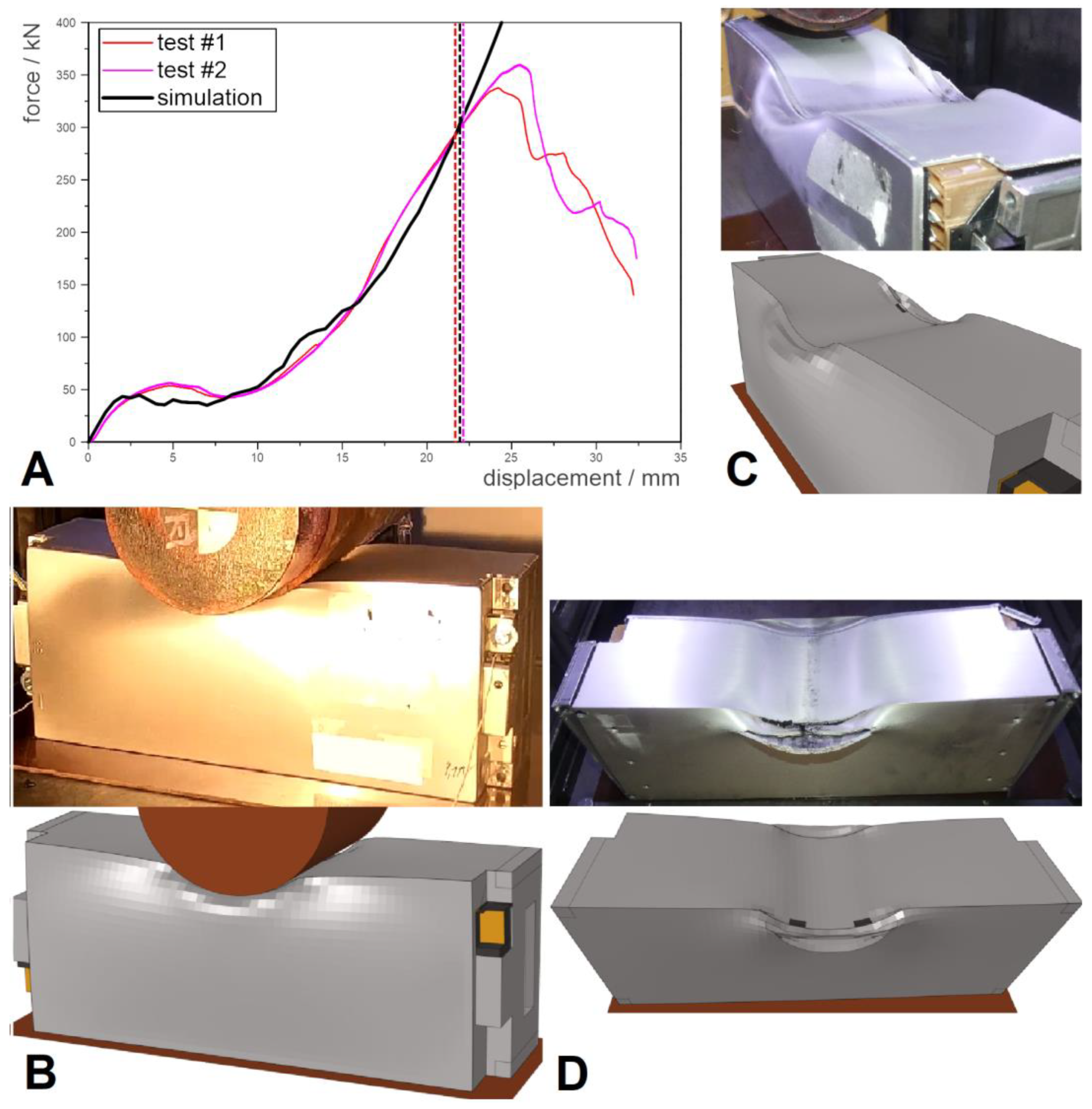
6. Results of Module Simulation
7. Conclusions
7.1. Methods
7.2. Results
7.3. Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Parliament. EU Ban on the Sale of New Petrol and Diesel Cars from 2035 Explained. 2023. Available online: https://www.europarl.europa.eu/news/en/headlines/economy/20221019STO44572/eu-ban-on-sale-of-new-petrol-and-diesel-cars-from-2035-explained (accessed on 9 February 2023).
- Sæther, S.R. Mobility at the crossroads-Electric mobility policy and charging. Transp. Res. Part A 2022, 157, 144–159. [Google Scholar] [CrossRef]
- Houache, M.S.E.; Yim, C.-H.; Karkar, Z.; Abu-Lebdeh, Y. On the Current and Future Outlook of Battery Chemistries for Electric Vehicles—Mini Review. Batteries 2022, 8, 70. [Google Scholar] [CrossRef]
- Huang, Z.; Li, X.; Wang, Q.; Duan, Q.; Li, Y.; Li, L.; Wang, Q. Experimental investigation on thermal runaway propagation of large format lithium ion battery modules with two cathodes. Int. J. Heat Mass Transf. 2021, 172, 121077. [Google Scholar] [CrossRef]
- Korthauer, R. Handbuch Lithium-Ionen-Batterien; Springer Nature: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Chombo, P.V.; Laoonual, Y.; Wongwises, S. Lessons from the Electric Vehicle Crashworthiness Leading to Battery Fire. Energies 2021, 14, 4802. [Google Scholar] [CrossRef]
- Pierri, E.; Cirillo, V.; Vietor, T.; Sorrentino, M. Adopting a Conversion Design Approach to Maximize the Energy Density of Battery Packs in Electric Vehicles. Energies 2021, 14, 1939. [Google Scholar] [CrossRef]
- Kukreja, J.; Nguyen, T.; Siegmund, T.; Chen, W.; Tsutsui, W.; Balakrishnan, K.; Liao, H.; Parab, N. Crash analysis of a conceptual electric vehicle with a damage tolerant battery pack. Extreme Mech. Lett. 2016, 9, 371–378. [Google Scholar] [CrossRef]
- Asp, L.E.; Bouton, K.; Carlstedt, D.; Duan, S.; Harnden, R.; Johannisson, W.; Johansen, M.; Johansson, M.K.G.; Lindbergh, G.; Liu, F.; et al. A Structural Battery and its Multifunctional Performance. Adv. Energy Sustain. Res. 2021, 2, 2000093. [Google Scholar] [CrossRef]
- Duan, X.; Wang, H.; Jia, Y.; Wang, L.; Liu, B.; Xu, J. A multiphysics understanding of internal short circuit mechanisms in lithium-ion batteries upon mechanical stress abuse. Energy Storage Mater. 2022, 45, 667–679. [Google Scholar] [CrossRef]
- Nijman, E.; Buchegger, B.; Böhler, E.; Rejlek, J. Experimental Characterization and Dynamic Modelling of Electrical Cables. SAE Int. J. Adv. Curr. Pract. Mobil. 2022, 5, 888–896. [Google Scholar] [CrossRef]
- Zhu, J.; Wierzbicki, T.; Li, W. A review of safety-focused mechanical modeling of commercial lithium-ion batteries. J. Power Sources 2018, 378, 153–168. [Google Scholar] [CrossRef]
- Jantscher, K.; Breitfuß, C.; Miklau, M.; Ismail, K.; Dobusch, P. Virtual Detection of Mechanically Induced Short Circuits in a Cylindrical Lithium-Ion Battery Cell Based on Finite Element Simulation. Batteries 2021, 7, 79. [Google Scholar] [CrossRef]
- Bulla, M.; Schmandt, C.; Kolling, S.; Kisters, T.; Sahraei, E. An Experimental and Numerical Study on Charged 21700 Lithium-Ion Battery Cells under Dynamic and High Mechanical Loads. Energies 2022, 16, 211. [Google Scholar] [CrossRef]
- Jia, Y.; Gao, X.; Mouillet, J.-B.; Terrier, J.-M.; Lombard, P.; Xu, J. Effective thermo-electro-mechanical modeling framework of lithium-ion batteries based on a representative volume element approach. J. Energy Storage 2020, 33, 102090. [Google Scholar] [CrossRef]
- Zhu, F.; Zhou, R.; Sypeck, D.; Deng, J.; Bae, C. Failure behavior of prismatic Li-ion battery cells under abuse loading condition—A combined experimental and computational study. J. Energy Storage 2022, 48, 103969. [Google Scholar] [CrossRef]
- Logakannan, K.P.; Zhu, F.; Sypeck, D.; Xu, S.; Deng, J.; Kim, S. Testing and Modeling of Vehicle Li-Ion Battery Module with Prismatic Cells under Abuse Conditions. Energies 2023, 16, 1055. [Google Scholar] [CrossRef]
- Aiello, L.; Gstrein, G.; Erker, S.; Kaltenegger, B.; Ellersdorfer, C.; Sinz, W. Optimized Nail for Penetration Test on Lithium-Ion Cells and Its Utilization for the Validation of a Multilayer Electro-Thermal Model. Batteries 2022, 8, 32. [Google Scholar] [CrossRef]
- Qu, Y.; Xing, B.; Wang, C.; Xia, Y. Simplified layered model of pouch cell for varied load cases: An indentation and three-point bending study. J. Energy Storage 2022, 59, 106476. [Google Scholar] [CrossRef]
- Sahraei, E.; Hill, R.; Wierzbicki, T. Calibration and finite element simulation of pouch lithium-ion batteries for mechanical integrity. J. Power Sources 2012, 201, 307–321. [Google Scholar] [CrossRef]
- Qu, Y.; Ge, Y.; Xing, B.; Xia, Y.; Zhou, Q. Development of Detailed Model and Simplified Model of Lithium-Ion Battery Module under Mechanical Abuse; SAE Technical Paper 2022-01-7120; SAE International: Pittsburgh, PA, USA, 2022. [Google Scholar] [CrossRef]
- Xia, Y.; Wierzbicki, T.; Sahraei, E.; Zhang, X. Damage of cells and battery packs due to ground impact. J. Power Sources 2014, 267, 78–97. [Google Scholar] [CrossRef]
- Kalnaus, S.; Wang, H.; Watkins, T.; Simunovic, S.; Sengupta, A. Features of mechanical behavior of EV battery modules under high deformation rate. Extrem. Mech. Lett. 2019, 32, 100550. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, G.; Zhou, Q.; Shi, X.; Shi, F. Failure behaviours of 100% SOC lithium-ion battery modules under different impact loading conditions. Eng. Fail. Anal. 2017, 82, 149–160. [Google Scholar] [CrossRef]
- Essl, C.; Golubkov, A.W.; Fuchs, A. Comparing Different Thermal Runaway Triggers for Two Automotive Lithium-Ion Battery Cell Types. J. Electrochem. Soc. 2020, 167, 130542. [Google Scholar] [CrossRef]
- Kriston, A.; Kersys, A.; Antonelli, A.; Ripplinger, S.; Holmstrom, S.; Trischler, S.; Döring, H.; Pfrang, A. Initiation of thermal runaway in Lithium-ion cells by inductive heating. J. Power Sources 2020, 454, 227914. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Huang, X.; Hao, M.; Huang, X. Laser-induced thermal runaway dynamics of cylindrical lithium-ion battery. J. Energy Storage 2024, 86, 111337. [Google Scholar] [CrossRef]
- Essl, C.; Seifert, L.; Rabe, M.; Fuchs, A. Early Detection of Failing Automotive Batteries Using Gas Sensors. Batteries 2021, 7, 25. [Google Scholar] [CrossRef]
- Essl, C.; Golubkov, A.W.; Fuchs, A. Influence of Aging on the Failing Behavior of Automotive Lithium-Ion Batteries. Batteries 2021, 7, 23. [Google Scholar] [CrossRef]
- Ledinski, T.; Golubkov, A.W.; Schweighofer, O.; Erker, S. Arcing in Li-Ion Batteries. Batteries 2023, 9, 540. [Google Scholar] [CrossRef]
- Lai, W.-J.; Ali, M.Y.; Pan, J. Mechanical behavior of representative volume elements of lithium-ion battery modules under various loading conditions. J. Power Sources 2014, 248, 789–808. [Google Scholar] [CrossRef]
- Lai, W.-J.; Ali, M.Y.; Pan, J. Mechanical behavior of representative volume elements of lithium-ion battery cells under compressive loading conditions. J. Power Sources 2014, 245, 609–623. [Google Scholar] [CrossRef]
- Zhou, M.; Hu, L.; Chen, S.; Zhao, X. Different mechanical-electrochemical coupled failure mechanism and safety evaluation of lithium-ion pouch cells under dynamic and quasi-static mechanical abuse. J. Power Sources 2021, 497, 229897. [Google Scholar] [CrossRef]
- Schmid, A.; Pasquale, A.; Ellersdorfer, C.; Raffler, M.; Champaney, V.; Ziane, M.; Chinesta, F.; Feist, F. Mechanical Characterization of Li-Ion Cells and the Calibration of Numerical Models Using Proper Generalized Decomposition. In Proceedings of the ASME 2023 International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 29 October–2 November 2023. IMECE2023-113228. [Google Scholar] [CrossRef]
- GTM, Kraftaufnehmer. Kraftsensoren Serie, K. 2024. Available online: https://www.gtm-gmbh.com/fileadmin/08_Downloads/Datenblaetter/Kraftaufnehmer/K/Data_sheet_Series_K.pdf (accessed on 6 February 2024).
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 2002, 11, 357–372. [Google Scholar] [CrossRef]
- LS-Dyna Keyword User’s Manual-Volume II Material Models. 2023. Available online: https://ftp.lstc.com/anonymous/outgoing/jday/manuals/LS-DYNA_Manual_Volume_II_R11.pdf (accessed on 12 October 2023).
- Mises, R.V. Mechanik der festen Körper im plastisch-deformablen Zustand., Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Math. Phys. Kl. 1913, 1913, 582–592. [Google Scholar]
- Stander, N.; Basudhar, A.; Roux, W.; Witowski, K.; Eggleston, T.; Goel, T.; Graig, K. LS-OPT User’s Manual, Version 6.0; Livermore Software Technology Corp: Livermore, CA, USA, 2019. [Google Scholar]
- Stander, N.; Müllerschön, H. Introduction to LS-OPT-Class Notes; Livermore Software Technology Corp: Livermore, CA, USA, 2014. [Google Scholar]
- Euro NCAP. Side Pole. 2024. Available online: https://www.euroncap.com/en/car-safety/the-ratings-explained/adult-occupant-protection/lateral-impact/side-pole/ (accessed on 14 February 2024).
- Kisters, T.; Gilaki, M.; Nau, S.; Sahraei, E. Modeling of Dynamic Mechanical Response of Li-Ion cells with Homogenized Electrolyte-Solid Interactions. J. Energy Storage 2022, 49, 104069. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, Q.; Wang, T.; Ji, H.; Ji, Y.; Li, L.; Liu, Y. Experimental study on the dynamic behavior of prismatic lithium-ion battery upon repeated impact. Eng. Fail. Anal. 2020, 115, 104667. [Google Scholar] [CrossRef]
- Zhu, J.; Li, W.; Wierzbicki, T.; Xia, Y.; Harding, J. Deformation and failure of lithium-ion batteries treated as a discrete layered structure. Int. J. Plast. 2019, 121, 293–311. [Google Scholar] [CrossRef]
- Greve, L.; Fehrenbach, C. Mechanical testing and macro-mechanical finite element simulation of the deformation, fracture, and short circuit initiation of cylindrical Lithium ion battery cells. J. Power Sources 2012, 214, 377–385. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, J.; Zhang, C.; Xu, J. Mechanical integrity of 18650 lithium-ion battery module: Packing density and packing mode. Eng. Fail. Anal. 2018, 91, 315–326. [Google Scholar] [CrossRef]
- Sahraei, E.; Campbell, J.; Wierzbicki, T. Modeling and short circuit detection of 18650 Li-ion cells under mechanical abuse conditions. J. Power Sources 2012, 220, 360–372. [Google Scholar] [CrossRef]
- Raffler, M.; Sevarin, A.; Ellersdorfer, C.; Heindl, S.F.; Breitfuss, C.; Sinz, W. Finite element model approach of a cylindrical lithium ion battery cell with a focus on minimization of the computational effort and short circuit prediction. J. Power Sources 2017, 360, 605–617. [Google Scholar] [CrossRef]
- Total Materia. Aluminum 6063-T6. 2023. Available online: https://www.totalmateria.com/ (accessed on 2 February 2023).
- Aerospace Specification Metals Inc. Aluminum 5052-O. 2023. Available online: https://asm.matweb.com/search/SpecificMaterial.asp?bassnum=MA5052O (accessed on 2 February 2023).
- Rheinfelden. Technische Informationen Silafont-36. 2023. Available online: https://rheinfelden-alloys.eu/wp-content/uploads/2015/11/TDB_Silafont-36_AlSi10MnMg_DE_V2.pdf (accessed on 2 February 2023).
- Batz Burgel. Werkstoffdatenblatt Kupfer: CW004A (Cu-ETP 2.0065). 2023. Available online: https://batz-burgel.com/wp-content/uploads/data-de/BB_CW004A.pdf (accessed on 23 March 2023).
- MatWeb Material Property Data. Avient Edgetek MP-10GF/000 Modified PPO-10% Glass Fiber Reinforced. 2023. Available online: https://www.matweb.com/search/DataSheet.aspx?MatGUID=1befaa98cdaf40eeb5a31e3b99034325&ckck=1 (accessed on 2 February 2023).
- MatWeb Material Property Data. Kuraray HYBRAR® F3 Foam Compound. 2024. Available online: https://www.matweb.com/search/DataSheet.aspx?MatGUID=fb279f5743694afdb27c78066dd7d6e6 (accessed on 6 February 2024).
- Doughty, D.H.; Crafts, C.C. FreedomCAR Electrical Energy Storage System Abuse Test Manual for Electric and Hybrid Electric Vehicle Applications; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2006. [Google Scholar] [CrossRef]
- Lian, J.; Wierzbicki, T.; Zhu, J.; Li, W. Prediction of shear crack formation of lithium-ion batteries under rod indentation: Comparison of seven failure criteria. Eng. Frac. Mech. 2019, 217, 106520. [Google Scholar] [CrossRef]
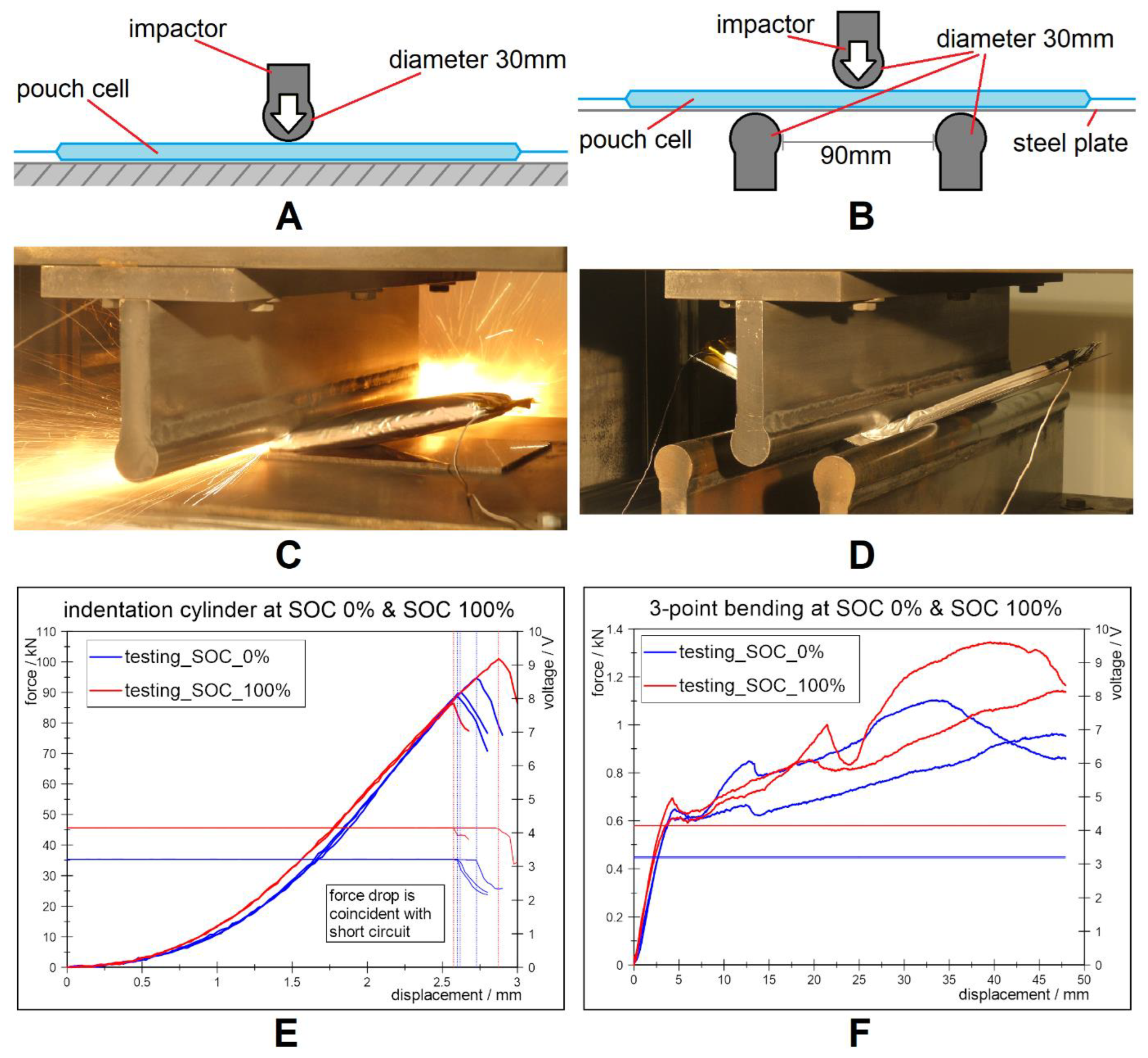
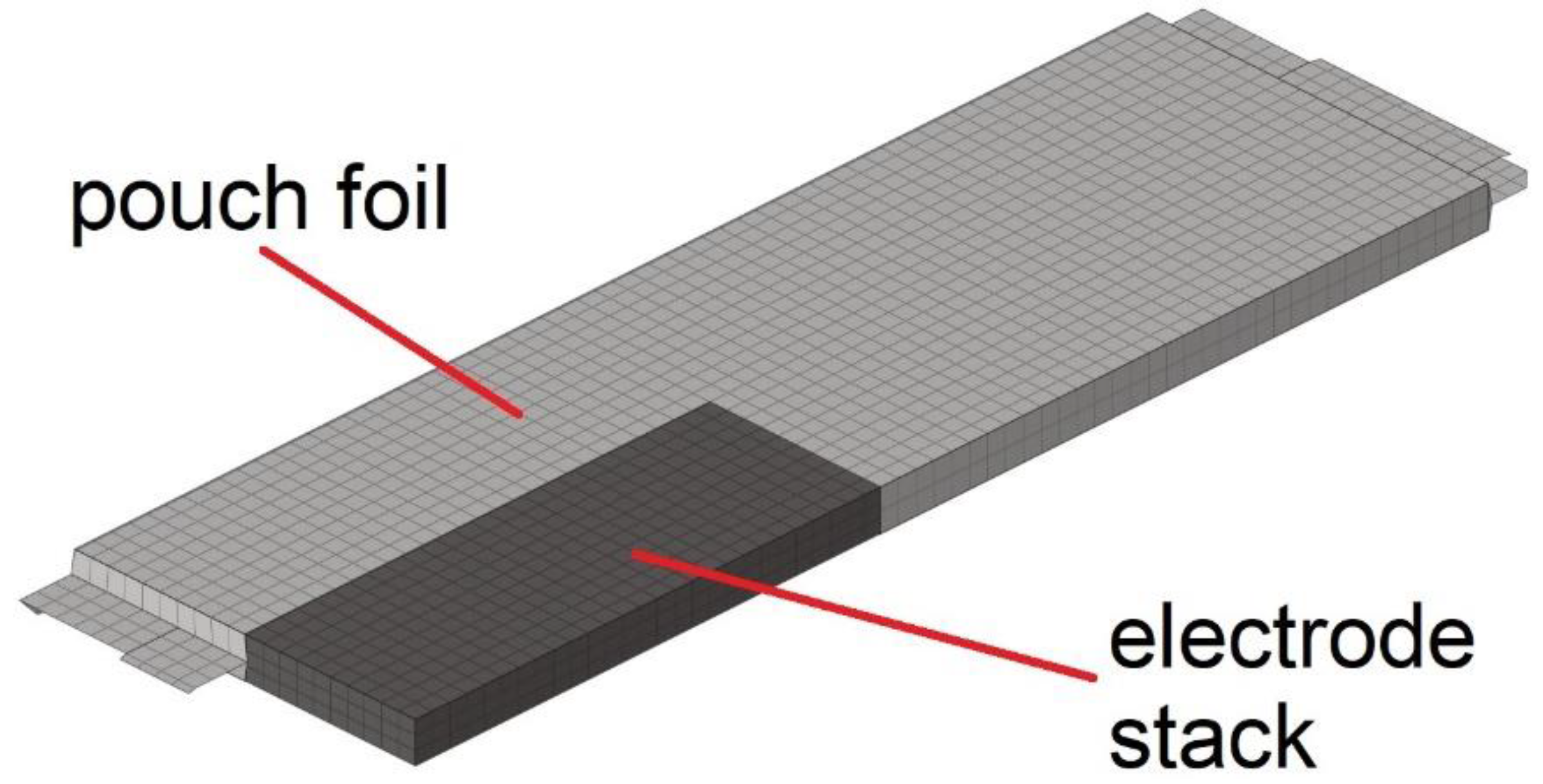
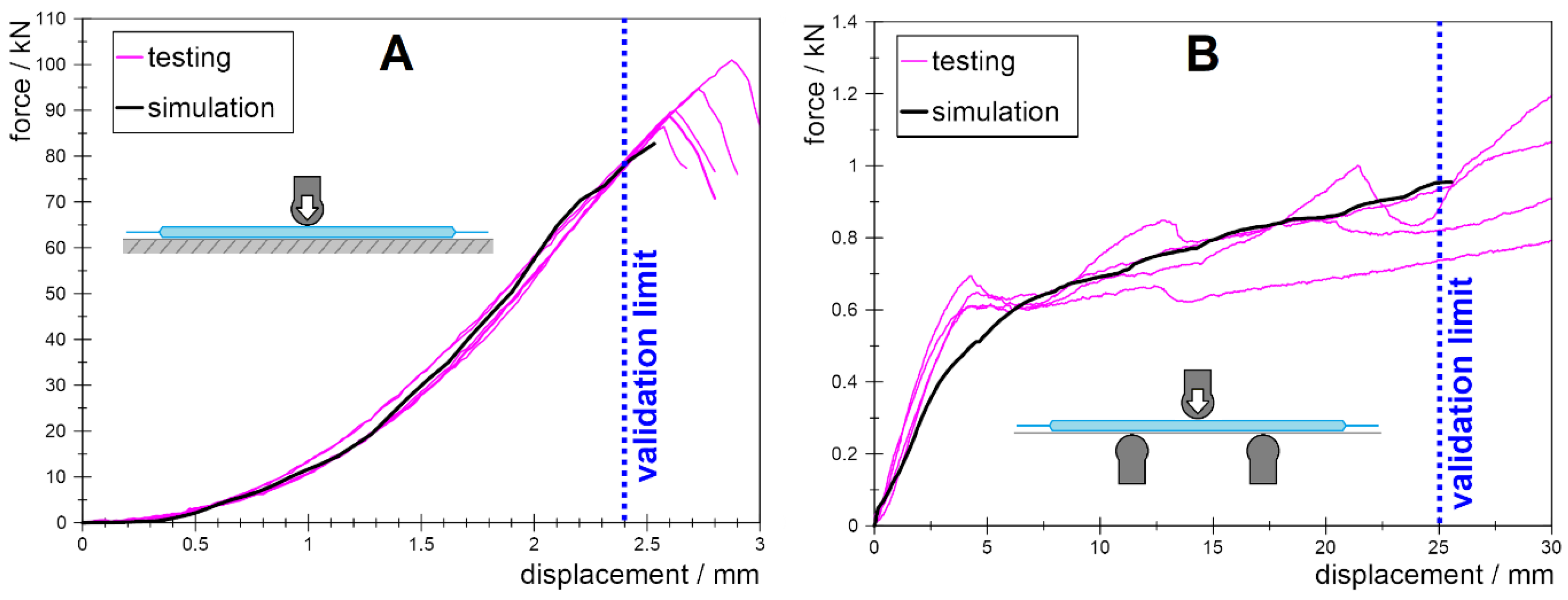

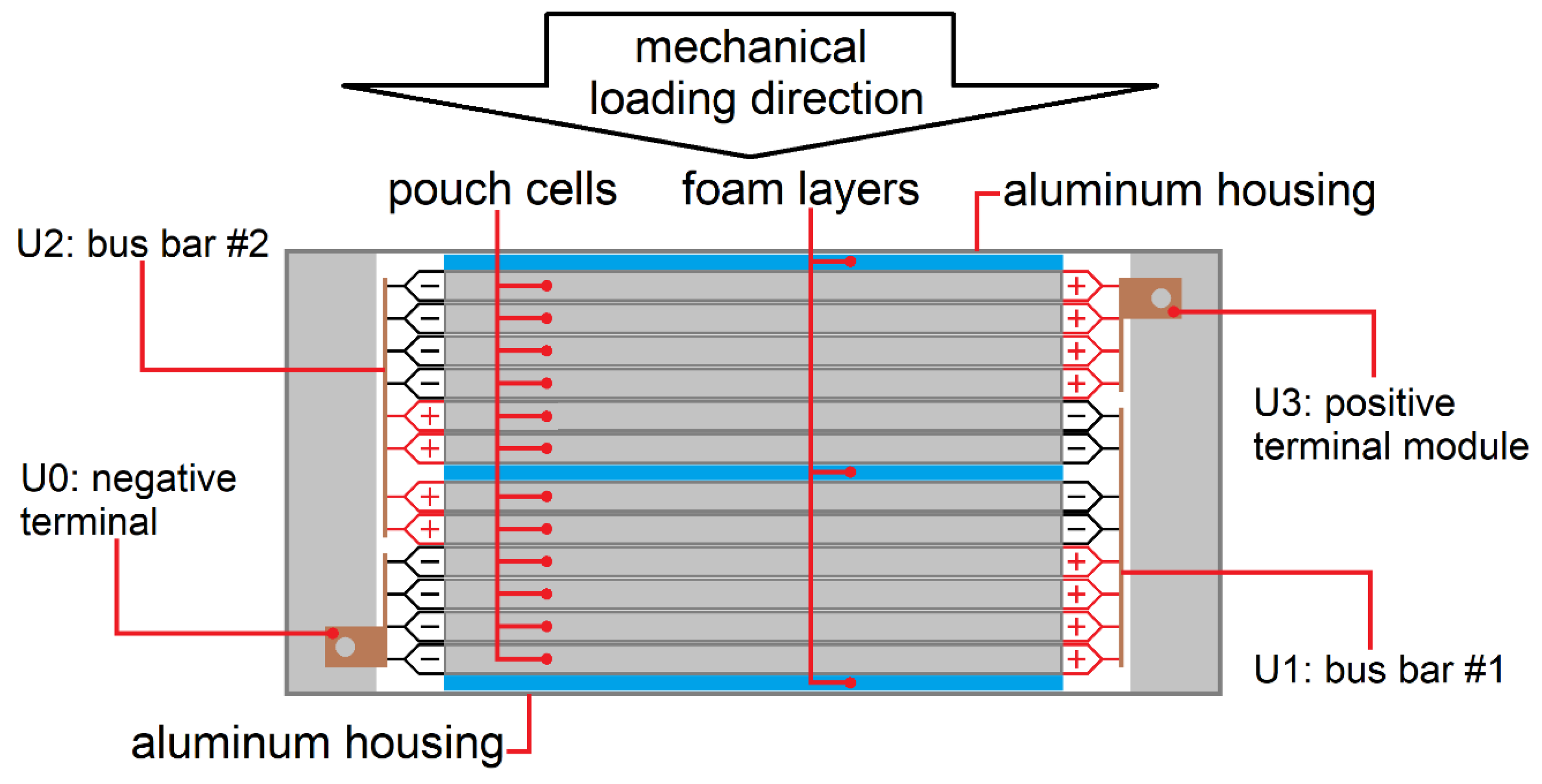

| Specimen | Length/mm | Width/mm | Height/mm | Chemistry | Anode Layers | Capacity |
|---|---|---|---|---|---|---|
| Pouch cell | 342 | 102 | 11.5 | NMC 811 | 38 | 71 Ah |
| Cell module | 380 | 152 | 108 | - | - | 12 cells (4 parallel and 3 serial) |
| Load Case | Number of Tests | SOC/% | Impactor Velocity/mm/min | Condition for Successful Test | Test Description |
|---|---|---|---|---|---|
| Indentation cylinder | 3 | 0 | 6 | Short circuit or 420 kN force | Deformation through cylindrical impactor |
| 2 | 100 | ||||
| 3-point bending | 2 + 1 failed | 0 | 60 | Short circuit or 50 mm impactor displacement | Bending deformation through cylindrical impactor and two cylindrical bearings; cell is supported on a 1.4301 steel plate, size (350 × 150 × 1) mm3 |
| 2 | 100 |
| Material Name | Module Component | Simulation Material Type | Literature Source |
|---|---|---|---|
| Aluminum 6063 | Side plates and bottom plate | *MAT_24 (elasto-plastic material [37]) | [49] |
| Aluminum 5052 | Lid | *MAT_24 | [50] |
| Silafont-36 | Cover on narrow sides | *MAT_24 | [51] |
| Cu-ETP | Busbars | [52] | |
| MPPO GF10 | Cell support parts, bus bar covers | *MAT_24 | [53] |
| Rubber foam | Foam layers | *MAT_24 | [54] |
| Model Property | Value |
|---|---|
| Number of elements | 476.866 |
| Element edge length (range) | 2.5–6.0 mm |
| Computation time (16 cores) | 349 min |
| Total simulation time | 25.0 ms |
| Elemental time step | 1.28 × 10−4 ms |
| Load Case | Number of Tests | SOC/% | Impactor Velocity/mm/min | Condition for Successful Test | Test Description |
|---|---|---|---|---|---|
| Indentation cylinder | 2 | 0 | 60 | Short circuit | Cylindrical impactor 150 mm diameter |
| Voltage Signal | Cells | Points for Measurement |
|---|---|---|
| V1 | Lower 4 cells | U0 and U1 |
| V2 | Middle 4 cells | U1 and U2 |
| V3 | Upper 4 cells | U2 and U3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jantscher, K.; Kreimaier, H.; Miralem, A.; Breitfuss, C. Development of a Mechanical Vehicle Battery Module Simulation Model Combined with Short Circuit Detection. Energy Storage Appl. 2024, 1, 19-34. https://doi.org/10.3390/esa1010003
Jantscher K, Kreimaier H, Miralem A, Breitfuss C. Development of a Mechanical Vehicle Battery Module Simulation Model Combined with Short Circuit Detection. Energy Storage and Applications. 2024; 1(1):19-34. https://doi.org/10.3390/esa1010003
Chicago/Turabian StyleJantscher, Klemens, Heimo Kreimaier, Alem Miralem, and Christoph Breitfuss. 2024. "Development of a Mechanical Vehicle Battery Module Simulation Model Combined with Short Circuit Detection" Energy Storage and Applications 1, no. 1: 19-34. https://doi.org/10.3390/esa1010003
APA StyleJantscher, K., Kreimaier, H., Miralem, A., & Breitfuss, C. (2024). Development of a Mechanical Vehicle Battery Module Simulation Model Combined with Short Circuit Detection. Energy Storage and Applications, 1(1), 19-34. https://doi.org/10.3390/esa1010003







