Model-Assisted Probabilistic Neural Networks for Effective Turbofan Fault Diagnosis
Abstract
1. Introduction
- -
- The diagnostic problem can be simplified/narrowed (for example, in cases where only fault detection is required);
- -
- A large amount of relevant data are available (for example, in cases where a performance model is available);
- -
- Simplicity is a factor.
2. Engine Performance Model and Representation of Physical Faults
3. Method Description
- One class, representing the healthy operation of the engine;
- Additional classes, each representing a faulty engine component operation.
- Measurements preprocessing;
- Engine health assessment;
- Generation of training patterns;
- Health assessment post-process.
- These parts are described in more detail in the following paragraphs.
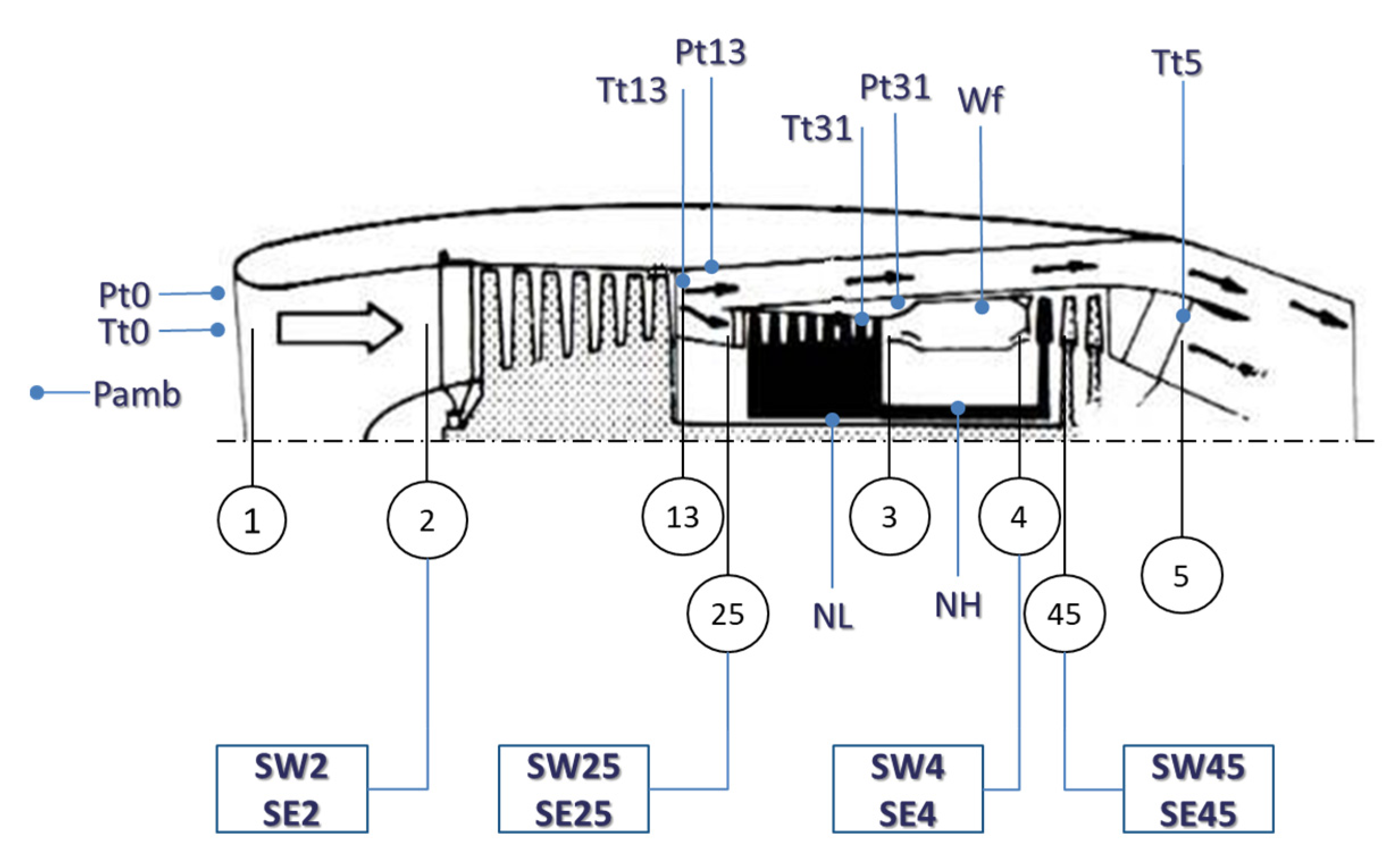
3.1. Measurements Preprocessing
- -
- The nominal values of the measured quantities used for condition monitoring Yo, for the given operating point . The delta ΔYx of a measurement, Yx, is then calculated as the percentage deviation of the Yi from its nominal value Yox;
- -
- The Jacobian matrix , at the specific operating point.
3.2. Engine Health Assessment
| is the output probability of the health condition of the engine represented by Class − i of the network, given the input deltas ΔY. | |
| is the a priori probability of the health condition of the engine represented by Class − i of the network. Each health condition is considered to have an equal a priori probability, thus: , where k is the number of considered classes. | |
| is the a priori probability of the input deltas ΔY. This acts as a normalization factor. As the considered classes are considered exhaustive and mutually exclusive, the sum of probabilities of all classes, given the input deltas ΔY, should be equal to 1. Therefore: | |
| is a smoothing factor that is calculated experimentally. A typical initial value is, generally, 0.1 for all classes, which is the value also considered here. | |
| is the dimension of vector ΔY. | |
| is the number of training patterns of Class − i. | |
| is the input deltas vector. | |
| is the j-th training pattern of Class − i. |
3.3. Generation of Training Patterns
3.4. Fault Identification
- (a)
- If the condition with the greatest probability represents healthy operation, the diagnostic procedure ends.
- (b)
- If any other class is tied with the maximum probability, a fault is considered to exist at the corresponding component. If the fault is located at a component with health parameters SWc and SEc, then the following is performed:
- We estimate the deviation of parameters SWc and SEc through the Jacobian pseudoinverse (PINV) equation as follows:is the vector of deviations of the health parameters:ΔY is the vector of deltas of input measurements Y, and is the nx2 submatrix of the Jacobian only associated with the health parameters ΔSWc and ΔSEc and is the corresponding pseudoinverse, which is a 2xn matrix.
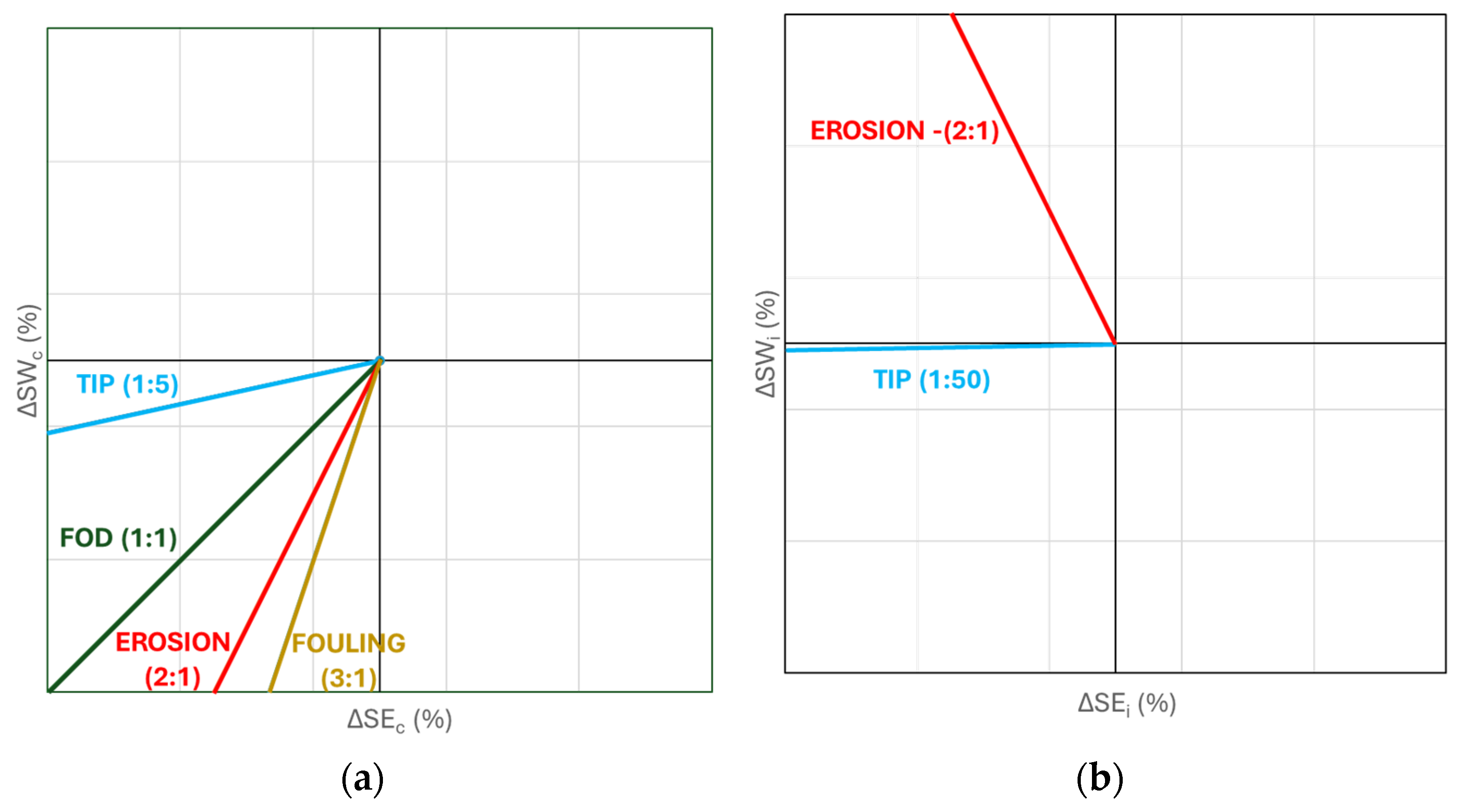
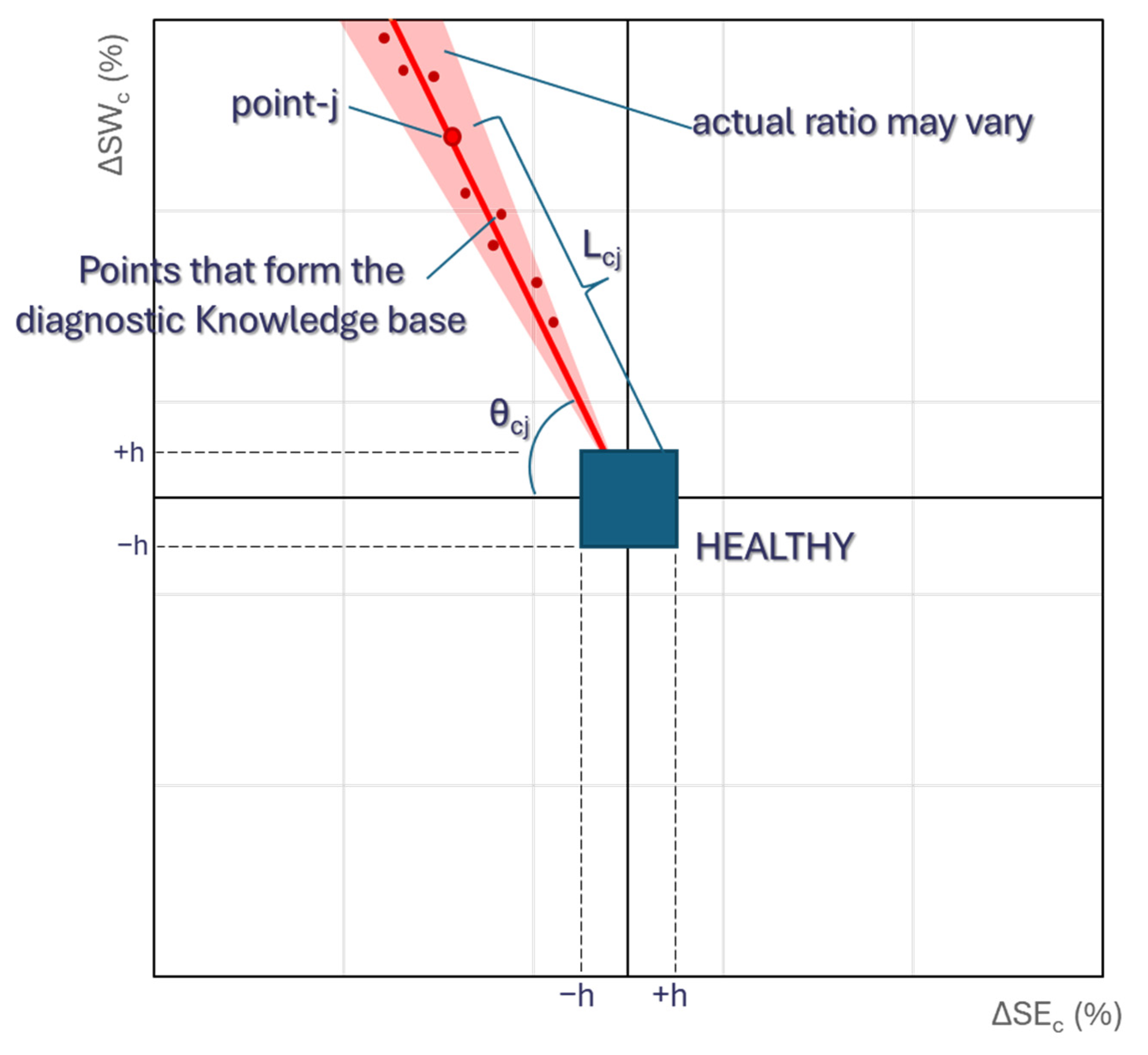
- The ratio of ΔSWc and ΔSEc is found:
- The calculated ratio ‘r’ is compared with the ratios of the considered faults of the affected component from the knowledge base. The fault with the closest ratio is the one that is present.
4. Application to a Mixed Flow Turbofan
4.1. Engine Description
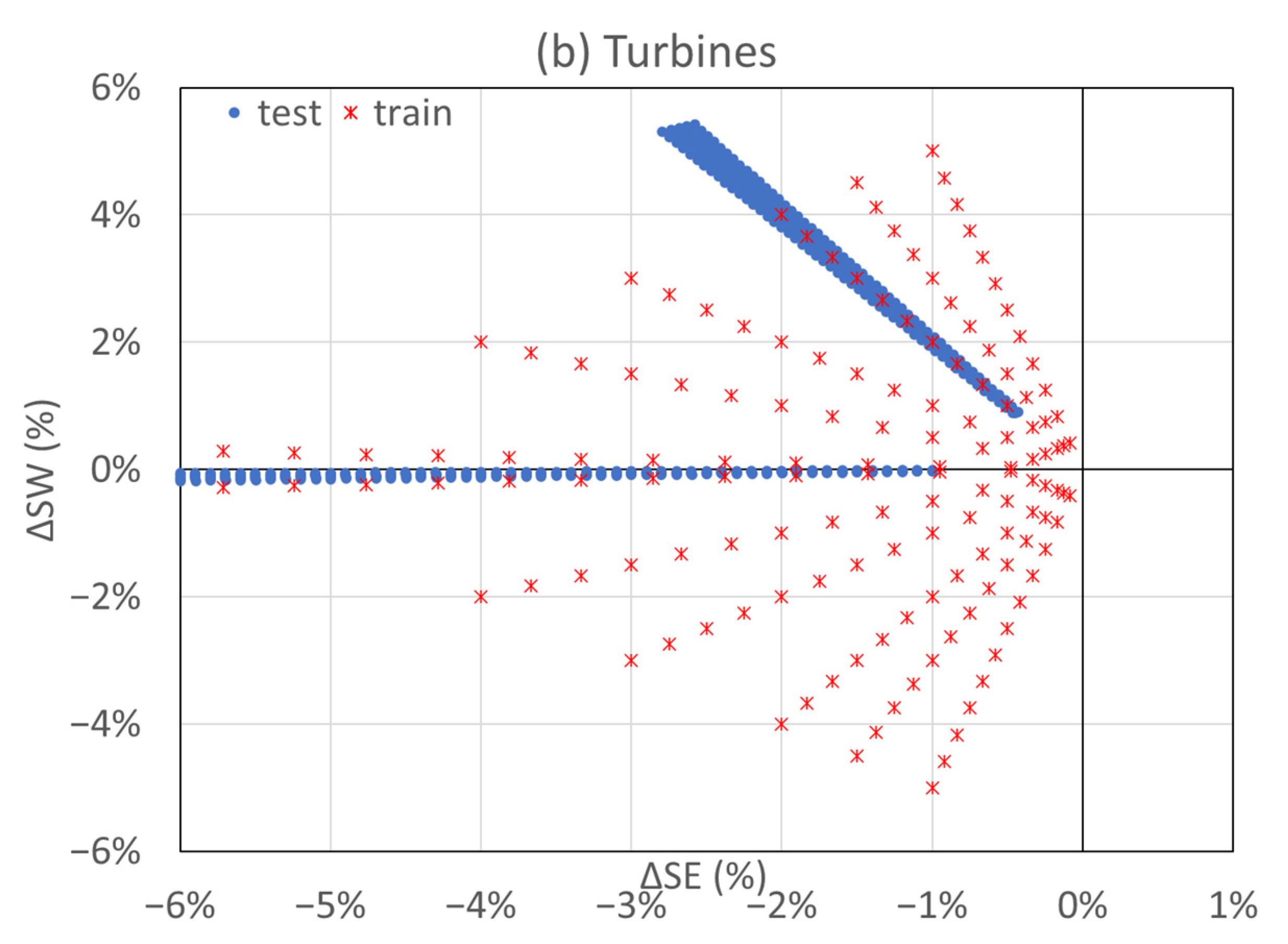
4.2. PNN Testing–Τraining Patterns
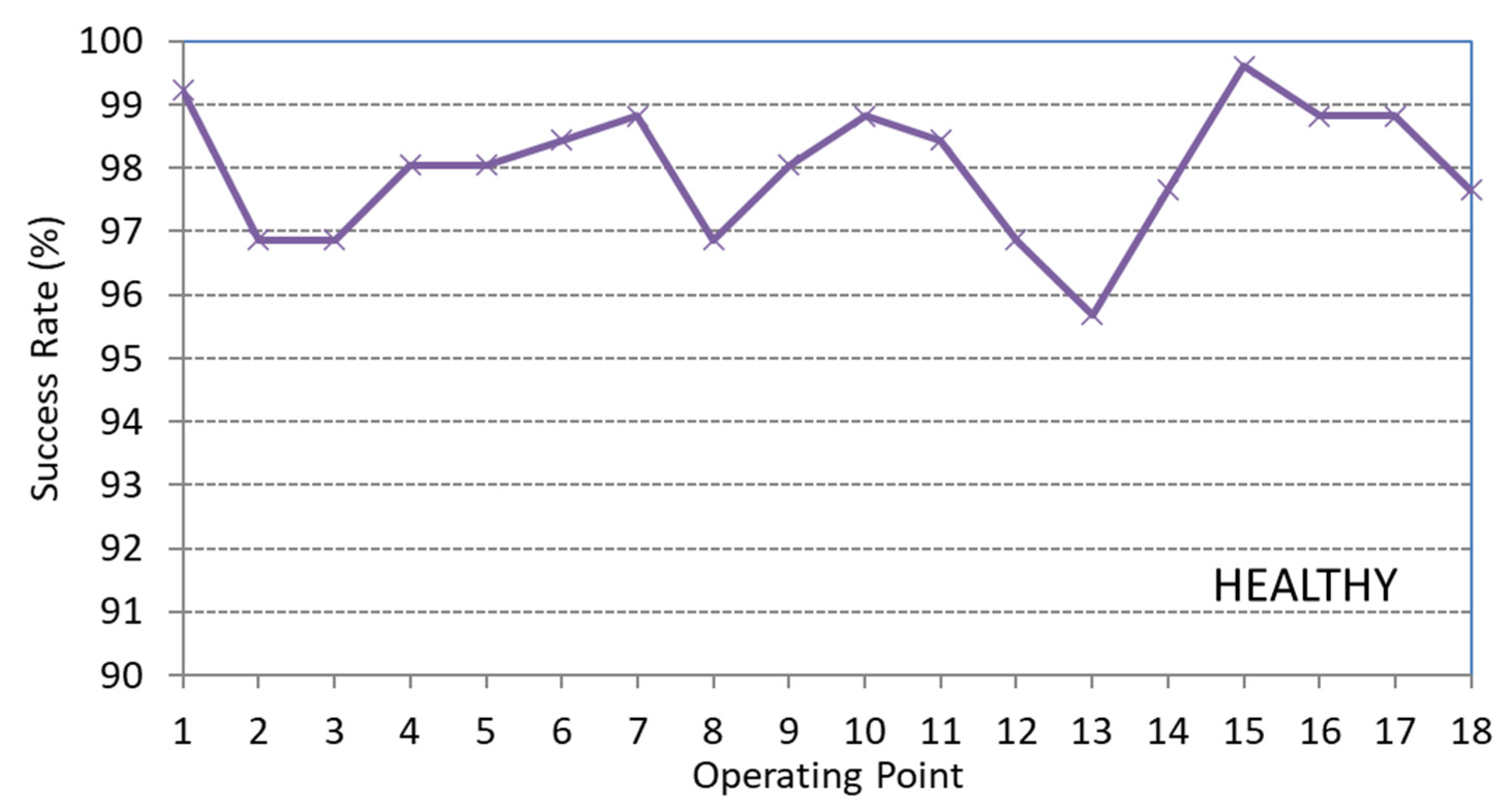
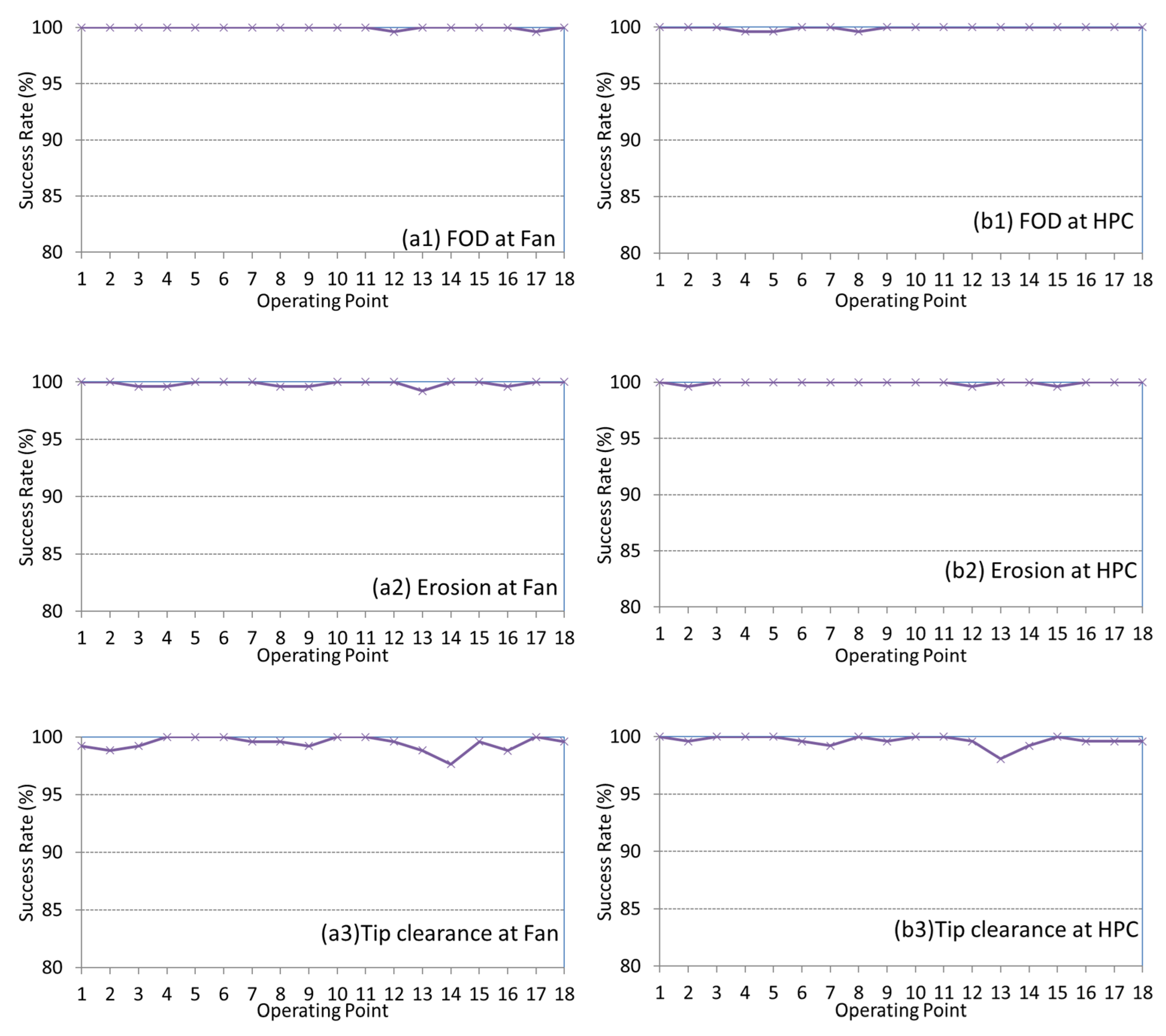
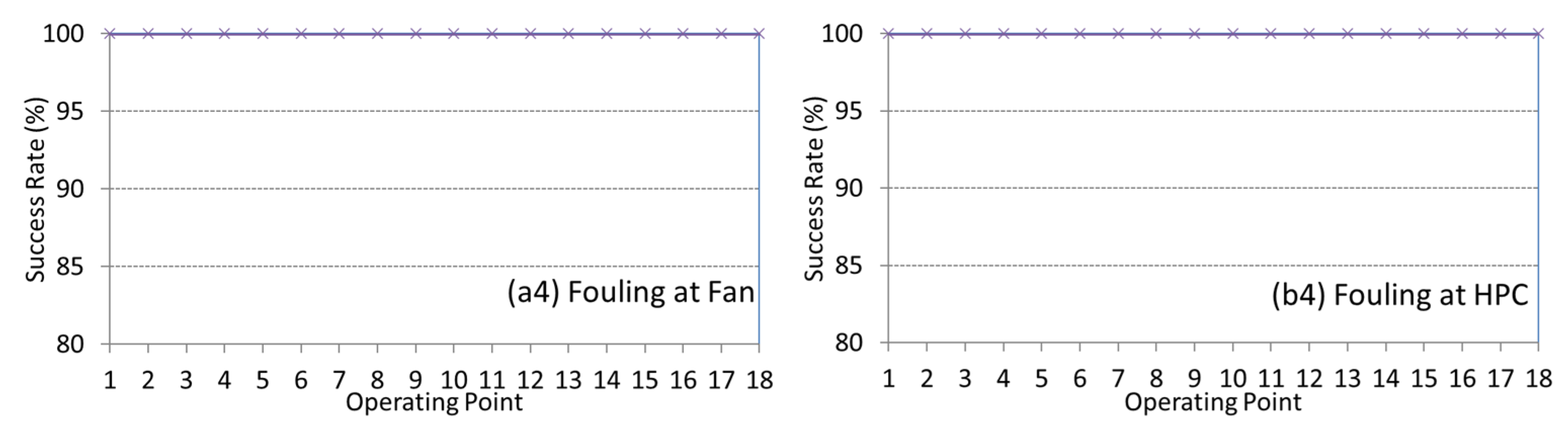
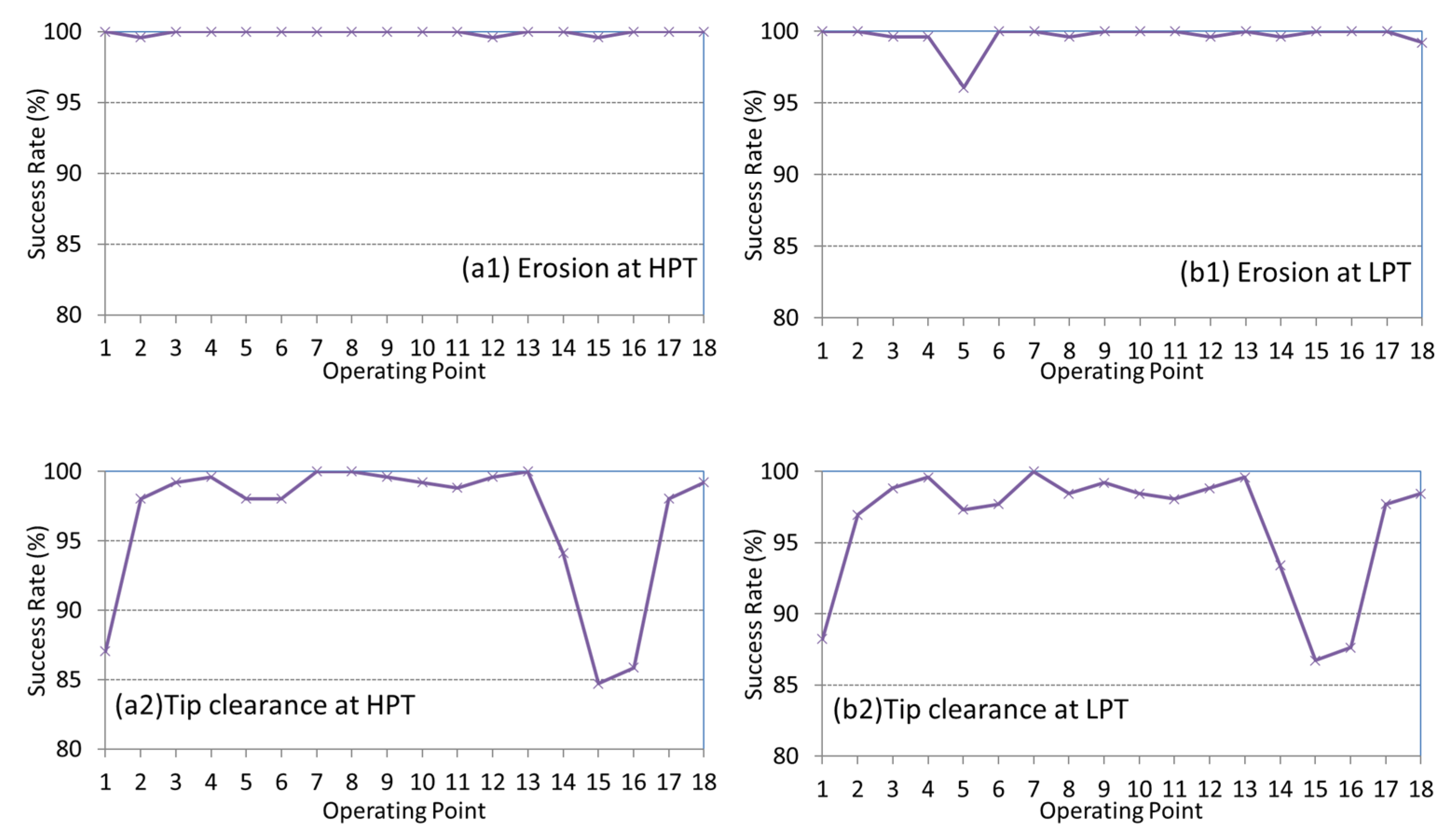
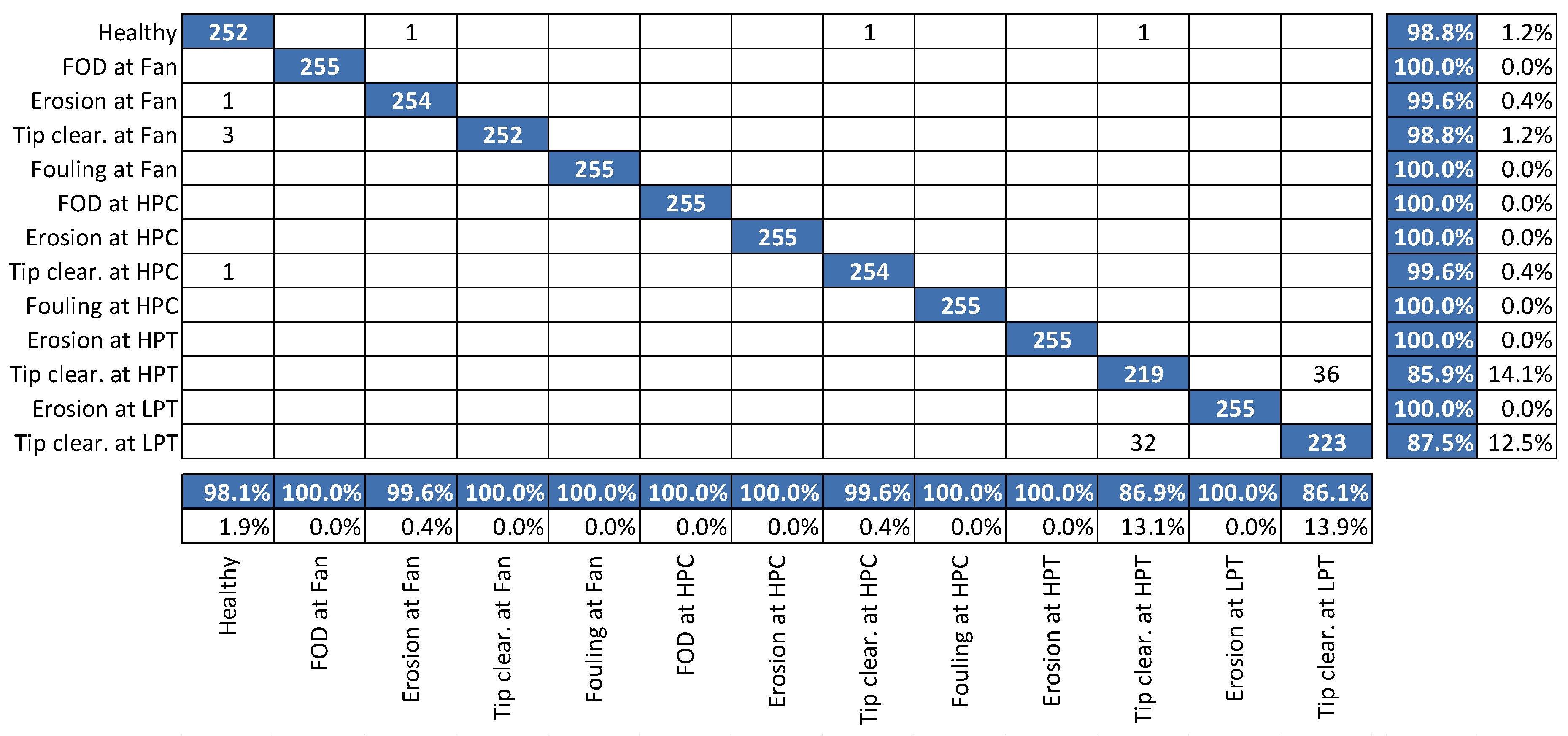
4.3. Diagnostic Method Efficiency
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Description of Training and Testing Patterns
| Fault Magnitudes (L) | Fault Ratios (tan(θ)) | No. of Training Patterns |
|---|---|---|
| −[0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0, 30] | +[0.05, 0.5, 1, 2, 3, 5] | 13 × 12 = 156 |
| +[0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0, 30] | −[0.05, 0.5, 1, 2, 3, 5] |
| Component | Fault | Fault Magnitudes (L) | Fault Ratios (tan(θ)) | No. of Test Patterns | ||||
|---|---|---|---|---|---|---|---|---|
| From | To | Step | From | To | Step | |||
| None | No fault | 0 | 0 | N/A | N/A | 255 | ||
| FAN | Tip clearance | −1 | −6 | 0.1 | 0.4 | 0.6 | 0.05 | 51 × 5 = 255 |
| FAN | Erosion | −1 | −6 | 0.1 | 1.9 | 2.1 | 0.05 | 51 × 5 = 255 |
| FAN | FOD | −1 | −6 | 0.1 | 0.9 | 1.1 | 0.05 | 51 × 5 = 255 |
| FAN | Fouling | −1 | −6 | 0.1 | −2.9 | −3.1 | 0.05 | 51 × 5 = 255 |
| HPC | Tip clearance | −1 | −6 | 0.1 | 0.1 | 0.3 | 0.05 | 51 × 5 = 255 |
| HPC | Erosion | −1 | −6 | 0.1 | 1.9 | 2.1 | 0.05 | 51 × 5 = 255 |
| HPC | FOD | −1 | −6 | 0.1 | 0.9 | 1.1 | 0.05 | 51 × 5 = 255 |
| HPC | Fouling | −1 | −6 | 0.1 | −2.9 | −3.1 | 0.05 | 51 × 5 = 255 |
| HPT | Tip clearance | −1 | −6 | 0.1 | 0.01 | 0.03 | 0.05 | 51 × 5 = 255 |
| HPT | Erosion | 1 | 6 | 0.1 | −1.9 | −2.1 | 0.05 | 51 × 5 = 255 |
| LPT | Tip clearance | −1 | −6 | 0.1 | 0.01 | 0.03 | 0.05 | 51 × 5 = 255 |
| LPT | Erosion | 1 | 6 | 0.1 | −1.9 | −2.1 | 0.05 | 51 × 5 = 255 |
Appendix B. Considered Operating Points and Measurement Noise of the Available Instrumentation
| OP id | Alt (ft) | dTisa | M | N1cor (%) |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 35 |
| 2 | 0 | 0 | 0 | 100 |
| 3 | 50 | 0 | 0.2 | 100 |
| 4 | 45,000 | 0 | 0.6 | 100 |
| 5 | 45,000 | 0 | 0.6 | 95 |
| 6 | 45,000 | 0 | 0.8 | 95 |
| 7 | 45,000 | 0 | 0.8 | 90 |
| 8 | 45,000 | 0 | 0.6 | 90 |
| 9 | 45,000 | 0 | 0.6 | 80 |
| 10 | 25,000 | 0 | 0.6 | 80 |
| 11 | 25,000 | 0 | 0.6 | 100 |
| 12 | 45,000 | 0 | 0.8 | 100 |
| 13 | 45,000 | 0 | 0.8 | 90 |
| 14 | 45,000 | 0 | 0.8 | 50 |
| 15 | 50 | 0 | 0.2 | 50 |
| 16 | 50 | 0 | 0.2 | 35 |
| 17 | 0 | 0 | 0 | 98.12 |
| 18 | 35,000 | 10 | 0.8 | 100 |
| Measurement | Symbol | Noise (%) |
|---|---|---|
| Ambient pressure | Pamb | 0.14 |
| Total pressure at station ‘0’ | Pt0 | 0.10 |
| Total temperature at station ‘0’ | Tt0 | 0.23 |
| LP shaft speed | NL | 0.05 |
| Fuel flow rate | Wf | 0.15 |
| HP shaft speed | NH | 0.05 |
| Total pressure at station ‘13’ | Pt13 | 0.17 |
| Total temperature at station ‘13’ | Tt13 | 0.23 |
| Total pressure at station ‘31’ | Pt31 | 0.17 |
| Total temperature at station ‘31’ | Tt31 | 0.10 |
| Total temperature at station ‘5’ | Tt5 | 0.10 |
| Total pressure at station ‘45’ | Pt45 | 0.17 |
References
- Fentaye, A.D.; Gilani, S.I.U.-H.; Baheta, A.T. Gas Turbine Gas Path Diagnostics: A Review. MATEC Web Conf. 2016, 74, 00005. [Google Scholar] [CrossRef]
- Vu, D.Q.; Razakarivony, S.; Marnissi, Y.; Nocture, M. A Comprehensive Literature Review on the Resolution of Turbine Engine Performances’ Inverse Problems. In Volume 4: Controls, Diagnostics, and Instrumentation, Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition, London, UK, 24–28 June 2024; American Society of Mechanical Engineers: New York, NY, USA, 2024; p. V004T05A045. [Google Scholar]
- Fentaye, A.D.; Baheta, A.T.; Gilani, S.I.; Kyprianidis, K.G. A Review on Gas Turbine Gas-Path Diagnostics: State-of-the-Art Methods, Challenges and Opportunities. Aerospace 2019, 6, 83. [Google Scholar] [CrossRef]
- Hanachi, H.; Mechefske, C.; Liu, J.; Banerjee, A.; Chen, Y. Performance-Based Gas Turbine Health Monitoring, Diagnostics, and Prognostics: A Survey. IEEE Trans. Reliab. 2018, 67, 1340–1363. [Google Scholar] [CrossRef]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Abdul Karim, Z.A. Performance-Based Health Monitoring, Diagnostics and Prognostics for Condition-Based Maintenance of Gas Turbines: A Review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef]
- De Castro-Cros, M.; Velasco, M.; Angulo, C. Machine-Learning-Based Condition Assessment of Gas Turbines—A Review. Energies 2021, 14, 8468. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E.; Gibson, S.; Cross, E.; Parente, A.; Vinuesa, R. Improving Aircraft Performance Using Machine Learning: A Review. Aerosp. Sci. Technol. 2023, 138, 108354. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Xiong, L.; Wang, J.; Luo, C.; Zhang, L.; Wang, K. Intelligent Fault Diagnosis Methods toward Gas Turbine: A Review. Chin. J. Aeronaut. 2024, 37, 93–120. [Google Scholar] [CrossRef]
- Hashmi, M.B.; Fentaye, A.D.; Mansouri, M.; Kyprianidis, K.G. A Comparative Analysis of Various Machine Learning Approaches for Fault Diagnostics of Hydrogen Fueled Gas Turbines. In Volume 4: Controls, Diagnostics, and Instrumentation, Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition, London, UK, 24–28 June 2024; American Society of Mechanical Engineers: New York, NY, USA, 2024; p. V004T05A050. [Google Scholar]
- Zhou, D.; Huang, D. A Review on the Progress, Challenges and Prospects in the Modeling, Simulation, Control and Diagnosis of Thermodynamic Systems. Adv. Eng. Inform. 2024, 60, 102435. [Google Scholar] [CrossRef]
- Mathioudakis, K.; Alexiou, A.; Aretakis, N.; Romesis, C. Signatures of Compressor and Turbine Faults in Gas Turbine Performance Diagnostics: A Review. Energies 2024, 17, 3409. [Google Scholar] [CrossRef]
- Urban, L.A. Gas Turbine Engine Parameter Interrelationships, 2nd ed.; HSD UTC: Windsor Locks, CT, USA, 1969. [Google Scholar]
- Urban, L.A.; Volponi, A.J. Mathematical Methods of Relative Engine Performance Diagnostics; SAE International: Warrendale, PA, USA, 1992; p. 922048. [Google Scholar]
- Doel, D. TEMPER—A Gas Path Analysis Tool for Commercial Jet Engines. J. Eng. Gas Turbines Power 1994, 116, 82–89. [Google Scholar] [CrossRef]
- Stamatis, A.; Mathioudakis, K.; Papailiou, K.D. Adaptive Simulation of Gas Turbine Performance. J. Eng. Gas Turbine Power 1990, 112, 168–175. [Google Scholar] [CrossRef]
- Li, Y.G. Gas Turbine Performance and Health Status Estimation Using Adaptive Gas Path Analysis. J. Eng. Gas Turbines Power 2010, 132, 041701. [Google Scholar] [CrossRef]
- Aretakis, N.; Roumeliotis, I.; Mathioudakis, K. Performance Model “Zooming” for In-Depth Component Fault Diagnosis. J. Eng. Gas Turbines Power 2011, 133, 031602. [Google Scholar] [CrossRef]
- Roumeliotis, I.; Aretakis, N.; Alexiou, A. Industrial Gas Turbine Health and Performance Assessment with Field Data. J. Eng. Gas Turbines Power 2017, 139, 051202. [Google Scholar] [CrossRef]
- Aretakis, N.; Mathioudakis, K.; Stamatis, A. Identification of Sensor Faults on Turbofan Engines Using Pattern Recognition Techniques. Control Eng. Pract. 2004, 12, 827–836. [Google Scholar] [CrossRef]
- Bunks, C.; Mccarthy, D.; Al-Ani, T. Condition-based maintenance of machines using hidden markov models. Mech. Syst. Signal Process. 2000, 14, 597–612. [Google Scholar] [CrossRef]
- Nadir, F.; Elias, H.; Messaoud, B. Diagnosis of Defects by Principal Component Analysis of a Gas Turbine. SN Appl. Sci. 2020, 2, 980. [Google Scholar] [CrossRef]
- Allen, C.W.; Holcomb, C.M.; De Oliveira, M. Gas Turbine Machinery Diagnostics: A Brief Review and a Sample Application. In Volume 6: Ceramics; Controls, Diagnostics and Instrumentation; Education, Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; Manufacturing Materials and Metallurgy; American Society of Mechanical Engineers: New York, NY, USA, 2017; p. V006T05A028. [Google Scholar]
- Luo, H.; Zhong, S. Gas Turbine Engine Gas Path Anomaly Detection Using Deep Learning with Gaussian Distribution. In Proceedings of the 2017 Prognostics and System Health Management Conference (PHM-Harbin), Harbin, China, 9–12 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Tamilselvan, P.; Wang, P. Failure Diagnosis Using Deep Belief Learning Based Health State Classification. Reliab. Eng. Syst. Saf. 2013, 115, 124–135. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Wang, J.-J.; Li, X.-Y.; Peng, G.-J.; Yang, Z. Extended Least Squares Support Vector Machine with Applications to Fault Diagnosis of Aircraft Engine. ISA Trans. 2020, 97, 189–201. [Google Scholar] [CrossRef]
- Zhou, D.; Yao, Q.; Wu, H.; Ma, S.; Zhang, H. Fault Diagnosis of Gas Turbine Based on Partly Interpretable Convolutional Neural Networks. Energy 2020, 200, 117467. [Google Scholar] [CrossRef]
- Cao, Q.; Chen, S.; Zheng, Y.; Ding, Y.; Tang, Y.; Huang, Q.; Wang, K.; Xiang, W. Classification and Prediction of Gas Turbine Gas Path Degradation Based on Deep Neural Networks. Int. J. Energy Res. 2021, 45, 10513–10526. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.G. Abrupt Fault Detection and Isolation for Gas Turbine Components Based on a 1D Convolutional Neural Network Using Time Series Data. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Virtual Event, 24–26 August 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar]
- Amare, F.D.; Gilani, S.I.; Aklilu, B.T.; Mojahid, A. Two-Shaft Stationary Gas Turbine Engine Gas Path Diagnostics Using Fuzzy Logic. J. Mech. Sci. Technol. 2017, 31, 5593–5602. [Google Scholar] [CrossRef]
- Wang, X.-X.; Ma, L.-Y. A Compact K Nearest Neighbor Classification for Power Plant Fault Diagnosis. J. Inf. Hiding Multimed. Signal Process. 2014, 5, 508–517. [Google Scholar]
- Romessis, C.; Mathioudakis, K. Bayesian Network Approach for Gas Path Fault Diagnosis. J. Eng. Gas Turbines Power 2006, 128, 64–72. [Google Scholar] [CrossRef]
- Bose, N.K.; Liang, P. Neural Network Fundamentals with Graphs, Algorithms and Applications; McGraw-Hill Series in Electrical and Computer Engineering; McGraw-Hill: New York, NY, USA, 1996; ISBN 978-0-07-006618-2. [Google Scholar]
- Specht, D.F. Probabilistic neural networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Mohebali, B.; Tahmassebi, A.; Meyer-Baese, A.; Gandomi, A.H. Chapter 14—Probabilistic neural networks: A brief overview of theory, implementation, and application. In Handbook of Probabilistic Models; Butterworth-Heinemann: Oxford, UK, 2020; pp. 347–367. ISBN 9780128165140. [Google Scholar] [CrossRef]
- Eustace, R.; Merrington, G. Fault Diagnosis of Fleet Engines Using Neural Networks. In Proceedings of the Twelfth International Symposium on Air Breathing Engines, Melbourne, Australia, 10–15 September 1995. paper no. ISABE 95-7085. [Google Scholar]
- Romesis, C.; Mathioudakis, K. Setting Up of a Probabilistic Neural Network for Sensor Fault Detection Including Operation with Component Faults. J. Eng. Gas Turbines Power 2003, 125, 634–641. [Google Scholar] [CrossRef]
- Romessis, C.; Stamatis, A.; Mathioudakis, K. A Parametric Investigation of the Diagnostic Ability of Probabilistic Neural Networks on Turbofan Engines. In Volume 4: Manufacturing Materials and Metallurgy; Ceramics; Structures and Dynamics; Controls, Diagnostics and Instrumentation; Education; IGTI Scholar Award, Proceedings of the ASME Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, Louisiana, USA, 4–7 June 2001; American Society of Mechanical Engineers: New York, NY, USA, 2001; p. V004T04A004. [Google Scholar]
- Aretakis, N.; Roumeliotis, I.; Alexiou, A.; Romesis, C.; Mathioudakis, K. Turbofan Engine Health Assessment From Flight Data. J. Eng. Gas Turbines Power 2015, 137, 041203. [Google Scholar] [CrossRef]
- Romessis, C.; Mathioudakis, K. Implementation of Stochastic Methods for Industrial Gas Turbine Fault Diagnosis. In Volume 1: Turbo Expo 2005, Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air, Reno, NV, USA, 6–9 June 2005; ASMEDC: New York, NY, USA, 2005; pp. 723–730. [Google Scholar]
- Butler, S.W.; Pattipati, K.R.; Volponi, A.; Hull, J.; Rajamani, R.; Siegel, J. An Assessment Methodology for Data-Driven and Model-Based Techniques for Engine Health Monitoring. In Volume 2: Aircraft Engine; Ceramics; Coal, Biomass and Alternative Fuels; Controls, Diagnostics and Instrumentation; Environmental and Regulatory Affairs, Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; ASMEDC: New York, NY, USA, 2006; pp. 823–831. [Google Scholar]
- Jiang, R.; Zhu, W. A PNN fault diagnosis method for gas turbine. In Proceedings of the World Automation Congress 2012, Puerto Vallarta, Mexico, 24–28 June 2012; pp. 1–4. [Google Scholar]
- Loboda, I.; Olivares Robles, M.A. Gas Turbine Fault Diagnosis Using Probabilistic Neural Networks. Int. J. Turbo Jet-Engines 2015, 32, 175–191. [Google Scholar] [CrossRef]
- Cao, Y.; Lv, X.; Han, G.; Luan, J.; Li, S. Research on Gas-Path Fault-Diagnosis Method of Marine Gas Turbine Based on Exergy Loss and Probabilistic Neural Network. Energies 2019, 12, 4701. [Google Scholar] [CrossRef]
- Alexiou, A.; Mathioudakis, K. Development of Gas Turbine Performance Models Using a Generic Simulation Tool. In Proceedings of the ASME Turbo Expo 2005, Reno, NV, USA, 6–9 June 2005; ASME: New York, NY, USA, 2005; pp. 185–194. [Google Scholar] [CrossRef]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Simon, D.L.; Borguet, S.; Leonard, O.; Zhang, X. Aircraft Engine Gas Path Diagnostic Methods: Public Benchmarking Results. J. Eng. Gas Turbines Power 2013, 136, 041201. [Google Scholar] [CrossRef]
- Koskoletos, O.; Aretakis, N.; Alexiou, A. Evaluation of Aircraft Engine Diagnostic Methods through ProDiMES. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]


| u | Symbol | f | Symbol |
|---|---|---|---|
| Ambient pressure | Pamb | FAN Flow factor | SW2 |
| Total pressure at station ‘0’ | Pt0 | FAN Efficiency factor | SE2 |
| Total temperature at station ‘0’ | Tt0 | HPC Flow factor | SW25 |
| LP shaft speed | NL | HPC Efficiency factor | SE25 |
| Y | Symbol | HPT Flow factor | SW4 |
| Fuel flow rate | Wf | HPT Efficiency factor | SE4 |
| HP shaft speed | NH | LPT Flow factor | SW45 |
| Total pressure at station ‘13’ | Pt13 | LPT Efficiency factor | SE45 |
| Total temperature at station ‘13’ | Tt13 | ||
| Total pressure at station ‘31’ | Pt31 | ||
| Total temperature at station ‘31’ | Tt31 | ||
| Total temperature at station ‘5’ | Tt5 |
| Class No. | Class Symbol | Class Description |
|---|---|---|
| 1 | HEALTHY | Healthy condition. All |ΔSW|, |ΔSE| ≤ 0.5% |
| 2 | FAN | Fault only in the FAN. |ΔSW2|, |ΔSE2| > 0.5%, |
| 3 | HPC | Fault only in the HPC. |ΔSW25|, |ΔSE25| > 0.5%, |
| 4 | HPT | Fault only in the HPT. |ΔSW4|, |ΔSE4| > 0.5%, |
| 5 | LPT | Fault only in the LPT. |ΔSW45|, |ΔSE45| > 0.5%, |
| Fault | Success Rate (%) | Difference | |
|---|---|---|---|
| 100 Rec. Avg. | 10 Rec. Avg. | ||
| Healthy | 98.06 | 95.17 | −2.89 |
| FanFOD | 99.98 | 99.42 | −0.56 |
| FanEros | 99.83 | 99.11 | −0.71 |
| FanTipRub | 99.52 | 98.46 | −1.06 |
| HPCFOD | 99.94 | 99.65 | −0.28 |
| HPCEros | 99.98 | 97.73 | −2.25 |
| HPCTipRub | 99.72 | 99.67 | −0.04 |
| HPCVGVp | 99.75 | 97.70 | −2.04 |
| HPCVGVm | 99.98 | 99.78 | −0.20 |
| HPTEros | 99.91 | 99.76 | −0.15 |
| HPTTipRub | 96.67 | 95.90 | −0.76 |
| LPTEros | 99.59 | 99.22 | −0.37 |
| LPTTipRub | 96.45 | 95.36 | −1.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romesis, C.; Aretakis, N.; Mathioudakis, K. Model-Assisted Probabilistic Neural Networks for Effective Turbofan Fault Diagnosis. Aerospace 2024, 11, 913. https://doi.org/10.3390/aerospace11110913
Romesis C, Aretakis N, Mathioudakis K. Model-Assisted Probabilistic Neural Networks for Effective Turbofan Fault Diagnosis. Aerospace. 2024; 11(11):913. https://doi.org/10.3390/aerospace11110913
Chicago/Turabian StyleRomesis, Christoforos, Nikolaos Aretakis, and Konstantinos Mathioudakis. 2024. "Model-Assisted Probabilistic Neural Networks for Effective Turbofan Fault Diagnosis" Aerospace 11, no. 11: 913. https://doi.org/10.3390/aerospace11110913
APA StyleRomesis, C., Aretakis, N., & Mathioudakis, K. (2024). Model-Assisted Probabilistic Neural Networks for Effective Turbofan Fault Diagnosis. Aerospace, 11(11), 913. https://doi.org/10.3390/aerospace11110913









