1. Introduction
It is well-known that the exhaustive physicochemical characterization of drugs in dissolution plays a crucial role in all stages associated with the R&D of homogenous liquid pharmaceutical dosage forms, especially those intended for parenteral administration in small volumes like ampules, because these products supply high doses of active pharmaceutical ingredients [
1,
2,
3,
4].
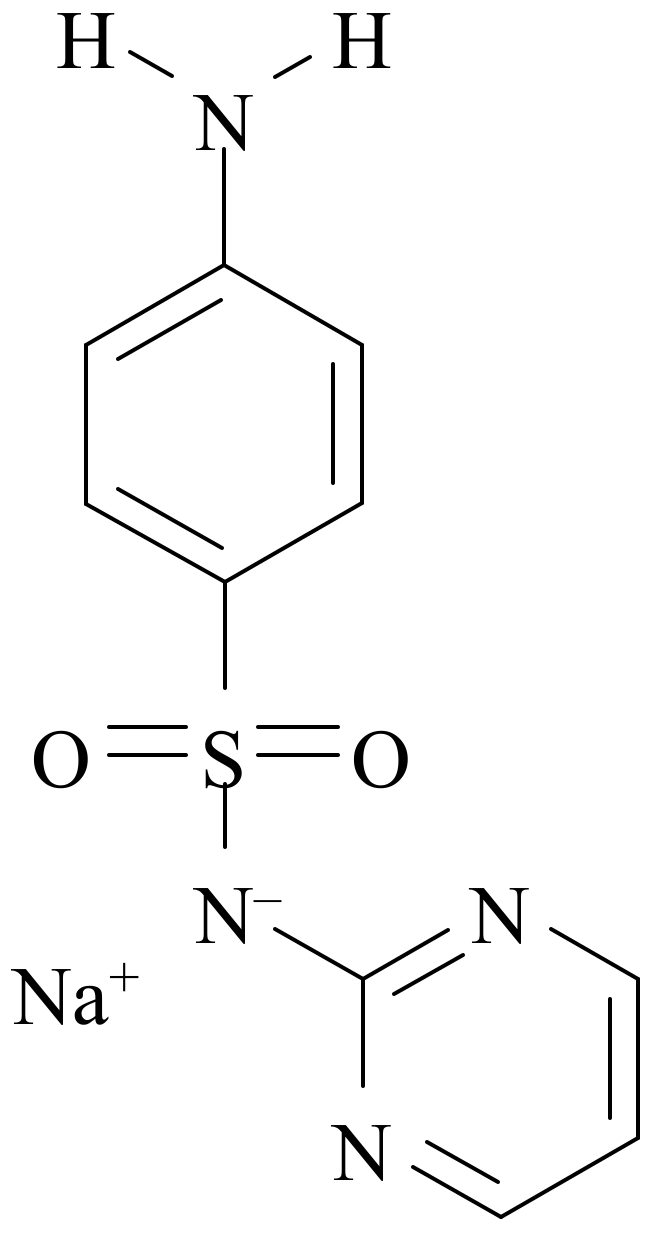
Sodium sulfadiazine (sodium [(4-aminophenyl)sulfonyl](2-pyrimidinyl)azanide, NaSD,
Figure 1) is a drug extensively used for the treatment of certain infections caused by several kinds of microorganisms [
5,
6,
7]. Although NaSD is widely used in therapeutics, its physicochemical information regarding its behavior in aqueous solutions is not yet complete. However, some physicochemical studies have been reported in the literature. Thus, the molar and mole fraction equilibrium solubility as well as the respective dissolution and mixing thermodynamic quantities in some ethanol–water blended solvents have been reported [
8,
9,
10]. Moreover, its equilibrium solubility and apparent specific volumes at saturation in different {cosolvent (1) + water (2)} mixtures at 25.0 °C have also been reported, involving propylene glycol, formamide,
N-methylformamide,
N,
N-dimethylformamide, dimethyl sulfoxide,
N-methyl-2-pyrrolidone, 1,4-dioxane, and methanol [
11,
12]. On the other hand, apparent molar volumes at several drug concentrations have been determined at several temperatures in aqueous–cosolvent media [
13,
14]. Ultimately, the molar electrical conductivity of this saline drug has also been studied as a function of drug concentration as a function of temperature [
15]. All these investigations have demonstrated the role of hydrophilic and hydrophobic hydration processes of this drug on the observed physicochemical magnitudes in aqueous media.
From a pharmaceutical viewpoint, the systematic searching, acquisition, and systematization of equilibrium solubility values and volumetric contributions of active pharmaceutical ingredients and excipients at saturation conditions in aqueous and non-aqueous cosolvent mixtures are very significant for theoretical and practical purposes. This is because cosolvent blends are frequently employed in pharmaceutical ingredient purification methods, dosage form preformulation studies, and the development and preparation of homogeneous liquid medicines, as already mentioned [
16,
17]. Therefore, it is almost mandatory for the global chemical and pharmaceutical community to systematically determine the solubility and specific volume contribution of every pharmaceutical agent.
Otherwise, the study of molar and specific volumes of every kind of pharmaceutical solute has been carried out basically with the aim of facilitating the design of liquid medicines on the one hand and also as an aid to proposing mechanisms for the transferring processes of drugs through biological membranes. Within the first group, studies have been carried out focused on the generation of useful information in the design of drug delivery systems, and as an example, the determination of partial specific volumes and critical micellar concentrations of surfactants from density measurements of their aqueous solutions [
18]; in a similar way, these determinations facilitate the proposal of novel calculation methods of partial molar volumes of surfactants dispersed at the micellar level owing to the difficulty observed in determining experimentally this property under extreme conditions [
19]. However, from density measurements, the apparent specific volumes of poly(ethylene oxide), poly(butylene oxide), poly(propylene oxide), and octadecyl chains in the micellar state as a function of temperature have been calculated and reported [
20]. Moreover, Sarazin and Francois, analyzing various polymers in solvents of differing molecular size and polarity, confirmed the dependence of their apparent specific volume on polymer molecular weight and solvent molar volume [
21]. Moreover, it is noteworthy that use of apparent specific volumes is relevant in chemical analysis varying from milk food science to blood biochemistry [
22,
23]. On the other hand, molar volumes are required to calculate Hildebrand solubility parameters as required for the estimation of the solubility of organic compounds [
24,
25]. Thus, partial molar volumes and solubility parameters of compounds of pharmaceutical interest such as some esters have been studied [
26]. Specifically, regarding the penetration of biological membranes, the solubility and partial molar volume of the ophthalmological drug physostigmine in binary mixtures of isopropanol–isopropyl myristate have been studied as an aid in clarifying the effects of these solvents on the penetration of physostigmine through biological membranes [
27].
The extended theory of regular solutions has been applied to explain and estimate the percutaneous absorption of different non-electrolytes or undissociated weak electrolytes by studying the solubility and partial molar volumes of these solutes in certain solvents, with the aim of finding application in the design of dermal controlled release systems. Some of these solutes correspond to certain alkanoic acids, theophylline, and adenosine, among others [
28,
29,
30].
In the research field related to identifying action mechanisms of active ingredients, the effect of volumetric properties has also been studied, as shown in the case of volatile anesthetics such as halothane, which have been evaluated for compressibility, molar volume, and partial molar volume in different solvents [
31,
32]. More recently, the partial molar volumes of some local anesthetics like lidocaine in water and ethanol were evaluated experimentally, and from these values the corresponding transfer volumes were calculated, and the respective interpretation was made in terms of solute–solvent interactions highlighting the role of the hydrophobicity of the compounds on the binding to the cell membrane [
33].
Other compounds of pharmaceutical interest studied include sodium salicylate, methyl orange, tryptophan, phenol and propranolol hydrochlorides, procaine, pilocarpene and ephedrine, whose volumes and apparent molal compressibilities have been determined as a contribution to the clarification of solute–solvent interactions in QSAR studies [
34]. A similar investigation was performed with tetracycline hydrochloride and chlortetracycline involving determining the partial molal volumes and compressibilities, interaction coefficients, and several thermodynamic activation parameters from ultrasonic speed, density, and viscosity measurements [
35]. Furthermore, the partial molal volumes at infinite dilution of different phenyl alkylamines have also been reported [
36]. Moreover, the volumetric properties of several other compounds, including active ingredients and excipients, have also been studied [
37,
38,
39,
40,
41]. Otherwise, apparent specific volumes have been correlated with primary tastes as well as with specific tastes like amino acids and sweetener agents [
42,
43,
44,
45,
46,
47,
48].
In this way, the present research studied the mass/volume (%
m/
v) and mass/mass (%
m/
m) percentages, equilibrium solubility, and apparent specific volume (
/mL/g) at saturation of NaSD (solute identified as component 3) in several aqueous–alcoholic binary mixtures at different temperatures from 5.0 to 35.0 °C. Thus, this research expands the available database of these properties reported earlier for other drugs and excipients in several binary and ternary aqueous–cosolvent mixtures that include some non-electrolyte organic compounds and active organic salts. These compounds and solvent systems include propranolol·HCl in aqueous binary mixtures of 1,4-dioxane, acetonitrile, polyethylene glycol 400, propylene glycol, and methanol at 25.0 °C [
49]; sodium naproxen, procaine·HCl, and lysine clonixinate in (propylene glycol + water) [
50] and (methanol + water) [
51] mixtures at 25.0 °C; lidocaine·HCl·H
2O in aqueous binary mixtures of polyethylene glycol 200, ethanol, and propylene glycol at 25.0 °C [
52]; and sodium diclofenac in aqueous binary mixtures of formamide,
N-methylformamide, and
N,
N,-dimethylformamide at 25.0 °C [
53]. All these reported physicochemical values of pharmaceutical compounds could be used for improving research and development activities.
Thus, it is noteworthy that these basic physicochemical properties of solid compounds in aqueous solutions have been key factors long time ago in the design of liquid dosage forms like syrups, elixirs, and injectable solutions, as well as in predicting the biological behavior of drugs [
54,
55].
2. Methods
The equilibrium solubility values of NaSD (CAS number: 547-32-0, molecular formula: C
10H
9N
4NaO
2S, molar mass: 272.26 g/mol, provider: Sigma-Aldrich, Burlington, MA, USA, mass fraction purity > 0.99) in binary mixtures of ethanol (CAS number: 64-17-5, molecular formula: C
2H
6O, molar mass: 46.07 g/mol, provider: Merck, Darmstadt, Germany, mass fraction purity > 0.995) and water (CAS number: 7732-18-5, obtained by distillation, conductivity < 2 μS/cm) as a function of mixture composition and temperature were expressed in molarity and mole fraction earlier [
10,
11]. Thus, these solubility values were determined at seven temperatures from 5.0 to 35.0 °C in EtOH mass fractions (
w1) from
w1 = 0.10 to
w1 = 0.90 varying by 0.10, studying nine binary mixtures and both pure solvents.
Classical shake-flask method and UV–vis spectrophotometry were employed for solubility determinations [
56,
57]. An excess of NaSD was added to 50 mL of each cosolvent mixture in stoppered dark glass flasks. Solid–liquid mixtures were stirred in a mechanical shaker (Burrel, Wrist Action Shaker, Model 75, Pittsburgh, PA, USA) at room temperature for at least four hours. After this, the flasks were kept at 35.0 ± 0.05 °C in recirculating thermostatic baths (Neslab RTE 10 Digital One, Thermo Electron Company, Waltham, MA, USA) with sporadic stirring at least for three days until equilibrium is obtained. After this time, the supernatant solutions were filtered (at isothermal conditions) using 0.45 μm pore diameter cartridges to ensure that they were free of particulate matter before sampling. NaSD concentrations at saturation were determined by measuring UV absorbance after appropriate gravimetric dilution with pure water and interpolation from a UV spectrophotometric calibration curve (UV/Vis BioMate 3 spectrophotometer, Thermo Electron Company, Waltham, MA, USA). Then, the temperature was diminished in successive steps of 5.0 °C following the same procedures indicated above to reach 5.0 °C as the lowest research temperature. All the solubility experiments were run at least in triplicate.
Moreover, in order to facilitate the transformation between volumetric and gravimetric concentration scales [
2,
58] and allow the calculation of apparent specific volumes of NaSD, the density of the saturated solutions at every temperature was determined with a digital density meter (DMA 45 Anton Paar, Graz, Austria) connected to a recirculating thermostatic bath (Neslab RTE 10 Digital One Thermo Electron Company, Waltham, MA, USA). All calculations, correlations, and plots were performed with different tools of MS Excel
® v. 2013.
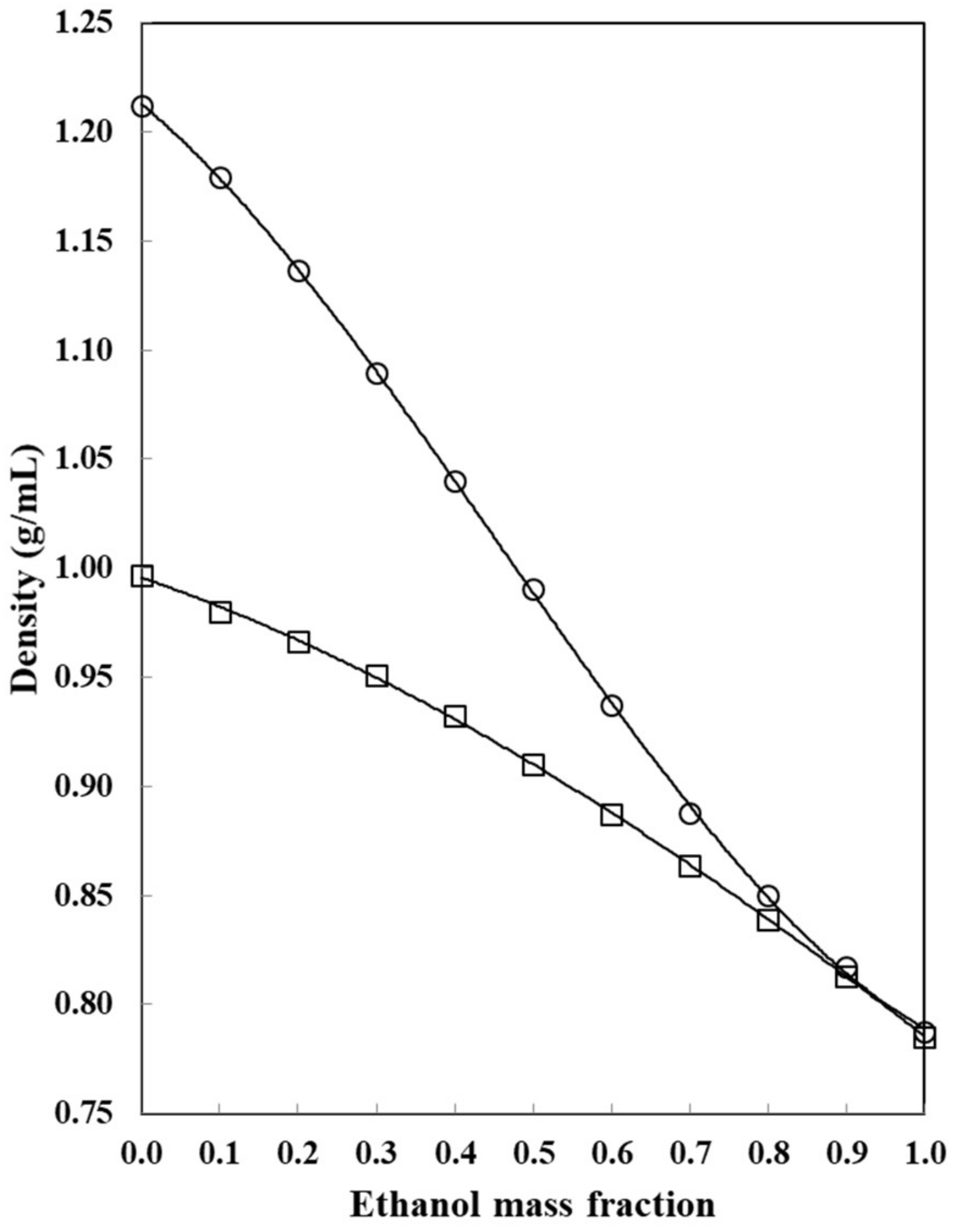
 : neat water;
: neat water;  : w1 = 0.10;
: w1 = 0.10;  : w2 = 0.20;
: w2 = 0.20;  : w1 = 0.30;
: w1 = 0.30;  : w1 = 0.40;
: w1 = 0.40;  : w1 = 0.50;
: w1 = 0.50;  : w2 = 0.60;
: w2 = 0.60;  : w1 = 0.70;
: w1 = 0.70;  : w1 = 0.80;
: w1 = 0.80;  : w1 = 0.90;
: w1 = 0.90;  : neat ethanol.
: neat ethanol.
 : neat water;
: neat water;  : w1 = 0.10;
: w1 = 0.10;  : w2 = 0.20;
: w2 = 0.20;  : w1 = 0.30;
: w1 = 0.30;  : w1 = 0.40;
: w1 = 0.40;  : w1 = 0.50;
: w1 = 0.50;  : w2 = 0.60;
: w2 = 0.60;  : w1 = 0.70;
: w1 = 0.70;  : w1 = 0.80;
: w1 = 0.80;  : w1 = 0.90;
: w1 = 0.90;  : neat ethanol.
: neat ethanol.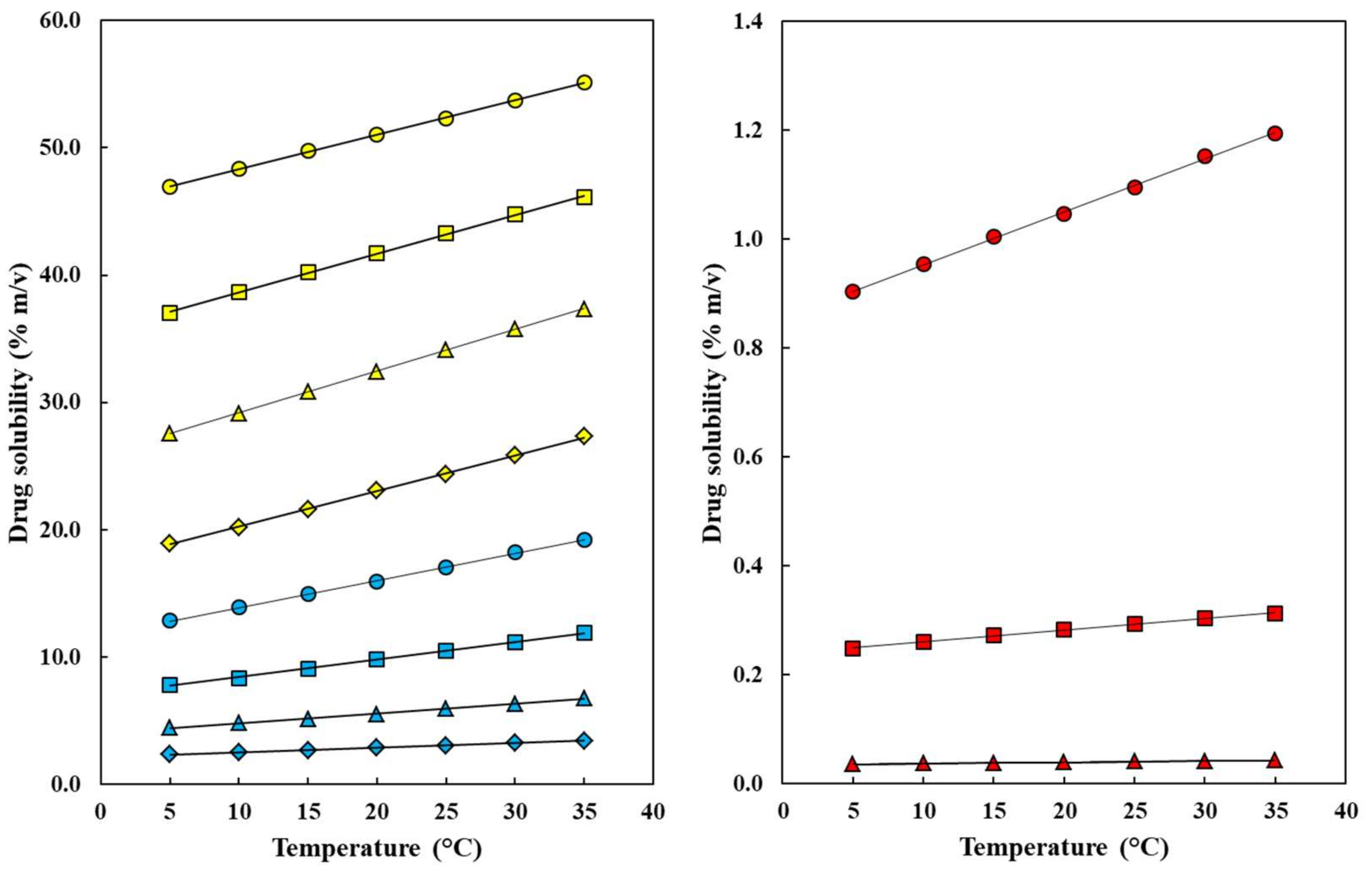
 : neat water;
: neat water;  : w1 = 0.10;
: w1 = 0.10;  : w2 = 0.20;
: w2 = 0.20;  : w1 = 0.30;
: w1 = 0.30;  : w1 = 0.40;
: w1 = 0.40;  : w1 = 0.50;
: w1 = 0.50;  : w2 = 0.60;
: w2 = 0.60;  : w1 = 0.70;
: w1 = 0.70;  : w1 = 0.80;
: w1 = 0.80;  : w1 = 0.90;
: w1 = 0.90;  : neat ethanol.
: neat ethanol.
 : neat water;
: neat water;  : w1 = 0.10;
: w1 = 0.10;  : w2 = 0.20;
: w2 = 0.20;  : w1 = 0.30;
: w1 = 0.30;  : w1 = 0.40;
: w1 = 0.40;  : w1 = 0.50;
: w1 = 0.50;  : w2 = 0.60;
: w2 = 0.60;  : w1 = 0.70;
: w1 = 0.70;  : w1 = 0.80;
: w1 = 0.80;  : w1 = 0.90;
: w1 = 0.90;  : neat ethanol.
: neat ethanol.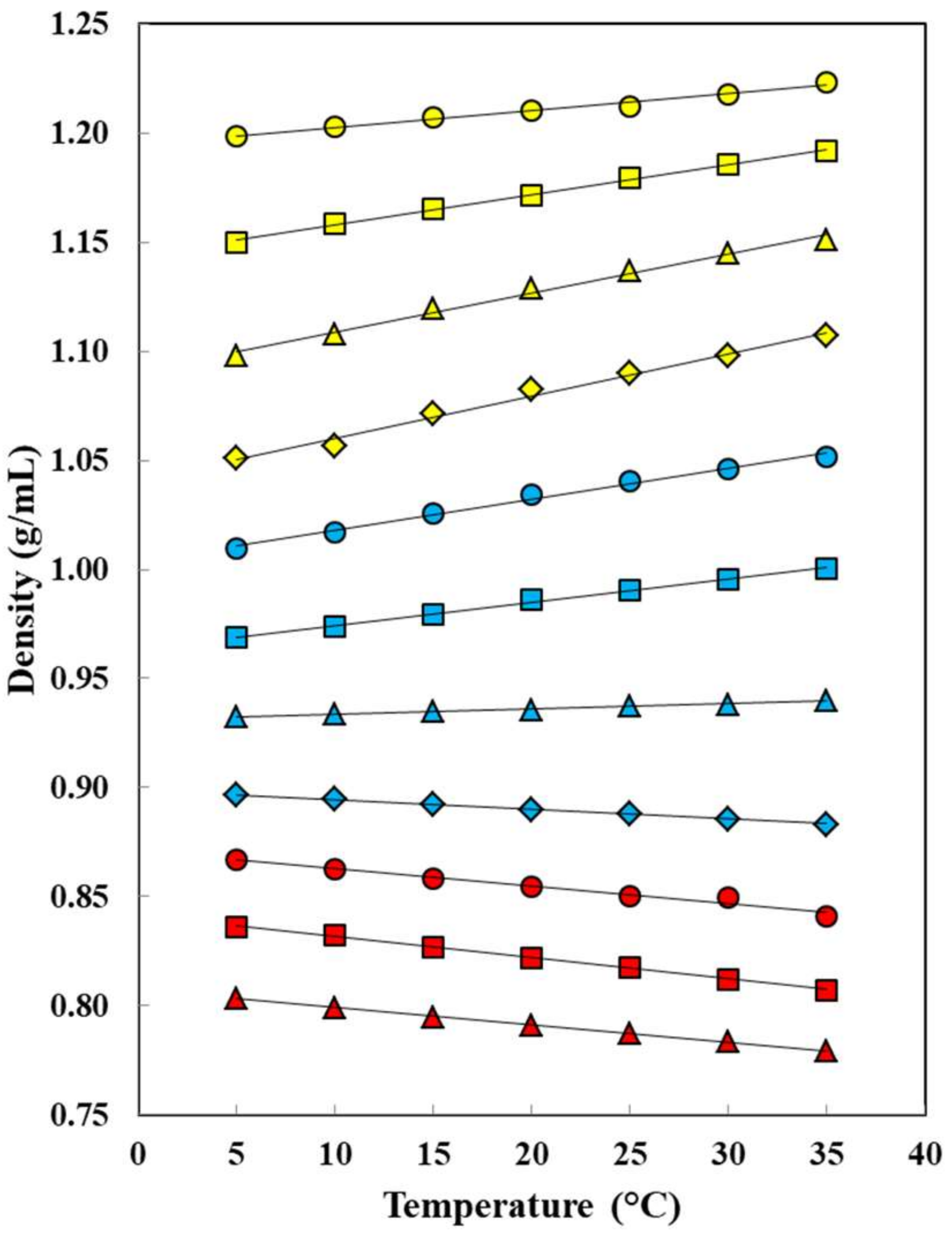
 : neat water;
: neat water;  : w1 = 0.10;
: w1 = 0.10;  : w2 = 0.20;
: w2 = 0.20;  : w1 = 0.30;
: w1 = 0.30;  : w1 = 0.40;
: w1 = 0.40;  : w1 = 0.50;
: w1 = 0.50;  : w2 = 0.60;
: w2 = 0.60;  : w1 = 0.70;
: w1 = 0.70;  : w1 = 0.80;
: w1 = 0.80;  : w1 = 0.90;
: w1 = 0.90;  : neat ethanol.
: neat ethanol.
 : neat water;
: neat water;  : w1 = 0.10;
: w1 = 0.10;  : w2 = 0.20;
: w2 = 0.20;  : w1 = 0.30;
: w1 = 0.30;  : w1 = 0.40;
: w1 = 0.40;  : w1 = 0.50;
: w1 = 0.50;  : w2 = 0.60;
: w2 = 0.60;  : w1 = 0.70;
: w1 = 0.70;  : w1 = 0.80;
: w1 = 0.80;  : w1 = 0.90;
: w1 = 0.90;  : neat ethanol.
: neat ethanol.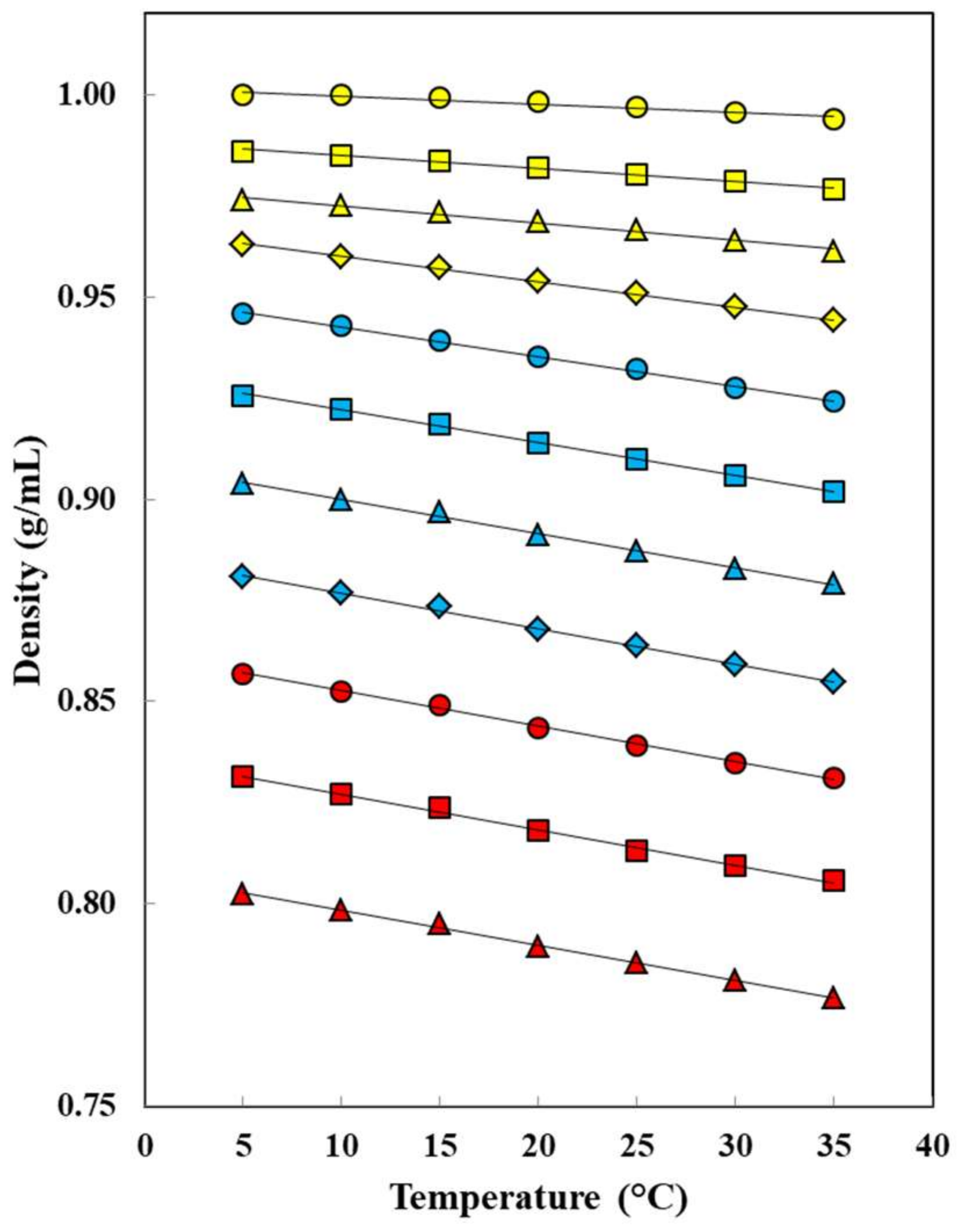
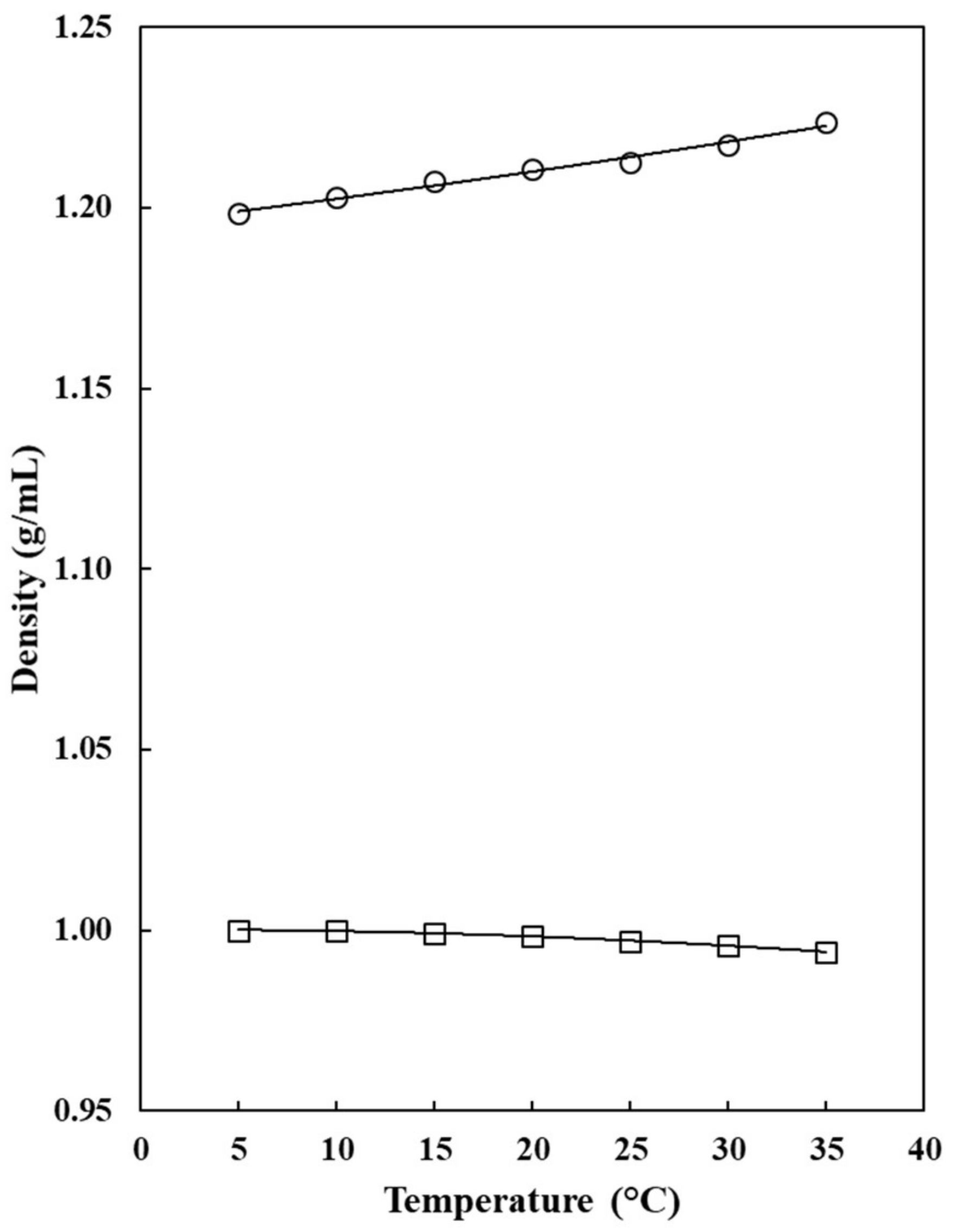
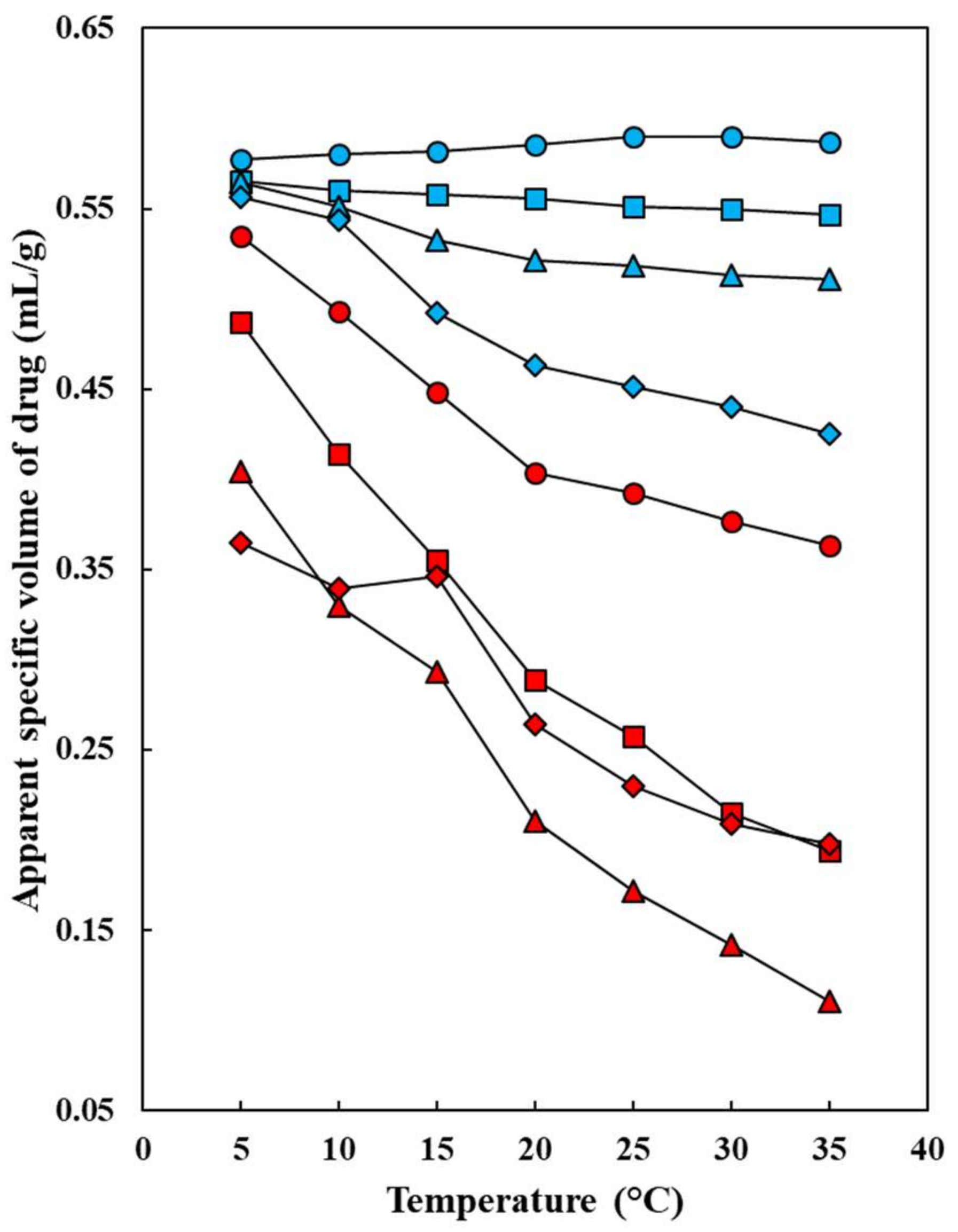
 : 5.0 °C;
: 5.0 °C;  : 10.0 °C;
: 10.0 °C;  : 15.0 °C;
: 15.0 °C;  : 20.0 °C;
: 20.0 °C;  : 25.0 °C;
: 25.0 °C;  : 30.0 °C;
: 30.0 °C;  : 35.0 °C.
: 35.0 °C.
 : 5.0 °C;
: 5.0 °C;  : 10.0 °C;
: 10.0 °C;  : 15.0 °C;
: 15.0 °C;  : 20.0 °C;
: 20.0 °C;  : 25.0 °C;
: 25.0 °C;  : 30.0 °C;
: 30.0 °C;  : 35.0 °C.
: 35.0 °C.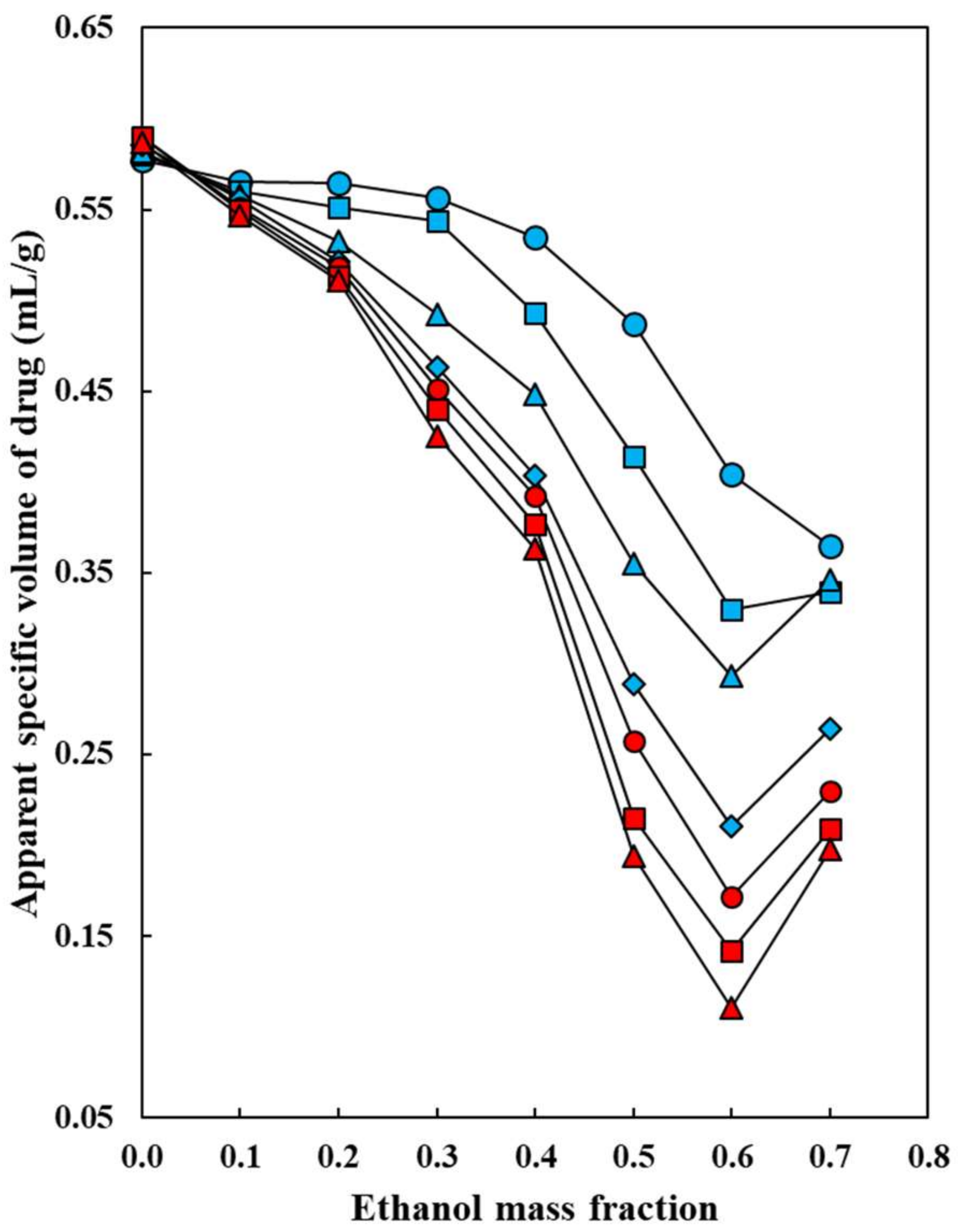
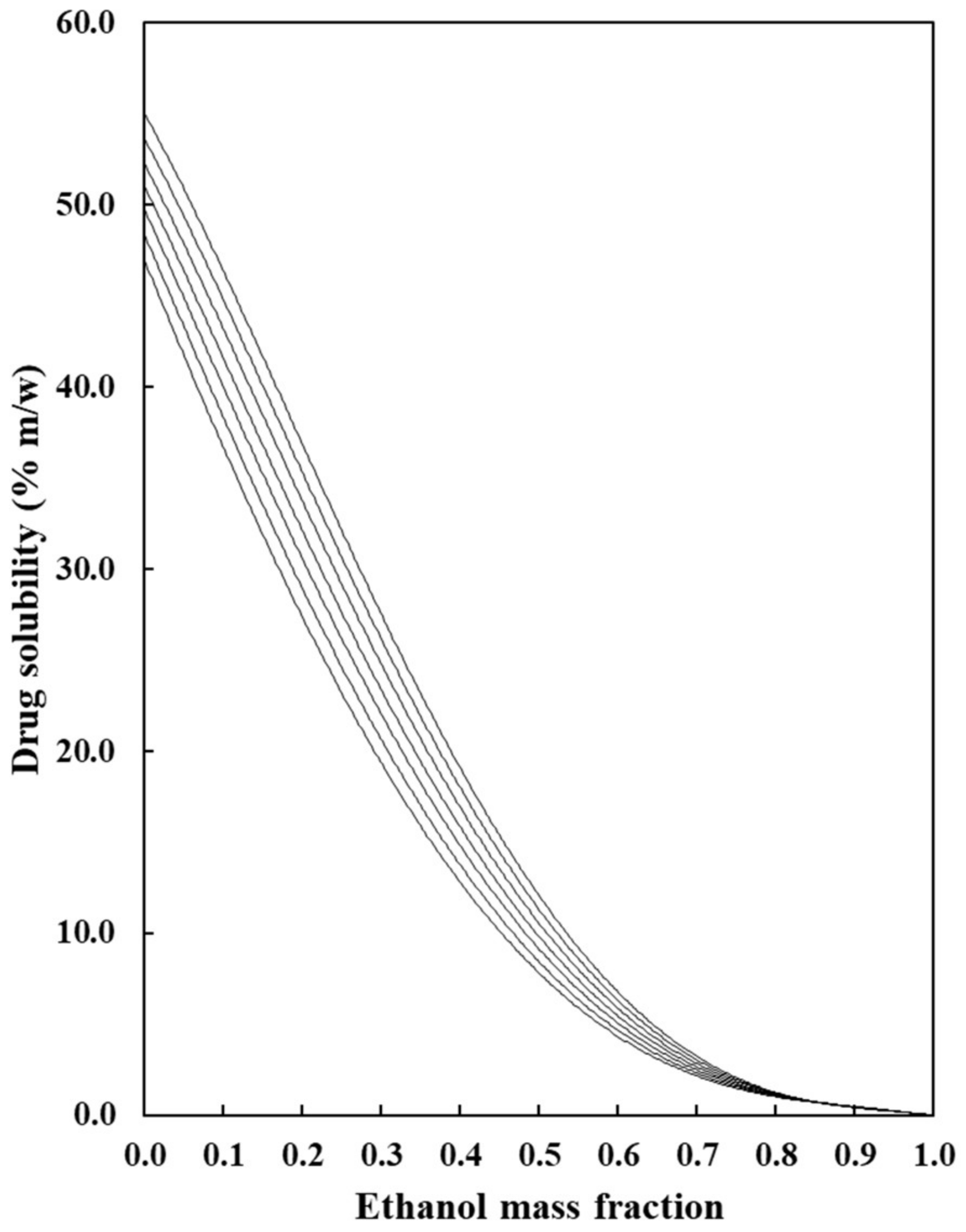
 : neat water;
: neat water;  : w1 = 0.10;
: w1 = 0.10;  : w2 = 0.20;
: w2 = 0.20;  : w1 = 0.30;
: w1 = 0.30;  : w1 = 0.40;
: w1 = 0.40;  : w1 = 0.50;
: w1 = 0.50;  : w1 = 0.60;
: w1 = 0.60;  : w1 = 0.70.
: w1 = 0.70.
 : neat water;
: neat water;  : w1 = 0.10;
: w1 = 0.10;  : w2 = 0.20;
: w2 = 0.20;  : w1 = 0.30;
: w1 = 0.30;  : w1 = 0.40;
: w1 = 0.40;  : w1 = 0.50;
: w1 = 0.50;  : w1 = 0.60;
: w1 = 0.60;  : w1 = 0.70.
: w1 = 0.70.