Energy and Grains Prices Cointegration and Causality Linkage

Abstract

Energy and grain markets are historically connected since oil, natural gas, and/or coal are used as inputs for fertilizers’ production or transportation costs. The recent rising prices in the energy market following important events such as the COVID-19 pandemic and the Russia-Ukraine conflict have again brought attention to researchers. The focus of this paper is to assess any changes in the relationships between crude oil, natural gas, and grain prices contributing to the review of the fuel-food relationship using time series models. Several techniques that account for structural breaks and regime shifts (Zivot-Andrews and Clemente, Montañés, Reyes unit root tests, Johansen’s cointegration test, and Toda-Yamamoto time domain causality test with time dummy variables for structural breaks, and Hatemi-J asymmetric causality test) are applied for monthly data covering the period from January 1982 to September 2022. The main result is that the neutrality hypothesis is still valid in light of recent developments in the respective markets (no significant linear causality and asymmetric causality were detected among the series).

1. Introduction

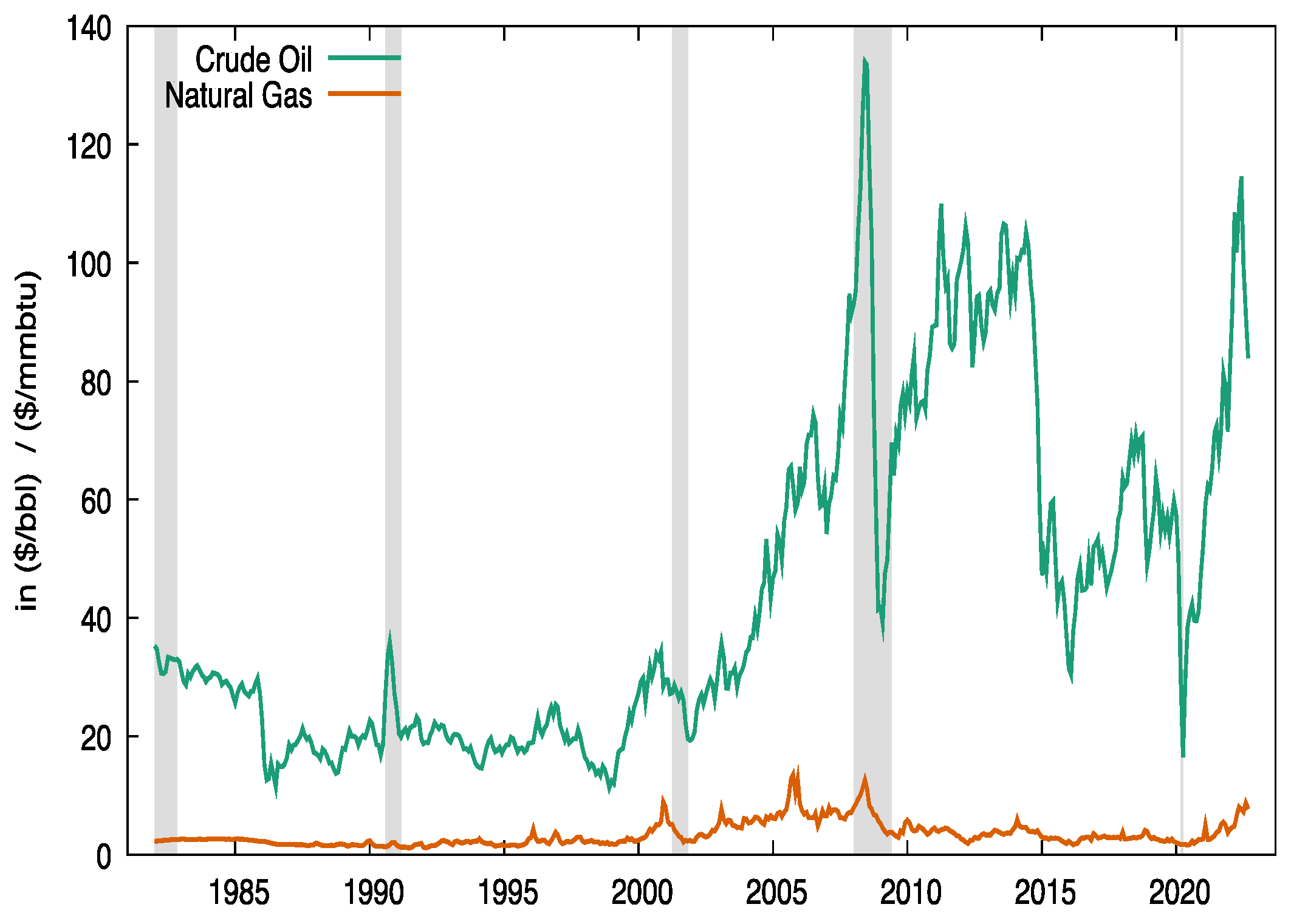
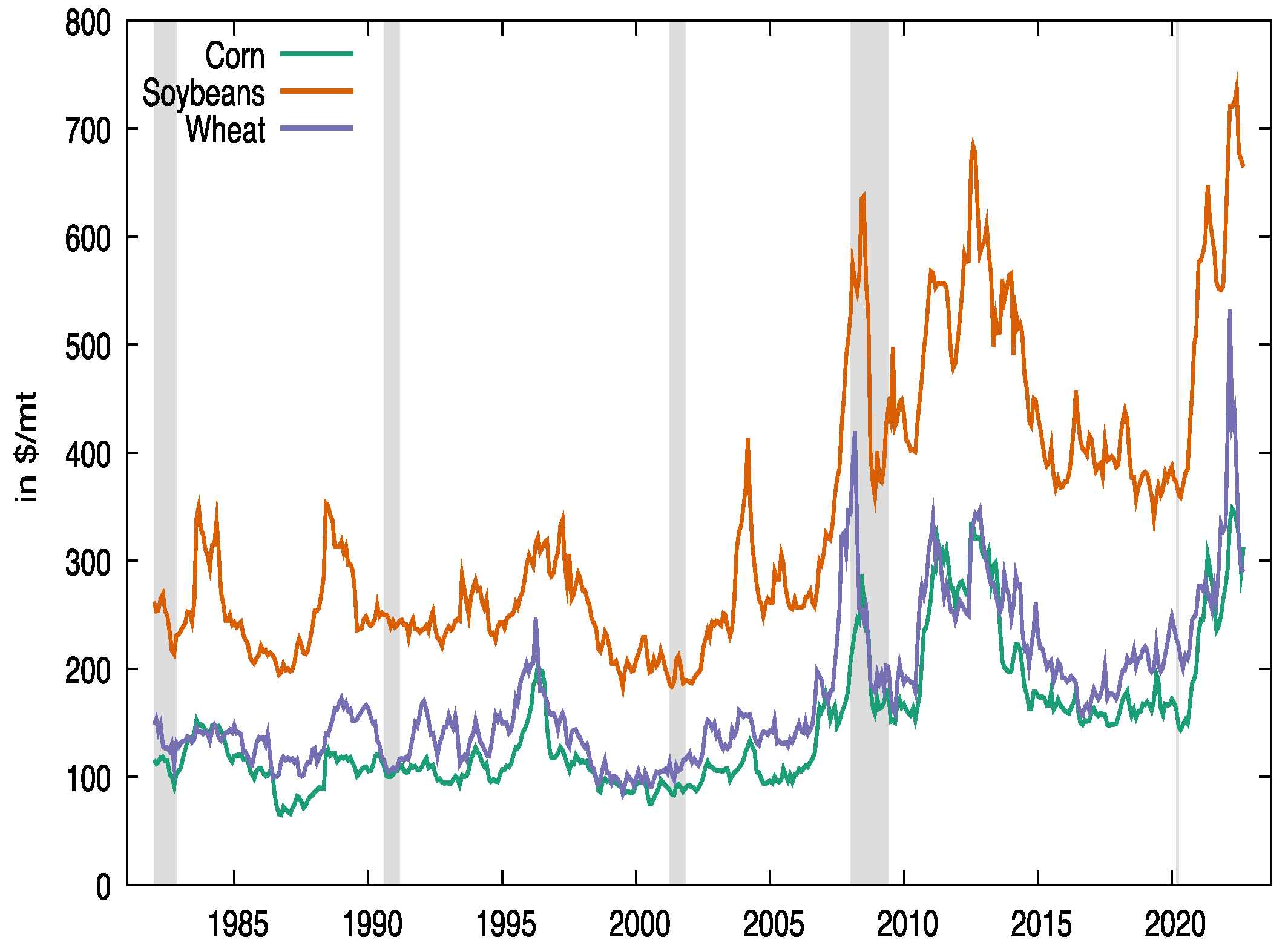
Agricultural commodity price drivers have gained special attention in the literature among researchers. Many indicators are identified [1,2,3]. Comparing graphically Figure 1 and Figure 2 it can be observed that grain prices react to the same economic dynamics as oil and natural gas prices (the vertical shadowed bars are the recession periods from the National Bureau of Economic Research, NBER).

Traditionally in the literature, the relationships between agricultural commodity and oil prices are seen on the supply-side (since oil is a factor in the production of fertilizers, both as energy during the production process or as transportation costs) and an increase in oil price leads to an increase in the agricultural commodity prices. On the demand side, in the context of biofuels developments, there is an increase in the price of corn and soybeans following the increase in oil prices since there is a higher demand for these commodities (for the production of biofuels, [4]).

One way to assess these relationship, is to trace the causality relationships between energy market prices and agricultural commodity prices. Two groups of authors are identified in the consulted literature.

Several researchers have stated the neutrality hypothesis, therefore, there is no causal relationship between them. Yu et al. [5] investigated the long-run linkage between several edible oil prices among them and crude oil prices for the period from January 1999 to March 2006. Using time series techniques, they found no significant impact of crude oil prices on edible oil prices. Zhang et al. [6]’s study was concentrated on the effect of crude oil prices on Chinese corn, soy meal, and pork prices. Using monthly prices from January 2000 to October 2007, they found no significant influence of crude oil prices on the rest of the variables. Gilbert [3] emphasized the role of oil price as a factor for the increase in food prices, linking it with the rise of demand for food crops in the context of biofuel purposes. Lombardi et al. [7] using a Factor-Augmented VAR approach, found no robust spillovers from oil to non-oil commodity prices. Kaltalioglu and Soytas [8] investigated for the period from January 1980 to April 2008, and the volatility spillover mechanism between oil, food items, and agricultural raw material price indexes found no volatility spillover from oil markets to food and agricultural raw material prices. [9] studied the response of U.S. cotton prices to the volatility in world crude oil prices, distinguishing the driven increase by crude oil demand or supply shocks. It was found that 0% of the variability in cotton prices was attributed to oil supply shocks.

Few studies find causality between oil and agricultural commodity prices. Hameed and Arshad [10] using monthly data from January 1983 to March 2008, and the bivariate co-integration approach with the Engle-Granger two-stage estimation procedure, it was found that in the long run there was a unidirectional causal relationship between petroleum price and the price of vegetable oils (palm, rapeseed, soybean, and sunflower). Cooke and Robles [11] using monthly data for the period from 2002–2009 for corn, wheat, rice, and soybeans prices, and first difference models and Granger causality tests, it resulted that oil price Granger causes soybeans and corn prices. Taghizadeh-Hesary et al. [12] using a panel VAR model and considering eight Asian economies, the relationship between energy and food prices was studied, confirming that oil price has had a significant impact on food prices during the period of study from 2000–2016. They suggested that oil price volatility represents a risk to food security and energy consumption; diversification in this sector will be in favor of both energy and food security (fossil fuels and renewable energy sources optimal combination). As an important input for goods and services production, it has a direct impact also on different sectors of economies such as agriculture [13]. The paper of Roman et al. [13] explored the relationship between crude oil and food price indexes (including meat, oils, cereals, sugar, and dairy), also stating the direction of the impact. Using different econometric techniques, for the period from 1990:01 to 2020:09, the authors identified cointegration relationships between crude oil and meat prices and short-term linkages with food, cereal, and vegetable oils with crude oil prices.

As essential for life, food products are considered in several articles regarding the relationship between food prices and crude oil prices. In this work, there are three main agricultural commodities selected, the grain category, such as wheat, corn, and soybeans, and their relationship with crude oil and natural gas prices, which is studied in terms of cointegration and causality. The hypothesis in the core of the work is as follows: “In light of the recent developments in the energy market, along the wide covered period of study, the neutrality hypothesis is still valid: there is no causal linkage between the energy market and grain prices?” and reflects also the motivation of this work.

The article is structured in sections: Section 2 summarizes data features and some preliminary tests, Section 3 lists all applied econometric techniques and the relevant findings, and Section 4 presents the conclusions and the implications of the results.

2. Data

From the category of agriculture commodities, three main grains are chosen (soybeans (Soybeans, from January 2021, U.S Gulf Yellow Soybean #2, CIF Rotterdam; December 2007 to December 2020, U.S. No. 2 yellow meal, CIF Rotterdam; previously US origin, nearest forward) wheat (Wheat (U.S.), no. 2, soft red winter, export price delivered at the US Gulf port for prompt or 30 days shipment), corn (Corn (U.S.), no. 2, yellow, f.o.b. US Gulf ports)). Graphical representations of the variables (expressed in real terms [14]) are provided below. The chosen period of study is January 1982–September 2022. The monthly time series are extracted from the World Bank [15], consisting of crude oil, natural gas, wheat, corn, and soybeans prices. To stabilize the variance of the series, the logs (of deflated series) are used during the analysis. The historical peak of crude oil prices was in July 2008, maintaining the same increasing tendency even after 2020. After the year 2018, the behavior was more volatile. The trend of natural gas shows some anticipated peaks compared to that of oil prices. After the year 2020, there was an increasing trend such as oil prices.

Figure 2 represents graphically the behavior of the three main grains (corn, wheat, and soybeans) price trend. Corn and wheat prices share similar movements between them, less with the soybeans price movements. All three grain prices react along the peaks of crude oil prices. After the year 2022, wheat and soybeans have reached the historical maximum, but corn has not.

2.1. Descriptive Statistics

In

Table 1. Summary statistics for series.

Variables	Mean	Std. Error	Skewness	Kurtosis	Min	Max	Jarque-Bera
Price series
Crude oil	47.650	24.755	0.72466	−0.28023	13.770	130.30	43.85 ***
Natural gas	3.8633	2.1723	1.9082	4.7503	1.4508	15.426	747.2 ***
Wheat	195.45	51.345	1.3727	4.2466	105.89	521.60	514.6 ***
Corn	162.37	48.759	1.0160	0.34770	87.957	328.28	85.53 ***
Soybeans	373.01	93.640	0.81051	−0.02508	227.18	705.03	52.9 ***
Log price series
Crude oil	3.7270	0.530741	−0.00449	−1.1594	2.6225	4.8698	27.05 ***
Natural gas	1.2288	0.4751129	0.60934	−0.15348	0.37209	2.7360	30.36 ***
Wheat	5.2441	0.2462605	0.34188	0.33268	4.6624	6.2569	11.64 ***
Corn	5.0492	0.2799538	0.49160	−0.51240	4.4769	5.7939	24.74 ***
Soybeans	5.8922	0.2397398	0.38740	−0.72974	5.4257	6.5582	22.8 ***

Note: *** respectively for 1% significance. Source: Author’s calculations.

there are the summarized descriptive statistics of the series, showcasing the initial information about volatilities and the distribution of the price series. Inside the energy market, crude oil is more volatile than natural gas; among grains, soybeans’ price is more volatile, followed by wheat and corn price, with a high degree of kurtosis and skewness that will decrease if price logs are considered. Testing for the normality of the series, the Jarque-Bera test statistics reject the null hypothesis of normality, for all series at 1% significance.

2.2. Multiple Structural Breaks Identification

Bai and Perron [16], as a methodology, considered multiple structural break models with $m$ breaks ($m+1$ breaks).

$$\begin{gathered} y_t=x_t^{\prime }\beta +z_t^{\prime }{\delta }_1+u_t, t=1,\dots .,T_1 \\ {y}_t=x_t^{\prime }\beta +z_t^{\prime }{\delta }_2+u_t, t=T_1+1,\dots .,T_2 \\ ................................................ \\ {y}_t=x_t^{\prime }\beta +z_t^{\prime }{\delta }_{m+1}+u_t, t=T_m+1,\dots .T \end{gathered}$$

(1)

where $y_t$ is the variable of interest, $x_t$ and $z_t$ are the regressors, and ${\beta }^1$ and ${\delta }_1$ are the respective vectors of coefficients, the breakpoints $\left(T_1\dots T_m\right)$ are treated as unknown.

Some restrictions are imposed and are defined in a set of small positive numbers $\epsilon : {\Lambda }_{\epsilon }=\left\{\left({\lambda }_1, \dots {\lambda }_m\right);\left| {\lambda }_{i+1}-{\lambda }_i\right|\ge \epsilon , {\lambda }_1\ge \epsilon ,{\lambda }_m\le 1-\epsilon \right\}$ for limiting each break date to be asymptotically different and bounded from the sample’s boundaries where ${\lambda }_i$ gives the break fraction $\left(T_i/T_m\right)$.

The method is based on the [16] least squares principle. For each partition $T_j$, the respective least squares estimate of ${\delta }_j$ is the product of minimizing the squared residuals’ sum $\sum _{i=1}^{m+1}\sum _{t=T_{i-1}+1}^{T_i}{\left(y_t-z_t^{\prime }{\delta }_i\right)}^2$. The regression estimators of parameters are linked with the estimated m-partition $\left(\widehat{\delta }=\widehat{\delta }\left(\left\{T_j\right\}\right)\right)$.

Bai and Perron [16] multiple structural breaks test was used to confirm some known dates as break dates in series (following the recessions from NBER displayed with the shadowed vertical bars in Figure 1 and Figure 2). The results are presented in

Table 2. Bai and Perron structural breaks test results.

Known Break Dates	W (tau)	Results
July 1990	17.36 **	Statistically significant
March 2001	71.09 ***	Statistically significant
December 2007	87.25 ***	Statistically significant
February 2022	3.01 **	Statistically significant

Note: **, *** respectively for 5 and 1% significance. Source: Author’s calculations.

as follows:

All the dates included in the table resulted as statistically significant as break dates for all series. Those dates coincide with the NBER recessions for the period. Break date identification directs the choice of all the following tests among them, which allows the presence of multiple (or at least one) structural breaks.

2.3. Pearson’s Correlation

Pearson’s correlation coefficients between variables for the whole period (subdivided following the identified structural breaks) are provided in

Table 3. Pearson’s correlation coefficients for series.

January 1982 to July 1990
	Crude oil	Natural gas	Wheat	Corn	Soybeans
Crude oil	1
Natural gas	0.8940 ***	1
Wheat	0.6822 ***	0.6908 ***	1
Corn	0.7614 ***	0.7858 ***	0.8628 ***	1
Soybeans	0.6104 ***	0.6055 ***	0.7495 ***	0.8763 ***	1
July 1990 to March 2001
Crude oil	1
Natural gas	0.4809 ***	1
Wheat	−0.2607 ***	−0.2556 ***	1
Corn	−0.2156 **	−0.1363	0.7281	1
Soybeans	−0.2074 **	−0.1072	0.5863	0.7449	1
March 2001 to December 2007
Crude oil	1
Natural gas	0.7096 ***	1
Wheat	0.4221 ***	0.1177	1
Corn	0.2533 **	0.0690	0.7605 ***	1
Soybeans	0.4293 ***	0.3592 ***	0.7432 ***	0.6327 ***	1
December 2007 to February 2022
Crude oil	1
Natural gas	0.6061 ***	1
Wheat	0.5060 ***	0.3138 ***	1
Corn	0.6067 ***	0.2516 ***	0.7633 ***	1
Soybeans	0.6406 ***	0.4116 ***	0.7379 ***	0.8334 ***	1
February 2022 to September 2022
Crude oil	1
Natural gas	−0.0458	1
Wheat	0.6423 *	−0.6776 *	1
Corn	0.7425 **	0.0514	0.5340	1
Soybeans	0.9172 **	0.0424	0.6315 *	0.8656 ***	1

Note: *, **, *** respectively for 10, 5, and 1% significance. Source: Author’s calculations.

.

What we can observe clearly is that taking into account the sub-periods created from the identified structural breaks in series: (1) for the period 1982:01–1990:07 strong positive, significant correlation was found between grain and oil and natural gas prices; (ii) for the period 1990:07–2001:03, weak, negative, significant correlation was found between grain and oil and natural gas prices (not significant for corn and soybeans prices with natural gas prices); (iii) for the period 2001:03–2007:12 the weak, significant correlation with crude oil prices persisted (in positive sign this time), while soybeans prices only were correlated significantly with natural gas prices; (iv) for the period 2007:12–2022:02 strong positive significant correlation with oil prices while with natural gas prices resulted a weaker correlation; (v) for the period 2022:02–2022:09 (the first months of the conflict Russia-Ukraine) grain lost the correlation with natural gas prices, and the correlation with oil prices was increased.

3. Techniques and Results

3.1. Time Series Stationarity Tests

In order to detect the (non)stationarity of the chosen series, unit root tests that account for structural breaks are applied. The Zivot-Andrews [17] unit root test (ZA) allows for one structural break in the time series. One of the model forms is the one applied here, a model that allows a one-time series level and slope trend change:

$$\Delta y_t=c+\alpha y_{t-1}+\beta t+\theta D{T}_t+\gamma D{U}_t+{\displaystyle \sum }_{j=1}^k{d}_j\Delta y_{t-j}+{\epsilon }_t,$$

(2)

where $D{U}_t$ in the above equation is a dummy variable respectively at each possible break date $TB,$ for a mean shift and $D{T}_t$ is the variable for the trend shift.

$$D{U}_t=[\begin{array}{cc}1 & t>TB\\ 0& otherwise\end{array} ; D{T}_t=[\begin{array}{cc} t-TB& t>TB\\ 0& otherwise\end{array}$$

The system of hypothesis is as follows:

Ho: α = 0, the series contain a unit root with a drift excluding any structural break,

Ha: α < 0, the series are trend-stationary, with one structural break, at an unknown time.

Behind the ZA unit root procedure, every potential break date is considered, and respectively, a regression is run. The break date that reaches the minimum of the one-sided t-statistic for testing $\widehat{\alpha }=1$. Since the covered period is large enough, thinking about another second structural break, is convenient in terms of unbiased unit root test results. Based on the Perron and Vogelsang’s [18] work, Clemente et al. [19] unit root test (CMR) is also applied as a validation for the ZA unit root test results (

Table 4. ZA, CMR-IO, CMR-AO unit root tests results.

	ZA		CMR-IO		CMR-AO
	Levels	1st diff.	Levels	1st diff.	Levels	1st diff.
Crude oil	−4.339 [2002m2]	−13.353 *** [2008m7]	−4.599 [1999m1, 2004m1]	−16.147 ** [2008m8, 2008m11]	−5.011 [2000m3, 2004m11]	−8.801 ** [2008m8, 2008m10]
Natural gas	−4.062 [1994m4]	−14.301 *** [2006m1]	−5.053 [1999m12, 2008m5]	−6.474 ** [2000m11, 2001m8]	−3.974 [1999m9, 2009m10]	−5.849 ** [1995m12, 2005m11]
Wheat	−4.861 [2006m7]	−20.084 *** [2008m4]	−3.418 [2007m4, 2008m2]	−9.086 ** [2008m2, 2008m12]	−3.218 [2007m10, 2007m12]	−7.513 ** [1986m8, 2007m7]
Corn	−3.999 [2006m7]	−17.182 *** [2008m7]	−3.646 [2006m7, 2013m4]	−9.194 ** [1988m5, 2008m9	−3.899 [2007m3, 2014m1]	−6.524 ** [1988m4, 2008m8]
Soybeans	−4.260 [2006m10]	−18.648 *** [2008m7]	−4.190 [2007m3, 2014m2]	−8.783 ** [1988m5, 2008m9]	−2.827 [2007m12, 2014m1]	−6.810 ** [1988m4, 2008m8]

Note: **, *** respectively for 5 and 1% significance; in brackets are the break dates. Source: Author’s calculations.

). Perron and Vogelsang [18] proposed a remedy to deal with the effect of the presence of structural breaks in series in the unit root tests results, allowing two forms of changes:

• The additive outlier (AO) model captures a sudden change,
• The innovational outlier (IO) model models a gradual shift in the mean of the series.

$T$ is the sample size, $T_b$ is the breakpoint ($1<T_b<T$), and the model is formalized as follows:

$$y_t=\delta D{T}_{bt}+ y_{t-1}+w_t, t=2\dots T,$$

(3)

with $D{T}_{bt}=1$ for $t=T_b+1$, and 0 otherwise, in the context of the null hypothesis $H_0$ of a unit root. Under the alternative hypothesis $H_a$:

$$y_t=c+\delta D{U}_t+w_t, t=2\dots T,$$

(4)

where $D{U}_t=1$ for $t>T_b$ and 0 otherwise. The test strategy is to estimate the regression:

$$y_t=\mu +\delta D{U}_t+\widetilde{y_t}.$$

(5)

Similar to the Augmented Dickey-Fuller (ADF) model, the below regression estimates $\alpha$ (if it is significantly less than one for stationary series).

$$\widetilde{y_t}={\displaystyle \sum }_{i=0}^k{w}_{i}D{T}_{bt-i}+\alpha {\tilde{y}}_{t-1}+{\displaystyle \sum }_{i=0}^k{\theta }_i\Delta {\tilde{y}}_{t-i}+e_t, t=k+2, \dots , T.$$

(6)

The transformation of the Equation (5) generates the finite AR model:

$$y_t=\mu +\delta D{U}_{t }+\vartheta D{T}_{bt}+\alpha y_{t-1}+{\displaystyle \sum }_{i=0}^k{\theta }_i\Delta y_{t-1}+e_t, t=k+2, \dots , T.$$

(7)

For both AO and IO models the breakpoint $T_b$ and the autoregressive order $k$ are unknown. Clemente et al. [19] extended the method with a double mean shift, for two breakpoints ($T_{b1}, T_{b2}$) also providing the critical values for the tests.

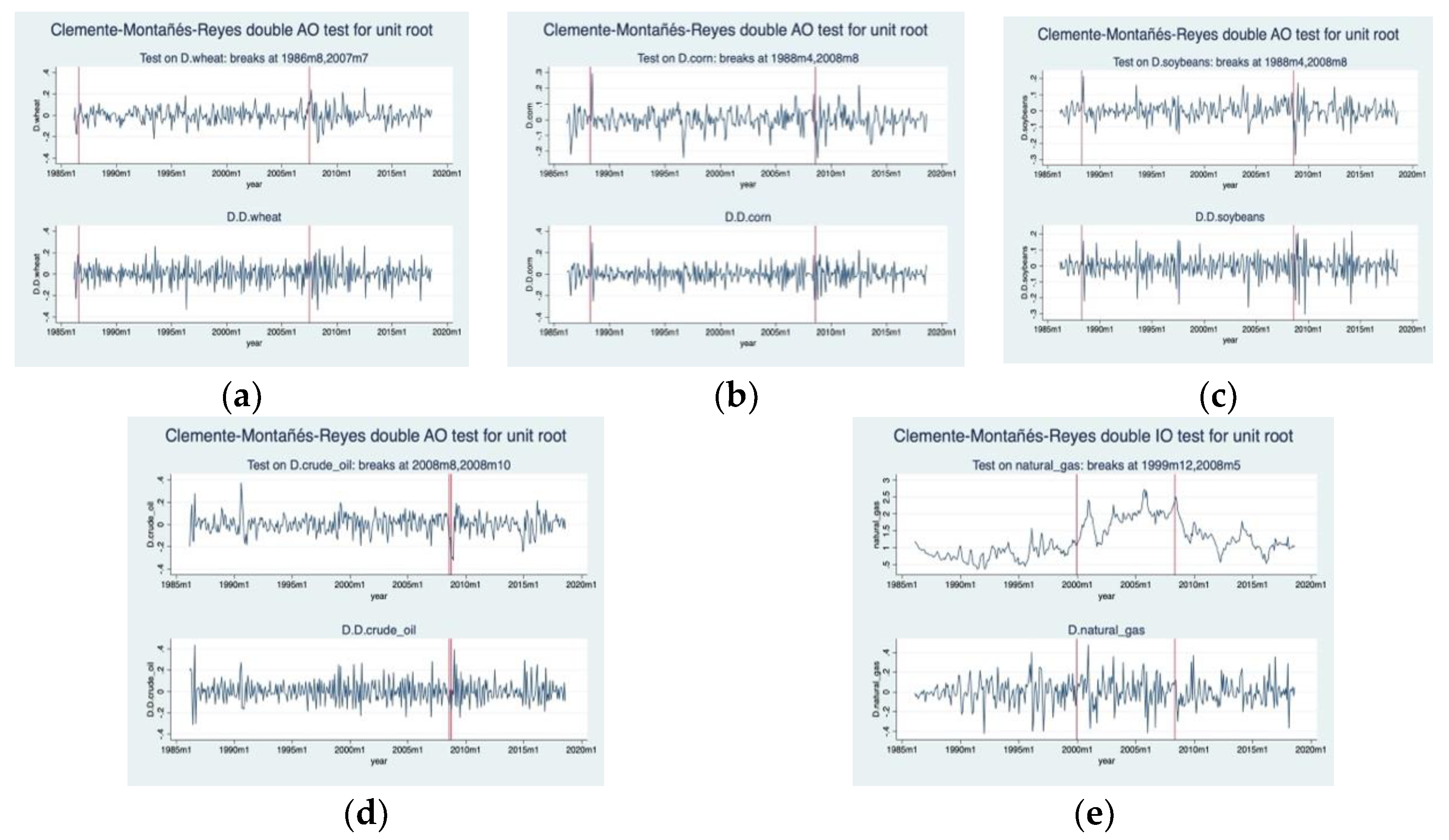
The results of ZA, CMR-IO, CMR-AO unit root tests are summarized in Table 4, which also identifies the breakpoints for the series in level and first difference. All series resulted nonstationary; integrated of order one, I(1), with both tests. Graphical representations of CMR-IO and CMR-AO tests are provided in Appendix A (Figure A1 and Figure A2).

3.2. Cointegration Estimation

Identifying the structural change in the data and checking for stationary of the time series are the preliminary steps needed to test for the presence of cointegration. Cointegration is an econometric technique that traces possible long-term correlations between time series processes, as introduced by Engle and Granger [20]. The time series resulted in nonstationary, and to check for more than one cointegrating relationship, the cointegration Johansen trace test (

Table 5. Johansen’s trace test (including exogenous variables and the time dummy variables for each of the four identified structural breaks) result.

Rank	Critical Value at 5%	LRtrace
0	192.89	272.8045
1	156.00	190.2569
2	124.24	115.8103 *
3	94.15	76.7200

Note: * selected rank; optimal lag length p = 2 (AIC). Source: Author’s calculations.

) will be used (instead of the Johansen maximum eigenvalue test). This test (the test is performed sequentially) has the following system of hypotheses:

Ho: at most zero cointegrating vector,

Ha: at most m-cointegrating vectors.

Johansen [21] (in)directly promotes the trace test as the most reliable with the argument that the maximum eigenvalue test depends on the initial value from which the test starts (the results from the test sequences may be affected).

As can be seen in the Johansen trace test, there is a cointegration of rank two between the variables for the whole period (a VECM analysis will be provided to explore the long-run relationships and to formalize them through equations). There are two linear combinations among the series in the long run. If there are shocks affecting individual series movements in the short run, they would converge with time in the long run.

3.3. The Vector Error Correction Model Approach Results

The VECM will be used as a convenient first approach (series are stationary in first difference, cointegrated) to get the first information about causality in the short and long run among variables. VECM model offers estimation in a system context providing information for interrelationships among series, thus reducing the bias endogeneity’s risk. The rank of cointegration includes addressing the problem of spurious regressions among non-stationary time series [22].

The system of the equations will be (without including the time dummy variables for each structural break for simplicity):

$$\begin{gathered} \Delta Whea{t}_t=\alpha +{{\displaystyle \sum }}_{\mathit{i}=\mathit{1}}^{\mathit{k}-\mathit{1}}{\mathit{\beta }}_{\mathit{i}}\Delta \mathit{W}\mathit{h}\mathit{e}\mathit{a}{\mathit{t}}_{\mathit{t}-\mathit{i}}+{{\displaystyle \sum }}_{j=1}^{k-1}{\gamma }_j\Delta Cor{n}_{t-j}+{{\displaystyle \sum }}_{m=1}^{k-1}{\delta }_m\Delta Soybean{s}_{t-m} \\ +{{\displaystyle \sum }}_{n=1}^{k-1}{\phi }_n\Delta Oi{l}_{t-n}+{{\displaystyle \sum }}_{p=1}^{k-1}{\varphi }_p\Delta Ga{s}_{t-p}+{\lambda }_{1}EC{T}_{t-1}+u_{1t} \\ \Delta Cor{n}_t=\sigma +{{\displaystyle \sum }}_{i=1}^{k-1}{\beta }_i\Delta Whea{t}_{t-i}+{{\displaystyle \sum }}_{\mathit{j}=\mathit{1}}^{\mathit{k}-\mathit{1}}{\mathit{\gamma }}_{\mathit{j}}\Delta \mathit{C}\mathit{o}\mathit{r}{\mathit{n}}_{\mathit{t}-\mathit{j}}+{{\displaystyle \sum }}_{m=1}^{k-1}{\delta }_m\Delta Soybean{s}_{t-m} \\ +{{\displaystyle \sum }}_{n=1}^{k-1}{\phi }_n\Delta Oi{l}_{t-n}+{{\displaystyle \sum }}_{p=1}^{k-1}{\varphi }_p\Delta Ga{s}_{t-p}+{\lambda }_{2}EC{T}_{t-1}+u_{2t} \\ \Delta Soybean{s}_t=\vartheta +{{\displaystyle \sum }}_{i=1}^{k-1}{\beta }_i\Delta Whea{t}_{t-i}+{{\displaystyle \sum }}_{j=1}^{k-1}{\gamma }_j\Delta Cor{n}_{t-j} \\ +{{\displaystyle \sum }}_{\mathit{m}=\mathit{1}}^{\mathit{k}-\mathit{1}}{\mathit{\delta }}_{\mathit{m}}\Delta \mathit{S}\mathit{o}\mathit{y}\mathit{b}\mathit{e}\mathit{a}\mathit{n}{\mathit{s}}_{\mathit{t}-\mathit{m}}+{{\displaystyle \sum }}_{n=1}^{k-1}{\phi }_n\Delta Oi{l}_{t-n}+{{\displaystyle \sum }}_{p=1}^{k-1}{\varphi }_p\Delta Ga{s}_{t-p} \\ +{\lambda }_{3}EC{T}_{t-1}+u_{3t} \\ \Delta Oi{l}_t=\upsilon +{{\displaystyle \sum }}_{i=1}^{k-1}{\beta }_i\Delta Whea{t}_{t-i}+{{\displaystyle \sum }}_{j=1}^{k-1}{\gamma }_j\Delta Cor{n}_{t-j}+{{\displaystyle \sum }}_{m=1}^{k-1}{\delta }_m\Delta Soybean{s}_{t-m} \\ +{{\displaystyle \sum }}_{\mathit{n}=\mathit{1}}^{\mathit{k}-\mathit{1}}{\mathit{\phi }}_{\mathit{n}}\Delta \mathit{O}\mathit{i}{\mathit{l}}_{\mathit{t}-\mathit{n}}+{{\displaystyle \sum }}_{p=1}^{k-1}{\varphi }_p\Delta Ga{s}_{t-p}+{\lambda }_{4}EC{T}_{t-1}+u_{1t} \\ \Delta Ga{s}_t=\rho +{{\displaystyle \sum }}_{i=1}^{k-1}{\beta }_i\Delta Whea{t}_{t-i}+{{\displaystyle \sum }}_{j=1}^{k-1}{\gamma }_j\Delta Cor{n}_{t-j} \\ +{{\displaystyle \sum }}_{m=1}^{k-1}{\delta }_m\Delta Soybean{s}_{t-m}+{{\displaystyle \sum }}_{n=1}^{k-1}{\phi }_n\Delta Oi{l}_{t-n} \\ +{{\displaystyle \sum }}_{\mathit{p}=\mathit{1}}^{\mathit{k}-\mathit{1}}{\mathit{\varphi }}_{\mathit{p}}\Delta \mathit{G}\mathit{a}{\mathit{s}}_{\mathit{t}-\mathit{p}}+{\lambda }_{5}EC{T}_{t-1}+u_{1t} \end{gathered}$$

(8)

The estimated cointegrating equations are included in Appendix A,

Table A1. VECM analysis results.

ECTs	D_Wheat	D_Corn	D_Soybeans	D_Crude_oil	D_Natural_gas
ECT1	−0.096 ***	0.067 ***	−0.003	−0.045 ***	−0.0116 ***
ECT2	0.026	0.073	0.04	0.040	0.125
Cointegrating equations
$EC{T}_1=Wheat-0.85Soybeans-0.54Oil+0.578Gas-0.04Break1-0.20Break2+0.6Break3-0.08Break4+0.95$ (0.000)  (0.000)  (0.000)  (0.55)  (0.03)  (0.000)  (0.68)
$EC{T}_2=Corn-1.18Soybeans-0.85Oil+0.79Gas-0.22Break1-0.09Break2+0.85Break3-0.29Break4+4.004$ (0.000)  (0.000)  (0.000)  (0.01)  (0.38)  (0.000)  (0.25)
$EC{T}_1=Soybeans-0.87Corn+0.72Oil-0.678Gas+0.19Break1+0.08Break2-0.72Break3+0.24Break4-3.39$ (0.000)  (0.000)  (0.000)  (0.007)  (0.38)  (0.000)  (0.25)
$EC{T}_2=Wheat-0.72Corn+0.07Oil+0.01Gas+0.11Break1-0.13Break2-0.01Break3+0.12Break4-1.92$ (0.000)  (0.24)  (0.85)  (0.007)  (0.023)  (0.827)  (0.35)
$EC{T}_1=Oil+12Wheat-8.83Corn+0.174Soybeans+1.42Break1-1.57Break2-0.29Break3+1.49Break4-23$ (0.000)  (0.000)  (0.93)  (0.010)  (0.003)  (0.64)  (0.35)
$EC{T}_2=Gas+13Wheat-8.2Corn-1.3Soybeans+1.2Break1-1.80Break2+0.76Break3+1.23Break4-20$ (0.000)  (0.000)  (0.51)  (0.03)  (0.001)  (0.25)  (0.46)

Note: *** denote the significance at 1% significance levels respectively; in parenthesis are the p-values; Breaks as in Table 2. Source: Author’s calculations.

, formalizing the long-run relationships among grain and energy commodity prices. Since the series are in logs, the coefficients in each of the cointegrating equations are interpreted as elasticity coefficients. For the first cointegrating equation, the ECT is negative and statistically significant, meaning that there is a long-run equilibrium where the series return after a short-run deviation or shock.

In the wheat price equation: a 1% change in the soybeans price, crude oil price, and natural gas price brings respectively a positive change of 0.85% and 0.54%, and a negative change of 0.58%; only the first three breaks are statistically significant (first cointegrating equation); 1% change in the corn price, crude oil price, and natural gas price brings a positive change of 0.72%, a negative change of 0.075, and a positive change of 0.01%, respectively; only break1 and break2 resulted statistically significant.

In the corn price equation: a 1% change in the soybeans price, crude oil price, and natural gas price brings respectively a positive change of 1.18% and 0.85%, and a negative change of 0.79%; only break1 and break3 resulted statistically significant.

In the soybeans price equation: a 1% change in the corn price, crude oil price, and natural gas price brings respectively a positive change of 0.87%, a negative change of 0.72%, and a positive change of 0.678%; only break1 and break3 resulted statistically significant.

In the crude oil price equation: a 1% change in the wheat price, corn price, and soybeans price brings respectively a negative change of 12%, a positive change of 8.83%, and a negative one of 0.174%, only break1 and break2 resulted statistically significant.

In the natural gas price equation: a 1% change in the wheat price, corn price, and soybeans price brings respectively a negative change of 13%, a positive change of 8.2% and 1.3%; only break1 and break2 resulted statistically significant.

For individual VECM models, their respective diagnostic statistics are presented in

Table A2. VECMs robustness tests results.

	LM Test	JB Test	Eigenvalue Stability Condition
1	97.6066	27.466 ***	checked
2		53.119 ***	checked
3		182.110 ***	checked
4		1970.155 ***	checked
5		311.418 ***	checked

Note: *** denotes 1% significance level; Lagrange-multiplier LM test, null hypothesis accepted: no autocorrelation at lag order 2 Jarque-Bera test, Ho is rejected: residuals are not symmetric and have an excess kurtosis (Not passing a test for normality at least asymptotically has no implications on the validity of either tests or estimators in VECMs). Source: Author’s calculations.

in the Appendix A. There is no autocorrelation at 5% significance at lag order 2 using the Lagrange- multiplier test, and the eigen stability condition is checked.

3.4. Toda Yamamoto Linear Causality Test

Toda-Yamamoto [23] developed a method that allows the existence of a Granger causal relationship between the variables to be estimated with the VAR (k+dmax) model with an augmented lag. Since our time series are I(1), the TY causality test method will be used, allowing us to work with the level values of the series. After determining the lag length (k) and maximum integration degree (dmax) of the model, a VAR (k+dmax) model is created, and the test is performed. The equations of the Toda-Yamamoto [23] causality test are as follows:

$$\begin{gathered} Y_t={\beta }_o+{\displaystyle \sum }_{i=1}^{k+dmax}{\beta }_{1i}{Y}_{t-1}+{\displaystyle \sum }_{i=1}^{k+dmax}{\beta }_{2i}{X}_{t-1}+{\epsilon }_{1t}, \\ {X}_t={\alpha }_o+{\displaystyle \sum }_{i=1}^{k+dmax}{\alpha }_{1i}{X}_{t-1}+{\displaystyle \sum }_{i=1}^{k+dmax}{\alpha }_{2i}{Y}_{t-1}+{\epsilon }_{2t }. \end{gathered}$$

(9)

The hypotheses tested using a Wald statistic are as follows:

$$\begin{gathered} \mathrm{Ho}: {\sum }_{\mathrm{i}=1}^{\mathrm{k}+\mathrm{dmax}}{\mathsf{\beta }}_{2\mathrm{i}}=0, {\mathrm{X}}_{\mathrm{t}-1} \mathrm{does} \mathrm{not} \mathrm{Granger} \mathrm{cause} {\mathrm{Y}}_{\mathrm{t}}, \\ \mathrm{Ha}: {\sum }_{\mathrm{i}=1}^{\mathrm{k}+\mathrm{dmax}}{\mathsf{\beta }}_{2\mathrm{i}}\ne 0, {\mathrm{X}}_{\mathrm{t}-1} \mathrm{does} \mathrm{Granger} \mathrm{cause} {\mathrm{Y}}_{\mathrm{t}}, \\ \mathrm{Ho}: {\sum }_{\mathrm{i}=1}^{\mathrm{k}+\mathrm{dmax}}{\mathsf{\alpha }}_{2\mathrm{i}} =0, {\mathrm{Y}}_{\mathrm{t}-1} \mathrm{does} \mathrm{not} \mathrm{Granger} \mathrm{cause} {\mathrm{X}}_{\mathrm{t}}, \\ \mathrm{Ha}: {\sum }_{\mathrm{i}=1}^{\mathrm{k}+\mathrm{dmax}}{\mathsf{\alpha }}_{2\mathrm{i}}\ne 0, {\mathrm{Y}}_{\mathrm{t}-1} \mathrm{does} \mathrm{Granger} \mathrm{cause} {\mathrm{x}}_{\mathrm{t}}. \end{gathered}$$

(10)

The rejection of the null hypothesis gives us information about the Granger causality between the series. In our case, the Toda Yamamoto time domain causality test is performed, including time dummy variables for all four breaks identified before, to account for them. As seen in

Table 6. Toda-Yamamoto causality test for the series.

	chi2	Results
$\mathrm{Crude} \mathrm{Oil} \nRightarrow$ Wheat	0.97478	lack of linear Granger causality
$\mathrm{Wheat} \nRightarrow$ Crude Oil	0.60606
$\mathrm{Crude} \mathrm{Oil} \nRightarrow$ Corn	0.30415
$\mathrm{Corn} \nRightarrow$ Crude Oil	0.86714
$\mathrm{Crude} \mathrm{Oil} \nRightarrow$ Soybeans	4.7469 *
$\mathrm{Soybeans} \nRightarrow$ Crude Oil	1.2936
$\mathrm{Natural} \mathrm{gas} \nRightarrow$ Wheat	1.6682	lack of linear Granger causality
$\mathrm{Wheat} \nRightarrow \mathrm{Natural} \mathrm{gas}$	0.74992
$\mathrm{Natural} \mathrm{gas} \nRightarrow$ Corn	1.3345
$\mathrm{Corn} \nRightarrow \mathrm{Natural} \mathrm{gas}$	0.788
$\mathrm{Natural} \mathrm{gas} \nRightarrow$ Soybeans	1.4962
$\mathrm{Soybeans} \nRightarrow \mathrm{Natural} \mathrm{gas}$	3.6855

Note: In parenthesis are the p-values; * respectively for 10% significance; $\nRightarrow$ lack of Granger causality null hypothesis. Source: Author’s calculations.

, it results in the lack of direct linear causality relationships from the energy market (oil and natural gas prices) to grain prices (wheat, corn, and soybeans), considering also the presence of structural breaks in the period of study. Only, a Granger causality only from crude oil to soybeans prices was detected at 10% significance.

3.5. Hatemi-J Asymmetric Causality Test

Hatemi-J [24] asymmetric causality test evaluates the causality relationship between the variables by separating the changes of the variables into positive and negative components. The test was developed because the assumption of symmetric causality tests that the effect of positive and negative shocks in the series is the same is insufficient to explain the existence of a causal relationship between the variables. The random walk model created to distinguish the negative and positive shocks of Hatemi-J [24] $y_{1t}$ and $y_{2t}$ series is as follows:

$$\begin{gathered} y_{1t}=y_{1,t-1}+{\epsilon }_{1t}=y_{1,0}+{{\displaystyle \sum }}_{i=1}^t{\epsilon }_{1i}, \\ {y}_{2t}=y_{2,t-1}+{\epsilon }_{2t}=y_{2,0}+{{\displaystyle \sum }}_{i=1}^t{\epsilon }_{2i}, \end{gathered}$$

(11)

where t = 1, 2, …, T specified in the model, $y_{1,0}$ and $y_{2,0}$ are the initial values, ${\epsilon }_{1i}$ and ${\epsilon }_{2i}$ are the white noise error terms. In the test, negative and positive shocks are expressed as follows:

$$\begin{gathered} {\epsilon }_{1i}^{-}=min\left({\epsilon }_{1i}, 0\right), {\epsilon }_{2i}^{-}=min\left({\epsilon }_{2i}, 0\right), \\ {\epsilon }_{1i}^{+}=max\left({\epsilon }_{1i}, 0\right), {\epsilon }_{2i}^{+}=max\left({\epsilon }_{2i}, 0\right). \end{gathered}$$

(12)

Thus, we find ${\epsilon }_{1t}={\epsilon }_{1t}^{+}+{\epsilon }_{1t}^{-},$ and ${\epsilon }_{2t}={\epsilon }_{2t}^{+}+{\epsilon }_{2t}^{-}$; the equations are rearranged as fol-lows:

$$\begin{gathered} y_{1t}=y_{1,t-1}+{\epsilon }_{1t}=y_{1,0}+{{\displaystyle \sum }}_{i=1}^t\left({\epsilon }_{1t}^{+}+{\epsilon }_{1t}^{-} \right), \\ {y}_{2t}=y_{2,t-1}+{\epsilon }_{2t}=y_{2,0}+{{\displaystyle \sum }}_{i=1}^t\left({\epsilon }_{2t}^{+}+{\epsilon }_{2t}^{-}\right). \end{gathered}$$

(13)

When the negative and positive shocks in the series are considered cumulatively:

$$\begin{gathered} y_{1t}^{-}={{\displaystyle \sum }}_{i=1}^t{\epsilon }_{1i}^{-}, y_{1t}^{+}={{\displaystyle \sum }}_{i=1}^t{\epsilon }_{2i}^{+}, \\ {y}_{2t}^{-}={{\displaystyle \sum }}_{i=1}^t{\epsilon }_{1i}^{-} , y_{2t}^{+}={{\displaystyle \sum }}_{i=1}^t{\epsilon }_{2i}^{+}. \end{gathered}$$

(14)

It resulted (

Table 7. Asymmetric causality Hatemi-J test results.

Direction of Causality	Wald Statistics	10% CV	5% CV	1% CV
Crude oil (+) to Wheat (+)	3.118	4.534	6.459	9.367
Crude oil (−) to Wheat (−)	0.588	4.917	6.706	9.804
Wheat (+) to Crude oil (+)	4.604 *	4.455	5.893	9.042
Wheat (−) to Crude oil (−)	5.298 *	4.691	6.172	10.542
Crude oil (+) to Corn (+)	1.402	4.313	5.763	11.806
Crude oil (−) to Corn (−)	0.060	4.869	6.371	11.122
Corn (+) to Crude oil (+)	1.751	4.693	6.409	12.727
Corn (−) to Crude oil (−)	1.331	4.686	5.795	9.259
Crude oil (+) to Soybeans (+)	0.033	4.448	5.976	11.238
Crude oil (−) to Soybeans (−)	2.265	4.951	6.289	9.584
Soybeans (+) to Crude oil (+)	2.197	4.930	7.063	12.447
Soybeans (−) to Crude oil (−)	5.561 *	4.916	6.472	12.762
Natural gas (+) to Wheat (+)	0.059	2.946	4.043	7.687
Natural gas (−) to Wheat (−)	0.149	2.915	3.906	7.015
Wheat (+) to Natural gas (+)	0.003	2.790	4.151	6.882
Wheat (−) to Natural gas (−)	0.290	2.816	3.926	6.489
Natural gas (+) to Corn (+)	0.493	2.817	4.116	8.153
Natural gas (−) to Corn (−)	0.207	4.722	6.300	10.052
Corn (+) to Natural gas (+)	1.173	2.746	3.747	6.953
Corn (−) to Natural gas (−)	0.947	4.642	6.046	10.413
Natural gas (+) to Soybeans (+)	0.006	2.283	3.333	7.672
Natural gas (−) to Soybeans (−)	0.852	2.770	4.195	7.636
Soybeans (+) to Natural gas (+)	0.998	2.527	3.670	9.051
Soybeans (−) to Natural gas (−)	0.171	2.711	3.729	6.609

Note: * denote the significance at 10% significance levels respectively. CV denotes the critical value; (+) and (−) represent positive and negative changes. Source: Author’s calculations.

) in an asymmetric causality relationship from positive (negative) changes in wheat prices to positive (negative) changes in crude oil prices at 10%, and from negative changes in soybeans prices to negative changes in crude oil prices at 10%. The rest of the pairs lack the presence of asymmetric Granger causality relationships, a result that is in line with the findings from the Toda-Yamamoto time domain Granger causality test.

4. Conclusions and Implications

This article explored the relationships between energy market prices and agricultural commodity prices. Monthly data for wheat, corn, soybeans, crude oil, and natural gas prices for the period from January 1982 to September 2022 were used to explore the potential cointegrating relationships between the variables. Since the presence of cointegration was traced, a VECM analysis was performed to formalize initially through equations the variables’ historical relationships. To identify the causality relationship between grain, crude oil, and natural gas prices, the Toda-Yamamoto time domain causality test and Hatemi-J asymmetric causality test were performed to complete the analysis. The choice for the causality tests is motivated to explore not only linear causality but also asymmetric causality among variables.

Cointegration of rank two was found among the variables (also considering time dummy variables for the four, identified structural breaks). There are long-run relationships between variables, empirically found using the Johansen’s trace test. This result gives us useful information about long-run relationships between grain and oil and natural gas prices. The co-movement between the series is clearer during peaks in energy market prices.

Using the VECM approach, some error correction terms were found negative and statistically significant, showing long-run causality relationships in the respective equations. Using the TY time domain causality test, no causal relationships from the energy market (oil and natural gas prices) to grain prices (wheat, corn, and soybeans) resulted.

Also, from Hatemi-J causality test, it resulted in only an asymmetric causality relationship from positive (negative) changes in wheat prices to positive (negative) changes in crude oil prices at 10%, and from negative changes in soybeans prices to negative changes in crude oil prices at 10%.

The work is in line with other similar works, proving the neutrality hypothesis: there is no linear and asymmetric causal linkage between the energy market and grain prices. The work contribution consists of a wide period of study (January 1982–September 2022), also considering natural gas prices from the energy market (not only crude oil prices as done usually). This last consideration was motivated by the increasing role of natural gas as an energy source, along with crude oil for food production and the recent developments in the respective markets, the Covid-19 period, and the first month of the Russia-Ukraine conflict. The main implication from the results is that explaining the increasing trend of grain prices is also useful to follow and consider the trend of biofuel production that can put upward pressure on food prices. In assessing the driving factors for grain prices, producers must consider a more complex picture, with not only crude oil and/or natural gas as the main drivers. This should be also the attention of policymakers in designing reforms and actions in the case of inflated prices in the energy and grain markets: limiting domestic prices rise (cutting taxes or implementing direct price subsidies) or allowing the international high prices to pass through (in a calibrated way) the domestic economy, keeping the protection of the most in need households a priority (directly affected by record food prices), along with providing them targeted transfers.

Also, a different nature should be considered of the causality between the energy and grain market: a non-linear one. Having a quantitative tool to measure the dynamic relationship between the energy market and grain prices will be helpful at producers’ and traders’ levels to better forecast their business operations and at the governmental level for food price policy adjustments.