Commodity and Equity Markets: Volatility and Return Spillovers
Abstract
:1. Introduction
2. Literature Review
3. Methodology
4. Data and Preliminary Analysis
5. Empirical Results
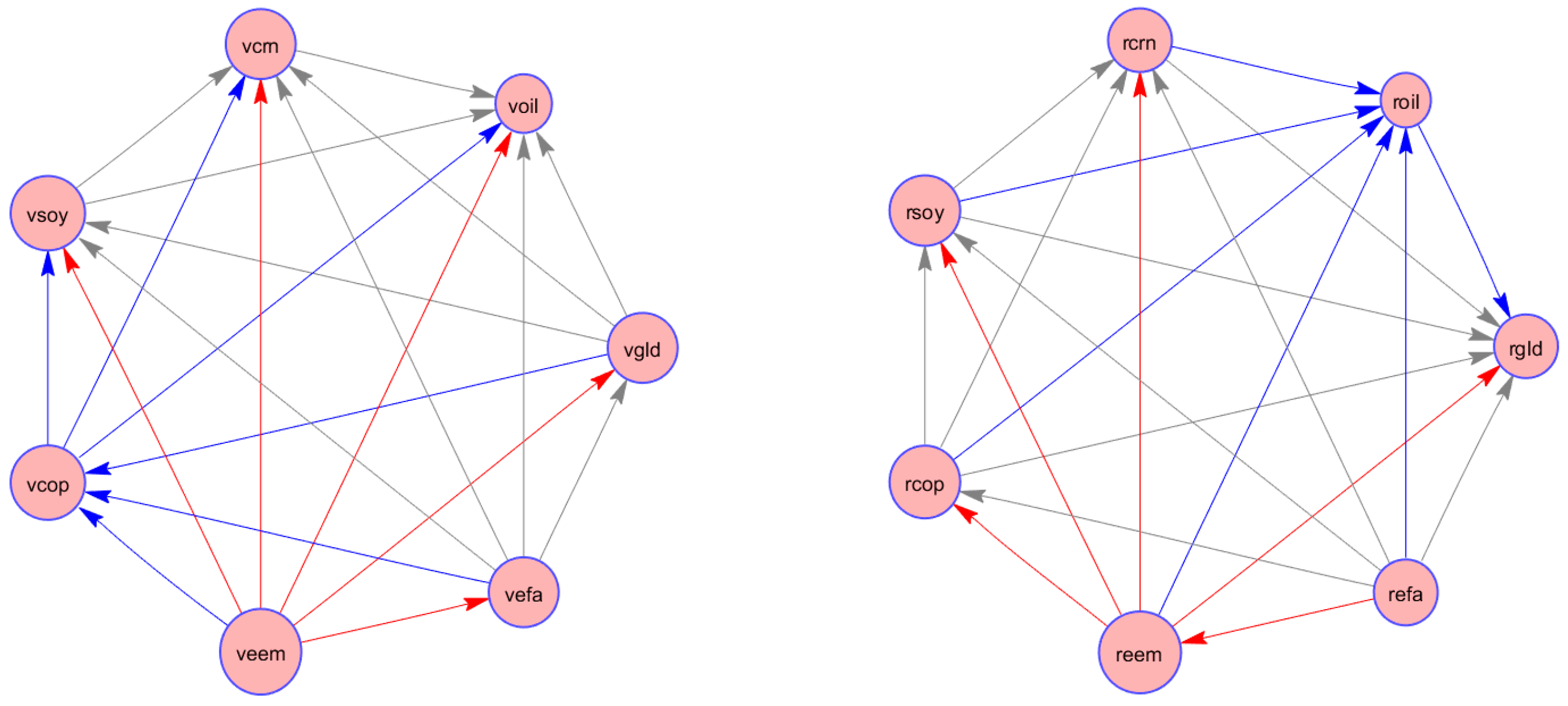
5.1. Full-Sample Spillover Analysis
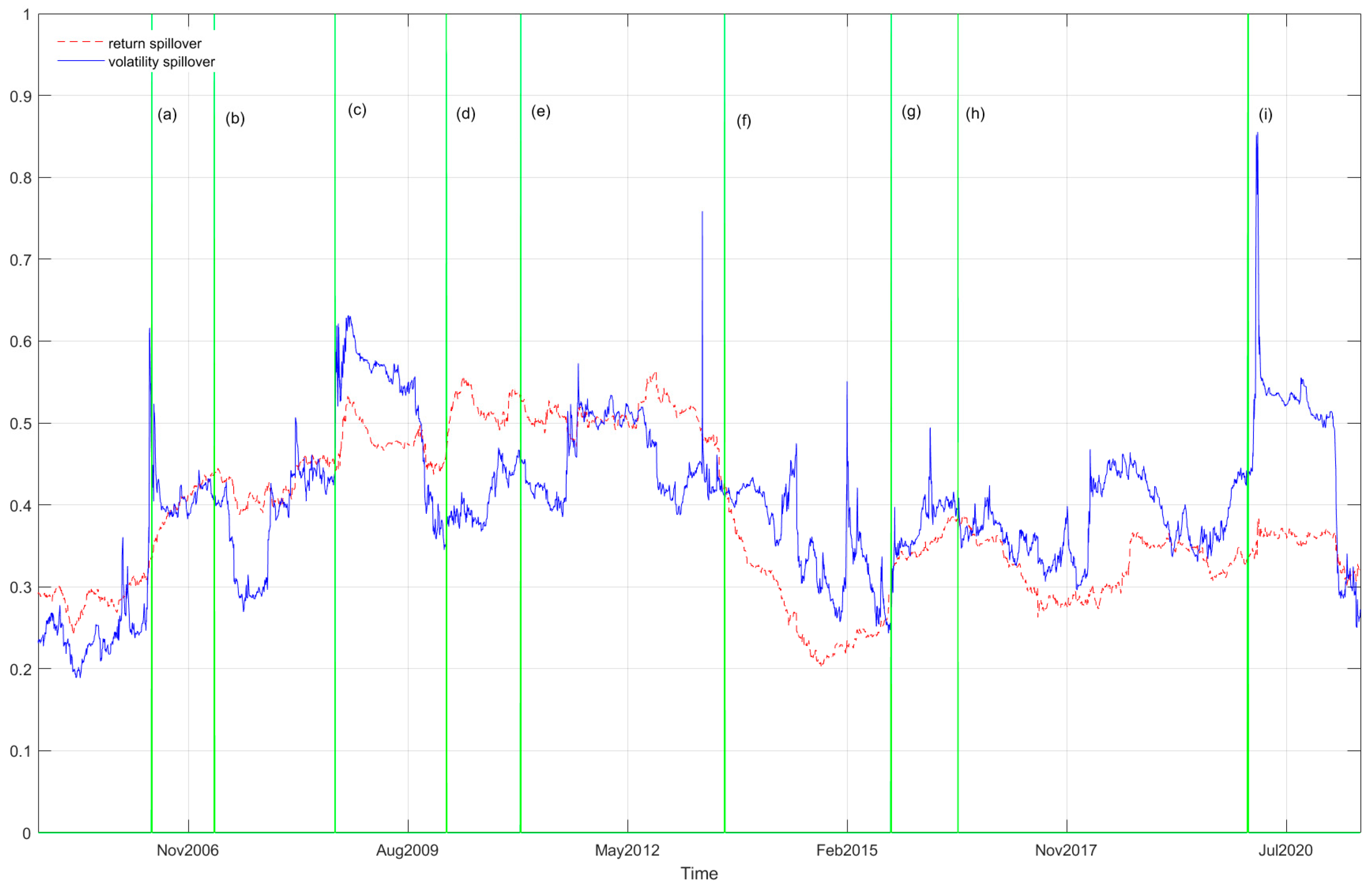
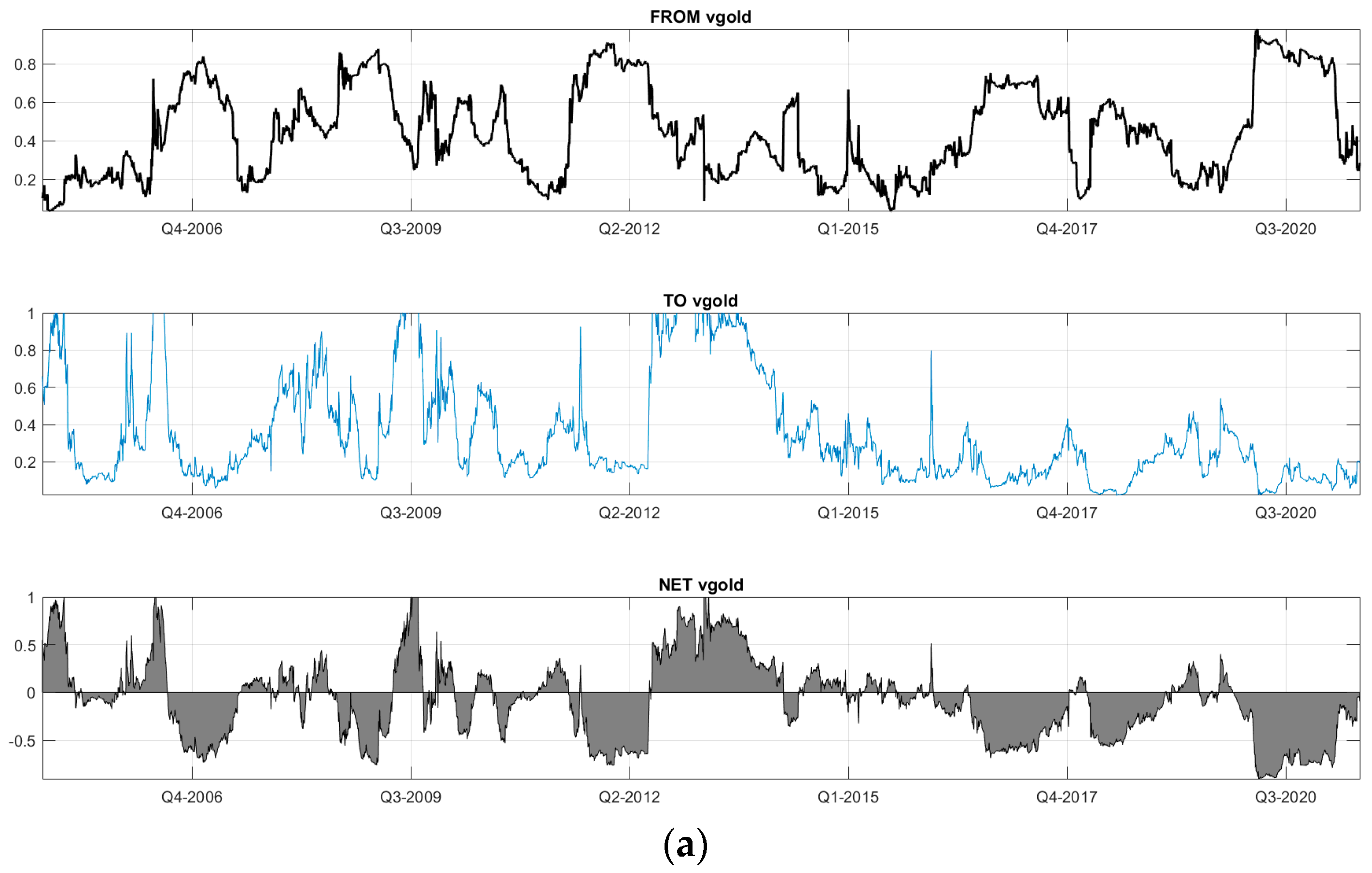
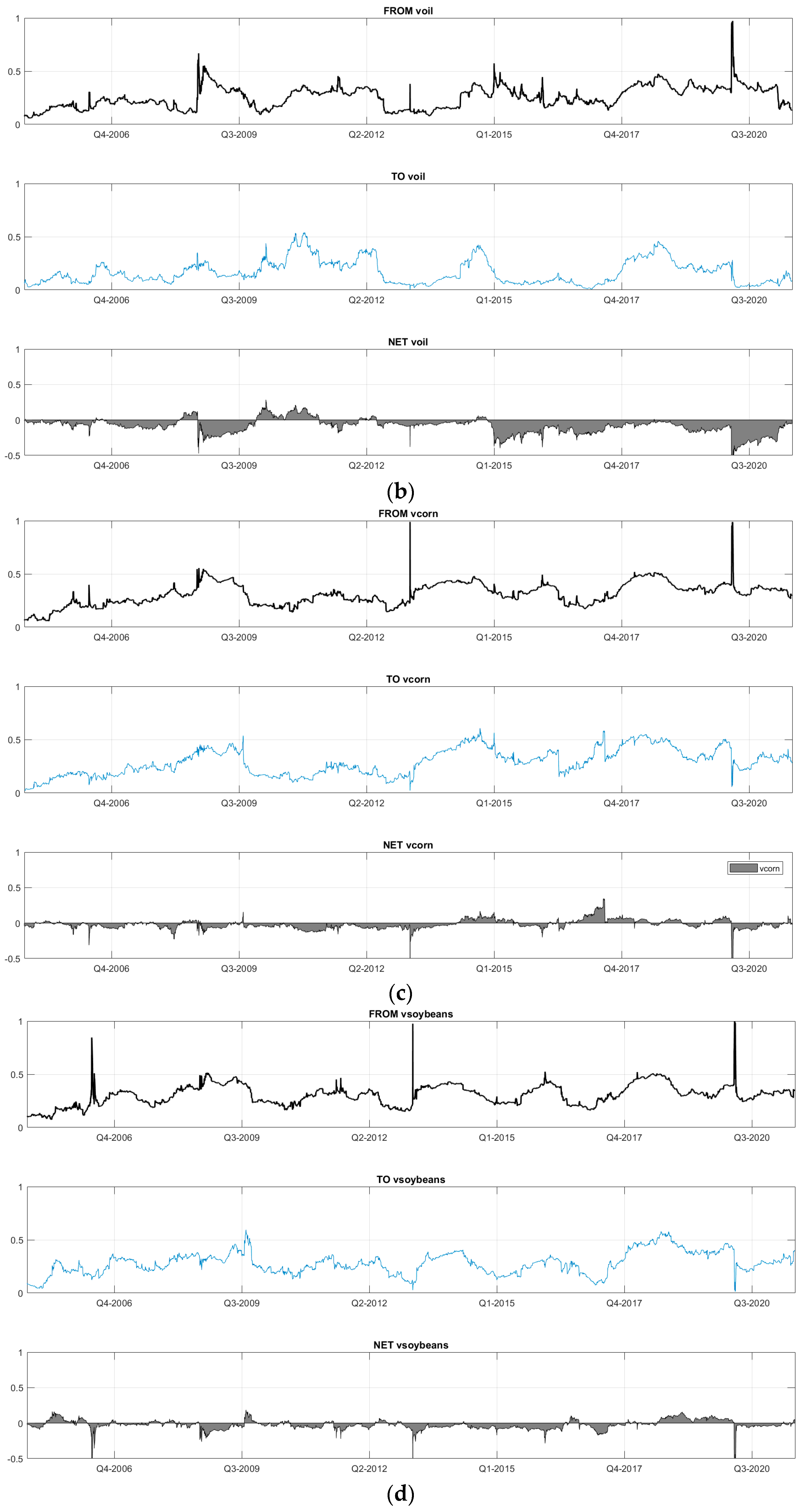
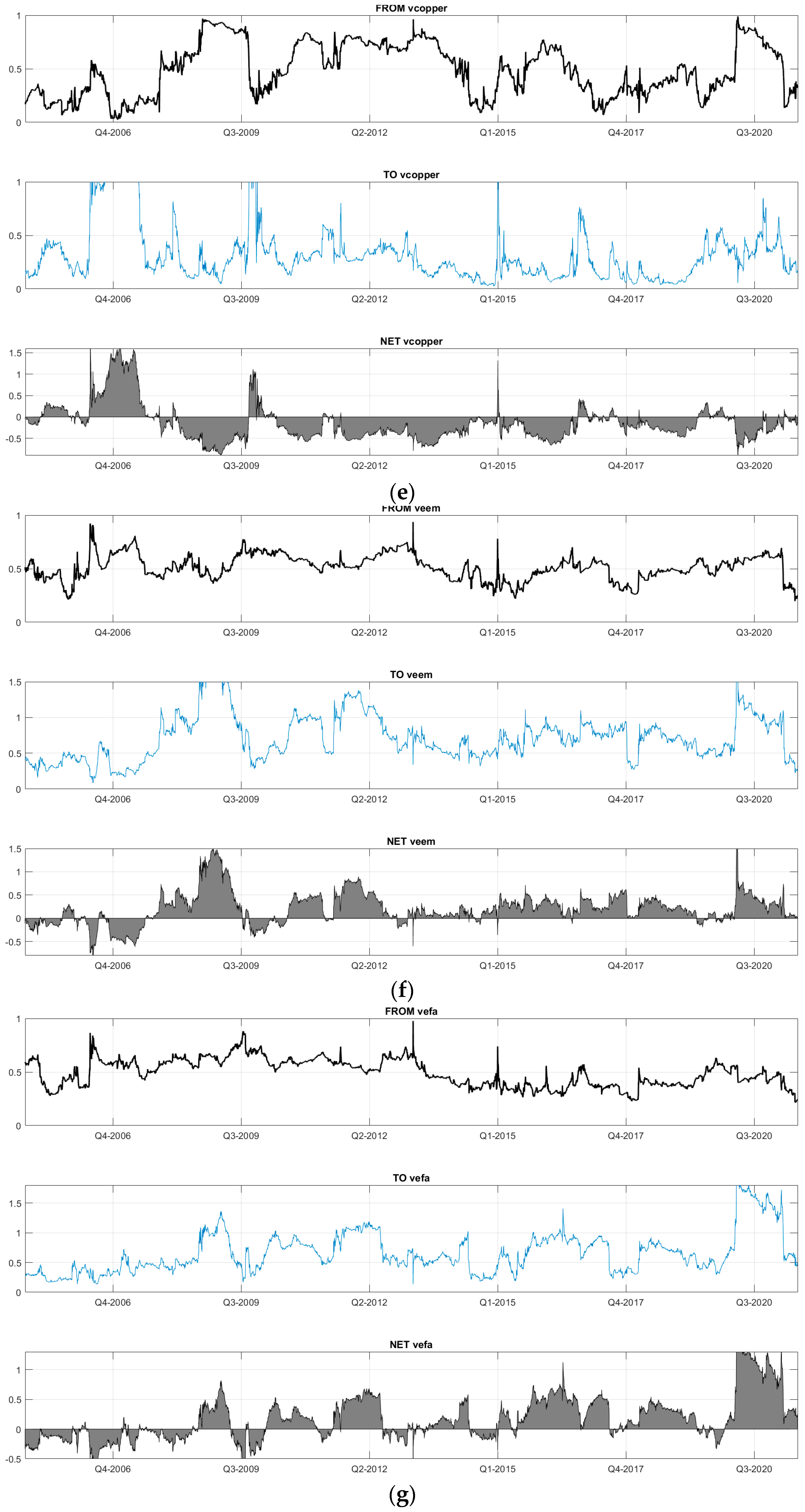
5.2. Dynamic Connectedness Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bheenick, E.; Brooks, R.; Do, H.; Smyth, R. Exploiting the heteroskedasticity in measurement error to improve volatility predictions in oil and biofuel feedstock markets. Energy Econ. 2020, 86, 104689. [Google Scholar] [CrossRef]
- Gong, X.; Lin, B. Forecasting the good and bad uncertainties of crude oil prices using HAR framework. Energy Econ. 2017, 67, 315–327. [Google Scholar] [CrossRef]
- Ma, F.; Liao, Y.; Zhang, Y.; Cao, Y. Harnessing jump component for crude oil volatility forecasting in the presence of extreme shocks. J. Empir. Financ. 2019, 52, 40–55. [Google Scholar] [CrossRef]
- Hasanov, A.; Poon, W.; Al-Freedi, A.; Heng, Z. Forecasting volatility in the biofuel feedstock mrakets in the presence of structural breaks: A comparison of alternative distribution functions. Energy Econ. 2018, 70, 307–333. [Google Scholar] [CrossRef]
- Klein, T.; Walter, T. Oil price volatility forecast with mixture memory GARCH. Energy Econ. 2016, 58, 46–58. [Google Scholar] [CrossRef] [Green Version]
- Chkili, W.; Hammoudeh, S.; Nguyen, D. Volatility forecasting and risk management for commodity markets in the presence of asymmetry and long memory. Energy Econ. 2014, 41, 1–18. [Google Scholar] [CrossRef]
- Haugom, E.; Langeland, H.; Molnar, P.; Westgaard, S. Forecasting volatility of the U.S. oil market. J. Bank. Financ. 2014, 47, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Arouri, M.; Lahiani, A.; Nguyen, D.K. Forecasting the conditional volatility of oil spot and futures prices with structural breaks and long memory models. Energy Econ. 2012, 34, 283–293. [Google Scholar] [CrossRef] [Green Version]
- Sadorsky, P. Modeling volatility and correlations between emerging market stock prices and the prices of copper, oil and wheat. Energy Econ. 2014, 43, 72–81. [Google Scholar] [CrossRef]
- Filis, G. Time-varing co-movements between stock market returns and oil price shocks. Int. J. Energy Stat. 2014, 2, 27–42. [Google Scholar] [CrossRef]
- Chang, K.-L.; McAleer, M.; Tansuchat, R. Conditional correlations and volatility spillovers between crude oil and stock index returns. N. Am. J. Econ. Financ. 2013, 25, 116–138. [Google Scholar] [CrossRef] [Green Version]
- Filis, G.; Degiannakis, S.; Floros, C. Dynamic correlation between stock market and oil prices: The case of oil-importing and oil-exporting countries. Int. Rev. Financ. Anal. 2011, 20, 152–164. [Google Scholar] [CrossRef]
- Mensi, W.; Beljid, M.; Boubaker, A.; Shunsuke, M. Correlations and volatility spillovers across commodity and stock markets: Linking energies, food, and gold. Econ. Model. 2013, 32, 15–22. [Google Scholar] [CrossRef] [Green Version]
- Sarwar, S.; Tiwari, A.K.; Tingqiu, C. Analyzing volatility spillovers between oil market and Asian stock markets. Resour. Policy 2020, 66, 101608. [Google Scholar] [CrossRef]
- Khalfaoui, A.; Boutahar, M.; Boubaker, H. Analyzing volatility spillovers and hedging between oil and stock markets: Evidence from wavelet analysis. Energy Econ. 2015, 49, 540–549. [Google Scholar] [CrossRef]
- Berger, T.; Uddin, G.S. On the dynamic dependence between equity markets, commodity futures and economic uncertainty indexes. Energy Econ. 2016, 56, 374–383. [Google Scholar] [CrossRef]
- Wang, X.; Lucey, B.; Huang, S. Can gold hedge against oil price movements: Evidence from GARCH-EVT wavelet modeling. J. Commod. Mark. 2021, 100226. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ. J. 2009, 119, 158–171. [Google Scholar] [CrossRef] [Green Version]
- Diebold, F.X.; Yilmaz, K. Better to Give than to Receive: Forecast-Based Measurement of Volatility Spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Kumar, M. Returns and volatility spillover between stock prices and exchange rates: Empirical evidence from IBSA countries. Int. J. Emerg. Mark. 2013, 8, 108–128. [Google Scholar] [CrossRef]
- Maghyereh, A.I.; Awartani, B.; Bouri, E. The directional volatility connectedness between crude oil and equity markets: New evidence from implied volatility indexes. Energy Econ. 2016, 57, 78–93. [Google Scholar] [CrossRef] [Green Version]
- Caloia, F.G.; Cipollini, A.; Muzzioli, S. Asymmetric semi-volatility spillover effects in EMU stock markets. Int. Rev. Financ. Anal. 2018, 57, 221–230. [Google Scholar] [CrossRef]
- Mensi, W.; Hkiri, B.; Al-Yahyaee, K.; Kang, S.H. Analyzing time–frequency co-movements across gold and oil prices with BRICS stock markets: A VaR based on wavelet approach. Int. Rev. Econ. Finance 2018, 54, 74–102. [Google Scholar] [CrossRef]
- BenSaïda, A.; Litimi, H.; Abdallah, O. Volatility spillover shifts in global financial markets. Econ. Model. 2018, 73, 343–353. [Google Scholar] [CrossRef]
- Yoon, S.-M.; Al Mamun, M.; Uddin, G.S.; Kang, S.H. Network connectedness and net spillover between financial and commodity markets. N. Am. J. Econ. Financ. 2019, 48, 801–818. [Google Scholar] [CrossRef]
- Balcilar, M.; Ozdemir, Z.A.; Ozdemir, H. Dynamic return and volatility spillovers among S&P 500, crude oil, and gold. Int. J. Financ. Econ. 2021, 26, 153–170. [Google Scholar]
- Akhtaruzzaman, M.; Boubaker, S.; Lucey, B.M.; Sensoy, A. Is gold a hedge or a safe-haven asset in the COVID–19 crisis? Econ. Model. 2021, 102, 105588. [Google Scholar] [CrossRef]
- Kang, S.; Hernandez, J.A.; Sadorsky, P.; McIver, R. Frequency spillovers, connectedness, and the hedging effectiveness of oil and gold for US sector ETFs. Energy Econ. 2021, 99, 105278. [Google Scholar] [CrossRef]
- Barunik, J.; Krehlik, T. Measuring the frequency dynamics of financial connectedness and systemic risk. J. Financ. Econ. 2018, 16, 271–296. [Google Scholar] [CrossRef]
| Variables | Mean | Std. Dev. | Min | Max | Skew. | Kurt. | JB | ADF |
|---|---|---|---|---|---|---|---|---|
| Panel A: Returns | ||||||||
| Gold | 0.033 | 1.149 | −9.821 | 8.643 | −0.344 | 8.424 | 0.0000 | −61.379 ** |
| Oil | 0.057 | 2.279 | −27.992 | 31.963 | 1.075 | 28.583 | 0.0000 | −53.306 ** |
| Soybeans | 0.02 | 1.4 | −13.843 | 20.321 | −0.036 | 20.031 | 0.0000 | −47.913 ** |
| Corn | 0.015 | 1.587 | −10.409 | 12.757 | 0.001 | 7.495 | 0.0000 | −50.865 ** |
| Copper | 0.033 | 1.799 | −11.693 | 11.769 | −0.202 | 7.168 | 0.0000 | −65.749 ** |
| EEM | 0.026 | 1.84 | −17.633 | 20.514 | 0.015 | 18.067 | 0.0000 | −73.936 ** |
| EFA | 0.013 | 1.387 | −11.837 | 14.745 | −0.407 | 16.566 | 0.0000 | −73.898 ** |
| Panel B: Volatility | ||||||||
| Gold | 2.809 | 0.263 | 2.35 | 3.73 | 0.962 | 3.676 | 0.0000 | −3.757 ** |
| Oil | 3.636 | 0.202 | 3.146 | 5.65 | 2.088 | 18.276 | 0.0000 | −4.464 ** |
| Soybeans | 3.174 | 0.154 | 2.858 | 4.741 | 2.251 | 14.042 | 0.0000 | −3.092 * |
| Corn | 3.319 | 0.129 | 3.043 | 4.474 | 2.382 | 14.614 | 0.0000 | −3.546 ** |
| Copper | 3.221 | 0.304 | 2.668 | 4.424 | 0.988 | 4.281 | 0.0000 | −3.618 ** |
| EEM | 3.103 | 0.387 | 2.468 | 5.008 | 1.562 | 6.651 | 0.0000 | −4.215 ** |
| EFA | 2.817 | 0.42 | 2.055 | 4.701 | 1.267 | 5.358 | 0.0000 | −4.584 ** |
| Panel A: Returns | |||||||
| Variables | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| (1) Gold | 1.000 | ||||||
| (2) Oil | 0.182 * | 1.000 | |||||
| (3) Soybeans | 0.146 * | 0.217 * | 1.000 | ||||
| (4) Corn | 0.147 * | 0.213 * | 0.563 * | 1.000 | |||
| (5) Copper | 0.339 * | 0.294 * | 0.222 * | 0.191 * | 1.000 | ||
| (6) EEM | 0.123 * | 0.252 * | 0.153 * | 0.130 * | 0.367 * | 1.000 | |
| (7) EFA | 0.120 * | 0.251 * | 0.143 * | 0.133 * | 0.370 * | 0.879 * | 1.000 |
| Panel B: Volatility | |||||||
| Variables | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| (1) Gold | 1.000 | ||||||
| (2) Oil | 0.232 * | 1.000 | |||||
| (3) Soybeans | 0.133 * | 0.067 * | 1.000 | ||||
| (4) Corn | 0.145 * | 0.108 * | 0.447 * | 1.000 | |||
| (5) Copper | 0.693 * | 0.180 * | 0.157 * | 0.173 * | 1.000 | ||
| (6) EEM | 0.721 * | 0.292 * | 0.153 * | 0.160 * | 0.722 * | 1.000 | |
| (7) EFA | 0.682* | 0.308 * | 0.135 * | 0.165 * | 0.639 * | 0.931 * | 1.000 |
| Volatility Spillover Table Rows (to), Columns (from), | |||||||||
| Gold | Oil | Soybeans | Corn | Copper | eem | efa | From Others | NDC | |
| gold | 51.497 | 0.518 | 0.307 | 0.316 | 2.057 | 23.817 | 21.487 | 48.503 | −25.709 |
| oil | 0.885 | 82.208 | 1.629 | 1.745 | 1.280 | 6.445 | 5.809 | 17.792 | −12.259 |
| soybeans | 0.635 | 1.397 | 76.634 | 17.360 | 1.324 | 1.148 | 1.502 | 23.366 | −3.487 |
| corn | 0.712 | 1.497 | 16.999 | 77.991 | 1.193 | 0.914 | 0.694 | 22.009 | −1.000 |
| copper | 9.936 | 0.672 | 0.413 | 1.003 | 47.631 | 24.688 | 15.658 | 52.369 | −38.516 |
| eem | 5.791 | 0.635 | 0.292 | 0.364 | 4.725 | 52.963 | 35.230 | 47.037 | 47.184 |
| efa | 4.834 | 0.815 | 0.239 | 0.222 | 3.274 | 37.210 | 53.408 | 46.592 | 33.787 |
| Contribution to others | 22.793 | 5.534 | 19.879 | 21.009 | 13.852 | 94.222 | 80.379 | ||
| Returns Spillover Table Rows (to), Columns (from), | |||||||||
| Gold | Oil | Soybeans | Corn | Copper | eem | efa | From Others | NDC | |
| gold | 81.240 | 2.770 | 1.800 | 1.730 | 8.970 | 1.950 | 1.540 | 18.760 | −4.110 |
| oil | 2.630 | 74.430 | 3.400 | 3.550 | 6.480 | 4.810 | 4.690 | 25.560 | −4.720 |
| soybeans | 1.460 | 3.170 | 68.450 | 21.680 | 2.430 | 1.400 | 1.410 | 31.550 | −1.060 |
| corn | 1.510 | 3.320 | 21.230 | 67.060 | 3.310 | 1.880 | 1.700 | 32.950 | −0.440 |
| copper | 6.930 | 5.340 | 2.190 | 3.000 | 63.170 | 9.900 | 9.470 | 36.830 | −1.340 |
| eem | 1.090 | 3.180 | 0.930 | 1.330 | 7.190 | 48.510 | 37.760 | 51.480 | 6.000 |
| efa | 1.030 | 3.060 | 0.940 | 1.220 | 7.110 | 37.540 | 49.090 | 50.900 | 5.670 |
| Contribution to others | 14.650 | 20.840 | 30.490 | 32.510 | 35.490 | 57.480 | 56.570 | ||
| Panel A: Spillovers Freq. Short-Term. Band 3.14 to 0.63, Corresponding to 1 Days to 5 Days. | |||||||||
| Gold | Oil | Soybeans | Corn | Copper | eem | efa | FROM_ABS | FROM_WTH | |
| gold | 66.200 | 2.180 | 1.390 | 1.430 | 7.610 | 1.270 | 1.100 | 2.14 | 2.59 |
| oil | 2.140 | 59.600 | 2.930 | 2.830 | 5.490 | 3.850 | 3.790 | 3 | 3.64 |
| soybeans | 1.390 | 2.970 | 53.600 | 17.360 | 2.840 | 1.460 | 1.270 | 3.9 | 4.72 |
| corn | 1.210 | 2.730 | 17.840 | 55.870 | 2.120 | 1.130 | 1.100 | 3.73 | 4.52 |
| copper | 5.620 | 4.380 | 2.380 | 1.740 | 53.110 | 7.520 | 7.430 | 4.15 | 5.03 |
| eem | 0.770 | 2.780 | 1.150 | 0.780 | 6.050 | 41.820 | 32.900 | 6.35 | 7.69 |
| efa | 0.710 | 2.590 | 1.060 | 0.760 | 5.890 | 31.750 | 41.850 | 6.11 | 7.4 |
| TO_ABS | 1.69 | 2.52 | 3.82 | 3.56 | 4.29 | 6.71 | 6.8 | 29.39 | |
| TO_WTH | 2.05 | 3.05 | 4.63 | 4.31 | 5.19 | 8.13 | 8.24 | 35.6 | |
| NET ABS | −0.45 | −0.48 | −0.08 | −0.17 | 0.14 | 0.36 | 0.69 | ||
| Panel B: Spillovers Freq. Medium-Term. Band 0.63 to 0.15, Corresponding to 5 Days to 21 Days. | |||||||||
| Gold | Oil | Soybeans | Corn | Copper | eem | efa | FROM_ABS | FROM_WTH | |
| gold | 11.100 | 0.440 | 0.250 | 0.270 | 1.010 | 0.500 | 0.320 | 0.4 | 3.1 |
| oil | 0.350 | 10.870 | 0.460 | 0.420 | 0.730 | 0.700 | 0.660 | 0.47 | 3.68 |
| soybeans | 0.100 | 0.270 | 9.880 | 2.850 | 0.340 | 0.310 | 0.310 | 0.6 | 4.63 |
| corn | 0.180 | 0.330 | 2.840 | 9.290 | 0.230 | 0.200 | 0.230 | 0.57 | 4.46 |
| copper | 0.960 | 0.710 | 0.450 | 0.330 | 7.450 | 1.750 | 1.510 | 0.82 | 6.33 |
| eem | 0.230 | 0.300 | 0.130 | 0.110 | 0.850 | 4.970 | 3.620 | 0.75 | 5.81 |
| efa | 0.230 | 0.350 | 0.110 | 0.130 | 0.900 | 4.280 | 5.350 | 0.86 | 6.67 |
| TO_ABS | 0.29 | 0.34 | 0.61 | 0.59 | 0.58 | 1.11 | 0.95 | 4.47 | |
| TO_WTH | 2.28 | 2.65 | 4.7 | 4.57 | 4.52 | 8.6 | 7.37 | 34.68 | |
| NET ABS | −0.11 | −0.13 | 0.01 | 0.02 | −0.24 | 0.36 | 0.09 | ||
| Pabel C: Spillovers Freq. Long-Term. Band 0.15 to 0.01, Corresponding to More than 21 Days. | |||||||||
| Long_Term | Gold | Oil | Soybeans | Corn | Copper | eem | efa | FROM_ABS | FROM_WTH |
| gold | 3.950 | 0.150 | 0.090 | 0.090 | 0.350 | 0.180 | 0.110 | 0.11 | 3.05 |
| oil | 0.140 | 3.960 | 0.160 | 0.150 | 0.260 | 0.260 | 0.240 | 0.14 | 3.78 |
| soybeans | 0.030 | 0.080 | 3.580 | 1.020 | 0.130 | 0.110 | 0.110 | 0.17 | 4.6 |
| corn | 0.060 | 0.110 | 1.000 | 3.290 | 0.080 | 0.070 | 0.080 | 0.16 | 4.38 |
| copper | 0.350 | 0.250 | 0.160 | 0.120 | 2.620 | 0.620 | 0.530 | 0.23 | 6.37 |
| eem | 0.090 | 0.100 | 0.040 | 0.040 | 0.300 | 1.720 | 1.250 | 0.21 | 5.69 |
| efa | 0.090 | 0.120 | 0.040 | 0.050 | 0.320 | 1.510 | 1.880 | 0.24 | 6.63 |
| TO_ABS | 0.29 | 0.34 | 0.61 | 0.59 | 0.58 | 1.11 | 0.95 | 1.26 | |
| TO_WTH | 0.09 | 0.09 | 0.17 | 0.17 | 0.16 | 0.31 | 0.27 | 34.49 | |
| NET ABS | −0.02 | −0.05 | 0 | 0.01 | −0.07 | 0.1 | 0.03 | ||
| Panel A: Spillovers Freq. Short-Term. Band 3.14 to 0.63, Corresponding to 1 Days to 5 Days. | |||||||||
| Gold | Oil | Soybeans | Corn | Copper | eem | efa | FROM_ABS | FROM_WTH | |
| gold | 0.370 | 0.000 | 0.000 | 0.000 | 0.000 | 0.030 | 0.030 | 0.01 | 0.03 |
| oil | 0.100 | 56.710 | 1.490 | 1.360 | 0.540 | 0.130 | 0.170 | 0.54 | 2.08 |
| soybeans | 0.100 | 1.290 | 48.500 | 10.860 | 0.210 | 0.110 | 0.050 | 1.8 | 6.93 |
| corn | 0.030 | 1.090 | 10.290 | 45.870 | 0.110 | 0.120 | 0.080 | 1.67 | 6.44 |
| copper | 0.010 | 0.000 | 0.000 | 0.000 | 0.380 | 0.050 | 0.040 | 0.01 | 0.06 |
| eem | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.590 | 0.260 | 0.04 | 0.15 |
| efa | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.340 | 0.800 | 0.05 | 0.19 |
| TO_ABS | 0.04 | 0.34 | 1.68 | 1.75 | 0.12 | 0.11 | 0.09 | 4.13 | |
| TO_WTH | 0.14 | 1.31 | 6.47 | 6.71 | 0.48 | 0.42 | 0.35 | 15.87 | |
| NET ABS | 0.03 | −0.2 | −0.12 | 0.08 | 0.11 | 0.07 | 0.04 | ||
| Panel B: Spillovers Freq. Medium-Term. Band 0.63 to 0.15, Corresponding to 5 Days to 21 Days. | |||||||||
| Gold | Oil | Soybeans | Corn | Copper | eem | efa | FROM_ABS | FROM_WTH | |
| gold | 1.040 | 0.000 | 0.000 | 0.000 | 0.020 | 0.040 | 0.060 | 0.02 | 0.16 |
| oil | 0.030 | 18.400 | 0.180 | 0.180 | 0.230 | 0.200 | 0.210 | 0.15 | 1.28 |
| soybeans | 0.060 | 0.150 | 21.140 | 4.420 | 0.110 | 0.070 | 0.030 | 0.69 | 5.97 |
| corn | 0.020 | 0.190 | 5.010 | 22.120 | 0.080 | 0.090 | 0.070 | 0.78 | 6.72 |
| copper | 0.030 | 0.000 | 0.010 | 0.000 | 1.150 | 0.130 | 0.130 | 0.04 | 0.37 |
| eem | 0.010 | 0.010 | 0.010 | 0.000 | 0.020 | 1.610 | 0.700 | 0.11 | 0.93 |
| efa | 0.020 | 0.020 | 0.000 | 0.000 | 0.010 | 0.910 | 2.190 | 0.14 | 1.19 |
| TO_ABS | 0.03 | 0.05 | 0.74 | 0.66 | 0.07 | 0.21 | 0.17 | 1.93 | |
| TO_WTH | 0.22 | 0.47 | 6.42 | 5.68 | 0.57 | 1.77 | 1.49 | 16.61 | |
| NET ABS | 0.01 | −0.1 | 0.05 | −0.12 | 0.03 | 0.1 | 0.03 | ||
| Panel C: Spillovers Freq. Long-Term. Band 0.15 to 0.01, Corresponding to More than 21 Days. | |||||||||
| Long_Term | Gold | Oil | Soybeans | Corn | Copper | eem | efa | FROM_ABS | FROM_WTH |
| gold | 50.040 | 0.520 | 0.310 | 0.300 | 2.050 | 23.790 | 21.390 | 6.91 | 11.07 |
| oil | 0.750 | 7.090 | 0.070 | 0.090 | 0.520 | 6.120 | 5.420 | 1.85 | 2.97 |
| soybeans | 0.550 | 0.050 | 8.340 | 1.720 | 0.890 | 0.740 | 0.610 | 0.65 | 1.04 |
| corn | 0.570 | 0.110 | 2.060 | 8.640 | 1.140 | 0.950 | 1.360 | 0.88 | 1.42 |
| copper | 9.860 | 0.670 | 0.990 | 0.410 | 46.130 | 24.530 | 15.470 | 7.42 | 11.89 |
| eem | 5.760 | 0.620 | 0.360 | 0.290 | 4.720 | 50.780 | 34.250 | 6.57 | 10.53 |
| efa | 4.800 | 0.790 | 0.220 | 0.230 | 3.280 | 35.980 | 50.400 | 6.47 | 10.37 |
| TO_ABS | 3.19 | 0.39 | 0.57 | 0.43 | 1.8 | 13.16 | 11.21 | 30.76 | |
| TO_WTH | 5.11 | 0.63 | 0.92 | 0.7 | 2.88 | 21.09 | 17.98 | 49.3 | |
| NET ABS | −3.72 | −1.46 | −0.08 | −0.45 | −5.62 | 6.59 | 4.74 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinho, C.; Maldonado, I. Commodity and Equity Markets: Volatility and Return Spillovers. Commodities 2022, 1, 18-33. https://doi.org/10.3390/commodities1010003
Pinho C, Maldonado I. Commodity and Equity Markets: Volatility and Return Spillovers. Commodities. 2022; 1(1):18-33. https://doi.org/10.3390/commodities1010003
Chicago/Turabian StylePinho, Carlos, and Isabel Maldonado. 2022. "Commodity and Equity Markets: Volatility and Return Spillovers" Commodities 1, no. 1: 18-33. https://doi.org/10.3390/commodities1010003
APA StylePinho, C., & Maldonado, I. (2022). Commodity and Equity Markets: Volatility and Return Spillovers. Commodities, 1(1), 18-33. https://doi.org/10.3390/commodities1010003






