Exploring Dependence Relationships between Bitcoin and Commodity Returns: An Assessment Using the Gerber Cross-Correlation
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Gerber Statistic
2.2. The Gerber Cross-Correlation
Inference Methods
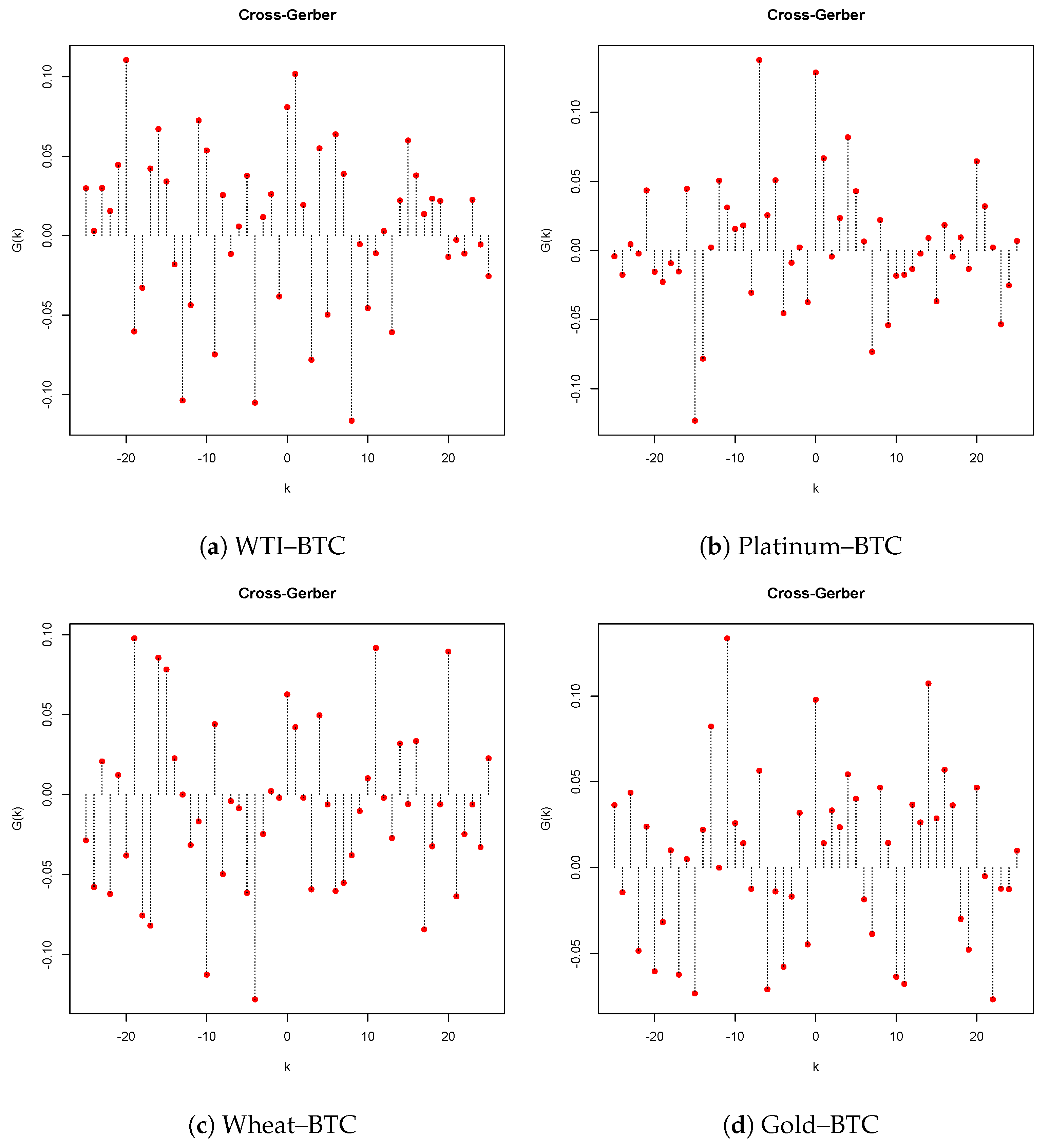
3. Data and Empirical Results
3.1. Data Description
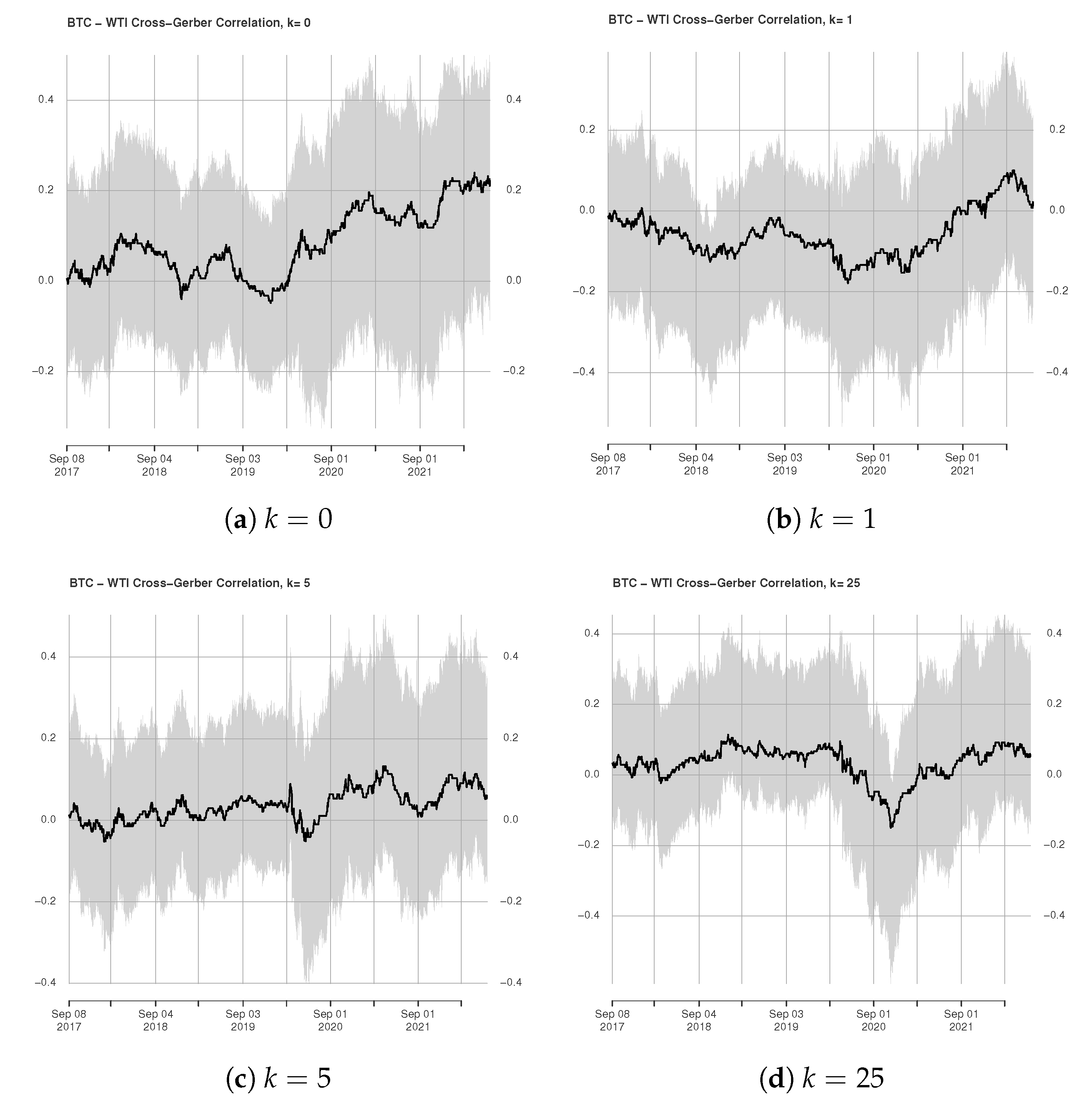
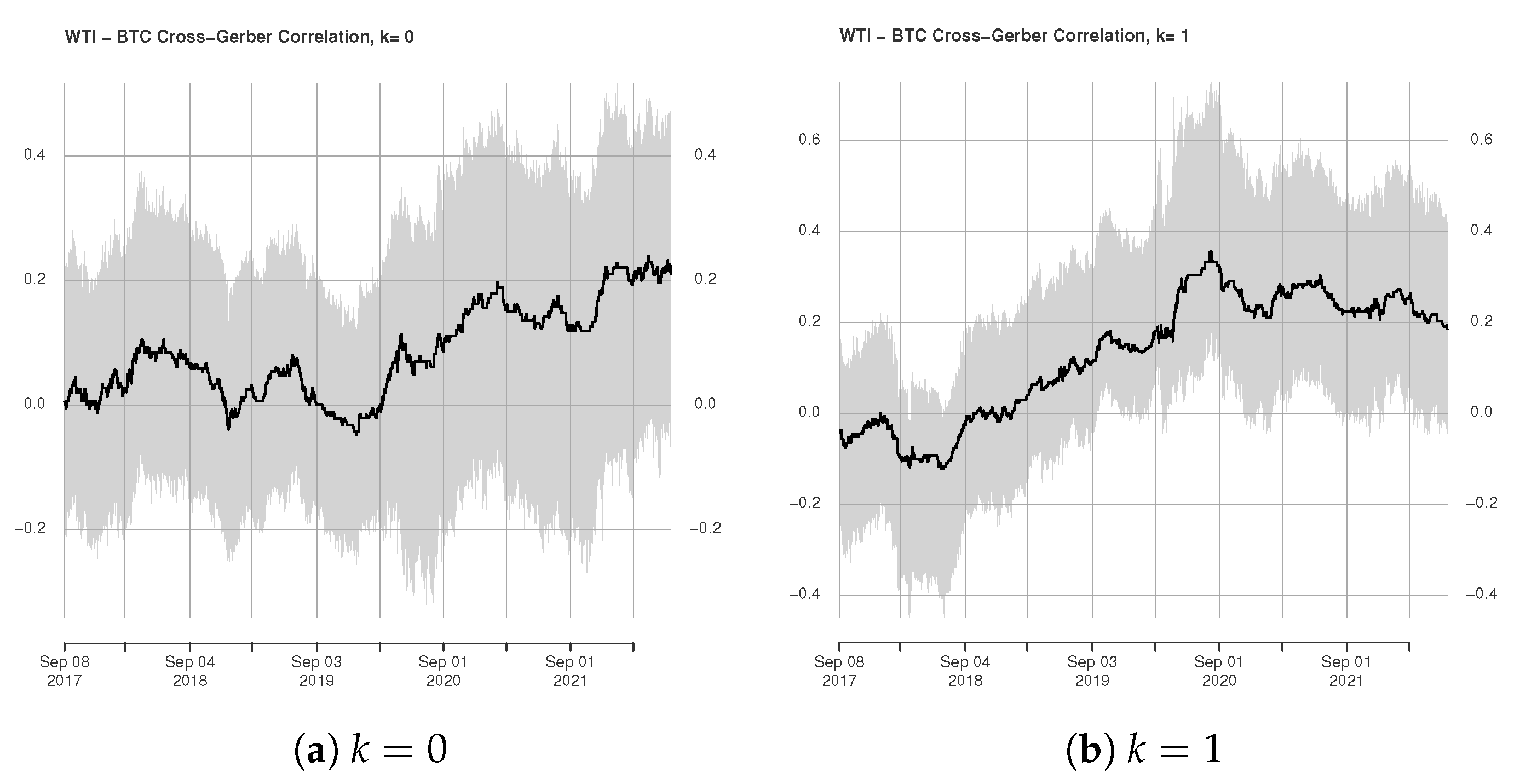
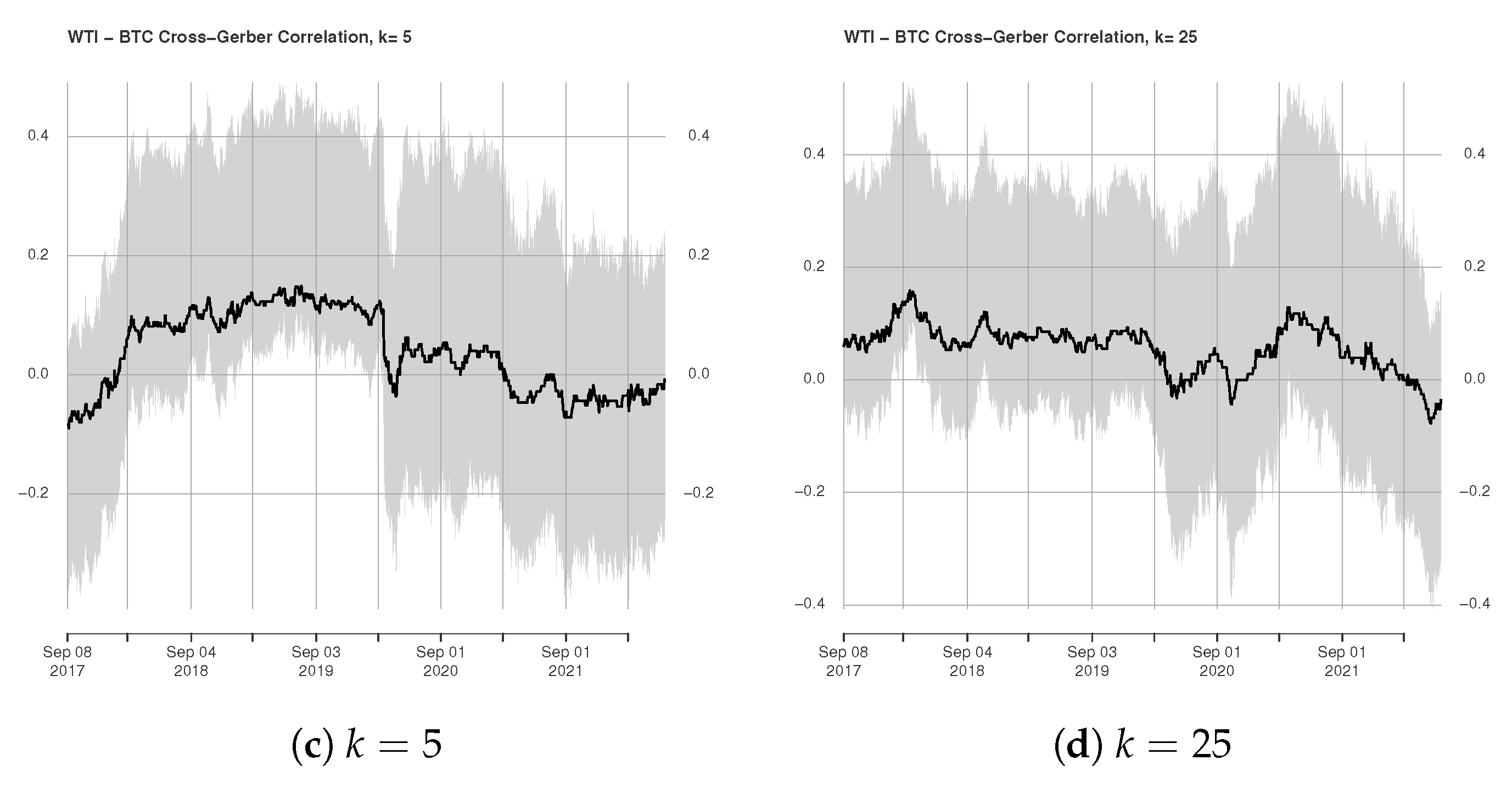
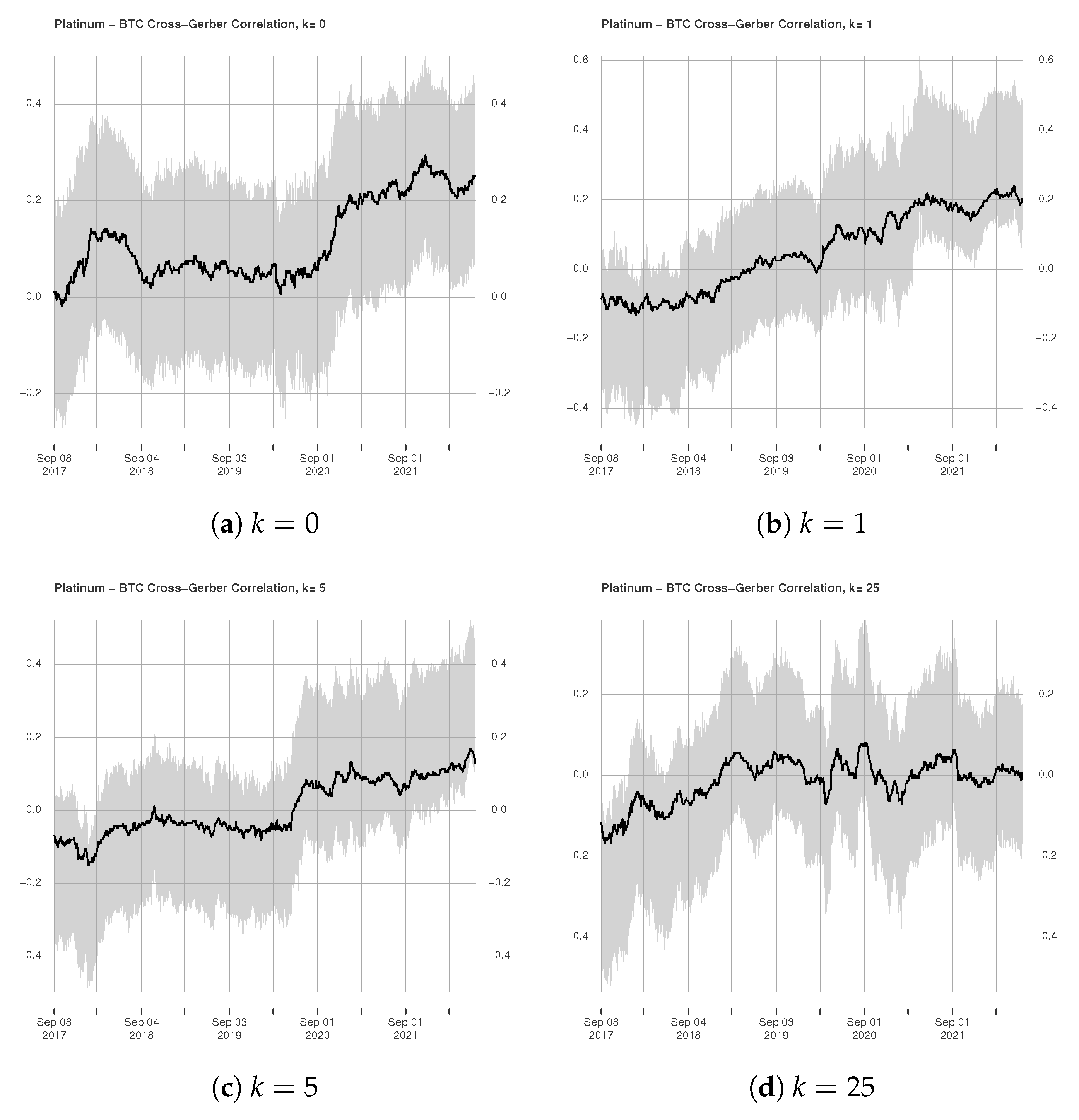
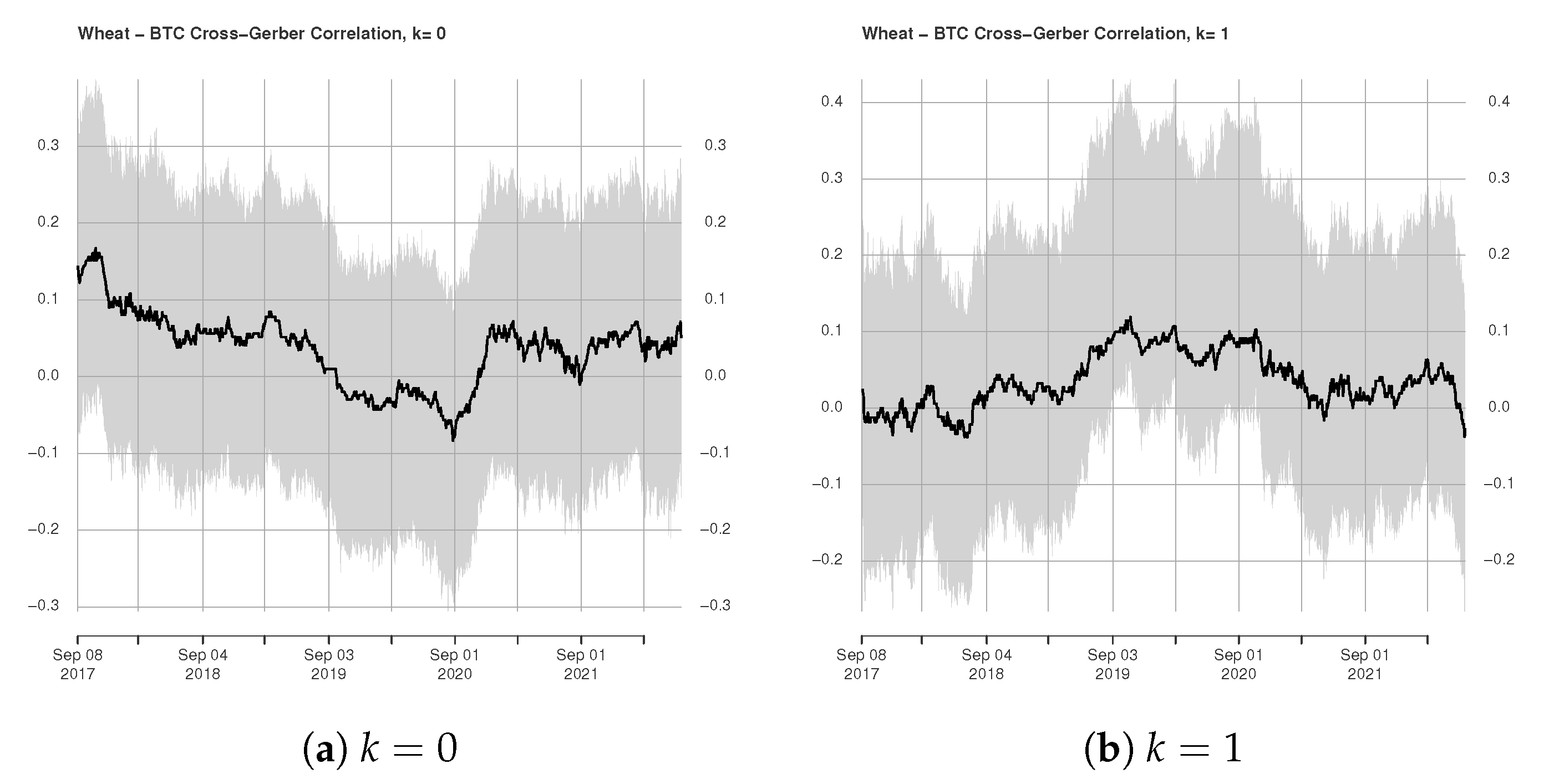
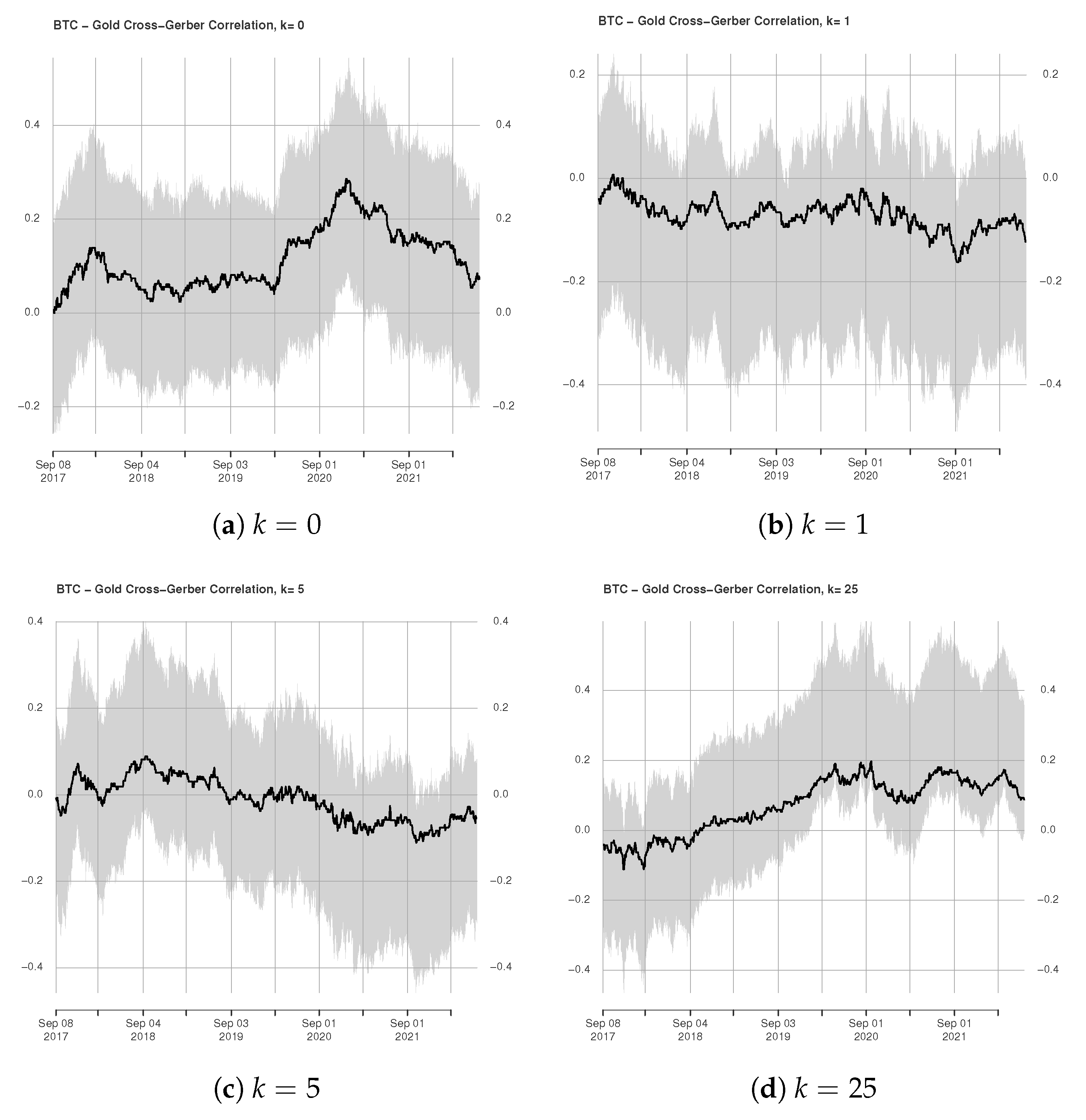
3.2. Rolling Window Estimation of Gerber Cross-Correlations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Almeida, J.; Gonçalves, T.C. A Systematic Literature Review of Volatility and Risk Management on Cryptocurrency Investment: A Methodological Point of View. Risks 2022, 10, 107. [Google Scholar] [CrossRef]
- Kristoufek, L. What Are the Main Drivers of the Bitcoin Price? Evidence from Wavelet Coherence Analysis. PLoS ONE 2015, 10, e0123923. [Google Scholar]
- Kjærland, F.; Khazal, A.; Krogstad, E.A.; Nordstrøm, F.B.G.; Oust, A. An Analysis of Bitcoin’s Price Dynamics. J. Risk Financ. Manag. 2018, 11, 63. [Google Scholar]
- Huynh, T.L.D.; Nasir, M.A.; Vo, X.V.; Nguyen, T.T. “Small things matter most”: The spillover effects in the cryptocurrency market and gold as a silver bullet. N. Am. J. Econ. Financ. 2020, 54, 101277. [Google Scholar]
- Klein, T.; Pham Thu, H.; Walther, T. Bitcoin is not the New Gold—A comparison of volatility, correlation, and portfolio performance. Int. Rev. Financ. Anal. 2018, 59, 105–116. [Google Scholar] [CrossRef]
- Wu, S. Co-movement and return spillover: Evidence from Bitcoin and traditional assets. SN Bus. Econ. 2021, 1, 1–16. [Google Scholar] [CrossRef]
- Elsayed, A.H.; Gozgor, G.; Yarovaya, L. Volatility and return connectedness of cryptocurrency, gold, and uncertainty: Evidence from the cryptocurrency uncertainty indices. Financ. Res. Lett. 2022, 47, 102732. [Google Scholar]
- Conrad, C.; Custovic, A.; Ghysels, E. Long- and Short-Term Cryptocurrency Volatility Components: A GARCH-MIDAS Analysis. J. Risk Financ. Manag. 2018, 11, 23. [Google Scholar] [CrossRef]
- Dai, M.; Qamruzzaman, M.; Hamadelneel Adow, A. An Assessment of the Impact of Natural Resource Price and Global Economic Policy Uncertainty on Financial Asset Performance: Evidence From Bitcoin. Front. Environ. Sci. 2022, 10, 897496. [Google Scholar] [CrossRef]
- Gerber, S.; Markowitz, H.; Ernst, P.A.; Miao, Y.; Javid, B.; Sargen, P. The Gerber Statistic: A Robust Co-Movement Measure for Portfolio Optimization. J. Portf. Manag. 2022, 48, 87–102. [Google Scholar]
- Algieri, B.; Leccadito, A.; Toscano, P. A Time-Varying Gerber Statistic: Application of a Novel Correlation Metric to Commodity Price Co-Movements. Forecasting 2021, 3, 339–354. [Google Scholar] [CrossRef]
- Zaremba, A.; Umar, Z.; Mikutowski, M. Commodity financialisation and price co-movement: Lessons from two centuries of evidence. Financ. Res. Lett. 2021, 38, 101492. [Google Scholar] [CrossRef]
- Politis, D.N.; Romano, J.P. The Stationary Bootstrap. J. Am. Stat. Assoc. 1994, 89, 1303–1313. [Google Scholar] [CrossRef]
- Patton, A.; Politis, D.N.; White, H. Correction to “Automatic Block-Length Selection for the Dependent Bootstrap” by D. Politis and H. White. Econom. Rev. 2009, 28, 372–375. [Google Scholar] [CrossRef]
- Ameur, H.B.; Ftiti, Z.; Louhichi, W. Revisiting the relationship between spot and futures markets: Evidence from commodity markets and NARDL framework. Ann. Oper. Res. 2022, 313, 171–189. [Google Scholar] [CrossRef]
- Algieri, B.; Leccadito, A. Assessing contagion risk from energy and non-energy commodity markets. Energy Econ. 2017, 62, 312–322. [Google Scholar] [CrossRef]
- Algieri, B.; Leccadito, A. Ask CARL: Forecasting tail probabilities for energy commodities. Energy Econ. 2019, 84. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T.; Kuck, K. Bitcoin, gold and the US dollar—A replication and extension. Financ. Res. Lett. 2018, 25, 103–110. [Google Scholar] [CrossRef]
- Baur, D.G.; Hoang, L. The Bitcoin gold correlation puzzle. J. Behav. Exp. Financ. 2021, 32, 100561. [Google Scholar] [CrossRef]
- Bouri, E.; Gupta, R.; Lahiani, A.; Shahbaz, M. Testing for asymmetric nonlinear short- and long-run relationships between bitcoin, aggregate commodity and gold prices. Resour. Policy 2018, 57, 224–235. [Google Scholar] [CrossRef]
- Jareño, F.; de la O. González, M.; López, R.; Ramos, A.R. Cryptocurrencies and oil price shocks: A NARDL analysis in the COVID-19 pandemic. Resour. Policy 2021, 74, 102281. [Google Scholar] [CrossRef]
- Aloui, R.; Aïssa, M.S.B.; Nguyen, D.K. Global financial crisis, extreme interdependences, and contagion effects: The role of economic structure? J. Bank. Financ. 2011, 35, 130–141. [Google Scholar] [CrossRef]





| Selected Commodities | |
|---|---|
| Ticker | Description |
| CL1 Comdty | Generic 1st Crude Oil WTI Futures |
| PL1 Comdty | Generic 1st Platinum futures |
| W1 Comdty | Generic 1st Wheat futures |
| GC1 Comdty | Generic 1st Gold futures |
| BTC | WTI | Platinum | Wheat | Gold | |
|---|---|---|---|---|---|
| Mean | 0.0015 | 0.0001 | −0.0002 | 0.0004 | 0.0002 |
| Standard Deviation | 0.0422 | 0.0325 | 0.0168 | 0.0193 | 0.0093 |
| Median | 0.0019 | 0.0013 | 0.0002 | −0.0002 | 0.0003 |
| Minimum | −0.4647 | −0.3454 | −0.1231 | −0.1130 | −0.0511 |
| Maximum | 0.2252 | 0.3196 | 0.1118 | 0.1970 | 0.0577 |
| Standard Error | 0.0010 | 0.0007 | 0.0004 | 0.0004 | 0.0002 |
| Skewness | −0.8523 | −0.7362 | −0.2743 | 0.5836 | −0.0783 |
| Kurtosis | 14.0416 | 29.3225 | 7.9913 | 10.2708 | 7.2735 |
| JB Stat | 10162.5935 | 56588.1481 | 2052.8205 | 4414.9624 | 1488.8657 |
| JB pval | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| = BTC, = WTI | = BTC, = Platinum | = BTC, = Wheat | = BTC, = Gold | |||||
| 1 | 2.8590 | 0.4570 | 2.7277 | 0.5500 | 0.0083 | 0.9600 | 3.8789 | 0.5790 |
| 5 | 28.8201 | 0.4320 | 11.9621 | 0.9000 | 40.5485 | 0.7110 | 13.3090 | 0.9120 |
| 10 | 46.9309 | 0.6870 | 53.2732 | 0.9080 | 74.0836 | 0.8400 | 31.3360 | 0.9640 |
| 25 | 137.9548 | 0.9130 | 112.1169 | 0.9880 | 166.4217 | 0.9670 | 120.1614 | 0.9920 |
| WTI, BTC | Platinum, BTC | Wheat, BTC | Gold, BTC | |||||
| 1 | 20.2080 | 0.0410 | 8.6844 | 0.5050 | 3.4788 | 0.4300 | 0.3950 | 0.7700 |
| 5 | 43.5911 | 0.2180 | 26.5014 | 0.8040 | 15.2411 | 0.8270 | 12.5860 | 0.8540 |
| 10 | 85.0695 | 0.2350 | 44.3850 | 0.9250 | 31.5308 | 0.9300 | 28.6693 | 0.9560 |
| 25 | 108.5652 | 0.8880 | 66.4093 | 0.9980 | 97.5479 | 0.9880 | 97.3701 | 0.9930 |
| BTC, WTI | BTC, Platinum | BTC, Wheat | BTC, Gold | |||||
| 1 | 12.0200 | 0.5480 | 0.9370 | 0.7950 | 16.1488 | 0.3110 | 13.1282 | 0.3170 |
| 5 | 58.6704 | 0.7580 | 14.5683 | 0.9510 | 52.9512 | 0.6780 | 97.1572 | 0.3190 |
| 10 | 178.7206 | 0.7110 | 75.9803 | 0.8770 | 94.2911 | 0.8270 | 260.5584 | 0.1840 |
| 25 | 672.2332 | 0.8990 | 183.1941 | 0.9870 | 275.7607 | 0.9490 | 684.0197 | 0.2120 |
| WTI,BTC | Platinum,BTC | Wheat,BTC | Gold,BTC | |||||
| 1 | 4.2667 | 0.6090 | 19.5400 | 0.1990 | 0.1041 | 0.9280 | 1.0248 | 0.7990 |
| 5 | 72.4407 | 0.6180 | 71.6663 | 0.4770 | 25.2471 | 0.8870 | 72.1157 | 0.4660 |
| 10 | 229.8511 | 0.3820 | 152.8596 | 0.5500 | 63.1620 | 0.9220 | 191.9757 | 0.2990 |
| 25 | 506.2262 | 0.5990 | 295.6690 | 0.9330 | 339.1286 | 0.8870 | 510.9055 | 0.3830 |
| BTC, WTI | BTC, Platinum | BTC, Wheat | BTC, Gold | |||||
| 1 | 1.8448 | 0.2820 | 16.9378 | 0.0000 | 9.4301 | 0.0380 | 17.7234 | 0.0000 |
| 5 | 17.9767 | 0.2060 | 60.2868 | 0.0020 | 69.5256 | 0.0000 | 74.4307 | 0.0000 |
| 10 | 31.2844 | 0.2050 | 118.3702 | 0.0000 | 137.8887 | 0.0000 | 135.3187 | 0.0000 |
| 25 | 53.1649 | 0.2070 | 308.7823 | 0.0000 | 333.0107 | 0.0000 | 316.5219 | 0.0000 |
| WTI, BTC | Platinum, BTC | Wheat, BTC | Gold, BTC | |||||
| 1 | 3.0219 | 0.2290 | 9.8020 | 0.0430 | 9.9330 | 0.0470 | 14.4043 | 0.0000 |
| 5 | 23.6538 | 0.1600 | 71.9153 | 0.0000 | 72.8432 | 0.0010 | 73.0970 | 0.0000 |
| 10 | 44.6466 | 0.1700 | 144.1266 | 0.0000 | 138.5131 | 0.0010 | 134.3093 | 0.0000 |
| 25 | 104.3157 | 0.1820 | 326.3295 | 0.0030 | 348.7731 | 0.0020 | 308.8461 | 0.0000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawuobahsumo, K.K.; Algieri, B.; Iania, L.; Leccadito, A. Exploring Dependence Relationships between Bitcoin and Commodity Returns: An Assessment Using the Gerber Cross-Correlation. Commodities 2022, 1, 34-49. https://doi.org/10.3390/commodities1010004
Lawuobahsumo KK, Algieri B, Iania L, Leccadito A. Exploring Dependence Relationships between Bitcoin and Commodity Returns: An Assessment Using the Gerber Cross-Correlation. Commodities. 2022; 1(1):34-49. https://doi.org/10.3390/commodities1010004
Chicago/Turabian StyleLawuobahsumo, Kokulo K., Bernardina Algieri, Leonardo Iania, and Arturo Leccadito. 2022. "Exploring Dependence Relationships between Bitcoin and Commodity Returns: An Assessment Using the Gerber Cross-Correlation" Commodities 1, no. 1: 34-49. https://doi.org/10.3390/commodities1010004
APA StyleLawuobahsumo, K. K., Algieri, B., Iania, L., & Leccadito, A. (2022). Exploring Dependence Relationships between Bitcoin and Commodity Returns: An Assessment Using the Gerber Cross-Correlation. Commodities, 1(1), 34-49. https://doi.org/10.3390/commodities1010004








