LINEX Loss-Based Estimation of Expected Arrival Time of Next Event from HPP and NHPP Processes Past Truncated Time

Abstract

This article introduces a computational tool for Bayesian estimation of the expected time until the next event occurs in both homogeneous Poisson processes (HPPs) and non-homogeneous Poisson processes (NHPPs), following a truncated time. The estimation utilizes the linear exponential (LINEX) asymmetric loss function and incorporates both gamma and non-informative priors. Furthermore, it presents a minimax-type criterion to ascertain the optimal sample size required to achieve a specified percentage reduction in posterior risk. Simulation studies indicate that estimators employing gamma priors for both HPP and NHPP demonstrate greater accuracy compared to those based on non-informative priors and maximum likelihood estimates (MLE), provided that the proposed data-driven method for selecting hyperparameters is applied.

1. Introduction

Let $\left\{N\right(t),t\ge 0\}$ be a counting process, where $N\left(t\right)$ denotes the number of events that occur by time t. Let $X_n$ denote the time between the $(n-1)$th and nth events of the process, $n\ge 1$. Let $S_{N\left(\tau \right)}$ denote the time of last arrival before a truncated time $\tau$ and $S_{N\left(\tau \right)+1}$ be the time of the first arrival after the time $\tau$. If $\{X_1,X_2,\dots \}$ is a sequence of identically independent distributed (iid) interarrival times of the events, then the process $\left\{N\right(t),t\ge 0\}$ is called a renewal process. One of the measures associated with a renewal process is the expected time of next arrival, $E\left[S_{N\left(\tau \right)+1}\right]$, after a specified time $\tau$. Note that $S_{N\left(t\right)}\le t$. Ref. [1] provides the well-known result $E\left[S_{N\left(\tau \right)+1}\right]=\mu (m\left(\tau \right)+1)$, where $\mu$ is the mean of the interarrival distribution and $m\left(\tau \right)=E\left[N\right(\tau \left)\right]$ is the renewal function. The proposed method presented in this article can be applied to any renewal process as long as $\mu$ and $m\left(\tau \right)$ can be expressed as closed functions of the parameter(s) of the renewal process. The estimation of $m\left(t\right)$ has been considered in the literature. For instance, [2] utilizes numerical methods based on an MCMC algorithm for estimating $m\left(t\right)$ when interarrival times follow a Pareto distribution.

The HPP is widely used in various fields of probability and applied statistics. Ref. [3] applied an HPP to model interarrivals of earthquakes. Ref. [4] provided a Bayesian approach to estimating the Poisson intensity function based on the Haar wavelet transform. The NHPP is also utilized in practice when the intensity function is not constant, as in the case of HPP. The NHPP model has numerous real-world applications. In the insurance industry, the occurrence of insurance claims can be effectively modeled using an NHPP. For example, the rate of car accident claims may increase during peak travel seasons or bad weather conditions. In financial market modeling, the arrival rate of transactions often exhibits time-varying characteristics. An NHPP can be considered to model these transactions. In software development, the NHPP can be considered as a possible model for the occurrence of software defects during testing. As testing progresses, the rate at which new defects are uncovered may decrease. Many authors have considered the power law (PL) intensity function for NHPP in the literature. Ref. [5] assumed that the failures of a system follow an NHPP with the PL intensity function and mentioned that the NHPP is a model commonly used to describe a system with minimal repairs. For minimal repair cases, it is assumed that the system is restored to its state immediately before the failure. This means the repair does not improve the system’s inherent reliability. Ref. [6] considered NHPP with linear and PL intensity functions to analyze COVID-19 cases. For NHPP, the rate of events (failures of a system) is not constant over time; it can increase or decrease, reflecting reliability growth or deterioration. Therefore, the occurrence rate is time-dependent. Under the PL intensity function, the failure intensity, or rate of failures per unit time, is modeled as a power function of time. The PL intensity is useful for systems undergoing continuous improvement or deterioration, where the reliability is not static. The PL mean-value function $\Lambda \left(t\right)$, and its intensity function $\lambda \left(t\right)={\displaystyle \frac{d\Lambda \left(t\right)}{dt}}$, respectively, are defined as

$$\Lambda (t)={({\displaystyle \frac{\tau }{\theta }})}^{\beta },\lambda (t)={\displaystyle \frac{\beta }{t}}{({\displaystyle \frac{\tau }{\theta }})}^{\beta },$$

where $\theta$ and $\beta$ are scale and shape parameters, respectively.

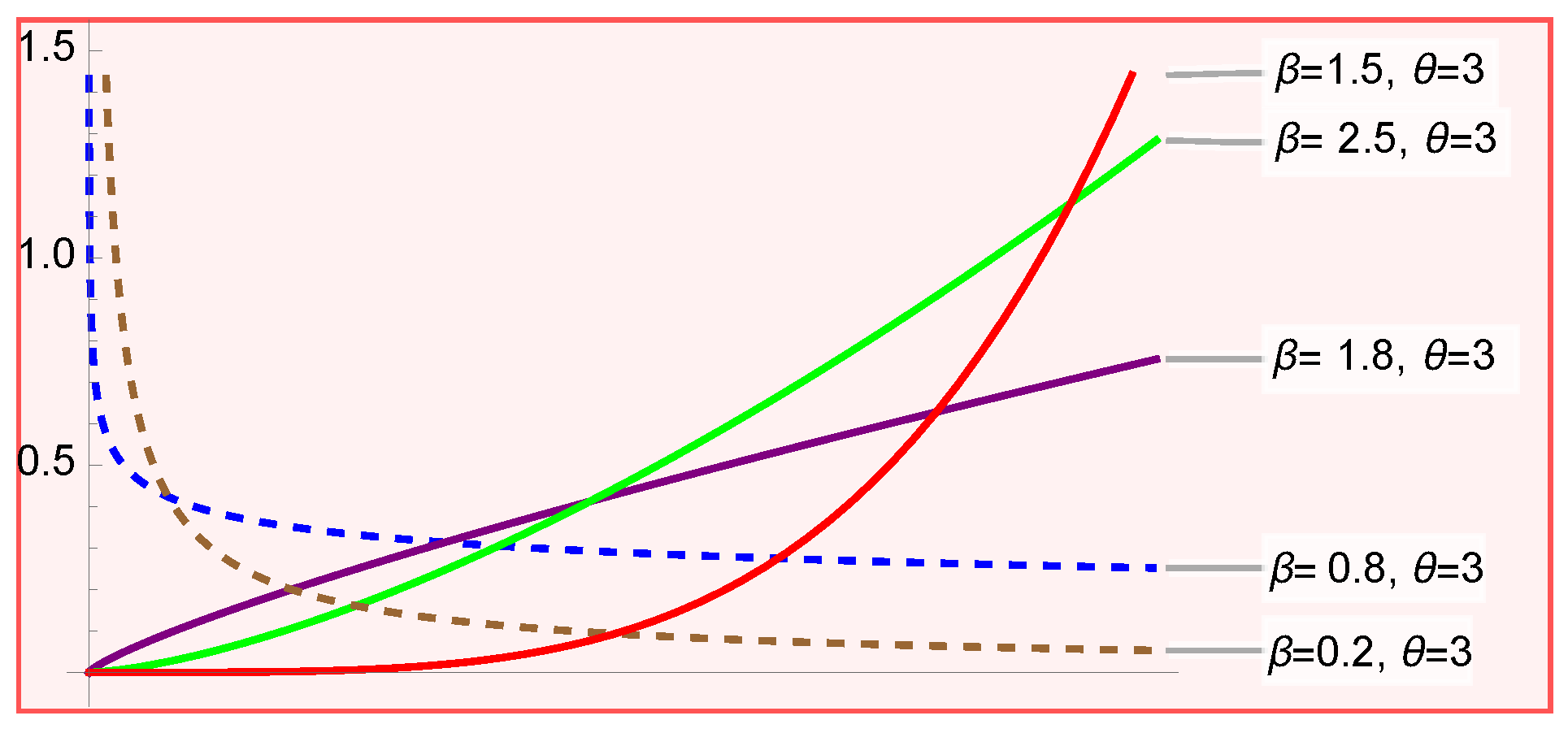
Figure 1 reveals that for $\beta <1$, the intensity function decreases, indicating that the occurrence rate of events diminishes. In the context of a repairable system, this suggests that minimal repairs are sufficient. Conversely, for $\beta >1$, the intensity function increases, indicating that failure rates rise.

The LINEX loss function has many advantages over other asymmetric loss functions, such as Mean Squared Error, Mean Absolute Error, and Binary Cross-Entropy, to name a few. The LINEX loss function provides different penalties based on whether the error is an overestimation or an underestimation, and the degree and direction of asymmetry can be controlled by choosing its parameter value (a positive value implies overestimation is more serious, and a negative value implies underestimation has a greater cost). The continuity and differentiability properties of the LINEX loss enable mathematical optimization to find the optimal Bayes estimate, and it converges to the quadratic loss function as its parameter approaches zero. Ref. [7] used the loss function to predict lower bounds for the number of points in regression models. The loss function penalizes underestimation at an exponential rate while penalizing overestimation only linearly. Ref. [8] considered the loss function to determine optimum process parameters for product quality. Ref. [9] utilized the loss function with a variable parameter and considered several distributions for the parameter to find Bayes risks. Ref. [10] applied the loss function to several resampling methods.

The main goal of this article is to provide novel Bayes estimators for the expected arrival of the event past a truncated time, $E\left[S_{N(\tau )+1}\right]$, utilizing the LINEX loss function for two cases: 1. $\{N(t),t\ge 0\}$ is assumed to be an HPP with rate $\lambda$; 2. $\{N(t),t\ge 0\}$ is assumed to be an NHPP with an intensity function $\lambda (t)$. For the HPP case, Laptance’s method for a twice-differentiable function was applied to obtain the Bayes estimator using gamma and non-informative priors. For the NHPP case, Bayes estimators based on gamma priors for the parameters of the PL intensity, as well as the Jeffreys prior, are applied to obtain Bayesian estimates. Additionally, the article provides closed formulas for the posterior risk based on informative and non-informative priors for both HPP and NHPP. It proposes a criterion based on a minimax-type method to determine the optimal sample size to satisfy a specified percentage decrease in posterior risk.

The remainder of this article is organized as follows: Section 2 consists of three subsections. It provides two Bayes estimators via gammas and the Jeffreys prior for the expected time of arrival of the event past a truncated time, assuming an HPP for the arrival times of events. Section 3 has three subsections. In this section, the NHPP is considered utilizing the PL intensity function. The computation of the Bayes estimates via gamma priors, as well as a non-informative prior, is discussed, and simulation results are presented. Section 4 has two subsections. In this section, a minimax-type algorithm is presented to compute the optimal sample size that meets a specified percentage decrease threshold level. In Section 5, a numerical example is presented to illustrate the computations involved in the goodness-of-fit of data to NHPP and the optimal sample size.

2. Homogeneous Poisson Process

For the HPP with rate $\lambda$, it is a well-known fact that $X_i\sim$ Exponential $(\lambda )$, $i=1,2,\dots$, with the probability density function (pdf) $f(x;\lambda )=\lambda e^{-\lambda x}$. It can be shown that $m(\tau )=\lambda \tau$ and $\mu =1/\lambda$; as a result, $E\left[S_{N(\tau )+1}\right]=\tau +1/\lambda$. Of course, this result can also be argued via the memoryless property of the Exponential distribution. Since the truncated time $\tau$ is given in advance, we concentrate on deriving the Bayes estimator of the rate of occurrence $\theta =1/\lambda$ based on a random sample $x_1,\dots ,x_n$. Let $v=\widehat{\theta }-\theta$ denote the error of estimating a parameter $\theta$ with an estimator $\widehat{\theta }$. The LINEX loss function is defined as

$$L(v)=q[e^{\omega v}-\omega v-1],\omega \ne 0,q>0$$

where $\omega$ and q are the shape and scale parameters, respectively, of the loss function. Without loss of generality, we let $q=1$. The shape parameter $\omega$ can take negative and positive values.

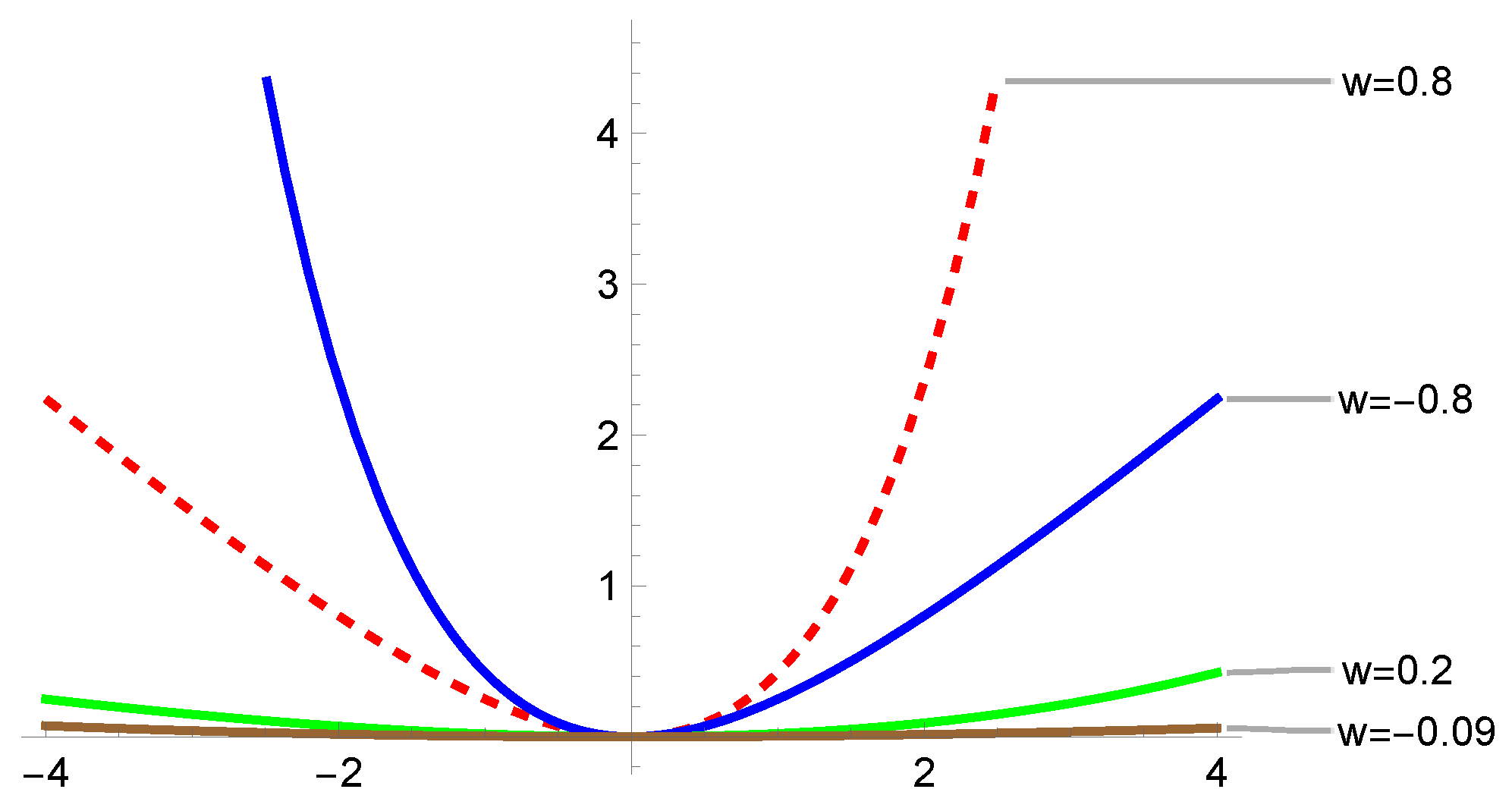
Figure 2 is the graph of the LINEX loss function, as defined above. Figure 2 reveals that for both $\omega >0$ and $\omega <0$, the loss function is asymmetric. For $\omega >0$ and $v>0$, overestimation is more severe than when $\omega >0$ and $v<0$. That is, for $v>0,\omega >0$, the loss function is greater (exponentially increases) than for $v<0,\omega >0$ (linearly increases). For example, LINEX $(v=2,\omega =0.8)=2.35$, while LINEX $(v=-2,\omega =0.8)=0.801$. On the other hand, when $\omega <0$, the loss function is almost linear for $v>0$ and almost exponential for $v<0$. Additionally, when the shape parameter $\omega$ in absolute value is less than 1 and is very small, the loss function is symmetric and resembles the squared-error loss function. It is worth mentioning that the squared error loss treats overestimation and underestimation equally, penalizing both with the square of the error. However, LINEX loss introduces asymmetry, allowing for different penalties for overestimation and underestimation, which are controlled by the parameter $\omega$.

The following Mathematica code provides a graph of the LINEX loss function for selected values of the shape parameter $\omega$ in Figure 2.

• ${\omega }_1=0.8$; ${\omega }_2=-0.8$; ${\omega }_3=0.2$; ${\omega }_4=-0.09;$ Plot[{Exp[v w1] − v w1 − 1, Exp[v w2] − v w2 − 1, Exp[v w3] − v w3 − 1, Exp[v w4] − v w4 − 1]}, {v, −4, 4}, PlotStyle → {{Red, Dashed}, Blue, Green, Brown}, PlotLabels → {“w = 0.8”, “w = −0.8”, “w = 0.2”, “w = −0.09”}]

Ref. [11] provides the general expression for the optimal Bayes estimator of $\theta$ with respect to the LINEX loss function as

$${\widehat{\theta }}_{Bayes}=-{\displaystyle \frac{\ln \left[M_{\theta }(-\omega )\right]}{\omega }}$$

(1)

where $M_{\theta }(-\omega )=E_{\theta }\left[e^{-\omega \theta }\right]$ is the moment generating function for the posterior distribution of $\theta$, and $E_{\theta }[.]$ denotes the expected value with respect to $\theta$.

2.1. Bayes Estimator Based on a Gamma Prior

The gamma distribution, as a prior distribution in Bayesian analysis, has many advantages. It is a natural and appropriate choice for modeling non-negative parameters such as variances, rates, and scale parameters. The distribution serves as a conjugate prior for several important likelihood functions, and by adjusting its parameters, the gamma distribution can adopt a variety of shapes, allowing for a flexible representation of prior beliefs. In this article, the gamma distribution is utilized for the parameters of HPP and NHPP. According to Laplace’s method, for a twice-differentiable function g(x), which has a unique global maximum at $x_0$ and for a large number n,

$${\int }_a^b{e}^{ng(x)}dx\approx \sqrt{{\displaystyle \frac{2\pi }{n|g^{″}(x_0)|}}{e}^{ng(x_0)}}.$$

(2)

Assume $\theta$ is a parameter with the prior distribution $\nu (\theta )$ and let $L(\theta ;\underline{x})$ denote the likelihood function. The moment generating function (mgf) for the posterior distribution of $\theta$ is

$$M_{(\theta )}(-\omega )={\displaystyle \frac{\int e^{-\omega \theta }\nu (\theta )L(\theta ;\underline{x})d\theta }{\int \nu (\theta )L(\theta ;\underline{x})d\theta }},$$

(3)

where $\underline{x}=(x_1,x_2,\dots x_n)$ is a random sample of interarrivals from the Exponential distribution. From (1), the LINEX Bayes estimator of $\theta$ is

$${\displaystyle \frac{-\ln \left[M_{(\theta )}(-\omega )\right]}{\omega }}.$$

Based on a sample $\underline{x}=(x_1,x_2,\dots ,x_n)$ of interarrival times from an HPP, the likelihood function is $L(\lambda ;\underline{x})=f(\underline{x};\lambda )={\lambda }^n{e}^{-\lambda s}$, where $s={\sum }_{i=1}^n{x}_i$. First, we consider a gamma prior for $\lambda$:

$${\nu }_1(\lambda )={\displaystyle \frac{{\beta }^{\alpha }}{\Gamma (\alpha )}}{\lambda }^{\alpha -1}{e}^{-\beta \lambda },\alpha >0,\beta >0.$$

(4)

It can be shown that the posterior pdf for $\lambda$ can be written as

$${\nu }_1(\lambda ;\underline{x})={\displaystyle \frac{L(\lambda ){\nu }_1(\lambda )}{{\int }_0^{\infty }L(\lambda ){\nu }_1(\lambda )d\lambda }}={\displaystyle \frac{{\lambda }^{n+\alpha -1}{e}^{-\lambda (s+\beta )}{(\beta +s)}^{n+\alpha }}{\Gamma (n+\alpha )}}$$

which is the pdf of gamma$(n+\alpha ,s+\beta )$. Therefore, the posterior distribution for $\theta =1/\lambda$ (which is the main parameter of interest), is inverse-gamma with the pdf

$${\nu }_1(\theta ;\underline{x})={\displaystyle \frac{{\theta }^{-(n+\alpha +1)}{e}^{\frac{-(s+\beta )}{\theta }}{(\beta +s)}^{n+\alpha }}{\Gamma (n+\alpha )}}.$$

(5)

Bayesian analysis assumes that some information is available on the hyperparameters $\alpha$ and $\beta$ based on the behavior of $\theta$. However, most of the time, such information is unavailable, and one can use a data-driven approach. This approach was implemented in ref. [2] and many other articles by the author. In the context of the present article, the MLE ${\widehat{\theta }}_{mle}$ is used to choose the hyperparameter values. Simulation studies in Section 2.3 indicate that for a smaller sample size, the Bayes estimator of ${\widehat{\theta }}_{Bayes}$ outperforms ${\widehat{\theta }}_{mle}$ in terms of accuracy as measured by the square root of average squared error (SASE). However, for large samples, the accuracy of MLE is comparable to that of the Bayes estimator. The numerical computations summarized in

Table 1. Mean and SASE of estimators for selected values of hyperparameters.

		$\mathit{\alpha }=5$	$\mathit{\lambda }=0.4$			$\mathit{\alpha }=50$	$\mathit{\lambda }=5$
$\mathit{\omega }$	$\mathit{n}$	${\widehat{\mathit{\theta }}}_{\mathit{mle}}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{g})}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{J})}$	$\mathit{\omega }$	$\mathit{n}$	${\widehat{\mathit{\theta }}}_{\mathit{mle}}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{g})}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{J})}$
0.02	10	2.5007	2.4954	2.2677	0.02	10	0.2003	0.2000	0.1821
		(0.7640)	(0.5434)	(0.7290)			(0.0633)	(0.0010)	(0.0603)
	50	2.4976	2.4965	2.4474		50	0.2003	0.2001	0.1964
		(0.3612)	(0.3342)	(0.3577)			(0.0274)	(0.0138)	(0.0271)
	100	2.5107	2.5096	2.4852		100	0.1996	0.1997	0.1977
		(0.2464)	(0.2368)	(0.2441)			(0.0206)	(0.0139)	(0.0206)
0.4	10	2.5156	2.4198	2.1869	0.4	10	0.2004	0.1999	0.1815
		(0.7925)	(0.5323)	(0.7316)			(0.0617)	(0.0104)	(0.0586)
	50	2.5226	2.4971	2.4488		50	0.2011	0.2005	0.1970
		(0.3748)	(0.3399)	(0.3633)			(0.0290)	(0.0146)	(0.0285)
	100	2.5043	2.4920	2.4673		100	0.2003	0.1999	0.1979
		(0.2584)	(0.2461)	(0.2554)			(0.0194)	(0.0130)	(0.0193)
1	10	2.4825	2.2902	2.0471	1	10	0.1999	0.1996	0.1799
		(0.8083)	(0.5354)	(0.7617)			(0.0651)	(0.0110)	(0.0614)
	50	2.5062	2.4491	2.3994		50	0.01994	0.1995	0.1951
		(0.3512)	(0.3150)	(0.3436)			(0.0279	(0.0140)	(0.0276)
	100	2.4980	2.4685	2.4434		100	0.1988	0.1991	0.1967
		(0.2589)	(0.2452)	(0.2566)			(0.0194)	(0.0130)	(0.0195)

,

Table 2. Mean and SASE of estimators for selected values of hyperparameters.

		$\mathit{\alpha }=5$	$\mathit{\lambda }=20$			$\mathit{\alpha }=50$	$\mathit{\lambda }=20$
$\mathit{\omega }$	$\mathit{n}$	${\widehat{\mathit{\theta }}}_{\mathit{mle}}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{g})}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{J})}$	$\mathit{\omega }$	$\mathit{n}$	${\widehat{\mathit{\theta }}}_{\mathit{mle}}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{g})}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{J})}$
0.02	10	0.0500	0.0500	0.0455	0.02	10	0.0501	0.0500	0.0456
		(0.0159)	(0.0113)	(0.0151)			(0.0160)	(0.0027)	(0.0152)
	50	0.0501	0.0501	0.0491		50	0.0501	0.0500	0.0491
		(0.0071)	(0.0066)	(0.0070)			(0.0070)	(0.0035)	(0.0070)
	100	0.0500	0.0500	0.0495		100	0.0497	0.0498	0.0492
		(0.0049)	(0.0048)	(0.0049)			(0.0050)	(0.0034)	(0.0050)
0.4	10	0.0498	0.0498	0.0452	0.4	10	0.0499	0.0499	0.0449
		(0.0155)	(0.0011)	(0.0149)			(0.0152)	(0.0025)	(0.0147)
	50	0.0499	0.0499	0.0489		50	0.0497	0.0498	0.0487
		(0.0069)	(0.0064)	(0.0068)			(0.0069)	(0.0035)	(0.0069)
	100	0.0501	0.0501	0.0496		100	0.00501	0.0500	0.0496
		(0.0048)	(0.0046)	(0.0048)			(0.0051)	(0.0034)	(0.0050)
1	10	0.0497	0.0497	0.0451	1	10	0.0496	0.0499	0.0450
		(0.0150)	(0.0113)	(0.0151)			(0.0160)	(0.0027)	(0.0153)
	50	0.0499	0.0498	0.0489		50	0.0497	0.0498	0.0487
		(0.0071)	(0.0066)	(0.0071)			(0.0071)	(0.0035)	(0.0070)
	100	0.0499	0.0499	0.0494		100	0.0498	0.0499	0.0493
		(0.0049)	(0.0047)	(0.0049)			(0.0048)	0.0032)	(0.0047)

and

Table 3. SASE for estimators: $n=100, \omega =1$.

$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\lambda }$	ML	Bayes(g)	Bayes(J)
5	3	5	(0.0196)	(0.0277)	(0.0195)
5	0.8	5	(0.0199)	(0.0191)	(0.0198)
5	2	25	(0.0040)	(0.0179)	(0.0040)
5	0.16	25	(0.0039)	(0.0036)	0.0039)
50	1.0	10	(0.0100)	(0.0736)	(0.0100)
50	4.9	10	(0.0101)	(0.0096)	(0.0010)
50	2	0.5	(0.1977)	(0.2002)	(0.1952)
50	98	0.5	(0.2008)	(0.1330)	(0.1992)

confirm the findings. Since

$$\theta \sim \mathrm{Inverse-Gamma}(\alpha ,\beta ),$$

we have,

$$E\left[\theta \right]={\displaystyle \frac{\beta }{\alpha -1}},Var(\theta )={\displaystyle \frac{{\beta }^2}{(\alpha -2){(\alpha -1)}^2}},\alpha >2.$$

In practice, where only one sample is available, the idea is to choose a large value for $\alpha$ to minimize the variance of the prior distribution, and then solve ${\widehat{\theta }}_{mle}={\displaystyle \frac{\beta }{\alpha -1}},$ for $\beta$. However, for the simulation studies, using selected “true” values of ${\alpha }_t$ and ${\theta }_t$, we let $\beta ={\theta }_t({\alpha }_t-1)$. The idea is to utilize the MLE and ensure the relation between hyperparameters is consistent with the information contained in the MLE. Simulations confirm that using this approach, the gamma-based Bayes estimator outperforms both ML-based and Jeffreys-based estimators in terms of accuracy.

The closed formula for the mgf of the posterior (5) can be written as

$$M_{\theta }(-\omega )={\displaystyle \frac{2{\left[(\beta +s)\omega \right]}^{0.5(n+\alpha )}{K}_{n+\alpha }(\sqrt{4\omega (\beta +s)}}{\Gamma (n+\alpha )}}$$

where

$$K_c(x)=0.5e^{-0.5c\pi i}{\int }_{-\infty }^{\infty }{e}^{-ix\sinh (v)-cv}dv$$

is the modified BesselK function. The mgf can also be expressed in a closed form that does not involve the BesselK function. From (5), we get

$$M_{\theta }(-\omega )={\displaystyle \frac{{(\beta +s)}^{n+\alpha }}{\Gamma (n+\alpha )}}{\int }_0^{\infty }{e}^{n{g}_1(\theta )}d\theta$$

where $g_1(\theta )=-(1/n)[\omega \theta +{\displaystyle \frac{(s+\beta )}{\theta }}+(n+\alpha +1)ln(\theta )]$. It can be shown that $g_1(\theta )$ has its global maximum at

$$k_1={\displaystyle \frac{-(n+\alpha +1)+\sqrt{{(n+\alpha +1)}^2+4\omega (s+\beta )}}{2\omega }}.$$

From (2), an approximate expression for the posterior mfg under the gamma prior for $\theta$, after many algebraic manipulations, can be written as

$$M_{\theta }(-\omega )\simeq {\displaystyle \frac{\sqrt{\frac{2\pi }{n}}{(s+\beta )}^{n+\alpha }{k}_1^{-(n+\alpha +1)}{e}^{-\omega k_1-(s+\beta )/k_1}}{\sqrt{\frac{(n+\alpha +1)k_1+2(s+\beta )}{n{k}_1^3}}\Gamma (n+\alpha )}},$$

(6)

As a result, the Bayes estimator is ${\widehat{\theta }}_{Bayes(g)}={\displaystyle \frac{-\ln \left[M_{\theta }(-\omega )\right]}{\omega }}$.

2.2. Bayes Estimator Using Jeffreys Prior

Often, the true values of hyperparameters for a prior distribution are unknown to practitioners, or they are difficult to guess based on the behavior of the parameter of interest. Sometimes, even the prior distribution itself cannot be guessed. In this section, the Jeffreys prior is considered to obtain a closed expression for the Bayes estimator. Using a sample $\underline{x}=(x_1,x_2,\dots ,x_n)$ from an Exponential($\lambda$) distribution, the likelihood function $L(\lambda ;\underline{x})={\lambda }^n{e}^{-\lambda s}$, and the Jeffreys prior

$${\nu }_2(\lambda )\propto \sqrt{I(\lambda )}=\lambda ,$$

where $I(\lambda )$ is the Fisher information. The posterior pdf for $\lambda$ is expressed as

$${\nu }_2(\lambda ;\underline{x})={\displaystyle \frac{s^{n+2}{\lambda }^{n+1}{e}^{-\lambda s}}{\Gamma (n+2)}},$$

(7)

which is the pdf of gamma($n+2,s$). From (7), the posterior pdf for $\theta ={\displaystyle \frac{1}{\lambda }}$ (the main parameter of interest) reduces to

$${\nu }_2(\theta ;\underline{x})={\displaystyle \frac{s^{n+2}{\theta }^{-(n+3)}{e}^{-s/\theta }}{\Gamma (n+2)}}.$$

As a result, the mgf for $\theta$ in this case is

$$M_{\theta }(-\omega )={\displaystyle \frac{2{(s\omega )}^{0.5(n+2)}{K}_{n+2}(\sqrt{4\omega s})}{\Gamma (n+2)}}$$

and can be approximated with

$${\displaystyle \frac{s^{n+2}}{\Gamma (n+2)}}{\int }_0^{\infty }{e}^{n{g}_2(\theta )}d\theta ,$$

(8)

where

$$g_2(\theta )=(-1/n)[\omega \theta +(n+3)ln(\theta )+s/\theta ],$$

with the global maximum $k_2={\displaystyle \frac{-(n+3)+\sqrt{{(n+3)}^2+4\omega s}}{2\omega }}$. From (2) and (8), the mgf simplifies to

$$M_{\theta }(-\omega )\simeq {\displaystyle \frac{\sqrt{2\pi k_2^3}{s}^{n+2}{k}_2^{-(n+3)}{e}^{-\omega k_2-s/k_2}}{\sqrt{(n+3)k_2-2s}\Gamma (n+2)}}$$

(9)

and then we compute ${\widehat{\theta }}_{Bayes(J)}={\displaystyle \frac{-\ln \left[M_{\theta }(-\omega )\right]}{\omega }}$.

2.3. Simulation Results for HPP

This section summarizes the simulation results to assess the accuracy of the estimators obtained in Section 2.1 and Section 2.2. It is worth mentioning that the mgf, $M_{\theta }(\omega ),\omega >0$, for the inverse-gamma distribution is not defined; however, for $\omega >0,M_{\theta }(-\omega )$ is defined. This is the main reason that in Table 1, Table 2 and Table 3 (Section 2.3), only a few selected positive values of $\omega$ are considered. Therefore, with this limitation, we are considering the cases where the loss function is asymmetric, with overestimation being more severe than underestimation. For example, in the design of a safety-critical system, overestimating might result in unnecessary maintenance. For selected values of input variables $w,n,\alpha$, and $\beta =\theta (\alpha -1)$ (see the discussion on choosing the hyperparameter values in Section 2.1), the simulation code generates N = 2000 samples from the Exponential distribution with the parameter $\lambda$. For every sample of size n, the approximate values of $-ln\left[M_{(\theta )}(-w)\right]/w$ using (6) and (9) are found. The code also computes the ML estimate of $\theta$. For each set of N simulated samples, the average of the estimates and the SASE, $\xi =\sqrt{{\displaystyle \frac{{\sum }_{i=1}^N{({\widehat{\theta }}_i-\theta )}^2}{N}}}$ are computed. The reason for using SASE as opposed to ASE, ${\sum }_{i=1}^N{\displaystyle \frac{{({\widehat{\theta }}_i-\theta )}^2}{N}}$, is that SASE resembles the standard deviation of a random variable, which is commonly used to compare variability. However, having SASE, one can obtain ASE based on SASE and vice versa. 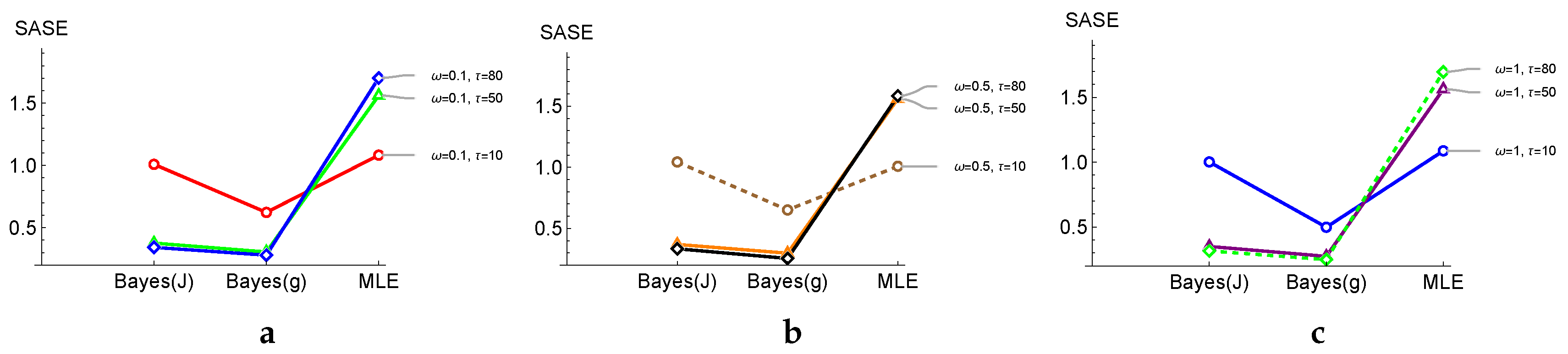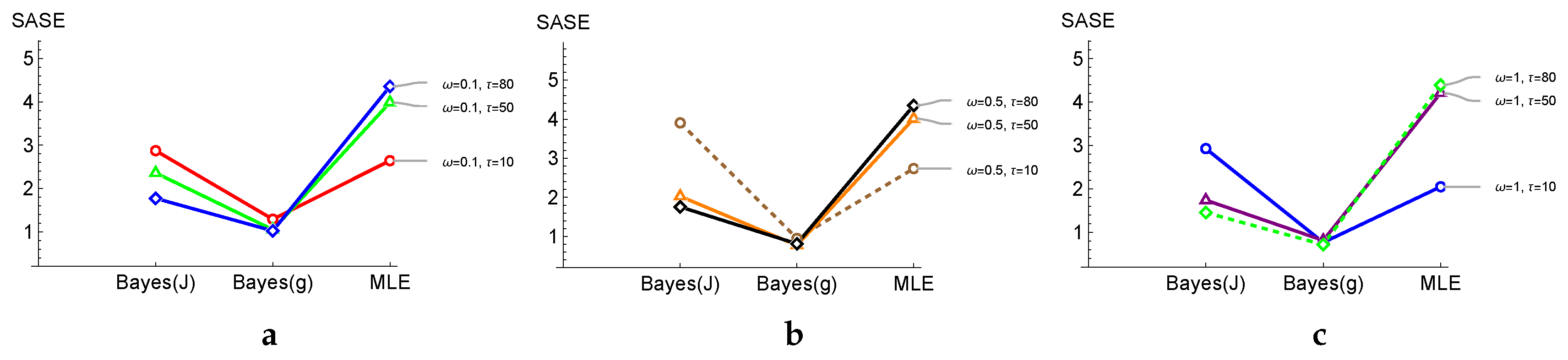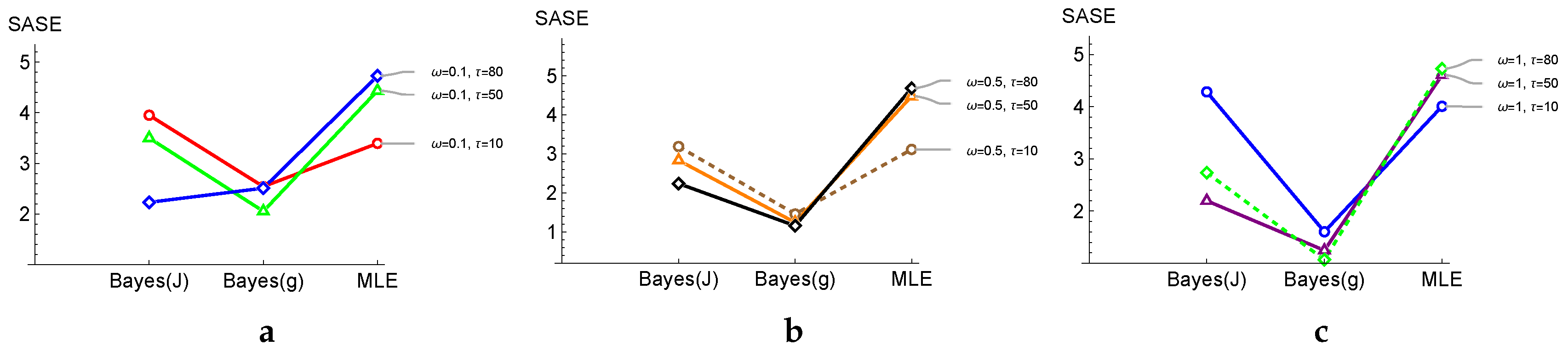Table 1 lists the averages and values of $\xi$ in parentheses. ${\widehat{\theta }}_{Bayes(g)}$ and ${\widehat{\theta }}_{Bayes(J)}$ denote Bayes estimates under gamma and Jeffreys priors, respectively. Table 1 reveals that as n increases, SASE decreases for all three estimators, regardless of the selected values for $\alpha ,\lambda ,n$, and $\omega$. ${\widehat{\theta }}_{Bayes(g)}$ outperforms ${\widehat{\theta }}_{Bayes(J)}$ with respect to their accuracy, as SASE for ${\widehat{\theta }}_{Bayes(g)}$ in boldface is smaller. Also, ${\widehat{\theta }}_{Bayes(J)}$ outperforms the MLE ${\widehat{\theta }}_{mle}={\displaystyle \frac{1}{s}}$, where $s={\sum }_{i=1}^n{x}_i$.

It is worth mentioning that $\theta ={\displaystyle \frac{1}{\lambda }}$ is the rate of occurrence of events under HPP, and that the estimator of $\theta$ is of primary interest, not $\lambda$. Note that MLEs of $\theta$ and $\lambda$ are functionally related. Although selected values of $\lambda$ are shown in the first row of Table 1, Table 2 and Table 3, the mean and SASE for ${\widehat{\theta }}_{mle}$, ${\widehat{\theta }}_{Baye{s}_{(}g)}$, and ${\widehat{\theta }}_{Bayes(J)}$ are provided in the main body of the tables. The SASE numbers in boldface in Table 1, Table 2 and Table 3 represent the smallest SASE values for selected values of the parameter $\omega$ of the LINEX loss, n, $\lambda$, and $\alpha$.

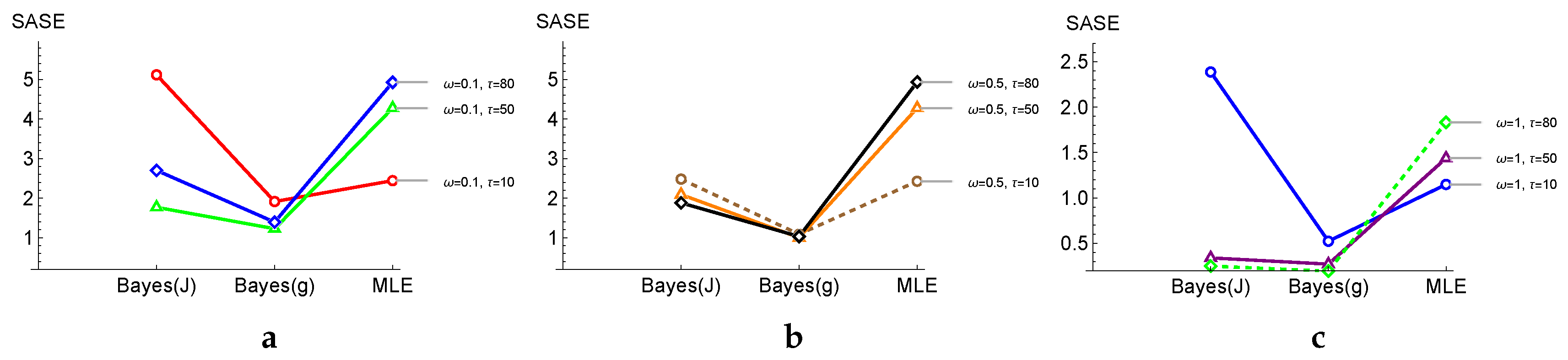
Table 3 lists four different selections for the parameters ($\alpha ,\lambda$). For each selection, two values for $\beta$ are listed. For instance, in the first row of the first selection, $(\alpha =5,\beta =3,\lambda =5)$, $\beta$ is not derived using the relation $\beta =\theta (\alpha -1)$. In contrast, in the second row, $(\alpha =5,\beta =0.8,\lambda =5)$ follows the relation as described in Section 2.1 for the hyperparameter $\beta$. We observe that with the second option, the estimator ${\widehat{\theta }}_{Bayes(g)}$, for all four cases, produces the smallest SASE. However, when the hyperparameters are selected arbitrarily, as in the first row for each case, the estimator ${\widehat{\theta }}_{Bayes(J)}$ has a slightly smaller or the same SASE value as the MLE, and ${\widehat{\theta }}_{Bayes(g)}$ is no longer the best estimator. This confirms that the selection of the hyperparameter value, as proposed, is important.

3. Non-Homogeneous Poisson Process (NHPP)

This section considers the NHPP with the PL intensity function. As mentioned earlier, the PL intensity function has many practical applications, such as in repairable systems.

3.1. Expected Time of Next Arrival After a Truncated Time

A few results by the author from [12] are used in this section.

Let $\{N(t),t\ge 0\}$ be an NHPP with an intensity function $\lambda (t)$ and mean-value function $E\left[N(\tau )\right]=\Lambda (\tau )={\int }_0^{\tau }\lambda (t)dt$, where $\tau$ is a predetermined truncated time; it can be shown that

$$E\left[S_{N(\tau )+1}\right]=e^{\Lambda (\tau )}{\int }_{\tau }^{\infty }t\lambda (t)e^{-\Lambda (v)}dt.$$

For a sequence of successive arrival (event) times $t_1<t_2,<\dots <t_n<\tau$, where $t_i$ is the ith event time, using the time-truncation sampling scheme, the log-likelihood function reduces to

$$l(t_1,\dots ,t_n,T)=e^{-\Lambda (t_n)}({\Pi }_{i=1}^n\lambda (t_i))\left\{e^{-[\Lambda (T)-\Lambda (t_n)]}\right\}=e^{-\Lambda (T)}{\Pi }_{i=1}^n\lambda (t_i),$$

And based on the PL mean-value function

$$\Lambda (\tau )=E\left[N(\tau )\right]={({\displaystyle \frac{\tau }{\theta }})}^{\beta },$$

the MLEs of the parameters are obtained as $\widehat{\beta }={\displaystyle \frac{n}{{\sum }_{i=1}^n\ln (\tau /t_i)}},\widehat{\theta }={\displaystyle \frac{\tau }{n^{1/\widehat{\beta }}}}.$

Letting $L=\Lambda (\tau )$ and using the following gamma priors for L and $\beta$:

$$\pi (L)=b^{-a}{L}^{a-1}{e}^{-L/b}/\Gamma (a),L>0,a>0,b>0,$$

$$\pi (\beta )=d^{-c}{\beta }^{c-1}{e}^{-\beta /d}/\Gamma (c),\beta >0,c>0,d>0,$$

the joint posterior pdf of ($L,\beta$) conditional on $\underline{t}$ and $\tau$ reduces to

$$\pi (L,\beta |\underline{t},\tau )\propto \Gamma \left(\beta |n+c,D\right)\Gamma (L|n+a,{\displaystyle \frac{b}{1+b}}),$$

(10)

where $D={\displaystyle \frac{d}{1+d{\sum }_{i=1}^n\ln (\tau /t_i)}}$ and $\Gamma (X|A,B)$ is the pdf of the gamma random variable X with parameters A and B. The form of $\pi (L,\beta |\underline{t},\tau )$ implies that, conditional on ($\underline{t}$ and $\tau$), $\beta$ and L are independent. It is noted in simulation studies that the hyperparameter d should be selected carefully so that D in the posterior pdf $\Gamma \left(\beta |n+c,D\right)$ is not a negative number. In general, small values less than 1 for the d do not cause any issues.

Consider a non-informative joint prior $\pi (\theta ,\beta )\propto {(\theta \beta )}^{-1}$, which has also been used by [12]. Based on the likelihood function, the non-informative prior, and $\widehat{\beta }={\displaystyle \frac{n}{{\sum }_{i=1}^n\ln (\tau /t_i)}}$, it is shown that the posterior pdf reduces to

$$\pi (L,\beta *|\underline{t},\tau )\propto {\displaystyle \frac{{(\beta *)}^{(\frac{p}{2}-1)}{e}^{-0.5\beta *}}{2^{\frac{p}{2}}\Gamma (\frac{p}{2})}}\times {\displaystyle \frac{e^{-L}{L}^{n-1}}{\Gamma (n)}},$$

(11)

The first term in the product on the right-hand side of (11) is the pdf of a scaled Chi-squared random variable $\beta *=({\displaystyle \frac{2n}{\widehat{\beta }}})\beta$ with $p=2(n-1)$ degrees of freedom, and the second term is the pdf of $\mathrm{gamma}(n,1)$. Therefore, the joint posterior is proportional to the product of the marginal posterior of L and $\beta *$. As a result, conditional on $\underline{t}$ and $\tau$, it is concluded that $\beta *$ and L are independent.

3.2. LINEX-Based Estimator of M via Gamma and Non-Informative Priors

We first consider an informative estimator for M using gamma priors. Recall (10), and the fact that conditional on $(t_1,t_2,\dots ,t_n,\tau )$, the variables $L,\beta$ are independent. The LINEX estimator is defined as

$${\widehat{M}}_{\mathrm{Bayes}(\mathrm{g})}=-{\displaystyle \frac{\ln \left[E_M(e^{-\omega M})\right]}{\omega }}.$$

And it can be shown that under the PL intensity function, we get

$$M=E\left[S_{N(\tau )+1}\right]=\tau L^{-1/\beta }{e}^L\Gamma (1+1/\beta ,L),$$

However, $E_M(e^{-\omega M})$, which the above LINEX estimator depends on and is defined as

$$E_M(e^{-\omega M})={\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\omega M}\Gamma \left(\beta |n+c,D\right)\Gamma (L|n+a,{\displaystyle \frac{b}{1+b}})d(\beta )d(L).$$

(12)

is intractable to derive as a closed formula. However, given the hyperparameters $a,b,c,d$ and $n,D$, a numerical integration method via Mathematica evaluates its value for the selected values of $\tau$ and $\omega$.

• From (11), the Bayes estimator for M based on the non-informative prior is given by

$${\widehat{M}}_{\mathrm{Bayes}(\mathrm{non-info})}=-{\displaystyle \frac{\ln \left[E_M(e^{-\omega M})\right]}{\omega }}$$

$$E_M(e^{-\omega M})={\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\omega M}\Gamma (0.5p,2)\Gamma (L|n,1)d(\beta *)d(L).$$

(13)

Similar to (12), the double integral (13) can be evaluated by Mathematica using a numerical method.

3.3. Simulation Results for NHPP

The summary of simulation studies for the NHPP case is given in

Table 4. Mean and SASE of estimators of M.

$(\mathit{b}=1.2,\mathit{d}=1.2$  ${\mathit{\theta }}_{\mathit{t}}=0.5$  ${\mathit{\beta }}_{\mathit{t}}=0.8)$					$(\mathit{b}=0.6,\mathit{d}=0.4$  ${\mathit{\theta }}_{\mathit{t}}=0.9$  ${\mathit{\beta }}_{\mathit{t}}=0.7)$
$\mathit{\omega }$	$\mathit{\tau }$	${\overline{\widehat{\mathit{M}}}}_{\mathit{mle}}$	${\overline{\widehat{\mathit{M}}}}_{\mathit{Bayes}(\mathit{g})}$	${\overline{\widehat{\mathit{M}}}}_{\mathit{Bayes}(\mathit{J})}$	$\mathit{\omega }$	$\mathit{\tau }$	${\overline{\widehat{\mathit{M}}}}_{\mathit{mle}}$	${\overline{\widehat{\mathit{M}}}}_{\mathit{Bayes}(\mathit{g})}$	${\overline{\widehat{\mathit{M}}}}_{\mathit{Bayes}(\mathit{J})}$
0.10	10	11.315	11.455	10.086	0.10	10	13.877	13.858	10.447
		(1.0088)	(0.6228)	(1.0824)			(5.1169)	(1.9138)	(2.4429)
	50	51.567	51.606	50.017		50	54.646	54.739	50.121
		(0.3765)	(0.3053)	(1.5618)			(1.7685)	(1.2273)	(4.2771)
	80	81.773	81.785	80.888		80	85.446	85.344	80.101
		(0.3422)	(0.2795)	(1.7017)			(2.7012)	(1.3934)	(4.9298)
0.50	10	11.350	11.336	10.074	0.50	10	13.581	13.172	10.439
		(1.0439)	(0.6509)	(1.0083)			(2.4807)	(1.0874)	(2.4270)
	50	51.641	51.650	50.018		50	54.828	54.469	50.121
		(0.3694)	(0.2976)	(1.5615)			(2.0907)	(1.0026)	(4.2774)
	80	81.768	81.750	80.245		80	85.246	84.961	80.0943
		(0.3337)	(0.2547)	(1.5839)			(1.8805)	(1.0295)	(4.9362)
1	10	11.337	11.264	10.079	1	10	11.611	11.450	10.148
		(1.0020)	(0.4986)	(1.0875)			(2.3862)	(0.5235)	(1.1486)
	50	51.598	51.605	50.0168		50	51.527	51.541	50.025
		(0.3505)	(0.2742)	(1.5628)			(0.3403)	(0.2714)	(1.4379)
	80	81.719	81.722	80.262		80	81.572	81.575	80.542
		(0.3161)	(0.2490)	(1.6964)			(0.2500)	(0.1955)	(1.8310)

and

Table 5. Mean and SASE of estimators of M.

$(\mathit{b}=0.2,\mathit{d}=0.2$  ${\mathit{\theta }}_{\mathit{t}}=2.2$  ${\mathit{\beta }}_{\mathit{t}}=0.85)$					$(\mathit{b}=0.5,\mathit{d}=0.5$  ${\mathit{\theta }}_{\mathit{t}}=0.4$  ${\mathit{\beta }}_{\mathit{t}}=0.95)$
$\mathit{\omega }$	$\mathit{\tau }$	${\overline{\widehat{\mathit{M}}}}_{\mathit{mle}}$	${\overline{\widehat{\mathit{M}}}}_{\mathit{Bayes}(\mathit{g})}$	${\overline{\widehat{\mathit{M}}}}_{\mathit{Bayes}(\mathit{J})}$	$\mathit{\omega }$	$\mathit{\tau }$	${\overline{\widehat{\mathit{M}}}}_{\mathit{mle}}$	${\overline{\widehat{\mathit{M}}}}_{\mathit{Bayes}(\mathit{g})}$	${\overline{\widehat{\mathit{M}}}}_{\mathit{Bayes}(\mathit{J})}$
0.10	10	13.391	14.102	10.967	0.10	10	13.587	15.330	11.487
		(2.8732)	(1.2899)	(2.6422)			(3.9508)	(2.5415)	(3.3944)
	50	54.441	54.343	50.207		50	55.793	55.6147	50.371
		(2.3591)	(1.0487)	(3.9872)			(3.5006)	(2.0538)	(4.4365)
	80	84.909	84.833	80.116		80	85.383	85.389	80.177
		(1.7714)	(1.0220)	(4.3568)			(2.2302)	(2.5106)	(4.7285)
0.50	10	13.403	13.272	10.687	0.50	10	13.357	13.732	11.005
		(3.9052)	(0.9498)	(2.7362)			(3.1895)	(1.4584)	(3.1140)
	50	54.517	54.240	50.170		50	55.382	54.686	50.321
		(2.0258)	(0.7738)	(4.0143)			(2.8345)	(1.2416)	(4.4807)
	80	84.810	84.437	80.123		80	85.6450	84.948	80.222
		(1.7561)	(0.8112)	(4.3501)			(2.2392)	(1.1570)	(4.6845)
1	10	13.370	12.873	10.490	1	10	14.023	13.189	10.435
		(2.9280)	(0.7653)	(2.0492)			(4.2846)	(1.6032)	(4.0081)
	50	51.174	51.781	50.069		50	54.722	53.951	50.190
		(1.7411)	(0.8125)	(4.2098)			(2.1968)	(1.2457)	(4.6089)
	80	84.515	81.183	80.081		80	85.572	84.161	80.175
		(1.4550)	(0.7159)	(4.3922)			(2.7352)	(1.0682)	(4.7296)

. Recall that to obtain an accurate Bayes estimator via the gamma prior, in simulation studies, a relatively large value for b and a small value for d (see the discussion in Section 3.1) are selected. Then, values of a and c are found via

$$a={\displaystyle \frac{L_t}{b}}c={\displaystyle \frac{{\beta }_t}{d}}.$$

The selections ensure

$$E\left[L\right]=abE\left[\beta \right]=cd,$$

and that the variance of both prior distributions for L and $\beta$ is small. As a result, the Bayes estimator using the gamma priors becomes more accurate than the ML estimator and the Bayes estimator using the non-informative prior. In a practical case, where only a sample on the arrival times of an NHPP is available, MLEs $\widehat{\beta }$ and $\widehat{\theta }$ (see Section 3.1) are found, and the b and d values are selected, as discussed. Then, using $\widehat{L}={({\displaystyle \frac{\tau }{\widehat{\widehat{\theta }}}})}^{\widehat{\beta }}$, we find the hyperparameter values $a={\displaystyle \frac{\widehat{L}}{b}},c={\displaystyle \frac{\widehat{\beta }}{d}}$. Recall that a value for a truncated time $\tau$ is given in advance.

For the selected “true” values (${\theta }_t,{\beta }_t$), hyperparameters $(b,d)$, truncated time $\tau$, and the parameter of LINEX loss $\omega$, Table 4 and Table 5 provide simulation summaries. Recall that the hyperparameters $(a,c)$, as discussed earlier in this section, are selected based on $(b,d)$. The mean and SASE, inside parentheses, for the three estimators ML, Bayes(g), and Bayes(J) for M are listed in the tables. For each combination of the selected input variables (${\theta }_t,{\beta }_t,b,d,\omega ,\tau$), N = 300 samples are generated from the NHPP with the power-law intensity. Examination of the tables reveals that regardless of the value of $\omega$, as $\tau$ increases (note that this makes the sample size n increase), SASE for MLE and Bayes(g) decreases, while SASE for Bayes (J) increases. For all three selected values $\omega =(0.1,0.5,1.0)$, when $\tau =10$, Bayes(J) has a smaller SASE than ML, but Bayes(g) outperforms both estimators. For all selected values of $\omega$, and $\tau =50$ and 80, MLE has a smaller SASE than Bayes(J), and Bayes (g) outperforms both MLE and Bayes(J) in terms of accuracy. The boldface numbers in parentheses, in Table 4 and Table 5, represent the smallest SASE among the three estimators. We can see that ${\widehat{M}}_{Bayes(g)}$, for all selected input values, has the smallest SASE. For a better visual comparison, Figure 2 and Figure 3 use Table 3 and Figure 4, Figure 5 and Figure 6 use Table 4 to provide a graphical presentation of the SASE values. The graphs also confirm that ${\widehat{M}}_{Bayes(g)}$ outperforms MLE and ${\widehat{M}}_{Bayes(J)}$ in all cases with the smallest SASE value.

Table 6. Sensitivity analysis for the estimators using selected distributions for $\theta$ and $\beta$.

$\mathit{b}=0.6$			$\mathit{d}=0.4$			$\mathit{b}=0.6$			$\mathit{d}=0.4$
$\mathit{\beta }\sim \mathrm{Uniform}(0.5,0.9)$, $\mathit{\theta }\sim \mathrm{Uniform}(1,3)$						$\mathit{\beta }\sim \mathrm{Uniform}(0.5,0.9)$, $\mathit{\theta }\sim \mathrm{Exponential}(0.5)$
$\mathit{\omega }$	$\mathit{\tau }$	$\overline{{\mathit{M}}_{\mathit{t}}}$	${\widehat{\mathit{\theta }}}_{\mathit{mle}}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{g})}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{J})}$	$\mathit{\omega }$	$\mathit{\tau }$	$\overline{{\mathit{M}}_{\mathit{t}}}$	${\widehat{\mathit{\theta }}}_{\mathit{mle}}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{g})}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{J})}$
0.8	10	14.81	(6.09)	(3.21)	(6.31)	0.8	10	12.49	(2.36)	(0.77)	(2.59)
	30	37.43	(6.66)	(5.57)	(10.19)		30	39.15	(11.29)	(9.74)	(14.16)
0.2	10	15.63	(3.66)	(1.80)	(6.31)	0.2	10	18.41	(9.44)	(7.63)	(11.38)
	30	39.09	(7.90)	(4.39)	(9.72)		30	38.41	(12.44)	(3.07)	(8.57)
$\mathit{b}=\mathbf{0}.\mathbf{8}$			$\mathit{d}=\mathbf{0}.\mathbf{3}$			$\mathit{b}=\mathbf{0}.\mathbf{8}$			$\mathit{d}=\mathbf{0}.\mathbf{3}$
$\mathit{\beta }\sim \mathrm{Gamma}(10,0.08)$, $\mathit{\theta }\sim \mathrm{Uniform}(1,3)$						$\mathit{\beta }\sim \mathrm{Gamma}(10,0.08)$, $\mathit{\theta }\sim \mathrm{Exponential}(0.67)$
$\mathit{\omega }$	$\mathit{\tau }$	$\overline{{\mathit{M}}_{\mathit{t}}}$	${\widehat{\mathit{\theta }}}_{\mathit{mle}}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{g})}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{J})}$	$\mathit{\omega }$	$\mathit{\tau }$	$\overline{{\mathit{M}}_{\mathit{t}}}$	${\widehat{\mathit{\theta }}}_{\mathit{mle}}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{g})}$	${\widehat{\mathit{\theta }}}_{\mathit{Bayes}(\mathit{J})}$
0.8	10	17.29	(14.54)	(13.85)	(15.33)	0.8	10	14.39	(7.75)	(6.79)	(8.37)
	30	39.38	(16.72)	(12.89)	(15.90)		30	34.69	(3.96)	(3.42)	(7.28)
0.2	10	14.98	(5.81)	(3.80)	(7.35)	0.2	10	14.36	(4.79)	(3.03)	(6.09)
	30	37.10	(22.29)	(9.95)	(10.61)		30	41.34	(11.25)	(9.30)	(16.03)

provides a summary of the sensitivity analysis. Four combinations of distributions for the parameters of the PL intensity function under an NHPP are shown in the table. For each combination, 100 samples are generated from the distributions, and the SASEs of the three estimators for $M=E\left[S_{N(\tau )+1}\right]$ are listed in the table. The numbers in each row in boldface represent the smallest SASE. We note that ${\widehat{\theta }}_{Bayes(g)}$ has the smallest precision in all cases across the table. For each combination of the distributions, we also provide $\overline{M_t}$ that represents the average of the “true” values of M based on simulated values of $\theta$ and $\beta$.

4. Optimal Sample Size: A Minimax-Type Approach

In this section, an algorithm is proposed for determining the optimal value of n, given that an HPP or NHPP is intended to be observed for a specified time T. There are many optimal designs for finding $\tau$ and n in the Bayesian framework. For instance, [13] provides optimal designs for Bayesian estimation of an HPP rate $\lambda$ for a set of loss functions; however, LINEX loss was not considered. The article presents two sequential methods and a non-sequential method to find conditions for the optimal stopping time $\tau$ and n. The process involves a substantial number of computations. Ref. [14] considered an algorithm to determine the optimal stopping time of an HPP where the cost of observations grows linearly with $\tau$.

In this article, we approach the problem computationally and propose a minimax-type method. Suppose the process is intended to be observed for time T. We are interested in finding the sufficient/optimal number of events n before time T that meets the specified risk level. This would help avoid waiting for all events to occur by time T.

The steps for computing the optimal sample size are similar for HPP and NHPP cases. Code B (see the Supplementary Materials) provides the computation of the optimal sample size based on the gamma priors for the NHPP case using the PL intensity function. The following steps are implemented in Code B.

• Select a specialized percentage decrease threshold value $\delta$ for the risk. In Code B, we used 0.05. Select $\omega$, and the maximum intended time T, to observe the events. Choose values for the hyperparameters b and d. T must be large enough to ensure that at least the initial arrival times do not exceed T; otherwise, the value of the optimal n would not converge.
• Using the current arrival times $t_1,\dots ,t_n$, up to $t_n$, compute the MLEs $\widehat{\beta },\widehat{\theta }$, which are the parameters of the PL intensity function. These estimates, along with the hyperparameters a and c, must be updated (see Section 3.3) as more data become available.
• Compute the risks $R_g(n,a,b,c,d,T,\omega )$ and $R_g(n+1,a,b,c,d,T,\omega )$ using (17), Section 4.2. Note that to find the latter risk, MLEs, and the hyperparameters ($a,c$), values within the while loop must be updated.
• If ${\displaystyle \frac{R_g(n,a,b,c,d,T,\omega )-R_g(n+1,a,b,c,d,T,\omega )}{R_g(n,a,b,c,d,T,\omega )}}<\delta$, the latest value of n would be the optimal value based on the specifications; otherwise, in the while loop, increase the value of n by one, and repeat Steps 2–4. The code stops when the best value of n is identified.

4.1. The Case of HPP

Since $\{N(t),t\ge 0\}$ is an HPP with the rate $\lambda$, $P(N(T)=n)={\left({\displaystyle \frac{T}{\theta }}\right)}^n{e}^{-\left(\frac{T}{\theta }\right)}/n!$, and as a result, using (7), the posterior distribution of $\theta$ is given by

$${\nu }_1(\theta ;n)={\displaystyle \frac{{\theta }^{-(n+\alpha +1)}{e}^{-\frac{(T+\beta )}{\theta }{(\beta +T)}^{n+\alpha }}}{\Gamma (n+\alpha )}}$$

which is the pdf of the inverse-gamma $(n+\alpha ,\beta +T)$, with $E\left[\theta \right|n]={\displaystyle \frac{\beta +T}{n+\alpha -1}}$.

For an estimator $W(\underline{x})$ of a parameter $\theta$, based on data $\underline{x},$ the LINEX loss is

$$L(W(\underline{x})-\theta )=e^{\omega (W(\underline{x})-\theta )}-\omega (W(\underline{x})-\theta )-1.$$

The posterior risk of the estimator with respect to a posterior pdf $\pi (\theta |\underline{x})$ is defined as

$$R(W(\underline{x})|\underline{x})=e^{wW(\underline{x})}{\int }_{-\infty }^{\infty }{e}^{-w\theta }\pi (\theta |\underline{x})d\theta -wW(\underline{x})+w{\int }_{-\infty }^{\infty }\theta \pi (\theta |\underline{x})d\theta -1.$$

Using the above remark, it can be shown that the risk of the Bayes rule, ${\widehat{\theta }}_{Bayes(g)}={\displaystyle \frac{-\ln \left[M_{\theta }(-\omega )\right]}{\omega }}$, simplifies to

$$R_g(n,T,\alpha ,\beta )=\ln \left[M_{\theta }(-\omega )\right]+{\displaystyle \frac{\omega (\beta +T)}{n+\alpha -1}}$$

(14)

where

$$M_{\theta }(-\omega )={\displaystyle \frac{2{\left[(\beta +T)\omega \right]}^{0.5(n+\alpha )}{K}_{n+\alpha }(\sqrt{4\omega (\beta +T)})}{\Gamma (n+\alpha )}}.$$

For a given value of T, $R_g(n,T,\alpha ,\beta )$ is decreasing in n, with the limit approaching zero as n increases. Since the longest time that the process is to be observed is T, the optimal value for n is proposed to be the smallest n for which the percentage decrease in the risk is less than a specified threshold $\delta$. That is

$${\displaystyle \frac{R_g(n,T,\alpha ,\beta )-R_g(n+1,T,\alpha ,\beta )}{R_g(n,T,\alpha ,\beta )}}<\delta ,$$

(15)

where $\delta$ is a small number such as 0.05. The above criteria guarantee that increasing n to $n+1$ does not significantly reduce $Rg(n,T\alpha ,\beta )$. Computationally, it is easy to find the optimal value of n once $\alpha$, $\beta$, T, and $\delta$ are given. It can also be shown that for the Jeffreys prior, the risk of the Bayes rule can be expressed as

$$R_J(n,T)=\ln \left[M_{\theta }(-\omega )\right]+{\displaystyle \frac{\omega T}{n+1}}$$

where $M_{\theta }(-\omega )={\displaystyle \frac{2{(T\omega )}^{0.5(n+2)}{K}_{n+2}(\sqrt{4\omega T})}{\Gamma (n+2)}}.$ For this case, the optimal value of n can also be obtained using the same criterion as in (15).

Given a data set $x_1,\dots ,x_N$ from Exponential$(\lambda )$, the Mathematica code (A), based on the gamma prior, uses a while loop to find the optimal value for n. We only provide the code for the gamma prior case, as ${\mathrm{Bayes}}_{(g)}$ outperforms the ${\mathrm{Bayes}}_{(J)}$ estimator regarding accuracy (see Table 1 and Table 2). Note that the values for $\alpha ,\delta ,T,$ and $\omega$ should be selected by a user, and that T must be large enough so that ${\sum }_{k=1}^j{x}_k<T$ for any values of j in the loop, while the condition (15) is being checked. It is worth noting that the computations for the risks in (15) are sequential. That is, the MLE $\widehat{\theta }$ is updated as $x_j$ is added to the sample $x_1,\dots ,x_j$ in the While loop. As a result, the risks in (15) are updated in the loop.

Table 7. Optimal n for HPP with $\delta =0.01,0.05$.

$\mathit{\lambda }$	$\mathit{\alpha }$	$\mathit{\omega }$	$\mathit{\delta }$	n	$\mathit{\lambda }$	$\mathit{\alpha }$	$\mathit{\omega }$	$\mathit{\delta }$	n
0.4	2	0.02	0.01	118.5	20	2	0.02	0.01	99.6
		0.02	0.05	20.3			0.02	0.05	19.0
		0.4	0.01	120.4			0.4	0.01	99.6
		0.4	0.05	20.4			0.4	0.05	19.0
		1	0.01	121.7			1	0.01	99.5
		1	0.05	20.4			1	0.05	19.0
0.2	5	0.02	0.01	114.5	20	5	0.02	0.01	96.7
		0.02	0.05	17.2			0.02	0.05	16.0
		0.4	0.01	115.8			0.4	0.01	96.5
		0.4	0.05	17.3			0.4	0.05	16.0
		1	0.01	119.2			1	0.01	96.5
		1	0.05	17.3			1	0.05	16.0

provides simulation results for the average values of the optimal n for selected values of $\lambda ,\alpha ,\delta ,$ and $\omega$ for the gamma prior case.

Table 7 reveals that for the selected $\lambda ,\alpha$, and $\omega$, a smaller $\delta$ leads to a larger n, as expected. The optimal sample size is smaller for a larger value of the hyperparameter $\alpha$ (which provides a more accurate Bayes estimate; see Section 2.3). Also, for any selected values of $\lambda ,\alpha$, and $\delta$, the three values of $\omega$ provide almost similar optimal sample sizes.

4.2. The Case of NHPP

Recall that the gamma-based and non-informative-based Bayes estimators are numerically computed using (12) and (13). Based on the LINEX loss, like in Section 4.1, the risk of the Bayes rule under LINEX loss can be written as

$$\ln \left[E_M(e^{-\omega M})\right]+\omega E\left[M\right].$$

(16)

The expected values in (16), for both gamma and non-informative prior cases, are based on the corresponding posterior distributions (10) and (11). Therefore, the risks based on gamma and non-informative priors, respectively, can be computed via

$$\begin{gathered} R_g(n,a,b,c,d,T,\omega )=\ln [{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\omega M}\Gamma \left(\beta |n+c,D\right)\Gamma (L|n+a,{\displaystyle \frac{b}{1+b}})d(\beta )d(L)] \\ +\omega {\int }_0^{\infty }{\int }_0^{\infty }M\Gamma \left(\beta |n+c,D\right)\Gamma (L|n+a,{\displaystyle \frac{b}{1+b}})d(\beta )d(L). \end{gathered}$$

(17)

$$\begin{gathered} R_{\mathrm{Non-info}}(n,T,\omega )=\ln [{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\omega M}\Gamma (0.5p,2)\Gamma (L|n,1)d(\beta *)d(L)] \\ +\omega {\int }_0^{\infty }{\int }_0^{\infty }M\Gamma (0.5p,2)\Gamma (L|n,1)d(\beta *)d(L). \end{gathered}$$

(18)

Given a data set $t_1,\dots ,t_N$ on arrival times from the NHPP with the power-law intensity, the Mathematica code (B) uses a while loop to find the optimal value for n. We only provide the code for the gamma prior case, as ${\mathrm{Bayes}}_{(g)}$ outperforms the ${\mathrm{Bayes}}_{(non-info)}$ estimator regarding accuracy (see Table 4 and Table 5). As in Section 4.1, we are interested in the smallest values of n for which

$${\displaystyle \frac{R_g(n,a,b,c,d,T,\omega )-R_g(n+1,a,b,c,d,T,\omega )}{R_g(n,a,b,c,d,T,\omega )}}<\delta .$$

(19)

A user should select the values for the hyperparameters b and d, and T must be large enough so that for the sum of interarrival times, we have ${\sum }_{k=0}^j(t_{k+1}-t_k)<T$. That is, $t_j<T$, with $t_0=0$. This should be true for any value of j in the loop while condition (19) is being checked. It is worth noting that the computations for the risks in (19) are sequential. That is, the MLEs

$$\widehat{\beta }={\displaystyle \frac{j}{{\sum }_{k=1}^j\ln (T/t_k)}},\widehat{\theta }={\displaystyle \frac{T}{j^{1/\widehat{\beta }}}},$$

from Section 3.1 are updated as $t_j$ is added to the sample $t_1,\dots ,t_j$ in the while loop. As a result, the risks in (19) are updated in the loop. As mentioned in Section 3.3, to get a more accurate Bayes_(g), using the data-driven approach, a large value for hyperparameter b and a small value for d (to ensure that D in $\Gamma \left(\beta |n+c,D\right)$ is not a negative number) are selected, and then the hyperparameters c and d are found using the MLEs. That is,

$$a=({\displaystyle \frac{1}{b}}){({\displaystyle \frac{T}{\widehat{\theta }}})}^{\widehat{\beta }}c={\displaystyle \frac{\widehat{\beta }}{d}}.$$

It is noted that the second double integral on the far right in (17) cannot be computed via a numerical integration method in Mathematica. Therefore, we use the Monte Carlo method to simulate $m=5000$ independent samples from $\Gamma \left(\beta |j+c,D\right)$ and $\Gamma (L|j+a,{\displaystyle \frac{b}{1+b}})$ for each iteration based on the sample size j in the loop to approximate the second integral.

Table 8. Optimal n for NHPP with $\delta =0.05$.

$\mathit{\theta }$	$\mathit{\beta }$	b	d	w	n	$\mathit{\theta }$	$\mathit{\beta }$	b	d	w	n
1.2	0.8	2	0.2	0.02	19.8	0.8	0.7	3	0.8	0.02	21.2
				0.4	28.3					0.4	37.8
				1.0	14.1					1.0	15.1
1.2	0.8	2	0.6	0.02	19.6	0.8	0.7	3	0.8	0.02	30.3
				0.4	35.7					0.4	37.8
				1.0	15.8					1.0	15.1
1.2	0.8	2	1.2	0.02	19.3	0.8	0.7	4	0.6	0.02	20.6
				0.4	31.7					0.4	38.3
				1.0	13.2					1.0	18.6
1.2	0.8	2	0.1	0.02	19.8	0.8	0.95	4	0.6	0.02	17.0
				0.4	35.9					0.4	36.0
				1.0	15.7					1.0	13.7
0.8	0.7	4	0.4	0.02	22.7	5	1.5	8	0.5	0.02	16.3
				0.4	35.6					0.4	33.6
				1.0	17.8					1.0	10.7
5	1.5	8	0.8	0.02	17.6	1.5	0.5	8	0.5	0.02	23.3
				0.4	32.6					0.4	39.0
				1.0	10.2					1.0	18.9

provides simulation results for the average values of the optimal n for selected values of $b,d,\delta$, and $\omega$ based on (19).

From a practical perspective, when performing data analysis, one must select an appropriate value for $\omega$ that matches the specific application. Several options are available, some of which are discussed in the literature but are not covered in this article.

• $\omega$ can be modeled as a random variable with a probability distribution. In this case, the Bayes estimator is obtained by taking the expected value of the LINEX-based estimator; see [8]. Therefore, with this approach, a specific value for $\omega$ is not chosen.
• A cost function depending on $\omega$ can be incorporated with the LINEX loss function, and the value of $\omega$ that minimizes this cost function is selected.

For this article, as previously noted, negative values of $\omega$ make it computationally impossible to provide Bayes estimates of the expected arrival past a truncated time for the HPP and NHPP cases. We considered only selected positive values in all tables. Due to this limitation, the proposed methods are applicable when overestimating the expected arrival beyond a truncated time is more critical than underestimating. We suggest selecting several potential values of ${\omega }_1,{\omega }_2,\dots ,{\omega }_k$ where the choices can be based on previous similar applications, if available. For ${\omega }_j,j=1,2,\dots ,k$, compute risks (14) and (17) for HPP and NHPP cases, respectively, using the informative priors (which, as shown by simulations, are more accurate than non-informative priors) and then choose the $\omega$ that yields the smallest risk value.

5. Numerical Example

The following data represents the arrival of 31 events. The data is generated from an NHPP. The purpose of this example is to provide computational steps for the goodness-of-fit of the data to the NHPP, using the MLEs of the parameters for the NHPP under the PL intensity to determine the appropriate values (see Section 4.2) for the hyperparameters $a,b,c,d$, and find the optimal sample size.

t = {0.10, 0.30, 1.05, 1.40, 1.94, 4.55, 5.60, 6.39, 16.87, 18.52, 23.74, 23.92, 27.27, 33.24, 34.17, 42.67, 43.49, 43.94, 44.44, 49.19, 63.13, 71.07, 78.60, 84.15, 85.02, 87.32, 89.98, 90.86, 102.44, 106.18, 117.6}

• where $\tau$ = 200; ref. [15] considered the Laplace statistic (LS)

$$S_n=\sqrt{{\displaystyle \frac{12}{n}}}\sum _{i=1}^n\left({\displaystyle \frac{\Lambda (t_i,\widehat{\beta })}{\Lambda (\tau ,\widehat{\beta })}}-0.5\right)$$

to assess the goodness-of-fit of an NHPP for several intensity functions, including power-law intensity. $\Lambda (t_i,\widehat{\beta })$ denotes the mean-value function evaluated at time $t_i$. The test statistic rejects an NHPP if

$$|S_n|>z_{\alpha /2}\sqrt{\nu (\widehat{\beta })},$$

where

$$\nu (\beta )=1-12{\beta }^2{\tau }^{-2\beta }{\left(0.5{\tau }^{\beta }\ln (\tau )-{\displaystyle \frac{{\tau }^{\beta }(-1+2\beta \ln (\tau )}{4\beta }}\right)}^2=0.25.$$

Based on the above data, the MLE for $\beta$ is $\widehat{\beta }=0.436625$, and $S_n=-0.823817$. Note that the estimated value of the parameter $\theta$ is not involved in the test statistic. Since

$$|S_n|\ngtr z_{\alpha /2}\sqrt{{\displaystyle \frac{1}{4}}}=1.96/2=0.98,$$

the null hypothesis that t is from the NHPP with the PL intensity is not rejected at the 0.05 significance level. Using $b=4$ and $d=0.4$ for the hyperparameters (see Section 4.2 for the selection of hyperparameters a and c) and $T=200$, the optimal sample sizes based on $\delta =0.05$ and $\delta =0.01$, respectively, are $n=20$ and $n=24$, via the Mathematica Code B.

6. Summary

This article presents a computational method for estimating the expected arrival time of an event beyond a truncated time under the HPP and NHPP models. Two priors are proposed for the HPP case. The gamma prior outperforms the Jeffreys prior in accuracy. For the NHPP case, the power-law intensity function is utilized. Simulations indicate that using gamma priors for the parameters of the intensity function results in more accurate estimates than the non-informative prior discussed in the article. Calculating Bayes estimates for the NHPP case involves a numerical integration method implemented in Mathematica. Given the maximum observation time T for HPP or NHPP, as data points collected in real time, it may be useful to determine the optimal sample size so that the percentage reduction in risk, as a function of sample size, meets a specific threshold. We propose a minmax-type approach to identify this optimal sample size. A sensitivity analysis for the NHHP case confirms that the Bayes estimator based on an informative prior is more precise than the MLE and the Bayes estimator based on the Jeffreys prior. Codes A and B in Supplementary Materials provide the optimal sample sizes for the HPP and NHPP cases.