Predictive Framework for Regional Patent Output Using Digital Economic Indicators: A Stacked Machine Learning and Geospatial Ensemble to Address R&D Disparities
Abstract
1. Introduction
- (1)
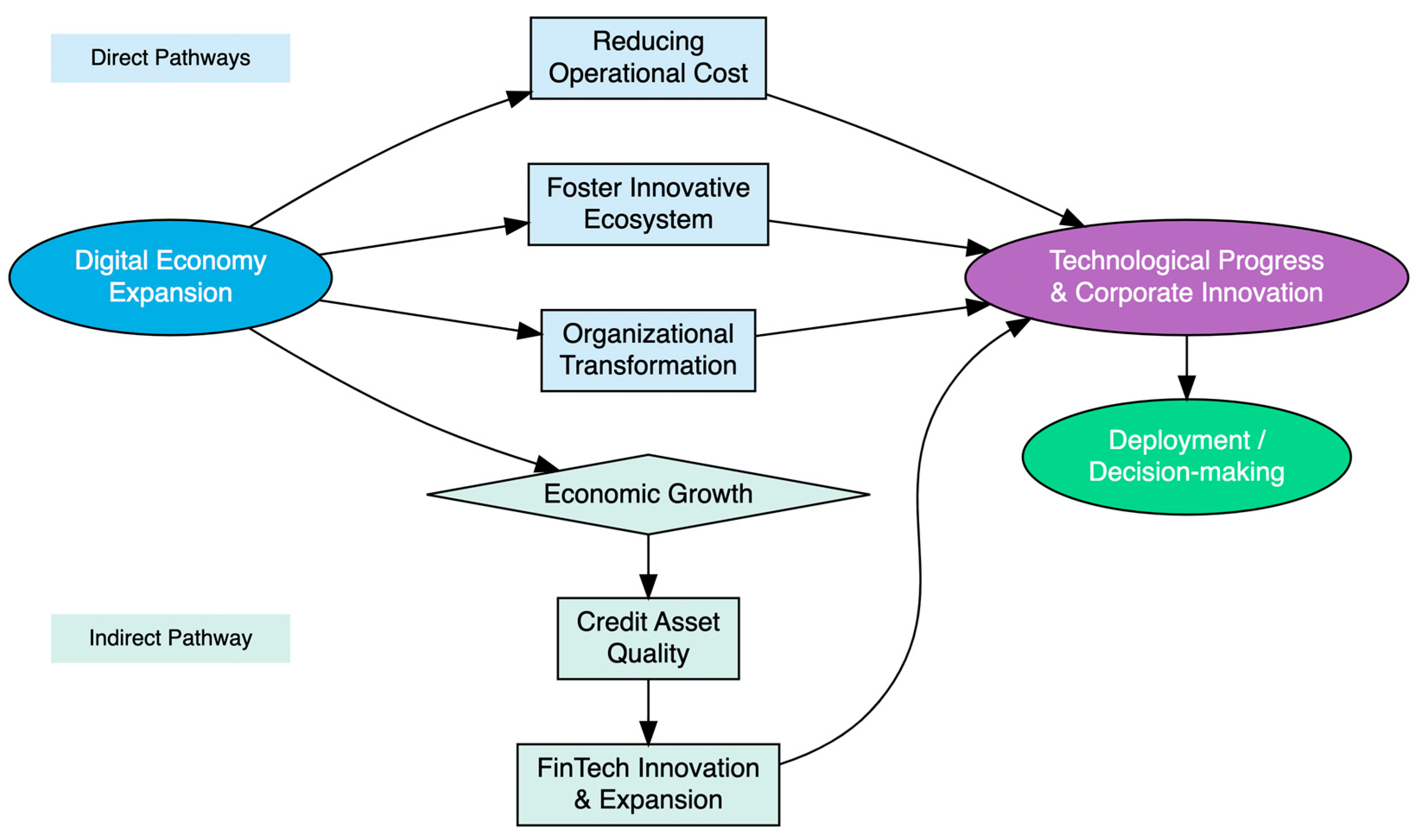
- This study introduces a novel hybrid framework that evaluates spatial autocorrelation measures in parallel with ML modeling and uses the resulting spatial insights to guide the potential embedding of spatial features into the ML algorithms. This dual-track approach serves two distinct purposes: first, spatial insights provide explicit regional decision-making guidance that complements and runs alongside ML results, helping to contextualize predictions within broader spatial patterns; and second, they enhance the robustness and accuracy of the ML models themselves by informing the modeling process and allowing for more realistic predictions that account for the regional interdependencies and spatial dynamics of innovation activity.
- (2)
- By conducting spatial analysis separately but in close dialogue with ML modeling, this study presents an innovative and replicable framework for applying machine learning to geospatial data. This framework not only improves predictive accuracy and robustness but also produces richer, spatially informed policy insights that can be integrated with the machine learning results. It holds significant promise for adaptation to other domains where geographic context is critical, thereby advancing the frontier of machine learning applications for spatially structured data in decision making, especially in the context of regional development and policy design.
- (3)
- Finally, this section situates this study within the context of emerging research from 2023 to 2024 on innovation and development. Unlike much of the current literature that relies on spatial analysis and traditional statistical methods, this work makes a distinctive contribution by explicitly integrating spatial thinking with ensemble machine learning techniques. The resulting framework offers more direct, actionable, and monitorable insights that can effectively support targeted regional innovation policies and inform strategies for high-quality regional development through spatially aware predictive monitoring.
2. Literature Review
2.1. The Role of the Digital Economy in Enhancing Corporate R&D
2.2. The Role of FinTech in Advancing R&D Investment
2.3. Synergies Between Digital Economy and FinTech in Advancing R&D
3. Materials and Methods
3.1. Variables Selection and Data Processing
3.2. Spatial Relationship of Variables
3.3. Machine Learning Models for R&D Prediction
3.3.1. Support Vector Machine (SVM)
3.3.2. Extreme Learning Machine (ELM)
3.3.3. Random Forest (RF)
3.3.4. XGBoost
3.4. Stacking Ensemble
3.5. Model Training and Validation
3.6. Testing and Performance Evaluation
4. Results
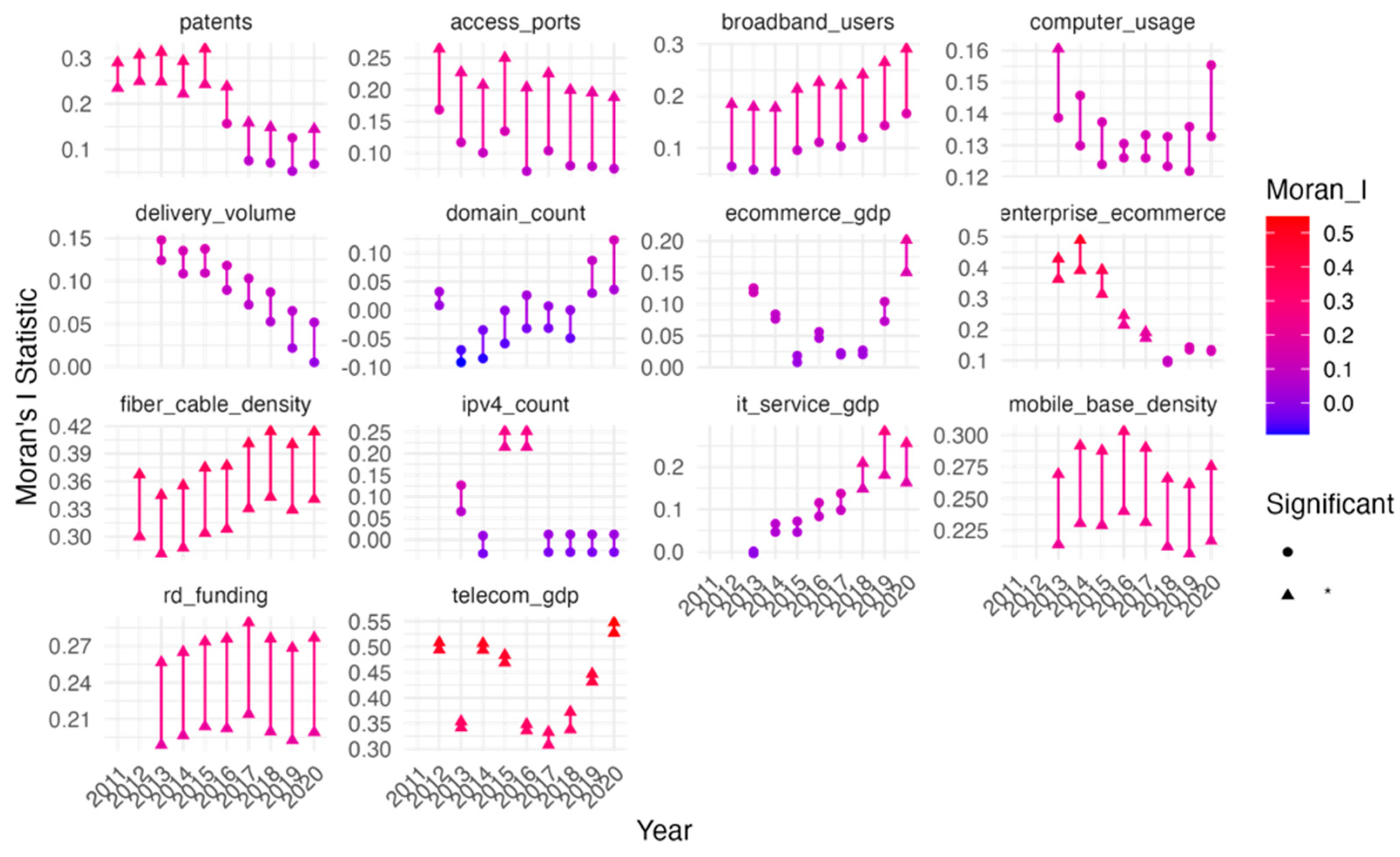
4.1. Spatial Correlation Analysis
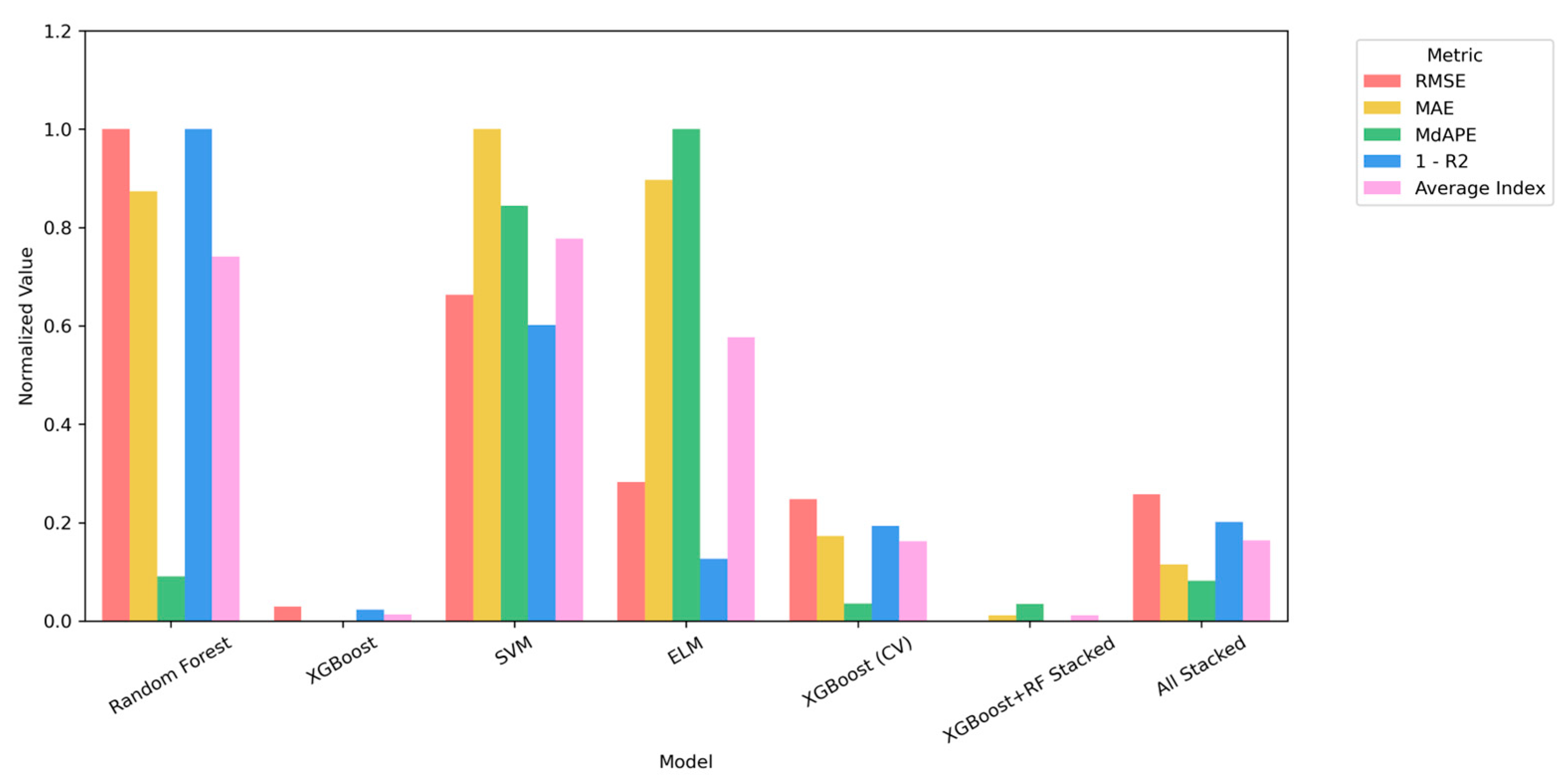
4.2. Machine Learning Outcomes
4.2.1. Model Parameters
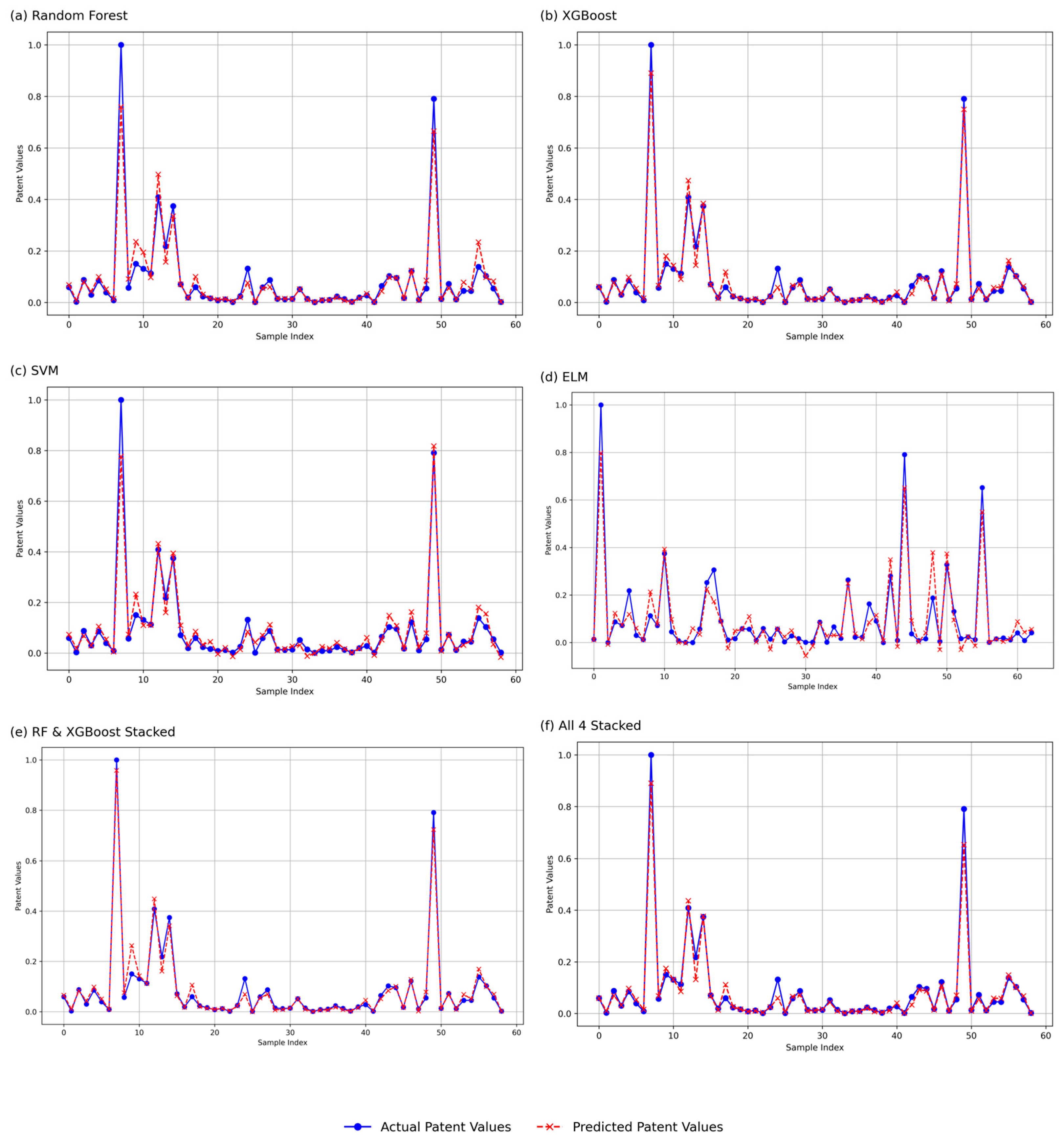
4.2.2. Empirical Prediction Results
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Weight Type | Moran’s Mean | Moran’s p-Value | Moran’s Significant Years | Moran’s Total Years | Moran’s Proportion Significant | Geary’s Mean | Geary’s p-Value | Geary’s Significant Years | Geary’s Total Years | Geary’s Proportion Significant |
|---|---|---|---|---|---|---|---|---|---|---|---|
| access_ports | Binary | 0.211909 | 2.70 × 10−2 | 8 | 8 | 1 | 0.792435 | 0.103647 | 1 | 8 | 0.125 |
| access_ports | Row-standardized | 0.095211 | 1.73 × 10−1 | 0 | 8 | 0 | 0.943141 | 0.348676 | 0 | 8 | 0 |
| broadband_users | Binary | 0.226952 | 2.26 × 10−2 | 8 | 8 | 1 | 0.778581 | 0.093397 | 1 | 8 | 0.125 |
| broadband_users | Row-standardized | 0.106632 | 1.57 × 10−1 | 0 | 8 | 0 | 0.934157 | 0.330132 | 0 | 8 | 0 |
| computer_usage | Binary | 0.127828 | 7.62 × 10−2 | 0 | 8 | 0 | 0.566018 | 0.028701 | 8 | 8 | 1 |
| computer_usage | Row-standardized | 0.141443 | 7.30 × 10−2 | 1 | 8 | 0.125 | 0.695284 | 0.028113 | 8 | 8 | 1 |
| delivery_volume | Binary | 0.105563 | 1.09 × 10−1 | 0 | 8 | 0 | 0.752825 | 0.157597 | 0 | 8 | 0 |
| delivery_volume | Row-standardized | 0.072743 | 1.93 × 10−1 | 0 | 8 | 0 | 1.016883 | 0.537215 | 0 | 8 | 0 |
| domain_count | Binary | 0.017021 | 3.54 × 10−1 | 0 | 8 | 0 | 0.788724 | 0.213897 | 1 | 8 | 0.125 |
| domain_count | Row-standardized | −0.03557 | 5.12 × 10−1 | 0 | 8 | 0 | 0.975974 | 0.446764 | 0 | 8 | 0 |
| ecommerce_gdp | Binary | 0.064524 | 2.05 × 10−1 | 1 | 8 | 0.125 | 0.590345 | 0.048219 | 5 | 8 | 0.625 |
| ecommerce_gdp | Row-standardized | 0.079589 | 1.93 × 10−1 | 1 | 8 | 0.125 | 0.755151 | 0.078031 | 2 | 8 | 0.25 |
| enterprise_ecommerce | Binary | 0.227441 | 4.68 × 10−2 | 5 | 8 | 0.625 | 0.564358 | 0.020763 | 6 | 8 | 0.75 |
| enterprise_ecommerce | Row-standardized | 0.264951 | 4.86 × 10−2 | 5 | 8 | 0.625 | 0.640183 | 0.027061 | 6 | 8 | 0.75 |
| fiber_cable_density | Binary | 0.315709 | 1.11 × 10−5 | 8 | 8 | 1 | 0.339695 | 0.019099 | 8 | 8 | 1 |
| fiber_cable_density | Row-standardized | 0.385109 | 5.96 × 10−7 | 8 | 8 | 1 | 0.435242 | 0.00133 | 8 | 8 | 1 |
| ipv4_count | Binary | 0.085914 | 1.93 × 10−1 | 2 | 8 | 0.25 | 0.635364 | 0.095414 | 2 | 8 | 0.25 |
| ipv4_count | Row-standardized | 0.043446 | 3.34 × 10−1 | 2 | 8 | 0.25 | 0.885228 | 0.260824 | 0 | 8 | 0 |
| it_service_gdp | Binary | 0.096039 | 1.50 × 10−1 | 3 | 8 | 0.375 | 0.619787 | 0.066267 | 3 | 8 | 0.375 |
| it_service_gdp | Row-standardized | 0.141866 | 1.23 × 10−1 | 3 | 8 | 0.375 | 0.722599 | 0.072284 | 4 | 8 | 0.5 |
| mobile_base_density | Binary | 0.222615 | 4.16 × 10−3 | 8 | 8 | 1 | 0.41174 | 0.017976 | 8 | 8 | 1 |
| mobile_base_density | Row-standardized | 0.280395 | 1.11 × 10−3 | 8 | 8 | 1 | 0.532612 | 0.003765 | 8 | 8 | 1 |
| patents | Binary | 0.217555 | 2.51 × 10−2 | 7 | 8 | 0.875 | 0.736945 | 0.136887 | 1 | 8 | 0.125 |
| patents | Row-standardized | 0.141918 | 1.06 × 10−1 | 3 | 8 | 0.375 | 0.974252 | 0.445514 | 0 | 8 | 0 |
| rd_funding | Binary | 0.27263 | 5.11 × 10−3 | 8 | 8 | 1 | 0.744202 | 0.104182 | 0 | 8 | 0 |
| rd_funding | Row-standardized | 0.199609 | 3.31 × 10−2 | 8 | 8 | 1 | 0.869696 | 0.196437 | 0 | 8 | 0 |
| telecom_gdp | Binary | 0.412085 | 9.78 × 10−4 | 8 | 8 | 1 | 0.512501 | 0.002287 | 8 | 8 | 1 |
| telecom_gdp | Row-standardized | 0.417459 | 1.41 × 10−3 | 8 | 8 | 1 | 0.532877 | 0.00165 | 8 | 8 | 1 |
| Model | Tuning Applied | Base Models | Meta-Learner | Hyperparameters (Tuned/Applied) |
|---|---|---|---|---|
| XGBoost | Default | N/A | N/A | n_estimators = 100, max_depth = 6, learning_rate = 0.1, subsample = 1, colsample_bytree = 1, objective = ‘reg:squarederror’ |
| Random Forest | Default | N/A | N/A | n_estimators = 100, max_depth = 6, random_state = 42 |
| SVM | Tuned | N/A | N/A | Kernel = ‘rbf’; GridSearchCV tuning for C, gamma |
| Meta-Model (XGBoost) | Tuned | N/A | N/A | GridSearchCV tuning for learning_rate, n_estimators, max_depth, subsample, colsample_bytree |
| Stacked Model (Full Ensemble) | N/A | XGBoost, RF, SVM, ELM | XGBoost | XGBoost: objective = ‘reg:squarederror’, n_estimators = 100, max_depth = 6RF: n_estimators = 100, max_depth = 6, random_state = 42SVM: kernel = ‘rbf’ELM: n_hidden = 1000 |
| Stacked Model (RF + XGBoost) | N/A | XGBoost, RF | Linear Regression | XGBoost: booster = ‘gbtree’, learning_rate = 0.2, n_estimators = 300, max_depth = 6, subsample = 0.8, colsample_bytree = 1.0, objective = ‘reg:squarederror’RF: n_estimators = 300, max_depth = 6, min_samples_split = 2, min_samples_leaf = 1, random_state = 42 |
References
- Cao, S.; Feng, F.; Chen, W.; Zhou, C. Does Market Competition Promote Innovation Efficiency in China’s High-Tech Industries? Technol. Anal. Strateg. Manag. 2020, 32, 429–442. [Google Scholar] [CrossRef]
- Chen, Z.; Xing, R. Digital Economy, Green Innovation and High-Quality Economic Development. Int. Rev. Econ. Financ. 2025, 99, 104029. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, S. The Impact of Digital Economy Development on Industrial Restructuring: Evidence from China. Sustainability 2023, 15, 10847. [Google Scholar] [CrossRef]
- Song, M.; Pan, H.; Vardanyan, M.; Shen, Z. Evaluating the Energy Efficiency-Enhancing Potential of the Digital Economy: Evidence from China. J. Environ. Manag. 2023, 344, 118408. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, D.; Chen, Y. Theoretical Framework and Research Prospect of the Impact of China’s Digital Economic Development on Population. Front. Earth Sci. 2022, 10. [Google Scholar] [CrossRef]
- China Daily|Nation’s Digital Push Gaining Speed, Edge. Available online: https://www.nda.gov.cn/sjj/ywpd/sjzg/0519/20250519222423223703950_pc.html (accessed on 16 June 2025).
- Pradhan, R.P.; Arvin, M.B.; Norman, N.R.; Bennett, S.E. Financial Depth, Internet Penetration Rates and Economic Growth: Country-Panel Evidence. Appl. Econ. 2016, 48, 331–343. [Google Scholar] [CrossRef]
- Al-Zoubi, W.K. Economic Development in the Digital Economy: A Bibliometric Review. Economies 2024, 12, 53. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, Z.; Liang, S. Digital Economy, Entrepreneurship, and High-Quality Economic Development: Empirical Evidence from Urban China. Front. Econ. China 2022, 17, 393–426. [Google Scholar] [CrossRef]
- Zhou, Q.; Cheng, C.; Fang, Z.; Zhang, H.; Xu, Y. How Does the Development of the Digital Economy Affect Innovation Output? Exploring Mechanisms from the Perspective of Regional Innovation Systems. Struct. Change Econ. Dyn. 2024, 70, 1–17. [Google Scholar] [CrossRef]
- Xing, M.; Gong, C.; Moon, G.-H.; Ge, X. Digital Economy, Dual Innovation Capability and Enterprise Labor Productivity. Int. Rev. Financ. Anal. 2025, 101, 104005. [Google Scholar] [CrossRef]
- Bartel, A.; Ichniowski, C.; Shaw, K. How Does Information Technology Affect Productivity? Plant-Level Comparisons of Product Innovation, Process Improvement, and Worker Skills. Q. J. Econ. 2007, 122, 1721–1758. [Google Scholar] [CrossRef]
- Wang, Y.; Han, P. Digital Transformation, Service-Oriented Manufacturing, and Total Factor Productivity: Evidence from A-Share Listed Companies in China. Sustainability 2023, 15, 9974. [Google Scholar] [CrossRef]
- Xia, L.; Baghaie, S.; Sajadi, S.M. The Digital Economy: Challenges and Opportunities in the New Era of Technology and Electronic Communications. Ain Shams Eng. J. 2024, 15, 102411. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Y.; Sun, H.; Tang, Y.; Li, J. How Digital Transformation Enhances Corporate Innovation Performance: The Mediating Roles of Big Data Capabilities and Organizational Agility. Heliyon 2024, 10, e34905. [Google Scholar] [CrossRef] [PubMed]
- Hall, B.H. The Financing of Research and Development. Oxf. Rev. Econ. Policy 2002, 18, 35–51. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Z.; Lu, M.; Xu, Z.; Zhang, Y. Does FinTech Constrain Corporate Misbehavior? Evidence from Research and Development Manipulation. Emerg. Mark. Financ. Trade 2023, 59, 3129–3151. [Google Scholar] [CrossRef]
- Du, L.; Geng, B. Financial Technology and Financing Constraints. Financ. Res. Lett. 2024, 60, 104841. [Google Scholar] [CrossRef]
- Wang, J.; Yao, Y.; Ge, H.; Wang, J. The Impact of Digital Inclusive Finance on SME Innovation. Sustainability 2025, 17, 3633. [Google Scholar] [CrossRef]
- Wang, J.-H.; Wu, Y.-H.; Yang, P.Y.; Hsu, H.-Y. Sustainable Innovation and Firm Performance Driven by FinTech Policies: Moderating Effect of Capital Adequacy Ratio. Sustainability 2023, 15, 8572. [Google Scholar] [CrossRef]
- Basu, S.; Fernald, J.G. Information and Communications Technology as a General Purpose Technology: Evidence from U.S. Industry Data. Ger. Econ. Rev. 2007, 8, 146–173. [Google Scholar] [CrossRef]
- Óskarsdóttir, M.; Bravo, C.; Sarraute, C.; Vanthienen, J.; Baesens, B. The Value of Big Data for Credit Scoring: Enhancing Financial Inclusion Using Mobile Phone Data and Social Network Analytics. Appl. Soft Comput. 2019, 74, 26–39. [Google Scholar] [CrossRef]
- Rizvi, S.K.A.; Rahat, B.; Naqvi, B.; Umar, M. Revolutionizing Finance: The Synergy of Fintech, Digital Adoption, and Innovation. Technol. Forecast. Soc. Change 2024, 200, 123112. [Google Scholar] [CrossRef]
- Ugur, M.; Trushin, E. Information Asymmetry, Risk Aversion and R&D Subsidies: Effect-Size Heterogeneity and Policy Conundrums. Econ. Innov. New Technol. 2023, 32, 1190–1215. [Google Scholar] [CrossRef]
- Lee, S.; Kim, M.-S.; Park, Y. ICT Co-Evolution and Korean ICT Strategy—An Analysis Based on Patent Data. Telecommun. Policy 2009, 33, 253–271. [Google Scholar] [CrossRef]
- da Silveira, F.; Ruppenthal, J.E.; Lermen, F.H.; Machado, F.M.; Amaral, F.G. Technologies Used in Agricultural Machinery Engines That Contribute to the Reduction of Atmospheric Emissions: A Patent Analysis in Brazil. World Pat. Inf. 2021, 64, 102023. [Google Scholar] [CrossRef]
- Wagner, S.; Wakeman, S. What Do Patent-Based Measures Tell Us about Product Commercialization? Evidence from the Pharmaceutical Industry. Res. Policy 2016, 45, 1091–1102. [Google Scholar] [CrossRef]
- Tapscott, D. The Digital Economy: Promise and Peril in the Age of Networked Intelligence; McGraw-Hill: New York, NY, USA, 1996; ISBN 978-0-07-062200-5. [Google Scholar]
- CAICT-WHITE PAPER. Available online: https://www.caict.ac.cn/english/research/whitepapers/index_9.html (accessed on 30 April 2025).
- Zou, S.; Liao, Z.; Fan, X. The Impact of the Digital Economy on Urban Total Factor Productivity: Mechanisms and Spatial Spillover Effects. Sci. Rep. 2024, 14, 396. [Google Scholar] [CrossRef]
- Ren, S.; Hao, Y.; Xu, L.; Wu, H.; Ba, N. Digitalization and Energy: How Does Internet Development Affect Chi-na’s Energy Consumption? Energy Econ. 2021, 98, 105220. [Google Scholar] [CrossRef]
- Chen, K.; Fan, Y. Selection of R&D Techniques: The Influence of Spillover Effects and Government Subsidies. Transp. Res. Part E Logist. Transp. Rev. 2025, 194, 103879. [Google Scholar] [CrossRef]
- Lyu, Y.; Peng, Y.; Liu, H.; Hwang, J.-J. Impact of Digital Economy on the Provision Efficiency for Public Health Services: Empirical Study of 31 Provinces in China. Int. J. Environ. Res. Public Health 2022, 19, 5978. [Google Scholar] [CrossRef]
- Xiaoyan, D.; Jiangnan, Z.; Xuelian, G.; Ali, M. The Impact of Informatization on Agri-Income of China’s Rural Farmers: Ways for Digital Farming. Front. Sustain. Food Syst. 2024, 8. [Google Scholar] [CrossRef]
- Saveleva, N.A.; Erdakova, V.P.; Ugriumov, E.S.; Yudina, T.A. The Role of the Digital Economy in the Retail Sphere. In Artificial Intelligence: Anthropogenic Nature vs. Social Origin, Proceedings of the 13th International Scientific and Practical Conference (ISC Conference–Volgograd 2020), Volgograd, Russia, 19–20 March 2020; Popkova, E.G., Sergi, B.S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Advances in Intelligent Systems and Computing; pp. 104–110. [Google Scholar]
- Jones, C.I.; Tonetti, C. Nonrivalry and the Economics of Data. Am. Econ. Rev. 2020, 110, 2819–2858. [Google Scholar] [CrossRef]
- Mayo, J.W.; Wallsten, S. From Network Externalities to Broadband Growth Externalities: A Bridge Not yet Built. Rev. Ind. Organ 2011, 38, 173–190. [Google Scholar] [CrossRef]
- Tang, C.; Xu, Y.; Hao, Y.; Wu, H.; Xue, Y. What Is the Role of Telecommunications Infrastructure Construction in Green Technology Innovation? A Firm-Level Analysis for China. Energy Econ. 2021, 103, 105576. [Google Scholar] [CrossRef]
- Forés, B.; Camisón, C. Does Incremental and Radical Innovation Performance Depend on Different Types of Knowledge Accumulation Capabilities and Organizational Size? J. Bus. Res. 2016, 69, 831–848. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Q.; Shi, R.; Zhang, K.; Wang, X. How the Digital Economy Enables Regional Sustainable Development Using Big Data Analytics. Sustainability 2023, 15, 13610. [Google Scholar] [CrossRef]
- Shao, B.; Wang, H. Digital Economy, Industrial Structure Advancement and Human Capital Accumulation. Financ. Res. Lett. 2025, 83, 107727. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, W. Impact of FDI and R&D on China’s Industrial CO2 Emissions Reduction and Trend Prediction. Atmos. Pollut. Res. 2019, 10, 1627–1635. [Google Scholar] [CrossRef]
- Sun, J.; Wu, X. Research on the Mechanism and Countermeasures of Digital Economy Development Promoting Carbon Emission Reduction in Jiangxi Province. Environ. Res. Commun. 2023, 5, 035002. [Google Scholar] [CrossRef]
- Zhou, F.; Deng, H. Creation or Disruption? Doubts from the Internet Applications in China’s Rural Sector. J. Innov. Knowl. 2023, 8, 100450. [Google Scholar] [CrossRef]
- Wang, Y.; Phillips, F.; Yang, C. Bridging Innovation and Commercialization to Create Value: An Open Innovation Study. J. Bus. Res. 2021, 123, 255–266. [Google Scholar] [CrossRef]
- Opler, T.C.; Titman, S. Financial Distress and Corporate Performance. J. Financ. 1994, 49, 1015–1040. [Google Scholar] [CrossRef]
- Romito, S.; Vurro, C. Non-Financial Disclosure and Information Asymmetry: A Stakeholder View on US Listed Firms. Corp. Soc. Responsib. Environ. Manag. 2021, 28, 595–605. [Google Scholar] [CrossRef]
- Brown, J.R.; Martinsson, G.; Petersen, B.C. Law, Stock Markets, and Innovation. J. Financ. 2013, 68, 1517–1549. [Google Scholar] [CrossRef]
- Grennan, J.; Michaely, R. Fintechs and the Market for Financial Analysis. J. Financ. Quant. Anal. 2021, 56, 1877–1907. [Google Scholar] [CrossRef]
- Lyu, Y.; Ji, Z.; Zhang, X.; Zhan, Z. Can Fintech Alleviate the Financing Constraints of Enterprises?—Evidence from the Chinese Securities Market. Sustainability 2023, 15, 3876. [Google Scholar] [CrossRef]
- Boot, A.; Hoffmann, P.; Laeven, L.; Ratnovski, L. Fintech: What’s Old, What’s New? J. Financ. Stab. 2021, 53, 100836. [Google Scholar] [CrossRef]
- Bollaert, H.; Lopez-de-Silanes, F.; Schwienbacher, A. Fintech and Access to Finance. J. Corp. Financ. 2021, 68, 101941. [Google Scholar] [CrossRef]
- Berg, T.; Burg, V.; Gombović, A.; Puri, M. On the Rise of FinTechs: Credit Scoring Using Digital Footprints. Rev. Financ. Stud. 2020, 33, 2845–2897. [Google Scholar] [CrossRef]
- Cookson, J.A.; Niessner, M. Why Don’t We Agree? Evidence from a Social Network of Investors. J. Financ. 2020, 75, 173–228. [Google Scholar] [CrossRef]
- Tang, M.; Hou, Y. (Greg); Goodell, J.W.; Hu, Y. Fintech and Corporate Risk-Taking: Evidence from China. Financ. Res. Lett. 2024, 64, 105411. [Google Scholar] [CrossRef]
- Cheng, M.; Qu, Y. Does Bank FinTech Reduce Credit Risk? Evidence from China. Pac.-Basin Financ. J. 2020, 63, 101398. [Google Scholar] [CrossRef]
- Ashta, A.; Herrmann, H. Artificial Intelligence and Fintech: An Overview of Opportunities and Risks for Banking, Investments, and Microfinance. Strateg. Change 2021, 30, 211–222. [Google Scholar] [CrossRef]
- Li, H.; Lu, Z.; Yin, Q. The Development of Fintech and SME Innovation: Empirical Evidence from China. Sustainability 2023, 15, 2541. [Google Scholar] [CrossRef]
- Dong, X.; Yu, M. Does FinTech Development Facilitate Firms’ Innovation? Evidence from China. Int. Rev. Financ. Anal. 2023, 89, 102805. [Google Scholar] [CrossRef]
- Chaudhry, S.M.; Ahmed, R.; Huynh, T.L.D.; Benjasak, C. Tail Risk and Systemic Risk of Finance and Technology (FinTech) Firms. Technol. Forecast. Soc. Change 2022, 174, 121191. [Google Scholar] [CrossRef]
- Tyagi, A. Risk Management in Fintech. In The Emerald Handbook of Fintech; Baker, H.K., Filbeck, G., Black, K., Eds.; Emerald Publishing Limited: Leeds, UK, 2024; pp. 157–175. ISBN 978-1-83753-609-2. [Google Scholar]
- Chen, X.; Yan, D.; Chen, W. Can the Digital Economy Promote FinTech Development? Growth Change 2022, 53, 221–247. [Google Scholar] [CrossRef]
- Oliveira, L.; Fleury, A.; Fleury, M.T. Digital Power: Value Chain Upgrading in an Age of Digitization. Int. Bus. Rev. 2021, 30, 101850. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, F. How Does the Digital Economy Drive High-Quality Regional Development? New Evidence from China. Eval. Rev. 2024, 48, 893–917. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, D.; Kong, Q.; Tan, F. Digital Infrastructure and Economic Growth: Evidence from Corporate Investment Efficiency. Int. Rev. Econ. Financ. 2025, 98, 103854. [Google Scholar] [CrossRef]
- Bu, Y.; Du, X.; Wang, Y.; Liu, S.; Tang, M.; Li, H. Digital Inclusive Finance: A Lever for SME Financing? Int. Rev. Financ. Anal. 2024, 93, 103115. [Google Scholar] [CrossRef]
- Bukht, R.; Heeks, R. Defining, Conceptualising and Measuring the Digital Economy. Int. Organ. Res. J. 2017, 13, 143–172. [Google Scholar] [CrossRef]
- Zhang, T.; Li, N. Measurement of the Scale and Development Trend of Digital Economy Core Industries in China’s Provinces. Procedia Comput. Sci. 2024, 242, 1218–1225. [Google Scholar] [CrossRef]
- Nagaoka, S.; Motohashi, K.; Goto, A. Chapter 25-Patent Statistics as an Innovation Indicator. In Handbook of the Economics of Innovation; Hall, B.H., Rosenberg, N., Eds.; Elsevier: North Holland, The Netherlands, 2010; Volume 2, pp. 1083–1127. [Google Scholar]
- Burhan, M.; Singh, A.K.; Jain, S.K. Patents as Proxy for Measuring Innovations: A Case of Changing Patent Filing Behavior in Indian Public Funded Research Organizations. Technol. Forecast. Soc. Change 2017, 123, 181–190. [Google Scholar] [CrossRef]
- Shahidan, N.H.; Latiff, A.S.A.; Wahab, S.A. Sustainable Technology Development during Intellectual Property Rights Commercialisation by University Startups. Asia Pac. J. Innov. Entrep. 2023, 17, 176–194. [Google Scholar] [CrossRef]
- Du, Z.-Y.; Wang, Q. Digital Infrastructure and Innovation: Digital Divide or Digital Dividend? J. Innov. Knowl. 2024, 9, 100542. [Google Scholar] [CrossRef]
- Logue, D.; Williamson, P.; Roberts, A.; Luo, Y.; Barrett, M. Digital Innovation, Platforms, and Global Strategy. Inf. Organ. 2025, 35, 100562. [Google Scholar] [CrossRef]
- Lukhmanov, Y.; Tsakalerou, M. Impact of Innovation-Enabling Technologies on Business Performance: An Empirical Study. In Smart Mobile Communication & Artificial Intelligence, Proceedings of the 15th IMCL Conference, Thessaloniki, Greece, 9–10 November 2023; Auer, M.E., Tsiatsos, T., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 197–207. [Google Scholar]
- Kaiser, H.F. The Application of Electronic Computers to Factor Analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Svanberg, J.; Ardeshiri, T.; Samsten, I.; Öhman, P.; Neidermeyer, P. Prediction of Controversies and Estimation of ESG Performance: An Experimental Investigation Using Machine Learning. In Handbook of Big Data and Analytics in Accounting and Auditing; Rana, T., Svanberg, J., Öhman, P., Lowe, A., Eds.; Springer Nature: Singapore, 2023; pp. 65–87. ISBN 978-981-19-4460-4. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Zhang, J. New Machine Learning Algorithm: Random Forest. In Proceedings of the Information Computing and Applications, Chengde, China, 14–16 September 2012; Liu, B., Ma, M., Chang, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 246–252. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Wallach, D.; Goffinet, B. Mean Squared Error of Prediction as a Criterion for Evaluating and Comparing System Models. Ecol. Model. 1989, 44, 299–306. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Armstrong, J.S.; Collopy, F. Error Measures for Generalizing about Forecasting Methods: Empirical Comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef]
| Layer | Variable | Variable Abbreviation | Reason for Classification |
|---|---|---|---|
| Core Layer | IPv4 Address Count | ipv4_count | IPv4 addresses are fundamental to Internet infrastructure, aligning with IT consulting and telecommunications. |
| Internet Domain Count | domain_count | Internet domains are essential for online services and software-driven activities. | |
| Broadband Internet Users | broadband_users | Broadband access is critical infrastructure for IT services, telecommunications, and digital operations. | |
| Internet Access Ports | access_ports | Internet access ports support foundational IT infrastructure and digital industrial content. | |
| Long-Distance Fiber Optic Cable Length per Unit Area | fiber_cable_density | Fiber optic cables are the backbone of telecommunications and digital industrial services. | |
| Mobile Base Station Density | mobile_base_density | Mobile base stations are critical infrastructure for telecommunications and IT services. | |
| IT Service Revenue as Percentage of GDP | it_service_gdp | IT services, including software development and consulting, are central to the core digital economy. | |
| Telecom Services Revenue as Percentage of GDP | telecom_gdp | Telecom services form a foundational part of the digital industrial content in the core layer. | |
| Broad Layer | E-commerce Revenue as Percentage of GDP | ecommerce_gdp | E-commerce aligns with the broad layer as a key component of digital trade and algorithmic economic activities. |
| Express Delivery Volume | delivery_volume | Express delivery supports the e-commerce ecosystem, which is part of the broad layer. | |
| Proportion of Enterprises Engaged in E-commerce | enterprise_ecommerce | E-commerce enterprise participation is part of the broad layer, supporting the digital trade economy. | |
| Narrow Layer | R&D Funding | rd_funding | R&D funding drives digital services, platform innovations, and advancements in the digital economy. |
| Number of Computers Used per 100 Employees | computer_usage | Computer usage supports the platform economy and digital services by enabling productivity tools and platforms. |
| Model | Sample Size | RMSE | MAE | MdAPE (%) | R2 | t-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Random Forest—Training | 136 | 0.0194 | 0.01 | 10.28 | 0.9838 | 0.3392 | 0.735 |
| Random Forest—Testing | 59 | 0.0449 | 0.0212 | 18.9 | 0.9309 | 0.1251 | 0.9008 |
| XGBoost—Training | 136 | 0.0006 | 0.0004 | 0.56 | 1 | 0 | 1 |
| XGBoost—Testing | 59 | 0.0253 | 0.0136 | 16.84 | 0.978 | 0.6143 | 0.5414 |
| SVM—Training | 136 | 0.0088 | 0.0076 | 12.3 | 0.9966 | 0.0574 | 0.9543 |
| SVM—Testing | 59 | 0.0381 | 0.0223 | 36.01 | 0.9501 | 0.1805 | 0.8574 |
| ELM—Training | 136 | 0.0249 | 0.0194 | 33.42 | 0.9683 | −0.0002 | 0.9999 |
| ELM—Testing | 59 | 0.0304 | 0.0214 | 39.56 | 0.973 | −0.2136 | 0.8316 |
| XGBoost—Training (CV) | 136 | 0.0005 | 0.0004 | 0.64 | 1 | −0.0008 | 0.9994 |
| XGBoost—Testing (CV) | 59 | 0.0297 | 0.0151 | 17.65 | 0.9698 | −0.1971 | 0.8444 |
| XGBoost-RF Stacked Model—Training | 136 | 0.0127 | 0.0067 | 5.41 | 0.993 | 0.4404 | 0.6603 |
| XGBoost-RF Stacked Model—Testing | 59 | 0.0247 | 0.0137 | 17.62 | 0.9791 | 0.0171 | 0.9864 |
| 4-Model Stacked—Training | 136 | 0.0007 | 0.0005 | 0.6538 | 1 | 0 | 1 |
| 4-Model Stacked—Testing | 59 | 0.0299 | 0.0146 | 18.7018 | 0.9694 | 1.5252 | 0.1327 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, A.; Wang, P. Predictive Framework for Regional Patent Output Using Digital Economic Indicators: A Stacked Machine Learning and Geospatial Ensemble to Address R&D Disparities. Analytics 2025, 4, 18. https://doi.org/10.3390/analytics4030018
Zhao A, Wang P. Predictive Framework for Regional Patent Output Using Digital Economic Indicators: A Stacked Machine Learning and Geospatial Ensemble to Address R&D Disparities. Analytics. 2025; 4(3):18. https://doi.org/10.3390/analytics4030018
Chicago/Turabian StyleZhao, Amelia, and Peng Wang. 2025. "Predictive Framework for Regional Patent Output Using Digital Economic Indicators: A Stacked Machine Learning and Geospatial Ensemble to Address R&D Disparities" Analytics 4, no. 3: 18. https://doi.org/10.3390/analytics4030018
APA StyleZhao, A., & Wang, P. (2025). Predictive Framework for Regional Patent Output Using Digital Economic Indicators: A Stacked Machine Learning and Geospatial Ensemble to Address R&D Disparities. Analytics, 4(3), 18. https://doi.org/10.3390/analytics4030018






