Abstract
Food commodities and energy bills have experienced rapid undulating movements and hikes globally in recent times. This spurred this study to examine the possibility that the shocks that arise from fluctuations of one market spill over to the other and to determine how time-varying the spillovers were across a time. Data were daily frequency (prices of grains and energy products) from 1 July 2019 to 31 December 2022, as quoted in markets. The choice of the period was to capture the COVID pandemic and the Russian–Ukrainian war as events that could impact volatility. The returns were duly calculated using spreadsheets and subjected to ADF stationarity, co-integration, and the full BEKK-GARCH estimation. The results revealed a prolonged association between returns in the energy markets and food commodity market returns. Both markets were found to have volatility persistence individually, and time-varying bidirectional transmission of volatility across the markets was found. No lagged-effects spillover was found from one market to the other. The findings confirm that shocks that emanate from fluctuations in energy markets are impactful on the volatility of prices in food commodity markets and vice versa, but this impact occurs immediately after the shocks arise or on the same day such variation occurs.
1. Introduction
Global markets serve as dynamic frameworks that facilitate the exchange of goods and services between buyers and sellers on a worldwide scale. These intricate systems operate across various sectors, including equities, bonds, futures, energy and food commodities, etc. Participants in these markets, ranging from individual investors to institutional entities, engage in investing capital to optimise wealth or secure positive returns. However, these markets are not insulated; instead, they are deeply interconnected with global economic phenomena. The unfolding of economic events triggers a spectrum of investor responses, leading to fluctuations in market prices and ultimately influencing investment returns. These fluctuations are what the macroeconomic literature refers to as volatility. Volatility is a change, usually of a continuous nature, through a specified period. It is a market concept used as a risk measure [1].
Volatility is defined in econometrics as the extent of variance or dispersion of a financial or economic indicator over a period. It is a critical term in the research field of financial markets since it assists analysts and researchers in understanding the risk connected with a stock or exchange [2]. Volatility is essential in finance because it influences pricing choices, risk management, portfolio diversification, and optimisation. As a result, investors and financial analysts watch volatility to aid improved forecasting and adequate portfolio diversification [3]. Volatility could be assessed using the standard deviation of historical price returns of assets. Future volatility could also be anticipated and projected using option prices, and market investors use this to evaluate market mood and unpredictability. More complex volatility assessments use autoregressive conditional heteroscedasticity and stochastic volatility models.
From a more practical perspective, global conditions in recent times have comprised chaotic situations disrupting lifestyles, macroeconomic conditions, and policies across different regions. First, the coronavirus pandemic abruptly struck, making news of death trolls, infected cases, and lockdowns, negatively impacting economic activities and upscaling the recession [4,5]. As economies recovered from the outbreak, the Russian–Ukraine war began hampering global supplies of energy fuels and food commodities. Food commodities have experienced rapid undulating movements skyrocketing with the current food crises worldwide due to the halt in supplies from Ukraine and Russia, which are global suppliers of cereals such as wheat and oilseeds [6]. Similar observations have also been noticed in the energy markets. In the past year, energy prices across Brent crude, coal, and European Natural Gas (ENG) have experienced fluctuations, with ENG and coal recording their highest price in August and July 2022, respectively [4].
Barbaglia, L. et al. posit that commodity markets (and, by implication, energy and other global markets) have become saturated with larger volumes of transactions and rapid fluctuations that have weakened the usage of mere supply–demand analysis in providing explanations for volatilities [1]. Furthermore, they raise that volatility in a specific market arrangement could be spread to another given the interconnectedness of markets in recent times [1], even though studies such as Chia-Lin et al. have confirmed possibilities of volatility of two market instruments occurring independently of each other [7]. Considering the preceding, investors and other players in the energy and commodity markets seek insight into whether presently occurring volatility in the energy market can influence the future fluctuations of the commodity market and vice versa. Market participants also strive to be aware of how this volatility transmits in whichever direction occurs if it exists. Knowledge of the existence and pattern of volatility transmission or spillover is also considered pivotal because it serves as a better pedestal for informed decision-making and risk exposure-reducing mechanisms for affected investors [8].
In many developing countries, heavy reliance is placed on energy and food imports, rendering them particularly susceptible to the impacts of market volatility. Significant fluctuations in these essential markets can result in substantial shifts in import costs, exerting strain on the balance of payments and fiscal stability of these nations. Understanding the patterns and transmission of volatility within these markets is deemed crucial by policymakers and governments in these regions, as effective strategies are sought to mitigate the adverse effects of uncertainty and market fluctuations in food and oil markets.
It is anticipated in this study that the recent notable volatility experienced in energy and food prices has fostered interconnectedness between these markets. This expectation is rooted in the recognition that energy serves as a critical input in food production processes, while food items, in turn, are utilised in the manufacture of biofuel products [9]. Consequently, an investigation into volatility spillover effects is undertaken to ascertain both the univariate volatility within the energy and commodity markets and the occurrence of volatility transmission between these domains.
To address these research inquiries, the BEKK_GARCH model was employed to estimate individual market volatilities and the transmission of these volatilities across both energy and commodity markets. Insights generated by our model include time-based conditional variance, conditional covariance, conditional correlation charts, and volatility matrix estimates. The dataset utilised in this study encompasses calculated returns or rates of change derived from daily listed prices in both energy and commodity markets, commonly employed in volatility studies.
The article is divided into four sections. Based on theory and empirical findings, the Section 1 critically evaluates the existing literature on volatility in both markets and volatility spillovers between the markets. It draws on a review to carve out a literature gap that this research will fill. The following section elucidates the methodology to be employed in the conduct of this research. It describes the research’s philosophical thought, strategy, data collection details, and data scrutiny methods needed to answer formulated research questions. The following section contains outputs from data analysis and discussions of findings based on outputs. It also entails the comparison of findings with those of previous related works. The Section 6 highlights the summary of findings, conclusions drawn from the research work, recommendations for industry based on findings, and suggestions for future research based on current study limitations.
2. Related Literature
2.1. Theoretical Background
Volatility spillover, delineated as the propagation of fluctuation shocks across markets, underscores the interconnected nature of financial landscapes as expounded in the finance and economics literature. This paper delves into two pivotal theoretical frameworks explicating this interconnection: contagion theory and information transmission theory.
The contagion theory posits a widely adopted framework in economics and finance, elucidating the shocks and disturbances stemming from interactions among multiple market arrangements, thereby shaping the volatility and performance of said markets. It delineates a scenario wherein the conditions of one market can reverberate across others, amplifying volatility and risk within the concerned markets and the broader financial system. Its inception traces back to the seminal work of Kaminsky, Lizondo, and Reinhart in 1998, who scrutinised the contagion impacts of the 1997 Asian financial crisis, uncovering the diffusion of shocks from weaker economies to other countries within the continent before extending to global financial markets [10].
Davidescu et al. referenced Forbes and Rigobon as scholars instrumental in establishing a framework for discerning contagion effects across diverse markets [10]. Their analysis of global financial crises, including those in Asia and Russia in 1997 and 1998, utilising a factor model, revealed a common and idiosyncratic volatility element across these markets. This underscores the manifestation of contagion effects during financial crises, precipitating volatility spillover.
Moreover, the applicability of the contagion theory extends to elucidating events stemming from the COVID-19 pandemic, wherein economic and financial disruptions in one country swiftly disseminated globally. Notably, Balcilar et al. identified contagion impacts between the British and American stock exchanges during the pandemic [11], while Corbet et al. scrutinised cryptocurrency markets, unveiling evidence of contagion effects on market fluctuations [12]. This theory posits that uncertainty and apprehension in one market can induce investor migration to other markets, exacerbating instability shocks [13]. Pertinent to the present study, the contagion theory underscores the interconnectedness of commodity and energy markets, highlighting the potential for volatility in one market to precipitate ripple effects in others.
In tandem, the information transmission theory is a pertinent framework in financial economics, delineating the nexus between news or information about a specific market or asset class and the ensuing performance and volatility across related asset classes or markets. Pioneered by the works of Granger and Engle, leveraging conditional volatility and autoregressive conditional heteroscedasticity (ARCH) models, this theory elucidates how news or information from one market can override other determining factors, catalysing volatility escalation in other markets [14].
Baur et al. substantiated this theory’s tenets by examining British and American stock market interactions [15]. Additionally, other studies have observed spillover effects from macroeconomic news releases on various markets, including stock, cryptocurrency, and forex markets, particularly in the contemporary era where social media and the internet facilitate rapid dissemination of news and market information [16,17].
The application of the information transmission theory underscores the pivotal role of news and market information in eliciting volatility across disparate markets. For instance, new information concerning the energy market can influence investor expectations and behaviour in commodity markets and vice versa, precipitating heightened volatility and spillovers [10].
2.2. Examining Interconnected Volatility: Spillovers between Energy Prices and Commodities
Loutfi defines volatility as the rate of price increase or decrease of a security within a specific range of returns, providing detailed insights into price behaviour and shifts within defined time frames [18]. Investors and policymakers rely on risk information and expectations to formulate efficient risk management strategies such as diversification and hedging [3]. Creti et al. observe that investment substitution strategies are contingent upon insights derived from studying the volatility structures of commodities or stocks [19]. The occurrence of volatility is driven by various factors, including economic events such as the COVID-19 pandemic and intrinsic characteristics of market instruments such as earnings, influencing investor behaviour and resulting in market volatility.
Bergmann et al. suggest that studying price transmission and its internal dynamics aids in analysing prices of different commodities or similar commodities in different locations [20]. Price transmission examines the relationship between predictable commodity prices, while price volatility transmission explores how unpredictable prices or price uncertainty in one market affects another [21]. The interaction among different financial markets’ volatilities, resulting in market instability, is called volatility spillover. Volatility spillover denotes the interdependence or interaction between different markets, leading to instability in one market and affecting others [22].
Commodity markets encompass exchanges of products derived from the primary economic sector, including both agricultural and non-agricultural products. These tangible products are direct inputs or raw materials for producing other goods, including precious metals, cotton, oil, cocoa, and gold. However, the dynamic nature of the business environment necessitates further research on price movement, particularly regarding food commodities [23].
Garg et al. identify factors contributing to volatility in commodity markets, including political instability, rising disposable income, growing demand, and price speculation [23]. Other determinants include increased production levels; inflation; energy prices; fertiliser supply; forces of supply and demand; and natural disasters such as floods, earthquakes, and hurricanes [24,25,26].
Energy prices have remained volatile globally over the past few decades. Liu and Serletis report significant variations in crude oil prices in 2020, with a 51% decrease in February and a 28% increase in April [27]. This volatility extends to natural gas and hydrocarbon production, attributed to significant economic and socio-political events creating uncertainties impacting demand and supply forces [28].
Pantos identifies factors affecting energy price volatility, including political policies, oil and gas output levels, decreased nuclear power usage, and increased reliance on sustainable sources [29]. Policies and regulations aim to improve market integration in managing energy price volatility, reducing uncertainties and volatility spillover [23].
The energy market plays a crucial role in the global industry, with virtually all sectors relying on it for operations, administration, and distribution. Efimova and Serletis note significant daily and hourly fluctuations in energy prices, underscoring the importance of accurately forecasting energy market volatility for hedging and derivatives trading [30]. However, the unpredictability of energy prices, like other market instruments, poses challenges to accurate forecasting, influenced by factors such as demand for crude oil, government policies, political instability, natural catastrophes, and energy waste [31,32].
Energy and commodity market rates are closely related as principal inputs to production processes. Volatility spillover between these markets’ prices has garnered attention from scholars and investors. The extant literature identifies a strong connection linking prices of food and energy market products internationally, with spillover occurring from food commodity prices to energy prices or vice versa [33].
Before 2006, commodity prices experienced relatively low volatility; however, this trend shifted dramatically following the global financial crisis of 2007–2009, with volatility spillovers from energy prices identified as a significant determinant [34,35]. The biofuel and financialisation channels are the two primary channels facilitating this spillover [36]. The biofuel channel results from increased biofuel production as governments seek to reduce reliance on crude oil and combat global warming. On the other hand, financialisation involves large volumes of investment capital flowing into the market, integrating commodities into financial markets, and boosting correlation with other asset classes [37].
While volatility spillovers have been observed before and during financial crisis periods, their occurrence remains debatable, with studies reporting either bidirectional or unidirectional volatility transfers [38,39,40]. Geopolitical events and macroeconomic factors also play significant roles in volatility spillovers between energy and commodity markets, further highlighting the complex nature of their interaction [41,42].
2.3. Empirical Review on Volatility Spillovers between Energy and Commodity Prices
Volatility spillovers or transmission between commodities and energy prices have been the subject of empirical research in recent decades. This can be attributed, among other reasons, to the close relationship between both markets, as energy is a vital input for many commodity markets.
Dinku and Worku gathered statistics on agro-commodity retail prices in Ethiopia spanning between 2010 and 2020 to determine the best-suited GARCH models for commodity markets [43]. The study employed asymmetric GARCH models to assess the volatile returns on investments in agricultural commodities. Specifically, it utilised threshold GARCH and exponential GARCH models from the asymmetric GARCH family to analyse price fluctuations across various commodities over time. The findings revealed that the Econometric GARCH model proved most suitable for certain commodities, while TGARCH estimation offered a better fit for others. However, none of the models provided the optimal fit for wheat price fluctuations during the sampled periods. Overall, the study successfully identified time-varying conditional volatility, indicating that shocks today continue to impact variance forecasts for multiple future periods [43].
Trujillo-Barrera et al. examined current volatility transfers from crude oil futures in the United States using the GJR-GARCH and VECM models. The spillover discovered ran from maise to ethanol markets and vice versa, although the ethanol market is slightly stronger. The proportion of maise and ethanol price fluctuation directly related to petroleum market volatility is around 10 per cent to 20 per cent but rose to about 45 per cent during the economic chaos when the global need for oil shifted substantially. Volatility transmission from maise to the ethanol market is also observed, but not vice versa [34]. The findings shed light on the magnitude of fluctuation links between energy and agriculture investment arrangements at high price volatility and considerable production of substantial corn-based ethanol output. Creti et al. explored the relationships of returns on prices for twenty-five commodity instruments and equities, focusing on extracted raw materials in the energy sector. The study showed that the associations between commodities and equity markets are time-dependent and are very unstable, especially following the financial crisis of 2007–2008, using the DCC GARCH estimation [19].
Chen et al. examined the impact of volatility spills among crude oil and markets for agricultural commodities since the beginning of the global financial distress. They found significant proof of mutual volatility spillovers across both market arrangements, with spills observed from crude oil markets to others [44]. Mensi et al. researched petroleum values, forex rates, and secondary securities markets in developing countries. The study found that volatility is transferred from the energy market to other markets using a bivariate GARCH model [45]. Related studies such as Kocak et al. also found similar proof of the volatility dissemination between the energy and stock markets in the United States, UK, Germany, and Japan [46]. Zhang et al. found unidirectional evidence of volatility spillovers from the energy market to Chinese agricultural futures markets. The shocks become more significant at higher volatility levels in energy listings [47].
Chen et al. used a dynamic conditional correlation model to assess the spillover effect of energy prices on the price of four agro commodities (corn, soybeans, wheat, and sugar) [44], while Fosu et al. used the VAR-BEKK-GARCH tool to ascertain the spillover impacts on the prices of five agro products (maise, soybeans, wheat, cotton, and sugar) with a VAR-BEKK-GARCH model [48]. Both works reported significant effects between energy costs and the prices of agricultural commodities.
Using the vector auto-regressive model, Barbaglia et al. investigated volatility spillovers over a broad spectrum of energy, agro, and biofuel commodities. They suggest the t-lasso method for obtaining a central VAR to estimate the possibility of a fat-tailed collection of errors within the specified model [1]. The empirical investigation reveals instability spillovers across oil and biofuels and between oil and agricultural commodities.
Kaulu illustrated how crude oil costs affect maise and copper costs. The relationship between oil costs and food and metal prices is studied using vector error correction and autoregressive estimators. The commodity price statistics range from January 1982 to June 2021 and include the mean monthly cost for petroleum, copper, and corn. The study was again run on a subset of the original dataset from 2000 to June 2021 for robustness. At the threshold of five per cent, a long-run association was discovered between petroleum and the price of copper and between maise and crude oil prices for the study periods from 1982 to 2021. The same could not be said for the smaller sample from 2000 to 2021. Granger causation from petroleum prices to prices of specified food and metal markets was not established. The study’s weaknesses and recommendations for further research are also discussed [49]. This study’s drawback is that it concentrated on the optimum choice of portfolios for investors instead of overall economic policy suggestions.
Umar et al. assessed the interdependence of bivariate and joint returns and variability among various agro-produce and oil price shocks, employing the fresh Time-Varying Parameter Vector Autoregression (TVP-VAR) methodology. Using data from 7 January 2000 to 17 September 2020, the study focused on crucial durations of economic distress over the past twenty yearly periods, namely the Global Financial Crisis (GFC), the dot-com bubble, and the coronavirus pandemic crisis. The core findings reveal that the volatility of oil risk surpasses shocks in oil needs, which is more significant than supply shocks in oil markets. Furthermore, the dynamic volatility connectedness varies across periods, increasing during economic distress eras. Overall, the association within net returns experienced significant growth within the three major crisis times examined [50]. Consequently, the differences between the transmitting grain markets and receiving other food commodities markets became more evident in the heat of the coronavirus pandemic and GFC blasts.
Lu et al. investigated the characteristics and patterns of how variability spreads from crude oil to agro-produce markets and vice versa since the financial crisis of 2008 and 2009. The study utilised a dynamic bivariate autoregressive model to investigate the spillover effects across long, mid, and short periods. During the crisis, bidirectional volatility spillovers were observed between crude oil and agricultural commodity markets in the short term. However, in the aftermath of the crisis, evidence supported the transmission of corn’s long-term and mid-term variabilities to crude oil variability. These findings suggest a diminished level of integration between crude oil and agricultural markets following the distress period [36]. However, the HAR model limits the study because it may not capture non-linear connections in the markets examined, given that it assumes linear relationships between variables.
Yanpeng et al. investigated the prolonged interdependence and causality of prices in the crude oil and agro-produce market arrangements. Time series over long years were utilised to identify demand and supply shocks that arose in both economic areas of focus in the calm era and shocks that emerged in the market’s unstable periods. The study generally used the entire rolling window and bootstrap sample causality tests for this purpose. Findings contrast sharply with most research articles attributing fluctuations in agro-produce prices to oil considerations [51]. Contrarily, findings support the existence of mutual causality and demonstrate that agro-produce prices affect oil prices just as much as the other way around.
Efimova and Serletisy examined energy price volatility, focusing on wholesale oil, natural gas, and electricity prices, using daily data on U.S. energy markets from 2001 to 2013. The data were analysed using the univariate GARCH modelling and tri-variate BEKK and DCC models, allowing the investigation of interdependence and interactions among the various markets. The study found similar evidence from both univariate and multivariate models, although the univariate model provided a more accurate estimate of the interactions among the markets [30]. Lin et al. also conducted a tri-variate analysis using the VAR-BEKK-GARCH-X model on data from 2007 to 2018. The study examined the transmission influence of volatilities due to economic and financial crises on the commodities market as evaluated by the Baltic Dry Index (BDI). A significant transmission effect was found only during periods of global financial distress, such as 2008/2009 and 2014–2016 [52]. Yu et al. (2018) also found a similar pattern for the energy market during financial crises. The study relied on the VAR-BEKK-GARCH model to evaluate variability transfer among the US and China crude oil market (WTI) and stock markets. They found that the 2008 financial crisis stimulated increased variability and interdependence across the oil and securities markets. This suggests that financial and economic disturbances are determinants of volatility spillovers or transmission in the energy and commodities markets [53].
Gardebroek and Hernandez explored the turbulent flow among petroleum, ethanol, and rising prices in the USA. To analyse the level of interconnection and fluctuation patterns across different markets, the study used a multivariate GARCH technique. The estimation results show a more vital link between the ethanol and maise trades in recent years, especially following 2006 when ethanol emerged as the sole substitute oxygenates for fuel. The authors, however, only found substantial fluctuation spillovers from maise to ethanol, not vice versa. The study did not document substantial mutual volatility from oil to corn prices [54]. Consequently, the findings do not support the proposition that energy market fluctuations increase price variability in the U.S. corn market.
Similarly et al. studied the symmetric and asymmetric effects exerted on India’s energy crops, such as sugarcane, soybeans, and wheat, from January 2016 to December 2020 by crude oil fluctuations. The threshold, exponential, and GARCH (1,1) models were used to test the data, and the findings show that petroleum prices had a considerable magnitude of effect on sugarcane and wheat but none on soybeans. Threshold GARCH results revealed a significant asymmetry across all agro-produces. Further coefficient of asymmetry showed that declining crude prices were more impactful on these crops than rising prices were, as confirmed by negative estimated values [55].
In the energy markets, Liu and Serletis made use of semi-parametric GARCH-in-Mean modelling on data from the start of 2002 to the end of 2021 to investigate price progression and variability characteristics of the natural gas, crude oil, and hydrocarbon-based gas liquids markets. The study provided empirical evidence that uncertainties in the market have been a significant source of shocks and volatility in crude oil returns. The study also recommended using the Frank copula to describe bivariate relationships among commodities in the energy market and the Clayton copula for the interaction between butane and ethane [27]. Also, Dutta and Noor looked at volatility interactions between oil and three significant non-energy assets. There was no indication of a volatility connection between agricultural and oil trading platforms using bivariate VAR-GARCH modelling during the data period [56]. However, findings show that oil fluctuations were crucial causal factors of instability in non-energy composite markets. The result was justified by the fact that petroleum-related goods constitute a core manufacturing input in metal sectors, making metal production heavily reliant on the market for crude oil.
Ghorbel and Jeribi provided evidence during the coronavirus pandemic and studied the variability spillover among energy and other financial commodities with the multivariate Markov-switching BEKK-GARCH model. The study found evidence of the transfer of fluctuation shocks from energy to other assets, with an indication of energy assets having a substantial degree of dynamic correlation with commodities indexes, proving the contagion influence of the pandemic on the markets [57].
Significant empirical evidence exists on volatility spillover or transmission across energy and commodity market arrangements. However, there are still some gaps in the literature that could be explored further. Some research works identified the roles played by global economic activity, financial crises, and geopolitical events as drivers of volatility spillovers [47,53,58]. The studies that examined the spillover effects across these particular markets were centred more on some farm commodities such as maise, soybeans, and wheat [16,44,55], leaving out several other commodities. A knowledge gap exists in the connected literature for further studies to provide empirical evidence on spillover dynamics across a broader range of energy and commodity markets.
Furthermore, limited evidence explains the spillover dynamics across energy and commodity markets as economies recover from the recent pandemic, combined with the effect of the ongoing Russian–Ukraine war, which has hampered global supplies of energy fuels and food commodities.
Therefore, based on the identified gap in the literature, this study estimates the univariate volatility in energy and commodity prices (individual volatility) and the occurrence of volatility spillover or transmission from one variable to another in consideration of the prevalent disruptions and shocks in the political and economic systems of the global financial markets.
3. Materials and Methods
3.1. Data Collection and Preparation
Data from reports on the commodity market and the energy market were used in the study. These reports were downloaded as CSV files from the Investing.com website (accessed 14 February 2023), a website that publishes statistics on indices of different financial, energy, and commodity markets in countries globally. The study’s data comprise energy and commodity (grains) prices used in related works [7,45]. The daily frequency data from July 2019 to 31 December 2022 formed the time horizon of the study. Daily frequency data are considered best for GARCH analysis because higher frequencies reveal volatility behaviour better. The description of the variables is provided in Table 1.

Table 1.
Description of variables.
Actual data for the study comprised returns (the change in daily prices) of both study variables (1).
where P1 = current daily rate.
P0 = immediate previous daily rate.
Collected data were first analysed with descriptive statistics comprising averages, normality distribution, and dispersion. The aim of descriptive statistics was to define patterns in the study data over the chosen period.
Inferential statistics used for data analysis comprised three general time series tests: unit root tests, co-integration diagnostics, and KPSS stationary test.
Unit root test: This test is conducted to decide on the constant nature of stationarity of the time series. This study employs the augmented Dickey–Fuller (ADF) tool. It is expected that the series is stationary at most at first, differing. Additionally, we employed the Phillips–Perron test (PP).
The Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test is used for testing a null hypothesis that an observable time series is stationary around a deterministic trend (i.e., trend stationary) against the alternative of a unit root [59].
Co-integration test: If unit roots existed in the time series, they were subjected to the Johansen co-integration to determine whether a long-term connection exists between the variables.
After confirming stationarity at the level or first differencing and establishing the presence or absence of long-term connection between variables, the data needed to be examined empirically for ARCH effects.
Test for ARCH effects: GARCH is only applicable to time series if ARCH effects exist within the time series. ARCH effects show conditional heteroscedasticity in datasets and imply that the variance of the data does not remain constant across different periods. The data for the study were tested appropriately for the presence of ARCH effects before GARCH models were used.
The multivariate BEKK-GARCH technique was conducted on study data using R-Studio’s MTS package to confirm the presence of ARCH effects. Other studies that used this technique for volatility spillovers include Mensi et al. [45] and Yu et al. [53]. The tests provided empirical evidence for the acceptance or rejection of the formulated hypotheses.
3.2. Model Specification
There is a discussion among the researchers about which of the models, BEKK-GARCH (developed by Engle and Kroner [60]) or DCC (developed by Engle [61]), is more precise. Caporin and McAleer performed an extensive analysis of the reasons for two similar models co-existing. They argued that BEKK is used to forecast conditional covariance and DCC to forecast conditional correlation. They also mentioned that the final choice must be made considering performance and appropriate framework [62]. Several studies showed that DCC is more suitable for portfolio analysis and BEKK for individual assets [63,64,65]. Therefore, for our study, we chose the BEKK-GARCH model.
As acceptable in macro-economic analysis, it was necessary to specify the univariate GARCH (p,q) model before the E_GARCH and BEKK-GARCH models. The inclusion of the univariate GARCH model prior to the models to be used is hinged on the understanding that the multivariate BEKK-GARCH model is an extension of the univariate model [66].
The conditional mean equation is as follows:
where = conditional expected returns.
= conditional heteroscedastic error.
The conditional variance equation is as follows:
where = GARCH term.
The multivariate full BEKK-GARCH is as follows:
The multivariate Full BEKK model was employed to measure volatility spillover between energy and commodity prices in global markets. Volatility spillovers can be unidirectional or bidirectional. It is unidirectional when the lagged volatility of one variable, A, affects the present volatility of another, B, but the lagged value of variable B is not significant in determining the current volatility of variable A. Bidirectional volatility spillovers have lagged values of both variables affect present values of the variables, respectively. Liu et al. also used this data analysis method to determine volatility spillover [67].
Model
The mean equation of the BEKK_GARCH model was specified according to Engle and Kroner [60]:
where Rt(i) is the return on asset i in time t.
µ is the intercept term or constant in the mean equation; it represents the average return of the financial asset i when all other explanatory variables are zero.
is the coefficient associated with the lagged returns Rt(i); it represents the effect of the current period’s return on the current period’s return of the financial asset i.
is the coefficient associated with the lagged returns Rt−1(i); it represents the effect of the lagged (previous period’s) return on the current period’s return of the financial asset i.
is the error term or residual at time t.
The mean equation is expanded below, adapted from Liu et al. [67]:
where Rt(i) is the return on asset i in time t.
denotes the absolute value function, which ensures that the total return Rt(i) is non-negative.
Ret(i) represents the excess return of the asset i in time t.
Rct(i) represents the common return or systematic return of the asset i in time t.
and are the excess return and common return residuals or error terms for the asset i in time t.
is a matrix of coefficients representing the autoregressive parameters for the excess and common returns. It captures the lagged relationship between the excess and common returns at time t − 1.
and are the excess return and common return error terms or residuals for the asset i in time t − 1.
The conditional variance equation is given below:
where Ht is the conditional variance–covariance matrix.
C is a matrix of coefficients used to model the impact of exogenous variables on the conditional covariance matrix Ht.
A is a matrix of coefficients used to model the impact of lagged error terms on the conditional covariance matrix Ht.
is the vector of lagged error terms or residuals for the asset i in time t − 1.
B is a matrix of coefficients used to model the impact of lagged conditional covariance matrices on the conditional covariance matrix Ht.
, , , are transpose of matrices for A, B, C, , respectively.
Ht is the conditional variance—2 × 2 covariance matrix:
is the conditional covariance between the excess return and the common return (or the cross-covariance between the two variables) at time t for the asset i.
is the conditional covariance between the common return and the excess return (or the cross-covariance between the two variables) at time t for the asset i.
is conditional variance of the common return (or the second variable) at time t for the asset i. The equations are expanded below:
where are coefficients used in the equation to model the relationship between different variables.
Equations (7)–(10) express the transmission of volatility patterns from commodity markets to energy markets and vice versa.
The log-likelihood function for a Baba, Engle, Kraft, and Kroner estimation is as follows:
This function in a BEKK estimation quantifies a model’s goodness of fit to the data being analysed. It delivers a numerical metric that assesses the degree to which the BEKK model’s estimated parameters describe the covariance structure of multivariate time series. In a BEKK estimation, this function is the logarithm of the associated function of the probability density of the study time series, assuming a specified parametric shape for the covariance matrix of the series. It is essential to the maximum likelihood estimation (MLE) method. By maximising the log-likelihood function, it discovers the coefficient values that make the observed data most likely under the assumed BEKK model (Livingstone and Nur) [68]. A greater log-likelihood value indicates that the model better fits the data, showing that the estimated parameters properly represent the covariance patterns of the multivariate data.
The conditional log-likelihood function is presented as follows:
where represents the log-likelihood function, which is a function of the parameters of the model.
T is the total number of observations in the dataset or time periods.
represents the vector of residuals or error terms at time t, parameterised by .
4. Results
4.1. Data Presentation
As outlined in the preceding chapter, the study utilised daily price data from energy and commodities markets over a specific timeframe. These data, sourced from reputable market platforms, are detailed in the appendices section and are denominated in dollars. Although the data are presented graphically for clarity and convenience, the original figures are included for reference (Figure 1).
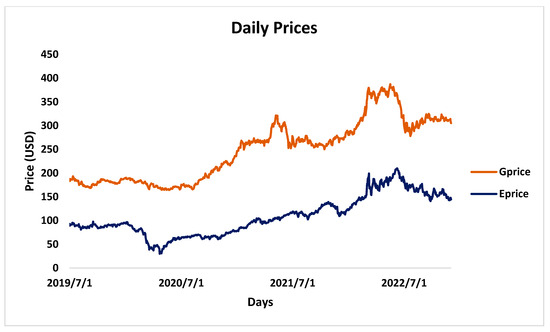
Figure 1.
Daily prices in energy and grains market (www.investing.com, accessed on 14 February 2023).
The plot in Figure 1 above shows grains and energy prices visualised with prices on the y-axis in USD and periods on the x-axis in chronological order. Grains ranged from USD 164.46 to USD 387.45 through the 866-day window under study, while energy prices fluctuated between USD 30.06 and USD 210 within the same period. For both markets, the study finds fair stability in the second half of 2019 before a weak plunge from January 2020 to May of the same year and a moderately consistent rise in prices for energy securities until March 2022. However, the commodities market experienced a short price spike between April and June of 2021. The plot also shows similar price movement between March 2022 and July 2022 with joint upward and downward movement, except that commodity markets fluctuated by higher magnitudes, as shown by the length and steepness of corresponding gradients. However, the raw price values were not used in the further analysis because GARCH modelling requires changes in target values to be analysed to reflect measures of volatility instead of direct values. These values are usually referred to as “returns”. The concept of returns in investment markets stems from favourable or adverse price changes in which investors record gains or losses, respectively. Returns are derived from expressing the difference in prices of a current and past period as a fraction of the price in the current period. Figure 2 and Figure 3 below are plots of calculated returns solved in spreadsheets for both grains and energy prices.
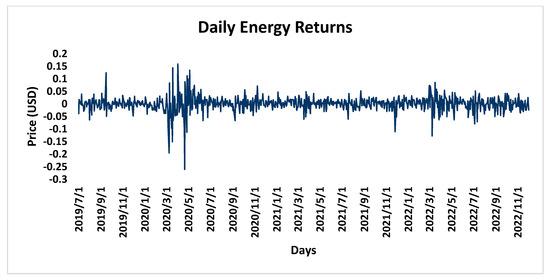
Figure 2.
Returns from daily prices in energy market (calculated by authors).
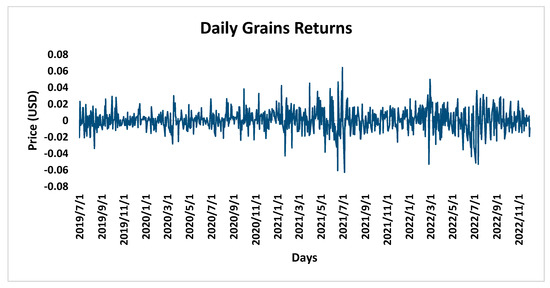
Figure 3.
Returns from daily prices in grains market (calculated by authors).
Energy returns were found to be fairly stable for most of the period. However, from March 2019 to May 2019, it experienced a notable increase in volatility, with daily returns experiencing more significant fluctuations. The same behaviour was seen in March 2022, although with a less vigorous intensity.
For grains, volatility was more noticeable, with spikes in June to July 2021, March 2022, and July 2022. Volatility follows an upward trend, with higher spikes seen in later years compared to earlier periods.
4.2. Descriptive Statistics
Descriptive statistics summarises the features of a dataset relating to specific variables. It is a concise approach to explaining and interpreting data without making inferences. Usually, descriptive statistics employed in academic research consist of measures of averages, dispersion, and normality of data. This study’s average measures are mean, minimum, and maximum statistics (Table 2). Dispersion in the dataset is measured using standard deviation, and kurtosis values give normality assessment.

Table 2.
Descriptive statistics of variables.
Throughout the period, grain prices averaged USD 248.03, while energy prices had a mean value of USD 108.72. All-time high values within the period of study were USD 387.45 and USD 210 in the grains and energy markets, respectively. The lowest prices in the same order were USD 164.6 and USD 30.06. Standard deviation statistics for grains and energy markets are 63.67 and 41.11, depicting values far from the mean and, thus, primarily spread. When examining returns, the mean return on grain prices is 0.065%, implying that, on average, alteration in grain prices is by 0.065%. Energy prices, in the same vein, have a 0.095% average daily return. The highest positive returns recorded in the energy market had prices rise by 15.9% in a single day, while the maximum rate of positive change per day in the grains market for the period had prices rise by 6.4%. Returns fell by 26%, depicting the deepest trough recorded in the energy market during the study period. Grains market had returns fall by at most 6% (minimum value = 0.06). Dispersion statistics were 0.13 and 0.29 for returns in grains and energy markets, respectively, showing that values were relatively clustered around mean values. Higher kurtosis values imply sharper peaks in the dataset, while lower values confirm that data distribution is flatter. By the rule of thumb, a kurtosis value above or below the absolute value of 3 shows that the dataset does not comply with assumptions of normality. Only returns from grain markets follow a normal distribution and are described as mesokurtic since the k statistic is approximately equal to 3 (k = 2.66 ≈ 3; probability of extreme or outlier values is zero). The kurtosis statistic of 13.89 for energy returns confirms that the dataset is leptokurtic (the distribution has a higher frequency of its values within the tail region and is most likely to have a higher frequency of extreme values). Datasets for the original prices of both markets have k values of −1.072 and −0.681. They are described as platykurtic (tails are thin, revealing that the distribution has a shallow frequency of outliers). Additionally, the Jarque–Bera test was performed (Table 3).

Table 3.
Jarque–Bera test results.
H0: Data are normally distributed;
Ha: Data are not normally distributed.
According to the data provided in Table 3, the null hypothesis shall be rejected; therefore, the data are not normally distributed.
4.3. Stationarity and Co-Integration Tests
Time series tend to vary over time. However, statistical inference requires the assumption that time series possess statistical properties that do not change over periods; in other words, time series do not exhibit long-term trends across the distribution [69]. The assumption of stationarity seeks to ensure that models are more reliable and forecasts are more accurate. Stationarity was tested using the augmented Dickey–Fuller tests, and outputs are contained in the table below (Table 4):

Table 4.
Stationarity of variables—augmented Dickey–Fuller test.
According to the literature, ADF statistics has the null hypothesis of data being stationary or constant with time, while the alternate hypothesis proposes that the dataset possesses a unit root.
H0: Time series is non-stationary or has a unit root;
Ha: Time series is stationary or has no unit root.
Higher absolute values of negative ADF statistics provide more substantial evidence of stationarity. However, a more accurate confirmation is the comparison of the derived p-value with the adopted p-value for the study, which, by rule of thumb, is 0.05 or 5% for research in social and business research. The acceptance of either of the hypotheses formulated above hinges on the significance of the statistic as determined by the p-value. A p-value higher than 0.05 depicts non-significance and acceptance of the null hypothesis, while values lower than 0.05 confirm significance, rejection of the null hypothesis, and acceptance of the alternate hypothesis. As shown in the stationarity table, most statistical tools use asterisks to denote significance at specified significance levels.
Outputs in Table 4 show that ADF statistics for energy returns is −29.34799, which is significant at 0.05, confirming the acceptance of the alternate hypothesis that the dataset is stationary. The same is found for grain returns with ADF statistic of −28.08475 with similar significance result. Therefore, datasets for both variables do not possess unit roots and are, thus, classified as stationary at the I(0) level.
Additionally, the Phillips–Perron unit root test and KPSS test for trend stationarity were performed (Table 5 and Table 6).

Table 5.
Phillips–Perron unit root test.

Table 6.
KPSS test.
H0: Time series has a unit root;
Ha: Time series has no unit root.
According to the results presented in Table 5, we can reject the null hypothesis at the significance level of 0.05. Therefore, the outcome of the test is consistent with the outcome of ADF statistics.
H0: The data are trend stationary;
Ha: The data are not trend stationary.
Since the p-value is greater than 0.05, we fail to reject the null hypothesis; the data are trend stationary.
Co-integration implies that time-series analysis requires that long-term relationships are tested among or between variables. Using the Johansen co-integration test, this study tests the long-term relationship between energy and grain market returns (Table 7). The toll is used because datasets for both variables are stationary at the same level; otherwise, the ARDL Bounds test would have been applied.

Table 7.
Johansen co-integration output.
The co-integration outcome in Table 7 shows that returns in both energy and grains markets have a long-term relationship as given by the ‘at most 1’ value of 0.1537 significant at 0.05 level as depicted by the asterisk. The existence of co-integration denotes an ongoing equilibrium interaction between returns in each of the markets under study, facilitating long-term modelling and forecasting of their trends.
4.4. Test for ARCH Effects
ARCH effects in a time series show that volatility clustering is visible in data distribution, mainly in financial time series within specific periods. Statistically, these effects reveal whether residuals are homoscedastic or heteroscedastic. When residuals are homoscedastic, it implies that the residuals across periods are equal or that the variance is approximately zero. Heteroscedastic residuals, on the other hand, imply that residuals have uneven variances [70]. As stated in the previous chapter, ARCH effects are a mandatory assumption for GARCH analysis and were thus conducted on both variables.
H0: ARCH effects are not present;
Ha: ARCH effects are present.
The acceptance of either hypothesis formulated above hinges on the significance of the statistic as determined by the p-value expressed in the time series sub-section testing stationarity. Table 8 contains statistics measuring ARCH effects in each variable distribution.

Table 8.
Heteroscedasticity test outputs.
Arch effects tests show values of 71.696 and 66.344 for energy market returns and 20.879 and 20.433 for grains market returns. All values are found to be significant (p < 0.05) and depict the acceptance of the alternate hypothesis that ARCH effects exist in both datasets. Finding ARCH effects confirms the suitability of the datasets for volatility modelling with GARCH estimations.
4.5. BEKK-GARCH Analysis
After the satisfaction of the ARCH effects condition, the BEKK-GARCH analysis was conducted on both variables to determine the existence of instability transmission across the two exchanges (Table 9).

Table 9.
BEKK-GARCH estimates.
A022 represents the constants in the variance equation in the energy market and are unconditional variance or long-term variance of returns from energy markets. Also called the intercept of the variance equation, the value 0.005558 captures the expected volatility if no past conditional variances or shocks from past volatility of the time series affect current volatility. In other words, it is the baseline variance around which the conditional variance revolves or varies. For commodity markets, baseline variance marked as A011 stood at 0.002689, revealing the fluctuations in returns that occur at a given time without interference from past volatility. Comparing baseline volatility values in both markets, the unconditional variance of energy returns is larger than the baseline value of commodity markets (0.005558 > 0.002689). Higher variance values denote increased turbulence and imply that the unconditional volatility in the energy market is higher than the inherent baseline volatility in commodity markets.
The following outcome analysed was the volatility persistence of each of the markets. Volatility persistence refers to the propensity of a set of financial time series to display a substantial level of autocorrelation in its fluctuation over time [71]. Volatility persistence suggests that times of turbulence are prone to be followed by periods of turbulence, while more stable periods tend to follow one another. To measure volatility persistence, the values labelled A11 and A22 were examined. Energy returns had a persistence measure of 0.35, implying a moderate degree of autocorrelation in the volatility of the time series, and this was also seen to be significant at 5% (p = 0.00 < 0.05). The persistence value also confirms that more volatile periods of returns were accompanied by more periods of like-elevated volatility. In contrast, periods of more stable movements were clustered around one another. The significance found proves that volatility in previous periods influences the volatility in returns in current periods. However, the low value, 0.35, indicates that the influence is not extremely strong since 0.35 is far from 1. In other words, the effect on current volatility does not occur immediately or does not stay too long in this market.
Concerning the commodity market, corresponding volatility persistence within own movements labelled as A11 was 0.25, which was significant, as confirmed by the p-value of less than 0.05. Persistence was found, as denoted by the significance, showing that fluctuations in grain returns of previous periods impact fluctuations in grain returns in current periods. However, persistence is weak, given its closeness to 0 more than proximity to 1. Comparing the volatility persistence of both energy and commodity returns, the volatility clustering in the commodity market is less than in the energy market (0.35 > 0.25).
The next stage of analysis is focused on volatility spillover impacts. Volatility spillover occurs when shocks from past fluctuations of a market influence the current fluctuations in another market. Before the analytical details, the study formulates a hypothesis from the study’s research objectives outlined in the introductory chapter. Formulating hypotheses in quantitative research is essential because it is the foundation for statistical approaches and reporting study findings [72].
The null and alternate hypotheses are formed for each question in line with hypothesis formulation patterns.
H0: No volatility spillover exists across commodity and energy markets.
Ha: There is volatility spillover across commodity and energy markets.
H0: Spillovers of volatility do not vary over time.
Ha: Spillovers of volatility vary over time.
As obtainable in decisions on probability values in other sections, accepting the null hypothesis as accurate is on the basis that the p-value surpasses 0.05 while rejecting the null hypothesis and accepting the alternate would hold when the p-value is less than 0.05.
In a BEKK-GARCH equation, the parameters B11, B12, B21, and B22 capture the spillover effect between two markets. These parameters represent the conditional covariance dynamics between the markets over a specified period. Generally, the spillover effect on the BEKK-GARCH output, as contained in Table 6, is measured numerically from a specific formula as given below:
The positive value depicts that past shocks emanating from volatility in one market will drive present fluctuations in the other. Precisely, B11 and B22 capture the contemporaneous effects: volatility spillover from one market to another within the same period. In contrast, B12 and B21 capture the lagged effects, the delayed spillover between markets.
Examining contemporaneous or the instantaneous spillover of return shocks from commodity markets to energy markets, the B11 coefficient, 0.945622, is applicable. The B11 coefficient is positive and has a corresponding probability value of 0.00, which validates the significance of the confidence level of the study. Therefore, return shocks in commodity markets are instantaneously transmitted to energy markets. Volatility within the commodity market in the current period significantly impacts the current volatility in the energy market. For the contemporaneous spillover from the energy market to the commodity market, the spillover effect is assessed with the B22 coefficient of 0.911215, which is positive and found to be significant (p < 0.05). This depicts that return volatility in energy markets is also instantaneously transferred to the commodity market. Volatility within energy markets in the current period considerably impacts today’s significant fluctuation in the commodity market. Larger values depict a more substantial contemporaneous spillover effect. This spells that although volatility transmits instantaneously and significantly from each of the markets to the other, the shocks from commodity markets are stronger in impacting the energy market than the shocks from the energy markets influence the commodity market on the same day (0.945622 > 0.911215).
On lagged spillover effects, spillover from the commodity market to the crude oil market is given by the B12 parameter of −0.00568. The negative coefficient, which is also insignificant (p > 0.13), confirms that the lagged effect spillover from the commodity market to the energy market is absent or very weak. More clearly stated, the volatility of returns in commodity markets in past periods does not reflect significantly on today’s movements in returns in the energy market. Also, lagged transmission effects from the energy market to commodity markets, as defined by the insignificant B21 coefficient of −0.0163, suggest that energy markets do not have lagged spillover transmission.
Finally, the log-likelihood value indicates a better fit of a BEKK model to the data, showing that the calculated parameters adequately reflect the covariance structure. It implies that the selected BEKK model is a suitable representation of a set of multivariate time series. From Table 6, the log-likelihood value is 4623.429 and can be categorised as a high positive value. Therefore, it assesses the BEKK model as an appropriate representation of the return’s series in the energy and grains markets. Clearly stated, shocks from energy markets from fluctuations in previous periods do not impact the volatility in commodity markets in subsequent periods.
4.6. Volatility Charts
Figure 4 contains the conditional variance and covariance of the two markets. A conditional variance chart is a graphical representation of the time-dependent volatility of specified time-related data. It reveals the pattern with which the variance of the series changes over time by capturing periods of high and more stable volatility.
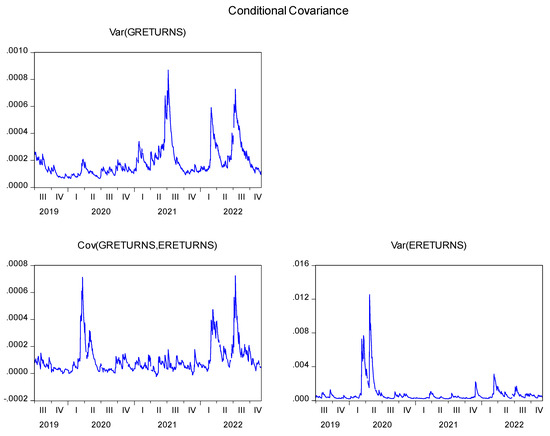
Figure 4.
Conditional variance and covariance charts.
The first chart, the only one on that row, illustrates the fluctuation patterns of returns in the grains or commodity arrangements. The graph shows clustering between April 2020, June 2021, October 2021, and March 2022. By clustering, the chart shows that the variance of the time series remains identical for an extended period, as seen in low-volatility days followed by low-volatility days; movements are fairly identical within this period. This is also referred to as persistence, which was significant in numerical measures. On patterns, the chart can be easily grouped into two regimes: the low volatility regime would extend from 2019 to 2020, and the other regime would be named the high volatility regime, given the spikes observed within the 2021 and 2022 periods. This confirms a point of structural break at the end of 2020, given that the volatility pattern shifted abruptly. Focusing on extreme events as denoted by spikes, an outlier volatility was found in the second quarter of 2021, while other spikes were found between the first and third quarters of 2022. The spikes are related to sudden shifts in investor sentiments, given shocks from the recovery from the COVID pandemic and the predicted food crisis due to the Russian–Ukrainian war.
The following chart examined from the figure illustrates conditional time-varying volatility in energy markets and is positioned rightwards on the second row. The graph shows clustering between April of 2020 and December of 2021 and the last three quarters of 2022. Low volatilities cluster around each other days within this period and provide evidence of volatility persistence as analysed previously. When observing the patterns of time-varying volatility, the chart does not reveal any structural breaks across the study period. Sharp spikes in outlier identification were found between the first two quarters of 2020. The spikes can be attributed to the news of disruption of economic activities in the advent of the coronavirus crisis. Much weaker spikes were also found between October 2021 and September 2022, and these sharp fluctuations are attributed to the Russian–Ukrainian war.
When comparing the plots in the variance charts of both markets, there are spikes in the first two quarters of 2020, except that the spikes are much more extreme in energy markets, unlike commodity markets with weak spikes in the period. Spikes observed from the first quarter of 2022 in commodity markets have corresponding movements in energy markets, although the spikes are much weaker. In the 2021 fiscal period, both markets had moved independently with tranquillity or stability of returns.
In the energy market and turbulence of returns in the commodity market, given that 2021 was the only annual period in which volatility operated independently and other periods had similar volatility behaviours, evidence exists on the contemporaneous impacts of both markets on each other.
The last chart in the figure is the covariance chart of G-returns and E-returns. Covariance measures the time-varying correlation between changes in a set of variables. A conditional covariance chart shows the time-varying covariance between two assets, providing insights into volatility transmission effects and the dynamic relationship between the assets across periods. Therefore, the conditional covariance graph above is a plot of the correlation of the volatility in energy returns and volatility in commodity returns conditional on periods. The relationship between the volatilities in both markets intensified in the first quarter of 2020 and the first and third quarters of 2022 between 0.0004 and 0.0007. Persistence is found from April 2020 to March 2022, suggesting a strong and continuous relationship between the assets, implying that the assets are interdependent. Shocks from one market impact volatility in the other market, and this spillover between the markets varies across periods.
Figure 5 presents the conditional correlation chart. Conditional correlation describes the dynamic relationship between returns of different financial instruments.
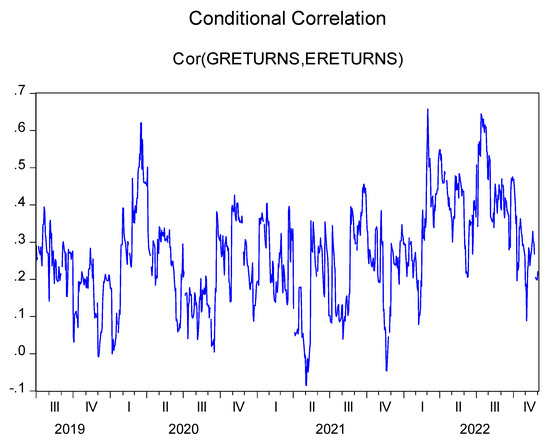
Figure 5.
Conditional correlation chart.
The conditional correlation graph above displays a largely volatile pattern. At the same time, the moving pattern from a general view is an ascending trend, with the association between energy returns and commodity returns from around −0.1 to about 0.65. The relationship between returns in both markets is also mostly positive, implying that energy and commodity returns are often directly associated with each other. In other words, the returns from both markets fluctuate in the same direction most of the time but at varying degrees, from being weakly to strongly correlated across periods. Persistence is also mostly short-lived as large ones, and vice versa, follow minor variances. The negative values of B21 and B12 also confirm that a change in volatility of one of the markets would negatively affect the relationship between both markets (conditional correlation) but on an insignificant scale.
4.7. Post-Diagnostic Checks
Although the log-likelihood value had been interpreted to support the significance of the model, it is recognised in the literature that the log-likelihood value does not indicate the economic or financial relevance of the computed parameters. As a result, researchers and analysts frequently employ other post-diagnostic tests to examine the BEKK model’s economic significance and the accuracy of its parameter estimations in capturing the complex nature of multivariate financial time series data. Post-diagnostic measures of the model were the test for heteroscedasticity and autocorrelation of residuals (Table 10 and Table 11).

Table 10.
Autocorrelation and partial correlation test.

Table 11.
Post-GARCH heteroscedasticity test.
Autocorrelation in residuals denotes that the model fails to incorporate all necessary information in the data, thus weakening the model. It also depicts the model under-fitting the data and failing to capture some time-dependent patterns in volatility. All p values are insignificant and confirm the absence of autocorrelation or partial correlation of residuals in the estimated GARCH model.
GARCH modelling incorporates lagged squared residuals in the conditional-variance specification. However, if the model fails to capture these ARCH effects adequately, it results in significant heterogeneity in the residuals (value where p < 0.05). As a post-diagnostic test, heteroscedasticity was also absent in residuals after the modelling, as the p-value was above 0.05. The absence of heteroscedasticity also indicates that the model captures essential nonlinearities. The model passed robustness checks and is thus valid according to econometric modelling.
5. Discussion
This study aimed to assess volatility transmission between energy and commodity markets, as well as the potential interdependence and spillover effects between both arrangements. The findings provide significant insights that help in grasping cross-market volatility patterns. The results tested time volatility within the individual markets before spillover parameters, and thus, own volatility in each of the markets is first discussed before spillover outcomes.
The energy and commodity markets had significant volatility. The price changes of energy products can be linked to the changing dynamics of demand and supply for crude oil. These changes could be caused by disruptions in oil production, adjustments in global oil consumption patterns, geopolitical events in oil-producing countries, and unexpected shifts in demand caused by economic events such as recession. Volatility in commodity markets, particularly in grains as a food item, was also discovered to be significant and relatively persistent. This can be attributed to being influenced by weather conditions, climate change effects, population growth, and changing food demands. Persistence found in markets confirms that future values can be predicted from past values with a significant level of accuracy. Periods of high covariance are specifically risky for investors with both asset classes in their portfolio, as negative returns imply negative returns in another inhibiting cushioning effect. Conversely, the assets may provide better diversification in periods of lower covariance.
The analysis also showed a bidirectional volatility transfer between the energy and commodity markets. Changes in one market’s volatility can affect and be affected by fluctuations in the other due to interconnectedness, shared resources, geopolitical events, economic growth, and technological shifts. Globalisation and financial integration have increased linkages between these markets, resulting in synchronised prices and trading behaviours. Moreover, investor behaviour, risk management, interconnected supply chains, and the integration of non-financial markets with financial markets are possible contributors to this volatility transfer. The study also highlights the impact of major global events like the COVID-19 pandemic and geopolitical conflicts on both markets, as volatility patterns were noticeably different within these periods on the plotted volatility charts.
Several studies have examined the interconnections and influences between commodity markets, mainly focusing on energy and agriculture commodities, and found interdependence between commodities and crude oil markets as follows:
Previous studies have consistently highlighted the interdependence between crude oil prices and agricultural commodity markets [1,36,51]. Xiarchos and Burnett studied volatility spillover between maise, energy commodities, and ethanol futures prices, indicating significant risk transfer [58]. Ghorbel and Jeribi examined variability spillover among energy and financial commodities during the pandemic, revealing fluctuation shocks transferring from energy to other assets [57]. Shahani and Taneja explored the impact of crude oil fluctuations on energy crops in India [55]. Significant effects on sugarcane and wheat were observed, with asymmetry in the impact of declining and rising crude prices. Lu et al. also found bivariate volatility spillovers between crude oil and agricultural commodities. The authors also found that the spillover was time-varying, with more volatility found in times of crisis—the 2008 global meltdown [36]. Similarly, Gardebroek and Hernandez studied turbulence flow among petroleum, ethanol, and maise prices. They found that volatility transfer occurred across the markets, and this spillover varied with time, with most volatility found after the 2006 fiscal year [54]. The present research aligned with these findings, demonstrating a significant bidirectional spillover between energy and commodity markets. This consistency underscores the enduring relevance of these market interactions.
The summarised comparative findings above are a collection of related works that found spillover from energy markets to commodity markets, on the one hand, and similar spillover from commodity markets to energy markets, showing strong interdependence of both markets and of various studies related to the interdependence between commodities, particularly crude oil and agricultural produce, are as follows:
However, nuanced differences emerge when examining the direction of volatility spillovers. Nazlioglu et al. analysed fluctuation dissemination between oil and specific agricultural commodities using causality in impulse response and variance functions. They reported that oil market volatility spreads to agricultural markets post-crisis, impacting agricultural investments [35]. However, spillover was univariate as volatility transfer was absent from agricultural investments to oil markets. Umar et al. also had shocks from oil volatility transmitted to the volatility behaviour of food commodities, particularly during economic distress [50]. However, the study did not record any spillover from food commodity markets to oil markets. This discrepancy with the present study’s findings could be attributed to the specific commodities considered in each of the studies used for comparative purposes or the evolution of market dynamics over time since both studies investigated spillovers before 2020. Lu et al. observed bidirectional volatility spillovers during the 2008 financial crisis [36]. In contrast, our study reveals a more pronounced effect of agricultural commodity volatility on crude oil prices after the coronavirus crisis and war outbreak.
Although the studies referenced delved into the intricate relationships between energy and agricultural commodity markets and found univariate or bivariate variability spillover across both market arrangements, a few studies negate the actual findings of this research as they found volatility of each of the two markets utterly independent of each other. Our results diverge from those of Dutta and Noor, who found no volatile connection between agricultural and oil trading platforms but identified oil fluctuations as causal factors for instability in non-energy composite markets due to their role in metal production [56]. Kaulu, in the same vein, found no impact of crude oil costs on maise prices, although Granger causalities and auto-regression models were used [49]. This discrepancy could be attributed to differences in data types, data periods, market conditions, or methodological approaches employed.
The present study provides a comprehensive exploration of the interplay between energy markets and commodity markets. While consistent with some prior findings, the study unveils context-specific effects that enrich the understanding of these complex relationships. This study extends the temporal scope of previous research, encompassing significant economic crises such as the recent COVID-19 pandemic and the Russian–Ukrainian war. This temporal extension, in alignment with the approach of Umar et al. [50], enables us to examine the varying dynamics of volatility connectedness during economic distress, further enriching our understanding of how shocks are transmitted through these markets.
The research not only offers theoretical insights but also practical implications. Directly identifying significant volatility spillovers affects risk management strategies for investors and policymakers alike. By shedding light on the dominant role of oil volatility shocks and their potential to amplify market uncertainties, the study contributes valuable insights that can inform decision-making during economic turbulence.
Moreover, the study findings confirm and extend the conclusions from earlier research. While it aligns with the observations made by studies like Xiarchos and Burnett regarding spillovers [58], the study also departs from the mutual causality inference proposed by Yanpeng et al. [51], highlighting a more transparent and less- biased relationship between grains and oil prices. This nuanced perspective contributes to a more comprehensive understanding of the mechanisms driving price movements across these markets.
Considering the evolution of research over time, this study contributes to the field’s understanding by incorporating the unique context of the coronavirus pandemic. Ghorbel and Jeribi have identified substantial dynamic correlations between energy assets and commodities indexes during the pandemic [57]. This is congruent with our observation of fluctuation shocks transferring from energy to grain commodity assets. This underscores the contagion influence of the pandemic on various markets, a facet that was less explored in earlier works. Considering the evolving landscape and unique market conditions, the contributions expand the knowledge base and pave the way for further investigation.
6. Conclusions
The summary of the findings is the following:
- Both energy and commodity markets have significant unconditional or baseline volatility. The results also confirm that commodity markets have less risk than energy markets.
- Volatility persistence is significant despite not being so strong in both markets. Persistence is also found to be weaker in the commodity market, confirming that volatility dissipates quickly or adjusts speedily to shocks in the market. Thus, market participants can predict future returns from past values with a significant level of accuracy.
- Volatility transmits instantaneously between energy and commodity markets, and these spillovers are also found to fluctuate across periods or vary with time. Therefore, there is a magnitude of real-time interlinkage between energy and commodity markets.
- Nevertheless, the transmission of fluctuation shocks from one market to another was insignificant when testing lagged effects. In other words, shocks from the volatility of past periods in each of the markets do not influence present fluctuations on a daily frequency.
The study explored the interconnections and transmission channels that lead to heightened volatility in both markets. Spillover effects fluctuated over time, reflecting the changing market dynamics and the evolving relationship between the two markets. The transmission was attributed to the increasing interconnectedness of markets, which can lead to stronger linkages between energy and commodity markets, making them more susceptible to spillover effects. Improved interconnectedness also supports market efficiency through a faster dissemination of information. With less information asymmetry, investors can access information better and make informed decisions on their investments in these markets, increasing the synchronisation of prices and trading behaviours across the global energy and commodity markets. As per global events, the existence of spillover of volatility-induced shocks between the markets is most likely partly responsible for economic disruptions globally in recent times from contagion effects that could arise from spillovers.
Overall, this research enhances the comprehension of the complex relationship between food and energy commodity markets, providing valuable indications for policymakers and market players seeking to navigate the challenges and opportunities presented by the bidirectional volatility spillover between these critical sectors.
Future research could entail the investigation of volatility spillovers at various price frequencies and exploring how these varying frequencies alter responses to changing economic and market situations. The role of localised or worldwide market integration in the transfer of volatility can also be measured by ascertaining the effect of cross-border trade, import/export patterns, and governmental interventions on volatility transmission across the energy and food commodity markets.
The outlined limitations represent precautions to be taken in generalising study results:
- Daily prices and returns were utilised in the study and are better for volatility modelling through GARCH, but this frequency has been criticised for increasing noise effects in modelling.
- The BEKK-GARCH model was used against other models that test volatility spillovers, which could yield conflicting results from the outcomes of others.
Author Contributions
Conceptualisation, T.P. and S.A.; methodology, S.A.; validation, T.P. and S.A.; formal analysis, T.P.; investigation, T.P. and S.A.; data curation, S.A.; writing—original draft preparation, S.A.; writing—review and editing, T.P.; visualisation, S.A.; supervision, T.P.; project administration, T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available at Investing.com (accessed on 14 February 2023).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Barbaglia, L.; Croux, C.; Wilms, I. Volatility spillovers in commodity markets: A large t-vector autoregressive approach. Energy Econ. 2020, 85, 104555. [Google Scholar] [CrossRef]
- Wang, L.; Ma, F.; Liu, J.; Yang, L. Forecasting stock price volatility: New evidence from the GARCH-MIDAS model. Int. J. Forecast. 2020, 36, 684–694. [Google Scholar] [CrossRef]
- Kalotychou, E.; Staikouras, S.K. An Overview of the Issues Surrounding Stock Market Volatility, Stock Market Volatility; Chapman & Hall: New York, NY, USA, 2009. [Google Scholar]
- World Bank. Commodity Markets Outlook. 2022. Available online: https://openknowledge.worldbank.org/bitstream/handle/10986/38160/CMO-October-2022-Special-Focus.pdf (accessed on 14 February 2023).
- Elgammal, M.M.; Ahmed, W.M.A.; Alshami, A. Price and volatility spillovers between global equity, gold, and energy markets prior to and during the COVID-19 pandemic. Resour. Policy 2021, 74, 102334. [Google Scholar] [CrossRef] [PubMed]
- OECD. The Impacts and Policy Implications of Russia’s Aggression against Ukraine on Agricultural Markets. 2022. Available online: https://www.oecd-ilibrary.org/docserver/0030a4cd-en.pdf?expires=1677677860&id=id&accname=guest&checksum=C8EA4D9474CA7E4C1CDF385FF7CE55E4 (accessed on 14 February 2023).
- Chang, C.-L.; Li, Y.; McAleer, M. Volatility Spillovers between Energy and Agricultural Markets: A Critical Appraisal of Theory and Practice. Energies 2018, 11, 1595. [Google Scholar] [CrossRef]
- Serra, T.; Zilberman, D. Biofuel-related price transmission literature: A review. Energy Econ. 2013, 37, 141–151. [Google Scholar] [CrossRef]
- Hasanov, A.; Poon, W.; Al-Freedi, A.; Heng, Z. Forecasting volatility in the biofuel feedstock markets in the presence of structural breaks: A comparison of alternative distribution functions. Energy Econ. 2018, 70, 307–333. [Google Scholar] [CrossRef]
- Davidescu, A.A.; Eduard, M.M.; Razvan, G.H.; Mihaela, G.; Oana, M.V. Exploring the contagion effect from developed to emerging CEE financial markets. Mathematics 2023, 11, 666. [Google Scholar] [CrossRef]
- Balcilar, M.; Demirer, R.; Gupta, R.; Wohar, M.E. The contagion effects of COVID-19 on US and UK stock markets: Evidence from early and late transmission stages. Financ. Res. Lett. 2020, 35, 101691. [Google Scholar]
- Corbet, S.; Lucey, B.; Yarovaya, L. Date-stamping the impact of the COVID-19 pandemic on cryptocurrency markets. Financ. Res. Lett. 2020, 35, 101554. [Google Scholar] [CrossRef]
- Bekaert, G.; Harvey, C.R.; Lundblad, C.T. Letting the data speak: Lessons from the financial crisis. J. Financ. 2013, 68, 2127–2177. [Google Scholar]
- Granger, C.W.J.; Engle, R.F. Co-integration and error correction: Representation, estimation, and testing. Econometrica 1987, 55, 251–276. [Google Scholar]
- Baur, D.G.; Lucey, B.M. Is gold a hedge or a safe haven? An analysis of stocks, bonds and gold. Financ. Rev. 2010, 45, 217–229. [Google Scholar] [CrossRef]
- Chen, Q.; Filardo, A.; He, D.; Zhu, F. News-based uncertainty measures for the US economy and their role in predicting output growth and recession probabilities. J. Futures Mark. 2018, 38, 1047–1069. [Google Scholar]
- Li, Z.; Li, X. Cryptocurrency return and volatility: Evidence from tweet sentiments. Econ. Model. 2018, 75, 373–383. [Google Scholar]
- Loutfi, J.A. Volatility Spillover Effects among Gold, Crude Oil and US Dollar Index: An analysis Using EGARCH Model. Published. Master’s Thesis, Notre Dame University-Louaize, Zouk Mosbeh, Lebanon, 2019. [Google Scholar]
- Creti, A.; Joets, M.; Mignon, V. On the links between stock and commodity markets’ volatility. Energy Econ. 2013, 37, 16–28. [Google Scholar] [CrossRef]
- Bergmann, D.; O’Connor, D.; Thümmel, A. An analysis of price and volatility transmission in butter, palm oil and crude oil markets. Agric. Food Econ. 2016, 4, 23. [Google Scholar] [CrossRef][Green Version]
- Assefa, T.T.; Meuwissen, M.P.M.; Oude-Lansink, A.G.J.M. A review of the effects of contextual factors on price volatility transmission in food supply chains. In Agricultural Markets Instability: Revisiting the Recent Food Crises; Garrido, A., Brümmer, B., M’Barek, R., Meuwissen, M., Morales-Opazo, C., Eds.; Routledge: London, UK; New York, NY, USA, 2016; pp. 85–97. [Google Scholar]
- Yonis, M. Stock Market Co-Movement and Volatility Spillover between USA and South Africa. Master’s Thesis, Umeå Universitet, Umeå, Sweden, 2014. [Google Scholar]
- Garg, M.; Singhal, S.; Sood, K.; Rupeika-Apoga, R.; Grima, S. Price discovery mechanism and volatility spillover between national agriculture market and national commodity and derivatives exchange: The study of the Indian agricultural commodity market. J. Risk Financ. Manag. 2023, 16, 62. [Google Scholar] [CrossRef]
- Krishnappa, B.; Murthy, T.K. Assessment of price volatility of commodities traded on MCX India and relationship between futures price of selected commodities and different parameters on economic factors affecting commodity markets. J. Posit. Sch. Psychol. 2022, 6, 5137–5161. [Google Scholar]
- Tadasse, G.; Algieri, B.; Kalkuhl, M.; Von Braun, J. Drivers and triggers of international food price spikes and volatility. In Food Price Volatility and Its Implications for Food Security and Policy; Springer: Cham, Switzerland, 2016; pp. 59–82. [Google Scholar]
- Ye, W.; Guo, R.; Deschamps, B.; Jiang, Y.; Liu, X. Macroeconomic forecasts and commodity futures volatility. Econ. Model. 2021, 94, 981–994. [Google Scholar] [CrossRef]
- Liu, J.; Serletis, A. Volatility and dependence in energy markets. J. Econ. Financ. 2023, 47, 15–37. [Google Scholar] [CrossRef]
- Clifford, C. How Higher and More Volatile Energy Prices Will Affect the Move to Clean Energy. EPIC. Energy Policy Institute University of Chicago. 2022. Available online: https://epic.uchicago.edu/news/how-higher-and-more-volatile-energy-prices-will-affect-the-move-to-clean-energy/ (accessed on 20 February 2023).
- Pantos, T. Volatility Spillovers in Electricity Markets: Evidence from the United States. In International Journal of Energy Economics and Policy. 2019. Available online: http://econjournals.com/index.php/ijeep/article/download/7563/4413 (accessed on 18 February 2023).
- Efimova, O.; Serletisy, A. Energy Markets Volatility Modelling Using GARCH Energy Economics. 2014. Available online: https://contacts.ucalgary.ca/info/econ/files/info/unitis/publications/1-4924855/Efimova_and_SerletisFeb14.pdf (accessed on 18 February 2023).
- Volpe, M.A. Who Controls Oil and Gas Prices in the United States? Business Week, 31 May 2022. Available online: https://www.newsweek.com/who-controls-oil-gas-prices-united-states-1710982 (accessed on 20 February 2023).
- Shively, B. How Much Primary Energy Is Wasted before Consumers See Value from Electricity? 2022. Available online: https://www.enerdynamics.com/Energy-Currents_Blog/How-Much-Primary-Energy-Is-Wasted-Before-Consumers-See-Value-from-Electricity.aspx (accessed on 20 February 2023).
- Trujillo-Barrera, A.; Mallory, M.; Garcia, P. Volatility spillovers in U.S. crude oil, ethanol, and corn futures markets. J. Agric. Resour. Econ. 2012, 37, 247–262. [Google Scholar]
- Yosthongngam, S.; Tansuchat, R.; Yamaka, W. Volatility spillovers between ethanol and corn prices: A Bayesian analysis. Energy Rep. 2022, 8 (Suppl. S10), 1030–1037. [Google Scholar] [CrossRef]
- Nazlioglu, S.; Erdem, C.; Soytas, U. Volatility spillover between oil and agricultural commodity markets. Energy Econ. 2013, 36, 658–665. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, L.; Liu, L. Volatility spillovers between crude oil and agricultural commodity markets since the financial crisis. Sustainability 2019, 11, 396. [Google Scholar] [CrossRef]
- Chan, W.H.; Shelton, B.; Wu, Y.W. Volatility spillovers arising from the financialization of commodities. J. Risk Financ. Manag. 2018, 11, 72. [Google Scholar] [CrossRef]
- Baffes, J.; Haniotis, T. Placing the 2006/08 commodity price boom into perspective. J. Agric. Econ. 2010, 61, 398–425. [Google Scholar]
- Chang, C.L.; McAleer, M. Aggregation, heterogeneity, and volatility: Evidence from energy and commodity markets. Int. Rev. Econ. Financ. 2013, 27, 416–431. [Google Scholar]
- Robe, M.A.; Wallen, J. Fundamentals, derivatives market information and oil price volatility. J. Futures Mark. 2016, 36, 317–344. [Google Scholar] [CrossRef]
- Ahmed, W.; Hu, J.; Mahmood, H. Volatility spillover between energy and agricultural commodity markets: A critical review of theory and practice. Renew. Sustain. Energy Rev. 2016, 65, 757–774. [Google Scholar]
- Zhang, Z.; Wang, Y.; Xiao, J.; Zhang, Y. Not all geopolitical shocks are alike: Identifying price dynamics in the crude oil market under tensions. Resour. Policy 2023, 80, 103238. [Google Scholar] [CrossRef]
- Dinku, T.; Worku, G. Asymmetric GARCH models on price volatility of agricultural commodities. SN Bus. Econ. 2022, 2, 181. [Google Scholar] [CrossRef]
- Wang, X.; Wu, C. Asymmetric volatility spillovers between crude oil and international financial markets. Energy Econ. 2018, 74, 592–604. [Google Scholar] [CrossRef]
- Mensi, W.; Tiwari, A.K.; Yoon, S.M. Dynamic spillovers between energy and commodity markets: The importance of period-specific shocks. Energy Econ. 2018, 75, 423–432. [Google Scholar]
- Kocak, E.; Sari, R. Oil prices and stock markets: A study of volatility spillovers. Energy Econ. 2016, 55, 107–117. [Google Scholar]
- Zhang, Y.J.; Yao, C.W.; Wei, Y.M. Spillover effects of crude oil price shocks on Chinese agricultural futures markets. Energy Econ. 2019, 81, 982–991. [Google Scholar]
- Fosu, S.; Danso, A.; Boako, G. The spillover effects of crude oil price volatility on agricultural commodities prices. Energy Rep. 2019, 5, 182–191. [Google Scholar]
- Kaulu, B. Effects of crude oil prices on copper and maize prices. Future Bus. J. 2021, 7, 54. [Google Scholar] [CrossRef]
- Umar, Z.; Jareño, F.; Escribano, A. Agricultural commodity markets and oil prices: An analysis of the dynamic return and volatility connectedness. Resour. Policy 2021, 73, 102147. [Google Scholar] [CrossRef]
- Yanpeng, S.; Nawazish, M.; Abdul, Q.; Hsin-Pei, H. Connectedness between oil and agricultural commodity prices during tranquil and volatile period. Is crude oil a victim indeed? Resour. Policy 2021, 72, 102131. [Google Scholar] [CrossRef]
- Lin, A.J.; Chang, H.Y.; Hsiao, J.L. Does the Baltic Dry Index drive volatility spillovers in the commodities, currency, or stock markets? Transp. Res. Part E Logist. Transp. Rev. 2019, 127, 265–283. [Google Scholar] [CrossRef]
- Yu, L.; Zha, R.; Stafylas, D.; He, K.; Liu, J. Dependences and volatility spillovers between the oil and stock markets: New evidence from the copula and VAR- BEKK-GARCH models. Int. Rev. Financ. Anal. 2020, 68, 101280. [Google Scholar] [CrossRef]
- Gardebroek, C.; Hernandez, M.A. Do energy prices stimulate food price volatility? Examining volatility transmission between US oil, ethanol and cornmarkets. Energy Econ. 2013, 40, 119–129. [Google Scholar] [CrossRef]
- Shahani, R.; Taneja, A. Dynamics of volatility behaviour and spillover from crude to energy crops: Empirical evidence from India. Energy Nexus 2022, 8, 100152. [Google Scholar] [CrossRef]
- Dutta, A.; Noor, H. Oil and non-energy commodity markets: An empirical analysis of volatility spillovers and hedging effectiveness. Cogent Econ. Financ. 2017, 5, 1324555. [Google Scholar] [CrossRef]
- Ghorbel, A.; Jeribi, A. Volatility spillovers and contagion between energy sector and financial assets during COVID-19 crisis period. Eurasian Econ. Rev. 2021, 11, 449–467. [Google Scholar] [CrossRef]
- Xiarchos, I.M.; Burnett, W.J. Dynamic volatility spillovers between agricultural and energy commodities. J. Agric. Appl. Econ. 2018, 50, 291–318. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Huang, Y.; Su, W.; Li, X. Comparison of BEKK GARCH and DCC GARCH Models: An Empirical Study. In Advanced Data Mining and Applications; Cao, L., Zhong, J., Feng, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6441, pp. 99–110. [Google Scholar] [CrossRef]
- Engle, R.; Kroner, K. Multivariate Simultaneous GARCH. Econom. Theory 1995, 11, 122–150. [Google Scholar] [CrossRef]
- Engle, R.F. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Caporin, M.; McAleer, M. Do we really need both BEKK and DCC? A Tale of two multivariate GARH Models. J. Econ. Surv. 2012, 26, 736–751. [Google Scholar] [CrossRef]
- Billio, M.; Caporin, M. A generalized dynamic conditional correlation model for portfolio risk evaluation. Math. Comput. Simul. 2009, 79, 2566–2578. [Google Scholar] [CrossRef]
- Caporin, M.; McAleer, M. Scalar BEKK and indirect DCC. J. Forecast. 2008, 27, 537–549. [Google Scholar] [CrossRef]
- Caporin, M.; McAleer, M. Ranking Multivariate GARCH Models by Problem Dimension. 2010. Available online: http://ssrn.com/abstract=1601236 (accessed on 1 February 2024).
- Liu, X.; An, H.; Huang, S.; Wen, S. The evolution of spillover effects between oil and stock markets across multi-scales using a wavelet-based GARCH–BEKK model. Phys. A-Stat. Mech. Its Appl. 2017, 465, 374–383. [Google Scholar] [CrossRef]
- Livingston, G.C.; Nur, D. Bayesian inference of multivariate-GARCH-BEKK models. Stat. Pap. 2023, 64, 1749–1774. [Google Scholar] [CrossRef]
- Enders, W. Applied Econometric Time Series, 4th ed.; John Wiley: New York, NY, USA, 2014. [Google Scholar]
- Schützenmeister, A.; Jensen, U.; Piepho, H.P. Checking normality and homoscedasticity in the general linear model using diagnostic plots, communications in statistics. Simul. Comput. 2012, 41, 141–154. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X.; Labys, P. The distribution of realized exchange rate volatility. J. Am. Stat. Assoc. 2001, 96, 42–55. [Google Scholar] [CrossRef]
- Binoy, S. Significance of hypothesis in research. Indian J. Holist. Nurs. 2019, 10, 31–33. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).