A Parallel Implementation of the Differential Evolution Method
Abstract
:1. Introduction
2. Method Description
2.1. The Original DE Method
| Algorithm 1: The steps of the base DE method |
|
2.2. Proposed Modifications
| Algorithm 2: The steps of the proposed method |
|
2.3. Propagation Mechanism
- 1.
- One to one. In this case, a random island will send to another randomly selected island its best value.
- 2.
- One to N. In this case, a random island will send its best value to all other islands.
- 3.
- N to one. In this case, all islands will inform a randomly selected island about their best value.
- 4.
- N to N. All islands will inform all the other islands about their best value.
2.4. Termination Rule
3. Experiments
3.1. Test Functions
- Bent-cigar function. The function iswith the global minimum . For the conducted experiments, the value was used.
- Bf1 function. The function Bohachevsky 1 is given by the equationwith .
- Bf2 function. The function Bohachevsky 2 is given by the equationwith .
- Branin function. The function is defined by with . The value of the global minimum is 0.397887 with .
- CM function. The cosine mixture function is given by the equationwith . For the conducted experiments, the value was used.
- Discus function. The function is defined aswith global minimum For the conducted experiments, the value was used.
- Easom function. The function is given by the equationwith and a global minimum of −1.0.
- Exponential function. The function is given byThe global minimum is located at with a value of . In our experiments, we used this function with and the corresponding functions are denoted by the labels EXP4, EXP16 and EXP64.
- Griewank2 function. The function is given byThe global minimum is located at the with a value of 0.
- Gkls function. is a function with w local minima, described in [56] with and n a positive integer between 2 and 100. The value of the global minimum is −1 and in our experiments, we used and .
- Hansen function. , . The global minimum of the function is −176.541793.
- Hartman 3 function. The function is given bywith and andThe value of the global minimum is −3.862782.
- Hartman 6 function.with and andThe value of the global minimum is −3.322368.
- High conditioned elliptic function, defined aswith global minimum ; the value was used in the conducted experiments
- Potential function. The molecular conformation corresponding to the global minimum of the energy of N atoms interacting via the Lennard–Jones potential [57] was used as a test case here. The function to be minimized is given by:In the experiments, two different cases were studied:
- Rastrigin function. The function is given by
- Shekel 7 function.
- Shekel 5 function.
- Shekel 10 function.
- Sinusoidal function. The function is given byThe global minimum is located at with . For the conducted experiments, the cases of and were studied. The parameter z was used to shift the location of the global minimum [58].
- Test2N function. This function is given by the equationThe function has in the specified range and in our experiments, we used .
- Test30N function. This function is given bywith . The function has local minima in the specified range, and we used in the conducted experiments.
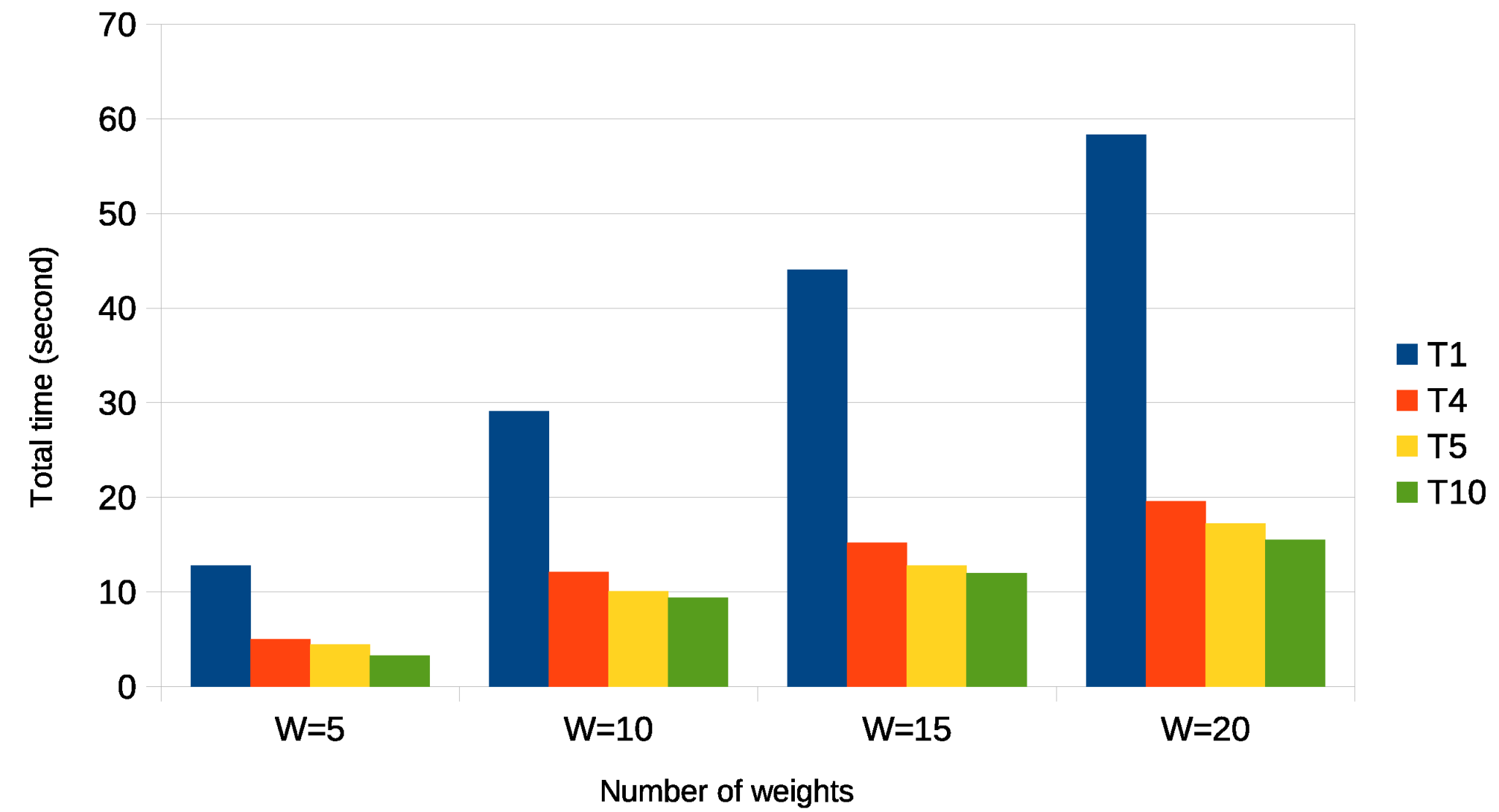
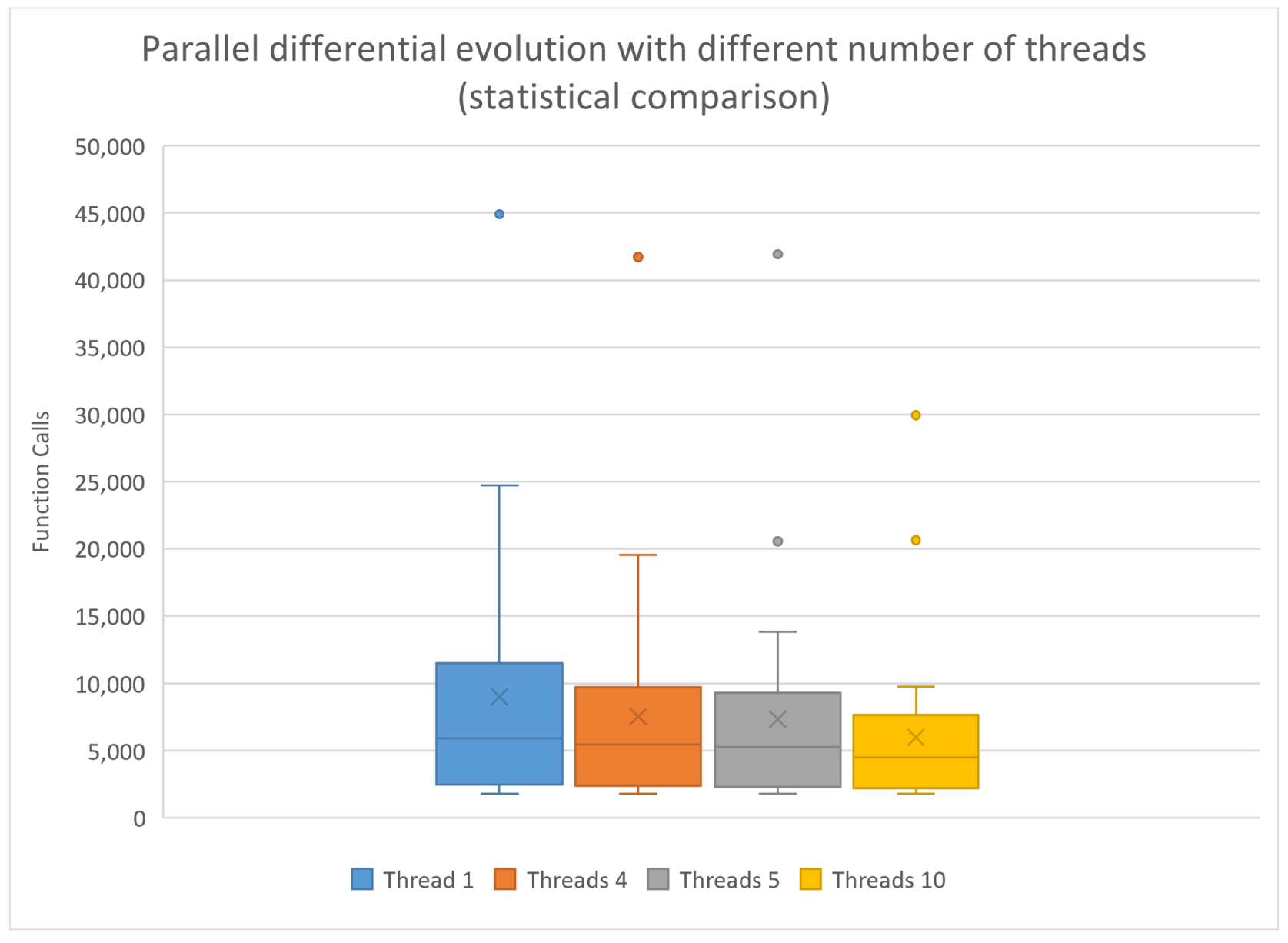
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Honda, M. Application of genetic algorithms to modelings of fusion plasma physics. Comput. Phys. Commun. 2018, 231, 94–106. [Google Scholar] [CrossRef]
- Luo, X.L.; Feng, J.; Zhang, H.H. A genetic algorithm for astroparticle physics studies. Comput. Phys. Commun. 2020, 250, 106818. [Google Scholar] [CrossRef] [Green Version]
- Aljohani, T.M.; Ebrahim, A.F.; Mohammed, O. Single and Multiobjective Optimal Reactive Power Dispatch Based on Hybrid Artificial Physics–Particle Swarm Optimization. Energies 2019, 12, 2333. [Google Scholar] [CrossRef] [Green Version]
- Pardalos, P.M.; Shalloway, D.; Xue, G. Optimization methods for computing global minima of nonconvex potential energy functions. J. Glob. Optim. 1994, 4, 117–133. [Google Scholar] [CrossRef]
- Liwo, A.; Lee, J.; Ripoll, D.R.; Pillardy, J.; Scheraga, H.A. Protein structure prediction by global optimization of a potential energy function. Biophysics 1999, 96, 5482–5485. [Google Scholar] [CrossRef] [Green Version]
- An, J.; He, G.; Qin, F.; Li, R.; Huang, Z. A new framework of global sensitivity analysis for the chemical kinetic model using PSO-BPNN. Comput. Chem. Eng. 2018, 112, 154–164. [Google Scholar] [CrossRef]
- Gaing, Z.-L. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Basu, M. A simulated annealing-based goal-attainment method for economic emission load dispatch of fixed head hydrothermal power systems. Int. J. Electr. Power Energy Syst. 2005, 27, 147–153. [Google Scholar] [CrossRef]
- Cherruault, Y. Global optimization in biology and medicine. Math. Comput. Model. 1994, 20, 119–132. [Google Scholar] [CrossRef]
- Lee, E.K. Large-Scale Optimization-Based Classification Models in Medicine and Biology. Ann. Biomed. Eng. 2007, 35, 1095–1109. [Google Scholar] [CrossRef]
- Price, W.L. Global optimization by controlled random search. J. Optim. Theory Appl. 1983, 40, 333–348. [Google Scholar] [CrossRef]
- Křivý, I.; Tvrdík, J. The controlled random search algorithm in optimizing regression models. Comput. Stat. Data Anal. 1995, 20, 229–234. [Google Scholar] [CrossRef]
- Ali, M.M.; Törn, A.; Viitanen, S. A Numerical Comparison of Some Modified Controlled Random Search Algorithms. J. Glob. 1997, 11, 377–385. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef] [Green Version]
- Eglese, R.W. Simulated annealing: A tool for operational research. Simulated Annealing Tool Oper. Res. 1990, 46, 271–281. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liu, J.; Lampinen, J. A Fuzzy Adaptive Differential Evolution Algorithm. Soft Comput. 2005, 9, 448–462. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.K.; Blackwell, T. Particle swarm optimization An Overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef] [Green Version]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning, Addison; Wesley Publishing Company: Reading, MA, USA, 1989. [Google Scholar]
- Michaelewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Grady, S.A.; Hussaini, M.Y.; Abdullah, M.M. Placement of wind turbines using genetic algorithms. Renew. Energy 2005, 30, 259–270. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Romeijn, H.E.; Tuy, H. Recent developments and trends in global optimization. J. Comput. Appl. Math. 2000, 124, 209–228. [Google Scholar] [CrossRef] [Green Version]
- Fouskakis, D.; Draper, D. Stochastic Optimization: A Review. Int. Stat. Rev. 2002, 70, 315–349. [Google Scholar] [CrossRef]
- Rocca, P.; Oliveri, G.; Massa, A. Differential Evolution as Applied to Electromagnetics. IEEE Antennas Propag. Mag. 2011, 53, 38–49. [Google Scholar] [CrossRef]
- Lee, W.S.; Chen, Y.T.; Kao, Y. Optimal chiller loading by differential evolution algorithm for reducing energy consumption. Energy Build. 2011, 43, 599–604. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H. Flexible job shop scheduling using hybrid differential evolution algorithms. Comput. Ind. 2013, 65, 246–260. [Google Scholar] [CrossRef]
- Xu, L.; Jia, H.; Lang, C.; Peng, X.; Sun, K. A Novel Method for Multilevel Color Image Segmentation Based on Dragonfly Algorithm and Differential Evolution. IEEE Access 2019, 7, 19502–19538. [Google Scholar] [CrossRef]
- Schutte, J.F.; Reinbolt, J.A.; Fregly, B.J.; Haftka, R.; George, A.D. Parallel global optimization with the particle swarm algorithm. Int. J. Numer. Methods Eng. 2004, 61, 2296–2315. [Google Scholar] [CrossRef]
- Larson, J.; Wild, S.M. Asynchronously parallel optimization solver for finding multiple minima. Math. Comput. 2018, 10, 303–332. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Tzallas, A.; Tsalikakis, D. PDoublePop: An implementation of parallel genetic algorithm for function optimization. Comput. Phys. Commun. 2016, 209, 183–189. [Google Scholar] [CrossRef]
- Kamil, R.; Reiji, S. An Efficient GPU Implementation of a Multi-Start TSP Solver for Large Problem Instances. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; pp. 1441–1442. [Google Scholar]
- Van Luong, T.; Melab, N.; Talbi, E.G. GPU-Based Multi-start Local Search Algorithms. In Learning and Intelligent Optimization; Coello, C.A.C., Ed.; LION 2011. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6683. [Google Scholar] [CrossRef] [Green Version]
- Barkalov, K.; Gergel, V. Parallel global optimization on GPU. J. Glob. Optim. 2016, 66, 3–20. [Google Scholar] [CrossRef]
- Weber, M.; Neri, F.; Tirronen, V. Shuffle or update parallel differential evolution for large-scale optimization. Soft Comput. 2011, 15, 2089–2107. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, X.; Li, J.; Li, S.; Wang, L. PDECO: Parallel differential evolution for clusters optimization. J. Comput. Chem. 2013, 34, 1046–1059. [Google Scholar] [CrossRef]
- Penas, D.R.; Banga, J.R.; Gonzalez, P.; Doallo, R. Enhanced parallel Differential Evolution algorithm for problems in computational systems biology. Appl. Soft Comput. 2015, 33, 86–99. [Google Scholar] [CrossRef] [Green Version]
- Sui, X.; Chu, S.C.; Pan, J.S.; Luo, H. Parallel Compact Differential Evolution for Optimization Applied to Image Segmentation. Appl. Sci. 2020, 10, 2195. [Google Scholar] [CrossRef] [Green Version]
- Skakovski, A.; Jędrzejowicz, P. An island-based differential evolution algorithm with the multi-size populations. Expert Syst. Appl. 2019, 126, 308–320. [Google Scholar] [CrossRef]
- Skakovski, A.; Jędrzejowicz, P. A Multisize no Migration Island-Based Differential Evolution Algorithm with Removal of Ineffective Islands. IEEE Access 2022, 10, 34539–34549. [Google Scholar] [CrossRef]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19–22 June 1996; pp. 519–523. [Google Scholar]
- F.Neri, E. Mininno, Memetic Compact Differential Evolution for Cartesian Robot Control. IEEE Comput. Intell. 2010, 5, 54–65. [Google Scholar] [CrossRef]
- Mininno, E.; Neri, F.; Cupertino, F.; Naso, D. Compact Differential Evolution. IEEE Trans. Evol. 2011, 15, 32–54. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Hachicha, N.; Jarboui, B.; Siarry, P. A fuzzy logic control using a differential evolution algorithm aimed at modelling the financial market dynamics. Inf. Sci. 2011, 181, 79–91. [Google Scholar] [CrossRef]
- Kaelo, P.; Ali, M.M. A numerical study of some modified differential evolution algorithms. Eur. J. Oper. 2006, 169, 1176–1184. [Google Scholar] [CrossRef]
- Corcoran, A.L.; Wainwright, R.L. A parallel island model genetic algorithm for the multiprocessor scheduling problem. In Proceedings of the 1994 ACM Symposium on Applied Computing, SAC ’94, Phoenix, AZ, USA, 6–8 March 1994; pp. 483–487. [Google Scholar]
- Whitley, D.; Rana, S.; Heckendorn, R.B. Island model genetic algorithms and linearly separable problems. In Evolutionary Computing; Series Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1305, pp. 109–125. [Google Scholar]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Ali, M.M. Charoenchai Khompatraporn, Zelda B. Zabinsky, A Numerical Evaluation of Several Stochastic Algorithms on Selected Continuous Global Optimization Test Problems. J. Glob. Optim. 2005, 31, 635–672. [Google Scholar] [CrossRef]
- Floudas, C.A.; Pardalos, P.M.; Adjiman, C.; Esposoto, W.; Gümüs, Z.; Harding, S.; Klepeis, J.; Meyer, C.; Schweiger, C. Handbook of Test Problems in Local and Global Optimization; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Gaviano, M.; Ksasov, D.E.; Lera, D.; Sergeyev, Y.D. Software for generation of classes of test functions with known local and global minima for global optimization. ACM Trans. Math. Softw. 2003, 29, 469–480. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the Determination of Molecular Fields. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar]
- Zabinsky, Z.B.; Graesser, D.L.; Tuttle, M.E.; Kim, G.I. Global optimization of composite laminates using improving hit and run. In Recent Advances in Global Optimization; ACM Digital Library: New York, NY, USA, 1992; pp. 343–368. [Google Scholar]
- Chandra, R.; Dagum, L.; Kohr, D.; Maydan, D.; McDonald, J.; Menon, R. Parallel Programming in OpenMP; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2001. [Google Scholar]
- Charilogis, V.; Tsoulos, I.G.; Tzallas, A.; Karvounis, E. Modifications for the Differential Evolution Algorithm. Symmetry 2022, 14, 447. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural networks and their applications. Rev. Sci. Instrum. 1994, 65, 1803–1832. [Google Scholar] [CrossRef]
- Raymer, M.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern Part B 2003, 33, 802–813. [Google Scholar] [CrossRef]
- Zhong, P.; Fukushima, M. Regularized nonsmooth Newton method for multi-class support vector machines. Optim. Methods Softw. 2007, 22, 225–236. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| NP | 200 agents |
| Propagation | 1-to-1 method |
| 5 iterations | |
| 2 islands | |
| CR | 0.9 for the crossover probability |
| M | 15 iterations |
| Function | Thread 1 | Threads 4 | Threads 5 | Threads 10 |
|---|---|---|---|---|
| BF1 | 5908 | 5517 | 5310 | 4887 |
| BF2 | 5415 | 5008 | 4888 | 4577 |
| BRANIN | 5467 | 4767 | 4535 | 3895 |
| CIGAR10 | 1886 | 1885 | 1885 | 1875 |
| CM4 | 2518 | 2432 | 2330 | 2243 (0.97) |
| DISCUS10 | 1818 | 1816 | 1814 | 1807 |
| EASOM | 1807 | 1802 | 1801 | 1791 |
| ELP10 | 44,910 | 41,731 | 41,930 | 29,944 |
| EXP4 | 1820 | 1816 | 1814 | 1806 |
| EXP16 | 1838 | 1835 | 1834 | 1830 |
| EXP64 | 1842 | 1840 | 1839 | 1838 |
| GKLS250 | 1987 | 1897 | 1879 | 1818 |
| GKLS350 | 2428 | 2373 | 2299 | 2195 |
| GRIEWANK2 | 5544 | 4811 | 4612 | 4208 |
| POTENTIAL3 | 11,121 | 7868 | 7260 | 5598 |
| POTENTIAL5 | 24,708 | 15,146 | 13,793 | 8620 |
| HANSEN | 23,035 | 13,602 | 12,178 | 9242 |
| HARTMAN3 | 3406 | 3198 | 3162 | 2883 |
| HARTMAN6 | 7611 | 6172 | 5739 | 4877 (0.97) |
| RASTRIGIN | 5642 | 4537 | 4386 | 3707 |
| ROSENBROCK4 | 11,859 | 10,441 | 10,139 | 9473 |
| ROSENBROCK8 | 21,640 | 19,536 | 20,560 | 20,654 |
| SHEKEL5 | 12,491 | 10,247 | 9754 | 5065 (0.80) |
| SHEKEL7 | 10,755 | 9183 | 8857 | 6996 |
| SHEKEL10 | 10,257 | 9002 | 8705 | 7283 |
| SINU4 | 6045 | 5473 | 5301 | 4434 |
| SINU8 | 9764 | 8132 | 7748 | 4523 |
| TEST2N4 | 8521 | 7487 | 7404 | 6834 |
| TEST2N5 | 10,218 | 8916 | 8715 | 8050 |
| TEST2N6 | 11,984 | 10,240 | 10,191 | 9175 |
| TEST2N7 | 15,674 | 13,983 | 13,341 | 9760 |
| TEST30N3 | 3720 | 3379 | 3349 | 2994 |
| TEST30N4 | 3728 | 3382 | 3363 | 3031 |
| Average | 298,267 | 249,454 | 242,715 | 197,913 (0.99) |
| Function | 1 to 1 | 1 to N | N to 1 | N to N |
|---|---|---|---|---|
| BF1 | 4887 | 4259 | 4209 | 2792 |
| BF2 | 4577 | 4021 | 3917 | 2691 |
| BRANIN | 3895 | 3378 | 3307 | 2382 |
| CIGAR10 | 1875 | 1874 | 1871 | 1873 |
| CM4 | 2243 (0.97) | 2173 | 2136 (0.97) | 2030 |
| DISCUS10 | 1807 | 1810 | 1808 | 1809 |
| EASOM | 1791 | 1790 | 1791 | 1789 |
| ELP10 | 29,944 | 42,025 | 22,876 | 19,117 |
| EXP4 | 1806 | 1807 | 1811 | 1806 |
| EXP16 | 1830 | 1829 | 1828 | 1824 |
| EXP64 | 1838 | 1838 | 1838 | 1836 |
| GKLS250 | 1818 | 1812 | 1810 | 1802 |
| GKLS350 | 2195 | 2163 | 2109 | 2011 (0.97) |
| GRIEWANK2 | 4208 | 3620 | 3514 | 2445 (0.80) |
| POTENTIAL3 | 5598 | 4445 | 4353 | 2521 |
| POTENTIAL5 | 8620 | 7475 | 7025 | 3374 |
| HANSEN | 9242 | 6075 | 6181 | 3135 |
| HARTMAN3 | 2883 | 2664 | 2593 | 2207 |
| HARTMAN6 | 4877 (0.97) | 4327 (0.83) | 4362 (0.80) | 2834 (0.57) |
| RASTRIGIN | 3707 | 3213 | 2870 | 2220 (0.90) |
| ROSENBROCK4 | 9473 | 8294 | 7883 | 7084 |
| ROSENBROCK8 | 20,654 | 24,470 | 15,919 | 19,272 |
| SHEKEL5 | 5065 (0.80) | 7556 | 5386 (0.93) | 4456 (0.70) |
| SHEKEL7 | 6996 | 7207 (0.90) | 6488 (0.93) | 4493 (0.80) |
| SHEKEL10 | 7283 | 6812 (0.93) | 6440 | 3916 (0.73) |
| SINU4 | 4434 | 4204 | 4020 | 2796 (0.97) |
| SINU8 | 4523 | 5386 | 4605 | 3341 (0.90) |
| TEST2N4 | 6834 | 5777 | 5625 | 3609 (0.97) |
| TEST2N5 | 8050 | 6695 (0.97) | 6647 | 4179 (0.73) |
| TEST2N6 | 9175 | 7770 (0.93) | 7660 | 4522 (0.53) |
| TEST2N7 | 9760 | 9259 (0.77) | 9081 | 5200 (0.57) |
| TEST30N3 | 2994 | 2814 | 2653 | 2210 |
| TEST30N4 | 3031 | 2797 | 2700 | 2107 |
| Average | 197,913 (0.99) | 201,649 (0.98) | 167,316(0.98) | 129,683 (0.91) |
| Function | Proposed | Original DE | DERL | DELB |
|---|---|---|---|---|
| BF1 | 4887 | 5516 | 2881 | 5319 |
| BF2 | 4577 | 5555 | 2895 | 5405 |
| BRANIN | 3895 | 5656 | 2857 | 4830 |
| CIGAR10 | 1875 | 88,396 | 66,161 | 58,460 |
| CM4 | 2243 (0.97) | 9107 | 3856 | 6014 |
| DISCUS10 | 1807 | 87,657 | 55,722 | 49,014 |
| EASOM | 1791 | 7879 | 7225 | 14,934 |
| ELP10 | 29,944 | 33,371 | 9345 | 39,890 |
| EXP4 | 1806 | 6027 | 2638 | 4142 |
| EXP16 | 1830 | 26,194 | 25,117 | 11,740 |
| EXP64 | 1838 | 26,497 | 27,831 | 18,346 |
| GKLS250 | 1818 | 3800 | 1983 | 3706 |
| GKLS350 | 2195 | 6206 | 2901 | 5027 |
| GRIEWANK2 | 4208 | 6365 | 3325 | 6165 |
| POTENTIAL3 | 5598 | 82,933 | 111,496 | 44,592 |
| POTENTIAL5 | 8620 | 24,118 | 61,694 | 46,557 |
| HANSEN | 9242 | 18,470 | 7123 | 12212 |
| HARTMAN3 | 2883 | 4655 | 2205 | 4124 |
| HARTMAN6 | 4877 (0.97) | 15,488 | 5343 | 7215 (0.93) |
| RASTRIGIN | 3707 | 6362 | 3102 | 5704 |
| ROSENBROCK4 | 9473 | 16,857 | 6679 | 10,411 |
| ROSENBROCK8 | 20,654 | 56,445 | 17,198 | 22,939 |
| SHEKEL5 | 5065 (0.80) | 13,079 | 5224 (0.90) | 8167 |
| SHEKEL7 | 6996 | 12,409 | 4994 (0.97) | 8093 |
| SHEKEL10 | 7283 | 13,238 | 5240 | 8822 |
| SINU4 | 4434 | 8977 | 3828 | 6052 |
| SINU8 | 4523 | 28,871 | 9318 | 10,157 |
| TEST2N4 | 6834 | 10,764 | 4529 | 7331 |
| TEST2N5 | 8050 | 15,568 | 5917 | 8969 |
| TEST2N6 | 9175 | 21,185 | 7613 | 10,648 |
| TEST2N7 | 9760 | 28,411 | 9492 | 12,252 |
| TEST30N3 | 2994 | 4965 | 2758 | 4693 |
| TEST30N4 | 3031 | 5123 | 2688 | 5153 |
| Average | 197,913 (0.99) | 706,144 | 491,178 (0.99) | 477,083 (0.99) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charilogis, V.; Tsoulos, I.G. A Parallel Implementation of the Differential Evolution Method. Analytics 2023, 2, 17-30. https://doi.org/10.3390/analytics2010002
Charilogis V, Tsoulos IG. A Parallel Implementation of the Differential Evolution Method. Analytics. 2023; 2(1):17-30. https://doi.org/10.3390/analytics2010002
Chicago/Turabian StyleCharilogis, Vasileios, and Ioannis G. Tsoulos. 2023. "A Parallel Implementation of the Differential Evolution Method" Analytics 2, no. 1: 17-30. https://doi.org/10.3390/analytics2010002
APA StyleCharilogis, V., & Tsoulos, I. G. (2023). A Parallel Implementation of the Differential Evolution Method. Analytics, 2(1), 17-30. https://doi.org/10.3390/analytics2010002





