Two-Component Unit Weibull Mixture Model to Analyze Vote Proportions ^†

Abstract

In this paper, we present a two-component Weibull mixture model. An important property is that this new model accommodates bimodality, which can appear in data representing phenomena in some heterogeneous populations. We provide statistical properties, such as the quantile function and moments. Additionally, the expectation-maximization (EM) algorithm is used to find maximum-likelihood estimates of the model parameters. Further, a Monte Carlo study is carried out to evaluate the performance of the estimators on finite samples. The new model’s relevance is shown with an application referring to the vote proportion for the Brazilian presidential elections runoff in 2018. The proportion of votes is an important measure in analyzing electoral data. Since it is a variable limited to the unitary interval, unit distributions should be considered to analyze its probabilistic behavior. Thus, the introduced model is suitable for describing the characteristics detected in these data, such as the asymmetric behavior, bimodality, and the unit interval as support. In the application, the superiority of the proposed model is verified when comparing the fit with the two-component beta mixture models.

1. Introduction

Finite mixture models appeared in a study on the asymmetry of grouped materials not being homogeneous [1], being useful in the presence of multimodality, heavy tails, and asymmetry [2]. Many works have appeared in the literature in the context of finite mixtures. For example, Jewell [3] proposed a model for exponential mixtures. Considering Weibull mixture models, we can cite [4] for characterizations of the failure rate function and [5] for reliability approximations. Recently, Huang et al. [6] analyzed individual periods in combined sea waves using parametric mixture models.

In data with limited support, beta mixture models have been studied by several authors. Ji et al. [7] proposed a study on the beta mixture to solve problems related to correlations of gene expression levels, Bouguila et al. [8] presented a study on Bayesian analysis, and Grün et al. [9] studied beta mixture in regression models. The Kumaraswamy mixture model is an alternative to the beta mixture models. Khalid et al. [10] carried out a Bayesian study on the three-component Kumaraswamy mixture.

In this paper, a new two-component mixture model is proposed as an alternative to model population heterogeneities in the unit support. We consider that each mixture component follows a unit Weibull ($\mathrm{UW}$) distribution [11]. Some of the contributions of this new distribution, the so-called Weibull mixture model of the two-component unit ($\mathrm{UWUW}$), are: (i) all estimation routines, including simulations and applications, are performed using the expectation-maximization (EM) algorithm, and (ii) applicability for electoral data modeling. The EM algorithm is a computational method used to calculate the maximum likelihood estimator (MLE) iteratively [12]. It is widely used to estimate the maximum probability for finite mixture models [13]. Finally, the adjustment to electoral data, defined as the district’s share of votes by the total number of valid votes cast in the district, the proportions of votes are useful since the electoral districts can vary considerably in the size of the population [14]. Additionally, this measure can analyze other characteristics of the electoral process, such as electoral volatility [15] and nationalization of electoral change [14]. The data set used refers to the proportions of votes in the Brazilian presidential elections runoff in 2018.

The rest of the work is organized as follows. In Section 2, the new mixture model is presented. Section 3 introduces the EM algorithm to perform maximum likelihood estimation for the $\mathrm{UWUW}$ model. In Section 4, an application is made with electoral data. The final considerations of this work are addressed in Section 5.

2. The Proposed Model

In this section, the two-component unit Weibull mixture distribution, so-denoted $\mathrm{UWUW}$, is introduced. Let X be a random variable with $\mathrm{UWUW}$ distribution. Then, its cdf is obtained as

$$\begin{array}{cc}\hfill F_{\mathrm{UWUW}}(x;\mathsf{\Theta })& =p{F}_{\mathrm{UW}}(x;{\mathit{\theta }}_1)+(1-p)F_{\mathrm{UW}}(x;{\mathit{\theta }}_2)\hfill \\ \hfill & =p{\tau }^{{[-logx/log{\mu }_1]}^{{\beta }_1}}+(1-p){\tau }^{{[-logx/log{\mu }_2]}^{{\beta }_2}},\hfill \end{array}$$

where ${\mathit{\theta }}_1$ = $({\mu }_1$, ${\beta }_1{)}^{\top }$, ${\mathit{\theta }}_2$ = (${\mu }_2$, ${\beta }_2{)}^{\top }$, ${\mu }_1$ and ${\mu }_2\in (0,1)$ are location parameters associated with the $\tau$th quantiles of each component of the mixture, ${\beta }_1$ and ${\beta }_2>0$ are shape parameters, and $\tau \in (0,1)$ is assumed to be known. One can note we use a parameterization based on quantiles to formulate each component of the mixture. The advantage of working with reparametrization in terms of quantiles is its flexibility to model data with heterogeneous conditional distributions [16,17]. The $\mathrm{UWUW}$ probability density function (pdf) is given by

$$\begin{array}{cc}\hfill f_{\mathrm{UWUW}}(x;\mathsf{\Theta })& =p{f}_{\mathrm{UW}}(x;{\mathit{\theta }}_1)+(1-p)f_{\mathrm{UW}}(x;{\mathit{\theta }}_2)\hfill \\ & =p\frac{{\beta }_{1}log\tau }{xlog{\mu }_1}{\left(\frac{logx}{log{\mu }_1}\right)}^{{\beta }_1-1}{\tau }^{{(logx/log{\mu }_1)}^{{\beta }_1}}\hfill \\ \hfill & +(1-p)\frac{{\beta }_{2}log\tau }{xlog{\mu }_2}{\left(\frac{logx}{log{\mu }_2}\right)}^{{\beta }_2-1}{\tau }^{{(logx/log{\mu }_2)}^{{\beta }_2}}.\hfill \end{array}$$

(1)

Figure 1 shows some plots of the $\mathrm{UWUW}$ pdf for some combinations of parameters and $\tau =0.5$, which reveals the high flexibility of the new distribution. It accommodates bimodal, unimodal, descending, and bath forms under different asymmetric characteristics. Additionally, it is possible to identify a bimodal form for different values of p. Hereafter, we denote X as a random variable following a $\mathrm{UWUW}$ distribution, this is, $X\sim \mathrm{UWUW}\left(\mathsf{\Theta }\right)$.

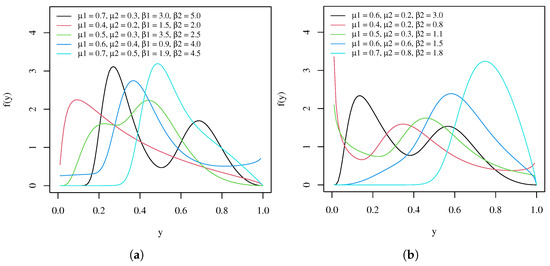
Figure 1. Plots of the $\mathrm{UWUW}$ density for some parameter values. (a) For $p=0.4$. (b) For $p=0.6$ and ${\beta }_1=3.0$.

3. Parameter Estimation

An approach to the iterative computation of MLEs when the observations can be treated as incomplete data is the well-known expectation-maximization (EM) algorithm. Considering the context of two-component mixture models, let $\mathit{x}=\{x_1,\dots ,x_n\}$ be a random sample of size n from a random variable X having pdf (4) with unknown parameter vector $\mathsf{\Theta }={({\mathit{\theta }}_1^{\top },{\mathit{\theta }}_2^{\top },p)}^{\top },$ where ${\mathit{\theta }}_1$ = (${\mu }_1$, ${\beta }_1{)}^{\top }$ and ${\mathit{\theta }}_2$ = (${\mu }_2$, ${\beta }_2{)}^{\top }$. It is customary to call $\mathit{x}$ of “incomplete data” since it is associated with a second component $\mathbf{z}=\{z_1,\dots ,z_n\}$ of unobserved values of a latent random variable Z. Each value $z_i$ of Z indicates which component of the mixture belongs to the ith observation $x_i$ such that

$$\begin{array}{c}\hfill z_i=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{x}_i\mathrm{has}\mathrm{pdf}{f}_{\mathrm{UW}}\left(x\right|{\mathit{\theta }}_{\mathbf{1}}),\hfill \\ 0\hfill & \mathrm{if}{x}_i\mathrm{has}\mathrm{pdf}{f}_{\mathrm{UW}}\left(x\right|{\mathit{\theta }}_{\mathbf{2}}),\hfill \end{array}\right.\end{array}$$

where $P(Z=1)=p$ and $P(Z=0)=1-p$. The complete-data specification is determined by the joint density of $(X,Z)$

$$\begin{array}{cc}\hfill f_{X,Z}(x_i,z_i;\mathsf{\Theta })=& {\left[p\frac{{\beta }_{1}log\tau }{x_{i}log{\mu }_1}{\left(\frac{log{x}_i}{log{\mu }_1}\right)}^{{\beta }_1-1}{\tau }^{{(log{x}_i/log{\mu }_1)}^{{\beta }_1}}\right]}^{z_i}\hfill \\ \hfill & \times {\left[(1-p)\frac{{\beta }_{2}log\tau }{xlog{\mu }_2}{\left(\frac{logx}{log{\mu }_2}\right)}^{{\beta }_2-1}{\tau }^{{(logx/log{\mu }_2)}^{{\beta }_2}}\right]}^{1-z_i},\hfill \end{array}$$

and based on it, the complete log-likelihood function, for the sample of size n, is given by

$$\begin{array}{cc}\hfill l_c\left(\mathsf{\Theta }\right)=& \sum _{i=1}^{n}log{f}_{X,Z}(x_i,z_i;\mathsf{\Theta })\hfill \\ \hfill =& \sum _{i=1}^n{z}_{i}log\left[p\frac{{\beta }_{1}log\tau }{x_{i}log{\mu }_1}{\left(\frac{log{x}_i}{log{\mu }_1}\right)}^{{\beta }_1-1}{\tau }^{{(log{x}_i/log{\mu }_1)}^{{\beta }_1}}\right]\hfill \\ \hfill & +\sum _{i=1}^n(1-z_i)log\left[(1-p)\frac{{\beta }_{2}log\tau }{xlog{\mu }_2}{\left(\frac{logx}{log{\mu }_2}\right)}^{{\beta }_2-1}{\tau }^{{(logx/log{\mu }_2)}^{{\beta }_2}}\right].\hfill \end{array}$$

(2)

The EM algorithm iterates, between two steps, to compute the MLEs of $\mathsf{\Theta }$. In the E-step or expectation step, due to  (2), is unobservable, it is replaced by its conditional expectation with respect to the conditional distribution of Z, given $\mathit{x}$ and the current parameter estimates. More specifically, in the $(k+1)$th iteration, the E-step computes    

$$\begin{array}{cc}\hfill Q(\mathsf{\Theta },{\mathsf{\Theta }}^{\left(k\right)})=& E_{{\mathsf{\Theta }}^{\left(\mathbf{k}\right)}}\left[l_c\left(\mathsf{\Theta }\right)|\mathit{x}\right]\hfill \\ \hfill =& \sum _{i=1}^{n}log{f}_{X,Z}(x_i,z_i;\mathsf{\Theta })\hfill \\ \hfill =& \sum _{i=1}^n{\overline{z}}_{i1}log\left[p\frac{{\beta }_{1}log\tau }{x_{i}log{\mu }_1}{\left(\frac{log{x}_i}{log{\mu }_1}\right)}^{{\beta }_1-1}{\tau }^{{(log{x}_i/log{\mu }_1)}^{{\beta }_1}}\right]\hfill \\ \hfill +& \sum _{i=1}^n{\overline{z}}_{i2}log\left[(1-p)\frac{{\beta }_{2}log\tau }{xlog{\mu }_2}{\left(\frac{logx}{log{\mu }_2}\right)}^{{\beta }_2-1}{\tau }^{{(logx/log{\mu }_2)}^{{\beta }_2}}\right],\hfill \end{array}$$

(3)

where

$$\begin{array}{c}\hfill {\overline{z}}_{i1}=\frac{p^{\left(k\right)}{f}_{UW}(x;{\mathit{\theta }}_{\mathbf{1}}^{\left(\mathbf{k}\right)})}{p^{\left(k\right)}{f}_{UW}(x;{\mathit{\theta }}_{\mathbf{1}}^{\left(\mathbf{k}\right)})+(1-p^{\left(k\right)})f_{UW}(x;{\mathit{\theta }}_{\mathbf{2}}^{\left(\mathbf{k}\right)})},\end{array}$$

$$\begin{array}{c}\hfill {\overline{z}}_{i2}=\frac{(1-p^{\left(k\right)})f_{UW}(x;{\mathit{\theta }}_{\mathbf{2}}^{\left(\mathbf{k}\right)})}{p^{\left(k\right)}{f}_{UW}(x;{\mathit{\theta }}_{\mathbf{1}}^{\left(\mathbf{k}\right)})+(1-p^{\left(k\right)})f_{UW}(x;{\mathit{\theta }}_{\mathbf{2}}^{\left(\mathbf{k}\right)})},\end{array}$$

and ${\mathsf{\Theta }}^{\left(\mathbf{k}\right)}={({\mathit{\theta }}_{\mathbf{1}}^{\left(\mathbf{k}\right)},{\mathit{\theta }}_{\mathbf{2}}^{\left(\mathbf{k}\right)},p^{\left(k\right)})}^{\top }$ are obtained from the kth iteration.

The M-step or maximization step, requires the maximization of (3) with respect to $\mathsf{\Theta }$. This is

$$\begin{array}{c}\hfill {\mathsf{\Theta }}^{(k+1)}={\displaystyle \underset{\mathsf{\Theta }}{arg\; max}}Q(\mathsf{\Theta },{\mathsf{\Theta }}^{\left(k\right)}).\end{array}$$

(4)

The vector ${\mathsf{\Theta }}^{(k+1)}$ is used to initialize the next iteration. Thus, the EM algorithm is initialized by the starting values ${\mathsf{\Theta }}^{\left(\mathbf{0}\right)}={({\mathit{\theta }}_{\mathbf{1}}^{\left(\mathbf{0}\right)},{\mathit{\theta }}_{\mathbf{2}}^{\left(\mathbf{0}\right)},p^{\left(0\right)})}^{\top }$ and the MLEs $\widehat{\mathsf{\Theta }}$ of $\mathsf{\Theta }$ are obtained by $\widehat{\mathsf{\Theta }}={\mathsf{\Theta }}^{(k+1)}$ when a convergence criterion $|{\mathsf{\Theta }}^{(k+1)}-{\mathsf{\Theta }}^{\left(k\right)}|<\epsilon$ is reached [12]. We set $\epsilon$ = 10,000. It should be noted that it is not possible to obtain analytical results from these expressions. It is necessary to perform this maximization by applying some iterative techniques, for example, Newton–Raphson’s method [18].

4. Application

In what follows, we present a case study that illustrates the suitability of the $\mathrm{UWUW}$ distribution for modeling real unit data sets. The database considered is the municipality’s vote proportion of the winning candidate in the Brazilian presidential elections runoff in 2018. Since it presents a bimodal shape, see Figure 2a, a unimodal distribution would not be appropriate to fit this data set. Therefore, the $\mathrm{UWUW}$ distribution is a suitable alternative to model these data. Its performance is compared with other double-bounded component mixtures that have already been studied in the literature: two-component beta mixture ($\mathrm{BB}$) model. In this paper, the parameterization proposed by [19] is considered to define the $\mathrm{BB}$ model, which has pdf given by

$$\begin{array}{cc}\hfill f(x;\mathsf{\Theta })& =p\frac{\mathsf{\Gamma }({\mu }_1+{\beta }_1)}{\mathsf{\Gamma }\left({\mu }_1\right)\mathsf{\Gamma }\left({\beta }_1\right)}{x}^{{\mu }_1-1}{(1-x)}^{{\beta }_1-1}+(1-p)\hfill \\ & \frac{\mathsf{\Gamma }({\mu }_2+{\beta }_2)}{\mathsf{\Gamma }\left({\mu }_2\right)\mathsf{\Gamma }\left({\beta }_2\right)}{x}^{{\mu }_2-1}{(1-x)}^{{\beta }_2-1},0<x<1,\hfill \end{array}$$

where $\mathsf{\Theta }={({\mu }_1,{\mu }_2,{\beta }_1,{\beta }_2,p)}^{\top }$, ${\mu }_1$ and ${\mu }_2\in (0,1)$ are location parameters associated with the mean of each mixture component, ${\beta }_1$ and ${\beta }_2$$>0$ are precision parameters, and $p\in (0,1)$ is the parameter that measures the weights of the mixture.

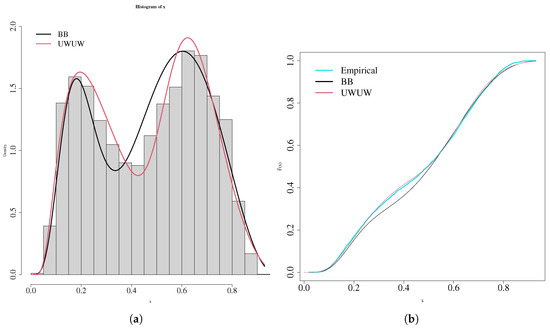
Figure 2. Estimated densities (a) and empirical cdf (b) of the $\mathrm{BB}$, $\mathrm{KWKW}$ and $\mathrm{UWUW}$ models.

For all competitive mixture models, the parameter estimation is carried out using the EM algorithm following the steps described in Section 3. The Corrected Anderson–Darling ($A^{*}$) [20], Cramér–von Misses ($W^{*}$) [21], and the Kolmogorov–Smirnov ($KS$) [22] statistics are calculated to assess the quality-of-fit for the three fitted models. The lower their values are, the better the model fit. All the analysis is performed using the R programming language, and the goodness-of-fit measures are computed using the AdequacyModel [23] subroutine.

Table 1 displays the parameter estimates, standard errors, and the model comparison criteria of the three considered models. The results indicate that the $\mathrm{UWUW}$ distribution provides the lowest values for all goodness-of-fit statistics. The $\mathrm{KWKW}$ presents the worse performance, not being an adequate alternative to fit these data.

Table 1. Parameter estimates and standard errors (given in parentheses) for the models fitted to Bolsonaro’s vote proportion in Brazilian presidential elections in 2018.

	$\widehat{{\mathit{\mu }}_1}$	$\widehat{{\mathit{\mu }}_2}$	$\widehat{{\mathit{\beta }}_1}$	$\widehat{{\mathit{\beta }}_1}$	$\widehat{\mathit{p}}$	${\mathit{W}}^{*}$	${\mathit{A}}^{*}$	$\mathit{KS}$
$\mathrm{BB}$	0.5816	0.1985	9.7510	29.3260	0.7268	1.2937	7.4584	0.0477
	(0.0035)	(0.0026)	(0.3201)	(1.3521)	-
$\mathrm{UWUW}$	0.2677	0.6491	2.7011	2.9611	0.5368	0.4119	3.6768	0.0153
	(0.0039)	(0.0027)	(0.0545)	(0.0567)	-

Figure 2a presents the histogram of the vote proportion data overlaid with the estimated densities of the fitted models. The bimodality of the data is confirmed, and the $\mathrm{UWUW}$ model provides the closest fit to the histogram. Clearly, the $\mathrm{KWKW}$ model is not adequate to fit these data. Further, Figure 2b gives plots of the empirical and estimated cdfs. This visual inspection favors the results in Figure 2a and Table 1, indicating that the proposed model is appropriate to fit these data. Thus, it can be an effective alternative to analyze vote proportions, being quite competitive with the $\mathrm{BB}$ model and providing consistently better fits than the $\mathrm{KWKW}$ model. Therefore, the $\mathrm{UWUW}$ provides a useful tool for modeling bimodal data restricted to the unit interval. Additionally, with the estimates of the mixture parameters, it is possible to identify that more than 50 % of the observations belong to the first mixture component. The estimated median of the first component is ${\widehat{\mu }}_1=0.2677$ and the estimated median of the second component is ${\widehat{\mu }}_2=0.6649$.

5. Conclusions

A two-component mixture model was defined to describe the heterogeneities of the population with the limited domain. The two-component unit Weibull mixture ($\mathrm{UWUW}$) model is formulated considering that each mixture component follows the unit Weibull distribution. Some of the main properties of $\mathrm{UWUW}$ have been presented, such as ordinary moments. The EM algorithm was used to obtain maximum likelihood estimates for the model parameters. To evaluate the performance of the EM algorithm, Monte Carlo simulations were performed. An application to electoral data illustrates the importance and potential of the new model. The motivating data set is about the vote proportions obtained by the winning candidate in the Brazilian presidential runoff elections in 2018. The results indicate that our proposal is adequate to fit this data set since it is suitable to analyze the asymmetric and bimodal behaviors. From the mixing parameter estimate, we can conclude that 53.68% of the observations are from the first component of the mixture with estimated median at ${\widehat{\mu }}_1=0.2677.$ The estimated median for the municipalites from the second mixture component was ${\widehat{\mu }}_2=0.6491.$ This application proved empirically that the $\mathrm{UWUW}$ performance may overcome other two-component mixture models based on other widely known unit distributions such as the beta and Kumaraswamy.