A Testing Coverage Based SRGM Subject to the Uncertainty of the Operating Environment ^†

Abstract

The number of software failures, software reliability, and failure rates can be measured and predicted by the software reliability growth model (SRGM). SRGM is developed and tested in a controlled environment where the operating environment is different. Many SRGMs have developed, assuming that the working and developing environments are the same. In this paper, we have developed a new SRGM incorporating the imperfect debugging and testing coverage function. The proposed model’s parameters are estimated from two real datasets and compared with some existing SRGMs based on five goodness-of-fit criteria. The results show that the proposed model gives better descriptive and predictive performance than the existing selected models.

1. Introduction

During the past four decades, various software reliability growth models (SRGM) [1,2,3,4,5,6,7] have been proposed to estimate reliability, predict the number of faults, determine the release time of the software, etc. Various proposed models have been developed based on different suppositions. For example, some models have discussed perfect debugging [1,7], and others have discussed imperfect debugging [3,4]. Some researchers have studied SRGM by considering a constant fault detection rate [1] or by the learning phenomenon [7]. During the testing and debugging process, various research papers have discussed resource allocation [8,9,10,11,12], testing effort [13,14], etc.

Most models have considered that the operating and testing environments are the same. In general, the software is implemented in the real working environment after the in-house testing process. In early 2000, researchers proposed different SRGMs incorporating uncertainty of the operating environment with new approaches. Teng and Pham [15] proposed a generalized SRGM considering the effects of the uncertainty of the working environment on software failure rate. Pham [6,16] presented an SRGM incorporating Vtub-shaped and Loglog fault detection rates subject to random environments, respectively. Li and Pham [17] discussed an SRGM where fault removal efficiency and error generation are incorporated together with the uncertainty of the operating environment. Li et al. [18] proposed a generalized SRGM incorporating the uncertainty of the operating environment.

This paper presents an SRGM incorporating imperfect debugging and testing coverage functions under the effects of a random field environment. The above discussed model [6,15,16,17,18] have assumed that the random variable $\eta$ follows Gamma distribution. In our model, we have assumed exponential distribution instead of the gamma distribution to keep less number of parameters in the model. We have validated the goodness-of-fit and predictability of the proposed model on two datasets. The remaining part of the paper is as follows. In Section 2, the explicit solution of the mean value function is derived. Numerical and data analysis is performed in Section 3. In Section 4, we summarize the paper’s conclusions.

2. Software Reliability Growth Model

The cumulative number of detected software faults follows non-homogeneous Poisson process (NHPP) and express as follows

$$P\{N\left(t\right)=n\}=\frac{{m\left(t\right)}^n}{n!}\exp (-m\left(t\right)),\mathrm{for}n=1,2,3,\dots .$$

(1)

The mean value function for the fault counting process is represented in terms of intensity function $\lambda \left(t\right)$ as

$$m\left(t\right)={\int }_0^t\lambda \left(s\right)ds.$$

(2)

The following assumptions are taken for the proposed model:

• The software fault detection follows the non-homogeneous Poisson process.
• Fault detection rate is proportional to the remaining faults in the software.
• After fault detection, the debugging process takes place immediately.
• During the testing process, new faults are introduced into the software.
• The testing coverage rate function is incorporated as the fault detection rate function.
• Random testing environment affects the fault detection rate.

Considering the above assumptions, the SRGM, with the uncertainty of the operating environment, is

$$\begin{array}{ccc}\hfill \frac{dm\left(t\right)}{dt}& =& \eta \frac{c^{\prime }\left(t\right)}{1-c\left(t\right)}\left\{N\left(t\right)-m\left(t\right)\right\},m\left(0\right)=0.\hfill \end{array}$$

(3)

where $\eta$ is random variable, $c\left(t\right)$ is the testing coverage function, $N\left(t\right)$ is the total fault present in the software at time t and $m\left(t\right)$ is cumulative number of software failure at time t.

Initially the software has N number of faults. During debugging phase new faults are introduced at a rate d. Therefore, the fault content function is

$$N\left(t\right)=N+dm\left(t\right)$$

(4)

The general solution for the MVF $m(\eta ,t)$ is given by

$$m(\eta ,t)=\frac{N}{1-d}\left(1-e^{-\eta {\int }_0^t(1-d)\frac{c^{\prime }\left(\tau \right)}{1-c\left(\tau \right)}d\tau }\right)$$

(5)

In order to find the mean value function $m\left(t\right)$, we have assume that, the random variable $\eta$ follows Exponential distribution, i.e., $\eta \sim exp\left(\alpha \right)$ and the probability density function of $\eta$ is given by

$$f\left(\eta \right)=\alpha e^{-\alpha \eta },\alpha >0\mathrm{and}\eta \ge 0.$$

(6)

An application of Laplace transformation of Equation (5) using Exponential distribution for random variable $\eta$, the mean value function $m\left(t\right)$ is given by:

$$\begin{array}{ccc}\hfill m\left(t\right)& =& \frac{N}{1-d}\left\{1-\left(\frac{\alpha }{\alpha +(1-d){\int }_0^t\frac{c^{\prime }\left(\tau \right)}{1-c\left(\tau \right)}d\tau }\right)\right\}\hfill \end{array}$$

(7)

In this paper, we have considered the following testing coverage rate function $c\left(t\right)$ as follows:

$$c\left(t\right)=1-e^{1-c^{t^b}},c>1,b>0$$

(8)

After substituting $c\left(t\right)$ in Equation (8), we obtained the following closed form of the solution of the mean value function $m\left(t\right)$ as:

$$m\left(t\right)=\frac{N}{1-d}\left\{1-\left(\frac{\alpha }{\alpha +(1-d)(c^{t^b}-1)}\right)\right\}.$$

(9)

Table 1 summarizes the MVF of the proposed model and other selected models, which are taken for comparison.

Table 1. Summary of SRGM.

No.	Model	MVF
1	Goel-Okumoto model [1]	$m\left(t\right)=a(1-e^{-bt})$
2	Delayed S-shaped model [19]	$m\left(t\right)=a(1-(1+bt)e^{-bt})$
3	Yamada ID model-I [3]	$m\left(t\right)=\frac{ab}{\alpha +b}(e^{\alpha t}-e^{-bt})$
4	Yamada ID model-II [3]	$m\left(t\right)=a(1-e^{-bt})(1-\frac{\alpha }{b})+\alpha at$
5	Yamada et al. (YExp) [20]	$m\left(t\right)=a\left\{1-e^{-\gamma \alpha (1-e^{-\beta t})}\right\}$
6	Yamada et al. (YRay) [20]	$m\left(t\right)=a\left\{1-e^{-\gamma \alpha (1-e^{-\beta t^2/2})}\right\}$
7	Pham-Zhang model [21]	$m\left(t\right)=\frac{1}{1+\beta e^{-bt}}\left((c+a)(1-e^{-bt})-\frac{ab}{b-\alpha }(e^{-\alpha t}-e^{-bt})\right)$
8	Pham-Zhang ID model [22]	$m\left(t\right)=a(1-e^{-bt})(1+(b+d)t+bd{t}^2)$
9	Proposed model	$m\left(t\right)=\frac{N}{1-d}\left\{1-\left(\frac{\alpha }{\alpha +(1-d)(c^{t^b}-1)}\right)\right\}$

3. Numerical and Data Analysis

3.1. Software Failure Data

The first dataset (DS-I) discussed in this paper is collected from the online IBM entry software package [2]. During the testing process of 21 weeks, 46 failures are observed. The second dataset (DS-II) is presented and collected from testing system at AT&T [23]. The system takes a total of 14 weeks to perform testing. As a result, 22 number of faults are experienced during the testing weeks.

3.2. Parameter Estimation and Goodness-of-Fit Criteria

Usually, the parameters of the SRGMs are estimated using the least square estimation (LSE) or maximum likelihood estimation (MLE) methods. We have used the least square estimation method to estimate the parameters of the proposed model and the parameter estimation is shown in Table 2.

Table 2. Parameter estimation for DS-I [2] and DS-II [23].

No.	Model	Parameter Estimate (DSI)	Parameter Estimate (DSII)
1	Goel-Okumoto model [1]	$\widehat{a}=192.3303$, $\widehat{b}=0.0121$	$\widehat{a}=23.0127, \widehat{b}=0.1884$
2	Delayed S-shaped model [19]	$\widehat{a}=77.253$, $\widehat{b}=0.0966$	$\widehat{a}=20.0045$, $\widehat{b}=0.5198$
3	Yamada ID model-I [3]	$\widehat{a}=38.1884$, $\widehat{b}=0.0439$, $\widehat{\alpha }=0.055$	$\widehat{a}=26.4815$, $\widehat{b}=0.13204$, $\widehat{\alpha }=0.00004$
4	Yamada ID model-II [3]	$\widehat{a}=1.7105$, $\widehat{b}=0.2959$, $\widehat{\alpha }=1.5247$	$\widehat{a}=17.5163$,$\widehat{b}=0.2657$, $\widehat{\alpha }=0.0251$
5	Yamada et al. (YExp) [20]	$\widehat{a}=1935.6515, \widehat{\gamma }=1.6636$,	$\widehat{a}=34.7439, \widehat{\gamma }=4.2853$,
		$\widehat{\alpha }=2.4954, \widehat{\beta }=0.0003$	$\widehat{\alpha }=0.2857, \widehat{\beta }=0.1061$
6	Yamada et al. (YRay) [20]	$\widehat{a}=77.8791, \widehat{\gamma }=2.5357$,	$\widehat{a}=20.7737, \widehat{\gamma }=3.7091$,
		$\widehat{\alpha }=0.5513, \widehat{\beta }=0.0045$	$\widehat{\alpha }=0.7458, \widehat{\beta }=0.0520$
7	Pham-Zhang model [21]	$\widehat{a}=83.1886, \widehat{b}=0.0747$, $\widehat{\beta }=0.0533$	$\widehat{a}=22.7269, \widehat{b}=0.223$, $\widehat{\beta }=0.0011$
		$\widehat{\alpha }=0.0838, \widehat{c}=8.0682$	$\widehat{\alpha }=4.1802, \widehat{c}=0.1$
8	Pham-Zhang ID model [22]	$\widehat{a}=75.7344, \widehat{b}=0.1001$, $\widehat{d}=0.001$	$\widehat{a}=19.4765, \widehat{b}=0.6924$, $\widehat{d}=0.113$
9	Proposed model	$\widehat{N}=3.1569, \widehat{d}=0.9527$,	$\widehat{N}=29.773, \widehat{d}=0.001$,
		$\widehat{\alpha }=6.5911$, $\widehat{b}=0.4806$, $\widehat{c}=3.8052$,	$\widehat{\alpha }=0.0006, \widehat{b}=1.082, \widehat{c}=1.0001$,

Several goodness-of-fit criteria are available to predict the best-fit model in the literature. Out of those, the standard criteria used to compare with the existing selected model are mean-squared error (MSE), predictive ratio risk (PRR), bias, variance, and root mean square prediction error (RMSPE). The smaller value of all goodness-of-fit criteria gives a better fit of the model.

The MSE measures the average of the deviation between the predicted values with the actual data [24] and is represented as

$$\mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n{(m\left(t_i\right)-y_i)}^2,$$

where n is the number of observations in the model.

The predictive ratio risk (PRR) gives the distance between the model estimates and actual data against the actual data and is defined as [25]

$$\mathrm{PRR}=\sum _{i=1}^n{\left(\frac{(m\left(t_i\right)-y_i)}{m\left(t_i\right)}\right)}^2$$

The bias is defined as the sum of the deviation of the model estimates testing curve from the actual data as [26]:

$$\mathrm{Bias}=\frac{1}{n}\sum _{i=1}^n(m\left(t_i\right)-y_i).$$

The variance is defined as [27]:

$$\mathrm{Variance}=\sqrt{\frac{{\sum }_{i=1}^n{\left(y_i-m\left(t_i\right)-\mathrm{Bias}\right)}^2}{n-1}}.$$

The root mean square prediction error (RMSPE) is defined as [27]

$$\mathrm{RMSPE}=\sqrt{{\mathrm{Variance}}^2+{\mathrm{Bias}}^2}.$$

where $m\left(t_i\right)$ is the predict fault at time $t_i$ and $y_i$ is the observed fault at time $t_i$.

3.3. Model Comparison for DS-I

Table 3 shows that the proposed model performs better regarding MSE, PRR, Bias, Variance, and RMSE criteria. The value of MSE, PRR, Bias, Variance, and RMSE of the proposed model are $1.168283,0.381616,$ −0.04598, 1.105182 and 1.106138, respectively, which is significantly smaller than the value of the other selected software reliability models. Figure 1a compared the proposed and existing models chosen with observed failure data. Figure 1b shows the relative errors of the proposed model in terms of the test week, which approach to zero compared to the other models. Overall, the proposed model is better than other selected existing models.

Table 3. Comparison criteria for DS-I.

No	MSE	PRR	Bais	Variance	RMSE
1	8.973872	1.019703	0.890848	3.452888	3.565957
2	1.480686	26.32063	−0.23211	1.313173	1.333528
3	4.057239	0.371741	−0.65302	2.06001	2.164841
4	1.458347	2.676588	−0.05303	1.241017	1.242149
5	6.245228	0.822893	0.844226	2.56076	2.696332
6	1.959292	55.68604	−0.39852	1.434314	1.488648
7	1.278945	2.729673	−0.0696	1.165397	1.167473
8	1.533603	40.66148	−0.25021	1.344427	1.367511
9	1.168283	0.381616	−0.04598	1.105182	1.106138

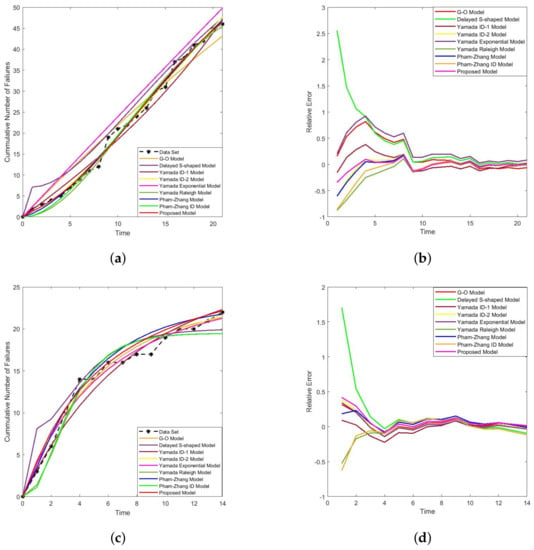
Figure 1. (a) Estimated MVFs for different selected and proposed model (DS-I). (b) Relative errors curve for different selected and proposed model (DS-I). (c) Estimated MVFs for different selected and proposed model (DS-II). (d) Relative errors curve for different selected and proposed model (DS-II).

3.4. Model Comparison for DS-II

The proposed model’s performance using LSE is evaluated in terms of MSE, PRR, Bias, Variance, and RMSE and shown in Table 4. From Table 4, we observe that the proposed models have the least value of MSE ($0.708826$), PRR ($0.117530$), Bias ($0.051773$), Variance ($0.878641$), and RMSE ($0.880165$) than the other models. The comparison between the proposed and selected model’s MVF is depicted in Figure 1c. Figure 1d shows the relative errors for different models and approaches rapidly to zero compared to other selected models. Overall, the proposed model also fits the DS-II better.

Table 4. Comparison criteria for DS-II.

No	MSE	PRR	Bias	Variance	RMSE
1	0.837889	0.126591	0.294310	1.087284	1.126412
2	1.409615	0.385109	−0.12266	1.251662	1.257659
3	1.394307	0.144932	−0.16151	1.225382	1.235980
4	0.718011	0.146291	0.168120	0.929816	0.944893
5	0.746532	0.135072	0.061377	0.896637	0.898735
6	2.027924	1.355159	−0.17989	1.477809	1.488717
7	1.526415	0.118110	0.879679	2.035660	2.217600
8	1.969308	2.921449	−0.17227	1.488848	1.498781
9	0.708826	0.117530	0.051773	0.878641	0.880165

4. Conclusions

Many SRGMs have been proposed on different realistic issues. This paper has incorporated imperfect debugging and the testing coverage rate function in the model. All the models discussed in Section 1 assumed that the uncertainty of the operating environment follows the gamma distribution. The main contribution of the model is implementing a random variable, which follows an exponential distribution. However, it is a special case of the gamma distribution and keeps fewer parameters in the model. The proposed model’s parameter is estimated using two datasets and validated over five goodness-of-fit criteria. The results show that the proposed model fits better than other selected models. In the future, we will incorporate multi-release and change-point concepts.