Numerical Solution of The Effects of Variable Fluid Properties on Biomagnetic Fluid over an Unsteady Stretching Sheet ^†

Abstract

In this paper, the effects of various fluid properties on two-dimensional unsteady biomagnetic fluid flow (blood) and heat transfer over a stretching sheet under the appearance of a magnetic dipole is investigated. The governing boundary layer equations are simplified via suitable transformation which are then solved using the bvp4c function approach in MATLAB software. The results indicate that fluid velocity and temperature are greatly influenced by the ferromagnetic interaction parameter. With increasing ferromagnetic number, fluid velocity drops but temperature increases. It is also found that the coefficient of skin friction and Nusselt number increase with an increase in values of thermal conductivity parameter. For certain parameter values, the results are also compared with previously published studies and they are found to be in acceptable agreement.

1. Introduction

The study of two-dimensional boundary layer flow and heat transfer of biomagnetic fluid over a stretching sheet with variable viscosity and thermal conductivity is very important due to its various applications in engineering, bio-medical, and industrial disciplines. Crane [1] was the first to study the steady two-dimensional boundary layer flow of a flat elastic sheet. Since then, the problem has been extensively studied by taking into account many different physical features, either separately or in various combinations. Shedzad et al. [2] analyzed the effect of thermophoresis mechanisms on mixed convection flow with different flow and thermal conditions. Elbashbeshy and Bazid [3] analyzed a similarity solution for the boundary layer equations which describes the unsteady flow and heat transfer over a stretching sheet. Mukhopadhyay [4] presented a solution for unsteady boundary layer flow over a stretching sheet with variable fluid viscosity and thermal diffusivity present in wall suction. The mathematical and numerical solutions for biomagnetic fluids dynamics (BFD) applications in cancer treatment is proposed by Misra et al. [5]. Bhatti et al. [6] analyzed the heat transfer properties and application of the blood clot with variable viscosity. Murtaza et al. [7] analyzed an extended biomagnetic fluid dynamics (BFD) model incorporating the principles of ferrohydrodynamics and magnetohydrodynamics. Misra et al. [8] investigated the biomagnetic fluid flow over a stretching sheet, considering the viscoelastic property of the fluid. Tzirtzilakis et al. [9] analyzed the study of two-dimensional, steady, laminar and incompressible biomagnetic fluid over a stretching sheet with heat transfer. In that study, the magnetization of the fluid varied with the magnetic field strength and the temperature.

To the authors’ best information, the investigations of blood flow affected by a magnetic field accompanied by variable fluid properties over an unsteady stretching sheet has not yet been studied. As we know that the blood properties, namely viscosity and thermal conductivity have a fundamental relationship with temperature. Therefore, the aim of this this paper is to fill up this gap via mathematical assumptions and computational solutions. The results indicate that blood flow in boundary layer is appreciably influenced by ferromagnetic number, which can be extremely helpful in cancer treatments as well as in practical medication delivery.

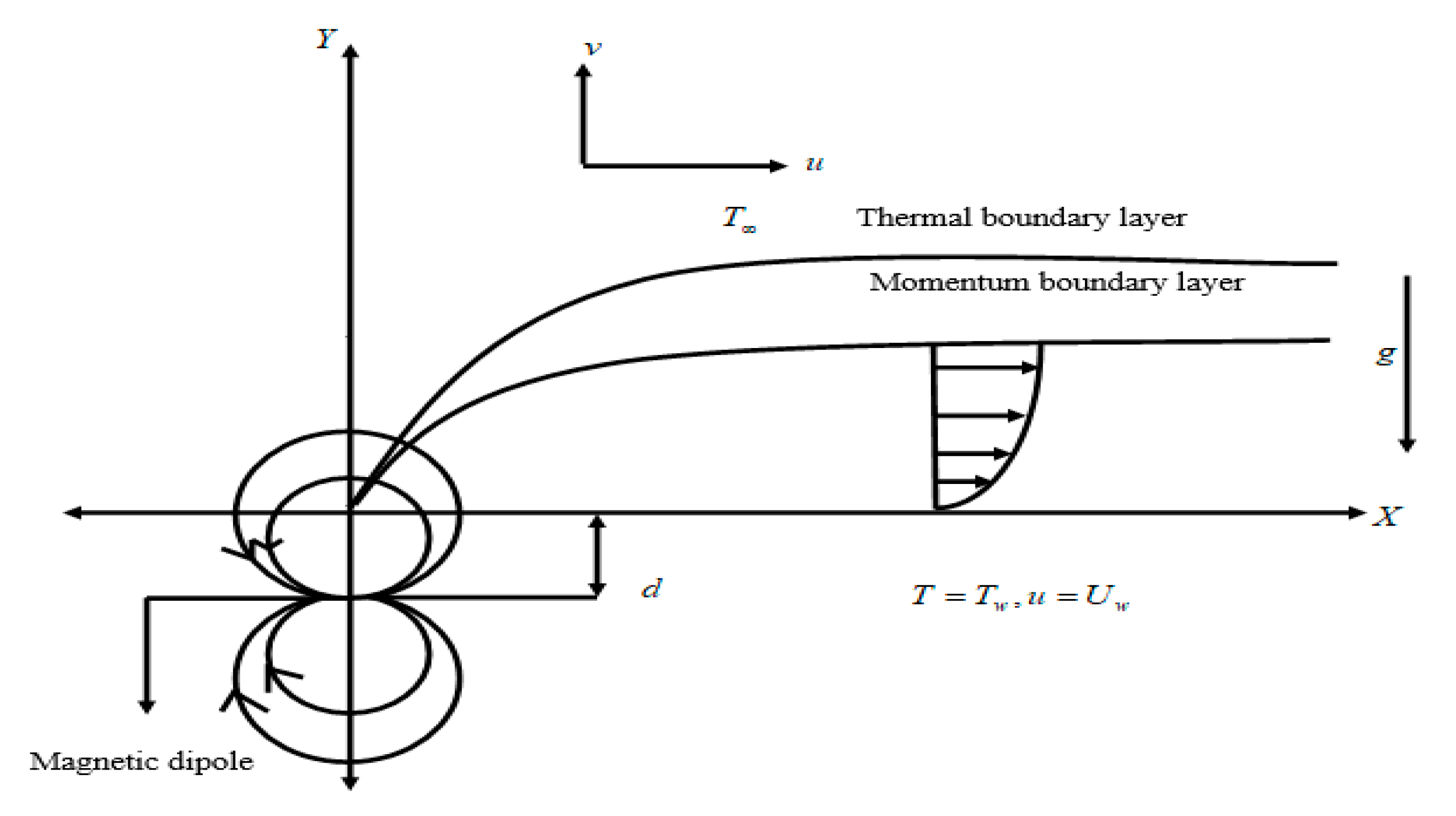
2. Model Description

In Figure 1, the horizontal line represents the $X$ axis and the perpendicular line represents the $Y$ axis. We considered that for time $t<0$, the fluid and heat flows are steady. The unsteady fluid and heat flows start at $t=0$, the sheet is being stretched with velocity $U_w\left(x,t\right)=ax{(1-ct)}^{-1}$ along the $X$ axis, keeping the origin fixed. The temperature of the sheet is $T_w\left(x,t\right)$, while the ambient blood temperature is $T_{\infty }$. Due to applied magnetic field in boundary domain, a magnetic dipole is produced and situated at a distance $d$ from the sheet. Therefore, the modified mathematical equations for governing the problem with the help of [10] can be expressed as:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{1}{{\rho }_{\infty }}\frac{\partial }{\partial y}\left(\mu \frac{\partial u}{\partial y}\right)+\frac{{\mu }_0}{{\rho }_{\infty }}\mathrm{{\rm M}}\frac{\partial \mathrm{H}}{\partial x}+g\beta \times \left(T-T\infty \right)$$

(2)

$${\rho }_{\infty }{C}_p\left(\frac{\partial \mathrm{{\rm T}}}{\partial t}+u\frac{\partial \mathrm{{\rm T}}}{\partial x}+v\frac{\partial \mathrm{{\rm T}}}{\partial y}\right)+{\mu }_{0}T\frac{\partial \mathrm{{\rm M}}}{\partial \mathrm{{\rm T}}}\left(u\frac{\partial \mathrm{H}}{\partial x}+v\frac{\partial \mathrm{H}}{\partial y}\right)=\frac{\partial }{\partial y}\left(K\frac{\partial \mathrm{{\rm T}}}{\partial y}\right)$$

(3)

The following are the boundary conditions:

$$\begin{array}{c}y=0:u=U_w,v=V_w\left(t\right),T=T_w\\ y\to \infty :u\to 0,T\to T_{\infty }\end{array}\}$$

(4)

where, $u$ and $v$ are the velocity components along the respective directions. ${\rho }_{\infty }$ is the fluid density, ${\upsilon }_{\infty }$ is the kinematic viscosity, $g$ is the acceleration due to gravity, ${\beta }^{*}$ is the coefficient of thermal expansion, $T$ is the fluid temperature, $C_p$ is the specific heat at constant pressure, $\mu$ is the co-efficient of viscosity, and $K$ is the variable thermal conductivity. Following Lai and Kulacki [11], the variable fluid viscosity can be simplified as:

$$\frac{1}{\mu }=\frac{1}{{\mu }_{\infty }}\left. [1+\gamma \left(T-T_{\infty }\right)\right]$$

(5)

Additionally, the thermal conductivity formula written as [12]:

$$K=K_{\infty }[1+\frac{{\mathsf{\xi }}_1}{\mathrm{\Delta }T}(T-T_{\infty })]$$

(6)

Here, ${\mathsf{\xi }}_1$ is a small parameter known as the variable thermal conductivity parameter. The magnetic field of intensity is given by [7,9]:

$\mathrm{H}\left(x,y\right)={[{\mathrm{H}}_x^2+{\mathrm{H}}_y^2]}^{\frac{1}{2}}=\frac{\gamma }{2\pi }\left. [\frac{1}{{\left(y+d\right)}^2}-\frac{x^2}{{\left(y+d\right)}^4}\right]$ where, fluid magnetization with temperature is given by: $M=k\left(T-T_{\infty }\right)$, where, $k$ is a pyromagnetic coefficient constant.

The following similarity variables are introduced:

$$\eta ={\left(\frac{a}{\left(1-ct\right){\upsilon }_{\infty }}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}y;\psi ={\left(\frac{a{\upsilon }_{\infty }}{\left(1-ct\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}xf\left(\eta \right); \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}$$

(7)

Therefore, Equations (2) and (3) are reduced as:

$$f\text{'}\text{'}\text{'}-\frac{1}{\left(\theta -{\theta }_r\right)}f\text{'}\text{'}\theta \text{'}+\left(\frac{\theta -{\theta }_r}{{\theta }_r}\right)A\left(f\text{'}+\frac{\eta }{2}f\text{'}\text{'}\right)+\left(\frac{\theta -{\theta }_r}{{\theta }_r}\right)\left(f{\text{'}}^2-ff\text{'}\text{'}-{\lambda }_1\theta \right)+\left(\frac{\theta -{\theta }_r}{{\theta }_r}\right)\frac{2\beta \theta }{{\left(\eta +{\alpha }_1\right)}^4}=0$$

(8)

$$\mathrm{Pr}\left(2A\theta +\frac{1}{2}\eta A\theta \text{'}+f\text{'}\theta -f\theta \text{'}\right)+\frac{2\beta \lambda \left(\theta +\epsilon \right)}{{\left(\eta +{\alpha }_1\right)}^3}f={\xi }_1\theta {\text{'}}^2+\left(1+{\xi }_1\theta \right)\theta \text{'}\text{'}$$

(9)

Subject to the boundary conditions,

$$\begin{array}{c}\eta =0:f^{\prime }\left(\eta \right)=1,f\left(\eta \right)=f_w,\theta \left(\eta \right)=1\\ \eta \to \infty :f^{\prime }\left(\eta \right)\to 0,\theta \left(\eta \right)\to 0\end{array}\}$$

(10)

where, $A=\frac{c}{a}$, $\mathrm{Pr}=\frac{C_p{\rho }_{\infty }{\upsilon }_{\infty }}{K_{\infty }}$, ${\lambda }_1=\frac{g{\beta }^{*}b}{a^2}$, $\lambda =\frac{a{\mu }_{\infty }^2}{{\rho }_{\infty }{K}_{\infty }\left(T_w-T_{\infty }\right)}$, $\epsilon =\frac{T_{\infty }}{T_w-T_{\infty }}$, $\beta =\frac{\gamma }{2\pi }\frac{k{\mu }_0{\rho }_{\infty }\left(T_w-T_{\infty }\right)}{{\mu }_{\infty }^2}$, ${\theta }_r=-\frac{1}{\gamma \left(T_w-T_{\infty }\right)}$, ${\alpha }_1={\left(\frac{a}{{\upsilon }_{\infty }\left(1-ct\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}d$, $f_w=-\frac{{\upsilon }_0}{\sqrt{a{\upsilon }_{\infty }}}$.

The important characteristics of the flow are skin friction coefficient and the Nusselt number, defined by,

$$C_f=-2\left(\frac{{\theta }_r}{\theta -{\theta }_r}\right){\mathrm{Re}}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}f\text{'}\text{'}\left(0\right); N{u}_x=-{\mathrm{Re}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\theta \text{'}\left(0\right)$$

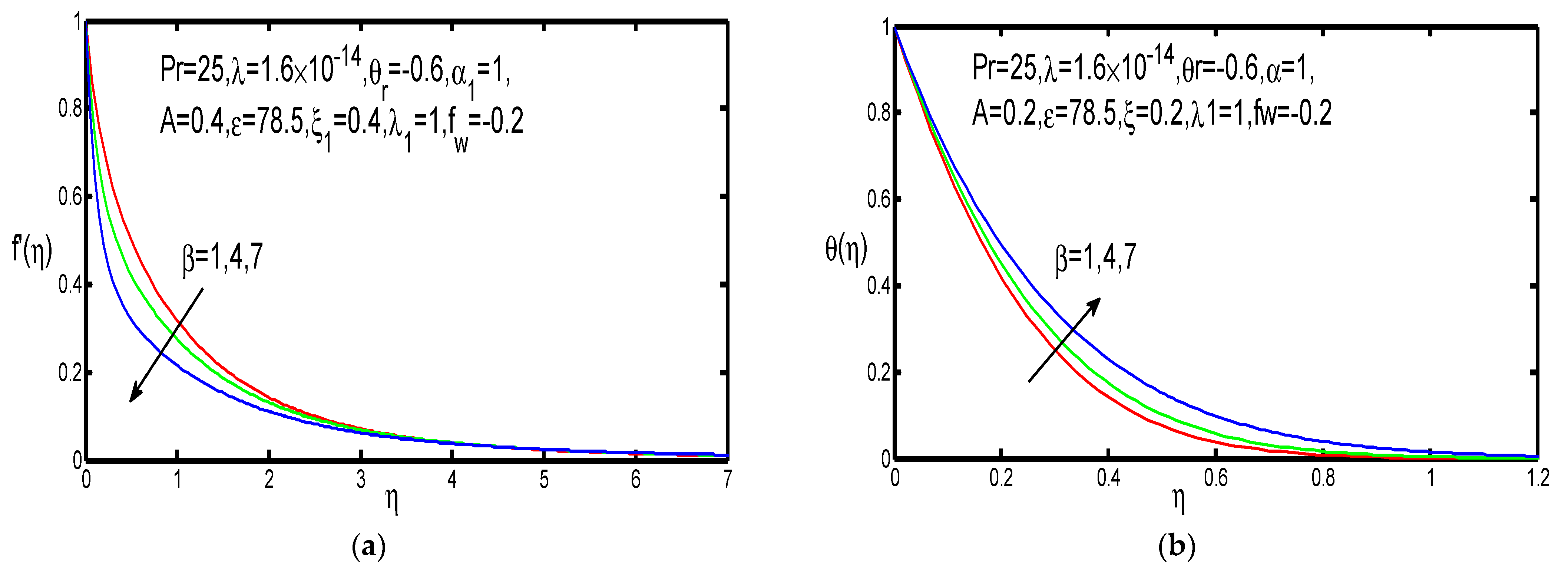
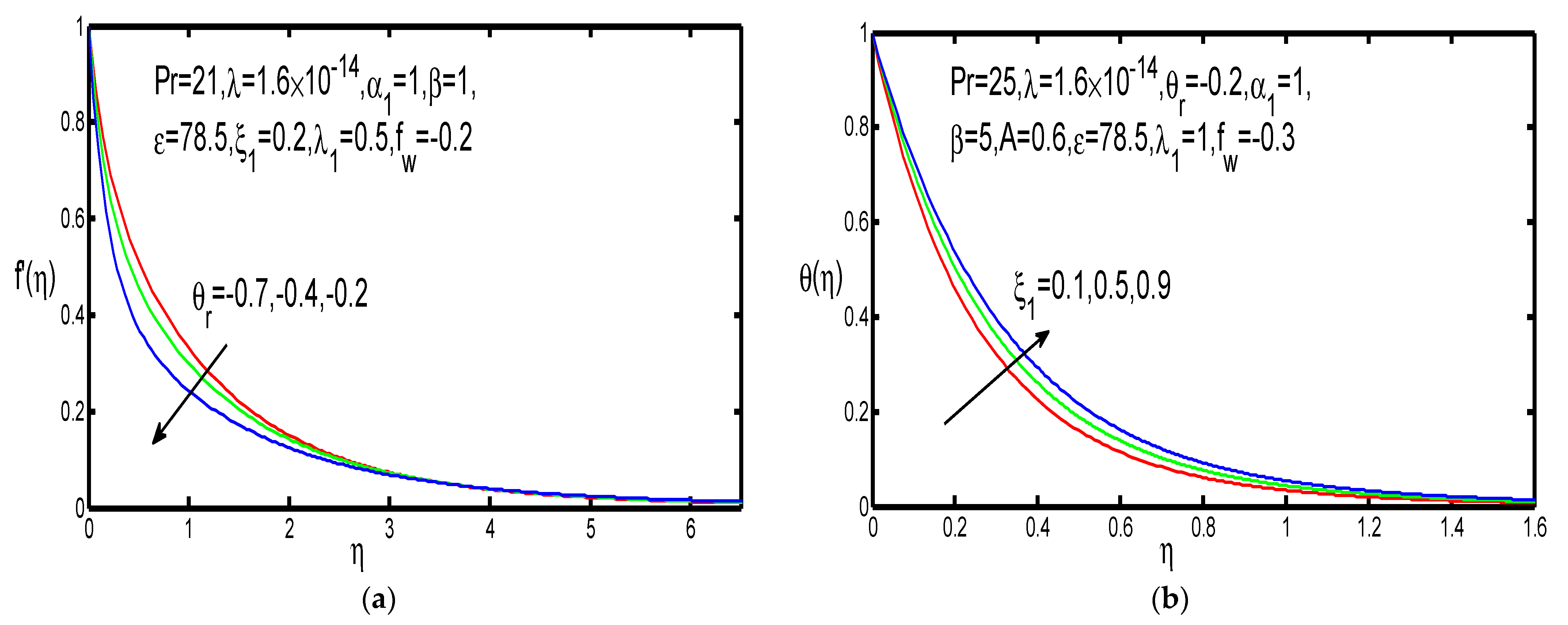
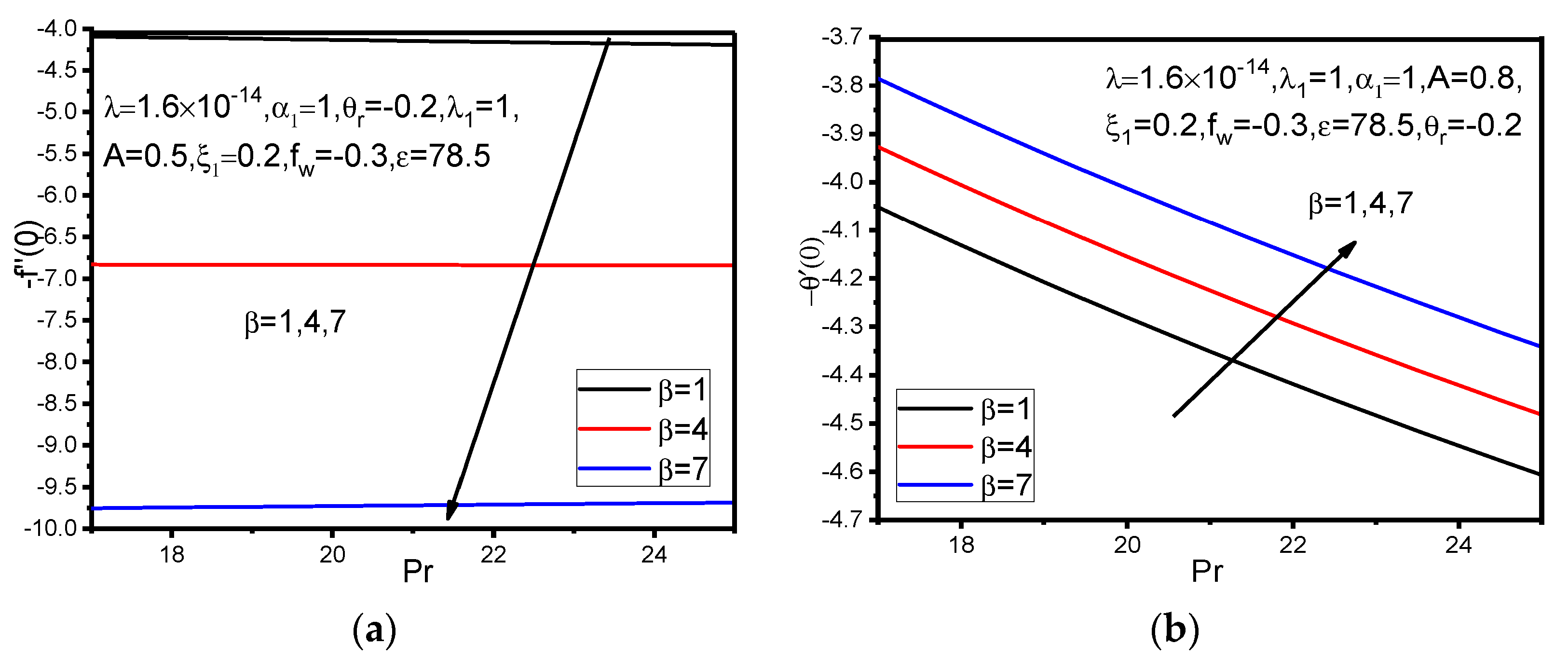
3. Results and Discussion

Computational solutions of ordinary differential equations (ODEs) are obtained using the well-known bvp4c technique in MATLAB. In order to assess the validity of the numerical analysis, a comparison has been conducted based on Pop et al. [13] for various values of the variable viscosity parameter when $\mathrm{Pr}=0.7$. The comparison shows an excellent agreement, as presented in

Table 1. Comparison values of $-f\text{'}\text{'}\left(0\right)$ and $-\theta \text{'}\left(0\right)$ for $\mathrm{Pr}=0.7$.

Viscosity	Present Results		Pop et al. [13]
${\theta }_r$	$-f\text{'}\text{'}\left(0\right)$	$-\theta \text{'}\left(0\right)$	$f\text{'}\text{'}\left(0\right)$	$\theta \text{'}\left(0\right)$
$-4$	$-0.507688$	$-0.344253$	$-0.5077877$	$-0.3442274$
$-2$	$-0.562720$	$-0.3350554$	$-0.5628924$	$-0.3348913$
$2$	$-0.278501$	$-0.380666$	$-0.2783288$	$-0.3806688$
4	$-0.369565$	$-0.366999$	$-0.3698711$	$-0.3667289$

.

The impacts of ferromagnetic interaction parameter on velocity and temperature profile are shown in Figure 2a,b. It is observed that with rising values of ferromagnetic number, blood velocity decreases but temperature accelerates. This is caused due to the polarization of blood. By applying a strong magnetic field on boundary domain, a resist force, which known as Kelvin force, has been produced. As a result, the flow in the boundary layer slows down.

Figure 3a,b show the variations caused by variable viscosity parameter and thermal conductivity parameter in velocity and temperature profiles, respectively. It is seen that blood velocity gradually decreased with increasing values of viscosity parameter. Physically, larger values of viscosity parameter suggest a greater temperature difference between the blood surface and the surrounding air. On the other hand, temperature enhanced with an increase in thermal conductivity parameter (see Figure 3b).

Finally, the variations in skin friction coefficient and the rate of heat transfer for various values of ferromagnetic numbers against Prandtl number are presented in Figure 4a,b. It is seen that skin friction declines whereas the rate of heat transfer is enhanced with increasing ferromagnetic number.

4. Conclusions

On the basis of the computational outcomes, we can summarize our results with the following statements:

(i)

Fluid velocity is reduced for large values of ferromagnetic number and viscosity variation parameter.

(ii)

For increasing values of ferromagnetic number and thermal conductivity parameter, temperature distributions are increased.

(iii)

Skin friction coefficient decreases with increasing ferromagnetic number, whereas a reverse phenomenon is observed in the rate of heat transfer.