Extracting Salient Facts from Company Reviews with Scarce Labels ^†

Abstract

In this paper, we propose the task of extracting salient facts from online company reviews. Salient facts present unique and distinctive information about a company, which helps the user in deciding whether to apply to the company. We formulate the salient fact extraction task as a text classification problem, and leverage pretrained language models to tackle the problem. However, the scarcity of salient facts in company reviews causes a serious label imbalance issue, which hinders taking full advantage of pretrained language models. To address the issue, we developed two data enrichment methods: first, representation enrichment, which highlights uncommon tokens by appending special tokens, and second, label propagation, which interactively creates pseudopositive examples from unlabeled data. Experimental results on an online company review corpus show that our approach improves the performance of pretrained language models by up to an F1 score of 0.24. We also confirm that our approach competitively performs well against the state-of-the-art data augmentation method on the SemEval 2019 benchmark even when trained with only 20% of training data.

1. Introduction

Online reviews are an essential source of information. More than 80% of people read online reviews before reaching decisions [1]. This trend also applies to job seekers. Before applying to open positions, job seekers often read online employee reviews about hiring experience and work environment on Indeed, LinkedIn, and other channels. However, the overabundance of reviews can render them cumbersome to read. For example, there are 63,400 reviews about Amazon on Indeed. Furthermore, job seekers must skim through several subjective comments in the reviews to find concrete information about a company of interest.

Alternatively, job seekers can find such concrete information (e.g.,

Table 1. Sample sentences from an online review and expert article about Google.

Online	Good work place, best pay, awesome company.
Expert	In the event of your death, Google pays your family 50% of your salary each year.

) in expert articles about companies on websites such as Business Insider [2,3] and FutureFuel [4]. However, such expert articles are typically written only for very popular companies and do not cover the global majority of companies. Online company reviews, on the other hand, are available for a vast number of companies, as (former) company employees submit reviews about a company to review platforms such as Glassdoor. Therefore, we aim to automatically extract unique and distinctive information from online reviews.

We refer to informative descriptions in online reviews as salient facts. In order to derive a formal definition of salient facts, we conducted an inhouse study where we asked three editors to inspect 43,000 reviews about Google, Amazon, Facebook, and Apple. The editors discussed salient and nonsalient sentences in the reviews, and concluded that a salient fact mentions an uncommon attribute about a company and/or describes some quantitative information of an attribute. Attributes of a company include employee perks, onsite services and amenities, the company culture, and the work environment. We further validated our definition by looking into expert articles, and confirmed that the articles were extensively composed of the same properties. For example, 4 of the 8 benefits mentioned in an article [2] about Google used less-known attributes such as food variety, fitness facilities, and pet policy. The other 4 of 8 benefits used numeric values, such as 50% retirement pension match.

In this paper, we propose the novel task of salient fact extraction and formulate it as a text classification problem. With this formulation, we could automate filtering company reviews that contain salient information about the company. Pretrained models [5,6,7] are a natural choice for such tasks [8,9] since they generalize better when the training data for the task are extremely small. We, therefore, adopted BERT [5] for our extraction task. However, generating even a small amount of task-specific balanced training data is challenging for salient fact extraction due to the scarcity of salient sentences in the reviews. Naively labeling more sentences to address the scarcity can be prohibitively expensive. As such, even pretrained models that perform robustly in few-shot learning cannot achieve good enough performance when used directly for this task.

In this work, we propose two data enrichment methods, representation enrichment and label propagation, to address the scarcity of salient facts in training data. Our representation enrichment method is based on the assumption that salient sentences tend to mention uncommon attributes and numerical values. We can, therefore, enrich training data using automatically identified uncommon attributes and numeric descriptions from review corpora. Specifically, we append special tags to sentences that mention uncommon attributes and numerical values to provide additional signals to the model. Our label propagation method is based on the idea that we can use a small set of seed salient sentences to fetch similar sentences from unlabeled reviews that are likely to be salient. This can help in improving the representation of salient sentences in the training data. Our methods are applicable to a wide variety of pretrained models [5,6,7].

We conducted extensive experiments to benchmark the extraction performance and demonstrate the effectiveness of our proposed methods. Our methods could improve the F1 scores of pretrained models by up to 0.24 on salient fact extraction, which is 2.2 times higher than the original F1 scores. This is because our models could identify more uncommon attributes and more quantitative descriptions than directly using pretrained language models can.Our models could also better distinguish between expert- and employee-written reviews.

To summarize, our contributions are the following: (1) We practice a new review mining taskcalled salient fact extraction using pretrained language models and data augmentation in an end-to-end manner. The task faced an extremely low ratio (i.e., <10%) of salient facts in raw reviews. (2) The best-performing methods still require massive labels in the tens of thousands, because trained models and augmented examples tend to be biased towards majority examples. To alleviate this problem, we leveraged a series of improvements to ensure that the model training and data augmentation worked effectively for the desired minority examples. (3) An extension of our method demonstrates that it generalizes well and could reduce the labeling cost for new domain adaption (e.g., transferring to a product domain achieves an improved label ratio from 5% to 43%) of the same task and for similar tasks that deal with minority review comment extraction (e.g., suggestion mining requires a reduced amount of labels by 75% to hit the performance of UDA semisupervised learning [10]). To facilitate future research, we publicized our implementations and experimental scripts (https://github.com/megagonlabs/factmine, accessed on 22 August 2020). We did not release the company dataset due to copyright issues. However, we aim to release datasets of similar tasks to benchmark the performance of different methods. We also released a command-line programming interface that renders our results readily reproducible.

2. Characterization of Salient Facts

The cornerstone towards automatic extraction is to understand what renders a review (or sentence in a review) salient. To this end, we first inspected raw online reviews to derive a definition of salient facts. We then analyzed expert articles to ensure that the derived definition is valid (Figure 1).

2.1. Review Corpus Annotation and Analysis

We produced inhouse annotation to understand what review sentences are deemed salient facts for human readers.We collected 43,000 company reviews about Google, Amazon, Facebook, and Apple. We split each review into sentences using NLTK [11]. Then, we inspected all the sentences and selected salient sentences according to our understanding of the corresponding companies.

Table 2. Sample salient facts extracted from online reviews.

Example 1. Google also has 25+ cafes and microkitchens every 100 ft. (Google)

Example 2. Dogs allowed in all the buildings I’ve been to (including some dog parks in the buildings!) (Amazon)

shows example sentences that were labeled salient.

Sentences labeled salient described more uncommon attributes than nonsalient sentences did. Uncommon attributes include real-world objects and services such as cafes, kitchens, dog parks. They are typically not provided by all companies and can help job seekers differentiate between companies. Furthermore, salient sentences use quantitative descriptions (e.g., 25+ and 100 ft in Table 2). Quantities often represent objective information and vary across companies, even for the same attribute, thereby helping job seekers in differentiating between companies.

These properties are not exhibited by nonsalient sentences. As shown in

Table 3. Example non-salient sentences and reasons.

Reason	Example
noquantity	awesome place to work, great salary, smart people
personal	I couldn’t imagine a better large corporate culture that still tries to be agile
common	Salary, perks, and benefits
noattribute	ok ok ok ok ook
incomplete	five single words for this
sentimental	great, happy, cool, friendly, doable, beautiful, awesome, nice, good, big
invalid	good fv gt tr tr yt y
irrelevant	Best friendly free cab cool no target

, most nonsalient sentences mention solely common attributes (e.g., place, salary and people), disclose purely personal sentiments (e.g., awesome, great, cool), or are noisy (e.g., invalid or incomplete texts). Different kinds of nonsalient sentences and their ratios are shown in Figure 1.

2.2. Expert Article Analysis

We analyze expert-written reviews to investigate if they exhibited characteristics of salient facts i.e., describe an uncommon attribute and/or use quantitative descriptions. First, we compare frequencies of a set of attribute words across expert sentences and review sentences. The used expert sentences attributed words that were infrequent in the review sentences. For example, frequencies of death, family (commonly mentioned in expert reviews for Google) in review sentences were 0.01% and 0.15%, respectively. In contrast, frequencies of place, pay (commonly mentioned in review sentences for Google) were 3.44% and 1.28%, respectively. This observation supports our definition.

Next, we inspected if the expert sentences used more quantitative descriptions than randomly selected review sentences. For example, 4 of the 7 expert sentences describing most benefits of Google used quantitative descriptions such as 10 years, USD 1000 per month, 18–22 weeks, and 50% match. On the other hand, none of the 7 sentences randomly sampled from reviews mentioned any quantities. In fact, most of them used subjective descriptions such as nice, interesting, and great. This observation supports our characterization of salient facts.

3. Methodology

Owing to the recent success of pretrained models in information extraction tasks, we adopted these models for salient fact extraction. We first describe how we modelled salient fact extraction as a sentence classification task over pretrained models. We describe technical challenges unique to this task. We then describe two methods, representation enrichment and label propagation, to address these challenges.

3.1. Pretrained Model and Fine Tuning

The goal of a supervised-learning model for salient fact extraction tasks is to predict the correct label for an unseen review sentence: 1 if the sentence is salient, and 0 otherwise. The model is trained using a set of labeled text instances ${(t,l)}_i$, where t is a sentence and l is a binary label. By seeing a number of training instances, the model learns to discriminate between positive and negative instances. However, supervised learning is sensitive to the coverage of salient sentences in the review corpus. It can yield suboptimal models when faced with imbalanced datasets.

Pretrained models, on the other hand, tend to be more robust to such imbalances and generalize better. These models project a text instance t into a high-dimensional vector (e.g., 768 in BERT), such that text instances sharing similar words or synonyms have similar vectors. Since predictions are based on dense-vector representations, they can predict the same label for semantically equivalent instances (e.g., cafe and coffee) without having seen them explicitly during training. As a result, pretrained models require far fewer salient sentences than supervised models trained from scratch do.

Despite their better generalizability, pretrained models struggle to make correct predictions for sentences with unseen attributes or quantities if their synonyms didn’t appear in the training set. As a result, a training set should contain as many infrequent attributes and quantitative descriptions as possible for optimal performance of pretrained models. However, due to the inherent scarcity of infrequent attributes and quantitative descriptions, the models can only see a limited amount of salient facts (and thus infrequent attributes and quantities) during training. We propose representation enrichment and label propagation methods to address these challenges. We next describe these methods in more detail.

3.2. Representation Enrichment

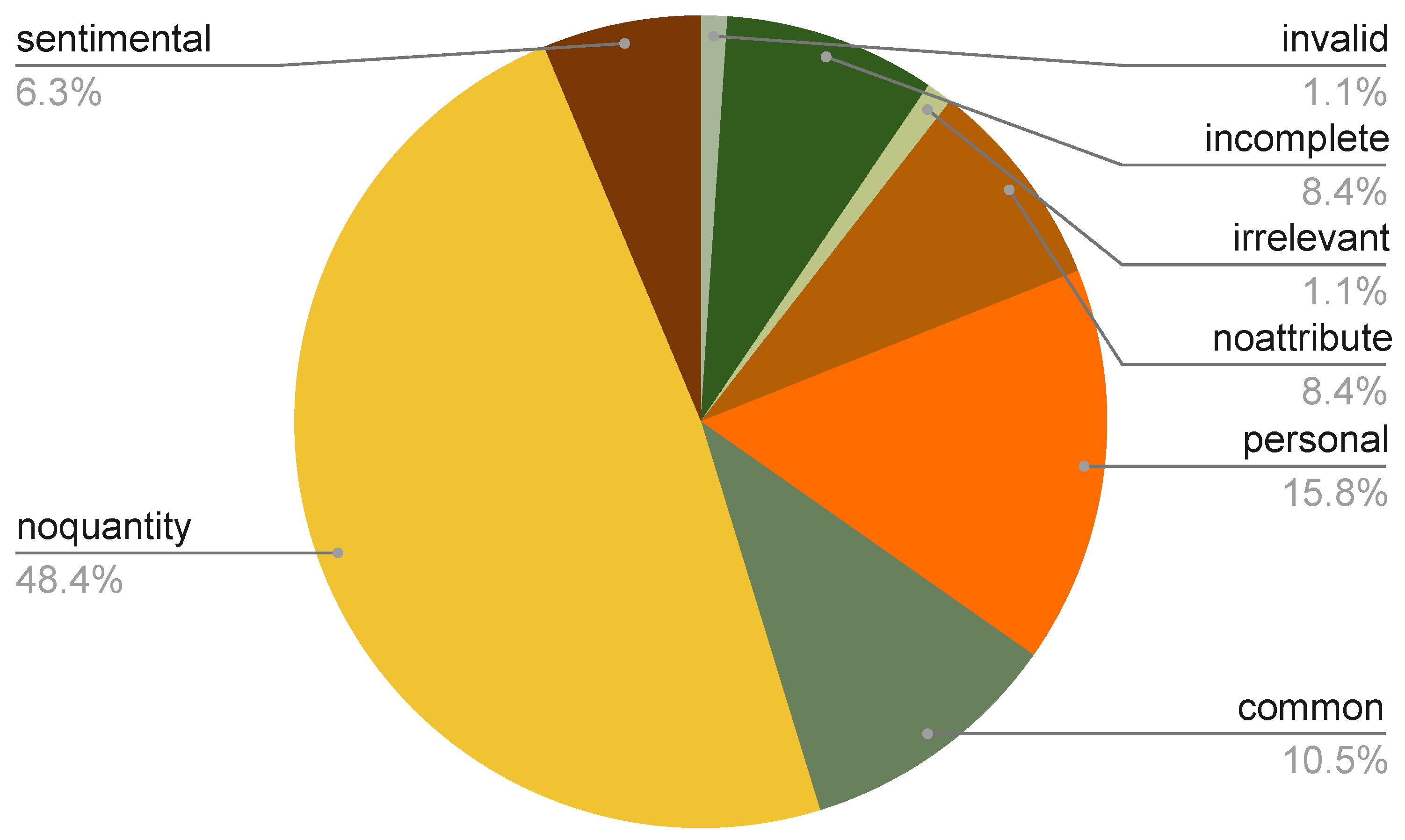
In our empirical experiment, we observed that only 0.55% of labeled sentences were considered to be positive (i.e., salient facts.). Given such an extremely small number of positive examples, there is a chance that the learning algorithm cannot generalize the model using the training set as it may not cover sufficient patterns of salient facts. As a result, a trained model may not be able to recognize salient facts with different linguistic patterns than those of the training instances. In this paper, we considered that we could alleviate the issue by incorporating prior knowledge about the task. Salient facts contain relatively uncommon attributes and/or quantitative descriptions, so we aimed to implement those functions into the model.

Since models may meet unseen salient facts during prediction, we developed a representation enrichment method to help the models in recognizing their attributes and quantities for prediction. The method appends a special tag to text instances if they contain tokens related to uncommon attributes or quantitative descriptions. The model can learn that a text instance containing the special tag tends to be a salient fact. During prediction, even if a model does not recognize unseen tokens in a salient fact instance, the model can recognize the special tag and make accurate prediction.

The expansion process begins by selecting a set of salient tokens. The salient tokens are those common words that appear in the review corpus to describe uncommon attributes or quantities. The expansion process comprises two steps. The first step identifies a list of salient tokens as part of the inputs to Algorithm 1. The second step takes the list and a special tag token (e.g., “salient” for uncommon attribute token list) to run Algorithm 1. The algorithm iterates all text instances. If a text instance contains any token of the list, the algorithm appends a special tag to it. All instances that contain salient tokens share the same tag. After the two steps, both groups of tagged and untagged text instances are fitted to train the extraction model. After the model is trained, it is used to produce predictions for salient facts.

Uncommon attribute token list: we used a two-step method to discover tokens that are used in the corpus to describe uncommon attributes. First, we identified nouns, since attribute tokens are mostly nouns. We used NLTK to extract noun words. Second, we ranked the nouns by their IDF scores. The IDF of a noun w is calculated as $log(T/|\left\{d\right|d\in D\wedge w\in d\left\}\right|)$, where T is the total number of sentences and $\left|\right\{d|d\in D\wedge w\in d\}|$ is the number of sentences that contain the noun token w. Nouns that appeared the least frequently (i.e., top 1000 words based on the IDF scores) in the review corpus were considered to be uncommon attribute tokens. We next inspect the top list to label tokens that are used to describe uncommon attributes. The purpose was to exclude nonattribute words. By applying this two-step method, we successfully constructed a list of uncommon attribute tokens.

Quantitative description token list: we curated a list of tokens that are used to describe quantities. The list contains three types of tokens: digit, numeric, and unit. Digit tokens include all integer numbers from 0 to 9 and any integers composed of the 10 integers. Numeric (https://helpingwithmath.com/cha0301-numbers-words01/, accessed on 22 August 2020) are word descriptions of numbers, and representatives are hundreds, thousands, and millions. Unit (https://usma.org/detailed-list-of-metric-system-units-symbols-and-prefixes, accessed on 22 August 2020) consist of commonly used measurements that often appear in quantitative descriptions, and some examples include hour and percentage. Digit, numeric, and unit form a comprehensive coverage of word tokens that people commonly use in quantitative descriptions. We last inspected the set of tokens and curated a final list of tokens for quantitative descriptions.

Algorithm 1 Representation enrichment.

Input: Text instance t with tokens $t_1,t_2,\cdots ,t_k$, list l of salient tokens, and special token s

Output: A new text instance $t_{new}$

1: $t_{new}\leftarrow t$

2: for $i\leftarrow 1$ to k do

3:   if $t_i\in l$ then

4:      $t_{new}\leftarrow t_{new}+s$

5:      return $t_{new}$

6:    end if

7: end for

8: return $t_{new}$

3.3. Label Propagation

Due to the extremely sparse positive examples for salient facts, the training procedure may fail to generalize the model. To alleviate the issue, we augmented training data by searching similar instances.

Candidate Selection: we show the label propagation process in Algorithm 2. The process takes salient fact instance t from existing training data as input. Then, it searches the m-most similar instances from unlabeled text instances (denoted as $u_1,u_2,\cdots ,u_n$.) As the similarity function, we used the Jaccard score as defined in Equation (1), where $V_t$ and $V_u$ denote the distinct vocabulary sets of t and u respectively. The score is 1 if two texts share exactly same vocabulary sets, and 0 if they do not share any common tokens.

$$J(t,u)=|V_t\cap V_u|/|V_t\cup V_u|$$

(1)

To obtain vocabulary sets, we used the BERT WordPiece tokenizer to split the text into tokens by matching character sequence with a predefined vocabulary of about 30,000 [5]. Since an unlabeled corpus contains abundant text instances, Algorithm 2 can help in retrieving the instances that are the most similar to salient facts to expand our training set.

Algorithm 2 Label propagation: candidate selection.

Input: Salient instances set T, unlabeled instances set U, similarity function $sim(t,u)$, candidate size m.

Output: Candidate instances set C of size m

1: Candidate set $C\leftarrow \left[\right]$

2: for t in T do

3:    for $i\leftarrow 1$ to n do

4:      $s\leftarrow sim(t,u_i)$

5:      $C\leftarrow C+(u_i,s)$

6:    end for

7: end for

8: $C=deduplicate\left(C\right)$

9: Sort C by score

10: return $C[1:m]$

Reranking: Jaccard score favors frequent word tokens such as stopwords. Therefore, a negative instance can be ranked high and returned as a candidate if it contains a lot of stopwords. To solve this issue, we introduced a reranking operator that sorts all candidates by their relative affinity to positive and negative examples in the training set, as shown in Algorithm 3. For every candidate c, we calculated two scores, i.e., textual affinity $ta$ and semantic affinity $sa$, which were used to measure the overall distances to a group of examples G.

$$avg\_dist(c,G)=1/\left|G\right|\ast \sum _{e\in G}(1-J(c,e))$$

(2)

$$ta(c,X,Y)=\frac{avg\_dist(c,\left\{x_i\right|x_i\in X,y_i=0\})}{avg\_dist(c,\left\{x_i\right|x_i\in X,y_i=1\})}$$

(3)

Textual affinity $ta$ was defined as Equation (3) to measure the relative affinity of a candidate c to the positive- and negative-example groups of the training set. Affinity is measured by counter average distance (see Equation (2)). Greater textual affinity is better, which means that c has smaller distance to the positive group and larger distance to the negative group. Intuitively, textual affinity favors candidate c that shares many common tokens with positive examples, while such tokens are not common (e.g., stopwords) in negative examples.

$$sa(c,X,Y)=discriminator(X,Y).estimate\left(c\right)$$

(4)

Textual affinity cannot recognize semantically connected words (e.g., million and billion). Therefore, we introduced semantic affinity $sa$ as defined in Equation (4). Semantic affinity requires a discriminator that uses word embeddings as input representation. In other words, a discriminator can recognize semantically connected words through similar word vectors. Next, we trained the discriminator using the training set, so that the discriminator learned to predict whether an input sentence is a positive example according to its word vectors. The trained discriminator is used to estimate the probability of candidate c belonging to the positive group. In our experiments, we used BERT as the discriminator and took the product of textual affinity $ta$ and semantic affinity $sa$ to yield the best F1 scores.

Lastly, we sorted all candidates in descending order by their overall affinity score (i.e., textual affinity × semantic affinity). We returned the top $pk$ as positive examples, and tail $nk$ as negative examples, where $pk$ and $nk$ are user-defined parameters. In our experiments, label propagation performed reasonably well if $\frac{pk}{pk+nk}$ equalled to the label ratio, and $pk+nk$ equalled to the training size but was smaller than half the size of unlabeled examples.

Algorithm 3 Label propagation: reranking.

Input: Candidate collection C, training set $X,Y$, number of pseudopositive examples $pk$, and negative examples $nk$

Output:$pk$ positive and $nk$ negative pseudoexamples

1: Reranking set $R\leftarrow \left[\right]$

2: for c in C do

3:    ta = textual_affinity(c, X, Y)

4:    estimator = BERT (X, Y)

5:    sa = semantic_affinity(c, estimator)

6:    $R\leftarrow R+(c,ta\ast sa)$

7: end for

8: $R.sorted(key=lambda(c,s):-s)$

9: return head $pk$ and tail $nk$ of R as positive and negative pseudoexamples

3.4. Additional Training Techniques

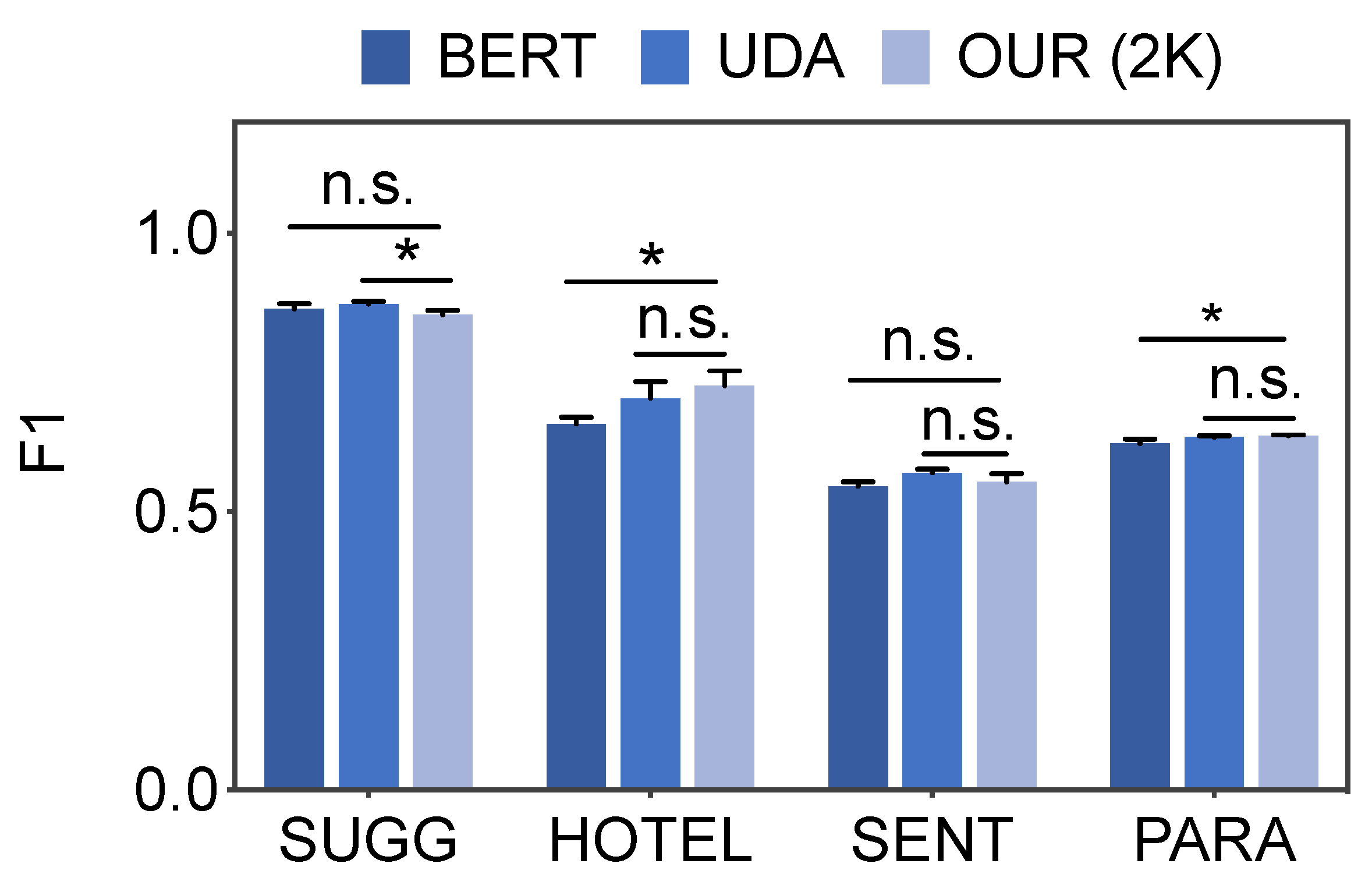
Fine tuning pretrained language models is limited in batch size due to GPU memory capacity. For example, the maximal batch size that BERT base model can process on a 16 GB GPU is around 64. Given the extremely low label ratio (e.g., 5%), it is possible that a batch may not contain any positive examples. Consequently, the trained model may exhibit significant biases against positive examples. To alleviate this problem, we leveraged two fine-tuning techniques, namely, thresholding and choosing the best snapshot (described below), to enable the trained model to weigh more on the positive examples.

Thresholding: pretrained models such as BERT adopt argmax to predict the label of an example. First, the pretrained model outputs two probability scores for the same example, indicating the likelihood of this example belonging to the negative or positive class. Next, argmax selects the class of a larger score as the final prediction. Experiments showed that the average positive probability was much smaller than negative probability; thus, we replaced argmax with thresholding that only concerned the positive prediction score. Thresholding sorts all examples by positive prediction scores and varies a threshold from the highest to the lowest score. We tried 100 different thresholds at equal intervals between highest and lowest, and chose the threshold that led to the largest F1 on the training set.

Choose best snapshot: due to severe label imbalance, a model could achieve the best performance during its training snapshots. A potential reason is that the model met the highest-quality positive and negative examples at the snapshots. Therefore, we set a fixed number of snapshots and inspected the model during each snapshot. We compared the model performance between two consecutive snapshots and checkpointed the model if better performance was observed.

4. Experiments

In this section, we first examine the extraction performance of pretrained models BERT, ALBERT, and RoBERTa. We then show the effectiveness of our proposed data enrichment methods by conducting an ablation study with the pretrained models.

Datasets: we obtained company reviews from an online company review platform for job seekers. We use the reviews of two companies (Google and Amazon) for evaluation. We chose these companies because their expert articles were also available for comparison. We first split the reviews into sentences using the NLTK sentence tokenizer [11]. For Google, we used all 13,101 sentences from the reviews. For Amazon, we randomly sampled 10,000 sentences. We then asked four editors to finish labeling these sentences (1 or 0) on the basis of their salience. We randomly sampled 100 sentences (50 positive and 50 negative) and asked two editors to label them. There was Cohen’s kappa agreement of 0.9 between the editors. This agreement is higher than the agreement scores reported in previous studies related to our work e.g., 0.81 from a SEMEVAL-2019 Competition task 9 [8] and 0.59 from TipRank [12]).

Hyperparameters: we split the labeled dataset into training and test sets at a ratio of 4:1. For training the pretrained models, we set the number of epochs to 5, max sequence length to 128, and batch size to 32. We used the F1 score of the positive class (i.e., salient) to measure the performance of a model. Since a model may achieve the best F1 score in the middle of training, we inspected a model 15 times during training and reported the best F1 score of the 15 snapshots.

4.1. Effectiveness of Pretrained Models

We first compare the performance of pretrained models and other supervised learning algorithms, namely, logistic regression (LR), support vector machine (SVM), convolutional neural network (CNN), and recurrent neural network with long short-term memory (LSTM). We used the same configuration to train and evaluate all models. Unsurprisingly, all pretrained models consistently outperformed other models on the two datasets (as shown in

Table 4. F1 scores of BERT, ALBERT (ALB.), RoBERTa (ROB.), LR, SVM, CNN, and LSTM on Google and Amazon datasets. The best score for each dataset is in bold.

Dataset	BERT	ALB.	ROB.	LR	SVM	CNN	LSTM
Google	0.33	0.30	0.19	0.13	0.17	0.17	0.17
Amazon	0.27	0.13	0.20	0.13	0.12	0.03	0.07

). BERT achieved the highest F1 scores with absolute F1 gain as high as 0.16 and 0.14 on Google and Amazon, respectively. These results indicate that the pretrained models are suited for the salient fact extraction task.

4.2. Effectiveness of Representation Enrichment

To investigate the effectiveness of representation enrichment, we curated two lists, one for uncommon attribute descriptions and one for quantitative descriptions. We separately applied the two lists for each pretrained model, and report their F1 scores in

Table 5. F1 score of BERT, ALBERT (ALB.), RoBERTa (ROB.) when using representation enrichment. F1 improvements compared with direct use of pretrained models (see Table 4) marked in orange. Best scores marked in bold.

Expansion	Dataset	BERT	ALB.	ROB.
Uncommon	Google	0.38 (+0.05)	0.43(+0.13)	0.19 (+0.00)
Uncommon	Amazon	0.29 (+0.02)	0.28 (+0.15)	0.35(+0.15)
Quantitative	Google	0.38 (+0.05)	0.40(+0.10)	0.32 (+0.13)
Quantitative	Amazon	0.27 (+0.00)	0.2 (+0.7)	0.44(+0.24)

. We also computed the F1 scores before and after representation enrichment.

We first evaluated the effect of representation enrichment using uncommon attribute token list (Uncommon). As shown in Table 5, Uncommon could improve the F1 score of BERT, which appeared to be the best model, as shown in Table 4, from 0.33 to 0.38 on Google and from 0.27 to 0.29 on Amazon, so improvement was 0.05 and 0.02, respectively. More importantly, Uncommon also improved the F1 scores of models ALBERT and RoBERTa on both Google and Amazon. ALBERT achieved the greatest F1 improvement (0.13 on Google and 0.15 on Amazon) and outperformed BERT. RoBERTa achieved 0.15 F1 improvement and outperformed BERT on Amazon. Results indicate that representation enrichment with an uncommon attribute token list is generic and can improve the extraction performance of various pretrained models.

We next evaluated the effect of representation enrichment using quantitative description token list (Quantitative). As shown in Table 5, Quantitative consistently improved F1 scores for all models. In particular, ALBERT achieved F1 improvement of 0.10 on Google, while RoBERTa an F1 improvement of 0.24 on Amazon. The final F1 score of RoBERTa was 0.44 on Amazon, and the score was record-high in Amazon extraction performance. Results further verified that representation enrichment, in particular the quantitative description token list, is a general method that works with various pretrained models.

4.3. Effectiveness of Label Propagation

Label propagation boosts the number of training samples by retrieving similar texts from unlabeled corpora. To evaluate the effect of label propagation, we retrieved three of the most similar texts for each salient fact and use them as positive examples for training. Since Google and Amazon had 62 and 66 salient facts, we retrieved 186 and 198 sentences, respectively. We report the F1 scores of BERT, ALBERT, and RoBERTa in

Table 6. F1 score of BERT, ALBERT (ALB.), RoBERTa (ROB.) when using label propagation. F1 improvement compared with direct use of pretrained models (see Table 4) are marked in orange. Best scores are marked in bold.

Dataset	BERT	ALB.	ROB.
Google	0.48(+0.15)	0.37 (+0.07)	0.36 (+0.17)
Amazon	0.28 (+0.01)	0.22 (+0.09)	0.29(+0.07)

. We also calculated the F1 improvements before and after the label propagation.

Pretrained models achieved better F1 scores with label propagation. F1 improvement ranged from 0.07 to 0.17 on Google, and 0.01 to 0.09 on Amazon. RoBERTa showed the largest improvement of 0.17 on Google, where its F1 score rose up to 0.36 from 0.19, which did not leverage label propagation (see Table 4). On Google, BERT achieved0.15 F1 improvement and a record-high F1 score of 0.48. Results suggest that label propagation can boost the performance of various pretrained models.

5. Extension

In this section, we extend our method to a new domain and similar tasks that deal with imbalanced datasets to verify whether our task and method had much generality.

5.1. New Domain

We defined the concept of salient fact from analyzing company reviews. We then attempted to transfer the concept to a new domain, i.e., product reviews. First, we directly deployed a trained company model on product review sentences to predict their probability of saliency. Next, we sorted all sentences by saliency score in descending order, and present the top 100 to 4 human annotators. We asked annotators to give label every sentence with positive or negative indicating salient or nonsalient, respectively. We also asked annotators to label randomly sampled 100 sentences for comparison.

We report the averaged ratio of positive examples for four headset products, i.e., plantronic, jawbone, Motorola, and Samsung, in

Table 7. Ratio of sentences that human annotators feel salient before and after transferring trained company model to product reviews.

	Plantronic	Jawbone	Motorola	Samsung
random	0.05	0.08	0.08	0.06
transfer	0.40	0.37	0.38	0.39

. According to the results, transferring consistently increased the label ratio by a large margin for all four products. The margin varied from 3× to 7×. Results suggest that the definition of salient facts is general enough to be applied to the product domain. For quick demonstration, we release all sentence samples in our public codebase.

5.2. Similar Public Task

We extended the label propagation algorithm to similar tasks since the algorithm was designed to be general. We conducted experiments to compare our method with the state-of-the-art baselines on public tasks that regard minority comment extraction. We obtained four public datasets that contained binary labels for training extraction models. SUGG [8] comes from SEMEVAL 2019 task 9; positive example means that it contains customer suggestions for software improvement. HOTEL [13] was derived from the Hotel domain with, positive example indicating that it carries customer-to-customer suggestions for accommodation. SENT [14] contains sentence-level examples, and a positive label means the sentence contains tips for PHP API design. PARA [14] comes from the same source of SENT, but contain paragraph-level examples. The ratio of positive examples for SUGG, HOTEL, SENT, and PARA was 26%, 5%, 10%, 17%, respectively. All four datasets contained a training set and a test set at 4:1 ratio.

We adopted UDA [10] as a strong baseline method. UDA uses BERT as base model and augments every example in the training set using back translation from English to French then back to English. The example and its back translation are fed into model training to minimize KL divergence, so that the two examples are projected to close vector representations. We ran UDA and BERT on the full training set, and our method on only 2000 training examples. Our F1 scores and those of BERT and UDA are shown

Table 8. F1 of four public tasks for minority comment extraction. All baselines use full training examples. Our method used 2000, yet could match the performance of baselines.

	SUGG (8.5k)	HOTEL (6k)	SENT (9.1k)	PARA (5.2k)
BERT (full)	0.8571	0.6467	0.5413	0.6297
UDA (full)	0.8695	0.7290	0.5614	0.6322
Ours (2k)	0.8673	0.7244	0.5416	0.6514

. The average F1 of BERT, UDA, and ours was 0.6687, 0.6980, and 0.6961, respectively. BERT performed the worst because it does not use any data augmentation, so it suffers the most from label imbalance. UDA and ours performed similarly across all the datasets, yet UDA used full training examples, but ours used only 23.52%, 33.33%, 21.97%, and 38.46% of the examples on SUGG, HOTEL, SENT, and PARA, respectively. UDA favors mild data augmentation due to the usage of KL divergence and back translation mostly change one or two word tokens in an example. However, the mild design choice was too conservative to efficiently augment minority examples in imbalanced datasets (thus requiring a higher volume of augmented data). Therefore, a more aggressive design choice such as ours, which can return new sentences as augmented examples, is needed for the widespread existence of imbalanced datasets.

5.3. Statistical Significance

We conducted experiments to evaluate the statistical significance or randomness of our results. Specifically, we set different random seeds to run BERT, UDA, and our method on SUGG, HOTEL, SENT, and PARA. The number of training examples for SUGG, HOTEL, SENT, and PARA was 8500, 6000, 9100, and 5200, respectively. For every dataset, we fed full training examples to BERT and UDA, but only 2000 to our method. We repeated the same experiment three times and reported F1 scores. Statistical analysis was performed using GraphPad Prism 7, and statistical significance was determined using one-way ANOVA followed by Tukey’s multiple-comparison test. We calculated the mean, SD, and p value with Student’s t test. Significance: not significant (n.s.) $p>0.5$, * $p<0.05$, ** $p<0.01$, *** $p<0.001$.

Comparison results of BERT, UDA, and ours (2000) on SUGG, HOTEL, SENT, and PARA shown in Figure 2. When comparing BERT with ours (2000), BERT showed no significant difference on SUGG and SENT, and worse performance on HOTEL and PARA. Results suggest that ours (2000) could outperform BERT even with fewer training examples. When comparing UDA and ours (2000), the two methods showed no significant difference on SENT and PARA. On HOTEL, UDA was better, but on SUGG it showed worse performance. Results suggest that ours (2000) could achieve equally good performance as that of UDA with much fewer training examples.

6. Related Work

Informative reviews: extracting informative reviews drives broad applications in web mining, while the definition of informativeness varies across application domains. TipRank [12] extracts short and practical sentences from TripAdvisor reviews to prepare travellers for upcoming trips. AR-Miner [15] and DeepTip [14] highlight useful comments in software reviews to notify developers of potential artifact issues. AMPERE [16] extracts argumentative sentences from paper reviews to help authors improve their manuscripts. In addition to the above research, there are many works targeting different domains such as products [17,18,19], restaurants [20,21,22], and hotels [13,23,24]. These works align with discovering helpful reviews to save reader time. Unlike existing works, our paper targets the company domain, where understanding a company heavily relies on knowledge of uncommon attributes and quantitative information, as indicated by expert-written reviews. Therefore, our definition of salient facts serves as another dimension to analyze massive reviews, and our work complements existing efforts towards mining the most useful information from reviews.

Supervised learning: existing works mostly adopt supervised learning when developing automatic extractors because supervised models can automatically learn to differentiate positive and negative instances from human labels. There are three popular categories of supervised models, depending on input sequence representation: word occurrence models [12,13,15], such as logistic regression [25] and support vector machine [26], representing a text as a bag of words and thus suffering from limited vocabulary when the number of training data is small. Word vector models [8,13,14,17,27,28], such as convolutional neural networks [29] and long short-term memory [30], represent a text as a matrix of word embeddings and can thereby process unseen words through their embeddings. Recently, pretrained models [8,9], such as BERT [5], ALBERT [6], and RoBERTa [7], have emerged representing a text as a high-dimensional vector by aggregating word embeddings. Due to the high dimension (e.g., 768 in BERT) and large-scale parameters (e.g., 110M in BERT) for aggregation, pretrained models appear to be the most promising solutions for extractions. In fact, among all different models, pretrained models achieved the best F1 scores and are thus the base models for our work.

Label scarcity: the problem of salient fact extraction falls into the big category of text classification. However, the unique challenge here is label sparsity. The ratios of salient facts in raw reviews are extremely low (<10%) due to the nature of uncommon attributes and quantitative descriptions that require solid domain-specific knowledge from crowd reviewers. As a result, collecting a large number of salient facts for model training is very difficult. We thus propose a label propagation method to expand existing salient facts with two benefits. First, the method expands the input tokens of a input sentence towards instructing pretrained models about whether the input carries uncommon attributes or quantitative descriptions. Second, the method fetches more salient fact instances from the ample unlabeled corpus to enable pretrained models seeing more salient facts. The label propagation method was specifically designed to suit the nature of uncommon attributes and quantitative information, and is thus complementary to existing techniques such as data augmentation [31,32,33] and active learning [34,35,36]. A combination of existing techniques can further improve extraction quality. However, it is nontrivial to adapt existing techniques here due to increased algorithmic complexity; therefore, incorporating existing techniques is a fascinating future direction for this work.

7. Extraction

In this section, we present extracted salient facts for qualitative analysis. We used BERT as the representative pretrained models. We also present extractions using existing solutions.

7.1. Extraction Comparison

We present salient facts extracted from reviews about Google on

Table 9. Extractions of various methods on Google dataset with attributes and descriptions marked in red and blue, respectively. Our extractions revealed finer-grained attributes (see red) and distilled numeric knowledge (see blue).

Method	Extractions
Ours	on campus laundry rooms, lots of gyms, cars on demand in case you have to drive during the day. Flexible working hours, 90% of health insurance paid for, 12 weeks paid parental leave as a secondary care giver, free breakfast/lunch/dinner.
TextRank	lots of happy hours and the free food is as great as everyone says it is. Solving challenging and interesting problems that matter to people.
Kmeans	Interestingwork. Google.
Longest	Chapter 4 of “English to Go” deals with Aeon, one of the other mega English teaching companies, and is entitled “Aeon’s Cult of Impersonality.” An earlier chapter, chapter 2, that deals specifically with NOVA doesn’t delve into the cultlike training...
Random	freefood. awesomeplace to work, great salary, smart people.

. We also present salient facts extracted by baseline algorithms TextRank, K-means, Longest, and Random. TextRank [37] formulates sentences and their similarity relation into a graph, and extracts texts with the highest PageRank weights. K-means clusters sentences into a number of centroids and extracts the centroid sentences. Longest chooses the longest sentence from the corpus. Random randomly selects sentences from the corpus. These algorithms form a complete set of existing solutions for mining informative texts from a large corpus.

Finer-grained attribute discovery: extraction examples show that our method extracted salient facts that contained finer-grained attributes than those extracted by the baseline methods. Representative attributes include laundry room, gyms, cars, and museum tickets. These attributes describe concrete properties about the company and are less common in the company domain. In contrast, extractions by the existing solutions tend to contain common attributes such as food, problem, work, salary, or people, which are popular and general topics about companies. The extractions by Longest did not reveal company attributes since the method retrieves long yet fake reviews that are copies of external literature. Results suggest that salient facts are informative when presenting specific or unique attributes of a company to readers.

Numeric knowledge distillation: our extractions distill numeric knowledge compared with extractions from existing solutions. Representative knowledge includes 90% paid health insurance, 12 weeks paid parental leave, and free meals provided by the company. Knowledge is objective since it quantitatively describes attributes. In contrast, extractions from existing solutions mostly use subjective descriptions such as “lots of”, “great”, and “awesome”. These subjective descriptions are biased towards reviewers. Results suggest that salient facts can provide unbiased and reliable descriptions to readers.

7.2. Expert Comment Recognition

Online comments are written by different people. Some writers with better knowledge about entities tend to give comments that are more informative. We refer to such writers as experts, and their comments as expert comments. In order to show the most informative comments to readers, a salient fact extractor should rank expert comments higher than other comments.

To understand whether our trained model could rank expert comments higher, we curated a collection of comments from online company reviews and FutureFuel. Online comments are those that we labeled as nonsalient (some representatives are in Table 3) and were thereby treated as nonexpert reviews. FutureFuel comments are those that came from invited writers and were thereby treated as expert reviews. We then sorted the collection of nonexpert and expert comments by prediction scores in descending order. A higher prediction score indicated a higher probability to be an expert comment.

Ranking results of Google and Amazon datasets are shown in

Table 10. Number of expert comments in top list after sorting all comments by prediction scores. Baseline randomly shuffles all comments.

Google (14 Expert Comments + 14 Online Comments)
Top List	Ours	Baseline
Top 4	4	2
Top 10	9	5
Top 14	13	7
Amazon (16 Expert Comments + 16 Online Comments)
Top List	Ours	Baseline
Top 4	4	2
Top 10	9	5
Top 16	15	8

. In the optimal case, all comments in the top-k list were expert comments. We show the number of expert comments of our model and a baseline that randomly shuffles all comments. Our model consistently achieved better results than the baseline in both the Google and the Amazon dataset, as shown in Table 10. In top 4 lists, all comments returned by our models were expert comments. In top 10 lists, 9 comments were expert comments in both Google and Amazon. Results indicate that our model could identify expert comments with nearly 100% accuracy. In the collection or comments that came from different people, our models could effectively recognize comments that had been written by experts, could and this ensure that readers are shown the most informative contents.

8. Conclusions

In this paper, we proposed a task of extracting salient facts from online company reviews. In contrast to reviews written by experts, only a few online reviews contain useful and salient information about a particular company, which creates a situation where the solution can only rely on highly skewed and scarce training data. To address the data scarcity issue, we developed two data enrichment methods, (1) representation enrichment and (2) label propagation, to boost the performance of supervised learning models. Experimental results showed that our data enrichment methods could successfully help in training a high-quality salient fact extraction model with fewer human annotations.