Long-Tail Zero and Few-Shot Learning via Contrastive Pretraining on and for Small Data †
Abstract
:1. Introduction
- RQ-1: Does a large pretrained language model, in this case, RoBERTa [13], achieve good long-tail class prediction performance (Section 5.1)?
- RQ-2: Can we extend language models such that a small language model can retain accurate long-tail information, with overall training that is computationally cheaper than fine-tuning RoBERTa?
- RQ-3: What are the long-tail prediction performance benefits of small CLMs that unify self-supervised and supervised contrastive learning?
Contributions
2. Related Work
2.1. Long-Tail Compression
2.2. Contrastive Learning Benefits
2.3. Long-Tail Learning
2.4. Negative and Positive Generation
2.5. Data and Parameter Efficiency
2.6. Label Denoising
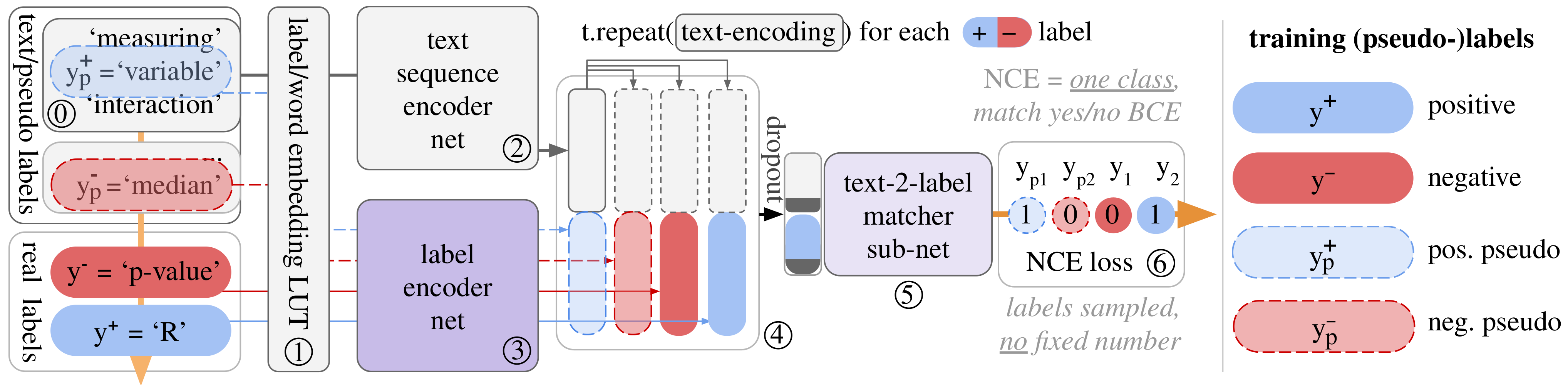
3. CLESS: Unified Contrastive Self-supervised to Supervised Training and Inference
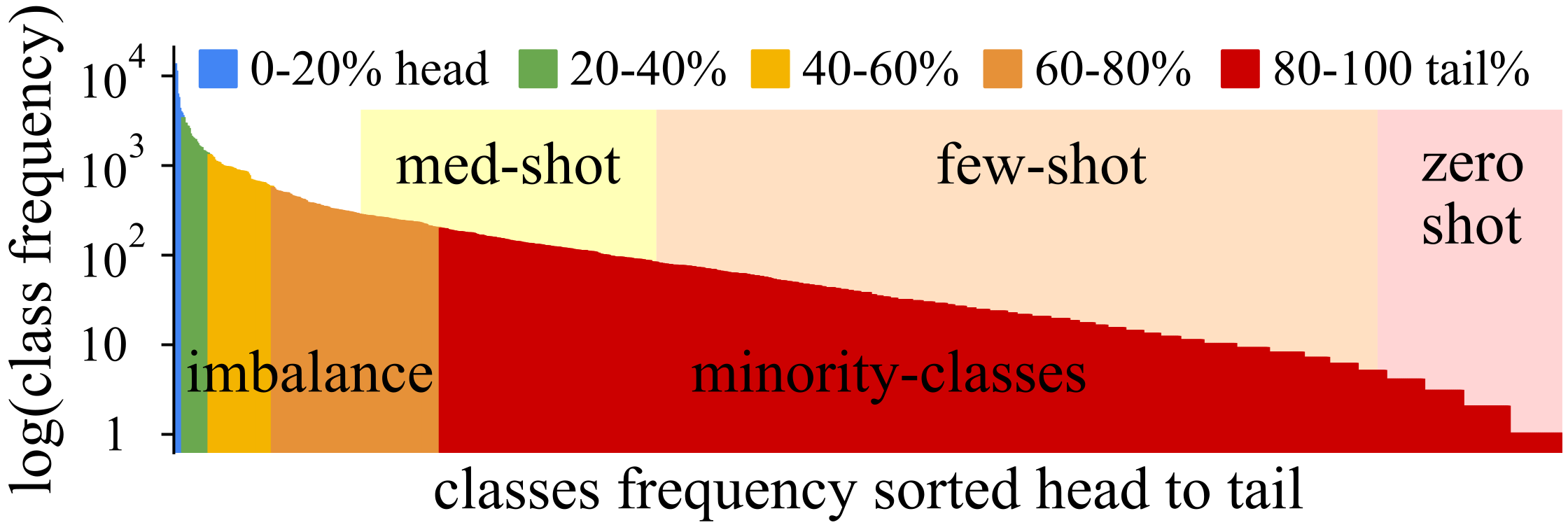
4. Data: Resource Constrained, Long-Tail, Multi-Label, Tag Prediction
- Long-tail evaluation metrics and challenges:
5. Results
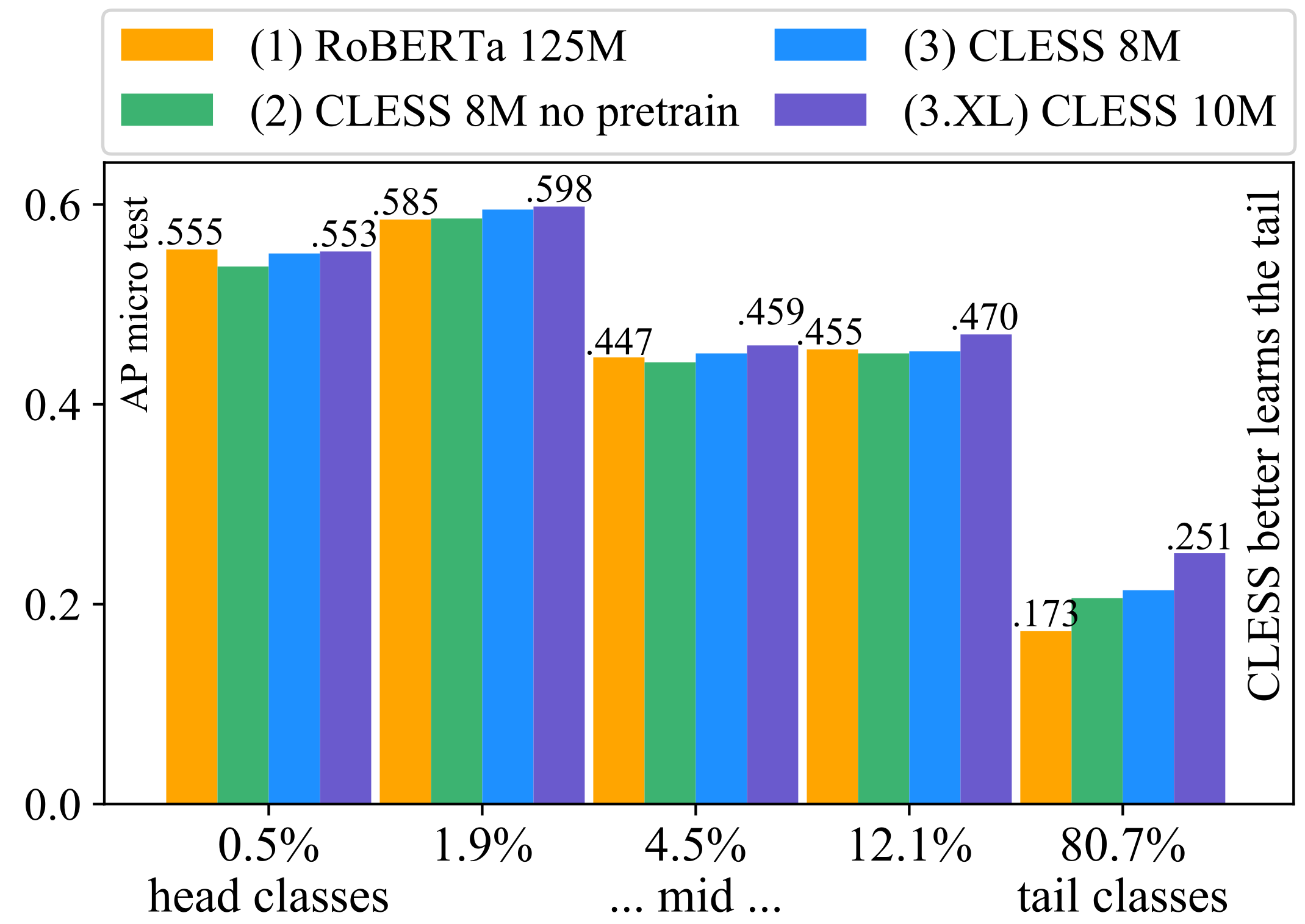
5.1. (RQ-1+2): Long-Tail Capture of RoBERTa vs. CLESS
5.1.1. RoBERTa: A Large Pretrained Model Does Not Guarantee Long-Tail Capture
5.1.2. CLESS: Contrastive Pretraining Removes the Need for Model Compression
5.1.3. Practical Computational Efficiency of Contrastive Language Modeling
5.2. (RQ-3.1-2): Contrastive Zero-Shot Long-Tail Learning
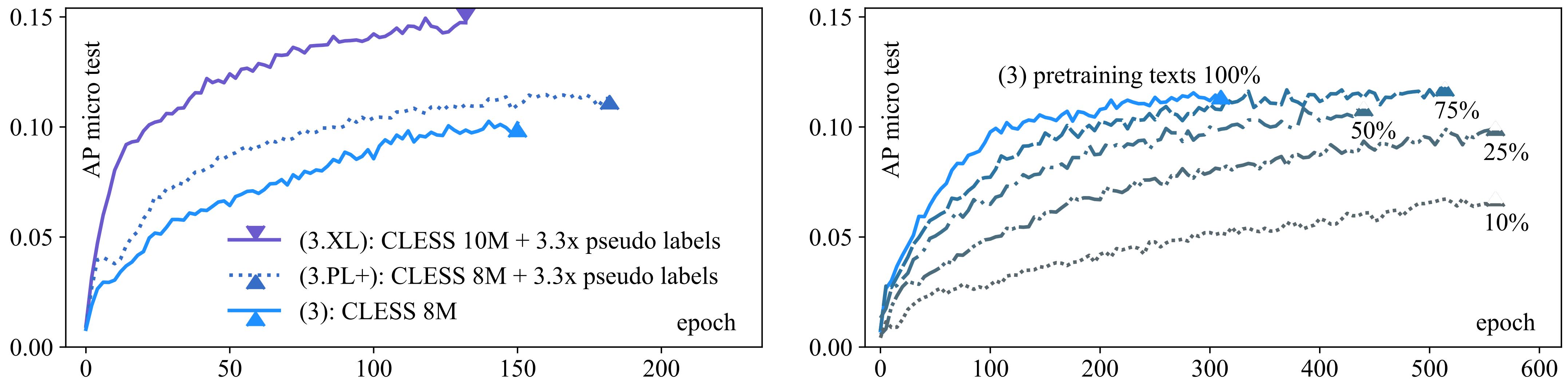
5.2.1. (RQ-3.1): More Self-supervision and Model Size Improve Zero-Shot Long-Tail Capture
5.2.2. RQ-3.2: Contrastive pretraining Leads to Data-Efficient Zero-Shot Long-Tail Learning
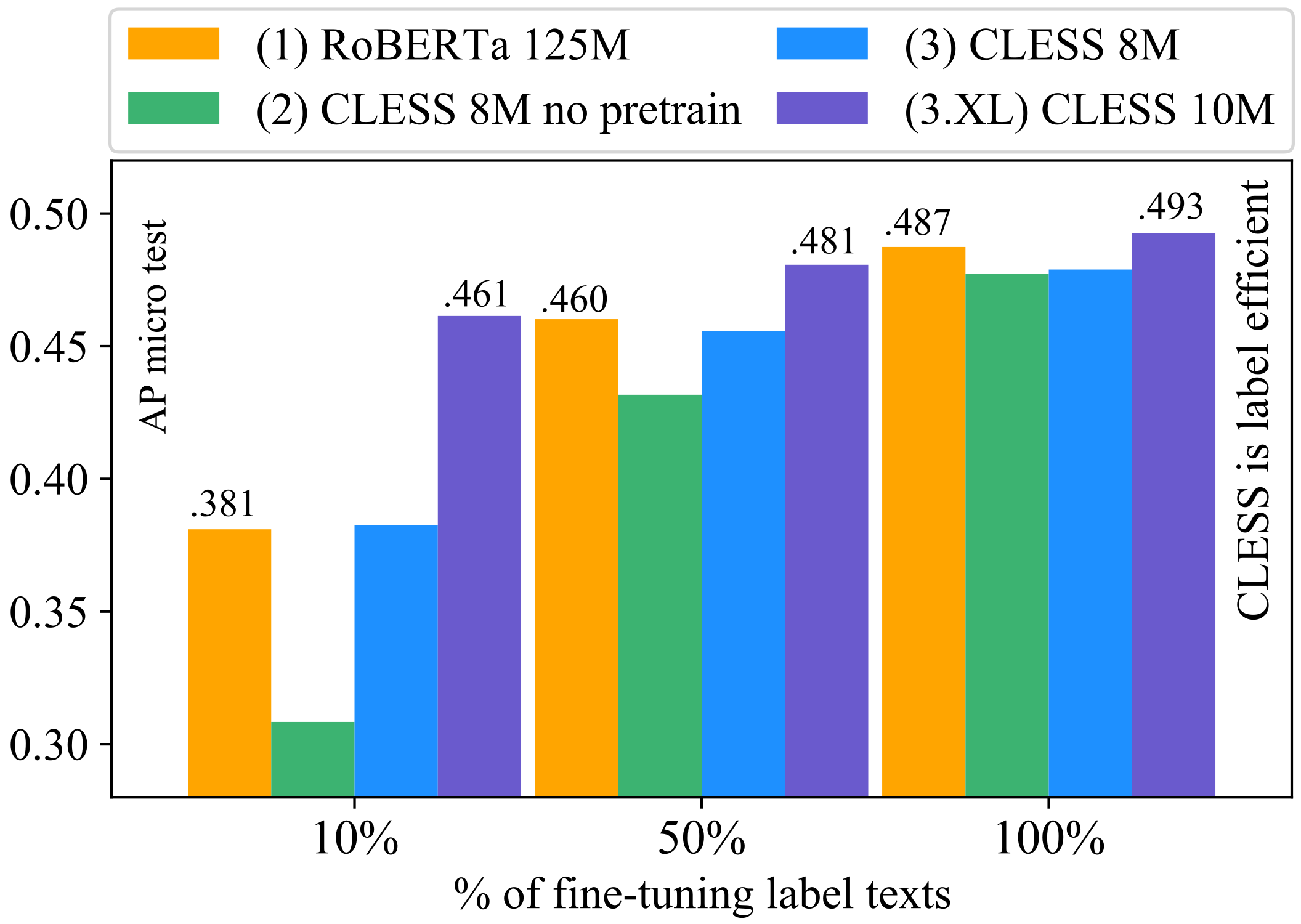
5.3. (RQ-3.3): Few-Shot Long-Tail Learning
6. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Layer Type | Literature Reported Data Requirements | Trainable Parameters | |
| Convolution | small (*) | 8M-10M (CLESS) | |
| Self-Attention | large to web-scale (*) | 125M (RoBERTa) |
Appendix C
| Filter size: num filters | {1: 57, 2: 29, 3: 14}, {1:100, 2:100, 1:100},{1: 285, 2: 145, 3: 70}, {1:10, 10:10, 1:10}, {1:15, 2:10, 3:5}, {1:10}, {1:100}, {10:100} |
| lr | 0.01, 0.0075, 0.005, 0.001, 0.0005, 0.0001 |
| bs (match size) | 1024, 1536, 4096 |
| max-k | 1, 3, 7, 10 |
| match-classifier | two_layer_classifier, ’conf’:[{’do’: None|.2, ’out_dim’: 2048|4196|1024}, {’do’:None|0.2}]}, one_layer_classifier, ’conf’:[{’do’:.2}]} |
| label encoder | one_layer_label_enc, ’conf’:[{’do’:None|.2, ’out_dim’: 100}, one_layer_label_enc, ’conf’:[{’do’: .2, ’out_dim’: 300} |
| seq encoder | one_layer_label_enc, ’conf’:[{’do’:None|.2, ’out_dim’: 100}, one_layer_label_enc, ’conf’:[{’do’: .2, ’out_dim’: 300} |
| tune embedding: | True, False |
| #real label samples: | 20, 150, 500 (g positives (as annotated in dataset), b random negative labels—20 works well too) |
| #pseudo label samples: | 20, 150, 500 (g positives input words, b negative input words)—used for self-superv. pretraining |
| optimizer: | ADAM—default params, except lr |
References
- Hooker, S.; Courville, A.; Clark, G.; Dauphin, Y.; Frome, A. What Do Compressed Deep Neural Networks Forget? arXiv 2020, arXiv:1911.05248. [Google Scholar]
- Hooker, S. Moving beyond “algorithmic bias is a data problem”. Patterns 2021, 2, 100241. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Miao, Z.; Zhan, X.; Wang, J.; Gong, B.; Yu, S.X. Large-Scale Long-Tailed Recognition in an Open World. In Proceedings of the IEEE CVPR, Long Beach, CA, USA, 16–20 June 2019; pp. 2537–2546. [Google Scholar] [CrossRef] [Green Version]
- D’souza, D.; Nussbaum, Z.; Agarwal, C.; Hooker, S. A Tale of Two Long Tails. arXiv 2021, arXiv:2107.13098. [Google Scholar]
- Hu, N.T.; Hu, X.; Liu, R.; Hooker, S.; Yosinski, J. When does loss-based prioritization fail? arXiv 2021, arXiv:2107.07741. [Google Scholar]
- Hooker, S.; Moorosi, N.; Clark, G.; Bengio, S.; Denton, E. Characterizing and Mitigating Bias in Compact Models. In Proceedings of the 5th ICML Workshop on Human Interpretability in Machine Learning (WHI), Virtual Conference, 17 July 2020. [Google Scholar]
- Zhuang, D.; Zhang, X.; Song, S.L.; Hooker, S. Randomness In Neural Network Training: Characterizing The Impact of Tooling. arXiv 2021, arXiv:2106.11872. [Google Scholar]
- Chang, W.C.; Yu, H.F.; Zhong, K.; Yang, Y.; Dhillon, I. X-BERT: eXtreme Multi-label Text Classification with using Bidirectional Encoder Representations from Transformers. arXiv 2019, arXiv:1905.02331. [Google Scholar]
- Joseph, V.; Siddiqui, S.A.; Bhaskara, A.; Gopalakrishnan, G.; Muralidharan, S.; Garland, M.; Ahmed, S.; Dengel, A. Reliable model compression via label-preservation-aware loss functions. arXiv 2020, arXiv:2012.01604. [Google Scholar]
- Blakeney, C.; Huish, N.; Yan, Y.; Zong, Z. Simon Says: Evaluating and Mitigating Bias in Pruned Neural Networks with Knowledge Distillation. arXiv 2021, arXiv:2106.07849. [Google Scholar]
- Jiang, Z.; Chen, T.; Mortazavi, B.J.; Wang, Z. Self-Damaging Contrastive Learning. Proc. Mach. Learn. Res. PMLR 2021, 139, 4927–4939. [Google Scholar]
- Rogers, A.; Kovaleva, O.; Rumshisky, A. A Primer in BERTology: What We Know About How BERT Works. Trans. Assoc. Comput. Linguist. 2020, 8, 842–866. [Google Scholar] [CrossRef]
- Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. RoBERTa: A Robustly Optimized BERT Pretraining Approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
- Liu, J.; Chang, W.; Wu, Y.; Yang, Y. Deep Learning for Extreme Multi-label Text Classification. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Shinjuku, Tokyo, Japan, 7–11 August 2017; pp. 115–124. [Google Scholar] [CrossRef]
- Pappas, N.; Henderson, J. GILE: A Generalized Input-Label Embedding for Text Classification. Trans. Assoc. Comput. Linguistics 2019, 7, 139–155. [Google Scholar] [CrossRef]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer. J. Mach. Learn. Res. 2020, 21, 1–67. [Google Scholar]
- Graf, F.; Hofer, C.; Niethammer, M.; Kwitt, R. Dissecting Supervised Constrastive Learning. Proc. Mach. Learn. Res. PMLR 2021, 139, 3821–3830. [Google Scholar]
- Zimmermann, R.S.; Sharma, Y.; Schneider, S.; Bethge, M.; Brendel, W. Contrastive Learning Inverts the Data Generating Process. Proc. Mach. Learn. Res. PMLR 2021, 139, 12979–12990. [Google Scholar]
- Zhang, H.; Xiao, L.; Chen, W.; Wang, Y.; Jin, Y. Multi-Task Label Embedding for Text Classification. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 2–4 November 2018; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; pp. 4545–4553. [Google Scholar] [CrossRef] [Green Version]
- Musgrave, K.; Belongie, S.J.; Lim, S. A Metric Learning Reality Check. In Proceedings of the Computer Vision-ECCV 2020-16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 681–699. [Google Scholar] [CrossRef]
- Rethmeier, N.; Augenstein, I. A Primer on Contrastive Pretraining in Language Processing: Methods, Lessons Learned and Perspectives. arXiv 2021, arXiv:2102.12982. [Google Scholar]
- Saunshi, N.; Plevrakis, O.; Arora, S.; Khodak, M.; Khandeparkar, H. A Theoretical Analysis of Contrastive Unsupervised Representation Learning. Proc. Mach. Learn. Res. PMLR 2019, 97, 5628–5637. [Google Scholar]
- Khosla, P.; Teterwak, P.; Wang, C.; Sarna, A.; Tian, Y.; Isola, P.; Maschinot, A.; Liu, C.; Krishnan, D. Supervised Contrastive Learning. In Advances in Neural Information Processing Systems 33 (NeurIPS 2020); Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 18661–18673. [Google Scholar]
- Ostendorff, M.; Rethmeier, N.; Augenstein, I.; Gipp, B.; Rehm, G. Neighborhood Contrastive Learning for Scientific Document Representations with Citation Embeddings. arXiv 2022, arXiv:2202.06671. [Google Scholar]
- Wang, T.; Isola, P. Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere. Proc. Mach. Learn. Res. PMLR 2020, 119, 9929–9939. [Google Scholar]
- Mnih, A.; Teh, Y.W. A Fast and Simple Algorithm for Training Neural Probabilistic Language Models. In Proceedings of the 29th International Conference on International Conference on Machine Learning (ICML’12), Edinburgh, UK, 26 June–1 July 2012; Omnipress: Madison, WI, USA; pp. 419–426. [Google Scholar]
- Şerbetci, O.N.; Möller, S.; Roller, R.; Rethmeier, N. EffiCare: Better Prognostic Models via Resource-Efficient Health Embeddings. AMIA Annu. Symp. Proc. 2020, 2020, 1060–1069. [Google Scholar]
- Kim, K.M.; Hyeon, B.; Kim, Y.; Park, J.H.; Lee, S. Multi-pretraining for Large-scale Text Classification. In Findings of the Association for Computational Linguistics: EMNLP 2020; Cohn, T., He, Y., Liu, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 2041–2050. [Google Scholar] [CrossRef]
- Tay, Y.; Dehghani, M.; Gupta, J.; Bahri, D.; Aribandi, V.; Qin, Z.; Metzler, D. Are Pre-trained Convolutions Better than Pre-trained Transformers? arXiv 2021, arXiv:2105.03322. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning Transferable Visual Models From Natural Language Supervision. Proc. Mach. Learn. Res. PMLR 2021, 139, 8748–8763. [Google Scholar]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. Proceedings of NAACL-HLT 2019, Minneapolis, MN, USA, 2–7 June 2019; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 4171–4186. [Google Scholar] [CrossRef]
- Liu, L.; Liu, X.; Gao, J.; Chen, W.; Han, J. Understanding the Difficulty of Training Transformers. arXiv 2020, arXiv:2004.08249. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016. pp. 2818–2826. [CrossRef] [Green Version]
- Gao, T.; Yao, X.; Chen, D. SimCSE: Simple Contrastive Learning of Sentence Embeddings. arXiv 2021, arXiv:2104.08821. [Google Scholar]
- Ma, Z.; Collins, M. Noise Contrastive Estimation and Negative Sampling for Conditional Models: Consistency and Statistical Efficiency. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 3698–3707. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, R.; Shan, S.; Chen, X. Transferable Contrastive Network for Generalized Zero-Shot Learning. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision, ICCV 2019, Seoul, Korea, 27 October–2 November 2019; pp. 9764–9773. [Google Scholar] [CrossRef] [Green Version]
- Simoncelli, E.P.; Olshausen, B.A. Natural image statistics and neural representation. Annu. Rev. Neurosci. 2001, 24, 1193–1216. [Google Scholar] [CrossRef] [Green Version]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Lukasik, M.; Bhojanapalli, S.; Menon, A.; Kumar, S. Does label smoothing mitigate label noise? Proc. Mach. Learn. Res. PMLR 2020, 119, 6448–6458. [Google Scholar]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, (ICML 2006), Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar] [CrossRef] [Green Version]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Learning from Imbalanced Data Sets; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Gururangan, S.; Marasović, A.; Swayamdipta, S.; Lo, K.; Beltagy, I.; Downey, D.; Smith, N.A. Don’t Stop Pretraining: Adapt Language Models to Domains and Tasks. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Virtual Conference, 6–8 July 2020; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 8342–8360. [Google Scholar] [CrossRef]
- Poerner, N.; Waltinger, U.; Schütze, H. Inexpensive Domain Adaptation of Pretrained Language Models: Case Studies on Biomedical NER and Covid-19 QA. In Findings of the Association for Computational Linguistics: EMNLP 2020; Cohn, T., He, Y., Liu, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 1482–1490. [Google Scholar] [CrossRef]
- Tai, W.; Kung, H.T.; Dong, X.; Comiter, M.; Kuo, C.F. exBERT: Extending Pre-trained Models with Domain-specific Vocabulary Under Constrained Training Resources. In Findings of the Association for Computational Linguistics: EMNLP 2020; Cohn, T., He, Y., Liu, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 1433–1439. [Google Scholar] [CrossRef]
- Rethmeier, N.; Plank, B. MoRTy: Unsupervised Learning of Task-specialized Word Embeddings by Autoencoding. In Proceedings of the 4th Workshop on Representation Learning for NLP, RepL4NLP@ACL 2019, Florence, Italy, 2 August 2019; pp. 49–54. [Google Scholar] [CrossRef]
- Augenstein, I.; Ruder, S.; Søgaard, A. Multi-Task Learning of Pairwise Sequence Classification Tasks over Disparate Label Spaces. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), New Orleans, LA, USA, 1–6 June 2018; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; pp. 1896–1906. [Google Scholar] [CrossRef] [Green Version]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Frankle, J.; Carbin, M. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Rethmeier, N.; Saxena, V.K.; Augenstein, I. TX-Ray: Quantifying and Explaining Model-Knowledge Transfer in (Un-)Supervised NLP. In Proceedings of the Proceedings of the Thirty-Sixth Conference on Uncertainty in Artificial Intelligence, UAI 2020, Toronto, ON, Canada, 3–6 August 2020. [Google Scholar]
- Augenstein, I.; Lioma, C.; Wang, D.; Chaves Lima, L.; Hansen, C.; Hansen, C.; Simonsen, J.G. MultiFC: A Real-World Multi-Domain Dataset for Evidence-Based Fact Checking of Claims. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 4685–4697. [Google Scholar] [CrossRef]
- Ma, Z.; Sun, A.; Yuan, Q.; Cong, G. Tagging Your Tweets: A Probabilistic Modeling of Hashtag Annotation in Twitter. In Proceedings of the 23rd ACM International Conference on Information and Knowledge Management (CIKM ’14), Shanghai, China, 3–7 November 2014; Li, J., Wang, X.S., Garofalakis, M.N., Soboroff, I., Suel, T., Wang, M., Eds.; Association for Computing Machinery: New York, NY, USA, 2014; pp. 999–1008. [Google Scholar]
- Liu, Q.; Kusner, M.J.; Blunsom, P. A Survey on Contextual Embeddings. arXiv 2020, arXiv:2003.07278. [Google Scholar]
- Yogatama, D.; de Masson d’Autume, C.; Connor, J.; Kociský, T.; Chrzanowski, M.; Kong, L.; Lazaridou, A.; Ling, W.; Yu, L.; Dyer, C.; et al. Learning and Evaluating General Linguistic Intelligence. arXiv 2019, arXiv:1901.11373. [Google Scholar]
- Merity, S.; Xiong, C.; Bradbury, J.; Socher, R. Pointer Sentinel Mixture Models. arXiv 2017, arXiv:1609.07843. [Google Scholar]
- Wang, C.; Ye, Z.; Zhang, A.; Zhang, Z.; Smola, A.J. Transformer on a Diet. arXiv 2020, arXiv:2002.06170. [Google Scholar]
- Bender, E.M.; Gebru, T.; McMillan-Major, A.; Shmitchell, S. On the Dangers of Stochastic Parrots: Can Language Models Be Too Big? In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency (FAccT ’21), Virtual Conference, 3–10 March 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 610–623. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Advances in Neural Information Processing Systems 30 (NIPS 2017); Curran Associates Inc.: Red Hook, NY, USA, 2017; ISBN 9781510860964. [Google Scholar]
- Hooker, S. The Hardware Lottery. Commun. ACM 2020, 64, 58–65. [Google Scholar] [CrossRef]
- Dodge, J.; Ilharco, G.; Schwartz, R.; Farhadi, A.; Hajishirzi, H.; Smith, N.A. Fine-Tuning Pretrained Language Models: Weight Initializations, Data Orders, and Early Stopping. arXiv 2020, arXiv:2002.06305. [Google Scholar]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and Policy Considerations for Deep Learning in NLP. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 3645–3650. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, M.; Baker, D.; Moorosi, N.; Denton, E.; Hutchinson, B.; Hanna, A.; Gebru, T.; Morgenstern, J. Diversity and Inclusion Metrics in Subset Selection. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, New York, NY, USA, 7–9 February 2020; Association for Computing Machinery: New York, NY, USA, 2020. pp. 117–123. [CrossRef] [Green Version]
- Waseem, Z.; Lulz, S.; Bingel, J.; Augenstein, I. Disembodied Machine Learning: On the Illusion of Objectivity in NLP. arXiv 2021, arXiv:2101.11974. [Google Scholar]
- Jiang, Y.; Neyshabur, B.; Mobahi, H.; Krishnan, D.; Bengio, S. Fantastic Generalization Measures and Where to Find Them. arXiv 2019, arXiv:1912.02178. [Google Scholar]
- He, F.; Liu, T.; Tao, D. Control Batch Size and Learning Rate to Generalize Well: Theoretical and Empirical Evidence. In NeurIPS; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rethmeier, N.; Augenstein, I. Long-Tail Zero and Few-Shot Learning via Contrastive Pretraining on and for Small Data. Comput. Sci. Math. Forum 2022, 3, 10. https://doi.org/10.3390/cmsf2022003010
Rethmeier N, Augenstein I. Long-Tail Zero and Few-Shot Learning via Contrastive Pretraining on and for Small Data. Computer Sciences & Mathematics Forum. 2022; 3(1):10. https://doi.org/10.3390/cmsf2022003010
Chicago/Turabian StyleRethmeier, Nils, and Isabelle Augenstein. 2022. "Long-Tail Zero and Few-Shot Learning via Contrastive Pretraining on and for Small Data" Computer Sciences & Mathematics Forum 3, no. 1: 10. https://doi.org/10.3390/cmsf2022003010
APA StyleRethmeier, N., & Augenstein, I. (2022). Long-Tail Zero and Few-Shot Learning via Contrastive Pretraining on and for Small Data. Computer Sciences & Mathematics Forum, 3(1), 10. https://doi.org/10.3390/cmsf2022003010






