The Design of a 140 GHz 28 nm CMOS Vector-Sum Phase Shifter Based on Gilbert Cell and Current-Steering Amplifiers
Abstract
1. Introduction
2. Comparison of Gilbert Cell and Current-Steering Variable Gain Amplifier
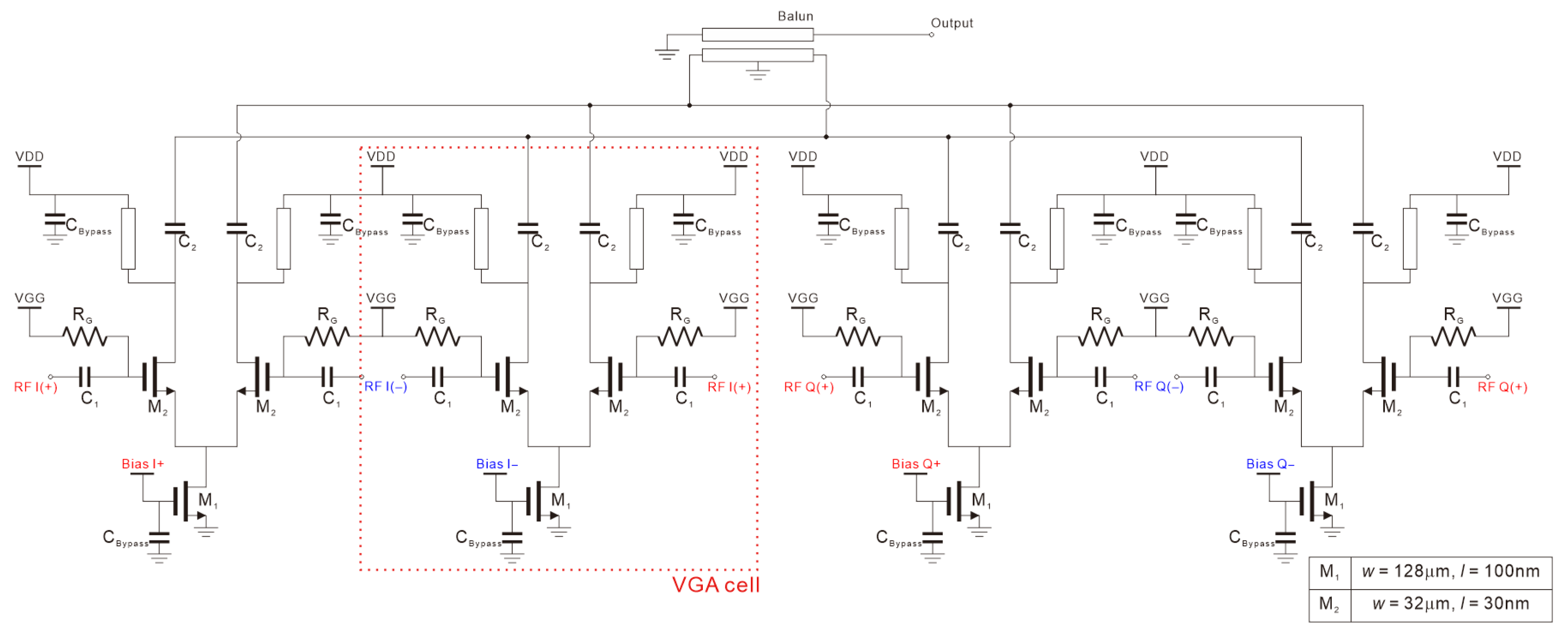
2.1. Conventional Gilbert Cell-Based VGA Design
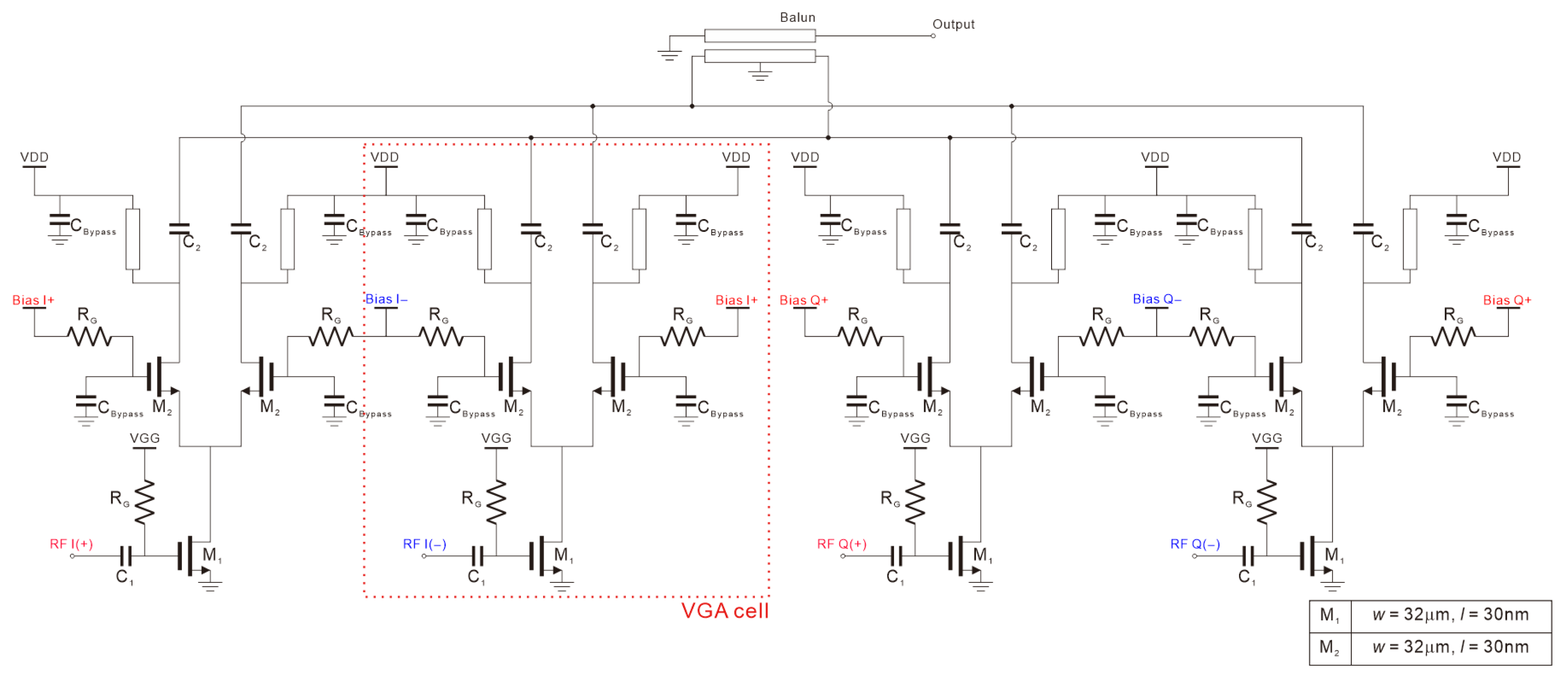
2.2. High-Gain Current-Steering VGA Design
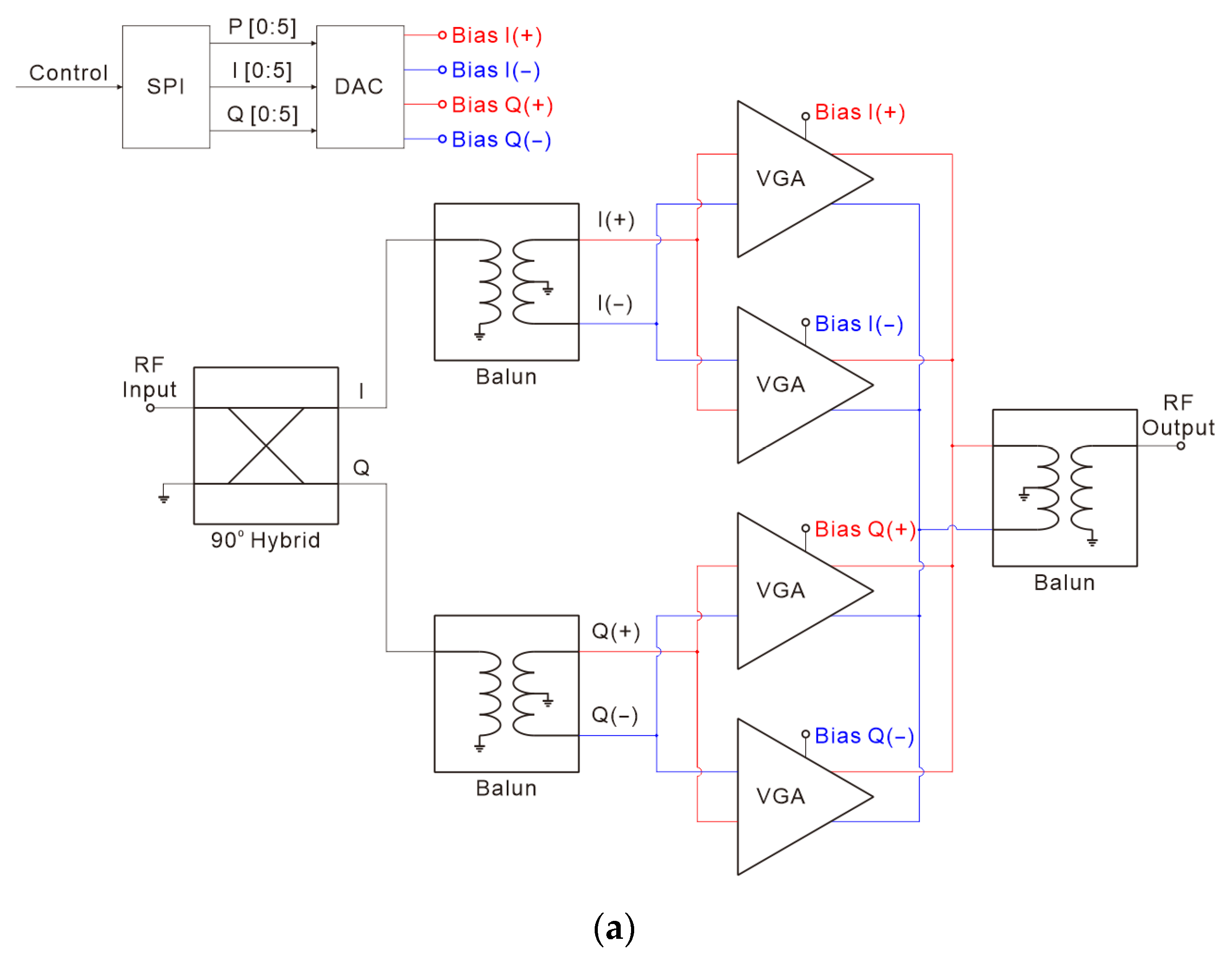
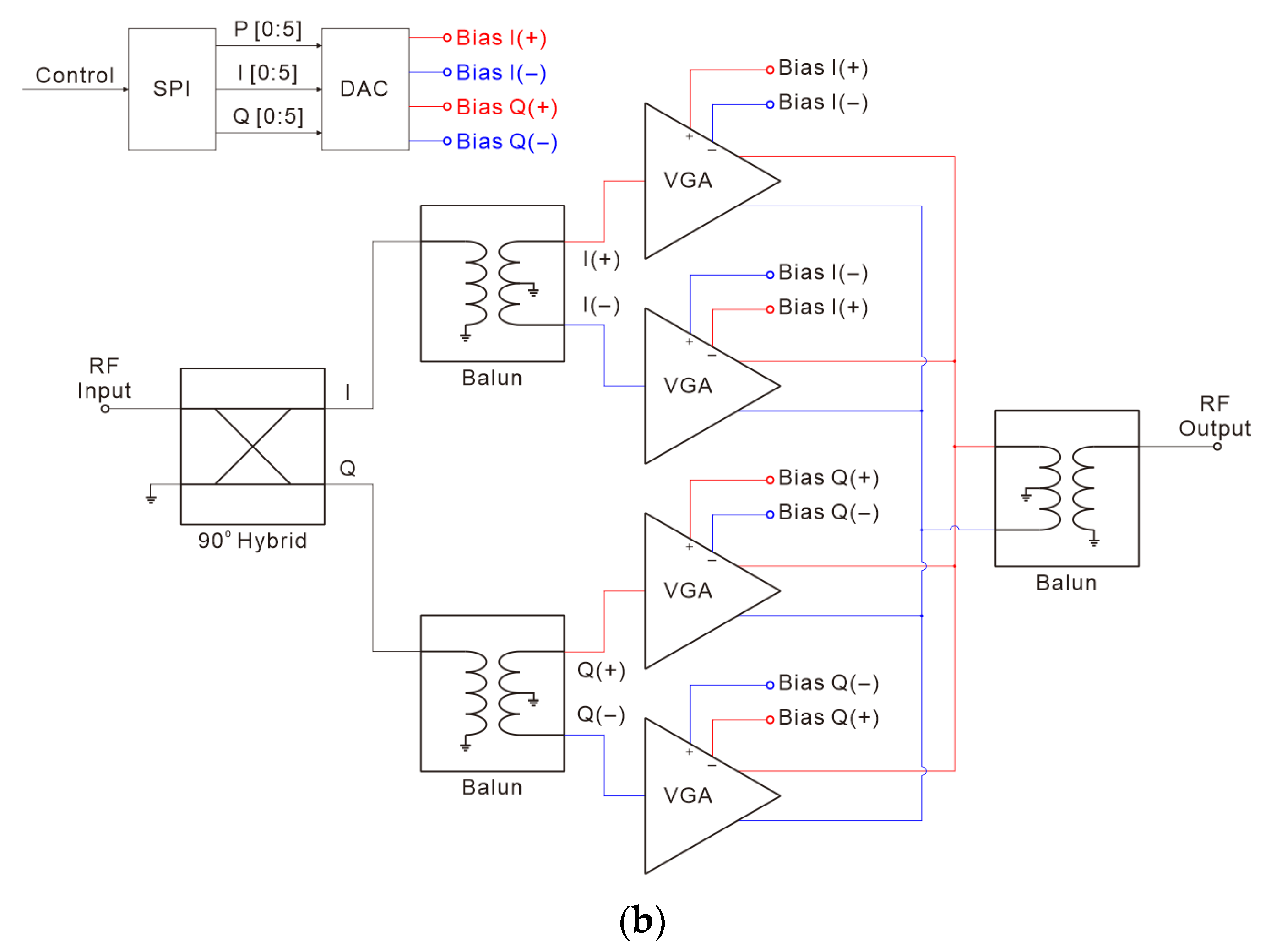
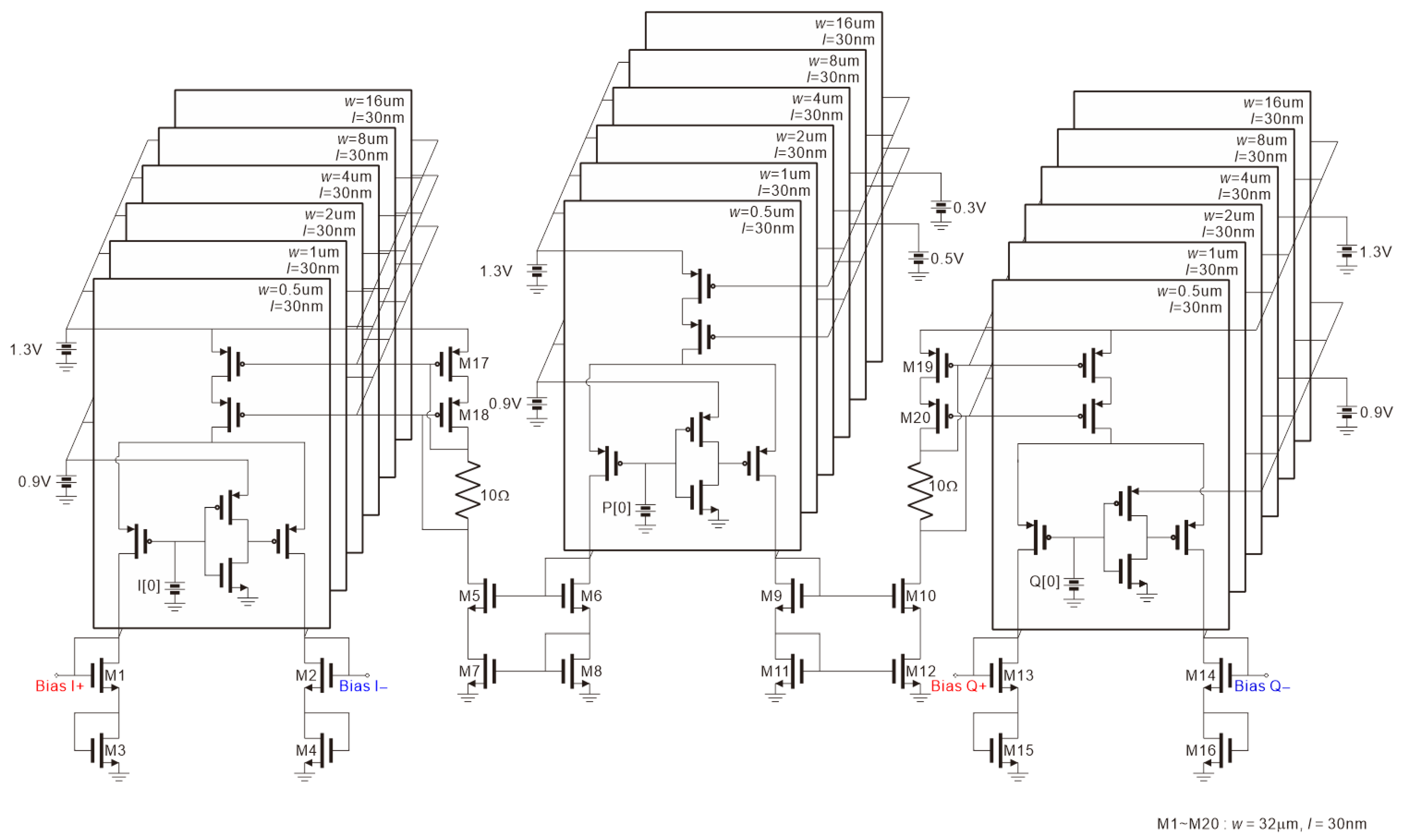
3. Proposed Phase Shifter Design Using Dual VGAs
3.1. DAC for Gilbert Cell-Based Amplifier
3.2. DAC for Current-Steering Amplifier
3.3. I/Q Generator
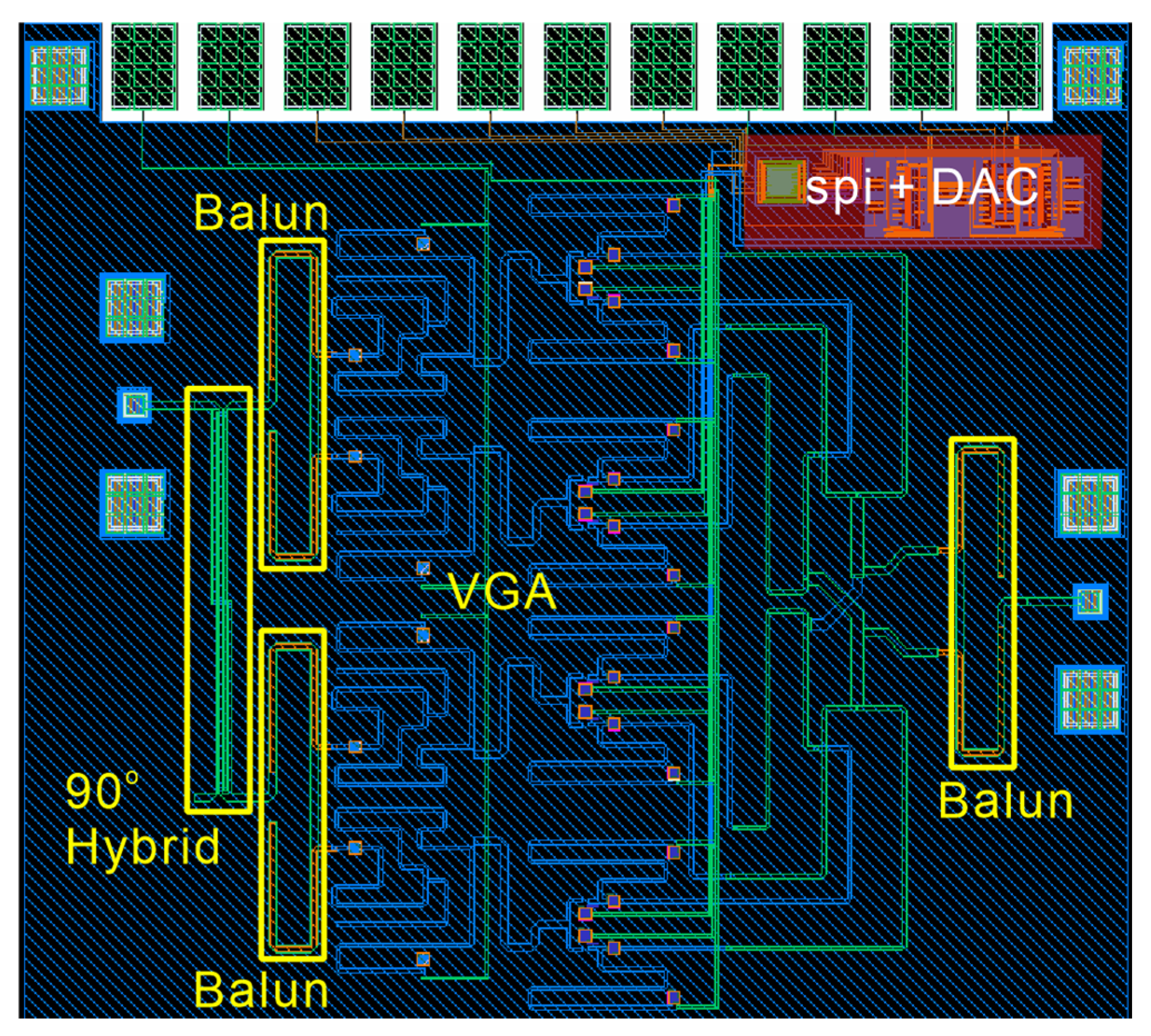
3.4. Integrated Phase Shifter Design
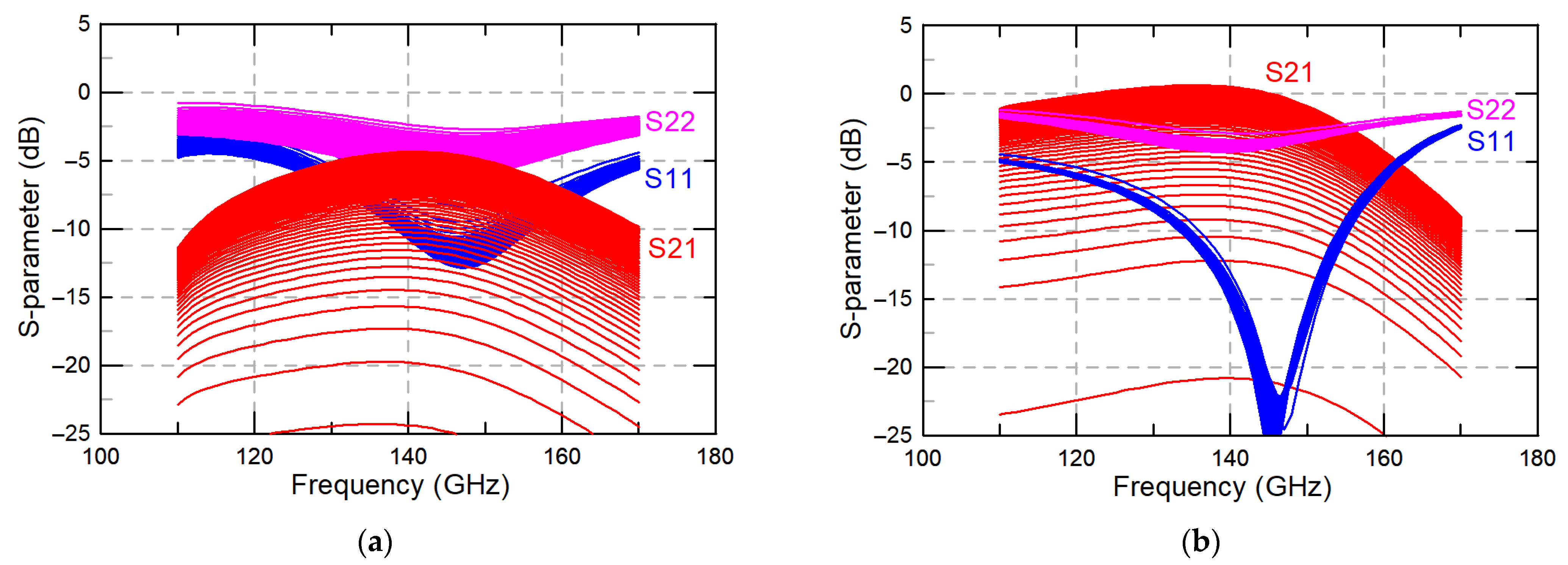
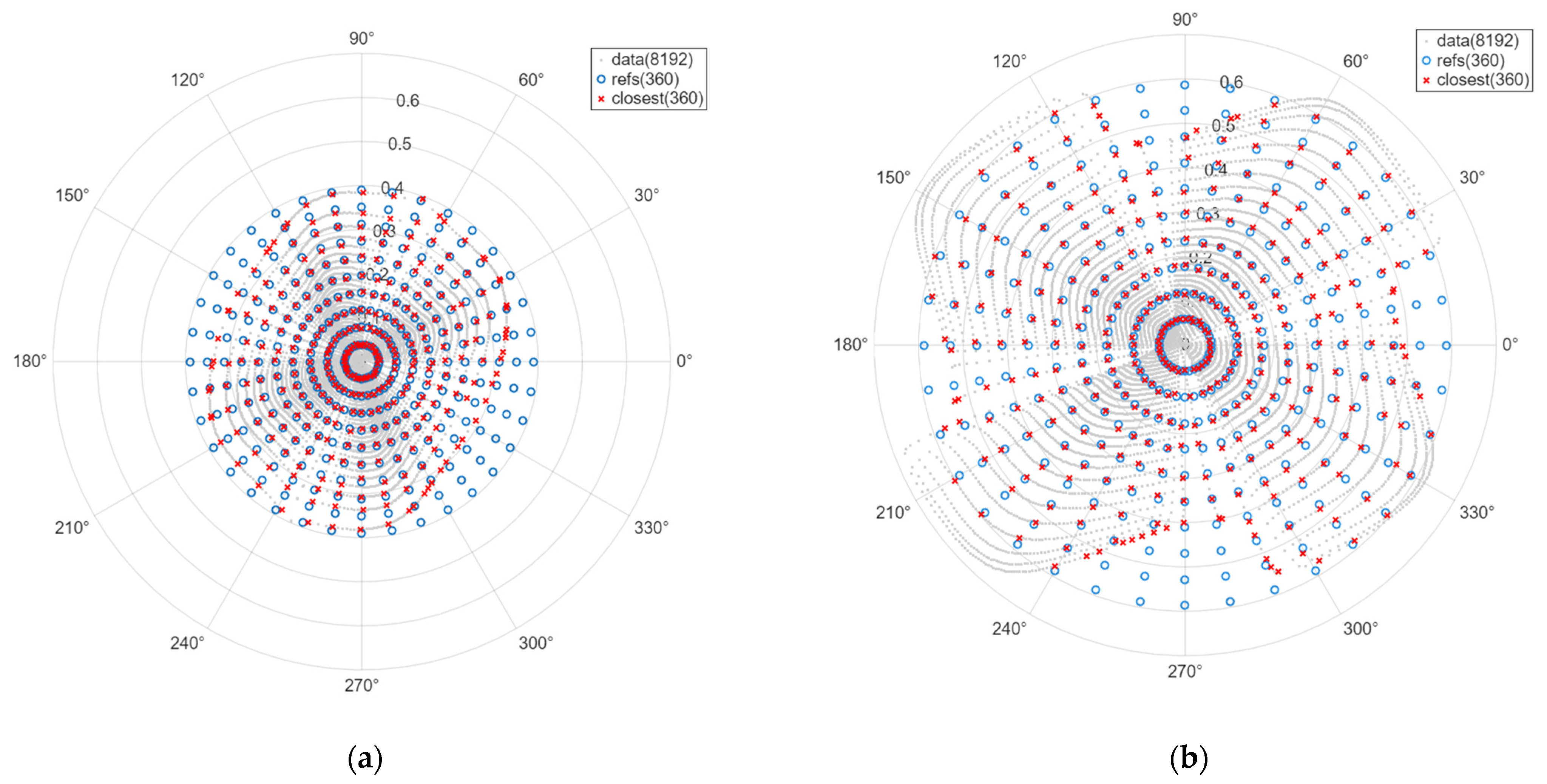
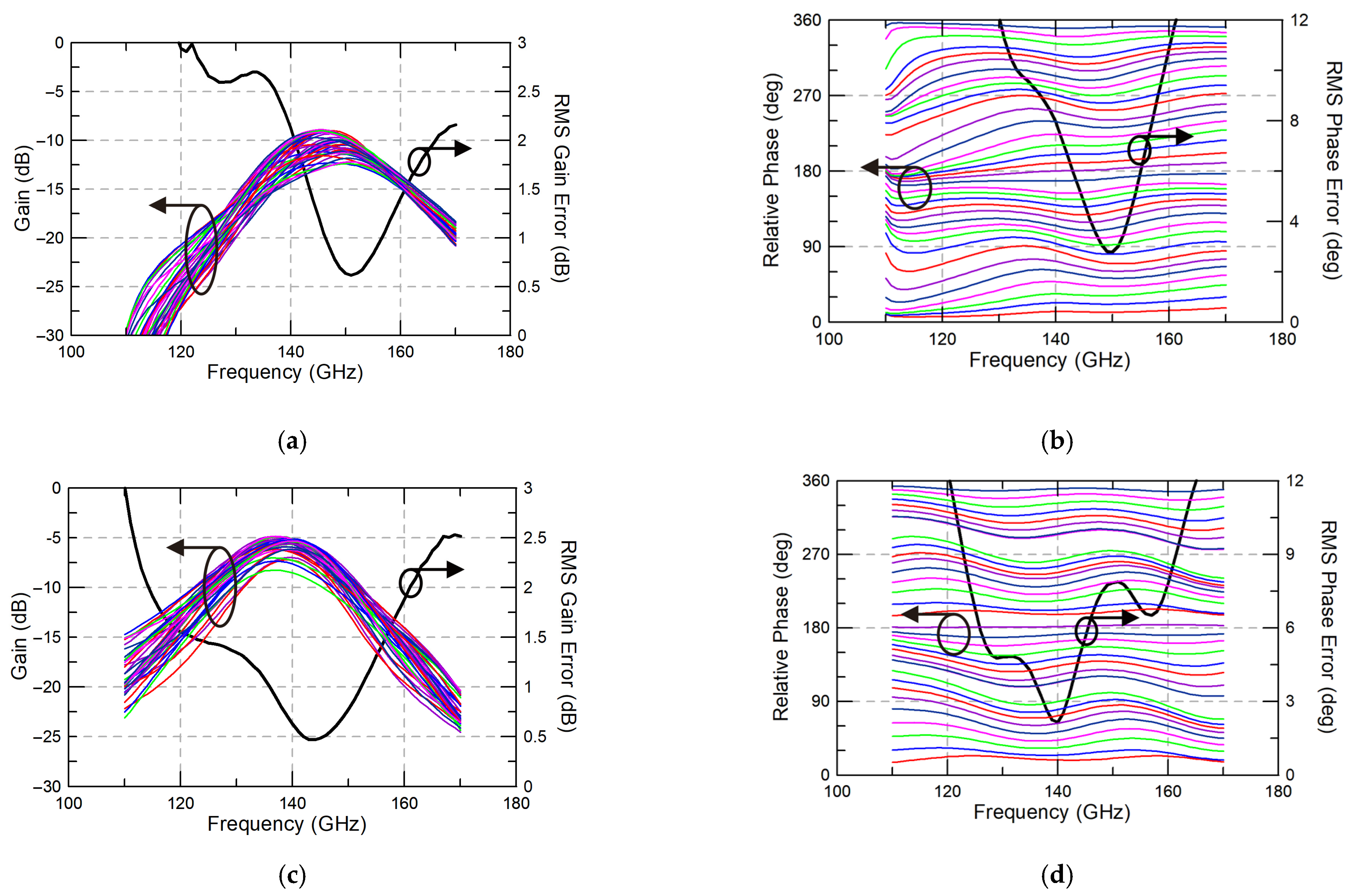
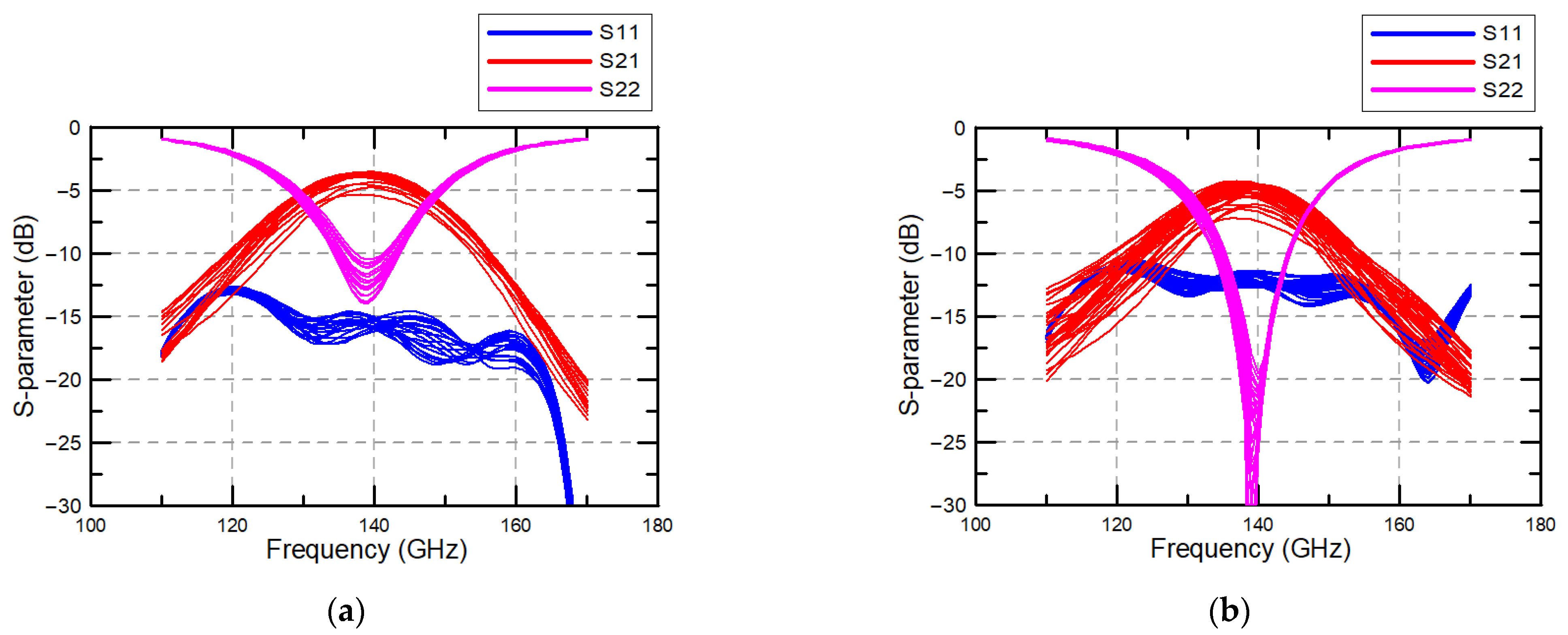
4. Simulation Results for the Proposed Phase Shifter
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frecassetti, M.G.L.; Sevillano, J.F.; del Rio, D.; Saglam, M.I.; Lamminen, A.; Ermolov, V. D-Band Backhaul and Fronthaul Solutions for 5G Radio Access Network. In Proceedings of the 2022 52nd European Microwave Conference (EuMC), Milan, Italy, 27–29 September 2022; Volume 52, pp. 772–775. [Google Scholar]
- Wang, H.; Guo, H.; Zhang, X.; Chi, T. A Packaged D-Band Transmitter with a Multifeed Lens Antenna Achieving 25.3 dBm Single-Element EIRP for 2-D Scalable Arrays. In Proceedings of the 2025 IEEE Custom Integrated Circuits Conference (CICC), Boston, MA, USA, 13–17 April 2025; pp. 1–3. [Google Scholar]
- Li, S.; Zhang, Z.; Rupakula, B.; Rebeiz, G.M. An Eight-Element 140-GHz Wafer-Scale IF Beamforming Phased-Array Receiver with 64-QAM Operation in CMOS RFSOI. IEEE J. Solid-State Circuits 2022, 57, 385–399. [Google Scholar] [CrossRef]
- Cho, M.K.; Baek, D.; Kim, J.G. An X-Band 5 Bit Phase Shifter with Low Insertion Loss in 0.18 μm SOI Technology. IEEE Microw. Wireless Compon. Lett. 2012, 22, 648–650. [Google Scholar] [CrossRef]
- Gu, P.; Zhao, D.; You, X. Analysis and Design of a CMOS Bidirectional Passive Vector-Modulated Phase Shifter. IEEE Trans. Circuits Syst. I 2021, 68, 1398–1408. [Google Scholar] [CrossRef]
- Li, W.T.; Chiang, Y.C.; Tsai, J.H.; Yang, H.Y.; Cheng, J.H.; Huang, T.W. 60-GHz 5-bit Phase Shifter with Integrated VGA Phase-Error Compensation. IEEE Trans. Microw. Theory Tech. 2013, 61, 1224–1235. [Google Scholar] [CrossRef]
- Li, T.W.; Wang, H. A Millimeter-Wave Fully Integrated Passive Reflection-Type Phase Shifter with Transformer-Based Multi-Resonance Loads for 360° Phase Shifting. IEEE Trans. Circuits Syst. I 2018, 65, 1406–1419. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, M.; Xie, Q.; Wang, Z. A D-band quadrature-hybrids-based 5-bit vector-modulated phase shifter with low RMS phase error. Electron. Lett. 2022, 58, 717–719. [Google Scholar] [CrossRef]
- Wang, S.; Park, J.; Hong, S. A K-Band Variable-Gain Phase Shifter Based on Gilbert-Cell Vector Synthesizer with RC-RL Poly-Phase Filter. IEEE Microw. Wireless Compon. Lett. 2021, 31, 393–396. [Google Scholar] [CrossRef]
- So, C.; Sung, E.T.; Hong, S. A 60-GHz Variable-Gain Phase Shifter with an Active RL Poly-Phase Filter. IEEE Trans. Microw. Theory Tech. 2023, 71, 593–601. [Google Scholar] [CrossRef]
- Sung, E.-T.; Wang, S.; Hong, S. A 60-GHz Polar Vector Modulator with Lookup Table-Based Calibration. IEEE Microw. Wireless Compon. Lett. 2021, 31, 572–574. [Google Scholar] [CrossRef]
- Najmussadat, M.; Ahamed, R.; Varonen, M.; Parveg, D.; Kantanen, M.; Halonen, K.A.I. 220–240-GHz High-Gain Phase Shifter Chain and Power Amplifier for Scalable Large Phased-Arrays. IEEE Access 2023, 11, 23565–23577. [Google Scholar] [CrossRef]
- So, C.; Sung, E.-T.; Hong, S. A 60-GHz Variable Gain Phase Shifter Based on Body Floated RF-DAC Structure. IEEE Trans. Circuits Syst. II 2022, 69, 4749–4753. [Google Scholar] [CrossRef]
- Rao, S.G.; Cressler, J.D. A D-Band Reflective-Type Phase Shifter Using a SiGe PIN Diode Resonant Load. IEEE Microw. Wireless Compon. Lett. 2022, 32, 1191–1194. [Google Scholar] [CrossRef]
- Yishay, R.B.; Elad, D. D-Band 360° Phase Shifter with Uniform Insertion Loss. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium—IMS, Philadelphia, PA, USA, 10–15 June 2018; pp. 868–870. [Google Scholar]
- Karakuzulu, A.; Eissa, M.H.; Kissinger, D.; Malignaggi, A. Broadband 110–170 GHz True Time Delay Circuit in a 130-nm SiGe BiCMOS Technology. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 775–778. [Google Scholar]
- Abbasi, M.; Lee, W. A D-band Calibration-Free Passive 360° Phase Shifter with 1.2°RMS Phase Error in 45 nm RFSOI. In Proceedings of the 2023 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), San Diego, CA, USA, 11–13 June 2023. [Google Scholar]
- Kim, I.; Koo, H.; Kim, W.; Hong, S. A D-Band Differential Phase Shifter Based on a Transmission Delay Line with Variable Inductors and Capacitors. IEEE Microw. Wireless Technol. Lett. 2025, 35, 59–62. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, M.; Geng, X.; Wang, K.; Xie, Q.; Wang, Z. A 0.0325-mm2 114-to-147-GHz 6-Bit Passive Vector-Modulated Phase Shifter with MN-Embedded Isolated Power Combiner Achieving <3.7° RMS Phase Error in 65-nm CMOS. IEEE Trans. Circuits Syst. I 2023, 70, 4394–4405. [Google Scholar]
- Testa, P.V.; Carta, C.; Ellinger, F. A 160–190-GHz Vector-Modulator Phase Shifter for Low-Power Applications. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 86–89. [Google Scholar] [CrossRef]
- del Rio, D.; Gurutzeaga, I.; Berenguer, R.; Huhtinen, I.; Sevillano, J.F. A Compact and High-Linearity 140-160 GHz Active Phase Shifter in 55 nm BiCMOS. IEEE Microw. Wireless Compon. Lett. 2021, 31, 157–160. [Google Scholar]
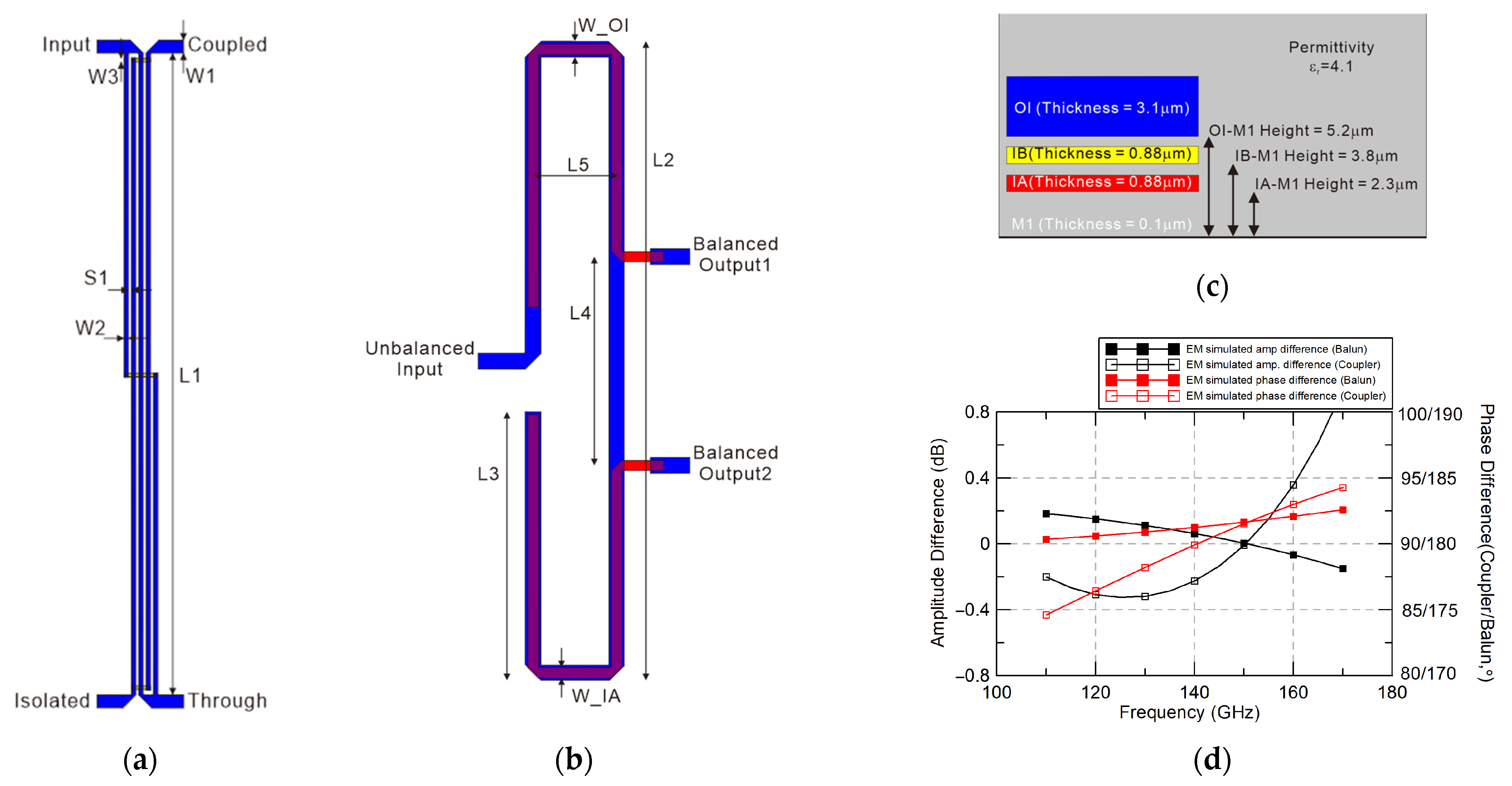
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| W1 (Port width) | 6 μm | L1 (Conductor length) | 303 μm |
| W2 (Conductor width) | 2 μm | S1 (Conductor spacing) | 1.5 μm |
| W3 (Bridge IB Layer width) | 1.5 μm | ||
| W_IA (Balun IA Layer width) | 4 μm | W_OI (Balun OI Layer width) | 6 μm |
| L2 | 245 μm | L3 | 103 μm |
| L4 | 80 μm | L5 | 32 μm |
| Ref. | Topology | Freq. (GHz) | Tech. | Dissipated Power (mW) | Peak Gain (dB) | Max. RMS Gain Error (dB) | Phase Shift Range (deg.) | Phase Resolution (bits) | Max. RMS Phase Error (deg.) |
|---|---|---|---|---|---|---|---|---|---|
| [14] | RTPS + PI | 130–150 | 90 nm SiGe | 21 | −5.5 | 1.25 | 360 | - | 13 |
| [15] | RTPS + PI | 116–128 | 0.12-μm SiGe | - | −5.8 | 0.6 | 360 | 5 | 2.2 |
| [16] | TTD | 110–170 | 130 nm SiGe | 6.22 | −20~−22 | 1.4 | TTD (max 6.64 ps) | 4 | - |
| [17] | STPS | 140 | 45 nm RFSOI | 0 | −9.7~−11.6 | 0.5 | 360 | 5 | 1.2 |
| [18] | TDL | 120–146 | 40 nm CMOS | - | −17.2 | - | 180 | 5 | 0.4 |
| [19] | VSPS (Passive) | 114–147 | 65 nm CMOS | 0 | −16.5 A | 1.5 | 360 | 6 | 3.7 |
| [20] | VSPS | 162–190 | 130 nm SiGe | 12.4 | −6.2 | 1 | 360 | 4 | 8 |
| [21] | VSPS | 140–160 | 55 nm BICMOS | 50 | −4.5 A | 1.4 | 360 | 5 | 7.5 |
| This work | VSPS | 140–157 S | 28 nm CMOS | 49 S | −9.5 S | 2 S | 360 | 8 | 6 S |
| This work | VSPS | 129–144 S | 28 nm CMOS | 29 S | −5.1 S | 1.3 S | 360 | 8 | 4.8 S |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.; Lee, J.-H.; Kim, M. The Design of a 140 GHz 28 nm CMOS Vector-Sum Phase Shifter Based on Gilbert Cell and Current-Steering Amplifiers. Chips 2025, 4, 50. https://doi.org/10.3390/chips4040050
Cho J, Lee J-H, Kim M. The Design of a 140 GHz 28 nm CMOS Vector-Sum Phase Shifter Based on Gilbert Cell and Current-Steering Amplifiers. Chips. 2025; 4(4):50. https://doi.org/10.3390/chips4040050
Chicago/Turabian StyleCho, Junyung, Jung-Hyun Lee, and M. Kim. 2025. "The Design of a 140 GHz 28 nm CMOS Vector-Sum Phase Shifter Based on Gilbert Cell and Current-Steering Amplifiers" Chips 4, no. 4: 50. https://doi.org/10.3390/chips4040050
APA StyleCho, J., Lee, J.-H., & Kim, M. (2025). The Design of a 140 GHz 28 nm CMOS Vector-Sum Phase Shifter Based on Gilbert Cell and Current-Steering Amplifiers. Chips, 4(4), 50. https://doi.org/10.3390/chips4040050






