A Perspective on Analog and Mixed-Signal IC Design Amid Semiconductor Paradigm Shifts
Abstract
1. Introduction
1.1. Growing Complexity, Engineering Challenges
1.2. Full-Stack Engineering
1.3. Analog Circuits Are Subject to the Same Driving Forces—What Can Be Done?
2. Tackling Complexity: A Multi-Level Approach
2.1. System Level
2.1.1. Merge and Relocate Functions
2.1.2. Specialize the Hardware to Better Fit to the Signal or the Application Characteristics
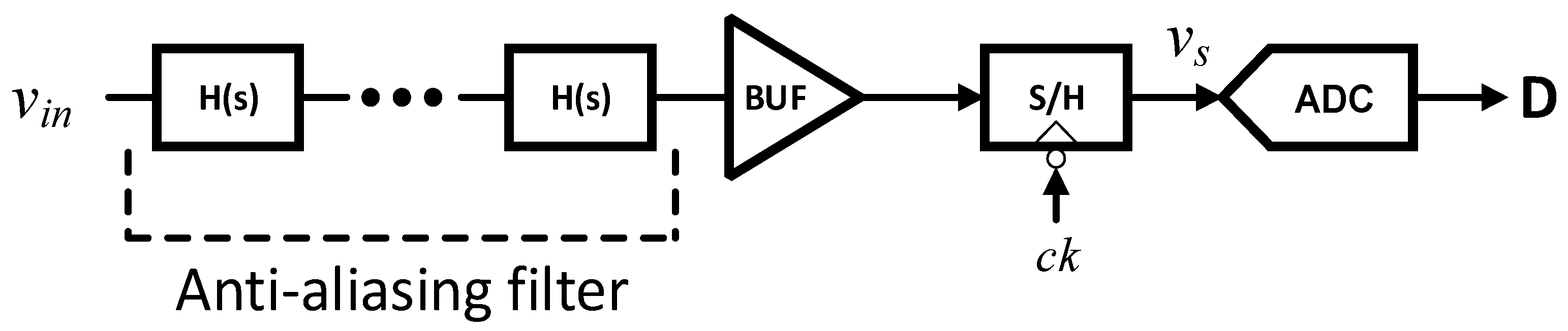
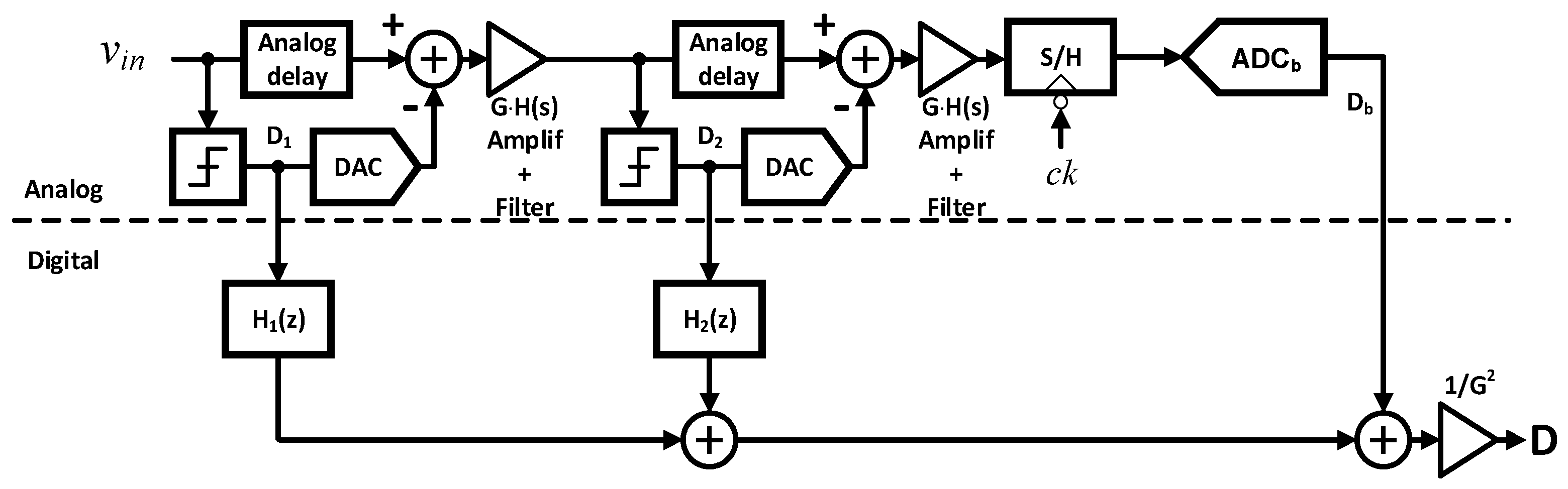
2.1.3. Transform the Signal to Fit or Simplify the Hardware
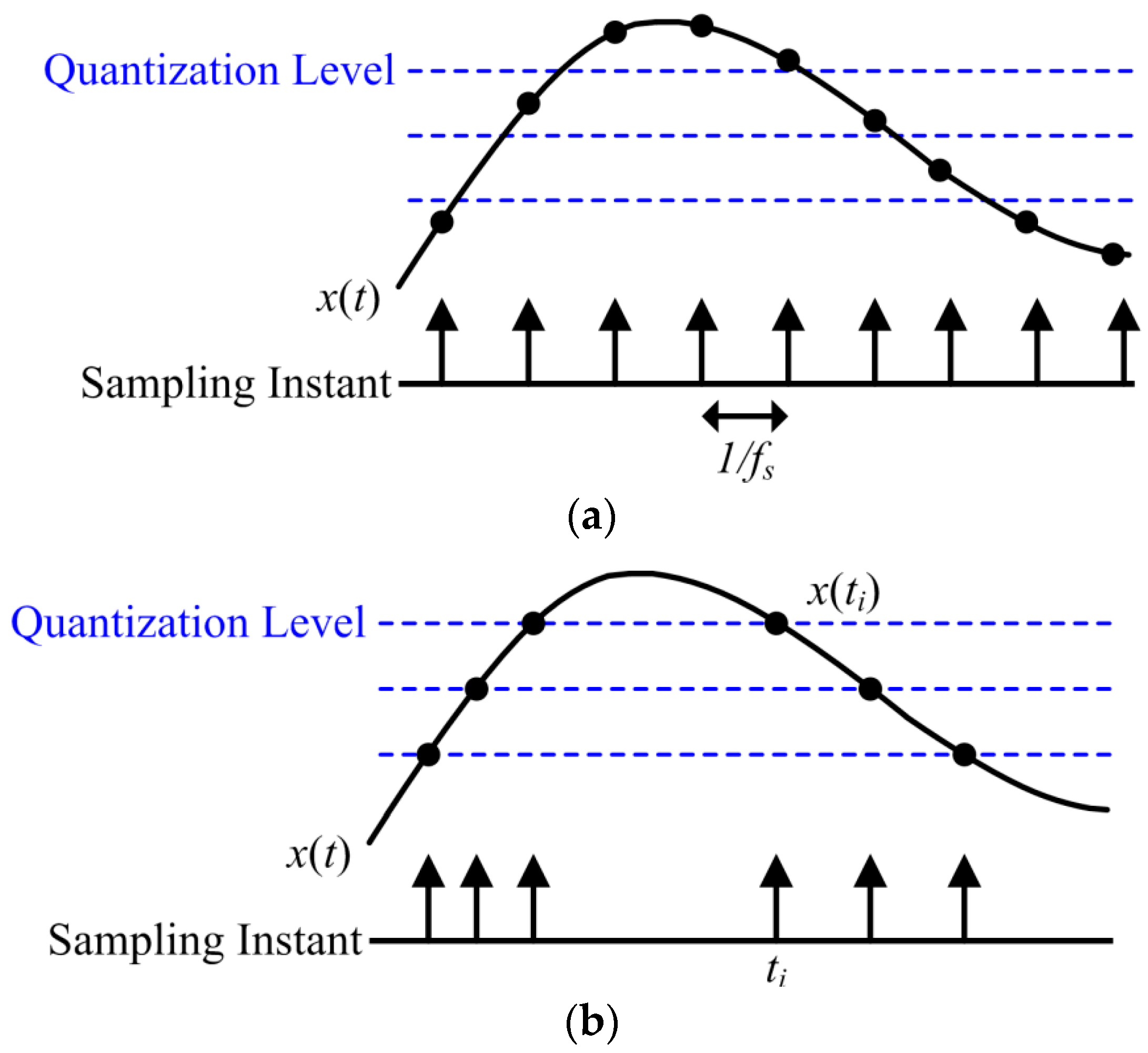
2.1.4. Capture the Information, Not the Data
- Combining separate functions into more efficient hybrid structures.
- Relocating sensitive circuit blocks to resolve PPA bottlenecks.
- Re-framing the entire processing chain by leveraging the signal’s unique characteristics.
2.2. Functional Level
2.2.1. Analog Versus Digital
2.2.2. When a Few Neurons Are Better than a Microprocessor
2.3. Transistor Level
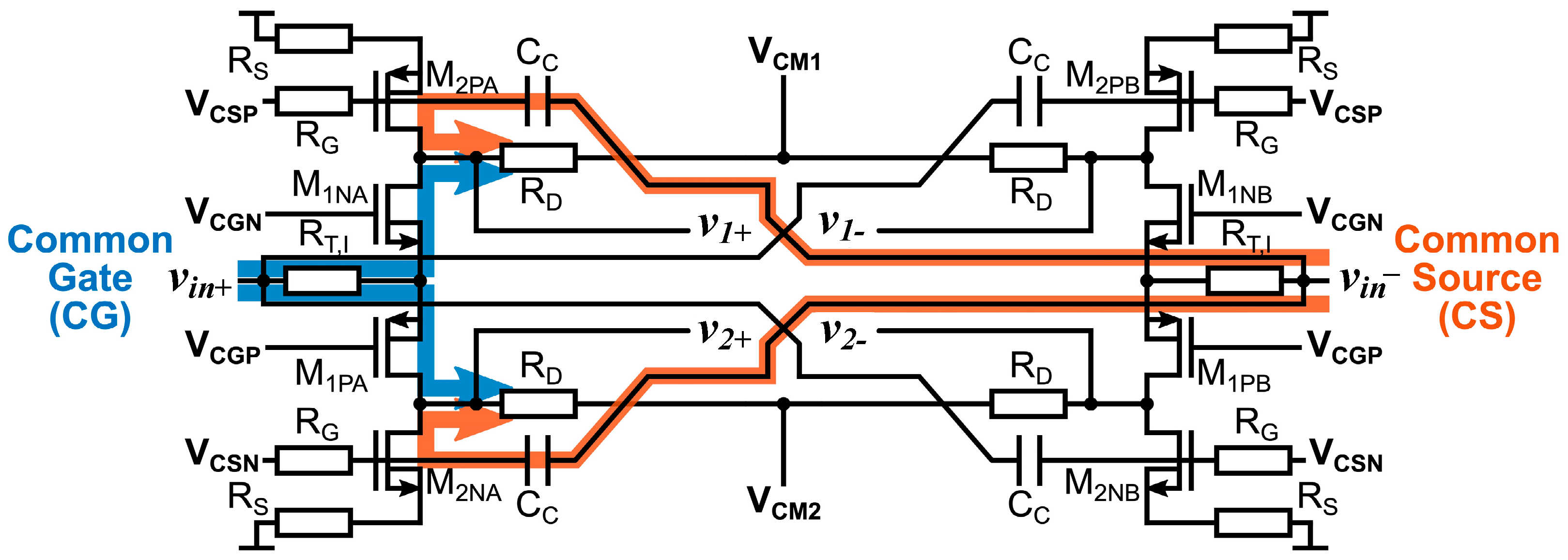
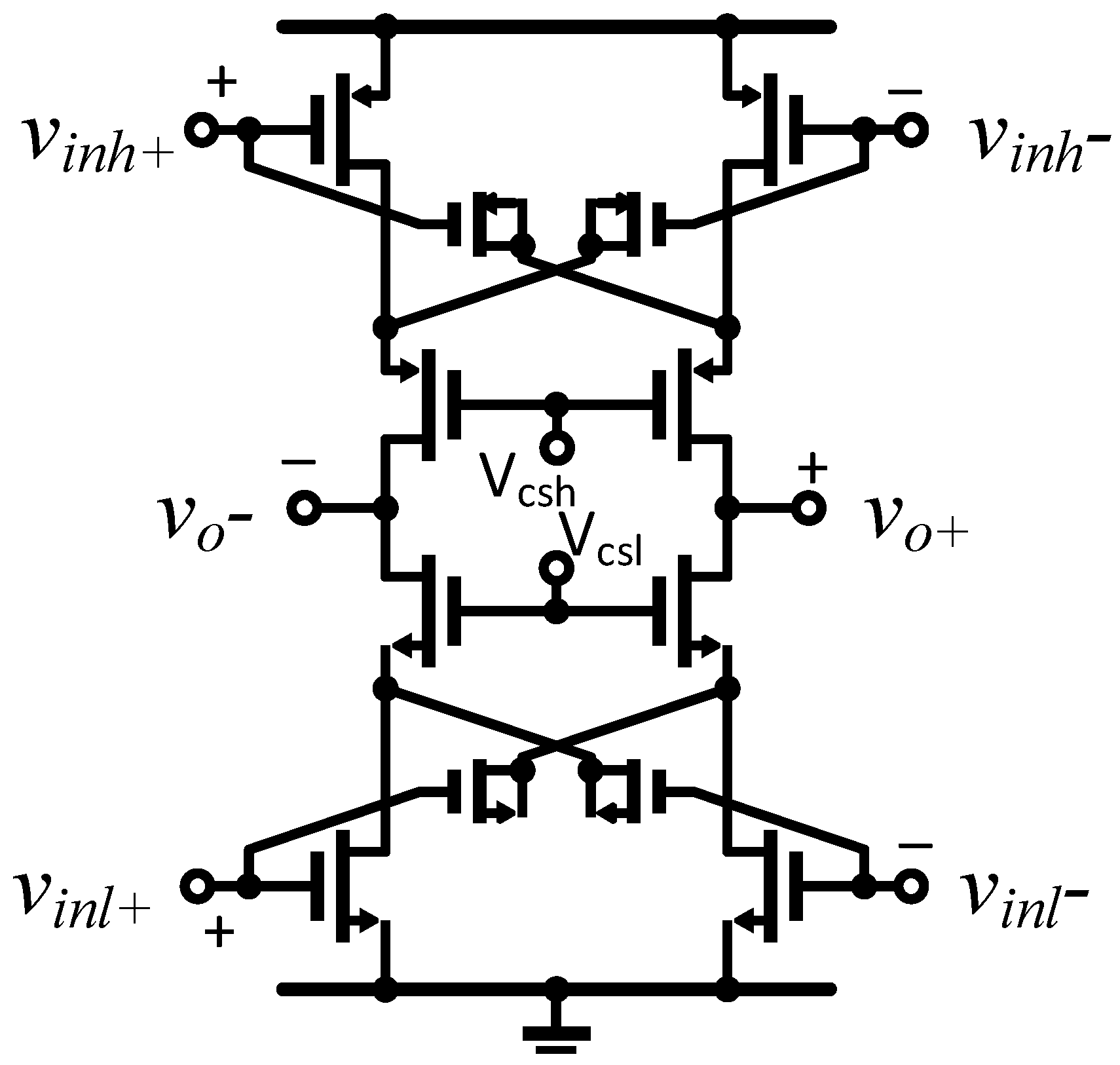
2.3.1. When Less Is More
2.3.2. Nature Is Frugal: The Brain Is Analog
2.4. Summary
3. Conclusive Considerations
3.1. Blur the Disciplinary and Departmental Barriers
3.2. Abstract, Collapse, Repeat
3.3. EDA Considerations
3.4. Workforce Development Considerations
3.5. Smarter or More Productive?
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AA | Anti-Aliasing |
| ACIM | Analog Compute in Memory |
| ADC | Analog to Digital Converter |
| AI | Artificial Intelligence |
| AMS | Analog and Mixed-Signal |
| BCI | Brain Computer Interface |
| BJT | Bipolar Junction Transistor |
| BP | Band Pass |
| CDR | Clock and Data Recovery |
| CIM | Compute in Memory |
| CT | Continuous Time |
| DLL | Delay Locked Loop |
| DCIM | Digital Compute in Memory |
| DPD | Digital Pre-Distortion |
| DSP | Digital Signal Processor |
| DT | Discrete Time |
| ECG | Electrocardiogram |
| EDA | Electronic Design Automation |
| FD-SOI | Fully Depleted Silicon on Insulator |
| FFE | Feedforward Equalizer |
| FIA | Floating Inverter Amplifier |
| GPU | Graphics Processing Unit |
| HI | Heterogeneous Integration |
| IC | Integrated Circuit |
| ICT | Information and Communication Technology |
| IP | Intellectual Property |
| MAC | Multiply and Accumulate |
| mmWave | millimeter Wave |
| MOS | Metal Oxide Semiconductor |
| NUS | Non-Uniform Sampling |
| OEM | Original Equipment Manufacturer |
| OOB | Out Of Band |
| PA | Power Amplifier |
| PLL | Phase Locked Loop |
| PPA | Performance, Power and Area |
| PVT | Process Voltage Temperature |
| RF | Radio Frequency |
| S/H | Sample and Hold amplifier |
| SERDES | SERializer/DESerializer |
| SoC | System on a Chip |
| SQNR | Signal-to-Quantization Ratio |
| TDC | Time-to-Digital Converter |
| TPU | Tensor Processing Unit |
| ULP | Ultra-Low Power |
| ULV | Ultra-Low Voltage |
References
- Manganaro, G. Rethinking mixed-signal IC design. In Proceedings of the 2024 IEEE European Solid-State Electronics Research Conference (ESSERC), Bruges, Belgium, 9–12 September 2024; pp. 552–556. [Google Scholar]
- Semiconductor Research Corporation. Microelectronics Advanced Packaging Technologies Roadmap (MAPT); Full Report; Semiconductor Research Corporation: Durham, NC, USA, 2023; Available online: https://srcmapt.org/ (accessed on 11 August 2025).
- Karl, E.; Park, J.-S. Forum 2: Energy-efficient AI-computing systems for large-language models. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; pp. 593–596. [Google Scholar]
- Liang, B.-S. AI computing design trends for LLMs in the generative AI era. Presented at the IEEE International Symposium on Circuits and Systems, London, UK, 25–28 May 2025. [Google Scholar]
- Liu, M.; Wong, H.-S. How We’ll Reach a 1 Trillion Transistor GPU, IEEE Spectrum, 28 March 2024. Available online: https://spectrum.ieee.org/trillion-transistor-gpu (accessed on 11 August 2025).
- Moore, S.M. Cerebras Unveils Its Next Waferscale AI Chip, IEEE Spectrum, 13 March 2024. Available online: https://spectrum.ieee.org/cerebras-chip-cs3 (accessed on 11 August 2025).
- Sivaram, S.; Ilkbahar, A. Searching for nonlinearity: Scaling limits in NAND flash. In Proceedings of the 2023 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Kyoto, Japan, 11–15 June 2023; pp. 1–4. [Google Scholar]
- Zhang, K. Semiconductor Industry: Present & Future. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; pp. 10–15. [Google Scholar]
- Das, S.; Wuu, J. Forum 1: Efficient Chiplets and die-to-die Communications. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; pp. 589–592. [Google Scholar]
- Hung, C.-M. Semiconductor Chip Design in a Legoland. In Proceedings of the 2023 IEEE Asian Solid-State Circuits Conference (A-SSCC), Haikou, China, 5–8 November 2023; pp. 1–4. [Google Scholar]
- Dally, W. Hardware for Deep Learning. In Proceedings of the 35th Hot Chips Symposium, Stanford, CA, USA, 27–29 August 2023; Stanford University: Standford, CA, USA, 2023. Available online: https://hc2023.hotchips.org/ (accessed on 11 August 2025).
- Moore, S.M. The Secret to Nvidia’s AI Success, IEEE Spectrum, 7 September 2023. Available online: https://spectrum.ieee.org/nvidia-gpu (accessed on 11 August 2025).
- Wirth, N. A plea for lean software. Computer 1995, 28, 64–68. [Google Scholar] [CrossRef]
- Hussain, A. Software Sucks, But It Doesn’t Have to: How to make leaner, greener software. IEEE Spectrum 2024, 61, 2. [Google Scholar] [CrossRef]
- Belay, A.; Leiserson, C.E. EVOLVE: Next Generation Software Efficiency@CSAIL. In Proceedings of the CSAIL Alliances Annual Meeting, Cambridge, MA, USA, 2–4 April 2024; Massachusetts Institute of Technology: Cambridge, MA, USA, 2024. Available online: https://cap.csail.mit.edu/annual-meeting-2024-key-takeaways#evolve (accessed on 11 August 2025).
- Rapp, M.; Amrouch, H.; Lin, Y.; Yu, B.; Pan, D.Z.; Wolf, M.; Henkel, J. MLCAD: A Survey of Research in Machine Learning for CAD Keynote Paper. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 3162–3181. [Google Scholar]
- Shi, Z.; Pan, H.; Khan, S.; Li, M.; Liu, Y.; Huang, J.; Zhen, H.-L.; Yuan, M.; Chu, Z.; Xu, Q. DeepGate2: Functionality-Aware Circuit Representation Learning. In Proceedings of the 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Francisco, CA, USA, 29 October–2 November 2023; pp. 1–9. [Google Scholar]
- Park, H.; Abdullatif, M.; Chen, E.; Elmallah, A.; Nehal, Q.; Gandara, M.; Liu, T.-B.; Khashaba, A.; Lee, J.; Kuan, C.-Y.; et al. A 4.63 pJ/b 112 Gb/s DSP-Based PAM-4 Transceiver for a Large-Scale Switch in 5 nm FinFET. In Proceedings of the 2023 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 19–23 February 2023; pp. 5–7. [Google Scholar]
- Li, G.; Garg, A.; He, T.; Singh, U.; Zhang, J.; Rao, L.; Liu, C.; Nazari, M.; Liu, Y.; Liu, Y.; et al. A 600 Gb/s DP-QAM64 Coherent Optical Transceiver Frontend with 4 × 105 GS/s 8b ADC/DAC in 16 nm CMOS. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 19–23 February 2024; pp. 338–340. [Google Scholar]
- Teh, M.Y.; Wu, Z.; Glick, M.; Rumley, S.; Ghobadi, M.; Bergman, K. Performance trade-offs in reconfigurable networks for HPC. J. Opt. Commun. Netw. 2022, 14, 454–468. [Google Scholar] [CrossRef]
- Montazerolghaem, M.A.; de Vreede, L.N.; Babaie, M. A 300 MHz-BW, 27-to-38 dBm In-Band OIP3 sub-7 GHz Receiver for 5 G Local Area Base Station Applications. In Proceedings of the 2023 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 19–23 February 2023; pp. 292–294. [Google Scholar]
- Workshop on System Design Considerations for Advanced Radios. In Proceedings of the 2022 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Denver, CO, USA, 19–21 June 2022.
- Cintuglu, M.H.; Mohammed, O.A.; Akkaya, K.; Uluagac, S.A. A Survey on Smart Grid Cyber-Physical System Testbeds. IEEE Commun. Surv. Tutor. 2017, 19, 446–464. [Google Scholar]
- Guthaus, M.; Batten, C.; Brunvand, E.; Gaillardon, P.E.; Harris, D.; Manohar, R.; Mazumder, P.; Pileggi, L.; Stine, J. NSF Integrated Circuits Research, Education and Workforce Final Report. arXiv 2023, arXiv:2311.02055. [Google Scholar]
- Manganaro, G.; Kwak, S.U.; Cho, S.; Pulincherry, A. A behavioral modeling approach to the design of a low jitter clock source. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 2003, 50, 804–814. [Google Scholar] [CrossRef]
- de la Rosa, J. Sigma-Delta modulators: Tutorial overview, design guide, and state-of-the-art survey. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1–21. [Google Scholar]
- Tegazzini, L.; Di Meo, G.; De Caro, D.; Strollo, A.G.M. High-Precision MUX-based digital delay interpolators based on a novel transistor sizing algorithm. IEEE Trans. Circuits Syst. II Express Briefs 2025, 72, 938–942. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Y.; Qiu, J.; Huang, H.; Sun, Z.; Xu, D.; Zhang, H.; Wang, Y.; Pang, J.; Li, Z.; et al. A fully-synthesizable fractional-N injection-locked PLL for digital clocking with triangle/sawtooth spread-spectrum modulation capability in 5-nm. IEEE Solid-State Circuits Lett. 2020, 3, 34–37. [Google Scholar]
- Nauta, B. Racing Down the Slopes of Moore’s Law. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; pp. 16–23. [Google Scholar]
- Pavan, S.; Manivannan, S.; Basavaraj, N. Analysis and Design of Wideband Filtering ADCs Using Continuous-Time Pipelining. IEEE J. Solid-State Circuits 2024, 59, 268–281. [Google Scholar]
- Pavan, S. Tutorial: Fundamentals of Continuous-Time ADCs. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024. [Google Scholar]
- Mittal, R.; Shibata, H.; Patil, S.; Krommenhoek, E.; Shrestha, P.; Manganaro, G.; Chandrakasan, A.P.; Lee, H.-S. A 6.4-GS/s 1-GHz BW Continuous-Time Pipelined ADC with Time-Interleaved Sub-ADC-DAC Achieving 61.7-dB SNDR in 16-nm FinFET. IEEE J. Solid-State Circuits 2024, 59, 1158–1170. [Google Scholar]
- Tsividis, Y. Event-Driven Data Acquisition and Digital Signal Processing—A Tutorial. IEEE Tran. Circuits Syst. II Express Briefs 2010, 57, 577–581. [Google Scholar]
- Wu, T.-F.; Dey, S.; Chen, M.S.-W. A Nonuniform Sampling ADC Architecture with Reconfigurable Digital Anti-Aliasing Filter. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1639–1651. [Google Scholar]
- Wu, T.-F.; Ho, C.-R.; Chen, M.S.-W. A Flash-Based Non-Uniform Sampling ADC with Hybrid Quantization Enabling Digital Anti-Aliasing Filter. IEEE J. Solid-State Circuits 2017, 52, 2335–2349. [Google Scholar]
- Ayesh, M.; Mahapatra, S.; Yang, C.; Chen, M.S.-W. A 0.072 mm2 18-to-21 GHz Non-Uniform Sub-Sampling Receiver with a Non-Uniform Discrete-Time FIR Filter Achieving 42 dB Blocker Rejection in 28 nm CMOS. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; pp. 92–94. [Google Scholar]
- Yang, C.; Ayesh, M.; Zhang, A.; Wu, T.-F.; Chen, M.S.-W. A 29-mW 26.88-GHz Non-Uniform Sub-Sampling Receiver Front-End Enabling Spectral Alias Spreading. In Proceedings of the 2020 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Los Angeles, CA, USA, 21–23 June 2020. [Google Scholar]
- Yang, C.; Su, S.; Ayesh, M.; Mahapatra, S.; Hamada, N.; Chenna, V.; Hashemi, H.; Chen, M.S.-W. A Blocker-Tolerant Receiver with VCO-Based Non-Uniform Multi-Level Time-Approximation Filter. IEEE J. Solid-State Circuits 2025, 60. [Google Scholar]
- Allstot, D.; Rovatti, R.; Setti, G. Special issue on Compressed Sensing. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012, 2, 337–339. [Google Scholar] [CrossRef]
- Yazicigil, R.T.; Haque, T.; Kinget, P.R.; Wright, J. Taking Compressive Sensing to the Hardware Level: Breaking Fundamental Radio-Frequency Hardware Performance Tradeoffs. IEEE Signal Process. Mag. 2019, 36, 81–100. [Google Scholar]
- Verhelst, M.; Bahai, A. Where Analog Meets Digital: Analog-to-Information Conversion and Beyond. IEEE Solid-State Circuits Mag. 2015, 7, 67–80. [Google Scholar]
- Guo, W.; Kim, Y.; Tewfik, A.H.; Sun, N. A Fully Passive Compressive Sensing SAR ADC for Low-Power Wireless Sensors. IEEE J. Solid-State Circuits 2017, 52, 2154–2167. [Google Scholar] [CrossRef]
- Liu, J.; Allstot, D.J. Compressed Sensing Σ-Δ Modulators and a Recovery Algorithm for Multi-Channel Wireless Bio-Signal Acquisition. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 1429–1438. [Google Scholar] [CrossRef]
- Bajor, M.; Haque, T.; Han, G.; Zhang, C.; Wright, J.; Kinget, P.R. A Flexible Phased-Array Architecture for Reception and Rapid Direction-of-Arrival Finding Utilizing Pseudo-Random Antenna Weight Modulation and Compressive Sampling. IEEE J. Solid-State Circuits 2019, 54, 1315–1328. [Google Scholar] [CrossRef]
- Pelissier, M.; Studer, C. Non-Uniform Wavelet Sampling for RF Analog-to-Information Conversion. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 471–484. [Google Scholar] [CrossRef]
- Yazicigil, R.T.; Haque, T.; Whalen, M.R.; Yuan, J.; Wright, J.; Kinget, P.R. Wideband Rapid Interferer Detector Exploiting Compressed Sampling with a Quadrature Analog-to-Information Converter. IEEE J. Solid-State Circuits 2015, 50, 3047–3064. [Google Scholar] [CrossRef]
- Jang, M.; Hays, M.; Yu, W.-H.; Lee, C.; Caragiulo, P.; Ramkaj, A.T.; Wang, P.; Phillips, A.J.; Vitale, N.; Tandon, P.; et al. A 1024-Channel 268-nW/Pixel 36 × 36 μm2/Channel Data-Compressive Neural Recording IC for High-Bandwidth Brain-Computer Interfaces. IEEE J. Solid-State Circuits 2024, 59, 1123–1136. [Google Scholar] [CrossRef]
- Manganaro, G. An Introduction to High Sample Rate Nyquist Analog-to-Digital Converters. IEEE Open J. Solid-State Circuits Soc. 2022, 2, 82–102. [Google Scholar] [CrossRef]
- Manganaro, G.; Rakuljic, N. Receiver Signal Chains with Low Power Drivers and Driver Optimization. US Patent US2020030 4135A1, 2019.
- Ali, A.M.A.; Dinc, H.; Bhoraskar, P.; Bardsley, S.; Dillon, C.; McShea, M.; Periathambi, J.P.; Puckett, S. A 12-b 18-GS/s RF Sampling ADC with an Integrated Wideband Track-and-Hold Amplifier and Background Calibration. IEEE J. Solid-State Circuits 2020, 55, 3210–3224. [Google Scholar] [CrossRef]
- Digitally Enhanced Mixed Signal Systems; Jabbour, C., Desgreys, P., Dallet, D., Eds.; IET Press: London, UK, 2019. [Google Scholar]
- Doufana, M.; Park, C.W.; Bahoura, M. A neural network based on-line adaptive predistorter for power amplifier. In Proceedings of the 2010 IEEE 11th Annual Wireless and Microwave Technology Conference (WAMICON), Melbourne Beach, FL, USA, 12–13 April 2010. [Google Scholar]
- Zhang, Y.; Chen, Q.; Gao, K.; Chen, W.; Feng, H.; Feng, Z.; Ghannouchi, F.M. A Novel Digital Predistortion Coefficients Prediction Technique for Dynamic PA Nonlinearities Using Artificial Neural Networks. IEEE Microw. Wirel. Technol. Lett. 2024, 34, 1115–1118. [Google Scholar] [CrossRef]
- Rakuljic, N.; Speir, C.; Otte, E.; Bray, J.; Petersen, C.; Manganaro, G. In-situ nonlinear calibration of a RF signal chain. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018. [Google Scholar]
- Dubois, S.; Lelong, B.; Hode, J.-M.; Ferre, G.; Dallet, D. Linearization of Intermodulation Distortion using a derivative extended model and three-tone signal identification. IEEE Trans. Instrum. Meas. 2025, 74, 1–12. [Google Scholar] [CrossRef]
- Boumard, S.; Lasanen, M.; Apilo, O.; Hekkala, A.; Cassan, C.; Verdeil, J.-P.; David, J.; Phichon, L. Power consumption trade-off between power amplifier OBO, DPD, and clipping and filtering. In Proceedings of the 2014 26th International Teletraffic Congress (ITC), Karlskrona, Sweden, 9–11 September 2014. [Google Scholar]
- Lu, E.; Li, W.-K.; Deng, Z.; Rostami, E.; Wu, P.-A.; Chang, K.-M.; Chuang, Y.-C.; Lai, C.-M.; Chen, Y.-C.; Peng, T.-H.; et al. A 4 × 4 Dual-Band Dual-Concurrent WiFi 802.11ax Transceiver with Integrated LNA, PA and T/R Switch Achieving +20 dBm 1024-QAM MCS11 Pout and −43 dB EVM Floor in 55 nm CMOS. In Proceedings of the 2020 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 16–20 February 2020. [Google Scholar]
- Park, K.; Shim, M.; Ko, H.-G.; Jeong, D.-K. A 6.4-to-32 Gb/s 0.96 pJ/b Referenceless CDR Employing ML-Inspired Stochastic Phase-Frequency Detection Technique in 40 nm CMOS. In Proceedings of the 2020 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 124–126. [Google Scholar]
- Wang, Z.; Megahed, M.; Chun, Y.; Anand, T. A Machine Learning Inspired Transceiver with ISI-Resilient Data Encoding: Hybrid-Ternary Coding + 2-Tap FFE + CTLE + Feature Extraction and Classification for 44.7 dB Channel Loss in 7.3pJ/bit. In Proceedings of the 2021 Symposium on VLSI Circuits, Kyoto, Japan, 13–19 June 2021; pp. 1–2. [Google Scholar]
- Zhang, T.; Cao, Y.; Zhang, S.; Chen, C.; Ye, F.; Ren, J. Machine Learning Based Prior-Knowledge-Free Calibration for Split Pipelined-SAR ADCs with Open-Loop Amplifiers Achieving 93.7-dB SFDR. In Proceedings of the ESSCIRC 2019—IEEE 45th European Solid State Circuits Conference (ESSCIRC), Cracow, Poland, 23–26 September 2019; pp. 189–192. [Google Scholar]
- Ware, E.; Correll, J.; Lee, S.; Flynn, M. 6GS/s 8-channel CIC SAR TI-ADC with Neural Network Calibration. In Proceedings of the ESSCIRC 2022—IEEE 48th European Solid State Circuits Conference (ESSCIRC), Milan, Italy, 19–22 September 2022; pp. 325–328. [Google Scholar]
- Bhanushali, S.; Maiti, D.; Bikkina, P.; Mikkola, E.; Sanyal, A. Circuits-informed machine learning technique for blind open-loop digital calibration of SAR ADC. In Proceedings of the 2025 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), San Francisco, CA, USA, 15–17 June 2025; pp. 151–154. [Google Scholar]
- Ramkaj, A.; Cantoni, A.; Manganaro, G.; Devarajan, S.; Steyaert, M.; Tavernier, F. A 30 GHz-BW < −57 dB-IM3 Direct RF Receiver Analog Front End in 16 nm FinFET. In Proceedings of the 2022 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Honolulu, HI, USA, 13–17 June 2022; pp. 100–101. [Google Scholar]
- Hsieh, C.E.; Manganaro, G.; Liao, S.-H.; Weng, J.; Fan, T.-Y.; Chin, A.; Hung, T.-C.; Wu, J.X.; Lo, C.-L.; Pan, A.; et al. A Power- and Area-Efficient 4 nm Self-Calibrated 12 b/16 GS/s Hierarchical Time-Interleaving ADC. In Proceedings of the 2025 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 16–20 February 2025; pp. 438–440. [Google Scholar]
- Mangelsdorf, C. The Comparator Vanishes [Shop Talk: What You Didn’t Learn in School]. IEEE Solid-State Circuits Mag. 2023, 15, 17–24. [Google Scholar] [CrossRef]
- Johnson, B.; Molnar, A. An Orthogonal Current-Reuse Amplifier for Multi-Channel Sensing. IEEE J. Solid-State Circuits 2013, 48, 1487–1496. [Google Scholar] [CrossRef]
- Tian, Y.; Qin, Z.; Yu, Y.; Gao, G.; Liao, X.; Liu, L. A Low-Noise and Low-Power Multi-Channel ECG AFE Based on Orthogonal Current-Reuse Amplifier. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 3167–3177. [Google Scholar] [CrossRef]
- Wang, P.-Y.; Su, G.-Y.; Chang, Y.-C.; Chang, D.-C.; Hsu, S.S.H. A Transformer-Based Current-Reuse QVCO With an FoM Up to −200.5 dBc/Hz. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 749–753. [Google Scholar] [CrossRef]
- Fan, C.; Yin, J.; Lim, C.-C.; Mak, P.-I.; Martins, R.P. A 9 mW 54.9-to-63.5 GHz Current-Reuse LO Generator with a 186.7 dBc/Hz FoM by Unifying a 20 GHz 3rd-Harmonic-Rich Current-Output VCO, a Harmonic-Current Filter and a 60 GHz TIA. In Proceedings of the 2020 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 282–284. [Google Scholar]
- Huang, S.; Zhang, Z.; He, X.; Gu, M.; Tao, Y.; Zhong, Y.; Sun, N.; Jie, L. A 70 dB SNDR 80 MHz BW Filter-Embedded Pipeline-SAR ADC Achieving 172 dB FoMs with Progressive Conversion and Floating-Charge-Transfer Amplifier. In Proceedings of the 2025 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 16–20 February 2025; pp. 318–320. [Google Scholar]
- Chen, Z.; Shen, L.; Ye, S.; Gao, J.; Li, J.; Cui, J.; Xu, X.; Luan, Y.; Zhang, H.; Ye, L.; et al. 182.3 dB FoMs 50 MS/s Pipelined-SAR ADC using Cascode Capacitively Degenerated Dynamic Amplifier and MSB Pre-Conversion Technique. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; pp. 174–176. [Google Scholar]
- Je, M. Tutorial: Process-Scalable Low-Power Amplifiers. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024. [Google Scholar]
- Allen, P.W.; Blalock, B.J.; Rincon, G.A. A 1 V CMOS op amp using bulk-driven MOSFETs. In Proceedings of the 1995 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 15–17 February 1995; pp. 192–193. [Google Scholar]
- Clerc, S.; Di Gilio, T.; Cathelin, A. (Eds.) The Fourth Terminal; Springer: Berlin, Germany, 2020. [Google Scholar]
- Gerfers, F. (Ed.) Bulk-Driven Circuit Techniques for CMOS FDSOI Processes; Springer: Berlin, Germany, 2025. [Google Scholar]
- Holloway, P.R. One Transistor, Two Transistors, Three. IEEE Solid-State Circuits Mag. 2013, 5, 21–28. [Google Scholar] [CrossRef]
- Pretl, H.; Eberlein, M. Fifty Nifty Variations of Two-Transistor Circuits: A tribute to the versatility of MOSFETs. IEEE Solid-State Circuits Mag. 2021, 13, 38–46. [Google Scholar] [CrossRef]
- Mead, C. Neuromorphic electronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef]
- Vittoz, E.A. Future of analog in the VLSI environment. In Proceedings of the IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 1–3 May 1990; Volume 2, pp. 1372–1375. [Google Scholar]
- Sarpeshkar, R. Analog Versus Digital: Extrapolating from Electronics to Neurobiology. Neural Comput. 1998, 10, 1601–1638. [Google Scholar] [CrossRef]
- Manganaro, G. Another look at Cellular Neural Networks. In Proceedings of the 2021 17th International Workshop on Cellular Nanoscale Networks and their Applications (CNNA), Catania, Italy, 29 September–1 October 2021; pp. 1–4. [Google Scholar]
- Lammie, C.; Büchel, J.; Vasilopoulos, A.; Le Gallo, M.; Sebastian, A. The inherent adversarial robustness of analog in-memory computing. Nat. Commun. 2025, 16, 1756. [Google Scholar] [CrossRef]
- Murmann, B. Mixed-Signal Computing for Deep Neural Network Inference. IEEE Trans. Very Large Scale Integr. Syst. 2021, 29, 3–13. [Google Scholar] [CrossRef]
- Fick, L.; Skrzyniarz, S.; Parikh, M.; Henry, M.B.; Fick, D. Analog Matrix Processor for Edge AI Real-Time Video Analytics. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2022; pp. 260–262. [Google Scholar]
- Leroux, N.; Manea, P.P.; Sudarshan, C.; Finkbeiner, J.; Siegel, S.; Strachan, J.P.; Neftci, E. Analog in-memory computing attention mechanism for fast and energy-efficient large language models. Nat. Comput. Sci. 2025, 5, 813–824. [Google Scholar]
- Sun, J.; Houshmand, P.; Verhelst, M. Analog or Digital In-Memory Computing? Benchmarking Through Quantitative Modeling. In Proceedings of the 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Francisco, CA, USA, 29 October–2 November 2023; pp. 1–9. [Google Scholar]
- Sperling, E. How AI Will Impact Chip Design And Designers. Semiconductor Engineering, 31 July 2025. Available online: https://semiengineering.com/how-ai-will-impact-chip-design-and-designers/ (accessed on 11 August 2025).
- Lu, J.; Lei, L.; Huang, J.; Yang, F.; Shang, L.; Zeng, X. Automatic Op-Amp Generation From Specification to Layout. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 4378–4390. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, J.; Zhao, W.-S.; Zhang, L. Automated Topology Synthesis of Analog Integrated Circuits With Frequency Compensation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2025, 44, 832–844. [Google Scholar] [CrossRef]
- Beaulieu, P.-O.; Dumesnil, E.; Nabki, F.; Boukadoum, M. Analog RF Circuit Sizing by a Cascade of Shallow Neural Networks. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 4391–4401. [Google Scholar] [CrossRef]
- Abel, I.; Neuner, M.; Graeb, H.E. A Hierarchical Performance Equation Library for Basic Op-Amp Design. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 1976–1989. [Google Scholar]
- Collini, L.; Hennessee, A.; Karri, R.; Garg, S. Can Reasoning Models Reason about Hardware? An Agentic HLS Perspective. In Proceedings of the 2025 IEEE International Conference on LLM-Aided Design (ICLAD), Stanford, CA, USA, 26–27 June 2025; pp. 188–194. [Google Scholar]
- Chen, P.-H.; Lin, Y.-S.; Lee, W.-C.; Leu, T.-Y.; Hsu, P.-H.; Dissanayake, A.; Oh, S.; Chiu, C.-S. MenTeR: A fully-automated Multi-agenT workflow for end-to-end RF/Analog Circuits Netlist Design. In Proceedings of the 2025 IEEE International Conference on LLM-Aided Design (ICLAD), Stanford, CA, USA, 26–27 June 2025; pp. 124–132. [Google Scholar]
- Wu, Z.; Savidis, I. Edge-weighted Graph Neural Networks for Post-placement Interconnect Capacitance Estimation of Analog Circuits. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 19–22 May 2024. [Google Scholar]
- Kochar, D.V.; Wang, H.; Chandrakasan, A.P.; Zhang, X. LEDRO: LLM-Enhanced Design Space Reduction and Optimization for Analog Circuits. In Proceedings of the 2025 IEEE International Conference on LLM-Aided Design (ICLAD), Stanford, CA, USA, 26–27 June 2025; pp. 141–148. [Google Scholar]
- Ghose, A.; Kahng, A.B.; Kundu, S.; Wang, Z. ORFS-Agent: Tool-Using Agents for Chip Design Optimization. arXiv 2025, arXiv:2506.08332. [Google Scholar]
- Nauta, B. AD Converter Figures of Merit: From a Meaningful Metric to a Design Disaster, Forum 4: Highlights of Data-Converter R&D in the Past 5 Years: A Comprehensive Overview. In Proceedings of the 2025 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 16–20 February 2025; pp. 635–637. [Google Scholar]
- Callandra, A. Barometers and Analog Design. In Analog Circuits Design: Art, Science and Personalities (EDN); Williams, J., Ed.; Butterworth-Heinemann: Oxford, UK, 1991; ISBN 978-0750696401. [Google Scholar]
- Mangelsdorf, C. Encouraging innovation in Analog IC Design. IEICE Trans. Electron. 2023, E106.C, 516–520. [Google Scholar] [CrossRef]
| Abstraction Level | Representative Techniques | Remarks | Possible Power Savings | Possible Area Savings |
|---|---|---|---|---|
| System (2.1) | Re-arrange, merge/split functional blocks (2.1.1) | Performance metrics’ trade-offs can enable optimal implementations | From marginal to >10 times | From marginal to 1.5 times |
| NUS, compressive sampling, feature extraction and application-specific processing (2.1.2)–(2.1.3) | Highly application dependent. May require post-processing. | From marginal to >100 times | Up to 5 times | |
| Functional (2.2) | Digital Nonlinear Correction (2.2.1) | Highly application dependent. | From marginal to >2 times. | Up to 2 times. |
| Neural Approximation (2.2.2) | ||||
| Transistor (2.3) | Complementary/Current re-use/composite topologies/bulk-driven (2.3.1) | Involves supply/signal swing trade-offs | Up to ~2 times | Up to ~2 times |
| Dynamic Amps/Floating Inverters (2.3.1) | PVT sensitive. Low frequency operation. | >>10 times | Marginal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manganaro, G. A Perspective on Analog and Mixed-Signal IC Design Amid Semiconductor Paradigm Shifts. Chips 2025, 4, 42. https://doi.org/10.3390/chips4040042
Manganaro G. A Perspective on Analog and Mixed-Signal IC Design Amid Semiconductor Paradigm Shifts. Chips. 2025; 4(4):42. https://doi.org/10.3390/chips4040042
Chicago/Turabian StyleManganaro, Gabriele. 2025. "A Perspective on Analog and Mixed-Signal IC Design Amid Semiconductor Paradigm Shifts" Chips 4, no. 4: 42. https://doi.org/10.3390/chips4040042
APA StyleManganaro, G. (2025). A Perspective on Analog and Mixed-Signal IC Design Amid Semiconductor Paradigm Shifts. Chips, 4(4), 42. https://doi.org/10.3390/chips4040042