Hardware-Described Nanoscale Carry-Save Adder in Quantum-Dot Cellular Automata: An Optimised Design and Evaluation Framework
Abstract
1. Introduction
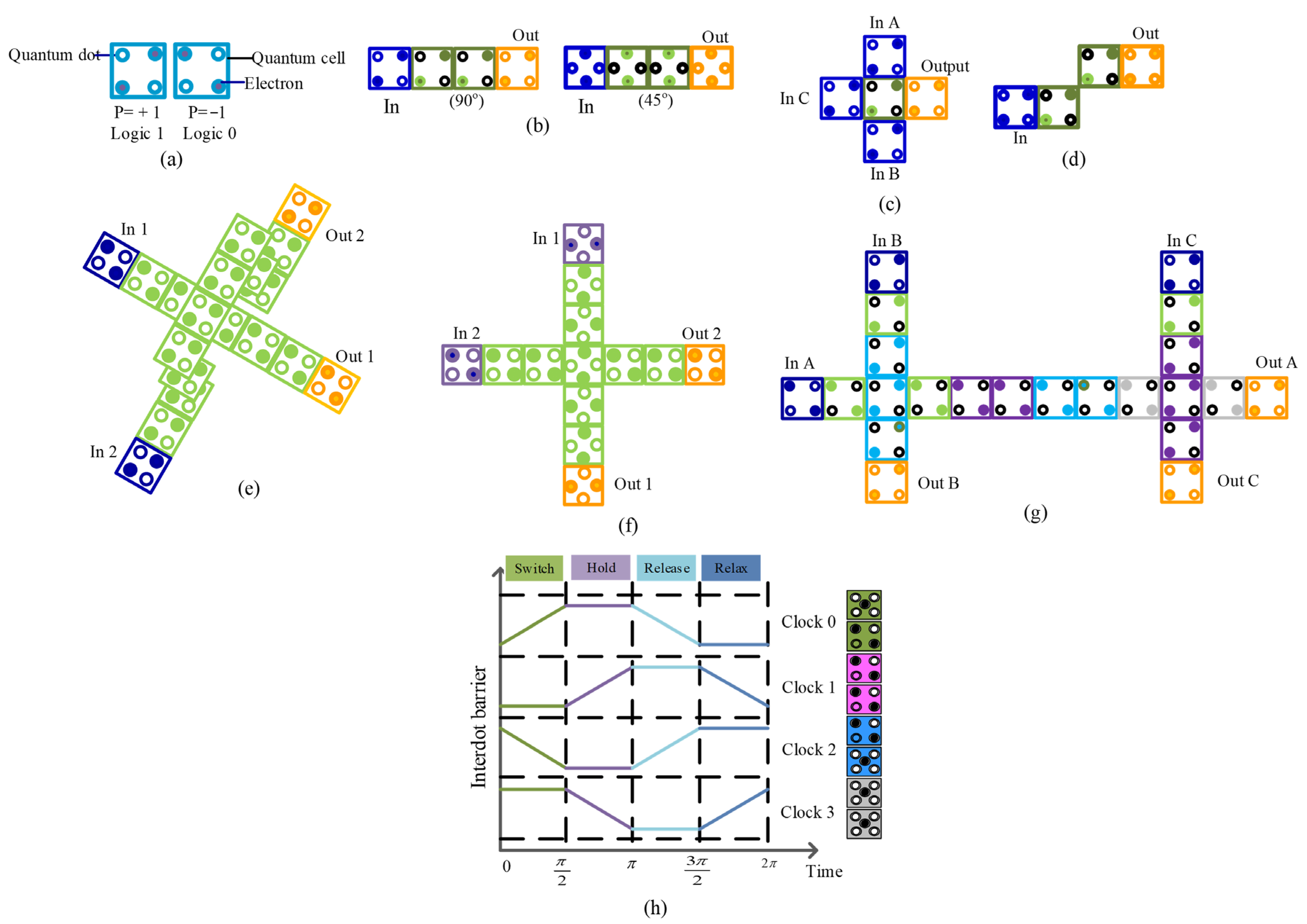
2. Theoretical Foundations of Quantum-Dot Cellular Automata
3. Review of Existing Research and Developments
4. Design and Development of the Proposed QCAFA and CSA
4.1. Systematic Placement Methodology and Automation Strategy
4.2. Limitations of QCADesigner and Assumptions in Simulation
4.3. Implementation Challenges and Strategic Solutions
4.4. Potential Real-World Applications and Technological Impact
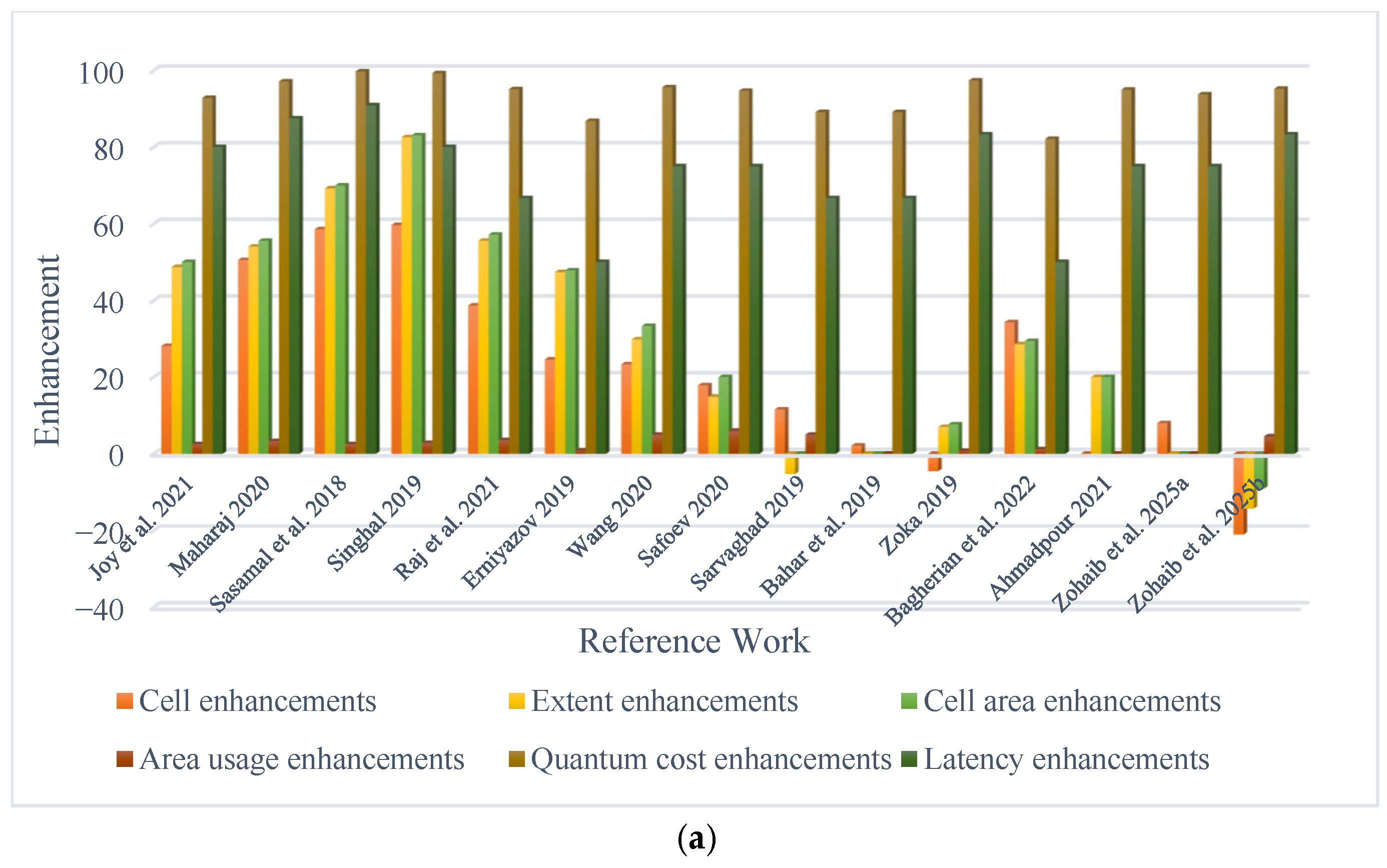
5. Comparative Analysis and Performance Evaluation
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Najmaei, S.; Glasmann, A.L.; Schroeder, M.A.; Sarney, W.L.; Chin, M.L.; Potrepka, D.M. Advancements in materials, devices, and integration schemes for a new generation of neuromorphic computers. Mater. Today 2022, 59, 80–106. [Google Scholar] [CrossRef]
- Radamson, H.H.; Zhu, H.; Wu, Z.; He, X.; Lin, H.; Liu, J.; Xiang, J.; Kong, Z.; Xiong, W.; Li, J.; et al. State of the art and future perspectives in advanced CMOS technology. Nanomaterials 2020, 10, 1555. [Google Scholar] [CrossRef]
- Lent, C.S.; Isaksen, B.; Lieberman, M. Molecular quantum-dot cellular automata. J. Am. Chem. Soc. 2003, 125, 1056–1063. [Google Scholar] [CrossRef] [PubMed]
- Walus, K.; Jullien, G.A.; Dimitrov, V.S. Computer arithmetic structures for quantum cellular automata. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1435–1439. [Google Scholar]
- Jain, V.; Sharma, D.K.; Gaur, H.M.; Singh, A.K.; Wen, X. Comprehensive and comparative analysis of QCA-based circuit designs for next-generation computation. ACM Comput. Surv. 2023, 56, 1–36. [Google Scholar] [CrossRef]
- Ahmadpour, S.S.; Noorallahzadeh, M.; Al-Khafaji, H.M.R.; Darbandi, M.; Navimipour, N.J.; Javadi, B.; Ain, N.U.; Hosseinzadeh, M.; Yalcin, S. A new energy-efficient design for quantum-based multiplier for nano-scale devices in internet of things. Comput. Electr. Eng. 2024, 117, 109263. [Google Scholar] [CrossRef]
- Hofmann, S.; Walter, M.; Wille, R. Efficient and Scalable Post-Layout Optimization for Field-coupled Nanotechnologies. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2025, 44, 3790–3803. [Google Scholar] [CrossRef]
- Abdullah-Al-Shafi, M.; Bahar, A.N. An Architecture of 2-Dimensional 4-Dot 2-Electron QCA Full-adder and Subtractor with Energy Dissipation Study. Act. Passiv. Electron. Compon. 2018, 2018, 5062960. [Google Scholar] [CrossRef]
- Abdullah-Al-Shafi, M. Integration of nano routers into cryptographic circuits for scalable QCA architectures. Discov. Quantum Sci. 2025, 1, 2. [Google Scholar] [CrossRef]
- Gladshtein, M. Quantum-dot cellular automata serial decimal digit multiplier. J. Comput. Electron. 2025, 24, 54. [Google Scholar] [CrossRef]
- Vahabi, M.; Rahimi, E.; Bahar, A.N.; Wahid, K.A. Design of an energy efficient approximate BinDCT module in quantum cellular automata. Sci. Rep. 2025, 15, 19744. [Google Scholar] [CrossRef]
- Abdullah-Al-Shafi, M. Innovative reliable nanoscale QCA circuits for advanced morphological image processing. AIP Adv. 2025, 15, 045303. [Google Scholar] [CrossRef]
- Ahmadpour, S.S.; Jafari Navimipour, N.; Mosleh, M.; Noorallahzadeh, M.; Kassa, S.; Ahmed, S. A new fault-tolerance majority voter circuit for quantum-based nano-scale digital systems. J. Comput. Electron. 2025, 24, 149. [Google Scholar] [CrossRef]
- Seyedi, S.; Abdoli, H. A fault tolerant CSA in QCA technology for IoT devices. Sci. Rep. 2025, 15, 3396. [Google Scholar] [CrossRef] [PubMed]
- Abdullah-Al-Shafi, M.; Islam, M.S.; Bahar, A.N. 5-Input majority gate based optimized full-adder circuit in nanoscale coplanar quantum-dot cellular automata. Int. Nano Lett. 2020, 10, 177–195. [Google Scholar] [CrossRef]
- Zohaib, M.; Navimipour, N.J.; Aydemir, M.T.; Ahmadpour, S.S. A New Nano-Design of High-Speed Arithmetic and Logic Unit for Signal Processing Devices Based on Quantum-dot Technology. Nano Commun. Netw. 2025, 44, 100574. [Google Scholar] [CrossRef]
- Abdullah-Al-Shafi, M. RAM, DEMUX and ALU in nanoscale: A quantum-dot cellular automata-based architecture. Discov. Electron. 2025, 2, 26. [Google Scholar] [CrossRef]
- Marjeghal, M.A.; Sabbaghi-Nadooshan, R.; Ashrafian, A. A novel fault-tolerant T flip-flop in ternary QCA. Analog. Integr. Circuits Signal Process. 2025, 124, 56. [Google Scholar] [CrossRef]
- Vahabi, M.; Rahimi, E.; Lyakhov, P.; Otsuki, A. A novel QCA circuit-switched network with power dissipation analysis for nano communication applications. Nano Commun. Netw. 2023, 35, 100438. [Google Scholar] [CrossRef]
- Khan, A.; Shaw, R.K.; Bahar, A.N. A neural cantonese speech converter using QCA for nanocomputing. Comput. Electr. Eng. 2025, 126, 110536. [Google Scholar] [CrossRef]
- Seyedi, S.; Abdoli, H. Efficient design and implementation of approximate FA, FS, and FA/S circuits for nanocomputing in QCA. PLoS ONE 2024, 19, e0310050. [Google Scholar] [CrossRef]
- Ahmadpour, S.S.; Navimipour, N.J.; Ain, N.U.; Kerestecioglu, F.; Yalcin, S.; Avval, D.B.; Hosseinzadeh, M. Design and implementation of a nano-scale high-speed multiplier for signal processing applications. Nano Commun. Netw. 2024, 41, 100523. [Google Scholar] [CrossRef]
- Hasani, B.; Navimipour, N.J. A new design of a carry-save adder based on quantum-dot cellular automata. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 993–999. [Google Scholar] [CrossRef]
- Joy, U.B.; Chakraborty, S.; Tasnim, S.; Hossain, M.S.; Siddique, A.H.; Hasan, M. Design of an Area Efficient Quantum Dot Cellular Automata Based Full-Adder Cell Having Low Latency. In Proceedings of the 2nd International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 5–7 January 2021; pp. 689–693. [Google Scholar]
- Maharaj, J.; Muthurathinam, S. Effective RCA design using quantum dot cellular automata. Microprocess. Microsyst. 2020, 73, 102964. [Google Scholar] [CrossRef]
- Sasamal, T.N.; Singh, A.K.; Mohan, A. An efficient design of quantum-dot cellular automata based 5-input majority gate with power analysis. Microprocess. Microsyst. 2018, 59, 103–117. [Google Scholar] [CrossRef]
- Singhal, R.; Perkowski, M. Comparative Analysis of Full-Adder Custom Design Circuit Using Two Regular Structures in Quantum-Dot Cellular Automata (QCA). In Proceedings of the 49th International Symposium on Multiple-Valued Logic (ISMVL), Fredericton, NB, Canada, 21–23 May 2019; pp. 194–199. [Google Scholar]
- Raj, M.; Gopalakrishnan, L.; Ko, S.B. Design and analysis of novel QCA full-adder-subtractor. Int. J. Electron. Lett. 2021, 9, 287–300. [Google Scholar] [CrossRef]
- Erniyazov, S.; Jeon, J.C. Carry save adder and carry look ahead adder using inverter chain based coplanar QCA full-adder for low energy dissipation. Microelectron. Eng. 2019, 211, 37–43. [Google Scholar] [CrossRef]
- Wang, L.; Xie, G. A novel XOR/XNOR structure for modular design of QCA circuits. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3327–3331. [Google Scholar] [CrossRef]
- Safoev, N.; Jeon, J.C. Design of high-performance QCA incrementer/decrementer circuit based on adder/subtractor methodology. Microprocess. Microsyst. 2020, 72, 102927. [Google Scholar] [CrossRef]
- Sarvaghad-Moghaddam, M.; Orouji, A.A. New symmetric and planar designs of reversible full-adders/subtractors in quantum-dot cellular automata. Eur. Phys. J. D 2019, 73, 125. [Google Scholar] [CrossRef]
- Bahar, A.N.; Ahmad, F.; Wani, S.; Al-Nisa, S.; Bhat, G.M. New modified-majority voter-based efficient QCA digital logic design. Int. J. Electron. 2019, 106, 333–348. [Google Scholar] [CrossRef]
- Zoka, S.; Gholami, M. A novel efficient full-adder–subtractor in QCA nanotechnology. Int. Nano Lett. 2019, 9, 51–54. [Google Scholar] [CrossRef]
- Bagherian Khosroshahy, M.; Abdoli, A.; Rahmani, A.M. Design and power analysis of an ultra-high speed fault-tolerant full-adder cell in quantum-dot cellular automata. Int. J. Theor. Phys. 2022, 61, 23. [Google Scholar] [CrossRef]
- Ahmadpour, S.S.; Mosleh, M. Ultra-efficient adders and even parity generators in nano scale. Comput. Electr. Eng. 2021, 96, 107548. [Google Scholar] [CrossRef]
- Zohaib, M.; Navimipour, N.J.; Aydemir, M.T.; Ahmadpour, S.S. A nano-scale design of arithmetic and logic unit for energy-efficient signal processing devices based on a quantum-based technology. Clust. Comput. 2025, 28, 340. [Google Scholar] [CrossRef]
- De, D.; Das, J.C. Design of novel carry save adder using quantum dot-cellular automata. J. Comput. Sci. 2017, 22, 54–68. [Google Scholar] [CrossRef]
- Khan, A.; Bahar, A.N.; Arya, R. Efficient design of vedic square calculator using quantum dot cellular automata (QCA). IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1587–1591. [Google Scholar] [CrossRef]
- Amiri, M.; Dousti, M.; Mohammadi, M. Design and implementation of carry-save adder using quantum-dot cellular automata. J. Supercomput. 2024, 80, 1554–1567. [Google Scholar] [CrossRef]
- Menon, A.; Miftah, S.; Kundu, S.; Kundu, S.; Srivastava, A.; Raha, A.; Sonnenschien, G.; Banerjee, S.; Mathaikutty, D.; Basu, K. Enhancing large language models for hardware verification: A novel systemverilog assertion dataset. ACM Trans. Des. Autom. Electron. Syst. 2025. [Google Scholar] [CrossRef]
- Cirstea, M.; Benkrid, K.; Dinu, A.; Ghiriti, R.; Petreus, D. Digital electronic system-on-chip design: Methodologies, tools, evolution, and trends. Micromachines 2024, 15, 247. [Google Scholar] [CrossRef]
- Ardesi, Y.; Beretta, G.; Vacca, M.; Piccinini, G.; Graziano, M. Impact of molecular electrostatics on field-coupled nanocomputing and quantum-dot cellular automata circuits. Electronics 2022, 11, 276. [Google Scholar] [CrossRef]
- Ardesi, Y.; Garlando, U.; Riente, F.; Beretta, G.; Piccinini, G.; Graziano, M. Taming molecular field-coupling for nanocomputing design. ACM J. Emerg. Technol. Comput. Syst. 2022, 19, 1–24. [Google Scholar] [CrossRef]
- Walus, K.; Dysart, T.J.; Jullien, G.A.; Budiman, R.A. QCADesigner: A rapid design and simulation tool for quantum-dot cellular automata. IEEE Trans. Nanotechnol. 2004, 3, 26–31. [Google Scholar] [CrossRef]
- Pudi, V.; Sridharan, K. Low complexity design of ripple carry and Brent–Kung adders in QCA. IEEE Trans. Nanotechnol. 2011, 11, 105–119. [Google Scholar] [CrossRef]
- Macrae, R.M. Mixed-valence realizations of quantum dot cellular automata. J. Phys. Chem. Solids 2023, 177, 111303. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, L. Quantum-dot cellular automata as a potential technology for designing nano-scale computers: Exploring the state-of-the-art techniques and suggesting the opportunities for the future. Optik 2022, 265, 169431. [Google Scholar] [CrossRef]
- Majeed, A.; Alkaldy, E. A new approach to bypass wire crossing problem in QCA nano technology. Circuit World 2023, 49, 145–152. [Google Scholar] [CrossRef]
- Safaiezadeh, B.; Mahdipour, E.; Haghparast, M.; Sayedsalehi, S.; Hosseinzadeh, M. Design and simulation of efficient combinational circuits based on a new XOR structure in QCA technology. Opt. Quantum Electron. 2021, 53, 684. [Google Scholar] [CrossRef]
- Jeon, J.C.; Seo, C. Design of Fixed Cell-Based PLG Using Quantum-Dot Cellular Automata for Efficiency and Reliability of Digital Systems. IEEE Access 2024, 12, 187868–187876. [Google Scholar] [CrossRef]
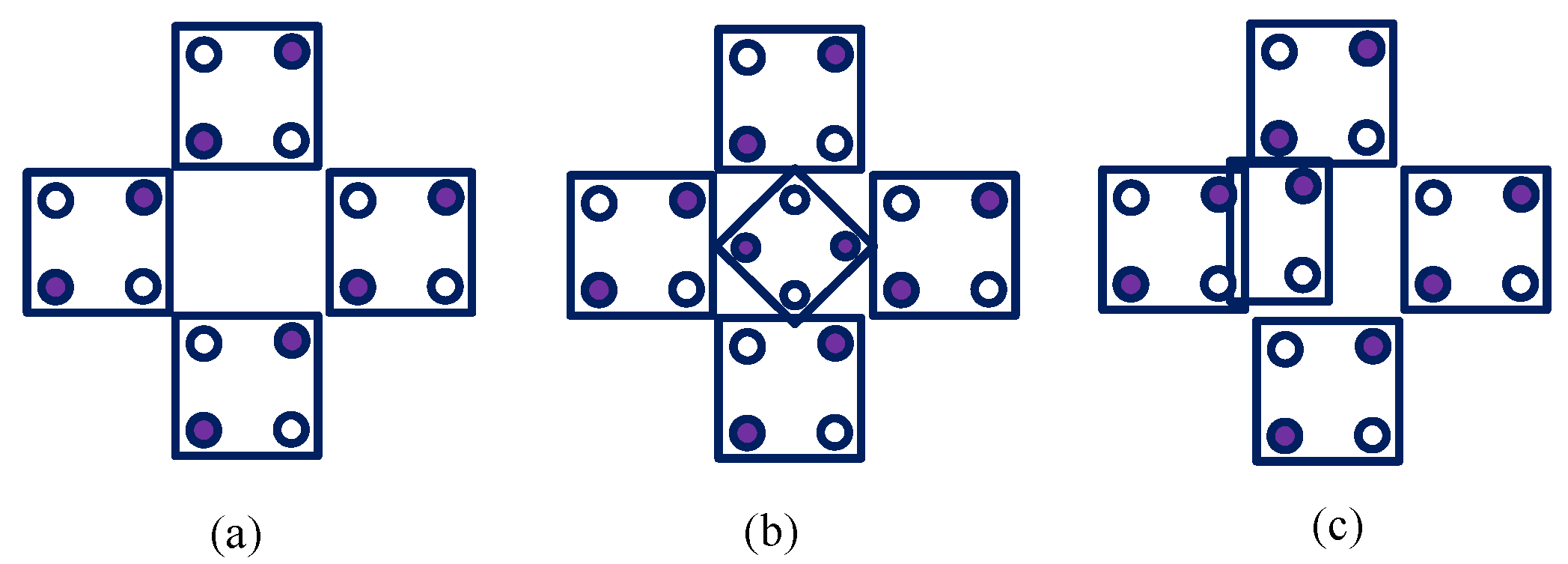
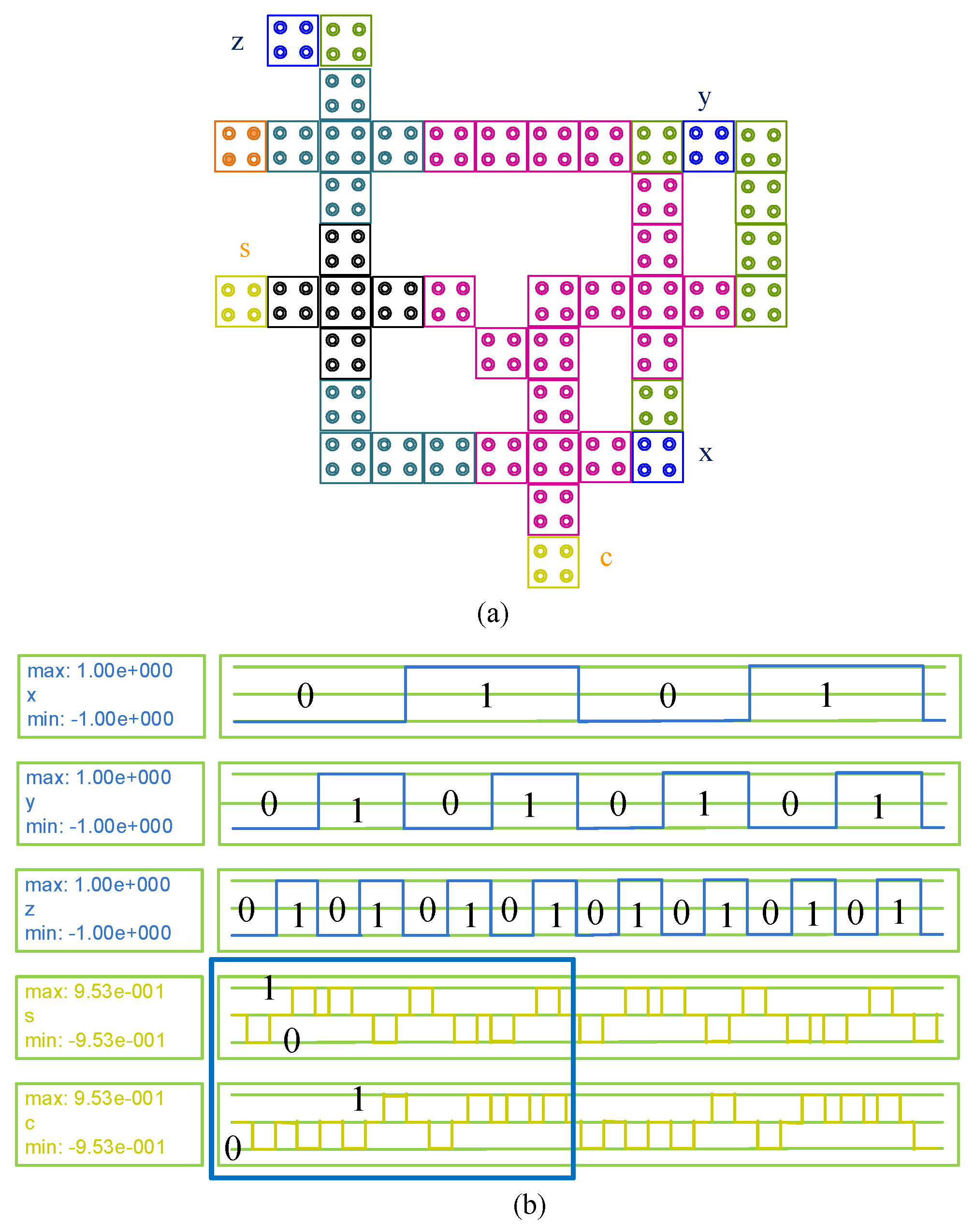



| Input | Output Response | |||
|---|---|---|---|---|
| x | y | z | s | c |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
| QCAFA | CSA |
|---|---|
| design.sv: function full_adder (x, y, z): s = x ^ y ^ z c = (x & y) | (y & z) | (x & z) return (s, c) | design.sv: MODULE full_adder: INPUTS: x, y, z (1-bit each) OUTPUTS: s (sum), c (carry) s = x XOR y XOR z c = (x AND y) OR (y AND z) OR (x AND z) END MODULE // Carry-Save Adder Module (main design) MODULE carry_save_adder: INPUTS: x1, y1, z1 (Triplet 1) x2, y2, z2 (Triplet 2) x3, y3, z3 (Triplet 3) x4, y4, z4 (Triplet 4) OUTPUTS: s1, s2, s3 (Sum outputs from triplets 1–3) s4, s5, s6 (Carry outputs from triplets 1–3) INTERNAL SIGNALS: fa1_s, fa1_c (Full adder 1 outputs) fa2_s, fa2_c (Full adder 2 outputs) fa3_s, fa3_c (Full adder 3 outputs) fa4_s, fa4_c (Full adder 4 outputs—unused) fa1 = full_adder (x1, y1, z1) → (fa1_s, fa1_c) fa2 = full_adder (x2, y2, z2) → (fa2_s, fa2_c) fa3 = full_adder (x3, y3, z3) → (fa3_s, fa3_c) fa4 = full_adder (x4, y4, z4) → (fa4_s, fa4_c) s1 = fa1_s s2 = fa2_s s3 = fa3_s s4 = fa1_c s5 = fa2_c s6 = fa3_c END MODULE |
| testbench.sv x, y, z = 0 s, c = 0 dut = full_adder (x, y, z, s, c) dump_file (“full_adder.vcd”) dump_vars (tb_full_adder) for i in [0, 1, 2, 3, 4, 5, 6, 7]: {x, y, z} = i wait (10) log (time, x, y, z, s, c) end_simulation () | testbench.sv MODULE tb_carry_save_adder: SIGNALS: x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4 SIGNALS: s1, s2, s3, s4, s5, s6 dut = carry_save_adder (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4, s1, s2, s3, s4, s5, s6) INITIAL: SET (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4) = 12′b000000000000 WAIT 10 time units SET (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4) = 12′b010101010101 WAIT 10 time units SET (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4) = 12′b111111111111 WAIT 10 time units SET (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4) = 12′b110011001100 WAIT 10 time units SET (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4) = 12′b101010101010 WAIT 10 time units SET (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4) = 12′b100100100100 WAIT 10 time units SET (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4) = 12′b110110110110 WAIT 10 time units SET (x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4) = 12′b001100110011 WAIT 10 time units CALL $finish () INITIAL: CALL $dumpfile (“carry_save_adder.vcd”) CALL $dumpvars (0, tb_carry_save_adder) INITIAL: MONITOR ( “Time = %0t: In1 = %b%b%b In2 = %b%b%b In3 = %b%b%b In4 = %b%b%b | Out = %b%b%b%b%b%b”, $time, x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4, s1, s2, s3, s4, s5, s6) END MODULE |
| Adders | Cell Intricacy | Space in (µm2) | Cell Space (µm2) | Area Engagement (%) | Resource Cost | Latency | Cell Ratio | Robustness/Fault Tolerance |
|---|---|---|---|---|---|---|---|---|
| In [24] | 64 | 0.078 | 0.024 | 30.77 | 0.035 | 1.25 | 1.39 | Not discussed |
| In [25] | 93 | 0.087 | 0.027 | 31.03 | 0.087 | 2 | 2.02 | Not discussed |
| In [26] | 111 | 0.13 | 0.040 | 30.77 | 0.9831 | 2.75 | 2.41 | Cell displacement and cell misalignment |
| In [27] | 114 | 0.23 | 0.071 | 30.87 | 0.359 | 1.25 | 2.48 | Not discussed |
| In [28] | 75 | 0.09 | 0.028 | 31.11 | 0.051 | 0.75 | 1.63 | Missing cell defects, misalignment defects, additional cell defects, and struck-at-faults |
| In [29] | 61 | 0.076 | 0.023 | 30.26 | 0.019 | 0.5 | 1.33 | Not discussed |
| In [30] | 60 | 0.057 | 0.018 | 31.58 | 0.057 | 1 | 1.30 | Not discussed |
| In [31] | 56 | 0.047 | 0.015 | 31.91 | 0.047 | 1 | 1.22 | Not discussed |
| In [32] | 52 | 0.038 | 0.012 | 31.58 | 0.023 | 0.75 | 1.13 | Cell displacement and cell misalignment |
| In [33] | 47 | 0.04 | 0.012 | 30.00 | 0.023 | 0.75 | 1.02 | Not discussed |
| In [34] | 44 | 0.043 | 0.013 | 30.23 | 0.096 | 1.5 | 0.96 | Not discussed |
| In [35] | 70 | 0.056 | 0.017 | 30.36 | 0.014 | 0.5 | 1.52 | Fault-tolerant |
| In [36] | 46 | 0.05 | 0.015 | 30.00 | 0.05 | 1 | 1.00 | Not discussed |
| In [37] | 50 | 0.04 | 0.012 | 30.00 | 0.04 | 1 | 1.08 | Not discussed |
| In [16] | 38 | 0.035 | 0.011 | 31.43 | 0.0525 | 1.5 | 0.826 | Not discussed |
| Proposed | 46 | 0.04 | 0.012 | 30.00 | 0.0025 | 0.25 | 1.00 | Not evaluated |
| Layouts | Cell (%) | Space (%) | Cell Space (%) | Area Usage (%) | Resource Cost (%) | Latency (%) |
|---|---|---|---|---|---|---|
| In [24] | 28.13 | 48.72 | 50.00 | 2.50 | 92.86 | 80.00 |
| In [25] | 50.54 | 54.02 | 55.56 | 3.32 | 97.13 | 87.50 |
| In [26] | 58.56 | 69.23 | 70.00 | 2.50 | 99.75 | 90.91 |
| In [27] | 59.65 | 82.61 | 83.10 | 2.82 | 99.30 | 80.00 |
| In [28] | 38.67 | 55.56 | 57.14 | 3.57 | 95.10 | 66.67 |
| In [29] | 24.59 | 47.37 | 47.83 | 0.86 | 86.84 | 50.00 |
| In [30] | 23.33 | 29.82 | 33.33 | 5.00 | 95.61 | 75.00 |
| In [31] | 17.86 | 14.89 | 20.00 | 5.99 | 94.68 | 75.00 |
| In [32] | 11.54 | −5.26 | 0.00 | 5.00 | 89.13 | 66.67 |
| In [33] | 2.13 | 0.00 | 0.00 | 0.00 | 89.13 | 66.67 |
| In [34] | −4.55 | 6.98 | 7.69 | 0.76 | 97.40 | 83.33 |
| In [35] | 34.29 | 28.57 | 29.41 | 1.19 | 82.14 | 50.00 |
| In [36] | 0.00 | 20.00 | 20.00 | 0.00 | 95.00 | 75.00 |
| In [37] | 8.00 | 0.00 | 0.00 | 0.00 | 93.75 | 75.00 |
| In [16] | −21.05 | −14.29 | −9.09 | 4.55 | 95.24 | 83.33 |
| CSA | Cell Intricacy | Space in (µm2) | Cell Space (µm2) | Area Employment (%) | Resource Cost | Latency | Cell Ratio |
|---|---|---|---|---|---|---|---|
| In [23] | 347 | 0.37 | 0.11 | 29.73 | 1.87 | 2.25 | 0.82 |
| In [29] | 696 | 0.66 | 0.20 | 30.30 | 4.13 | 2.50 | 1.64 |
| In [38] | 525 | 0.55 | 0.17 | 30.91 | 2.78 | 2.25 | 1.24 |
| In [40] | 521 | 0.62 | 0.19 | 30.65 | 1.90 | 1.75 | 1.23 |
| In [45] | 815 | 0.738 | 0.23 | 31.17 | 11.81 | 4 | 1.92 |
| In [46] | 698 | 0.618 | 0.19 | 30.74 | 9.89 | 4 | 1.65 |
| Proposed | 424 | 0.56 | 0.17 | 30.36 | 1.72 | 1.75 | 1 |
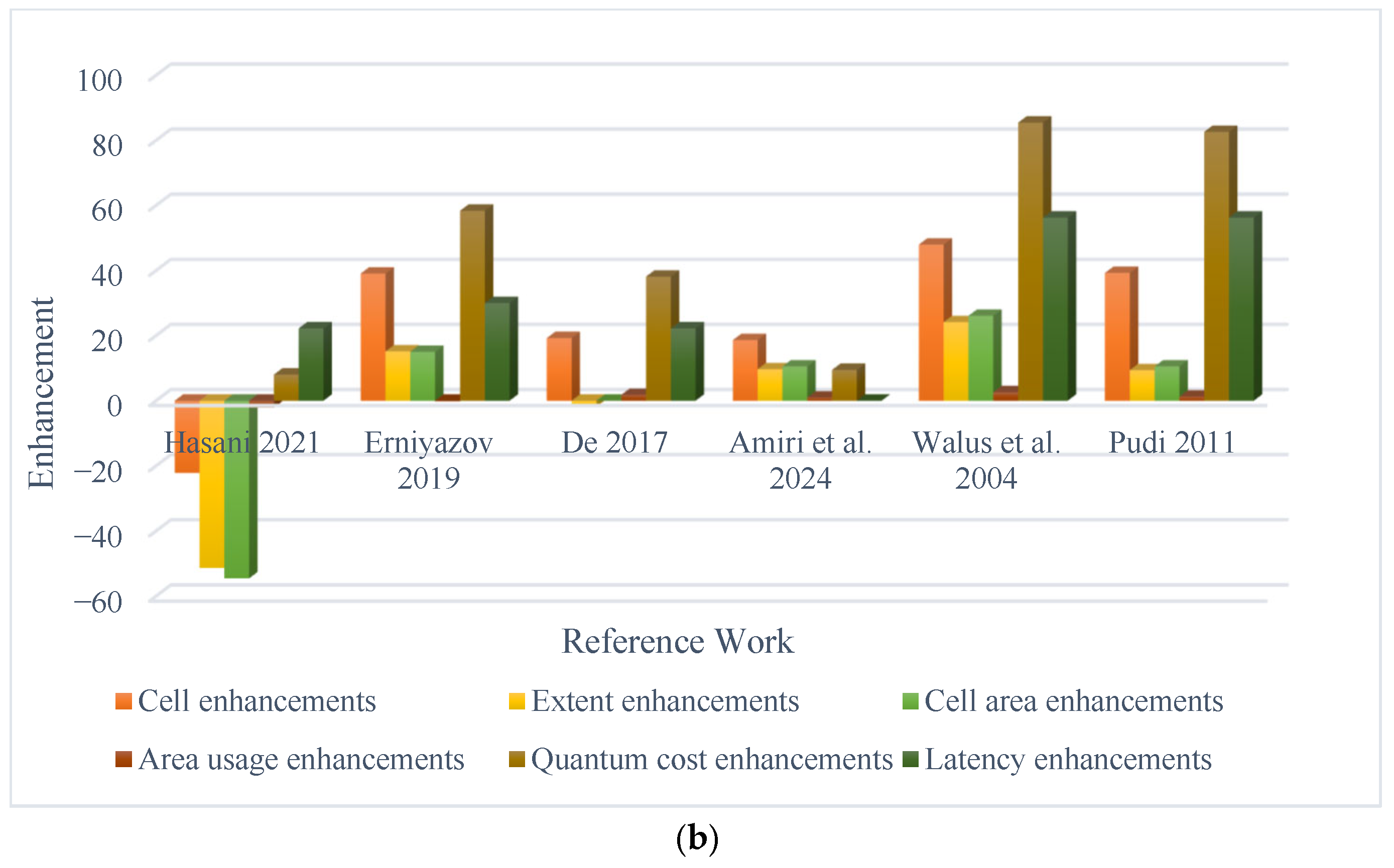
| QCA Layout | Cell Block (%) | Extent (%) | Cell Area (%) | Area Usage (%) | Resource Cost (%) | Latency (%) |
|---|---|---|---|---|---|---|
| In [23] | −22.19 | −51.35 | −54.55 | −2.12 | 8.02 | 22.22 |
| In [29] | 39.08 | 15.15 | 15.00 | −0.20 | 58.35 | 30.00 |
| In [38] | 19.24 | −1.82 | 0.00 | 1.78 | 38.13 | 22.22 |
| In [40] | 18.62 | 9.68 | 10.53 | 0.95 | 9.47 | 0.00 |
| In [45] | 47.98 | 24.12 | 26.09 | 2.60 | 85.44 | 85.44 |
| In [46] | 39.26 | 9.39 | 10.53 | 1.24 | 82.61 | 56.25 |
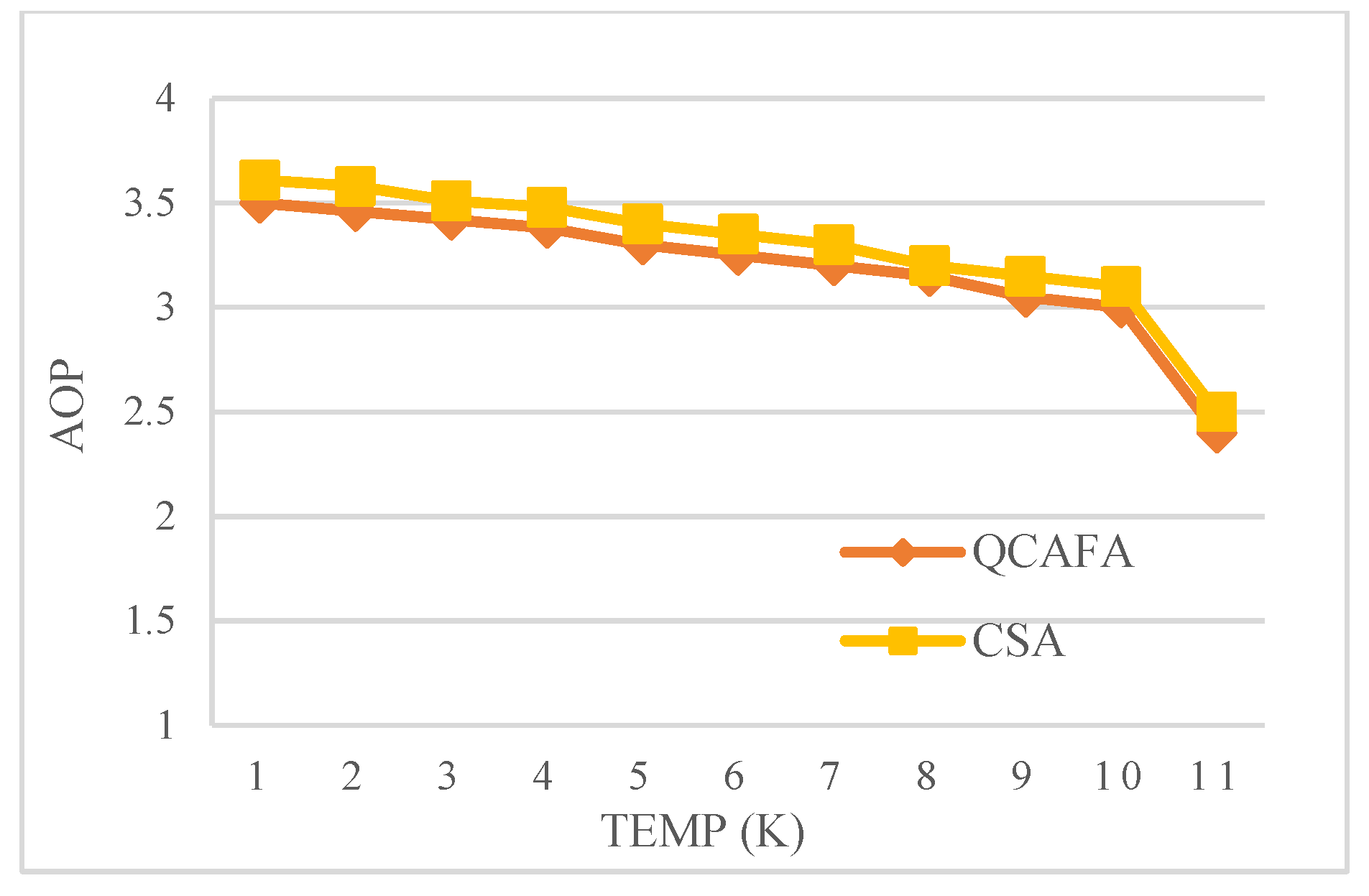
| QCA Architecture | Depletion of Total Energy | Depletion of Average Energy |
|---|---|---|
| Proposed QCAFA | 1.34 eV | 1.18 eV |
| Proposed CSA | 3.80 eV | 3.60 eV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah-Al-Shafi, M. Hardware-Described Nanoscale Carry-Save Adder in Quantum-Dot Cellular Automata: An Optimised Design and Evaluation Framework. Chips 2025, 4, 43. https://doi.org/10.3390/chips4040043
Abdullah-Al-Shafi M. Hardware-Described Nanoscale Carry-Save Adder in Quantum-Dot Cellular Automata: An Optimised Design and Evaluation Framework. Chips. 2025; 4(4):43. https://doi.org/10.3390/chips4040043
Chicago/Turabian StyleAbdullah-Al-Shafi, Mohammad. 2025. "Hardware-Described Nanoscale Carry-Save Adder in Quantum-Dot Cellular Automata: An Optimised Design and Evaluation Framework" Chips 4, no. 4: 43. https://doi.org/10.3390/chips4040043
APA StyleAbdullah-Al-Shafi, M. (2025). Hardware-Described Nanoscale Carry-Save Adder in Quantum-Dot Cellular Automata: An Optimised Design and Evaluation Framework. Chips, 4(4), 43. https://doi.org/10.3390/chips4040043






